| Issue |
A&A
Volume 597, January 2017
|
|
|---|---|---|
| Article Number | A117 | |
| Number of page(s) | 5 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201629526 | |
| Published online | 13 January 2017 | |
Power requirements for cosmic ray propagation models involving diffusive reacceleration; estimates and implications for the damping of interstellar turbulence
1 Dublin Institute for Advanced Studies, School of Cosmic Physics, 31 Fitzwilliam Place, Dublin 2, Ireland
e-mail: LD@cp.dias.ie
2 MPI für Extraterrestrische Physik, Postfach 1312, 85741 Garching, Germany
Received: 13 August 2016
Accepted: 21 October 2016
We make quantitative estimates of the power supplied to the Galactic cosmic ray population by second-order Fermi acceleration in the interstellar medium, or as it is usually termed in cosmic ray propagation studies, diffusive reacceleration. Using recent results on the local interstellar spectrum, following Voyager 1’s crossing of the heliopause, we show that for parameter values, in particular the Alfvén speed, typically used in propagation codes such as GALPROP to fit the B/C ratio, the power contributed by diffusive reacceleration is significant and can be of order 50% of the total Galactic cosmic ray power. The implications for the damping of interstellar turbulence are briefly considered.
Key words: cosmic rays / ISM: structure / turbulence / acceleration of particles
© ESO, 2017
1. Introduction
In most discussions of cosmic ray propagation it is assumed that the cosmic rays are produced in discrete sources, generally taken to be supernova remnants (SNRs), although there is increasing interest in and evidence for possible additional classes of sources, see e.g. the presentations in the recent conference organised by Tibolla & Drury (2014), and the recent exciting evidence for acceleration of protons to PeV energies in the Galactic centre region (H.E.S.S. Collaboration et al. 2016). They then diffuse through the interstellar medium and an extended cosmic ray halo before escaping from the Galaxy. This diffusion is not just in space, but also in momentum, if, as is inevitably the case, the magnetic fields that scatter the particles are not purely static but are in random motion with characteristic velocities of order the Alfvén speed. This leads to a certain amount of second-order Fermi acceleration during propagation, an effect which for historical reasons is usually referred to as “reacceleration”. There has been a long and inconclusive debate as to the importance of reacceleration, but there is no doubt that the idea is attractive for a variety of reasons, and physically the effect must occur at some level. For clarity we note that the term “reacceleration” is also sometimes used to refer to the acceleration by supernova remnants (SNR) shocks of pre-existing ambient cosmic rays; in this paper we do not consider this shock reacceleration process and are exclusively concerned with diffusive reacceleration.
One of the strongest arguments in favour of diffusive reacceleration is that it allows a rather natural fit to the low energy boron to carbon data. This was persuasively argued by Heinbach & Simon (1995) who showed that with reacceleration the B/C data could be well fit with a single power-law dependence of the escape path-length as a function of rigidity, whereas in a leaky-box model one had to suppose an unnatural decrease in the path-length at low energies. The fact that the inferred power-law dependence of the path-length also agreed with that predicted for Kolmogorov turbulence was seen as another positive feature of the model (although whether interstellar magnetic turbulence should be described by a Kolmogorov spectrum is another question).
This reacceleration by interstellar turbulence is a potentially significant contribution to the total Galactic cosmic ray source power (and of course also a potentially significant damping term for interstellar turbulence). This was qualitatively discussed in Thornbury & Drury (2014) and presented at the ICRC by Drury & Strong (2015) on the basis of analytic estimates. In this paper we seek to make quantitative estimates of the diffusive reacceleration power using both recent parametrisations of the local interstellar spectrum and the well-established cosmic ray propagation code GALPROP as first described in Strong & Moskalenko (1998). GALPROP has become the de facto reference model for cosmic ray propagation studies in our Galaxy and is thus an appropriate choice, but any other propagation model incorporating diffusive reacceleration should give very similar results, e.g. the DRAGON code of Evoli et al. (2016).
The power transferred to the cosmic rays comes of course at the expense of the general turbulence in the interstellar medium so we also evaluate a damping process for interstellar turbulence. An important aspect of this problem is that it depends (as we will see) sensitively on the low-energy form of the cosmic ray spectrum in interstellar space. Until recently this was largely unknown, but we now have direct in situ observations from the Voyager spacecraft of the cosmic ray spectrum beyond the heliopause which we can use to constrain the local interstellar spectra at sub-relativistic energies (Stone et al. 2013). There are also useful constraints from the diffuse gamma-ray emission of the Galaxy (Strong 2015) which are important as being independent of solar modulation and confirming the spectral break at GeV energies.
2. Reacceleration power
This section briefly reviews and expands on the main results of Thornbury & Drury (2014). The basic equation underpinning all diffusion models of cosmic ray transport, going back at least to the classic monograph of Ginzburg & Syrovatskii (1964) is 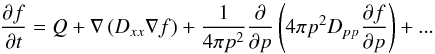 (1)Here f(x,p,t) is the isotropic part of the phase space density of a given species as a function of position x, scalar momentum p and time t and Q(x,p,t) is a source term representing the initial production and acceleration of cosmic rays. The spatial and momentum space diffusion coefficients are Dxx and Dpp respectively and will in general be functions of position, momentum, and time. On heuristic grounds (Thornbury & Drury 2014) the two diffusion coefficients are related by
(1)Here f(x,p,t) is the isotropic part of the phase space density of a given species as a function of position x, scalar momentum p and time t and Q(x,p,t) is a source term representing the initial production and acceleration of cosmic rays. The spatial and momentum space diffusion coefficients are Dxx and Dpp respectively and will in general be functions of position, momentum, and time. On heuristic grounds (Thornbury & Drury 2014) the two diffusion coefficients are related by 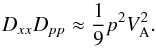 (2)Detailed calculations (Skilling 1975a,b,c), see also Eqs. (9.38) and (9.39) in Berezinskii et al. (1990), show that
(2)Detailed calculations (Skilling 1975a,b,c), see also Eqs. (9.38) and (9.39) in Berezinskii et al. (1990), show that 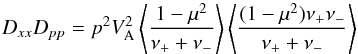 (3)where the angle brackets denote an average over an isotropic pitch angle distribution μ being the pitch angle cosine,
(3)where the angle brackets denote an average over an isotropic pitch angle distribution μ being the pitch angle cosine, 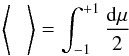 (4)and ν± is the rate of pitch-angle scattering off forward and backward propagating Alfvén waves. If the scattering rates are taken to be constant and equal we recover the naive heuristic result, but in general the scattering rates should be functions of the pitch angle and related to the wave spectrum through the gyro-resonant condition. This introduces a weak dependence on the shape of the wave spectrum, but not on its amplitude. Specifically, if we assume a power-law wave spectrum with W(k) ∝ k− a where ∫W(k) dk is the total energy content of the waves and k is the wave-number (a = 5/3 being a Kolmogorov spectrum for example).
(4)and ν± is the rate of pitch-angle scattering off forward and backward propagating Alfvén waves. If the scattering rates are taken to be constant and equal we recover the naive heuristic result, but in general the scattering rates should be functions of the pitch angle and related to the wave spectrum through the gyro-resonant condition. This introduces a weak dependence on the shape of the wave spectrum, but not on its amplitude. Specifically, if we assume a power-law wave spectrum with W(k) ∝ k− a where ∫W(k) dk is the total energy content of the waves and k is the wave-number (a = 5/3 being a Kolmogorov spectrum for example). 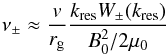 (5)where rg = p/eB0 is the particle gyroradius, B0 the background magnetic field, and the resonant condition is
(5)where rg = p/eB0 is the particle gyroradius, B0 the background magnetic field, and the resonant condition is 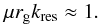 (6)Considered as a function of pitch angle the scattering rates thus scale as
(6)Considered as a function of pitch angle the scattering rates thus scale as 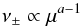 (7)so that (assuming ν+ = ν−)
(7)so that (assuming ν+ = ν−) 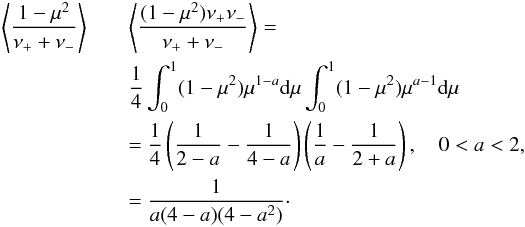 (8)Thus more generally
(8)Thus more generally 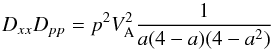 (9)which agrees with the simple heuristic estimate for a = 1.
(9)which agrees with the simple heuristic estimate for a = 1.
However if we hold μ fixed and look at the scattering rate as a function of particle momentum or gyro-radius, then 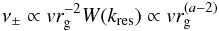 (10)and thus
(10)and thus 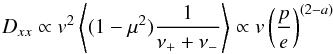 (11)which is the commonly used form, D ∝ vRδ or velocity times a power-law in particle rigidity (momentum per charge, which is directly proportional to the gyro-radius for fixed magnetic field). The power-law index of the rigidity dependence of the spatial diffusion coefficient, δ is thus related to that of the wave spectrum by
(11)which is the commonly used form, D ∝ vRδ or velocity times a power-law in particle rigidity (momentum per charge, which is directly proportional to the gyro-radius for fixed magnetic field). The power-law index of the rigidity dependence of the spatial diffusion coefficient, δ is thus related to that of the wave spectrum by  (12)and as is easily verified
(12)and as is easily verified 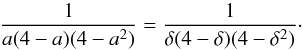 (13)In fact the denominator can be written
(13)In fact the denominator can be written 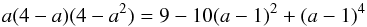 (14)which shows that it is symmetric about and has a local maximum at a = 1. Thus within this simple quasilinear theory of particle scattering we have
(14)which shows that it is symmetric about and has a local maximum at a = 1. Thus within this simple quasilinear theory of particle scattering we have 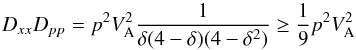 (15)which is essentially the form used by GALPROP, see Eq. (1) in Strong & Moskalenko (1998) derived from Seo & Ptuskin (1994), if their factor 4/3w is set to unity (the inclusion of w appears formally incorrect, but as it is treated as a constant of order unity it makes no difference to the results). It is interesting to note that for equal intensities of forward and backward propagating waves the naive scattering estimate corresponds to the minimum possible level of reacceleration, but of course lower values can be obtained with anisotropic wave fields.
(15)which is essentially the form used by GALPROP, see Eq. (1) in Strong & Moskalenko (1998) derived from Seo & Ptuskin (1994), if their factor 4/3w is set to unity (the inclusion of w appears formally incorrect, but as it is treated as a constant of order unity it makes no difference to the results). It is interesting to note that for equal intensities of forward and backward propagating waves the naive scattering estimate corresponds to the minimum possible level of reacceleration, but of course lower values can be obtained with anisotropic wave fields.
For convenience we will from now on write 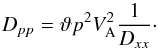 (16)For a Kolmogorov spectrum with δ = 1/3 we have ϑ = 81/385 ≈ 0.21 and the largest it can be is for δ = 1 where we have ϑ = 1/9 ≈ 0.11; the results of Strong & Moskalenko (1998) can be obtained by setting
(16)For a Kolmogorov spectrum with δ = 1/3 we have ϑ = 81/385 ≈ 0.21 and the largest it can be is for δ = 1 where we have ϑ = 1/9 ≈ 0.11; the results of Strong & Moskalenko (1998) can be obtained by setting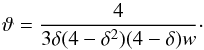 (17)The local reacceleration power density (energy per unit time and per unit volume) is shown in Thornbury & Drury (2014), assuming very reasonable regularity conditions on the particle distribution function, to be given by the integral over the particle spectrum,
(17)The local reacceleration power density (energy per unit time and per unit volume) is shown in Thornbury & Drury (2014), assuming very reasonable regularity conditions on the particle distribution function, to be given by the integral over the particle spectrum, 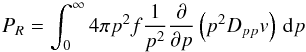 (18)which can be written, if Dpp is expressed in terms of Dxx using the above relation, as
(18)which can be written, if Dpp is expressed in terms of Dxx using the above relation, as ![\begin{equation} P_R = \int_0^\infty 4\pi p^2 f \left (\vartheta V_{\rm A}^2 p v\over D_{xx}\right) \left[ 4 + {\partial\!\ln(v/D_{xx})\over\partial\!\ln p}\right]\, {\rm d}p. \end{equation}](/articles/aa/full_html/2017/01/aa29526-16/aa29526-16-eq45.png) (19)If we parametrise the spatial diffusion in the usual fashion as
(19)If we parametrise the spatial diffusion in the usual fashion as 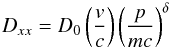 (20)where m is the particle mass and c the speed of light this can be written in the useful and rather transparent form
(20)where m is the particle mass and c the speed of light this can be written in the useful and rather transparent form 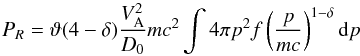 (21)which gives the local reacceleration power density in terms of a simple integral over the spectrum. The formula is interesting in that the term
(21)which gives the local reacceleration power density in terms of a simple integral over the spectrum. The formula is interesting in that the term 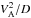 is a rate, mc2 is just the particle rest mass energy, and the integral is essentially just the total number density of cosmic ray particles biased by a power-law factor with exponent 1−δ. Thus the energy transfer is more or less as if all particles were acquiring their own rest mass energy on a time scale of
is a rate, mc2 is just the particle rest mass energy, and the integral is essentially just the total number density of cosmic ray particles biased by a power-law factor with exponent 1−δ. Thus the energy transfer is more or less as if all particles were acquiring their own rest mass energy on a time scale of 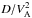 . Integrating this over the entire Galaxy then gives the total power transferred to the cosmic ray population from Alfvénic turbulence.
. Integrating this over the entire Galaxy then gives the total power transferred to the cosmic ray population from Alfvénic turbulence.
2.1. Numerical estimates using Voyager data
Numerical evaluation of this integral requires knowledge of the low-energy part of the interstellar cosmic ray spectrum, as noted in Thornbury & Drury (2014), and until recently this was quite poorly constrained. However the situation has dramatically changed with the recent passage of the Voyager spacecraft into the local interstellar medium which allows us for the first time to have access to in situ measurements of the low-energy cosmic ray flux just outside the heliosphere (Potgieter 2014). A useful analytic fit to the local interstellar flux of protons, JLIS, has been given by Vos & Potgieter (2015) in the form 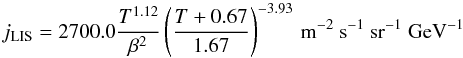 (22)where T is the kinetic energy in units of GeV and β = v/c is the dimensionless particle speed. Noting that dT = v dp and that p2f(p)v dp = j(T) dT where p is particle momentum and f is the phase space density we can convert this flux to a local interstellar phase space density via
(22)where T is the kinetic energy in units of GeV and β = v/c is the dimensionless particle speed. Noting that dT = v dp and that p2f(p)v dp = j(T) dT where p is particle momentum and f is the phase space density we can convert this flux to a local interstellar phase space density via 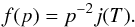 (23)In Fig. 1 we show the corresponding spectrum plotted slightly unconventionally as a differential number spectrum in log momentum; we plot the number of protons per logarithmic interval in momentum, 4πp3f(p) noting that the total number density of particles is just the area under this curve,
(23)In Fig. 1 we show the corresponding spectrum plotted slightly unconventionally as a differential number spectrum in log momentum; we plot the number of protons per logarithmic interval in momentum, 4πp3f(p) noting that the total number density of particles is just the area under this curve, 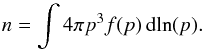 (24)Presenting the data in this way brings out just how sharply peaked the local interstellar cosmic ray proton spectrum is around 1 GeV. On a more conventional log log plot one can see that there are power-law tails extending to both lower and higher energies, see Fig. 2, but by far the dominant population, at least by number, are the mildly relativistic ones. It is interesting to note that this spectrum corresponds to a total number density of 1.2 × 10-3 cosmic ray protons per cubic meter locally, an energy density of 0.7 eV cm-3 and a pressure of 0.33 eV cm-3.
(24)Presenting the data in this way brings out just how sharply peaked the local interstellar cosmic ray proton spectrum is around 1 GeV. On a more conventional log log plot one can see that there are power-law tails extending to both lower and higher energies, see Fig. 2, but by far the dominant population, at least by number, are the mildly relativistic ones. It is interesting to note that this spectrum corresponds to a total number density of 1.2 × 10-3 cosmic ray protons per cubic meter locally, an energy density of 0.7 eV cm-3 and a pressure of 0.33 eV cm-3.
 |
Fig. 1 Local interstellar proton number spectrum from Vos & Potgieter (2015). |
 |
Fig. 2 Local interstellar proton number spectrum from Vos & Potgieter (2015) in a more conventional log log representation showing the power-law tails. |
 |
Fig. 3 Integral of (p/mc)1−δ weighted by the local interstellar proton number spectrum from Vos & Potgieter (2015) as a function of δ-note that the dimensions are m-3. The value for δ = 1 is just the cosmic ray number density. |
 |
Fig. 4 Local reacceleration power density from Eq. (21), the Vos and Potgieter local interstellar spectrum, VA = 30 km s-1 and D0 = 1028 cm2 s-1. |
We can now evaluate the integral in Eq. (21) over the local interstellar spectrum as parametrized by Vos and Potgieter. The result is shown in Fig. 3 and shows a very weak dependence on δ. In Fig. 4 we show the corresponding power density from Eq. (21) using 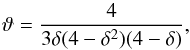 (25)and canonical values
(25)and canonical values 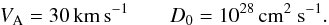 (26)We only plot the physically relevant range 0.3 <δ< 0.6 where we see that the power density is
(26)We only plot the physically relevant range 0.3 <δ< 0.6 where we see that the power density is 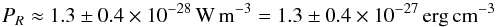 (27)if we now naively take the effective volume for the Galaxy to be 4 × 1061 m3 then the total power input from diffusive reacceleration can be estimated as 5 × 1033 W = 5 × 1040 erg s-1. This should be compared with the canonical estimate of the total cosmic ray Galactic luminosity of order 1034 W or 1041 erg s-1 (see discussion in Drury 2014, where it is noted that there is probably half a decade of systematic uncertainty in this estimate either way). Thus we have the, at first sight rather remarkable, result that diffusive reacceleration may be contributing as much as 50% of the total cosmic ray luminosity of the Galaxy!
(27)if we now naively take the effective volume for the Galaxy to be 4 × 1061 m3 then the total power input from diffusive reacceleration can be estimated as 5 × 1033 W = 5 × 1040 erg s-1. This should be compared with the canonical estimate of the total cosmic ray Galactic luminosity of order 1034 W or 1041 erg s-1 (see discussion in Drury 2014, where it is noted that there is probably half a decade of systematic uncertainty in this estimate either way). Thus we have the, at first sight rather remarkable, result that diffusive reacceleration may be contributing as much as 50% of the total cosmic ray luminosity of the Galaxy!
It is worth noting that if there is still some residual solar modulation beyond the heliopause, the local interstellar spectrum would have even more low energy particles and the diffusive reacceleration power would increase. Similarly, it is hard to believe that the local low-density bubble in which the solar system is located contains a significantly higher density of low-energy cosmic rays than the general Galactic average at the Sun’s distance from the Galactic centre; if anything, adiabatic expansion of the hot bubble would imply a slightly lower value. The ionization rates inferred from interstellar chemistry in molecular clouds also seem to indicate that the solar system cosmic ray environment is quite representative of the local Galaxy, as does the diffuse gamma-ray emission of the Galaxy (although at higher energies), see e.g. Grenier et al. (2015).
2.2. Estimates using GALPROP
As a cross-check on the above we now use the numerical CR-propagation package GALPROP1, using parameters which reproduce B/C with reacceleration, and then with the same parameters but without the reacceleration term, so that the difference in energy content is due to the reacceleration process2. The total CR proton energy content of the Galaxy is computed by integration over momentum and volume.
We base the calculation on the model z04LMS, which has reacceleration and a CR halo height of 4 kpc and VA = 30 km s-1Strong et al. (2010). This model has typical parameter values which reproduce B/C in reacceleration models (see also Trotta et al. 2011; Jóhannesson et al. 2016).
The CR proton energy content of the Galaxy is (8.1, 6.4) × 1055 erg with and without reacceleration respectively. Hence 1.7 × 1055 erg results from reacceleration, or ≈20% of the total; stated another way, the original energy injected by sources is boosted by ≈25%.
The luminosity of the Galaxy can be estimated from the total energy content using a value for the residence time of CR in the Galaxy. The total proton luminosity for our reacceleration model3 is 8 × 1040 erg s-1Strong et al. (2010), so the effective CR residence time is ≈ 3 × 107 yr. Hence the proton luminosity is 8.0, 6.3 × 1040 erg s-1 with and without reacceleration respectively. This is consistent with the analytical estimates in Sect. 2.1. Note that the relative values quoted above are independent of the assumed residence time.
3. Conclusions and implications for interstellar turbulence
Our estimates of the reacceleration power are necessarily approximate, but suffice to demonstrate that, for parameters chosen to reproduce B/C and commonly used in propagation calculations, the energy input via reacceleration is of order a quarter to half the total energy input. SNRs are then not “the sources of CR” in such models, at least not in the conventional sense! In retrospect this is perhaps not as surprising as it first seems. If the bulk of the energy resides in mildly relativistic and sub-relativistic particles, and if the spectrum in this region is to be significantly modified by reacceleration, then the energy input must be significant.
An interesting consequence is that the cosmic rays in such models must also damp interstellar turbulence and it is interesting to ask whether this is physically plausible and significant. Energetically it is not impossible. The main energy input into interstellar turbulence is generally taken to be the mechanical energy from expanding SNR shells and there is thus enough power input, but at quite large scales (Elmegreen & Scalo 2004; Scalo & Elmegreen 2004). The turbulence is normally assumed to be dissipated by non-linear cascading to high wave-number modes and the question is whether the cosmic rays can extract enough energy from the cascade at the scales which scatter mildly relativistic particles before thermal dissipation takes over. This is far from obvious, but if it is the case then the cosmic rays may define the inner scale of the interstellar turbulence. SNRs would then remain the ultimate engine driving cosmic ray acceleration, but through two channels; a direct one involving shock acceleration, and an indirect one mediated by interstellar turbulence.
Meanwhile it is essential to consider alternative explanations of the peak in the energy-dependence B/C, in particular convection gives a fairly natural mechanism (e.g. Korsmeier & Cuoco 2016) and there is evidence for a Galactic wind (e.g. Everett et al. 2012). The main message of this work is that behind the reacceleration term in the propagation codes there is a significant impact on the total energy budget of both the cosmic rays and the interstellar turbulence. It is not a free parameter than one can tune at will without physical consequences.
Current version available at https://sourceforge.net/projects/galprop
References
- Berezinskii, V. S., Bulanov, S. V., Dogiel, V. A., & Ptuskin, V. S. 1990, in Astrophysics of cosmic rays (Amsterdam: North Holland) [Google Scholar]
- Drury, L. O. 2014, ArXiv e-prints [arXiv:1412.1376] [Google Scholar]
- Drury, L. O., & Strong, A. W. 2015, ICRC2015 in Den Haag, PoS(ICRC2015)483 [arXiv:1508.02675] [Google Scholar]
- Elmegreen, B. G., & Scalo, J. 2004, ARA&A, 42, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Everett, J., Zweibel, E., Benjamin, B., et al. 2012, in EAS Pub. Ser. 56, ed. M. A. de Avillez, 73 [Google Scholar]
- Evoli, C., Gaggero, D., Vittino, A., et al. 2016, ArXiv e-prints [arXiv:1607.07886] [Google Scholar]
- Ginzburg, V. L., & Syrovatskii, S. I. 1964, in The Origin of Cosmic Rays, authorised english translation edn. (Oxford: Pergamon Press) [Google Scholar]
- Grenier, I. A., Black, J. H., & Strong, A. W. 2015, ARA&A, 53, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Heinbach, U., & Simon, M. 1995, ApJ, 441, 209 [NASA ADS] [CrossRef] [Google Scholar]
- H.E.S.S. Collaboration, Abramowski, A., Aharonian, F., et al. 2016, Nature, 531, 476 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Jóhannesson, G., Ruiz de Austri, R., Vincent, A. C., et al. 2016, ApJ, 824, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Korsmeier, M., & Cuoco, A. 2016, Phys. Rev. D 94, 123019 [Google Scholar]
- Potgieter, M. 2014, Brazilian J. Phys., 44, 581 [Google Scholar]
- Scalo, J., & Elmegreen, B. G. 2004, ARA&A, 42, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Seo, E. S., & Ptuskin, V. S. 1994, ApJ, 431, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Skilling, J. 1975a, MNRAS, 172, 557 [NASA ADS] [CrossRef] [Google Scholar]
- Skilling, J. 1975b, MNRAS, 173, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Skilling, J. 1975c, MNRAS, 173, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Stone, E. C., Cummings, A. C., McDonald, F. B., et al. 2013, Science, 341, 150 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Strong, A. W. 2015, ArXiv e-prints [arXiv:1507.05006] [Google Scholar]
- Strong, A. W., & Moskalenko, I. V. 1998, ApJ, 509, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Strong, A. W., Porter, T. A., Digel, S. W., et al. 2010, ApJ, 722, L58 [NASA ADS] [CrossRef] [Google Scholar]
- Thornbury, A., & Drury, L. O. 2014, MNRAS, 442, 3010 [NASA ADS] [CrossRef] [Google Scholar]
- Tibolla, O., & Drury, L. 2014, Nucl. Phys. B Proc. Suppl., 256, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Trotta, R., Jóhannesson, G., Moskalenko, I. V., et al. 2011, ApJ, 729, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Vos, E. E., & Potgieter, M. S. 2015, ApJ, 815, 119 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Local interstellar proton number spectrum from Vos & Potgieter (2015). |
| In the text | |
 |
Fig. 2 Local interstellar proton number spectrum from Vos & Potgieter (2015) in a more conventional log log representation showing the power-law tails. |
| In the text | |
 |
Fig. 3 Integral of (p/mc)1−δ weighted by the local interstellar proton number spectrum from Vos & Potgieter (2015) as a function of δ-note that the dimensions are m-3. The value for δ = 1 is just the cosmic ray number density. |
| In the text | |
 |
Fig. 4 Local reacceleration power density from Eq. (21), the Vos and Potgieter local interstellar spectrum, VA = 30 km s-1 and D0 = 1028 cm2 s-1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


