| Issue |
A&A
Volume 597, January 2017
|
|
|---|---|---|
| Article Number | A4 | |
| Number of page(s) | 22 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201526989 | |
| Published online | 19 December 2016 | |
(Sub)millimetre interferometric imaging of a sample of COSMOS/AzTEC submillimetre galaxies
III. Environments
1 Department of Physics, University of Zagreb, Bijenička cesta 32, 10000 Zagreb, Croatia
e-mail: vs@phy.hr
2 INAF–Osservatorio Astronomico di Bologna, via Ranzani, 1, Bologna 40127, Italy
3 Department of Physics, University of Helsinki, PO Box 64, 00014 Helsinki, Finland
4 Aix-Marseille Université, CNRS, Laboratoire d’Astrophysique de Marseille, UMR 7326, 13388 Marseille, France
5 Núcleo de Astronomía, Facultad de Ingeniería, Universidad Diego Portales, Av. Ejército 441, Santiago, Chile
6 Department of Astronomy, California Institute of Technology, MC 249-17, 1200 East California Blvd, Pasadena, CA 91125, USA
7 Department of Astronomy, University of Texas at Austin, 1 University Station C1400, Austin, TX 78712, USA
8 Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge, MA 02138, USA
9 Argelander Institute for Astronomy, Auf dem Hügel 71, 53121 Bonn, Germany
10 Sorbonne Universités, UPMC Univ. Paris 06, UMR 7095, Institut d’Astrophysique de Paris, 75005 Paris, France
11 Institut d’Astrophysique de Paris, UMR 7095 CNRS, Université Pierre et Marie Curie, 98bis boulevard Arago, 75014 Paris, France
12 Department of Astronomy, Cornell University, 220 Space Sciences Building, Ithaca, NY 14853, USA
13 Max-Planck-Institut für Extraterrestrische Physik, Postfach 1312, 85741 Garching bei München, Germany
14 Max Planck Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
15 Dark Cosmology center, Niels Bohr Institute, University of Copenhagen, Juliane Mariesvej 30, 2100 Copenhagen, Denmark
Received: 17 July 2015
Accepted: 4 April 2016
We investigate the environment of 23 submillimetre galaxies (SMGs) drawn from a signal-to-noise (S/N)-limited sample of SMGs originally discovered in the James Clerk Maxwell Telescope (JCMT)/AzTEC 1.1 mm continuum survey of a Cosmic Evolution Survey (COSMOS) subfield and then followed up with the Submillimetre Array and Plateau de Bure Interferometer at 890 μm and 1.3 mm, respectively. These SMGs already have well-defined multiwavelength counterparts and redshifts. We also analyse the environments of four COSMOS SMGs spectroscopically confirmed to lie at redshifts zspec > 4.5, and one at zspec = 2.49 resulting in a total SMG sample size of 28. We search for overdensities using the COSMOS photometric redshifts based on over 30 UV-NIR photometric measurements including the new UltraVISTA data release 2 and Spitzer/SPLASH data, and reaching an accuracy of σΔz/ (1 + z) = 0.0067 (0.0155) at z < 3.5 (>3.5). To identify overdensities we apply the Voronoi tessellation analysis, and estimate the redshift-space overdensity estimator δg as a function of distance from the SMG and/or overdensity centre. We test and validate our approach via simulations, X-ray detected groups or clusters, and spectroscopic verifications using VUDS and zCOSMOS catalogues which show that even with photometric redshifts in the COSMOS field we can efficiently retrieve overdensities out to z ≈ 5. Our results yield that 11 out of 23 (48%) JCMT/AzTEC 1.1 mm SMGs occupy overdense environments. Considering the entire JCMT/AzTEC 1.1 mm S/N ≥ 4 sample and taking the expected fraction of spurious detections into account, this means that 35–61% of the SMGs in the S/N-limited sample occupy overdense environments. We perform an X-ray stacking analysis in the 0.5–2 keV band using a 32″ aperture and our SMG positions, and find statistically significant detections. For our z < 2 subsample we find an average flux of (4.0 ± 0.8) × 10-16 erg s-1 cm-2 and a corresponding total mass of M200 = 2.8 × 1013M⊙. The z > 2 subsample yields an average flux of (1.3 ± 0.5) × 10-16 erg s-1 cm-2 and a corresponding total massof M200 = 2 × 1013M⊙. Our results suggest a higher occurrence of SMGs occupying overdense environments at z ≥ 3 than at z < 3. This may be understood if highly star-forming galaxies can only be formed in the highest peaks of the density field tracing the most massive dark matter haloes at early cosmic epochs, while at later times cosmic structure may have matured sufficiently that more modest overdensities correspond to sufficiently massive haloes to form SMGs.
Key words: galaxies: clusters: general / galaxies: evolution / galaxies: formation / large-scale structure of Universe / submillimeter: galaxies
© ESO, 2016
1. Introduction
Massive clusters of galaxies, the largest gravitationally bound objects in the Universe, are common in the local Universe, and they have been found up to z = 2.00 (Gobat et al. 2011, 2013). In a Lambda cold dark matter (ΛCDM) Universe it is expected that these systems descend from proto-clusters, which are early overdensities of massive galaxies that merge hierarchically and have the potential to form a virialised galaxy cluster by the present day (z = 0; Miley et al. 2004; Hatch et al. 2011; Chiang et al. 2013). Given the hierarchical growth of the proto-clusters, an enhanced galaxy interaction and merger rate within the systems is expected. This can trigger luminous active galactic nuclei (AGN) and/or starburst phenomena in the overdensity or proto-cluster member galaxies (e.g. Lehmer et al. 2009; Daddi et al. 2009; Capak et al. 2011; Walter et al. 2012). To date a few proto-clusters at z > 4 have been found hosting dusty, luminous starburst galaxies, the so-called submillimetre galaxies or SMGs (Daddi et al. 2009; Capak et al. 2011; Walter et al. 2012), by definition detected at wavelengths beyond 850 μm and up to a few millimetres (e.g. Blain et al. 2002, for a review).
With star formation rates (SFRs) of ~100–1000 M⊙ yr-1, SMGs are acknowledged to be the most powerful starbursts in the Universe (see Blain et al. 2002; and Casey et al. 2014, for reviews). They are promising candidates for the progenitors of the most massive elliptical galaxies seen in the present-day Universe (e.g. Lilly et al. 1999; Fu et al. 2013; Ivison et al. 2013; Toft et al. 2014; Simpson et al. 2014). Because early-type galaxies are predominantly found in clusters, the question arises whether SMGs are preferentially found to reside in galaxy overdensities, or are more likely to represent a field galaxy population – an issue that has not yet been systematically studied. Nonetheless, a number of SMGs have been found that are associated with galaxy overdensities, as summarised in Table 1.
Galaxy overdensities hosting SMGs in order of increasing redshift.
A number of studies have analysed the spatial clustering of SMGs (e.g. Blain et al. 2004; Hickox et al. 2012; Cowley et al. 2016; see also Almeida et al. 2011). For example, Hickox et al. (2012) have derived a spatial comoving correlation length of 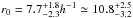 comoving Mpc (here we adopt h = 0.71; see below) for z = 1–3 SMGs, drawn from the 870 μm LABOCA Extended Chandra Deep Field South (ECDFS) Submillimetre Survey (LESS; Weiß et al. 2009). This suggests that the probability for an SMG to have another SMG within
comoving Mpc (here we adopt h = 0.71; see below) for z = 1–3 SMGs, drawn from the 870 μm LABOCA Extended Chandra Deep Field South (ECDFS) Submillimetre Survey (LESS; Weiß et al. 2009). This suggests that the probability for an SMG to have another SMG within 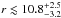 comoving Mpc is significantly higher than for a random spatial distribution. Their analysis further suggests that the z = 0 descendants of SMGs are typically massive (~2–3 L⋆, where L⋆ is a characteristic galaxy luminosity) elliptical galaxies residing in moderate to high-mass groups (
comoving Mpc is significantly higher than for a random spatial distribution. Their analysis further suggests that the z = 0 descendants of SMGs are typically massive (~2–3 L⋆, where L⋆ is a characteristic galaxy luminosity) elliptical galaxies residing in moderate to high-mass groups (![\hbox{$\log(M_\mathrm{halo} [h^{-1} {M_\odot}]) = 13.3^{+0.3}_{-0.5}$}](/articles/aa/full_html/2017/01/aa26989-15/aa26989-15-eq37.png) ), in agreement with the general view of this evolutionary sequence. Miller et al. (2015) studied whether SMG overdensities are tracers of the most massive structures of dark matter. Their simulation results suggest that SMG associations might be underdense in dark matter mass, while dark matter overdensities might be devoid of SMGs. The authors concluded that such complex biases of SMGs make them poor tracers of dark matter overdensities.
), in agreement with the general view of this evolutionary sequence. Miller et al. (2015) studied whether SMG overdensities are tracers of the most massive structures of dark matter. Their simulation results suggest that SMG associations might be underdense in dark matter mass, while dark matter overdensities might be devoid of SMGs. The authors concluded that such complex biases of SMGs make them poor tracers of dark matter overdensities.
A systematic study of overdensities around SMGs was performed by Aravena et al. (2010) who studied the environment of Max-Planck Millimetre Bolometer (MAMBO) 1.2 mm-detected SMGs in the COSMOS field (Bertoldi et al. 2007) searching for overdensities in BzK-selected galaxies. They identified three statistically significant compact overdensities at z = 1.4–2.5, and concluded that only ~30% of radio-identified bright SMGs in that redshift range form in galaxy number density peaks. As already noted by Aravena et al. (2010), studies purely based on the angular two-point correlation function measure the average clustering properties of SMGs, and these might be dominated by only a few significantly clustered systems. A systematic study of SMGs thus carries the advantage of identifying individual overdensities and studying the statistical clustering properties of the full sample, as well as the physical connection between the galaxies and their environment (e.g. Capak et al. 2011; Riechers et al. 2014). To date, however, no environmental analysis of individual SMGs in a well-selected sample of SMGs with secure counterparts has been performed. Here we perform such an analysis based on a sample of 23 SMGs drawn from the COSMOS JCMT/AzTEC 1.1 mm SMG sample (Scott et al. 2008), and associated with secure multiwavelength counterparts and (spectroscopic or photometric) redshifts (Younger et al. 2007, 2009; Smolčić et al. 2012a; Miettinen et al. 2015). Given the sparsity of well-selected SMG samples with secure counterparts and redshifts as well as exquisite data for large-scale structure studies this SMG sample is supplemented with four COSMOS SMGs that lie at spectroscopic redshifts of zspec > 4.5, and one that lies at zspec = 2.49 and was part of the SMG sample of Aravena et al. (2010). Hence, a total of 28 SMG environments are analysed in the present work.
Our SMG sample and observational data are described in Sect. 2. The overdensity analysis is presented in Sect. 3. The results are presented in Sect. 4, the spectroscopic verification of the identified overdensities in Sect. 5. The results are discussed in Sect. 6, and summarised in Sect. 7. We adopt a concordance ΛCDM cosmology, with the Hubble constant H0 = 71 km s-1 Mpc-1 (h ≡ H0/ (100 km s-1 Mpc-1) = 0.71), total (dark plus luminous baryonic) matter density Ωm = 0.27, and dark energy density ΩΛ = 0.73 (Spergel et al. 2007; Larson et al. 2011). Magnitudes in the present paper refer to the AB magnitude system (Oke 1974).
2. Data
2.1. SMG sample
2.1.1. Main SMG sample
The main sample of 23 SMGs studied here (main SMG sample hereafter) is taken from the JCMT/AzTEC 1.1 mm COSMOS survey S/N-limited sample identifying sources at 18″ angular resolution within 0.15 deg2 in the COSMOS field (Scott et al. 2008). Younger et al. (2007, 2009) followed up sources AzTEC1–15 with the Submillimetre Array (SMA) at 890 μm wavelength and ≲2″ angular resolution, and identified 17 counterparts to the initially selected 15 SMGs. Sources AzTEC16–30 were followed up by Miettinen et al. (2015) with the Plateau de Bure Interferometer (PdBI) at 1.3 mm and they identified 22 counterparts at this wavelength, yielding a total of 39 AzTEC1–30 counterparts identified at 890 μm (S/N ≥ 3.9) and 1.3 mm (S/N ≥ 4.5) wavelength. Using the COSMOS panchromatic data multi-wavelength counterparts were then associated to a subset of these sources by Younger et al. (2007, 2009), Smolčić et al. (2012a), Miettinen et al. (2015), and photometric redshifts computed via a standard χ2 minimisation spectral energy distribution (SED) fitting procedure and galaxy templates optimised for SMGs (Smolčić et al. 2012a; Miettinen et al. 2015; see also Smolčić et al. 2012b, for details). A comparison between spectroscopic and photometric redshifts yields an accuracy of such computed photometric redshifts of σΔz/ (1 + z) = 0.09 (see Smolčić et al. 2012a,b, for details). For the SMGs with no multi-wavelength counterparts lower redshift limits were computed using the millimetre-to-radio-flux ratio technique (see Miettinen et al. 2015).
An analysis of the number of spurious sources in the sample of the 39 counterparts of AzTEC1–30 detected at 890 μm (S/N ≥ 3.9) and 1.3 mm (S/N ≥ 4.5) with the SMA and PdBI, respectively, has been performed by both Younger et al. (2009), and Miettinen et al. (2015). While all sources with associated multi-wavelength counterparts are estimated to be real, eight spurious sources are expected among the 16 detections without associated multi-wavelength counterparts (i.e. two within the AzTEC7–15 SMA–890 μm sample, and six within the AzTEC16–30 PdBI–1.3 mm sample).
In summary, within the sample of 39 counterparts of AzTEC1–30 detected at 890 μm and 1.3 mm at ≲2″ angular resolution, seven have been associated with counterparts with spectroscopic redshifts, 16 with counterparts for which photometric redshifts (σΔz/ (1 + z) = 0.09) have been determined, and 16 for which only lower redshift (z ≳ 2) limits could be estimated. Out of the last 16 sources, eight are estimated to be spurious. We here exclude the SMGs with only lower redshift limits, and list in Table 2 the sources analysed here. Taking the expected spurious source fraction into account we estimate that the excluded percentage of SMGs amounts to 26%[=100% × (16–8)/(39–8)] of the total sample. This percentage is taken into account in the interpretation of our results in later sections.
2.1.2. Additional SMG sample
Given that well-selected samples of SMGs with secure counterparts and redshifts, as well as exquisite data for large-scale structure studies are still sparse in the literature, here we also analyse the environments of five more SMGs in the COSMOS field (additional SMG sample hereafter), four of which are spectroscopically confirmed to lie at zspec> 4.5 (see Smolčić et al. 2015, for more details), and one additional SMG (Cosbo-3) at zspec = 2.49 identified by Bertoldi et al. (2007), and further studied by Aravena et al. (2010) and Smolčić et al. (2012b). The additional SMG sample has a high degree of complementarity with the main SMG sample. While the inclusion of this sample induces a slight deviation from a S/N-limited sample, the main purpose of a S/N-limited sample is to minimise contamination from spurious sources, which the galaxies in the additional SMG sample are clearly not. Furthermore, any potential bias from the inclusion of these sources is more than compensated for by every galaxy in the additional SMG sample having a secure spectroscopic redshift, which dramatically decreases the uncertainty in overdensity association. In total, this yields 28 SMGs analysed here, the details of which are listed in Table 2.
Source list.
 |
Fig. 1 Comparison between photometric (zphot) and spectroscopic (zspec) redshifts in the COSMOS field for galaxies with zphot ≤ 3.5 (left panels) and zphot> 3.5 (right panels). The top panels show a direct comparison (with the one-to-one line indicated). The bottom panels show the distribution of the difference between the spectroscopic and photometric redshifts normalised to 1 + zspec. A Gaussian fit to the distribution is shown and the number of sources, the mean, and standard deviation are indicated in the panels. |
2.2. Redshift data
2.2.1. Catalogues
We use the most up-to-date version of the COSMOS photometric redshift catalogue (Laigle et al. 2016), which includes Y, J, H, anf Ks data from the UltraVISTA data release 2, and new SPLASH 3.6 and 4.5 μm Spitzer/IRAC data (Capak et al. 2007, and in prep.; McCracken et al. 2012; Ilbert et al. 2013). The catalogue was selected using the zYJHKs stacked mosaic and, thus, the number density of galaxies is high and well suited for our overdensity analysis. We here also make use of the COSMOS spectroscopic redshift catalogue (M. Salvato et al., in prep.), compiling all available spectroscopic redshifts, both internal to the COSMOS collaboration and from the literature (zCOSMOS, Lilly et al. 2007, 2009; IMACS, Trump et al. 2007; MMT, Prescott et al. 2006, VIMOS Ultra Deep Survey, VUDS, Le Fèvre et al. 2015; Subaru/FOCAS, T. Nagao et al., priv. comm.; and SDSS DR8 Aihara et al. 2011).
2.2.2. Photometric redshift accuracy
A key issue for the analysis presented here is whether photometric redshifts can efficiently be used for galaxy overdensity identification, especially at high redshifts (z ≳ 3.5) where the photometric redshift accuracy is lower compared to lower redshifts (e.g. Laigle et al. 2016). Hence, to test this, in Fig. 1 (left panels) we first compare the photometric (zphot) and spectroscopic (zspec) redshifts for 15 527 sources with secure spectroscopic redshifts up to zphot = 3.5 (i+ ≲ 25). In the figure, we also show the distribution of Δz/ (1 + zspec), where Δz is the difference between the spectroscopic and photometric redshifts. Consistent with the results from Ilbert et al. (2013), we find that the standard deviation of this distribution is only σΔz/ (1 + z) = 0.0067, which verifies the excellent photometric redshift accuracy at these redshifts.
To test whether the COSMOS photometric redshift catalogue can be efficiently used to search for overdensities at z > 3.5, in Fig. 1 (right panels) we show a comparison between photometric (3.5 ≲ zphot ≲ 6) and secure spectroscopic redshifts for 240 high-redshift sources in the COSMOS field. We find excellent agreement between the photometric and spectroscopic redshifts, with a standard deviation of σΔz/ (1 + z) = 0.0155. We also note that Le Fèvre et al. (2015) recently compared the VUDS spectroscopic redshifts with the same Ilbert et al. (2013) photometric redshift values as here and found similar results (see their Fig. 11). Because of the well known degeneracy in the SED fitting procedure between the Balmer-4000 Å and Lyα-1215 Å breaks, a fraction of high redshift (z > 2) sources might have a photometric redshift of less than unity (see, for example, Fig. 11 in Le Fèvre et al. 2015), which makes a high redshift photometric redshift sample partially incomplete. We estimate a completeness of 80% of our high-redshift photometric redshift selected sample based on the number of sources with zphot < 3.5 within the COSMOS spectroscopic sample with secure spectroscopic redshifts of zspec > 3.5. In summary, the photometric redshift accuracy in the COSMOS field is accurate enough for an overdensity analysis up to z < 6, as we show below.
3. Methodology
We search for galaxy overdensities around our SMGs, and determine their surface density profiles in a multistep process, described in detail in Sect. 3.1. Around each SMG’s position we first compute the galaxy overdensity parameter (δg) as a function of projected radius (r) for r = 0.5, 1, 2.5, and 5 arc minutes to assess potential small scale overdensities centred at the SMG. We then apply the Voronoi tessellation analysis (VTA; e.g. Ramella et al. 2001; Smolčić et al. 2007) at a 25′ × 25′ area surrounding the SMG to display the identified small scale overdensity and to identify further potential overdensities on larger scales close to the given SMG. As SMGs may not necessarily be located in the very centres of their host overdensities, using the VTA-overdense cells we recompute the centre of the overdensity. Using this newly defined overdensity centre we then re-compute the galaxy overdensity parameter (δg) of the structure as a function of projected radius in small steps (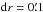 ) out to
) out to 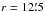 . We describe the quantification of the significance of the identified overdensities and false detection probabilities in Sect. 3.2, and we present further tests and verifications of the method in Appendix A.
. We describe the quantification of the significance of the identified overdensities and false detection probabilities in Sect. 3.2, and we present further tests and verifications of the method in Appendix A.
3.1. Searching for overdensities using photometric redshifts
To search for overdensities around our SMGs, we use the position and redshift of the target SMG. To analyse the environment of each SMG we use galaxies drawn from the COSMOS photometric redshift catalogue with i+ ≤ 25.5 assuring sample completeness and the most accurate photometric redshifts (see previous section and Laigle et al. 2016). To select large enough redshift bins to account for a variety of magnitude dependent photometric redshift uncertainties (see Ilbert et al. 2013; Laigle et al. 2016) we use all the galaxies in the photometric redshift catalogue with zphot = zSMG ± 3σΔz/ (1 + z)(1 + zSMG), where zSMG is the redshift of the SMG (we take σΔz/ (1 + z) = 0.007 (0.016) for zSMG ≤ 3.5 (>3.5); see Fig. 1 and Sect. 2.2.2 for details). In Appendix B, we present the results using all galaxies within a factor of two narrower bin (i.e. with zphot = zSMG ± 1.5σΔz/ (1 + z)(1 + zSMG)).
3.1.1. Small-scale overdensity search with central SMGs
We first search for small scale overdensities around our SMGs by computing the galaxy overdensity parameter in the vicinity of each SMG, i.e. within a distance of 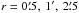 , and 5′ from the given SMG. The galaxy overdensity parameter, i.e. contrast above the background field, as a function of radius is defined as
, and 5′ from the given SMG. The galaxy overdensity parameter, i.e. contrast above the background field, as a function of radius is defined as 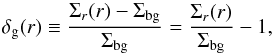 (1)where Σr and Σbg are the local galaxy, and the background galaxy surface density, respectively. The numerator in the first equality, Σr−Σbg ≡ ΔΣ, is the deviation of the local galaxy number density from that in the background field. The value of Σr was calculated as Σr = Nr/Ar, where Nr is the number of galaxies within the given redshift bin around the centre inside the search window of area Ar = π × r2 with r the search radius. Similarly, Σbg = Nbg/Abg, where Nbg is the number of galaxies satisfying the photometric redshift criterion within the large background area Abg. This was taken to be the effective area of the full COSMOS field for our small-scale SMG overdensity assessment. In the computation masked areas (due to e.g. saturated stars or corrupted data) in the COSMOS field have properly been taken into account.
(1)where Σr and Σbg are the local galaxy, and the background galaxy surface density, respectively. The numerator in the first equality, Σr−Σbg ≡ ΔΣ, is the deviation of the local galaxy number density from that in the background field. The value of Σr was calculated as Σr = Nr/Ar, where Nr is the number of galaxies within the given redshift bin around the centre inside the search window of area Ar = π × r2 with r the search radius. Similarly, Σbg = Nbg/Abg, where Nbg is the number of galaxies satisfying the photometric redshift criterion within the large background area Abg. This was taken to be the effective area of the full COSMOS field for our small-scale SMG overdensity assessment. In the computation masked areas (due to e.g. saturated stars or corrupted data) in the COSMOS field have properly been taken into account.
We, furthermore, compute for each radius the Poisson probability of observing ≥Nr objects when the expected number is nr = Σbg × Ar, p( ≥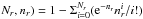 , and consider p ≤ 0.05 to be robust overdensity values.
, and consider p ≤ 0.05 to be robust overdensity values.
According to the above definition, δg = 0 ⇔ ΔΣ = 0 means there is no observed overdensity, while δg< 0 indicates an underdensity. As a general rule, the higher the value of δg, the higher the probability that the identified overdensity structure is a genuine galaxy (proto-)cluster or group (e.g. Chiang et al. 2013).
3.1.2. Voronoi tessellation analysis (VTA)
We next apply the VTA onto galaxies surrounding our SMGs. Voronoi tessellation is an efficient method to identify and visualise overdensities, and it has already been applied for the search of galaxy clusters by e.g. Ramella et al. (2001), Kim et al. (2002), Lopes et al. (2004), Smolčić et al. (2007), and Oklopčić et al. (2010). A major advantage of the VTA is that overdensities are identified irrrespective of their shape or galaxy properties. In general, a Voronoi tessellation, in the 2D case as in the present work, is a method to partition a plane into convex polygons called Voronoi cells (Dirichlet 1850; Voronoi 1908). When a 2D distribution of distinct points, generally called nuclei (that in our case are galaxies), is decomposed through the Voronoi tessellation algorithm, each resulting cell encloses exactly one seed point, and every position within a given cell is closer to the cell’s nucleus than to any other nucleus in the plane (Icke & van de Weygaert 1987). The higher the surface density of nuclei is, the smaller is the area of the cells; an overdensity region can be uncovered this way.
We apply the VTA on galaxies drawn from the COSMOS photometric redshift catalogue (i+ ≤ 25.5, zphot = zSMG ± 3σΔz/ (1 + z)(1 + zSMG)), as defined above, over an area larger than 25′ × 25′ surrounding the given SMG. To identify overdensities in the analysed region we make use of the inverse of the areas of the VTA cells (which effectively correspond to the local surface densities of given galaxies; ng hereafter). We first generate 10 Mock cataloguess with the same number of galaxies as present in the inner 1 deg2 of the COSMOS field, but with randomly distributed positions over this area (note that such a size is large enough to contain both overdensities, underdensities, and field galaxies). We then apply the VTA on each Mock catalogue and generate a cumulative distribution of ng, averaged over the ten iterations. Following Ramella et al. (2001), we define the value of ng that corresponds to the 80% quantile as the threshold above which a VTA cell is considered overdense.
3.1.3. Large-scale overdensity search for off-centre SMGs
As the small-scale δg computation (Sect. 3.1.1), and the VTA (Sect. 3.1.2) are centred at the position of the given SMG, we next redefine the centre of the potential overdensity by computing the median right ascension and median declination of VTA-identified overdense cells within r ≤ x′ from the SMG, where x is taken between 1′ and 10′ and determined in such a way that the surface density of the overdense VTA cells (i.e. number of overdense VTA cells over x2 × π) is maximised within this circular area.
With such defined overdensity centres we then re-compute the galaxy overdensity parameter, δg (Eq. (1)) out to 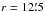 , in steps of d
, in steps of d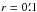 . To assess an average value of the background surface density and quantify its fluctuation for this analysis we use nine differently positioned, circular, and not overlapping Abg = 706.86 arcmin2 areas to compute the median value of the background surface density,
. To assess an average value of the background surface density and quantify its fluctuation for this analysis we use nine differently positioned, circular, and not overlapping Abg = 706.86 arcmin2 areas to compute the median value of the background surface density, 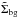 , and its standard deviation, σΣbg. This allows us to quantify the significance of δg(r) > 0 values by assigning errors on δg(r) = 0, i.e. σδg = 0(r). The errors reflect statistical fluctuations for ΔΣ = 0, and we compute them by taking Σr = Σbg and statistically propagating the errors of Σr and Σbg (≡σΣr and σΣbg, where the latter was defined above). This yields
, and its standard deviation, σΣbg. This allows us to quantify the significance of δg(r) > 0 values by assigning errors on δg(r) = 0, i.e. σδg = 0(r). The errors reflect statistical fluctuations for ΔΣ = 0, and we compute them by taking Σr = Σbg and statistically propagating the errors of Σr and Σbg (≡σΣr and σΣbg, where the latter was defined above). This yields ![\begin{equation} \label{eq:deltaerr} \sigma_{\delta_{\rm g}=0}(r) = \frac{1}{\tilde{\Sigma}_{\rm bg}} \left[ \sigma_{\Sigma_r(r)}^2 + \sigma_{\Sigma_{\rm bg}}^2 \right]^{1/2} . \end{equation}](/articles/aa/full_html/2017/01/aa26989-15/aa26989-15-eq173.png) (2)As Σr(r) is derived from rather small areas (Ar), σΣr will be dominated by Poisson errors (of the number of expected galaxies based on Σbg). Hence, we take
(2)As Σr(r) is derived from rather small areas (Ar), σΣr will be dominated by Poisson errors (of the number of expected galaxies based on Σbg). Hence, we take 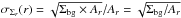 . Finally, to consider the overdensity centred at the newly defined centre as significant, at any given radius we require δg ≥ t × σδg = 0, where t is determined based on our simulations, detailed in the next subsection, in such a way that it reassures ≤20% of chance detections.
. Finally, to consider the overdensity centred at the newly defined centre as significant, at any given radius we require δg ≥ t × σδg = 0, where t is determined based on our simulations, detailed in the next subsection, in such a way that it reassures ≤20% of chance detections.
3.2. Assessing significance and false detection probabilities
To quantify false detection probabilities we make use of ten Mock catalogues generated for each SMG containing the same number of galaxies with z = zSMG ± 3σΔz/ (1 + z)(1 + z) present in the inner 1 deg2 of the COSMOS field, but with randomly distributed positions over this area (see Sect. 3.1.2). For 1000 random SMG positions we then search within each Mock catalogue for the number of occurrences with Nr ≥ 1,2,3 within r = 0.5′,1′. This corresponds to 10 000 Mock realisations per SMG. For each SMG in our sample this then sets the false detection probability within our small-scale overdensity search (see Sect. 3.1.1) out to r = 1′.
To quantify the false detection probability within our large-scale overdensity search with off-centre SMGs (see Sect. 3.1.3), we apply the same procedure as for the real SMGs to 100 random SMG positions. We first apply the VTA on the Mock cataloguess (including the random-SMG position per realisation), then redefine the potential overdensity centre for each random SMG, and finally derive δg as a function of r, centred at the newly defined overdensity centre. We lastly determine the number of δg/σδg ≥ 3, 4,...10 detections with the requirement that the distance between the random SMG position and the newly defined overdensity centre is less or equal to the same distance, as determined for the real SMG. We set a δg/σδg threshold value such that the fraction of such occurrences is ≤0.2. This process then yields, for each SMG in our sample, a unique δg/σδg threshold to assess the significance of the overdensity analysed around the newly defined centre.
4. Analysis and results
The overdensity search results are shown in Fig. C.1, where for each SMG in our sample we show i) the integral δg as a function of projected circular radius, centred on the SMGs position and out to r = 5′, which indicates the number of sources within a given radius (Nr, which also includes the SMG of interest); ii) the Voronoi diagram over a 25′ × 25′ area centred on the SMG’s position with overdense VTA cells, and the redefined overdensity centre indicated; and iii) δg as a function of radius out to 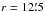 away from the newly defined overdensity centre, and its significance. In Sect. 4.1, we first investigate the small-scale (r ≤ 1′) overdensities centred on the SMG positions, and in Sect. 4.2 we investigate overdensities surrounding SMGs on larger scales and not necessarily with a centrally positioned SMG.
away from the newly defined overdensity centre, and its significance. In Sect. 4.1, we first investigate the small-scale (r ≤ 1′) overdensities centred on the SMG positions, and in Sect. 4.2 we investigate overdensities surrounding SMGs on larger scales and not necessarily with a centrally positioned SMG.
Small-scale overdensity search results.
4.1. Evidence for small (r ≤ 1′) scale overdensities around central SMGs
In Table 3, we list the number of sources (if larger than one) within r = 0.5′ or r = 1′ for the 28 SMGs in our sample. For each SMG we also list the Poisson probability of finding ≥Nr sources within this radius, as well as the false detection probability (PFD) to find ≥ Nr within r based on the results of our simulations using random SMG positions and Mock galaxy catalogues (see Sect. 3.2 for details). If we set the false detection probability to PFD ≤ 5%, we find five out of 23 (22%) systems in our main SMG sample, and three out of five (60%) systems in our additional SMG sample with Nr ≥ 2 values at r ≤ 1′ away from the SMG. This amounts to a total of 8/28 (29%) systems with significant small-scale overdensities. Note that with such a false detection probability we expect ≤1.15 false detections in the main SMG sample, and ≤0.25 in the additional SMG sample. If we restrict our main SMG sample to only the SMGs with spectroscopic redshifts, we find 2/6 (33%) SMGs with small-scale overdensities.
As discussed in Sect. 2, our main SMG sample was drawn from a S/N-limited sample of AzTEC/JCMT sources, and in addition to the 23 SMGs in our main SMG sample eight further SMGs have lower redshift limit estimates only and were, thus, not analysed here. If these eight SMGs were to exhibit the same small-scale environment properties as the 74% (=23/(23+8)) of the sample analysed here, the percentage of SMGs in the flux limited sample with small-scale overdensities would remain the same (22%). In the two extreme cases where all eight systems would either be or not be associated with small-scale overdensities, this percentage would range from 35% to 61%. In Appendix B, we compute these percentages for a narrower redshift width (Δz = zSMG ± 1.5σΔz/ (1 + z)(1 + zSMG)), and find statistically consistent results.
The scales (r ≤ 1′) tested here correspond to physical scales of less than 510, 470, 425, and 380 kpc at z = 2, 3, 4, and 5, respectively. These are the typical sizes of (proto-)groups (e.g. Diener et al. 2013), used a projected physical diameter of 500 kpc to search for proto-groups at 1.8 < z < 3). We thus further test whether any of our SMG systems has been detected via extended X-ray emission arising from thermal bremsstrahlung radiation of the intra-group/-cluster medium, heated during the gravitational collapse of the primordial density peaks.
The COSMOS field has been a target of several large programmes with both Chandra and XMM-Newton (Hasinger et al. 2007; Finoguenov et al. 2007; Elvis et al. 2009; Civano et al. 2016), which allow for a detection of emission from the hot gas of galaxy groups. The published catalogues combine X-ray and optical-NIR data to assign redshifts to the groups, and are limited to z ≃ 1 (Finoguenov et al. 2007; George et al. 2011), while most of our SMGs are at z > 1.
The expected diameter of a galaxy group at z ≳ 2 at the sensitivity limit of the X-ray survey is about 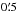 and brighter groups and clusters are expected to have even larger sizes. We find that only one source in our sample, Cosbo-3, is directly detected as an extended X-ray source in the 0.5–2 keV band. This is described in more detail in Wang et al. (2016) who estimate an X-ray luminosity of LX = 7 × 1043 erg s-1 in the rest-frame 0.1–2.4 keV band, and a total mass within r200 = 38″ of M200 = 4 × 1013M⊙. We have further verified that none of the extended X-ray sources in the COSMOS field, unidentified in the optical-NIR data, matches the position of any of the remaining SMGs in our sample. We note that the sensitivity of combined X-ray data only reaches roughly ~4 × 1013M⊙ at the redshifts of our SMG sample. To gain a deeper insight into the halo masses of our SMGs, we have performed a stacking analysis for the SMG systems (excluding Cosbo-3) outside the area confused with emission from other groups. We combine the data from Chandra and XMM-Newton in the 0.5–2 keV band, after subtracting the background and removing the emission on spatial scales of 16″, which removes point sources, X-ray jets as well as cores of groups and clusters (for details, see e.g. Finoguenov et al. 2015). We have separately searched for SMG halo detection on scales of 4″–16″ using Chandra data only, finding none.
and brighter groups and clusters are expected to have even larger sizes. We find that only one source in our sample, Cosbo-3, is directly detected as an extended X-ray source in the 0.5–2 keV band. This is described in more detail in Wang et al. (2016) who estimate an X-ray luminosity of LX = 7 × 1043 erg s-1 in the rest-frame 0.1–2.4 keV band, and a total mass within r200 = 38″ of M200 = 4 × 1013M⊙. We have further verified that none of the extended X-ray sources in the COSMOS field, unidentified in the optical-NIR data, matches the position of any of the remaining SMGs in our sample. We note that the sensitivity of combined X-ray data only reaches roughly ~4 × 1013M⊙ at the redshifts of our SMG sample. To gain a deeper insight into the halo masses of our SMGs, we have performed a stacking analysis for the SMG systems (excluding Cosbo-3) outside the area confused with emission from other groups. We combine the data from Chandra and XMM-Newton in the 0.5–2 keV band, after subtracting the background and removing the emission on spatial scales of 16″, which removes point sources, X-ray jets as well as cores of groups and clusters (for details, see e.g. Finoguenov et al. 2015). We have separately searched for SMG halo detection on scales of 4″–16″ using Chandra data only, finding none.
We extract the stacked X-ray flux using a 32″ diameter aperture centred on the SMG, removing source duplications. The selected aperture matches well the expected size of the X-ray emission from groups slightly below the X-ray detection threshold. The choice of aperture is determined by the source confusion on the flux level of interest, as discussed in Finoguenov et al. (2015). We perform a correction for missing flux when reporting the final values below. Given the redshift dependence of conversion factors, we have split the sample into two, z < 2 (eight systems) and z > 2 subsamples (19). To infer the total mass, we calculate the total luminosity, using the K corrections from the L−T (luminosity – temperature) relation and apply the L−M (luminosity – mass) relation of Leauthaud et al. (2010), using the iterative procedure described in Finoguenov et al. (2007). The scaling relation connecting the X-ray luminosity and the total mass at those fluxes (albeit at z < 1.6) has been verified through the stacked weak lensing analysis as well as clustering in Finoguenov et al. (2015). Furthermore, an agreement between the clustering analysis and X-ray stacking has been presented at z ~ 2 by Béthermin et al. (2014).
Large-scale overdensity search results.
The z < 2 subsample yields a 5σ detection with an average flux of (4.0 ± 0.8) × 10-16 erg s-1 cm-2 and a corresponding total mass of M200 = 2.8 × 1013M⊙ assuming z = 1.5. We can rule out a major contribution to the flux from point sources, based on the depth of Chandra observations.
The z > 2 subsample yields a marginally significant signal with average flux of (1.3 ± 0.5) × 10-16 erg s-1 cm-2 and a corresponding total mass of M200 = 2.5 × 1013M⊙ for redshifts between 2 and 3. Assuming z = 4 we estimate a total mass of M200 = 2.0 × 1013M⊙. At those fluxes we cannot rule out the contribution of point sources.
Overdensity search results based on small and large-scale analyses.
4.2. Evidence for overdensities around SMGs
While in the previous section we have analysed the environments of our SMGs at r ≤ 1′ scales, here we investigate the general environment of the SMGs in our sample, on small and large scales, without requiring that the SMG necessarily resides in the centre of the overdensity. As described in Sect. 3.1, for each SMG the potential overdensity centre was automatically relocated by taking the median RA and Dec of overdense VTA cells surrounding the SMG. This was done within a radius that maximises the number density of such cells within the encompassing circular area. The new centre positions and the radii maximising the VTA-overdense number densities are indicated in the middle panels in Fig. C.1, and the distances between the target SMGs and the newly defined overdensity centres are tabulated in Table 4. In Fig. C.1, we also show δg as a function of radius out to 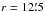 away from the overdensity centre, as well as its significance (δg/σδg = 0). For each SMG, the δg/σδg = 0 threshold above which our simulations yield ≤20% false detection probability is indicated in the panels. We find 9/23 (39%) systems within our main SMG sample, and 4/5 (80%) in our additional SMG sample with δg/σδg = 0 higher than the corresponding threshold. Out of the six SMGs in the main SMG sample with spectroscopic redshifts we find that three (50%) of the systems show evidence for overdensities. Combining this with the results of the small-scale overdensity search with central SMGs presented in the previous subsection we find a total of 11/23 (48%), 3/6 (50%), and 4/5 (80%) overdense systems in our main SMG sample, main SMG subsample with spectroscopic redshifts assigned to the SMGs, and additional SMG sample, respectively. The combined results are tabulated in Table 5. The analysis for a narrower redshift width (Δz = zSMG ± 1.5σΔz/ (1 + z)(1 + zSMG)) yields systematically lower percentages, yet consistent within the Poisson errors (see Appendix B for details).
away from the overdensity centre, as well as its significance (δg/σδg = 0). For each SMG, the δg/σδg = 0 threshold above which our simulations yield ≤20% false detection probability is indicated in the panels. We find 9/23 (39%) systems within our main SMG sample, and 4/5 (80%) in our additional SMG sample with δg/σδg = 0 higher than the corresponding threshold. Out of the six SMGs in the main SMG sample with spectroscopic redshifts we find that three (50%) of the systems show evidence for overdensities. Combining this with the results of the small-scale overdensity search with central SMGs presented in the previous subsection we find a total of 11/23 (48%), 3/6 (50%), and 4/5 (80%) overdense systems in our main SMG sample, main SMG subsample with spectroscopic redshifts assigned to the SMGs, and additional SMG sample, respectively. The combined results are tabulated in Table 5. The analysis for a narrower redshift width (Δz = zSMG ± 1.5σΔz/ (1 + z)(1 + zSMG)) yields systematically lower percentages, yet consistent within the Poisson errors (see Appendix B for details).
5. Spectroscopic verification of overdensity candidates
As our analysis is based on photometric redshifts, spectroscopic redshifts are required in order to confirm each identified overdensity. In order to fully assess the entire sample of photometric redshift overdensities reported here requires a dedicated spectroscopic campaign of the area surrounding each SMG (as in e.g. Riechers et al. 2014). Though such a comparison is not yet possible, a large number of spectroscopic redshifts at z > 2 in the COSMOS field exist mainly from the VUDS (Le Fèvre et al. 2015) and the zCOSMOS-deep surveys (S. Lilly et al., in prep.) from which we can make a preliminary assessment of the reliability of our photometric redshift measurements in recovering overdense regions. The VUDS spectroscopic redshift survey targeted ~8000 sources (i+ ≲ 25) at 2 < z ≲ 6 covering 1 deg2 in three fields (COSMOS, ECDFS, and VVDS-02h), of which approximately half are in the COSMOS field. The zCOSMOS survey assembled over 20 000 spectra in the COSMOS field in two phases, the magnitude limited zCOSMOS-bright survey (IAB < 22.5; Lilly et al. 2007, 2009) and the zCOSMOS-deep, with targets selected by a variety of colour and magnitude cuts (limited to i′ ≲ 24.5), from which we rely almost exclusively from the latter. The combination of the two surveys puts reliable1 spectroscopic redshifts of nearly 4000 unique galaxies at z > 2 at our disposal across the full COSMOS field. Based on the VUDS and zCOSMOS coverage of the COSMOS field, out of the 28 SMGs analysed here, 112 are in the redshift range where both surveys are sensitive (z > 2) and their projected surroundings (R < 5′) are sampled densely enough to potentially identify an overdensity. In the previous sections, we identified overdensities associated with eight out of these 11 systems3.
For each overdensity candidate at z > 2, we searched for associated spectroscopic members using a redshift window of zSMG ± 3σΔz/ (1 + z)(1 + z) and a 5′ radius for the spatial filter centred on the overdensity candidate centre. This size roughly matches that of proto-clusters found in VUDS (Cucciati et al. 2014; Lemaux et al. 2014) and in simulations (e.g. Chiang et al. 2013). For known overdensities in VUDS (hereafter proto-structures), the size of the filter was shrunk to the bounds of the proto-structure as determined in a method similar to that of Lemaux et al. (2014). The number of spectroscopic members of each overdensity candidate4 was used to determine the overdensity (δg) by contrasting with an identical measure in 1000 proto-structure-sized volumes (i.e. the filter size) in random locations in the field where similar spectroscopic sampling existed. For overdensity candidates at 2 < z < 4, the central redshift of each of the 1000 realisations was set to a random value between 2.2 <z < 4.2 to determine the density properties of the field at these epochs. For candidates at z > 4, a random redshift between 4 < z < 5 was used for each realisation as the number density of VUDS sources begins to decline rapidly above z ≳ 45. The magnitude of the overdensity, δg, along with its associated uncertainty was estimated for each overdensity candidate by fitting either a truncated Gaussian or a Poissonian function, the latter being generally reserved for the higher redshift overdensities where the number of galaxies in the filter is extremely small, to the distribution of the number of galaxies recovered in the 1000 observations of random spatial and redshift positions in the ranges given above (see Lemaux et al. 2014, for more details).
Out of the 11 candidates with the requisite coverage, we find three SMGs (AzTEC5, J1000+0234, and Cosbo-3) in environments which are, spectroscopically, significantly overdense systems with respect to the general VUDS+zCOSMOS field (i.e. ≳2.5σ, δg ≳ 4, with an average overdensity of ⟨ δg ⟩ ~ 5), and three SMGs (AzTEC18, AK03, and Vd-17871) in environments which are potentially overdense (i.e. ≳2σ, δg ≳ 1.5). This amounts to 3/8 (38%), and potentially 5/8 (62%) of the overdensities found to be statistically significant in the previous sections using our photometric redshift analysis. Note that the spectroscopic analysis retrieves one additional potential overdensity (AzTEC18), not identified within out photometric-redshift-based approach. However, this overdensity is identified when using a narrower redshift bin (see Appendix B, and Sect. 6.2).
We note that while the set of VUDS/zCOSMOS proto-structures in this field comprises a pure sample of genuine overdensities, the sample is not complete even in those areas which we have denoted as having the requisite spectroscopic coverage. The selection criteria of both the VUDS and zCOSMOS surveys is such that galaxies with stellar population older than ~1 Gyr are essentially absent, a population which may be more prevalent in high-density environments even at these redshifts (e.g. Kodama et al. 2007). In addition, the spatial sampling of the VUDS and zCOSMOS surveys in the area comprising the overdensity candidates is non-uniform in nearly all cases (see Fig. C.2 for an example) and is also a strong function of redshift, further diminishing our ability to spectroscopically confirm some candidates and limiting the conclusions that can be drawn from this analysis. Thus, a dedicated spectroscopic study of the remaining overdensity candidates is necessary to either confirm or deny their genuineness.
To date such spectroscopic studies have confirmed for example the proto-cluster nature of the structure associated with AzTEC3 (Capak et al. 2008; Riechers et al. 2014). Furthermore, A. Karim et al. (in prep.) show that the SMG Vd-17871 has a spectroscopically identified close companion, in accordance with the above estimated elevated galaxy density in its surroundings. Lastly, the structure associated with the SMG Cosbo-3, initially identified by Aravena et al. (2010), here spectroscopically identified has been independently confirmed, and studied in more detail based on optical and mm spectroscopic, and X-ray data in Casey et al. (2015) and Wang et al. (2016). In summary, we conclude that four (AzTEC5, J1000+0234, and Cosbo-3 based on VUDS and zCOSMOS data, and the structure associated with AzTEC3 via dedicated follow-up) out of eight overdensity candidates tested here (i.e. ~50%) have been independently spectroscopically identified. Adding to this the two spectroscopically identified ambiguous cases (AK03 and Vd-17871) this amounts to 6/8, i.e. 75% of the tested systems.
6. Discussion
6.1. Fraction of SMGs in overdense environments
Within our main SMG sample we have identified 5/23 overdensities showing evidence of small-scale overdensities, and six additional overdensities showing statistically significant overdensities with the SMG off-centre. This yields a percentage of 48% (11/23) of SMGs in our main SMG sample located in overdense environments. In Sect. 2, we estimated that in addition to these 23 SMGs drawn from a S/N-limited sample, eight further sources with only lower redshift limits are present (i.e. 16 in total out of which eight are expected to be spurious). If these eight sources with lower redshift limits on average have the same properties as the sources analysed, then the estimated percentage of SMGs occupying overdensities does not change. In the two extreme cases, however, where all eight systems would either occupy or not occupy overdensities this percentage would then range from 35% to 61%. Within our additional SMG sample, containing Cosbo-3 at zspec = 2.49, as well as AzTEC/C159, Vd-17871, J1000+1234, and AK03 at zspec> 4.5 we find 4/5 (80%) systems associated with overdensitites.
Only the spectroscopically verified Cosbo-3 proto-cluster (z = 2.49) has been directly detected in the X-rays, and has an estimated X-ray mass of M200 = 4 × 1013M⊙ (Wang et al. 2016). Stacking the X-ray data to search for extended haloes occupied by the SMGs in our sample in Sect. 4.1 we derived for the z< 2 subsample a total mass of M200 = 2.8 × 1013M⊙ assuming z = 1.5. For the z> 2 subsample we found a total mass of M200 = 2–2.5 × 1013M⊙ given the span in assumed redshift (from z = 2 to 4). This yields dark matter halo masses of the SMGs analysed here in the range of M200 = 2–3 × 1013M⊙, in reasonable agreement with dark matter halo masses derived by Hickox et al. (2012) based on a clustering analysis of LABOCA SMGs in the ECDFS field (![\hbox{$\log(M_\mathrm{halo}[h^{-1}~{M_\odot}])=12.8^{+0.3}_{-0.5}$}](/articles/aa/full_html/2017/01/aa26989-15/aa26989-15-eq244.png) ).
).
If we split our SMG sample in two redshift bins and use the errors on measurements based on a small number of events (Gehrels 1986), at z< 3 we find 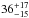 % (
% (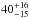 %) overdensities in the main (main plus additional) SMG sample, while this fraction increases to
%) overdensities in the main (main plus additional) SMG sample, while this fraction increases to 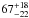 % (
% (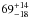 %) at z ≥ 3. Although the errors on these percentages are large, this could suggest that the occurrence of SMGs in overdensities at high redshift is higher. This is consistent with the picture that massive, highly star-forming galaxies can only be formed in the highest peaks of the density field tracing the most massive dark matter haloes at the earliest epochs (z ≥ 3; e.g. Kauffmann et al. 1999; Springel et al. 2005; see also discussion by Riechers et al. 2013). At later times, cosmic structure may have matured sufficiently that more modest overdensities correspond to sufficiently massive haloes to form SMGs (e.g. Hopkins et al. 2008; González et al. 2011; Amblard et al. 2011). However, a more detailed theoretical exploration of this aspect in the future is desirable in cosmological simulations, as well as more constraining observational data, as discussed below.
%) at z ≥ 3. Although the errors on these percentages are large, this could suggest that the occurrence of SMGs in overdensities at high redshift is higher. This is consistent with the picture that massive, highly star-forming galaxies can only be formed in the highest peaks of the density field tracing the most massive dark matter haloes at the earliest epochs (z ≥ 3; e.g. Kauffmann et al. 1999; Springel et al. 2005; see also discussion by Riechers et al. 2013). At later times, cosmic structure may have matured sufficiently that more modest overdensities correspond to sufficiently massive haloes to form SMGs (e.g. Hopkins et al. 2008; González et al. 2011; Amblard et al. 2011). However, a more detailed theoretical exploration of this aspect in the future is desirable in cosmological simulations, as well as more constraining observational data, as discussed below.
6.2. A grain of salt
We performed a statistical analysis of the environments of two samples of SMGs, i) a well-defined sample obtained via interferometric (SMA and PdBI) follow-up of a S/N-limited sample identified at 1.1 mm with AzTEC/JCMT over a 0.15 deg2 COSMOS subfield with photometric or spectroscopic redshifts assigned to the SMGs, ii) five additional SMGs with secure spectroscopic redshifts, one at zspec = 2.49, and four at zspec> 4.5. The analysis was performed using uniform selection and overdensity identification criteria for all SMGs in our sample, thus rendering a robust statistical result on the percentage of SMGs occupying overdense environments under the assumptions made. We here discuss a few caveats that may have an effect on the results of individual overdensities hosting our SMGs.
The analysis performed here is based on a galaxy sample limited to i+ ≤ 25.5, which assures the most accurate photometric redshifts in the COSMOS field (see Sect. 2.2.2). It, thus, does not take into account fainter galaxies that may be present in vicinity of, and be gravitationally bound to the SMGs analysed here. Furthermore, a 20% incompleteness in the photometric redshift catalogue at z> 3.5 (estimated in Sect. 2.2.2, and due to the well known degeneracy in the SED fitting procedure between the Balmer-4000 Å and Lyα-1215 Å breaks) may bias the results at high redshift low. On the other hand, catastrophic failures in photometric redshift solutions, estimated to amount to <15% for 3 <z< 6 (Laigle et al. 2016), could bias the results in some cases high. Furthermore, wrongly assigned redshifts to SMGs, and multiplicity of the SMGs at scales ≲2″ may bias the results in an unpredictable manner (see Koprowski et al. 2014; Miettinen et al. 2016; M. Aravena et al., in prep.).
Other caveats that may bias the derived overdensity percentage low are the width and centring of the redshift bin used for the analysis. The SMG redshift may not necessarily be coincident with the host overdensity’s redshift, nor does the extent of the overdensity in the z-direction need to be of certain width, but may vary from case-to-case. For example, as shown in Appendix B using a narrower redshift bin (Δz = zSMG ± 1.5σΔz/ (1 + z)(1 + zSMG)) we identify three additional overdensities6. Adding these to those identified above would then yield a total of 13/23 (56%), and 5/5 (100%) overdensities in our main and additional SMG samples, respectively, and an estimated range of 42–68% of SMGs occupying overdensities in our S/N-limited, 1.1 mm selected SMG sample (accounting for the expected spurious percentage in the sample). Furthermore, as already shown by Chiang et al. (2013), using photometric redshifts to search for overdensities dilutes the δg signal (see their Fig. 13), and we are, thus, likely to be biased in the present analysis towards detecting the most prominent overdensities only.
With the data in-hand it is impossible to address all the above described caveats in a robust way. The optimal solution would be a dedicated spectroscopic follow-up of all galaxies surrounding SMGs drawn from a well-selected, S/N-limited SMG sample within which each SMG has been assigned a secure spectroscopic redshift. With facilities like ALMA such samples may become reality in the near future.
7. Summary and conclusions
We carried out a search for galaxy overdensities around a sample of 28 SMGs in the COSMOS field lying at redshifts of z ≃ 0.8–5.3. We searched for overdensities using the COSMOS photometric redshifts based on over 30 UV-NIR photometric measurements including the new UltraVISTA data release 2 and Spitzer/SPLASH data, and reaching an accuracy of σΔz/ (1 + z) = 0.0067 (0.0155) at z< 3.5 ( >3.5). To identify overdensities we applied the Voronoi tessellation analysis, and derived the δg redshift-space overdensity estimator. Within the search it was not required that the SMG be in the centre of the potential overdensity. The approach was tested and validated via simulations, X-ray detected groups and clusters, and spectroscopically verified overdensities, which show that even with photometric redshifts in the COSMOS field we can efficiently retrieve overdensities out to z ≈ 5. Our main conclusions, based on this analysis are summarised as follows.
-
1.
Out of 28 SMGs in our sample 15 show evidenceof associated galaxy overdensities. Separating these into ourmain SMG sample of 23 SMGs drawn from a S/N-limited,1.1 mm AzTEC/JCMT SMG sample, and ouradditional SMG sample consisting of five SMGs withspectroscopic redshifts at z = 2.49 and z> 4.5, we find evidence for 11/23 and 4/5 systems, respectively, occupying overdense environments. Considering all sources in the S/N-limited AzTEC/JCMT sample, and taking into account the percentage of spurious sources, our results suggest that 35–61% of the SMGs in the 1.1 mm S/N-limited sample occupy overdense environments. As discussed in Sect. 6.2, these percentages are likely to be lower limits, as our analysis based on photometric redshifts may have missed the less prominent overdensities.
-
2.
Performing an X-ray stacking analysis using a 32″ aperture centred at the SMG positions for our z< 2 subsample, we found an average 0.5–2 keV X-ray flux of (4.0 ± 0.8) × 10-16 erg s-1 cm-2 and a corresponding total mass of M200 = 2.8 × 1013M⊙ assuming z = 1.5, and for the z> 2 subsample an average flux of (1.3 ± 0.5) × 10-16 erg s-1 cm-2 and a corresponding total mass of M200 = 2.5 × 1013M⊙ for redshifts between 2 and 3 (M200 = 2 × 1013M⊙ assuming z = 4).
Our results suggest a higher occurrence of SMGs occupying overdense environments at z ≥ 3 than at z< 3. This may be understood if massive, highly star-forming galaxies can only be formed in the highest peaks of the density field tracing the most massive dark matter haloes at early cosmic epochs, while at later times cosmic structure may have matured sufficiently that more modest overdensities correspond to sufficiently massive haloes to form SMGs. Further theoretical and observational efforts are needed to investigate this further.
AzTEC17a, AzTEC18, and AzTEC/C159, out of which AzTEC18 has also been verified as a potentially spectroscopic overdensity (see Sect. 5).
Acknowledgments
This research was funded by the European Union’s Seventh Framework programme under grant agreement 337595 (ERC Starting Grant, “CoSMass”). A.F. wishes to acknowledge Finnish Academy award, decision 266918. This work was supported in part by the National Science Foundation under Grant No. PHYS-1066293 and the hospitality of the Aspen Center for Physics. This work is partly based on data products from observations made with ESO Telescopes at the La Silla Paranal Observatory under ESO programme ID 179.A-2005 and and 185.A-0791 and on data products produced by TERAPIX and the Cambridge Astronomy Survey Unit on behalf of the UltraVISTA consortium. This research has made use of NASA’s Astrophysics Data System, and the NASA/IPAC Infrared Science Archive, which is operated by the JPL, California Institute of Technology, under contract with the NASA. We greatfully acknowledge the contributions of the entire COSMOS collaboration consisting of more than 100 scientists. More information on the COSMOS survey is available at http://www.astro.caltech.edu/~cosmos. We thank the VUDS team for making the data in the COSMOS field available prior to public release.
References
- Aihara, H., Allen de Prieto, C., An, D., et al. 2011, ApJS, 193, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Almeida, C., Baugh, C. M., & Lacey, C. G. 2011, MNRAS, 417, 2057 [NASA ADS] [CrossRef] [Google Scholar]
- Amblard, A., Cooray, A., Serra, P., et al. 2011, Nature, 470, 510 [NASA ADS] [CrossRef] [Google Scholar]
- Aravena, M., Bertoldi, F., Carilli, C., et al. 2010, ApJ, 708, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Aretxaga, I., Wilson, G. W., Aguilar, E., et al. 2011, MNRAS, 415, 3831 [NASA ADS] [CrossRef] [Google Scholar]
- Basilakos, S., & Plionis, M. 2001, ApJ, 550, 522 [NASA ADS] [CrossRef] [Google Scholar]
- Baugh, C. M., Benson, A. J., Cole, S., et al. 1999, MNRAS, 305, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Béthermin, M., Kilbinger, M., Daddi, E., et al. 2014, A&A, 567, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertoldi, F., Carilli, C., Aravena, M., et al. 2007, ApJS, 172, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Blain, A. W., Smail, I., Ivison, R. J., Kneib, J.-P., & Frayer, D. T. 2002, Phys. Rep., 369, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Blain, A. W., Chapman, S. C., Smail, I., & Ivison, R. 2004, ApJ, 611, 725 [NASA ADS] [CrossRef] [Google Scholar]
- Blanton, M., Cen, R., Ostriker, J. P., et al. 2000, ApJ, 531, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, R. G., Benson, A. J., Malbon, R., et al. 2006, MNRAS, 370, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Capak, P., Aussel, H., Ajiki, M., et al. 2007, ApJS, 172, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Capak, P., Carilli, C. L., Lee, N., et al. 2008, ApJ, 681, L53 [Google Scholar]
- Capak, P. L., Riechers, D., Scoville, N. Z., et al. 2011, Nature, 470, 233 [Google Scholar]
- Casey, C. M., Narayanan, D., & Cooray, A. 2014, Phys. Rep., 541, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Casey, C. M., Cooray, A., Capak, P., et al. 2015, ApJ, 808, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Chapman, S. C., Lewis, G. F., Scott, D., et al. 2001, ApJ, 548, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Chapman, S. C., Blain, A., Ibata, R., et al. 2009, ApJ, 691, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Chiang, Y.-K., Overzier, R., & Gebhardt, K. 2013, ApJ, 779, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Chiang, Y.-K., Overzier, R., & Gebhardt, K. 2014, ApJ, 782, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Civano, F., Marchesi, S., Comastri, A., et al. 2016, ApJ, 819, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Coupon, J., Kilbinger, M., McCracken, H. J., et al. 2012, A&A, 542, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cowley, W. I., Lacey, C. G., Baugh, C. M., & Cole, S. 2016, MNRAS, 461, 1621 [NASA ADS] [CrossRef] [Google Scholar]
- Cucciati, O., Zamorani, G., Lemaux, B. C., et al. 2014, A&A, 570, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Daddi, E., Dannerbauer, H., Stern, D., et al. 2009, ApJ, 694, 1517 [Google Scholar]
- Dannerbauer, H., Kurk, J. D., De Breuck, C., et al. 2014, A&A, 570, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Diener, C., Lilly, S. J., Knobel, C., et al. 2013, ApJ, 765, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Diener, C., Lilly, S. J., Ledoux, C., et al. 2015, ApJ, 802, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Dirichlet, G. L. 1850, J. Reine Angew. Math., 40, 209 [CrossRef] [Google Scholar]
- Elvis, M., Civano, F., Vignali, C., et al. 2009, ApJS, 184, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Finoguenov, A., Guzzo, L., Hasinger, G., et al. 2007, ApJS, 172, 182 [Google Scholar]
- Finoguenov, A., Tanaka, M., Cooper, M., et al. 2015, A&A, 576, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fry, J. N. 1996, ApJ, 461, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Fu, H., Cooray, A., Feruglio, C., et al. 2013, Nature, 498, 338 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N. 1986, ApJ, 303, 336 [NASA ADS] [CrossRef] [Google Scholar]
- George, M. R., Leauthaud, A., Bundy, K., et al. 2011, ApJ, 742, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Gobat, R., Daddi, E., Onodera, M., et al. 2011, A&A, 526, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gobat, R., Strazzullo, V., Daddi, E., et al. 2013, ApJ, 776, 9 [NASA ADS] [CrossRef] [Google Scholar]
- González, J. E., Lacey, C. G., Baugh, C. M., & Frenk, C. S. 2011, MNRAS, 413, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Hasinger, G., Cappelluti, N., Brunner, H., et al. 2007, ApJS, 172, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Hatch, N. A., De Breuck, C., Galametz, A., et al. 2011, MNRAS, 410, 1537 [NASA ADS] [Google Scholar]
- Hickox, R. C., Wardlow, J. L., Smail, I., et al. 2012, MNRAS, 421, 284 [NASA ADS] [Google Scholar]
- Hopkins, P. F., Hernquist, L., Cox, T. J., & Keres, D. 2008, ApJS, 175, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Icke, V., & van de Weygaert, R. 1987, A&A, 184, 16 [NASA ADS] [Google Scholar]
- Ilbert, O., McCracken, H. J., Le Fèvre, O., et al. 2013, A&A, 556, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ivison, R. J., Dunlop, J. S., Smail, I., et al. 2000, ApJ, 542, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Ivison, R. J., Greve, T. R., Smail, I., et al. 2002, MNRAS, 337, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Ivison, R. J., Swinbank, A. M., Smail, I., et al. 2013, ApJ, 772, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Jelić, V., Smolčić, V., Finoguenov, A., et al. 2012, MNRAS, 423, 2753 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., Colberg, J. M., Diaferio, A., & White, S. D. M. 1999, MNRAS, 307, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, R. S. J., Kepner, J. V., Postman, M., et al. 2002, AJ, 123, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Kodama, T., Tanaka, I., Kajisawa, M., et al. 2007, MNRAS, 377, 1717 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., Smith, K. M., Dunkley, J., et al. 2011, ApJS, 192, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Koprowski, M. P., Dunlop, J. S., Michałowski, M. J., et al. 2014, MNRAS, 444, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Kovač, K., Somerville, R. S., Rhoads, J. E., et al. 2007, ApJ, 668, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Laigle, C., McCracken, H. J., Ilbert, O., et al. 2016, ApJS, 224, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Lahav, O., Lilje, P. B., Primack, J. R., & Rees, M. J. 1991, MNRAS, 251, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, D., Dunkley, J., Hinshaw, G., et al. 2011, ApJS, 192, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Le Fèvre, O., Tasca, L. A. M., Cassata, P., et al. 2015, A&A, 576, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lehmer, B. D., Alexander, D. M., Geach, J. E., et al. 2009, ApJ, 691, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Lemaux, B. C., Cucciati, O., Tasca, L. A. M., et al. 2014, A&A, 572, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lilly, S. J., Eales, S. A., Gear, W. K. P., et al. 1999, ApJ, 518, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Lilly, S. J., Le Fèvre, O., Renzini, A., et al. 2007, ApJS, 172, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Lilly, S. J., Le Brun, V., Maier, C., et al. 2009, ApJS, 184, 218 [Google Scholar]
- Lopes, P. A. A., de Carvalho, R. R., Gal, R. R., et al. 2004, AJ, 128, 1017 [NASA ADS] [CrossRef] [Google Scholar]
- Ma, C.-J., Smail, I., Swinbank, A. M., et al. 2015, ApJ, 806, 257 [NASA ADS] [CrossRef] [Google Scholar]
- McCracken, H. J., Milvang-Jensen, B., Dunlop, J., et al. 2012, A&A, 544, A156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miettinen, O., Smolčić, V., Novak, M., et al. 2015, A&A, 577, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miettinen, O., Delvecchio, I., Smolčić, V., et al. 2016, A&A, 597, A5 (Paper IV) [Google Scholar]
- Miley, G. K., Overzier, R. A., Tsvetanov, Z. I., et al. 2004, Nature, 427, 47 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Miller, T. B., Hayward, C. C., Chapman, S. C., & Behroozi, P. S. 2015, MNRAS, 452, 878 [NASA ADS] [CrossRef] [Google Scholar]
- Oke, J. B. 1974, ApJS, 27, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Oklopčić, A., Smolčić, V., Giodini, S., et al. 2010, ApJ, 713, 484 [NASA ADS] [CrossRef] [Google Scholar]
- Prescott, M. K. M., Impey, C. D., Cool, R. J., & Scoville, N. Z. 2006, ApJ, 644, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Ramella, M., Boschin, W., Fadda, D., & Nonino, M. 2001, A&A, 368, 776 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Riechers, D. A., Capak, P. L., Carilli, C. L., et al. 2010, ApJ, 720, L131 [NASA ADS] [CrossRef] [Google Scholar]
- Riechers, D. A., Bradford, C. M., Clements, D. L., et al. 2013, Nature, 496, 329 [Google Scholar]
- Riechers, D. A., Carilli, C. L., Capak, P. L., et al. 2014, ApJ, 796, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Schinnerer, E., Carilli, C. L., Capak, P., et al. 2008, ApJ, 689, L5 [Google Scholar]
- Scott, K. S., Austermann, J. E., Perera, T. A., et al. 2008, MNRAS, 385, 2225 [NASA ADS] [CrossRef] [Google Scholar]
- Simpson, J. M., Swinbank, A. M., Smail, I., et al. 2014, ApJ, 788, 125 [Google Scholar]
- Smail, I., Ivison, R. J., Gilbank, D. G., et al. 2003, ApJ, 583, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Smolčić, V., Schinnerer, E., Finoguenov, A., et al. 2007, ApJS, 172, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Smolčić, V., Aravena, M., Navarrete, F., et al. 2012a, A&A, 548, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smolčić, V., Navarrete, F., Aravena, M., et al. 2012b, ApJS, 200, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Smolčić, V., Karim, A., Miettinen, O., et al. 2015, A&A, 576, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spergel, D. N., Bean, R., Doré, O., et al. 2007, ApJS, 170, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., White, S. D. M., Jenkins, A., et al. 2005, Nature, 435, 629 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Stevens, J. A., Ivison, R. J., Dunlop, J. S., et al. 2003, Nature, 425, 264 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Tamura, Y., Kohno, K., Nakanishi, K., et al. 2009, Nature, 459, 61 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Toft, S., Smolčić, V., Magnelli, B., et al. 2014, ApJ, 782, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Toshikawa, J., Kashikawa, N., Ota, K., et al. 2012, ApJ, 750, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Trump, J. R., Impey, C. D., McCarthy, P. J., et al. 2007, ApJS, 172, 383 [NASA ADS] [CrossRef] [Google Scholar]
- van Kampen, E., Percival, W. J., Crawford, M., et al. 2005, MNRAS, 359, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Voronoi, G. 1908, J. Reine Angew. Math., 134, 198 [Google Scholar]
- Walter, F., Decarli, R., Carilli, C., et al. 2012, Nature, 486, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, T., Elbaz, D., Daddi, E., et al. 2016, ApJ, 828, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Weiß, A., Kovács, A., Coppin, K., et al. 2009, ApJ, 707, 1201 [NASA ADS] [CrossRef] [Google Scholar]
- Yoshikawa, K., Taruya, A., Jing, Y. P., & Suto, Y. 2001, ApJ, 558, 520 [NASA ADS] [CrossRef] [Google Scholar]
- Younger, J. D., Fazio, G. G., Huang, J.-S., et al. 2007, ApJ, 671, 1531 [Google Scholar]
- Younger, J. D., Fazio, G. G., Huang, J.-S., et al. 2009, ApJ, 704, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Yun, M. S., Aretxaga, I., Gurwell, M. A., et al. 2015, MNRAS, 454, 3485 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Recovering known groups and simulated proto-clusters
To test our overdensity search method, described in detail in Sect. 3.1, at z < 1.5 we apply it to positions of X-ray detected groups in the COSMOS field taken from Finoguenov et al. (2007). We retrieve every single group with high significance. This is in accordance with results from previous studies that used the VTA with photometric redshifts to recover galaxy overdensities (Smolčić et al. 2007; Oklopčić et al. 2010; Jelić et al. 2012).
To test our overdensity search method at z > 1.5 we apply it to simulated proto-clusters at z = 2, 3, 4, and 5. We generate mock catalogues of proto-clusters following the overdensity profiles of proto-cluster galaxies with stellar mass M⋆ > 109M⊙ for three present-day cluster mass bins (Mz = 0 > 1015M⊙, Mz = 0 = 3–10 × 1014M⊙, and Mz = 0 = 1.37–3 × 1014M⊙) at redshifts 2, 3, 4, and 5 adopted from Chiang et al. (2013). Chiang et al. (2013) derived these stacked profiles based on about 3000 clusters from the Millennium Simulation, whose evolution they tracked from early cosmic times till today. The number of our generated galaxies as a function of distance from the proto-cluster centre is then set by the proto-cluster profiles for a given redshift (z = 2,3,4,5; see Fig. 3 in Chiang et al. 2013). We then further scatter the galaxies in redshift space (i) assuming a line-of-sight (LOS) velocity dispersion (in the range of 200–1000 km s-1, which corresponds to Δz ≤ 0.015); and (ii) taking the COSMOS photometric redshift uncertainty into account. Both the LOS velocity and σΔz/ (1 + z) distributions are taken to be Gaussian. Such generated cluster galaxies are then superposed onto background galaxies generated such that they (i) are uniformly distributed over a 1 deg2 field (at small and large scales); and (ii) follow the photometric redshift distribution of galaxies in the COSMOS field (i+ ≤ 25.5). We generated 100 simulated proto-clusters at each redshift, z = 2,3,4, and 5, and recover these with at least ≈3σδg significance.
This validates our approach to identify overdensities using photometric redshifts in the COSMOS field, in accordance with the results from Chiang et al. (2014) who searched for proto-cluster candidates in the COSMOS field at 1.6 < z < 3.1 using photometric redshifts, and identified 36 candidate systems.
Appendix B: Overdensity search within narrower redshift bins
Here we present the results of the overdensity search performed using galaxies with photometric redshifts zphot = zSMG ± 1.5σΔz/ (1 + z)(1 + zSMG). The small-scale and large-scale overdensity search results are listed in Tables B.1, and B.2, respectively, while the combined results are listed in Table B.3.
We find 6/23 (26%) small-scale overdensities in our main SMG sample, 4/6 (67%) in our main SMG subsample with spectroscopic redshifts for our SMGs, and 2/5 (40%) in our additional SMG sample. Within our overdensity search with potentially off-centre SMGs we find 5/23 (22%), 3/6 (50%), and 3/5 (60%) overdense systems in our main SMG sample, main SMG subsample with spectroscopic redshifts assigned to the SMGs, and additional SMG sample, respectively. In total, we find 7/23 (30%), and 3/5 (60%) overdensities in our main and additional SMG samples, respectively. Taking the expected spurious percentage in the S/N-limited 1.1 mm sample the SMGs were drawn from into account this amounts to a range of 19–45% of SMGs occupying overdense systems.
Combining all overdensities identified using both redshift ranges, Δz = zSMG ± k × σΔz/ (1 + z)(1 + zSMG), where k = 1.5 and 3, then yields a total of 13/23 (56%), and 5/5 (100%) overdensities in our main and additional SMG samples, respectively. Taking the expected spurious percentage into account would imply a range of 42–68% of SMGs occupying overdensities in our S/N-limited, 1.1 mm selected SMG sample.
Small-scale overdensity search results (using Δz = zSMG ± 1.5 × σΔz/ (1 + z)(1 + zSMG)).
Large-scale overdensity search results (using Δz = zSMG ± 1.5 × σΔz/ (1 + z)(1 + zSMG)).
Overdensity search results based on small and large-scale analyses (using Δz = zSMG ± 1.5 × σΔz/ (1 + z)(1 + zSMG)).
Appendix C: Additional figures
 |
Fig. C.1 Each row corresponds to one SMG. Left panel: δg versus radius, centred at the target SMG (see Sect. 3.1.1). The errors shown are Poisson errors. The number of sources found in a circular area (Nr), and the δg = 0 line are indicated. Also indicated are the points with Poisson probability p ≤ 0.05, as listed in the legend (see Sect. 3.1.1 for details). Middle panel: Voronoi tessellation analysis (VTA; blue lines) shown around each target SMG indicated by the thick red circle. Overdense VTA cells are coloured yellow. The area and density of the cells depend on the number of galaxies in the given redshift range (Δzphot), indicated above the panel. The overdensity centre is shown by the red cross, and the radius within which it was computed is indicated by the black circle (see Sect. 3.1.2 for details). Regions outlined by grey lines and curves indicate the masked areas in the COSMOS photometric catalogue. Right panel: the top panel shows δg versus radius, centred at the overdensity (indicated by the red cross in the middle panel). The SMG’s projected distance from the centre is indicated by the red downwards pointing arrow. The horizontal line indicates the value δg = 0. The meaning of various symbols and linestyles is listed in the legend. The bottom panel shows the significance of the overdensity (δg/σδg = 0) as a function of radius. The dashed horizontal line designates the threshold beyond which the false detection probability is ≤20% (see Sect. 3.1.3 for details). |
 |
Fig. C.1 continued. |
 |
Fig. C.1 continued. |
 |
Fig. C.1 continued. |
 |
Fig. C.1 continued. |
 |
Fig. C.1 continued. |
 |
Fig. C.1 continued. |
 |
Fig. C.1 continued. |
 |
Fig. C.2 Example of spectral, often non-uniform coverage, shown for the overdensity candidate (OC) associated with AzTEC18, confirmed to also yield a spectroscopic overdensity (see text for details). The left panel shows the galaxies with secure (filled symbols) and less secure (open symbols) spectroscopic redshifts in or outside the redshift range considered (2.92 <zOC ≤ 3.08), as listed in the legend. The circles illustrate radii of r = 1′, 5′, 10′. The panels on the right show the spectroscopic redshift distribution for galaxies within 5′ (top right) and 10′ (bottom right) from the overdensity candidate with secure (filled histogram) and less secure (open histogram) spectroscopic redshifts. |
All Tables
Small-scale overdensity search results (using Δz = zSMG ± 1.5 × σΔz/ (1 + z)(1 + zSMG)).
Large-scale overdensity search results (using Δz = zSMG ± 1.5 × σΔz/ (1 + z)(1 + zSMG)).
Overdensity search results based on small and large-scale analyses (using Δz = zSMG ± 1.5 × σΔz/ (1 + z)(1 + zSMG)).
All Figures
 |
Fig. 1 Comparison between photometric (zphot) and spectroscopic (zspec) redshifts in the COSMOS field for galaxies with zphot ≤ 3.5 (left panels) and zphot> 3.5 (right panels). The top panels show a direct comparison (with the one-to-one line indicated). The bottom panels show the distribution of the difference between the spectroscopic and photometric redshifts normalised to 1 + zspec. A Gaussian fit to the distribution is shown and the number of sources, the mean, and standard deviation are indicated in the panels. |
| In the text | |
 |
Fig. C.1 Each row corresponds to one SMG. Left panel: δg versus radius, centred at the target SMG (see Sect. 3.1.1). The errors shown are Poisson errors. The number of sources found in a circular area (Nr), and the δg = 0 line are indicated. Also indicated are the points with Poisson probability p ≤ 0.05, as listed in the legend (see Sect. 3.1.1 for details). Middle panel: Voronoi tessellation analysis (VTA; blue lines) shown around each target SMG indicated by the thick red circle. Overdense VTA cells are coloured yellow. The area and density of the cells depend on the number of galaxies in the given redshift range (Δzphot), indicated above the panel. The overdensity centre is shown by the red cross, and the radius within which it was computed is indicated by the black circle (see Sect. 3.1.2 for details). Regions outlined by grey lines and curves indicate the masked areas in the COSMOS photometric catalogue. Right panel: the top panel shows δg versus radius, centred at the overdensity (indicated by the red cross in the middle panel). The SMG’s projected distance from the centre is indicated by the red downwards pointing arrow. The horizontal line indicates the value δg = 0. The meaning of various symbols and linestyles is listed in the legend. The bottom panel shows the significance of the overdensity (δg/σδg = 0) as a function of radius. The dashed horizontal line designates the threshold beyond which the false detection probability is ≤20% (see Sect. 3.1.3 for details). |
| In the text | |
 |
Fig. C.1 continued. |
| In the text | |
 |
Fig. C.1 continued. |
| In the text | |
 |
Fig. C.1 continued. |
| In the text | |
 |
Fig. C.1 continued. |
| In the text | |
 |
Fig. C.1 continued. |
| In the text | |
 |
Fig. C.1 continued. |
| In the text | |
 |
Fig. C.1 continued. |
| In the text | |
 |
Fig. C.2 Example of spectral, often non-uniform coverage, shown for the overdensity candidate (OC) associated with AzTEC18, confirmed to also yield a spectroscopic overdensity (see text for details). The left panel shows the galaxies with secure (filled symbols) and less secure (open symbols) spectroscopic redshifts in or outside the redshift range considered (2.92 <zOC ≤ 3.08), as listed in the legend. The circles illustrate radii of r = 1′, 5′, 10′. The panels on the right show the spectroscopic redshift distribution for galaxies within 5′ (top right) and 10′ (bottom right) from the overdensity candidate with secure (filled histogram) and less secure (open histogram) spectroscopic redshifts. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


