| Issue |
A&A
Volume 596, December 2016
|
|
|---|---|---|
| Article Number | L4 | |
| Number of page(s) | 7 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201629769 | |
| Published online | 30 November 2016 | |
The SHARDDS survey: First resolved image of the HD 114082 debris disk in the Lower Centaurus Crux with SPHERE ⋆
1 European Southern Observatory, Alonso de Còrdova 3107, Vitacura, Casilla 19001, Santiago, Chile
e-mail: zwahhaj@eso.org
2 Institute of Astronomy, University of Cambridge, Madingley Road, Cambridge CB3 0HA, UK
3 Steward Observatory, Department of Astronomy, University of Arizona, 933 N. Cherry Avenue, Tucson, AZ 85721, USA
4 LESIA, Observatoire de Paris, PSL Research Univ., CNRS, Sorbonne Univ., UPMC Univ. Paris 06, Univ. Paris Diderot, Sorbonne Paris Cité, 92195 Meudon, France
5 Instituto Nacional de Astrofísica, Óptica y Electrónica, Luis Enrique Erro 1, Sta. Ma. Tonantzintla, Puebla, Mexico
6 UMI-FCA, CNRS/INSU (UMI 3386), France
7 Dept. de Astronomía, Universidad de Chile, Santiago, Chile
8 Univ. Grenoble Alpes, CNRS, IPAG, 38000 Grenoble, France
9 STAR Institute, Université de Liège, 19c Allée du Six Août, 4000 Liège, Belgium
10 Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA
11 Hubble Fellow at Jet Propulsion Laboratory, Caltech, 4800 Oak Grove Drive, Pasadena, CA 91109, USA
12 Department of Physics, Nagoya University, Nagoya, Aichi 464-8602, Japan
13 Dept. of Astronomy, California Institute of Technology, 1200 E. CA Boulevard, Pasadena, CA 91125, USA
14 ALMA Santiago Central Offices, Alonso de Còrdova 3107, Vitacura, Casilla 763 0355, Santiago, Chile
Received: 21 September 2016
Accepted: 7 November 2016
We present the first resolved image of the debris disk around the 16 ± 8 Myr old star, HD 114082. The observation was made in the H-band using the SPHERE instrument. The star is at a distance of 92 ± 6 pc in the Lower Centaurus Crux association. Using a Markov chain Monte Carlo analysis, we determined that the debris is likely in the form of a dust ring with an inner edge of 27.7+2.8-3.5 au, position angle –74.3°+0.5-1.5, and an inclination with respect to the line of sight of 6.7°+3.8-0.4. The disk imaged in scattered light has a surface density that is declining with radius of ~r-4, which is steeper than expected for grain blowout by radiation pressure. We find only marginal evidence (2σ) of eccentricity and rule out planets more massive than 1.0 MJup orbiting within 1 au of the inner edge of the ring, since such a planet would have disrupted the disk. The disk has roughly the same fractional disk luminosity (Ldisk/L∗ = 3.3 × 10-3) as HR 4796 A and β Pictoris, however it was not detected by previous instrument facilities most likely because of its small angular size (radius ~0.4′′), low albedo (~0.2), and low scattering efficiency far from the star due to high scattering anisotropy. With the arrival of extreme adaptive optics systems, such as SPHERE and GPI, the morphology of smaller, fainter, and more distant debris disks are being revealed, providing clues to planet-disk interactions in young protoplanetary systems.
Key words: stars: individual: HD 114082 / techniques: high angular resolution / planetary systems
The reduced images are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/596/L4
© ESO, 2016
1. Introduction
Debris disks are dust belts produced by collisions between planetesimals orbiting stars at ages ≳10 Myr (e.g., Backman & Paresce 1993; Wyatt 2008). Since the first image of a debris disk around β Pictoris (Smith & Terrile 1984), more than 80 debris disks have been resolved at optical, infrared, and submillimeter wavelengths1 (Choquet et al. 2016). Asymmetries in these dust disks are thought to be signs of interactions with unseen bodies, possibly of planetary mass; examples include offsets of the disk with respect to the star as in the case of HR 4796 A (Wahhaj et al. 2014; Thalmann et al. 2011; Schneider et al. 2009), a warp in the disk as in the case of the β Pictoris planetary system (Lagrange et al. 2012), or multiple gaps and rings as in the case of HD 141569 (Perrot et al. 2016; Biller et al. 2015). Indeed several debris disk systems have massive planets that have been directly imaged, but the planet-disk interactions are not always well understood (e.g., HR 8799, Booth et al. 2016; Fomalhaut, Kalas et al. 2008, 2013; β Pic, Lagrange et al. 2009, 2010, 2012; HD 106906, Kalas et al. 2015; Lagrange et al. 2016). Even toy model predictions are not easy to make (e.g., Mustill & Wyatt 2009; Rodigas et al. 2014). Moreover, significant asymmetries in the form of clumps in the debris disk of AU Mic have been recently attributed to a stellar wind around the M star primary, showing that such features need not be connected to orbiting companions (Boccaletti et al. 2015).
In order to be able to discern between different effects, it is essential to understand the optical properties of different grains and their dynamical properties as an ensemble across systems of different ages and around stars of different spectral types. With this goal in mind, we are undertaking the SPHERE High Angular Resolution Debris Disk Survey (SHARDDS, VLT program 096.C-0388, PI: J. Milli) project. Using adaptive optics (AO) imaging in H-band, we targeted 55 cold debris disks with high fractional luminosity (Ldust/L∗> 10-4) but that were never resolved in scattered light. Indeed, it was unclear why highly sensitive instruments such as the Hubble Space Telescope (HST) had been unable to detect most of these debris disks. One possibility was that the excess emission originated from disks with small angular separations from their primaries where HST and first generation AO instruments provided insufficient contrasts. With the advent of an extreme adaptive optics instrument like the Spectro-Polarimetric High-contrast Exoplanet REsearch (SPHERE; Beuzit et al. 2008), the detection of such disks is within reach.
In this paper, we present the first resolved image of a compact disk around the F3V star HD 114082 at a distance of 92 ± 6 pc with an age of 16 ± 8 Myr in the Lower Centaurus Crux association (Pecaut et al. 2012). The luminosity and mass estimates for the star are 3.6 ± 0.2 L⊙ and 1.4 M⊙, respectively (Pecaut et al. 2012). Debris disks in this age range represent an interesting evolutionary stage, as they fall between the 10 Myr old TW Hya association disks (HR 4796A, etc.; Stauffer et al. 1995) and those in the 20 Myr old β Pic association (Binks & Jeffries 2014).
2. Observation
We observed HD 114082 (F3V, V = 8.2) on UT Feb. 14, 2016 in the IRDIS (Dohlen et al. 2008) classical imaging mode of SPHERE (Beuzit et al. 2008) with pupil tracking for angular difference imaging (Liu 2004; Marois et al. 2006). The SPHERE instrument is equipped with the extreme adaptive optics system SAXO (Fusco et al. 2014), which corrects atmospheric turbulence at 1.38 kHz, using a 40 × 40 lenslet Shack-Hartmann sensor and a high order deformable mirror. The IRDIS instrument has a field of view (FoV) of 11′′ × 11′′ and a pixel scale of 12.251 ± 0.005 mas (SPHERE User manual).
We acquired 152 images, each with an integration time of 16 s. The sky rotated through 16.7° with respect to the detector during this sequence. The apodized Lyot mask, N_ALC_YJH_S, with an opaque mask of diameter 185 mas was used. Images in this mode are obtained in two channels simultaneously, both in the H-band (λ = 1.625μm, Δλ = 0.29μm). Since the simultaneous images are in the same band, they are just added together. The seeing ranged from 0.6′′ to 0.7′′ and the Strehl ratio estimated by SAXO was 65% to 75%, while the wind speed varied between 1.5 and 2 m/s.
The images were flatfielded and sky subtracted in the usual way. We also acquired off-mask unsaturated images of the star, through a neutral density filter. These are used to estimate the contrast achieved with respect to the star in the rest of the field. We also acquired images with four satellite spots equidistant (400 mas) from the star, which we later used to the determine the stellar position behind the mask. This is important when derotating images around an accurate center. The spots are created by introducing sine aberrations into the deformable mirror of the SAXO system.
3. Data reduction
 |
Fig. 1 Left: MLOCI+ADI reduction using the template in Fig. A.2. Right: best-fit model to MLOCI+ADI reduction obtained using the MCMC analysis in Sect. 4. |
Basic reduction was carried out using the SPHERE data reduction pipeline (Pavlov et al. 2008) to subtract backgrounds and apply bad pixel and flat-field corrections.
Since the total sky rotation was only 16.7° we expect significant self-subtraction of any disk. Nonetheless, a principal component analysis (PCA) reduction (Soummer et al. 2011) revealed an edge-on disk extending out to ~0.5′′ from the star. As in any ADI reduction, we try to subtract the star light from the science frames, which is decoupled from any off-axis astrophysical light source that rotates. In PCA, we construct an eigenbasis of images using the science frames, and construct a reference coronagraphic image using only a few of the largest components of this image projected onto the eigenbases. This method preferentially selects star light over the varying (rotating) signal, thus subtraction of the reference image reveals the underlying off-axis astrophysical source. The difference images are then derotated and combined.
For our reduction we found that applying the PCA algorithm to images divided into annular rings of ten pixels in width, starting at five pixels from the center, gave the best results. We used only the first seven principal components to construct the reference image for subtraction. The final reduced image is shown in Fig. A.1. We see a nearly edge-on, narrow ring with a large inner hole that is clearly visible on both sides of the star. We also performed a reference difference imaging (RDI) reduction, which is described in Appendix A.
To maximize the S/N of the disk, we use the MLOCI algorithm (Wahhaj et al. 2015). Here, the star subtraction and science combination steps are performed simultaneously, while preserving a given signal region and minimizing the rms in a given background region (Fig. A.2, right panel). In the reduced image of Fig. 1, we see that the inner hole is again clearly visible and so there is a brightness asymmetry across the short axis of the ring. However, there is some self-subtraction although less severe than before.
4. Analysis
All of our reduced images suffer from artifacts of the reduction process. Although it is possible to estimate the range of disk properties by subtracting simulated disks from the data set and repeating the reduction process to statistically analyse the residuals, the process is very computationally expensive. Moreover, since two of our methods are particularly resistent to disk self-subtraction effects, methods using simulated disks are not critical. Given the complexity of the ring structure seen, we need to consider nine disk parameters, a number that is very large for a Markov chain Monte Carlo (MCMC) analysis. These model parameters are the following: (1) dust surface density, Σ0; (2, 3) offsets of the disk from the star, x and y; (4) inclination to the line of sight (LOS), φ (0° indicating a pole-on orientation); (5) position angle (PA), measured east of north; (6) inner radius of ring, rin; (7) ring width, Δr; (8) ring tail, exponent of density profile, γ; and (9) Henyey-Greenstein scattering parameter, g.
We model the dust surface density as Σ(r) = 0 for r<rin, Σ(r) = Σ0 for r = rintorin + Δr, Σ(r) = Σ0r− γ for r>rin + Δr. Here, r is the distance from the star. The contrast of the disk is modeled as f(R) /f∗ = p(θ)ωΣ(r)/ ∥ R ∥ 2, where R = r + x + y, f∗ is the flux from the star and ω is the albedo. We can only constrain the product ωΣ0 now, but we break this degeneracy by considering infrared flux measurements later. The flat density segment (from rin to rin + Δr) is included to emulate a planetesimal “birth” ring, where large grains mostly unaffected by radiation pressure maintain their orbits. Beyond this radius, the density is described by a power law to model the distribution of small grains being blown out. Anisotropic scattering is described by the Henyey-Greenstein function, p(θ) = (1−g2)/(4π(1 + g2−2gcos(θ)))3/2, where θ is the angle wrt. the LOS.
As in Wahhaj et al. (2014), we use the Metropolis Hastings measure with MCMC to generate a sampling of the nine-dimensional parameter space, which is also an estimate of the relative probability distribution for the space; see that article for details. The relative probability of a model is e− χ2/ 2, where χ2 is the usual statistic for data and model image comparisons. The model and data are compared over an ellipse (aligned with the disk) of major axis 2′′ and minor axis 0.13′′, with the central circular region of radius 0.13′′ excluded. This region includes all regions of the disk that are significantly detected and an ample background region, but excludes regions containing mostly stellar residuals. Including background regions is important for constraining the edges of the ring. In total, it covers 226 resolution elements. However, we rescale this to count only 76 independent measurements that register above a detection level of 2σ. The flux uncertainty per pixel, used to calculate χ2, is the standard deviation of intensities in the matching region, but with the disk effectively removed by a filtering process. The technique is similar to that used in Wahhaj et al. (2013), except that it removes running flux averages over 15 pixels along the radial (instead of the azimuthal) direction with the star as center. To ensure good constraints, we examined the probability distribution of models from MCMC to make sure that the probability of each parameter agrees to within 10% over two different runs. Along with the best-fit parameter values, we list the 95% confidence internal for each parameter by rejecting 2.5% of the values on both extremes of the distribution (see Table B.1). Using the contrast measurement of the disk ansae from the LOCI+RDI reduction (Appendix A), we estimate ωΣ0 = 3.28 ± 0.14 × 10-3, which sets the overall intensity scale.
The parameter estimates obtained from the fits to the different reduced images are consistent in most cases, but some have non-overlapping confidence intervals with small fractional differences in the best estimates. This is true for the ring inclination where we have a ~5% difference (81° vs. 84.9°) and the inner radius of the ring with ~12% difference (25 au versus 28.5 au). Also, the PCA reduction is insensitive to scattering anisotropy due to disk self-subtraction and so we ignore its constraints on g. We believe that the non-overlapping constraints are due to small artifacts introduced into the final images from the reduction process. Since the MLOCI reduced image yields the smallest reduced χ2 (1.5), we adopt its parameter estimates as best, while reporting the extremes of the 2σ limits from the other reductions to be conservative in our constraints.
We repeat the MCMC analysis, comparing the spectral energy distribution (SED) models to the available photometry (Table B.2) with a0 (minimum grain radius), q (grain size distribution exponent), ωΣ0 as free parameters (see Appendix C). Meanwhile, rin, γ, and Δr are allowed to vary within the extremes of the ranges permitted by the image fits (see Table B.1). For all models, the total dust mass md in grains smaller than 4 mm (see Ertel et al. 2012) is calculated assuming a density of 2300 kg/m3. The 2σ constraints found were a0 = 5.0–18 μm and q = 3.9–7.8, while Md = 0.022–0.043 M⊕. Using the previous imaging constraints on ωΣ0 with the SED constraint on (1−ω)Σ0, we find the albedo, ω = 0.13–0.24. See Fig. C.1 for the best SED model fit to the photometry. Finally, the AKARI photometry suggests that there is excess emission at 9 μm coming from warmer dust than is detected in our scattered light images. We can explain this excess with a ring extending from 3–4 au with the same surface density as the birth ring. Of course this solution is not unique.
5. Discussion and conclusions
We have presented the first resolved image of the debris disk around HD 114082, a 16 ± 8 Myr old, F3V star in the Lower Centaurus Crux association. We estimate from the MCMC analysis of this H-band image that the disk has a birth ring with uniform density of width 1.9 au, outside of which the density falls off with a power-law index of 3.9
au, outside of which the density falls off with a power-law index of 3.9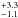 . This is the first detection of a debris disk from the SHARDDS program, which aimed to explain why some disks with estimated high fractional luminosities were not detected in scattered light.
. This is the first detection of a debris disk from the SHARDDS program, which aimed to explain why some disks with estimated high fractional luminosities were not detected in scattered light.
HD 114082 joins a family of debris ring systems that have been imaged with clear inner holes, for example, HD 181327 (Schneider et al. 2006), HD 207129 (Krist et al. 2010), HD 202628 (Krist et al. 2012), HR 4796 A (Wahhaj et al. 2014; Milli et al. 2015; Perrin et al. 2015), and HD 106906 (Kalas et al. 2015; Lagrange et al. 2016). Moreover, it is much like HR 4796 A, in that it also has significant scattering anisotropy (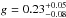 ), and has mid-sized grains (radius ~11 μm), indicating that their grain properties may be very similar. The blowout grain size due to radiation pressure is given by D = 2300 /ρ (L∗/L⊙)(M⊙/M∗)μm. The blowout size estimate for HD 114082 is thus 2.4 μm, which is much smaller than our estimated minimum grain size (~10 μm). The estimated dust density power-law index (~3.9) is much steeper than what is expected for a distribution dominated by radiation pressure blowout (1.5; Thébault & Wu 2008). The grain size power-law exponent (>3.9) is steeper than that of other debris disks but is still consistent with realistic collisional cascades (see discussion in MacGregor et al. 2016). Since the ring is relatively narrow, inner and outer shepherding planets may be necessary to maintain it. Although the disk center is not detectibly offset from the star along its apparent long axis, because of the high inclination of the disk, we can only constrain the offset along the short axis to <0.15′′. This would allow a brightness asymmetry of ~30%, accounting for the fact that the density of grains is smaller at the pericenter in a Keplerian disk (see Wahhaj et al. 2014). Thus, any such eccentricity or offset would be unable to explain the estimated brightness asymmetry factor (4 for g = 0.23) along the short axis, which in turn strengthens the scattering asymmetry claim. On the other hand, if we assume that the ~2σ level hint of an offset (~0.019′′; see Table B.1) along the long axis is real, the eccentricity would be ~0.02.
), and has mid-sized grains (radius ~11 μm), indicating that their grain properties may be very similar. The blowout grain size due to radiation pressure is given by D = 2300 /ρ (L∗/L⊙)(M⊙/M∗)μm. The blowout size estimate for HD 114082 is thus 2.4 μm, which is much smaller than our estimated minimum grain size (~10 μm). The estimated dust density power-law index (~3.9) is much steeper than what is expected for a distribution dominated by radiation pressure blowout (1.5; Thébault & Wu 2008). The grain size power-law exponent (>3.9) is steeper than that of other debris disks but is still consistent with realistic collisional cascades (see discussion in MacGregor et al. 2016). Since the ring is relatively narrow, inner and outer shepherding planets may be necessary to maintain it. Although the disk center is not detectibly offset from the star along its apparent long axis, because of the high inclination of the disk, we can only constrain the offset along the short axis to <0.15′′. This would allow a brightness asymmetry of ~30%, accounting for the fact that the density of grains is smaller at the pericenter in a Keplerian disk (see Wahhaj et al. 2014). Thus, any such eccentricity or offset would be unable to explain the estimated brightness asymmetry factor (4 for g = 0.23) along the short axis, which in turn strengthens the scattering asymmetry claim. On the other hand, if we assume that the ~2σ level hint of an offset (~0.019′′; see Table B.1) along the long axis is real, the eccentricity would be ~0.02.
The ring has a fractional width between 0.07–0.175. Consulting Eqs. (2) and (5) from Rodigas et al. (2014), we find that a putative planet interior of the disk should not be more massive than 1.0 MJup to have the desired broadening effect on the ring and should have an orbital radius of ~25 au. These constraints are more stringent that those obtained from the direct detection limits (see Appendix D).
Lastly, the non-detection of HD 114082 by past facilities despite having a large fractional infrared luminosity is likely due to three reasons: (1) a small disk radius (25–30 au) compared to other ring systems (>70 au); (2) a low albedo (~0.2); and (3) a relatively high scattering anisotropy (g ~ 0.23) that forces most of the light to be scattered behind the coronagraphic mask. Nevertheless, we expect more detections of narrow ring systems with smaller disks by extreme AO instruments like SPHERE and GPI, as such systems are predicted from dynamical analyses investigating the infrared excesses detected around young stars (Kobayashi & Löhne 2014).
The Catalog of Circumstellar Disks: http://www.circumstellardisks.org/
Acknowledgments
We would like to thank the ESO staff and the technical operators at the Paranal Observatory. O.A. is F.R.S.-FNRS Research Associate. O.A. and C.G.G. acknowledge support by the European Union through ERC grant number 337569. G.M.K. is supported by the Royal Society as a Royal Society University Research Fellow. C.B. has been supported by Mexican CONACyT research grant CB-2012-183007. E.C. acknowledges support for this work from NASA through Hubble Fellowship grant HST-HF2-51355 awarded by STScI, which is operated by the AURA, Inc., for NASA under contract NAS5-26555.
References
- Allard, F., Hauschildt, P. H., Alexander, D. R., Tamanai, A., & Schweitzer, A. 2001, ApJ, 556, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Backman, D. E., & Paresce, F. 1993, in Protostars and Planets III, eds. E. H. Levy, & J. I. Lunine, 1253 [Google Scholar]
- Backman, D. E., Witteborn, F. C., & Gillett, F. C. 1992, ApJ, 385, 670 [NASA ADS] [CrossRef] [Google Scholar]
- Beuzit, J.-L., Feldt, M., Dohlen, K., et al. 2008, in Instrumentation for Astronomy II, Proc. SPIE, 7014, 701418 [CrossRef] [Google Scholar]
- Biller, B. A., Liu, M. C., Rice, K., et al. 2015, MNRAS, 450, 4446 [NASA ADS] [CrossRef] [Google Scholar]
- Binks, A. S., & Jeffries, R. D. 2014, MNRAS, 438, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Boccaletti, A., Thalmann, C., Lagrange, A.-M., et al. 2015, Nature, 526, 230 [NASA ADS] [CrossRef] [Google Scholar]
- Booth, M., Jordán, A., Casassus, S., et al. 2016, MNRAS, 460, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, C. H., Mittal, T., Kuchner, M., et al. 2014, ApJS, 211, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Choquet, É., Perrin, M. D., Chen, C. H., et al. 2016, ApJ, 817, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, 2MASS All Sky Catalog of point sources [Google Scholar]
- Dohlen, K., Saisse, M., Origne, A., et al. 2008, in Telescopes and Instrumentation, Proc. SPIE, 7018, 701859 [CrossRef] [Google Scholar]
- Dohnanyi, J. S. 1969, J. Geophys. Res., 74, 2531 [NASA ADS] [CrossRef] [Google Scholar]
- Ertel, S., Wolf, S., Marshall, J. P., et al. 2012, A&A, 541, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fusco, T., Sauvage, J.-F., Petit, C., et al. 2014, in Adaptive Optics Systems IV, Proc. SPIE, 9148, 91481U [Google Scholar]
- Greenberg, J. M. 1979, in Infrared Astronomy, Proc. NATO Advanced Study Institute, eds. G. Setti, & G. G. Fazio, 51 [Google Scholar]
- Ishihara, D., Onaka, T., Kataza, H., et al. 2010, A&A, 514, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalas, P., Graham, J. R., Chiang, E., et al. 2008, Science, 322, 1345 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kalas, P., Graham, J. R., Fitzgerald, M. P., & Clampin, M. 2013, ApJ, 775, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Kalas, P. G., Rajan, A., Wang, J. J., et al. 2015, ApJ, 814, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Kobayashi, H., & Löhne, T. 2014, MNRAS, 442, 3266 [NASA ADS] [CrossRef] [Google Scholar]
- Krist, J. E., Stapelfeldt, K. R., Bryden, G., et al. 2010, AJ, 140, 1051 [NASA ADS] [CrossRef] [Google Scholar]
- Krist, J. E., Stapelfeldt, K. R., Bryden, G., & Plavchan, P. 2012, AJ, 144, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Lagrange, A., Gratadour, D., Chauvin, G., et al. 2009, A&A, 493, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lagrange, A.-M., Bonnefoy, M., Chauvin, G., et al. 2010, Science, 329, 57 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lagrange, A.-M., Boccaletti, A., Milli, J., Chauvin, G., & Others. 2012, A&A, 542, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lagrange, A.-M., Langlois, M., Gratton, R., et al. 2016, A&A, 586, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lieman-Sifry, J., Hughes, A. M., Carpenter, J. M., et al. 2016, ApJ, 828, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, M. C. 2004, Science, 305, 1442 [NASA ADS] [CrossRef] [Google Scholar]
- Löhne, T., Augereau, J.-C., Ertel, S., et al. 2012, A&A, 537, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- MacGregor, M. A., Wilner, D. J., Chandler, C., et al. 2016, ApJ, 823, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Marois, C., Lafrenière, D., Doyon, R., Macintosh, B., & Nadeau, D. 2006, ApJ, 641, 556 [Google Scholar]
- Milli, J., Mouillet, D., Lagrange, A.-M., et al. 2012, A&A, 545, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Milli, J., Mawet, D., Pinte, C., et al. 2015, A&A, 577, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mustill, A. J., & Wyatt, M. C. 2009, MNRAS, 399, 1403 [NASA ADS] [CrossRef] [Google Scholar]
- Pavlov, A., Feldt, M., & Henning, T. 2008, in Astronomical Data Analysis Software and Systems XVII, eds. R. W. Argyle, P. S. Bunclark, & J. R. Lewis, 394, 581 [Google Scholar]
- Pecaut, M. J., Mamajek, E. E., & Bubar, E. J. 2012, ApJ, 746, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Perrin, M. D., Duchene, G., Millar-Blanchaer, M., et al. 2015, ApJ, 799, 182 [Google Scholar]
- Perrot, C., Boccaletti, A., Pantin, E., et al. 2016, A&A, 590, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodigas, T. J., Malhotra, R., & Hinz, P. M. 2014, ApJ, 780, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, G., Silverstone, M. D., Hines, D. C., et al. 2006, ApJ, 650, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, G., Weinberger, A. J., Becklin, E. E., Debes, J. H., & Smith, B. A. 2009, AJ, 137, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, B. A., & Terrile, R. J. 1984, Science, 226, 1421 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Soummer, R., Brendan Hagan, J., Pueyo, L., et al. 2011, ApJ, 741, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Stauffer, J. R., Hartmann, L. W., & Barrado y Navascues, D. 1995, ApJ, 454, 910 [NASA ADS] [CrossRef] [Google Scholar]
- Thalmann, C., Janson, M., Buenzli, E., et al. 2011, ApJ, 743, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Thébault, P., & Wu, Y. 2008, A&A, 481, 713 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wahhaj, Z., Koerner, D. W., Backman, D. E., et al. 2005, ApJ, 618, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Wahhaj, Z., Liu, M. C., Biller, B. A., et al. 2013, ApJ, 779, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Wahhaj, Z., Liu, M. C., Biller, B. A., et al. 2014, A&A, 567, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wahhaj, Z., Cieza, L. A., Mawet, D., et al. 2015, A&A, 581, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [NASA ADS] [CrossRef] [Google Scholar]
- Wyatt. 2008, ARA&A, 46, 339 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Multiple reductions of the HD 114082 disk
 |
Fig. A.1 Left: H-band PCA Reduced image of HD 114082. A highly inclined ring with large inner hole can be clearly seen. Right: RDI+LOCI reduction of same data set. The ring does not undergo self-subtraction here, and flux levels are more reliable. |
 |
Fig. A.2 Left: MLOCI template. MLOCI works to preserve signal directly in the regions shown in white, while it tries to minimize noise in the solid blue elliptical region. Right: MLOCI+RDI reduction using the template on the left. Same as in Fig. A.1, the ring does not undergo self-subtraction and the flux levels are more reliable. |
Since the PCA reduction suffers from self-subtraction of the disk in the star subtraction process (see Milli et al. 2012), we need a higher fidelity image to confirm the ring morphology. The apparent sharpness of the image is also due to this self-subtraction effect that enhances the edges of the disk. We observed many stars without any sign of a disk in the SHARDDS program, and so we can use these as a library to construct reference images for star subtraction; this method is known as Reference Difference Imaging (RDI). The images from seven stars of similar brightness were selected for the library; these are HD 10472, HD 105, HD 377, HD 25457, HD 38207, HD 206893, and HD 69830. For each science image, we chose the most similar images from this library, by comparing the residual rms in the annular region between 15 and 50 pixels from the star, after they were scaled to minimize the residuals upon subtraction from the science image. All pixels for which the disk emission is noticeable were excluded from the match. Per science image, we selected a maximum of 60 library images, with the condition that they reduced the rms by >30%. At a minimum, we chose five of the best matches. On average, the matches reduced the rms by 38% to 55% (1σ range). For star subtraction, we used the LOCI algorithm (Lafreniere et al. 2006) to subtract the best linear combination of library (not science) images from each science image, in annular rings of 20 pixels, starting at 10 pixels separation from the star. The RDI reduced image, shown in Fig. A.1, thus has no self-subtraction of the disk. We estimate the contrast of the disk in this image using unsaturated images of the star, measuring 1.57 × 10-4 for the ring peak at the SE ansa.
We see the ring with very similar extent and morphology as in the PCA reduction, albeit with a less distinct inner hole. Although the disk is retrieved with higher fidelity, here the removal of the star is not as effective. Interestingly, we identify a new feature of the disk: over the short axis of emission, one side of the disk is noticeably brighter. This could be due to either forward or backward scattering.
We also perform an MLOCI reduction using only the library images for star subtraction (not images of the same star). We call this reduction MLOCI+RDI. The reduced image is shown in Fig. A.2. The star subtraction is much more effective and a brightness asymmetry across the short axis of the axis is seen again (see Sect. 3).
Appendix B: Constraints on debris ring properties and HD 114082 photometry
Ring parameters estimates and 2σ constraints from MCMC model comparisons.
Photometry and references.
Appendix C: Best SED model fits to HD 114082 photometry
 |
Fig. C.1 Photometry of HD 114082 showing excess flux (black dots) over the photosphere (red line). The blue solid line is the best-fit model SED corresponding to the MLOCI+ADI model in Table B.1 (disk inner radius of 27.6 au and γ = 3.9; see text for details) with a grain radius of 7.2 μm and grain size power-law index, q = 4.25. The dashed lines are the SED contributions of different grain diameters spaced evenly on a log scale (light green for 10 μm, blue for 19 μm, ..., purple for 1056 μm). |
The photometry beyond 5 μm where HD 114082 has a detectible excess flux over the photosphere is sparse. We use the available flux measurements presented in Table B.2 to constrain the dust properties of the system. The thermal emission at a particular wavelength from an annulus of infinitesimal width is modeled as
![$$f(r) = (1-\omega ) \Sigma(r) r^{-\gamma} \epsilon_{\lambda} B_{\nu}[T_p(a, r),\lambda]\left(\frac{2\pi r {\rm d}r}{D^2}\right) \rm ~Jy.$$](/articles/aa/full_html/2016/12/aa29769-16/aa29769-16-eq79.png) See Backman et al. (1992) and Wahhaj et al. (2005) for details. Here, the new parameters are ϵλ (=1.5a/λ when λ> 1.5a, but 1 otherwise; Greenberg 1979) the radiative efficiency, Bν the Planck function, a the grain radius, and D the distance to the system in parsecs. The grain temperature for moderately absorbing grains like “dirty ice” (e.g., Greenberg 1979) with radius a, is given by Tp(r) = 432(L∗/L⊙/a)0.2(r/ au)-0.4. We assume that the grain size distribution is given by n(a) da ~ a− q da and the grain radius ranges from a0 to a1(=2 mm). Here, q = 3.5 would correspond to a steady-state collisional cascade (Dohnanyi 1969). When a1 ≫ λ, the SED shape is not very sensitive to a1, since the number of large grains fall so steeply both in number and temperature. We compared our results to a quick run using the fitting tool SAnD (Ertel et al. 2012; Löhne et al. 2012) and found consistent results from this independent tool and modeling approach.
See Backman et al. (1992) and Wahhaj et al. (2005) for details. Here, the new parameters are ϵλ (=1.5a/λ when λ> 1.5a, but 1 otherwise; Greenberg 1979) the radiative efficiency, Bν the Planck function, a the grain radius, and D the distance to the system in parsecs. The grain temperature for moderately absorbing grains like “dirty ice” (e.g., Greenberg 1979) with radius a, is given by Tp(r) = 432(L∗/L⊙/a)0.2(r/ au)-0.4. We assume that the grain size distribution is given by n(a) da ~ a− q da and the grain radius ranges from a0 to a1(=2 mm). Here, q = 3.5 would correspond to a steady-state collisional cascade (Dohnanyi 1969). When a1 ≫ λ, the SED shape is not very sensitive to a1, since the number of large grains fall so steeply both in number and temperature. We compared our results to a quick run using the fitting tool SAnD (Ertel et al. 2012; Löhne et al. 2012) and found consistent results from this independent tool and modeling approach.
Appendix D: Detection limits on planetary companions
There are many point sources (>20) detected in the IRDIS field of view (11′′ × 11′′), but given that this is a dense stellar field and that the candidate separations are large (~45 au), they are very likely background stars. Follow-up observations will confirm or reject these as gravitationally bound companions by testing for common proper motion. The 5σ contrast from the PCA reduction was ΔH = 9.0 mag at 0.25′′ separation and 12.4 mag at 0.5′′ separation. According to the AMES-COND models (Allard et al. 2001), these detection limits correspond to 38 MJup and 16 MJup at 0.25 and 0.5′′ (or 23 au and 46 au), respectively. These limits are much less stringent than the limits we obtain from dynamical constraints considering the strength of companion and disk interaction (see Appendix A).
All Tables
All Figures
 |
Fig. 1 Left: MLOCI+ADI reduction using the template in Fig. A.2. Right: best-fit model to MLOCI+ADI reduction obtained using the MCMC analysis in Sect. 4. |
| In the text | |
 |
Fig. A.1 Left: H-band PCA Reduced image of HD 114082. A highly inclined ring with large inner hole can be clearly seen. Right: RDI+LOCI reduction of same data set. The ring does not undergo self-subtraction here, and flux levels are more reliable. |
| In the text | |
 |
Fig. A.2 Left: MLOCI template. MLOCI works to preserve signal directly in the regions shown in white, while it tries to minimize noise in the solid blue elliptical region. Right: MLOCI+RDI reduction using the template on the left. Same as in Fig. A.1, the ring does not undergo self-subtraction and the flux levels are more reliable. |
| In the text | |
 |
Fig. C.1 Photometry of HD 114082 showing excess flux (black dots) over the photosphere (red line). The blue solid line is the best-fit model SED corresponding to the MLOCI+ADI model in Table B.1 (disk inner radius of 27.6 au and γ = 3.9; see text for details) with a grain radius of 7.2 μm and grain size power-law index, q = 4.25. The dashed lines are the SED contributions of different grain diameters spaced evenly on a log scale (light green for 10 μm, blue for 19 μm, ..., purple for 1056 μm). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


