| Issue |
A&A
Volume 596, December 2016
|
|
|---|---|---|
| Article Number | A9 | |
| Number of page(s) | 5 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201629567 | |
| Published online | 21 November 2016 | |
Constraints on the size and dynamics of the J1407b ring system
1 RIKEN Advanced Institute for Computational Science, 7-1-26 Minatojima-minami-machi, Chuo-ku, Kobe, 650-0047 Hyogo, Japan
2 Sterrewacht Leiden, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
e-mail: steven@rieder.nl
Received: 22 August 2016
Accepted: 28 September 2016
Context. J1407 (1SWASP J140747.93-394542.6 in full) is a young star in the Scorpius-Centaurus OB association that underwent a series of complex eclipses over 56 days in 2007. To explain these, it was hypothesised that a secondary substellar companion, J1407b, has a giant ring system filling a large fraction of the Hill sphere, causing the eclipses. Observations have not successfully detected J1407b, but do rule out circular orbits for the companion around the primary star.
Aims. We test to what degree the ring model of J1407b could survive in an eccentric orbit required to fit the observations.
Methods. We run N-body simulations under the AMUSE framework to test the stability of Hill radius-filling systems where the companion is on an eccentric orbit.
Results. We strongly rule out prograde ring systems and find that a secondary of 60 to 100 MJup with an 11 yr orbital period and retrograde orbiting material can survive for at least 104 orbits and produce eclipses with similar durations as the observed one.
Key words: planets and satellites: dynamical evolution and stability - planets and satellites: rings
© ESO, 2016
1. Introduction
Giant planet formation consists of the transfer of material from the circumstellar environment to the circumplanetary environment. The change in angular momentum of the circumstellar material results in the formation of a disk of gas and dust surrounding the protoplanet (Ward & Canup 2010; Alibert et al. 2005). In our Solar system, the primordial gas is no longer present, but evidence of the circumplanetary disk exists in the form of coplanar moons and rings (e.g. see review by Tiscareno 2013). All Solar system gas giant ring systems show structure. This structure consists of gaps in the rings themselves and sudden changes of particle density as a function of radius from the planet.
The K5 pre-MS 16 Myr-old star J1407 showed a complex series of eclipses in 2007, lasting a total of 56 days, and a series of papers investigating the J1407 system (Mamajek et al. 2012; Van Werkhoven et al. 2014; Kenworthy et al. 2015; Kenworthy & Mamajek 2015) conclude that there is a secondary substellar companion (called J1407b) with a giant multi-ring system in orbit around the primary star. The ring system shows detailed structure down to the temporal resolution set by the diameter of the primary star and their mutual relative projected velocity. A study of the stability of a Hill sphere-filling system on a circular orbit has been explored in Zanazzi & Lai (2016). The derived diameter of the ring system combined with the observational limits set on the companion J1407b (as described in Van Werkhoven et al. 2014; Kenworthy et al. 2015) imply that J1407b is on an eccentric orbit about J1407.
In this paper we investigate the effects of an elliptical orbit on the stability of the ring system surrounding J1407b. Our goal is to determine whether there are any bound orbital solutions for the secondary companion that can explain both the derived relative velocity and the duration of the eclipse seen towards J1407.
To this end, we construct a model containing J1407, its companion J1407b and a co-planar disc around J1407b; based on the model in Kenworthy & Mamajek (2015). In Sect. 2, we describe this model and the parameters we investigate in this article. We run simulations of this model using AMUSE1 (Pelupessy et al. 2013; Portegies Zwart et al. 2013) with the Rebound/WHFast2 (Rein & Liu 2012; Rein & Tamayo 2015) N-body integrator. We give the resulting disc sizes and eclipse durations in Sect. 3 and discuss our results and the consequences in Sect. 4.
2. Description of the J1407b ring models
To investigate how the extent of a ring system around J1407b would change over time, we create a model consisting of J1407, companion J1407b on an eccentric orbit around J1407 and a disc of N particles around J1407b, initially in either prograde or retrograde circular orbits. Since the height to diameter ratio of the J1407b exorings is <0.01 (Mamajek et al. 2012), we limit our model to be co-planar with the secondary’s orbit.
For the orbital parameters of J1407b, we choose values based on the best fits found by Kenworthy et al. (2015). For all models, we choose a period of 11 yr, resulting in a semi-major axis a of 5.0 ± 0.1 AU, and a mass M of J1407 of 1.0 M⊙. We set the J1407b mass m to values between 20 and 100 MJup in steps of 20 MJup, as Kenworthy et al. (2015, Fig. 15) constrained the mass of J1407b for elliptic orbits to be up to 100 MJup.
We assume that the eclipse was observed at or very near its pericentre, since the orbital velocity is highest at this point and J1407b would likely have been detected if the long axis of the orbit were not aligned to the line of sight (Kenworthy et al. 2015).
The pericentric velocity of the system is 32 ± 2 km s-1 (Kenworthy et al. 2015, Fig. 11). This velocity is inferred from the stellar radius and the steepest gradient in the light curve, with the second-steepest gradient resulting in a velocity of 18 km s-1. To account for these velocities, while also investigating a slightly less extreme case, we choose values between 0.6 and 0.7 for the eccentricity e. This results in pericentric velocities between 27 and 33 km s-1 and pericentric distances between 1.5 and 2.0 AU. In Fig. 1 we show the orbit of model B80 as an example. We summarise the selected values in Table 1.
Orbital parameters of J1407b used for the different models.
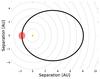 |
Fig. 1 Orbit of J1407b model B80, with J1407b located at pericentre. The J1407b system (red) is shown to scale for the initial size of the model. The size of the star (orange) is exaggerated by a factor 20. Grey circles indicate the distance to the star in AU, while the black ellipse shows the orbit. |
We initially place particles on equidistant rings, with equal distance between particles in each ring. We choose the number of particles in the nth ring to be 1 + 6n. To prevent artificially created rings, we then change the radial distance of each particle by a random value drawn evenly between ±0.5 × ΔR (with ΔR the distance between rings). We create 50 rings, scaling the system so that the outer ring is initially at the Hill radius of the system calculated at the companion’s pericentre (Eq. (1) Hamilton & Burns 1992). This results in initial radii ranging from 0.29 AU (for model C-20) to 0.66 AU (for model A-100). 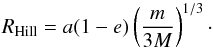 (1)Since the star’s influence is smallest for the innermost orbits, we limit the inner radius to 0.25 × RHill. This eliminates the first 12 rings of particles, while a significant fraction of orbits within the Hill radius is covered. As the timestep of our simulation scales with the orbital period of the particles, this also speeds up our simulation. The total number of disc particles in each of our models is N = 6992.
(1)Since the star’s influence is smallest for the innermost orbits, we limit the inner radius to 0.25 × RHill. This eliminates the first 12 rings of particles, while a significant fraction of orbits within the Hill radius is covered. As the timestep of our simulation scales with the orbital period of the particles, this also speeds up our simulation. The total number of disc particles in each of our models is N = 6992.
In this article, we limit ourselves to investigating the extent to which a disc can survive, while the creation and evolution of ring structure is left to future study. Since the mass of the disc is negligible compared to the secondary’s mass, we ignore the internal dynamics of the disc and make the disc particles massless, speeding up the calculations. At the start of each simulation, the secondary is at apastron, where the star’s initial influence on the system is minimal. We then run each model twice, once with prograde and once with retrograde orbiting particles.
As the simulation progresses, we remove all particles beyond 2 AU from the secondary; well beyond the Hill radius. We then calculate the eclipse duration at pericentre from the most distant particle on both sides of the star-secondary axis (dmin and dmax) and the secondary’s velocity relative to the star at that moment (vperi) (Eq. (2)). 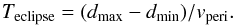 (2)
(2)
3. Size of the system
We simulate 105 yr (~9090 orbits of the secondary) of orbital evolution of the system, and compare the initial distribution of particles to their final distribution, noting the radius within which particles remain bound to the companion.
In Fig. 2, we plot the particle density of model B80, which has an initial radius of 0.53 AU. In the left panel, we show the system at initialisation; with black, red and blue particles representing particles that are unbound, bound in the retrograde case only and bound in the prograde case, respectively. In the middle and right panels we illustrate the same system after 105 yr of evolution for the retrograde and prograde case, respectively, using red for the retrograde case and blue for the prograde case.
 |
Fig. 2 Particle distributions for model B80, initial configuration (left, at apocentre) and after 105 yr for the retrograde (middle) and prograde (right) cases, respectively; both at pericentre. In the initial configuration; black, red and blue particles represent particles that are stripped, bound in only the retrograde case and bound in the prograde case, respectively. |
We find that prograde disc systems are severely disrupted, losing all particles initially further out than 0.45 ± 0.01 RHill within a few passages; whereas retrograde systems are stable out to much larger radii, gradually losing all particles with an initial radius over 0.64 ± 0.04 RHill. This is in agreement with classical results from e.g. Toomre & Toomre (1972), who studied similar interactions on a galaxy scale, and Morais & Giuppone (2012), who studied 3-body systems on planetary scale.
We also find that the initially circular ring particles become increasingly eccentric due to the periodic forcing of the companion’s eccentric orbit and periastron passage (in a similar manner as the effect described by Thébault et al. 2006). This initially leads to spiral patterns in the distribution of particles, which wind up, and are difficult to detect after more than a few hundred orbits.
The radius after 105 yr, measured along the axis perpendicular to the star-secondary axis, is 0.75 ± 0.04 × RHill and 0.46 ± 0.02 × RHill for retrograde and prograde systems, respectively. We use these values to plot the theoretical eclipse duration for all systems with an eccentricity between 0.59 and 0.71 and a companion mass between 10 and 110 MJup in Fig. 3.
 |
Fig. 3 Theoretical eclipse duration for retrograde (left) and prograde (right) systems, based on the size obtained from our simulations. Lines indicate equal eclipse durations (given in days), dashed lines are plotted for 56 ± 4 days. The positions of our models are indicated with squares. |
 |
Fig. 4 Evolution of the eclipse duration at pericentre for the simulation models. The hashed blue region indicates the observed duration of 56 ± 4 days, while the hashed turquoise region indicates the observed velocity of 32 ± 2 km s-1. The upper models with the longer eclipse duration are the retrograde models, the lower models are the prograde ones. The colour bar indicates the age of the model in log 10-scale: lightest is after 3000 yr, while darkest is after 105 yr. |
In Fig. 4, we show the evolution of the eclipse duration for each of our models at pericentre between 3000 and 105 yr, combined with the expected values from the observations. While the prograde systems only show a small change in eclipse duration during this time, the change in the retrograde systems is much larger, with the eclipse duration shortening by about 10 days.
The eclipse durations are up to ~40 days for prograde models. These models can therefore not explain the 56 day duration of the J1407b eclipse. These models would require either a much more massive companion or a much less eccentric orbit to work as a solution (Eq. (1)). Since a less eccentric orbit would result in a lower transverse velocity, this would be inconsistent with the derived velocity of 32 ± 2 km s-1 from Kenworthy et al. (2015). Similarly, Kenworthy et al. (2015) restricts the mass of J1407b to be <100 MJup at 3σ. As a result, any stable prograde orbit would be inconsistent with the observed and derived orbital parameters of J1407b.
In contrast, the eclipse lasts up to ~80 days for some of the retrograde models. In particular the highest-mass B models can have eclipses that last long enough, while still being within the margin of error for the derived velocity. If the system formed recently, lower values for the companion’s mass or orbits with higher eccentricity may also provide a solution in agreement with the observations. We therefore conclude that a giant ring system as proposed in Mamajek et al. (2012) can be a dynamically stable solution, but only if the rings are on a retrograde orbit, for relatively large masses of J1407b.
4. Results and discussion
4.1. Results from the simulations
Our main results from the simulations can be summarised as follows:
Retrograde ring systems can exist for at least 105 yr and produce eclipses that last 56 days in duration with a projected velocity consistent with that seen in the observational data (see Fig. 4). No prograde ring systems are large enough to explain the duration of the eclipse, since the outer rings are scattered within one or two orbits of the companion. Retrograde ring systems are typically 1.4 times the size of prograde ring systems, consistent with similar results from other simulations (Toomre & Toomre 1972; Morais & Giuppone 2012).
We constrain the mass of the secondary companion to be larger than the mass of 20 MJup expected by Kenworthy et al. (2015), closer to 100 MJup for the longest transit durations.
Initially circular particle orbits in the retrograde disc systems become eccentric over time. As a result, particles starting within the stable radius may be stripped. When the orbits change from circular to more eccentric, spiral patterns are seen in the distribution of particles, but these disappear over time.
4.2. Discussion
Lifetime of rings
We simulate a disc of circumsecondary material for a period of 105 yr. On this timescale, the discs shrink from RHill to 0.46 RHill and 0.75 RHill for pro- and retrograde orbits, respectively. For prograde orbits, this process is quick (within several orbits), whereas retrograde orbits shrink more gradually.
Since the system is significantly larger than its Roche limit (which is on the order of 0.001 AU for a Moon-like object), satellites may form in the disc. This is supported by the observed gaps in the eclipse (Kenworthy & Mamajek 2015). The timescale on which such satellites would form may help constrain the age of the ring system around J1407b.
Our simulations assume no new material is added to the system. However, on a timescale of 105 yr, we consider it likely to be replenished by material from a variety of sources, as J1407 is a young and dynamically active system (see Sect. 4.2 for a discussion of possible replenishment sources). The longer disruption timescale of retrograde systems would allow them to keep their size for a longer time in this case, while the disruption timescale for prograde systems is too short.
Retrograde rings
One of the strongest results out of our simulations is the implication that the rings are in retrograde motion. The additional stability of retrograde ring solutions over the equivalent prograde ring solutions is to the point that we can rule out all prograde ring solutions from being consistent with the observations. Explaining how a retrograde ring system in an highly eccentric orbit around a young star came to be contributes additional complexity to the giant exoring model presented in Kenworthy et al. (2015).
Two of the eight planets in our Solar system show evidence of giant impacts that resulted in high planetary inclinations with respect to the Ecliptic. In these cases, both the rings and planet have a large enough obliquity so that both planet and rings are retrograde. It is possible that such a collision between two rocky bodies in orbit around a planet results in a significant amount of retrograde moving material in the Hill sphere of J1407b, resulting in the rings we see today. Given that the height to diameter ratio of the J1407b exorings is <0.01 (Mamajek et al. 2012) and that there is radial structure at all spatial scales, the system is dynamically cold and any such retrograde generating event must have happened a dynamically long time ago.
Replenishment of rings
The ring lifetime may be boosted beyond that seen in our simulations via a process of replenishment of the rings. For debris disks, a collisional cascade from a reservoir of large bodies generates micron sized material that is seen in reflected light observations (Backman & Paresce 1993; Dent et al. 2000).
Processes that generate additional dust and ice in the J1407b Hill sphere may well include the tidal disruption of bodies that are captured by the gravity of J1407b, as suggested for the ice rings of Saturn (Canup 2010) and as seen in our own solar system when comets are tidally disrupted and captured by Jupiter, for example the tidal disruption of the comet Shoemaker-Levy 9 in July 1992 (Sekanina et al. 1994) that resulted in a string of icy cores surrounded by a dust cloud.
The presence of large numbers of comets in young planetary systems has been seen towards the beta Pictoris system (Ferlet et al. 1987; Lagrange-Henri et al. 1988, 1989; Kiefer et al. 2014) and those seen in transit towards KIC 8462852 (Boyajian et al. 2016).
Two possible tests for this hypothesis are (i) to carry out transmission spectroscopy of the ring system during the next eclipse and determine the age of the rings by looking for recently ground up material; and (ii) to see if the generated and disrupted dust is observed at thermal and longer wavelengths and at radii larger than the Hill sphere.
Uncertainty dominated by radius of star
The relative velocity of the star and ring system is derived from the gradient of the light curve measured towards J1407 (see Eq. (11) in Van Werkhoven et al. 2014),
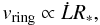 where the star is observed to change brightness at a maximum rate of approximately 3 L∗ day-1. The diameter of the ring system is simply vringTeclipse and relative velocity of the ring system is directly proportional to the radius of the star, and our greatest uncertainty in the size of the giant ring system is dominated by the uncertainty of the stellar size (Kenworthy et al. 2015).
where the star is observed to change brightness at a maximum rate of approximately 3 L∗ day-1. The diameter of the ring system is simply vringTeclipse and relative velocity of the ring system is directly proportional to the radius of the star, and our greatest uncertainty in the size of the giant ring system is dominated by the uncertainty of the stellar size (Kenworthy et al. 2015).
There is no direct measurement of the radius of the star, and it will not be resolvable using ground-based interferometers in the forseeable future, so we use the luminosity and effective temperature from stellar evolution models to derive the radius of the star. Additional constraints are set by rotational broadening of spectral absorption lines measured using CORALIE (Kenworthy et al. 2015), imposing a radius of R∗> 0.93 ± 0.02 R⊙. If the assumed radius of the star is smaller than stellar models predict, then the relative velocity and diameter of the ring system become smaller. This also decreases the derived eccentricity of the orbit of J1407b, easing the dynamical problem we face in this paper.
Non-azimuthal structures in the rings
An alternative explanation is that there is additional internal structure in the ring system that is non-azimuthally symmetric. The vector addition of J1407b’s orbital motion with the orbital motion of ring material can explain the high relative velocity, discussed in Van Werkhoven et al. (2014). As shown by our simulations, non-radial structures develop during periastron passage on dynamically short timescales that are comparable to the duration of the transit.
5. Conclusions
We have performed simulations that consist of a companion on an eccentric orbit consistent with the most probable orbital parameters as detailed in Kenworthy et al. (2015). A disk composed of particles initially orbiting the secondary in circular orbits out to the Hill radius are added and the simulation is run for 105 yr. The particles are run in both a prograde orbital sense and a retrograde sense. As expected, the prograde ring system loses a significant portion of its mass in a few orbits, and we do not find a stable prograde ring system consistent with the observed orbital parameters and eclipse duration. For the retrograde ring system, we find it retains a larger fraction of its mass out to larger radii, and for the proposed orbital parameters of J1407b, a disk size and orbital velocity consistent with observations is seen.
Circumplanetary disks are expected to be prograde with respect to the circumstellar disks they formed in. With a retrograde ring system, the question is raised as to how it came into existence. Uranus has a tilt of 98 degrees, with an associated ring system, but no consensus of how it ended up with this obliquity. Early theories suggested a single giant impactor caused the planet to tilt over (Safronov 1966), and possibly disrupt an initially circular orbit into the elliptical one we hypothesise. More recently, Morbidelli et al. (2012) show that a single impactor leads to retrograde motions in the rings and moons, and that a series of smaller impacts can preserve the orbital motion of the rings.
There is precedence for planets with retrograde orbits beyond our Solar system. Extrasolar planets have been detected with their orbital axes inclined by more than 90 degrees with respect to their star’s rotation axis (e.g. WASP-17b; Anderson et al. 2010). An interaction with a third companion in the system through the Kozai mechanism (Kozai 1962) is thought to provide the mechanism in these cases. The hypothesized third companion may still be within the J1407 system, but a deep direct imaging search with Keck reveals no candidates within 400 AU greater than 6 MJup (Kenworthy et al. 2015). An alternative explanation is that the third companion was ejected out of the system and is a free floating object. Evidence of strong gravitational scattering may be present in the distribution of dust within the J1407 system, and observations at sub-mm wavelengths with telescopes such as ALMA may provide additional information. One way to discriminate between these two hypotheses is to measure the planet’s obliquity and determine if it is greater than 90 deg, but this is not possible to test with current instruments. Spectroscopic measurements during the next eclipse, however, can reveal the orbital direction of the rings with respect to the rotation axis of the star and confirm the retrograde ring hypothesis.
Acknowledgments
We are grateful to Nathan de Vries, Lucie Jílková, Masaki Iwasawa, Erin L. Ryan and Eric Mamajek for many useful discussions, suggestions and comments that helped shape this work. We would also like to acknowledge the anonymous referee, whose comments helped improve this article. Finally, we are grateful to David Mikolas for alerting us to an inconsistency in an earlier version of this article.
References
- Alibert, Y., Mordasini, C., Benz, W., & Winisdoerffer, C. 2005, A&A, 434, 343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anderson, D. R., Hellier, C., Gillon, M., et al. 2010, ApJ, 709, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Backman, D. E., & Paresce, F. 1993, in Protostars and Planets III, eds. E. H. Levy, & J. I. Lunine, 1253 [Google Scholar]
- Boyajian, T. S., LaCourse, D. M., Rappaport, S. A., et al. 2016, MNRAS, 457, 3988 [NASA ADS] [CrossRef] [Google Scholar]
- Dent, W. R. F., Walker, H. J., Holland, W. S., & Greaves, J. S. 2000, MNRAS, 314, 702 [NASA ADS] [CrossRef] [Google Scholar]
- Ferlet, R., Vidal-Madjar, A., & Hobbs, L. M. 1987, A&A, 185, 267 [NASA ADS] [Google Scholar]
- Hamilton, D. P., & Burns, J. A. 1992, Icarus, 96, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Kenworthy, M. A., & Mamajek, E. E. 2015, ApJ, 800, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Kenworthy, M. A., Lacour, S., Kraus, A., et al. 2015, MNRAS, 446, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Kiefer, F., Lecavelier des Etangs, A., Boissier, J., et al. 2014, Nature, 514, 462 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kozai, Y. 1962, AJ, 67, 591 [Google Scholar]
- Lagrange-Henri, A. M., Vidal-Madjar, A., & Ferlet, R. 1988, A&A, 190, 275 [NASA ADS] [Google Scholar]
- Lagrange-Henri, A. M., Beust, H., Ferlet, R., & Vidal-Madjar, A. 1989, A&A, 215, L5 [NASA ADS] [Google Scholar]
- Mamajek, E. E., Quillen, A. C., Pecaut, M. J., et al. 2012, AJ, 143, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Morais, M. H. M., & Giuppone, C. A. 2012, MNRAS, 424, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Morbidelli, A., Tsiganis, K., Batygin, K., Crida, A., & Gomes, R. 2012, Icarus, 219, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Pelupessy, F. I., van Elteren, A., de Vries, N., et al. 2013, A&A, 557, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Portegies Zwart, S., McMillan, S. L. W., van Elteren, E., Pelupessy, I., & de Vries, N. 2013, Comp. Phys. Comm., 183, 456 [NASA ADS] [CrossRef] [Google Scholar]
- Rein, H., & Liu, S.-F. 2012, A&A, 537, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rein, H., & Tamayo, D. 2015, MNRAS, 452, 376 [NASA ADS] [CrossRef] [Google Scholar]
- Safronov, V. S. 1966, Soviet Ast., 9, 987 [NASA ADS] [Google Scholar]
- Sekanina, Z., Chodas, P. W., & Yeomans, D. K. 1994, A&A, 289, 607 [NASA ADS] [Google Scholar]
- Thébault, P., Marzari, F., & Scholl, H. 2006, Icarus, 183, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Tiscareno, M. S. 2013, Planetary Rings, eds. T. D. Oswalt, L. M. French, & P. Kalas, 309 [Google Scholar]
- Toomre, A., & Toomre, J. 1972, ApJ, 178, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Van Werkhoven, T. I. M., Kenworthy, M. A., & Mamajek, E. E. 2014, MNRAS, 441, 2845 [NASA ADS] [CrossRef] [Google Scholar]
- Ward, W. R., & Canup, R. M. 2010, AJ, 140, 1168 [NASA ADS] [CrossRef] [Google Scholar]
- Zanazzi, J. J., & Lai, D. 2016, MNRAS, in press, [arXiv:1605.02365] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Orbit of J1407b model B80, with J1407b located at pericentre. The J1407b system (red) is shown to scale for the initial size of the model. The size of the star (orange) is exaggerated by a factor 20. Grey circles indicate the distance to the star in AU, while the black ellipse shows the orbit. |
| In the text | |
 |
Fig. 2 Particle distributions for model B80, initial configuration (left, at apocentre) and after 105 yr for the retrograde (middle) and prograde (right) cases, respectively; both at pericentre. In the initial configuration; black, red and blue particles represent particles that are stripped, bound in only the retrograde case and bound in the prograde case, respectively. |
| In the text | |
 |
Fig. 3 Theoretical eclipse duration for retrograde (left) and prograde (right) systems, based on the size obtained from our simulations. Lines indicate equal eclipse durations (given in days), dashed lines are plotted for 56 ± 4 days. The positions of our models are indicated with squares. |
| In the text | |
 |
Fig. 4 Evolution of the eclipse duration at pericentre for the simulation models. The hashed blue region indicates the observed duration of 56 ± 4 days, while the hashed turquoise region indicates the observed velocity of 32 ± 2 km s-1. The upper models with the longer eclipse duration are the retrograde models, the lower models are the prograde ones. The colour bar indicates the age of the model in log 10-scale: lightest is after 3000 yr, while darkest is after 105 yr. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


