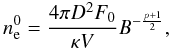| Issue |
A&A
Volume 596, December 2016
|
|
|---|---|---|
| Article Number | A30 | |
| Number of page(s) | 9 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201526825 | |
| Published online | 25 November 2016 | |
Gamma-ray emission from galaxy cluster outskirts versus radio relics
Astronomical Observatory, Jagiellonian University, ul. Orla 171, 30–244 Kraków, Poland
e-mail: grazyna@oa.uj.edu.pl; zdzislaw.golda@uj.edu.pl
Received: 24 June 2015
Accepted: 21 July 2016
Context. Galaxy cluster peripheries provide important information on the nature of ICM/IGM linkage. In this paper we consider potential future observations in the gamma-ray domain at cluster edges involving the radio relic phenomenon.
Aims. We focus on the spectral signature of gamma radiation that should be evident in the energy range of Fermi-LAT, i.e. ≳10-1 GeV and the CTA energy range ~102 GeV. The spectral signature results from a comparable gamma-ray flux due to the IC and π0 decay on the edge of the cluster, and its spectral position is a function of the magnetic field and relative efficiency of the acceleration of protons and electrons. We aim to draw attention to the dependence of the gamma-ray structure on the magnetic field value.
Methods. As an example, we carried out analyses of two types of non-thermal diffuse radio emission: the radio relic of A 2256 and the radio halo of Coma cluster. We suggest that in both cases the expected spatially correlated gamma-ray spectrum should have a characteristic structure that depends on the strength of the local magnetic field. In both of the clusters we calculated the combined flux of gamma radiation from the actual observational values of the used observables.
Results. The revealed spectral dependence on the magnetic field would allow us to relate the future spectral observations, in particular the position of the gamma-ray signature, to the value of the magnetic field in the border area between galaxy clusters and their connecting filaments, possibly constraining the estimated relative efficiency of particle acceleration at the edge of the cluster.
Key words: galaxies: clusters: intracluster medium / radiation mechanisms: non-thermal / gamma rays: galaxies: clusters
© ESO, 2016
1. Introduction
Clusters of galaxies are excellent laboratories for studying plasma physical processes. Combining cluster medium observables from the radio to gamma-ray domains enables us to probe the characteristics of intracluster plasma. The intracluster medium (ICM) is of interest for a number of reasons. With respect to the cosmological aspect, the most important things to understand concern the cluster formation and their subsequent evolution.
First, the important point here is the role of centrally located black holes and the processes underlying specific heating and cooling of nuclear regions of clusters. Second, the baryonic matter deficit in galaxy clusters is another issue to be debated. In practice, it reduces to the search for baryonic matter vestiges at the cluster outskirts in the form of cooler gas of the warm-hot intergalactic medium (WHIM). Third, the dynamic state of baryons in galaxy clusters and connecting filaments is in turn associated with the shock waves and accompanying turbulences occurring there. The role of these phenomena in the modelling of intergalactic cluster media is one of the motivations for studying shocks.
The main astrophysical motivation is to explain the whole variety of non-thermal and the thermal processes occurring at different spatial scales of clusters in both central regions, where the interaction of active galactic nucleus with the cluster medium is of primary importance, and other places, particularly at the periphery, with conditions favouring multi-frequency emissions.
We expect that the above interrelated approaches will finally yield a coherent picture of the ICM. This will allow us to answer the following key questions concerning the baryon fraction of clusters, which could be used as an estimator of the average baryon value for the Universe and to address other primordial problems: what causes the non-thermal high-energy cluster emission in the radio and hard X-ray (HXR) domains? What is the origin of the large-scale magnetic field and its long-standing evolution, and, particularly, its coupling to cosmic-ray (CR) physics, i.e. particle diffusion and transport (viscosity, conduction)? What is our understanding of the role and properties of turbulences within the ICM?
The presence of relativistic particles in the ICM manifests itself as diffuse radio emission in the form of cluster radio halos and relics. Natural tools for the study of these phenomena are synchrotron diagnostics as well as X-ray and, perhaps soon, gamma analyses.
The peripheral cluster regions in the context of the above questions have a particular significance. On the one hand, investigating cluster outskirts is very important because we can see a connection of clusters with the cosmic web via accretion of gas and subclusters, thus providing a viable cosmological probe. On the other hand, in these outer regions, closer to the sources of accretion from filaments, it is in a sense easier to study the physical properties of the ICM (e.g. non-thermal interactions), since they are much less complex than the central regions.
Recently, several informative observations have been made at cluster peripheries. The baryon content in outer regions has been estimated through Sunyaev-Zel’dovich effect and X-ray observations (e.g. Afshordi et al. 2007). For a number of galaxy clusters, measurements of intracluster gas temperature and entropy profiles, along with profiles of gas density, gas fraction, and mass, out to large radii, have also been performed (e.g. Reiprich et al. 2009; George et al. 2009; Sato et al. 2012) based on Suzaku data.
Signatures of giant shock waves seen as radio relics and arising from cluster mergers were discovered in the last years (e.g. Bagchi et al. 2006; van Weeren et al. 2011, 2010). The recent discovery of large-scale diffuse, non-thermal radio emission in PLCK G287.0+32.9 (Bagchi et al. 2011), which was confirmed by the Planck satellite in an all-sky blind search for new clusters through the Sunyaev-Zel’dovich effect, reveals a pair of giant (>1 Mpc) arcs-shaped peripheral radio relics.
These relic sources constitute unique signs of energetic mergers and shocks and a probe of the filamentary cosmic-web structure beyond the cluster virial radius. Although currently there is not too much other observational evidence about physical properties within cluster outskirts, numerical simulations tend to describe at least the thermodynamic state of the gas. They predict numerous shocks in the large-scale structure and are eventually able to reproduce the radio luminosity features through analysing the parameters of the merger shocks during their evolution.
In this paper, we focus on the external cluster features, i.e. locations of radio relics. Below we present the reasons behind our supposition that these radio-emitting, extended boundary areas should also show a certain brightness in gamma emission within the same timescale as radio emission. Then we are going to show that the spectral characteristics of emission depends on the strengths of peripheral magnetic fields in clusters.
In the frame of the model of radio relics adopted in the literature, we present in Sect. 2 the arguments in favour of the possibility of the occurrence of external gamma emission that is spatially correlated with the relic; in Sect. 3, we briefly discuss the mechanisms underlying production of gamma rays. In Sect. 4, we present the expected gamma-ray spectra for two well-known and analysed cases of galaxy clusters.
2. What we can see and what we expect to see at the edges of clusters
The extended radio emission regions that can be observed at the edges of many clusters (Hoeft & Brüggen 2007; Skillman et al. 2011; van Weeren et al. 2013; Bonafede et al. 2012), commonly referred to as relics, are associated with the recently shock-accelerated electrons. The origin of these boundary relativistic electrons is accounted for by the DSA acceleration mechanism in a moving forwards merger shock, which in many clusters can give spectral predictions that are consistent with the observed distribution of radio spectral index across the relic width (e.g. A 3667).
Below we consider a hypothesis that within the relic extent we can also expect an enhanced gamma emission. Therefore, first we present a possible origin of these gamma-ray, ring-like structures at the edges of clusters.
2 1. How do the main observables characterizing the relic area behave?
Very little is known to date about magnetic field properties in the cluster outskirts. However the mean magnetic field spatial profiles presented in the literature, which are beta-modelled and volume-weighted via synchrotron emission, (see e.g. Arieli et al. 2011) show a decrease of magnetic field strength within the virial radius of more than 2 orders of magnitude. This radial magnetic field distribution roughly agrees with the spatial distribution of the field inferred from RM measurements of a statistical sample of galaxy clusters (Clarke et al. 2001).
Also (Donnert et al. 2009, 2010) successfully fitted the predicted rotation measure signal of galaxy clusters to the observations. Their magnetic field profiles are in good agreement with the recent findings, showing that the radial magnetic field decline conforms to the density profile.
Energy density spatial profiles of the gas and CR in the ICM were recently discussed in the framework of large-scale cosmological shock simulations (e.g. Vazza et al. 2012; Burns et al. 2010); these profiles were also compared with the new observations of Suzaku, out to rvir ≈ r200 (Walker et al. 2012). The value r200 is the virial radius of a spherically collapsed cluster with a virial density ≈200 times the critical density of the Universe.The inconsistency of these profiles with the hydrostatic equilibrium assumption in the outer cluster regions suggests that the ICM pressure does not come solely from the thermal energy density at r ≈ rvir.
Also the underestimates (up to 30%) of galaxy cluster masses, which increase with r, can indicate the presence of greater amount of gas in the outskirts than it is predicted by an ordinary β model. This can result either from gas or subcluster accretion along the filaments entering clusters in these regions, such as from the existence of connections with the cosmic web, but also, in the case of an advanced outgoing merger, from the compressed post-shock gas. For both cases, the hydrostatic equilibrium assumption becomes invalid at the outskirts of clusters (Sato et al. 2012).
Several papers dealing with galaxy cluster merger simulations reveal the final radial profiles of various quantities, as compared to the initial radial profiles. This includes not only the plasma density and temperature profiles but also the velocity and entropy maps. In the latter case, the final profiles exhibit a large increase in entropy in the cluster outskirts, which can indicate the dissipative processes at work there, presumably associated with the strengthening of the shock.
The same trend is confirmed in radio profiles of gas density and in the temperature and entropy profiles recently presented in the paper of Vazza et al. (2012), including CR physics (CR injection, feedback, and acceleration efficiency).
The effects of CR input are particularly evident in the advanced phase of merging systems, where pressure of freshly injected CR’s at peripheral position can be comparable with the thermal pressure. The role of CR physics can be crucial in interpreting the recent Suzaku observation of a galaxy cluster close to r200 and beyond (Bautz et al. 2009; Simionescu et al. 2011) and in predicting their future non-thermal observations at larger radii.
The statements above and, in particular, the recent results concerning the dynamical role of CR in cluster outer regions makes us expect a diffusive gamma-ray emission in the same region, i.e. close to r200.
On the basis of all the mentioned observational indicators, we assume the following:
-
1.
The relic radio features are mainly generated through interiorforwards-propagating shocks associated with cluster mergers.This hypothesis is supported by simulations(e.g. Skillmanet al. 2011), which show thatalmost every cluster displays signs of radio relics at some stage ofits evolution, being highly dependent on the merger, the radioemission of which is associated with the merger shockparameters. However, the radio emission decreases when theICM overdensity value drops below ≈10 ÷ 30, which disfavours the possibility of attributing the relic feature to the accretion shock alone. Therefore we postulate here that the region located exactly between the outwards-going shock (≲rvir) and the accretion shock racc should be expected to show the multi-frequency, non-thermal emission, such as radio, gamma, and HXR. This also means that the relic feature is related to and dependent both on the merger and accretion shocks’ properties.
-
2.
An approaching merger shock together with a long-living accretion shock form a so-called double shock structure (Fig. 1), which provides for larger efficiencies both in injection and CR acceleration. When pre-shock gas density is slightly higher, which is the case in a forwarding shock, then the density of accelerated CRs is enhanced. The more considerable gas density at larger radii is due to adiabatic compression interior to accretion shock. This does not contradict that the ratio vsh/vsound still increases radially when approaching the outer region, in spite of gas redistribution due to the passage of the shock, which is obviously equivalent to a Mach number(M = vsh/vsound)increase of the merger shock. Apart from the increasing power of forwarding shock, in the vicinity of accretion shock we expect the presence of the older population, such as preexisting CRs, which also increases the acceleration efficiency for moderate M (Hong et al. 2014; Kang et al. 2012). Thus between the merger and the exterior strong accretion shock, the effective, i.e. combined, acceleration efficiency, must be enhanced and so is the flux of CRs accumulated between both shocks. Such a double shock structure has been previously discussed (Siemieniec-Ozieblo & Ostrowski 2000) in the context of UHECR acceleration in large-scale structures, showing a significant amplification of acceleration efficiency. The main consequence of accelerated particle confinement in two such converging flows is a hardening of the spectral index owing to inefficient particle escape from the acceleration region and, thus, to the diffusion enhancement between the shocks (see details in Siemieniec-Ozieblo & Ostrowski 2000). The exact formalism describing development of this double shock model in the current context will be presented in the next paper, which will include the analysis of diffusion of particles between two shocks: a forwarding merger shock and a stationary accretion shock.
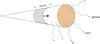 |
Fig. 1 Outline of the considered region of radio relic in between the outgoing merger shock and accretion shock for galaxy clusters. |
2 2. Do gamma-ray relics exist at the cluster outskirts?
Although no gamma-ray emission from the clusters observed by Fermi-LAT (e.g. Ackermann et al. 2010) has been detected to date, it is still expected to occur within the observationally established constraints. The (spatial profiles of) expected morphology and the spectrum of gamma-ray emission should depend on the relative contribution of two gamma-ray mechanisms dominant at the cluster outskirts. In the photon energy range, where the gamma-ray emission would have the maximal flux, i.e. 10-2 ÷ 102 GeV, both relativistic protons and primary electrons (via IC) should equally reveal their presence (see e.g. Fig. 1 in Pinzke & Pfrommer 2010).
Primary CR electrons contribute to an irregularly elongated relic feature seen in radio, HXR, and possibly in gamma-ray domains, due to synchrotron and inverse Compton (IC) processes. The timescales of these processes are relatively short for the electrons and typical magnetic field of the relic: tradio:synch + IC ~ 108 y, tHXR:IC ~ 107 ÷ 8 y; while tgamma:IC ~ 107 y.
The long-living gamma-ray emission that results from CR protons interacting with thermal gas protons is expected to be a dominant component everywhere but in the peripheral regions of the merging cluster, where it can have a value that is comparable to the primary IC emission. The maximum energy attainable by protons (E ~ 1019 eV) is determined by the time of the propagating merger shock, which is τshock ≈ 109 y.
All the above timescales can suggest that the relic sources can be treated as a sort of transient “flares” accompanied by X-ray, gamma, and radio emissions (Fig. 1).This simply means that the higher frequency used to observe the IC emission within the relic, the shorter the high-energy phenomenon to be found there corresponding to the shorter cooling time.
As one can see from Fig. 1, the possibility of observing a hypothetical gamma emission strongly depends on the direction of merger propagation. The most favourable case is the merger shock propagating close to the line of sight. It is obvious that its face-on geometry increases the detectability of relic radiation.
3. Gamma-ray spectral properties
In this paper we consider two instances of such sources: the cluster A 2256 and the Coma cluster as a reference case; the relic associated with the former is caused by a shock moving approximately along the line of sight. In this example, the modelled spectral index for the relic is very flat, suggesting that we observe the advanced phase of merger, in which the radio emission comes from freshly and efficiently accelerated electrons within the narrow volume around the shock.
In the case of A 2256, we have already proposed a coherent model consistently explaining the radio and HXR emissions (Siemieniec-Ozieblo & Pasternak 2011). One can find there some predictions concerning the gamma emission owing to π0-decay. The resulting gamma-ray flux estimated for the A 2256 relic is by 2 ÷ 3 orders of magnitude smaller than in the case of the halo of the Coma cluster. Now, we additionally calculate the primary IC component since at the cluster outskirts it should equally contribute to the gamma emission. Moreover, we expect that in the energy range covered by Fermi, the gamma-ray spectrum can show a specific concave structure in the relic location. This feature would result from comparable IC and π0-decay emissions in the energy range close to the π0 bump.
Potentially, the same characteristic could be produced on both sides of the π0 bump, i.e. also for E ≥ 10 GeV. Although we focus here on the energy regime accessible to the Fermi-LAT observations, one has to mention that an equally interesting domain with respect to both IC and pion-generated photons is expected at the CTA energy range, i.e. above a few tens of GeV. However, the observational verification of the expected structure at such a high-energy range significantly depends on the IC spectral index and thus it is distinctly visible only for flat spectra; cf. Fig. 2. In the energy range E ≥ 10 GeV, the location of the feature is extremely sensitive to the energy spectrum. As one can see in Fig. 2, the relative change of spectral index 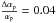 corresponds to ΔEcross of the order of 3 × 103 GeV in the CTA range.Another crucial assumption concerns the maximum energy of IC photons reaching the TeV range (e.g. Miniati 2003; Kushnir & Waxman 2009), which is connected with the uncertainty of maximum energy to which CR electrons can be accelerated in the double shock considered. We estimate the maximum energy of primary electrons in a standard way, i.e. by comparing the acceleration time, τacc (τacc ∝ γeB-1) with the cooling time due to IC and synchrotron processes tcool. This allows us to derive the maximal value of Lorentz factor for electrons
corresponds to ΔEcross of the order of 3 × 103 GeV in the CTA range.Another crucial assumption concerns the maximum energy of IC photons reaching the TeV range (e.g. Miniati 2003; Kushnir & Waxman 2009), which is connected with the uncertainty of maximum energy to which CR electrons can be accelerated in the double shock considered. We estimate the maximum energy of primary electrons in a standard way, i.e. by comparing the acceleration time, τacc (τacc ∝ γeB-1) with the cooling time due to IC and synchrotron processes tcool. This allows us to derive the maximal value of Lorentz factor for electrons 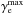 , which constrains the energy break in electron spectrum
, which constrains the energy break in electron spectrum 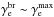 . The outskirt cluster region covered by the merger shock approaching the accretion shock, in which the acceleration occurs, is characterized by strong turbulence. Accordingly, we expect the effective Bohm diffusion assumption to be valid there. Ultimately, this results in a value of
. The outskirt cluster region covered by the merger shock approaching the accretion shock, in which the acceleration occurs, is characterized by strong turbulence. Accordingly, we expect the effective Bohm diffusion assumption to be valid there. Ultimately, this results in a value of 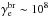 for a magnetic field B ~ 0.1 μG (
for a magnetic field B ~ 0.1 μG (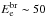 TeV), corresponding to the photon break energy
TeV), corresponding to the photon break energy 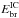 of ~1 TeV.
of ~1 TeV.
 |
Fig. 2 Comparison of Ecross dispersion for two slightly different spectral indices αp, for the IC and π0 fluxes in a wider energy range. |
The observed X-ray synchrotron emission in young supernova remnants (e.g. Vink et al. 2006) and the optical radiation in certain hotspots of radiogalaxies (e.g. Brunetti et al. 2003) can support an interpretation based on the existence of unbroken electron spectra in the extended energy range. We presume that the conditions for efficient particle acceleration are achieved in peripheral radio relics because of the double shock, which allows us to expect such extensive electron spectra with a synchrotron turnover corresponding to 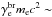 few TeV. Since the synchrotron emission from monoenergetic electrons with γe peaks around
few TeV. Since the synchrotron emission from monoenergetic electrons with γe peaks around 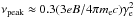 , then for electrons within the energy range ~
, then for electrons within the energy range ~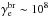 it corresponds to the break frequency νbr, peak ~ few 1015 Hz (for B ~ 0.1 μG), whose emission is beyond the observational limit. Therefore we assume that for observed peripheral relics with straight spectra, this trend continues up to the frequency νbr,peak. For the sake of illustration and to present a very approximate synchrotron flux estimation for Coma-like relics, we extrapolate the radio spectrum of a relic in Coma (cf. Fig. 1 in Atoyan & Völk 2000; Thierbach et al. 2003). The synchrotron emission generated by electrons with maximal energies (γe ~ 108) yields the value of flux, νsynFsyn, of ~108 Jy Hz; for this very rough estimation we took the radio spectral index ~1. These electrons, which are responsible for the non-observable synchrotron emission in the EUV range, scatter the relic photons to the energy range of ~1 TeV. For the magnetic field B ~ 0.1μG, the expected flux of IC emission νγFγ roughly falls within the range (1010 ÷ 1011) Jy Hz, which is consistent with the expectation delineated in Fig. 2.
it corresponds to the break frequency νbr, peak ~ few 1015 Hz (for B ~ 0.1 μG), whose emission is beyond the observational limit. Therefore we assume that for observed peripheral relics with straight spectra, this trend continues up to the frequency νbr,peak. For the sake of illustration and to present a very approximate synchrotron flux estimation for Coma-like relics, we extrapolate the radio spectrum of a relic in Coma (cf. Fig. 1 in Atoyan & Völk 2000; Thierbach et al. 2003). The synchrotron emission generated by electrons with maximal energies (γe ~ 108) yields the value of flux, νsynFsyn, of ~108 Jy Hz; for this very rough estimation we took the radio spectral index ~1. These electrons, which are responsible for the non-observable synchrotron emission in the EUV range, scatter the relic photons to the energy range of ~1 TeV. For the magnetic field B ~ 0.1μG, the expected flux of IC emission νγFγ roughly falls within the range (1010 ÷ 1011) Jy Hz, which is consistent with the expectation delineated in Fig. 2.
In discussing the gamma-ray spectra below, we consider the energy range limited by E ≤ 10 GeV. At the same time we emphasize that the expected shape of the concave spectrum is due to the physical reasons described above as follows:
-
very efficient injection of relativistic protons, which are alwaysexpected to be around in this region;
-
their efficient reacceleration due to a double shock; and
-
ρgas strengthened by a forwarding shock; numerical simulations predict gas clumping (Vazza et al. 2012, 2013; Eckert et al. 2013).
The possibility of gamma-ray spectral signature for E ≥ 100 MeV, and the factors controlling this effect are the subject of a follow-up analysis. The parameters presumably playing a major role in shaping the spectrum are: the value of the magnetic field, and the relative acceleration efficiency of protons to electrons in the considered region.
Below we concentrate primarily on the dependence of the gamma-ray spectral structure on the magnetic field.
First, we stress the energy ranges and timescales required in the radio relic model. For the Lorentz factors of electrons of 3 × 103 ÷ 107, the cooling time via IC is 109 y and 105 y, and the average energies obtained by microwave photons are ≈103 ÷ 1010 eV, respectively.
We limit ourselves to comparing gamma-ray emissions produced by two processes occurring in the location of radio relic at an edge of galaxy cluster and within the halo volume of another cluster owing to IC radiation of primary electrons and to π0 decay coming from pp interaction.
We expect that for a certain energy value E, the two fluxes will be comparable, and thus within the cooling timescales for electrons, the gamma radiation spectrum should reveal the structure (a sort of intermittent phenomena), indicating the presence of both types of relativistic particle populations.
The gamma-ray flux produced by interaction of CR protons with ambient relic/halo nuclei is given by 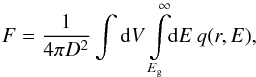 (1)where V is the relic volume and D is the luminosity distance. To calculate the value of gamma-ray emissivity from π0 decay, we used the formalism given in Pfrommer & Ensslin (2004), where
(1)where V is the relic volume and D is the luminosity distance. To calculate the value of gamma-ray emissivity from π0 decay, we used the formalism given in Pfrommer & Ensslin (2004), where ![\begin{eqnarray} q_{\pi^0}(r,E)&=&\sigma_{\rm pp}c\,n_{\rm N}(r)\;\xi^{2-\alpha_\gamma}\frac{n_{\rm p}(r)}{\rm GeV}\frac{4}{3\alpha_\gamma} \left(\frac{m_{\pi^0}c^2}{\rm GeV}\right)^{-\alpha_\gamma} \nonumber\\ &&~~\times\left[\left(\frac{2E}{m_{\pi^0}c^2}^{}\right)^{\delta\gamma}+\left(\frac{2E}{m_{\pi^0}c^2}\right)^{-\delta\gamma}\right]^{\alpha_\gamma/\delta\gamma}\cdot \label{eq:02} \end{eqnarray}](/articles/aa/full_html/2016/12/aa26825-15/aa26825-15-eq73.png) (2)Here αγ = αp = αe−1 is γ-ray spectrum index,
(2)Here αγ = αp = αe−1 is γ-ray spectrum index, 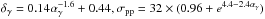 mbarn, mπ0c2/ 2 ≅ 67.5 MeV, ξ = 2, nN(r) = nth(r)/(1−0.5XHe)(XHe = 0.24), where nth(r) is the thermal electron density and np(r) is rescaled number density of CR protons (cf. Eq. (8) Pfrommer & Ensslin 2004) expressed by nth,αp,Xp.
mbarn, mπ0c2/ 2 ≅ 67.5 MeV, ξ = 2, nN(r) = nth(r)/(1−0.5XHe)(XHe = 0.24), where nth(r) is the thermal electron density and np(r) is rescaled number density of CR protons (cf. Eq. (8) Pfrommer & Ensslin 2004) expressed by nth,αp,Xp.
The contribution to the gamma-ray flux coming from IC-scattered photons on primary electrons expressed by emissivity qIC is given as ![\begin{eqnarray} q_{\rm IC}(r,E)&=&\left[\frac{m_{\rm e}c^2}{\rm GeV}\right]^{1-p}\!n_{\rm e}(r)\:\frac{8\pi^2r_{\rm e}^2}{h^3c^2}\:F(p)(kT)^2 \left[\frac{E}{kT}\right]^{\frac{-p+1}{2}}, \label{eq:03} \end{eqnarray}](/articles/aa/full_html/2016/12/aa26825-15/aa26825-15-eq85.png) (3)where
(3)where ![\begin{equation} F(p)=2^{p+3}\frac{p^2+4p+11}{(p+3)^2(p+5)(p+1)}\Gamma\left[\frac{p+5}{2}\right]\xi\left[\frac{p+5}{2}\right] \label{eq:04} \end{equation}](/articles/aa/full_html/2016/12/aa26825-15/aa26825-15-eq86.png) (4)and
(4)and 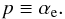 (5)The density ne(r), of CR electrons is often expressed by
(5)The density ne(r), of CR electrons is often expressed by 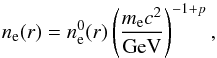 (6)which is related to the electron energy distribution in two equivalent notations as follows:
(6)which is related to the electron energy distribution in two equivalent notations as follows: 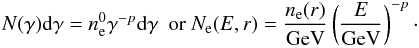 (7)These electrons are scattered off the CMB photons in the blackbody temperature T = 2.7 K. The analysis of gamma-ray spectrum, which is the combination of both processes, reduces to following up the competition of these mechanisms, which in turn appears to depend on the ratio K0 = ne/np. This quantity is in general not constrained by cosmic plasma physics and is often assumed as a constant. Nevertheless, its value is critical for the qπ/qIC ratio and, in general, changes with energy. Because of the CRe energy losses, the number density ratio K0 decreases with particle energy. In a zero-order approximation, if K0(E) = const. were valid, one could ask at what energy the both emissivities are comparable. Thus, a comparison of both processes with the assumed fixed values of index p and nth in qπ/qIC ∝ nthK0f(E) could lead to the possibility of estimating the relation K0(Ecross), see Fig. 3, and next allow us to evaluate the relative acceleration efficiency of electrons and protons. However, at energies around 1 GeV such an approach is not valid, as the electron losses through the IC process are significant here (energy distributions for e and p are not “parallel”) and thus K0 = K0(E) ≠ const. (e.g. Beck & Krause 2005). Therefore, below we concentrate on the input observables that are constrained by observational radio data and their implicit dependence on magnetic field B. To do this, we adopt any necessary radio observables from the literature data for the examined cluster. Thus, in the further, ne, np, nth and the proton spectral indices are taken according to the analysed cluster case (referring to Reimer et al. 2004; or Siemieniec-Ozieblo & Pasternak 2011, respectively). The procedure consists in attaching the values of variables resulting from the radio observation to the emissivities to reduce the number of parameters, i.e. the apparently high degree of degeneracy of the total gamma-ray flux.
(7)These electrons are scattered off the CMB photons in the blackbody temperature T = 2.7 K. The analysis of gamma-ray spectrum, which is the combination of both processes, reduces to following up the competition of these mechanisms, which in turn appears to depend on the ratio K0 = ne/np. This quantity is in general not constrained by cosmic plasma physics and is often assumed as a constant. Nevertheless, its value is critical for the qπ/qIC ratio and, in general, changes with energy. Because of the CRe energy losses, the number density ratio K0 decreases with particle energy. In a zero-order approximation, if K0(E) = const. were valid, one could ask at what energy the both emissivities are comparable. Thus, a comparison of both processes with the assumed fixed values of index p and nth in qπ/qIC ∝ nthK0f(E) could lead to the possibility of estimating the relation K0(Ecross), see Fig. 3, and next allow us to evaluate the relative acceleration efficiency of electrons and protons. However, at energies around 1 GeV such an approach is not valid, as the electron losses through the IC process are significant here (energy distributions for e and p are not “parallel”) and thus K0 = K0(E) ≠ const. (e.g. Beck & Krause 2005). Therefore, below we concentrate on the input observables that are constrained by observational radio data and their implicit dependence on magnetic field B. To do this, we adopt any necessary radio observables from the literature data for the examined cluster. Thus, in the further, ne, np, nth and the proton spectral indices are taken according to the analysed cluster case (referring to Reimer et al. 2004; or Siemieniec-Ozieblo & Pasternak 2011, respectively). The procedure consists in attaching the values of variables resulting from the radio observation to the emissivities to reduce the number of parameters, i.e. the apparently high degree of degeneracy of the total gamma-ray flux.
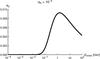 |
Fig. 3 Values of K0 as a function of Ecross, i.e. energy at which qπ flux is equal to qIC flux. |
4. Two examples of a putative gamma spectrum and its dependence on the magnetic field
The purpose of this analysis is to show that for both radio halo and radio relics in the galaxy clusters, a new (intermittent) feature is expected to appear in the gamma-ray spectrum in MeV energy range of Fermi-LAT observations. We also suppose that the energy at which this signature occurs is correlated with the value of the magnetic field (corresponding to the place where the emission comes from) via the relation of gamma-ray flux versus magnetic field. This relationship is by no means evident from the above formulae. The field B affects the value of gamma-ray flux via ne and/or nth. In the first case, B can be regarded as a link in modelling the observed synchrotron radiation F = F0(ne(B))ν− α, permitting agreement between the adopted model of radio emissivity and the observables that involve B. While nth can be associated with B through the magnetic field simulation to consistently match its spatial profile with RM observations, e.g. Bonafede et al. (2010, discussed below). Observational confirmation of this effect would be of particular importance for estimating the value of intergalactic magnetic field. This new method would be especially useful in the case of radio relics, which occur mostly at the edges of clusters. To illustrate this effect, we consider the expected gamma-ray spectra for the two cases well known in the literature, i.e. the radio halo of Coma cluster and the relic of A 2256 cluster.
For the Coma cluster, the basic observables concerning relativistic electrons (ne,αe) come from radio observations (Thierbach et al. 2003) while another observational quantity, X-ray emissivity, allows us to roughly estimate the density of thermal particles, nth ~ 10-3 cm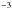 . This value corresponds to the thermal energy density uth ≅ 3.8 × 10-11 erg cm-3. Following Pinzke & Pfrommer (2010), we take the electron spectral index αe = 3.6, which correctly reproduces the radio flux density
. This value corresponds to the thermal energy density uth ≅ 3.8 × 10-11 erg cm-3. Following Pinzke & Pfrommer (2010), we take the electron spectral index αe = 3.6, which correctly reproduces the radio flux density 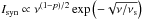 and νs = 0.44 GHz from Thierbach et al. (2003). The hypothetical magnetic field value B ~ 0.1 ÷ 1μG fits well within the range that allows us to reproduce the observed radio flux of synchrotron radiation. The above quantities can be used to calculate the expected value of qIC, according to the value of B. For the qπ0 ∝ np × nth, the CRe index is known, and thus (assuming a common acceleration mechanism) the spectral index of protons is also known. Then to eliminate np, instead of the parameter K0, we use the parameter X = np/nth (i.e. a rescaled version of Xp = ϵp/uth). Given that the proton injection to acceleration area depends highly on gas density, we assume that X ~ const. Furthermore, in the cluster outskirts we can perceive its high value as a result of a relatively high-energy content in CRp relative to nth (see e.g. Brunetti & Jones 2014).
and νs = 0.44 GHz from Thierbach et al. (2003). The hypothetical magnetic field value B ~ 0.1 ÷ 1μG fits well within the range that allows us to reproduce the observed radio flux of synchrotron radiation. The above quantities can be used to calculate the expected value of qIC, according to the value of B. For the qπ0 ∝ np × nth, the CRe index is known, and thus (assuming a common acceleration mechanism) the spectral index of protons is also known. Then to eliminate np, instead of the parameter K0, we use the parameter X = np/nth (i.e. a rescaled version of Xp = ϵp/uth). Given that the proton injection to acceleration area depends highly on gas density, we assume that X ~ const. Furthermore, in the cluster outskirts we can perceive its high value as a result of a relatively high-energy content in CRp relative to nth (see e.g. Brunetti & Jones 2014).
Thus taking the hadronic spectral index αp = 2.5 and the postulated ratio of number density of protons to the thermal gas Xp = 0.28 (for the sake of comparison with the results of Reimer et al. 2004) allows us first to calculate the needed density of np and ne and then to compute the emissivity of both processes supposed to produce gamma radiation. According to Eqs. (1)–(3), the total gamma-ray flux for different values of the magnetic field is shown in Fig. 4, which, together with Figs. 5 and 6, visualize how the spectral structure changes with decreasing thermal density. Despite the dominant role of the IC process in the energy range 10-4 ÷ 10-2 GeV, this spectral signature still is visible for the B fields <1 μG. The value of energy, Ecross at which both the gamma fluxes, i.e. for IC and π0 processes are comparable, changes with magnetic field B and density of thermal medium nth variations in the ICM.
 |
Fig. 4 Expected gamma-ray spectrum for thermal plasma density, nth = 10-4 cm |
The Ecross value decreases with increasing value of nth and with the value of B as well, while the flux Fν(Ecross) value increases with nth (Fig. 7). It should be noted that these two variables, i.e. B and nth, both depending on r, are not be treated as independent quantities. They usually scale according to the phenomenological formula 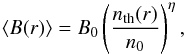 (8)where η ∈ (0.1 ÷ 1) and n0 = 3.4 × 10-3 cm
(8)where η ∈ (0.1 ÷ 1) and n0 = 3.4 × 10-3 cm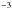 . Theoretically, the above relationship originates from the conservation law for magnetic flux during the gravitational collapse of a magnetized structure, when nth ~ Ba. However for the frozen-in magnetic field compression required by the power-law relation with plasma density, the average field B strongly depends on multiple parameterizations. The most important variables are related to compression symmetry and magnetic field amplification processes of different kinds during the cluster evolution. They play a significant role at the cluster outskirts because of constant accretion and mergers. Thus accepting the phenomenological approach by applying the above scaling relation, while it imposes some uncertainty, seems to be the only reliable way to interrelate these variables. The choice of right values of η and B0 is usually carried out by correlating the different observables (e.g. RM versus X-ray brightness); see for example Donnert et al. (2010) and Bonafede et al. (2012). To illustrate how to remove the degeneracy between nth and B, we take, following Donnert et al. (2010), η ~ 1 (Fig. 8). The value of energy at which the considered structure appears now depends only on the value of nth, which is a function of radial position of the examined region. This position can therefore be assumed to be the very place of structure occurrence that is associated with both nth and B. This seems to be very advantageous for clusters because the detector spread function at ~1 GeV range is typically of the order of the cluster size. On the other hand, the knowledge of Ecross value gives us a chance to estimate the value of magnetic field B, provided the scaling law for a given cluster is properly established. In general, by adopting such a scaling procedure between the cluster thermal density and its magnetic field, we can infer the following relation from the analysed requirement:
. Theoretically, the above relationship originates from the conservation law for magnetic flux during the gravitational collapse of a magnetized structure, when nth ~ Ba. However for the frozen-in magnetic field compression required by the power-law relation with plasma density, the average field B strongly depends on multiple parameterizations. The most important variables are related to compression symmetry and magnetic field amplification processes of different kinds during the cluster evolution. They play a significant role at the cluster outskirts because of constant accretion and mergers. Thus accepting the phenomenological approach by applying the above scaling relation, while it imposes some uncertainty, seems to be the only reliable way to interrelate these variables. The choice of right values of η and B0 is usually carried out by correlating the different observables (e.g. RM versus X-ray brightness); see for example Donnert et al. (2010) and Bonafede et al. (2012). To illustrate how to remove the degeneracy between nth and B, we take, following Donnert et al. (2010), η ~ 1 (Fig. 8). The value of energy at which the considered structure appears now depends only on the value of nth, which is a function of radial position of the examined region. This position can therefore be assumed to be the very place of structure occurrence that is associated with both nth and B. This seems to be very advantageous for clusters because the detector spread function at ~1 GeV range is typically of the order of the cluster size. On the other hand, the knowledge of Ecross value gives us a chance to estimate the value of magnetic field B, provided the scaling law for a given cluster is properly established. In general, by adopting such a scaling procedure between the cluster thermal density and its magnetic field, we can infer the following relation from the analysed requirement:
and finally 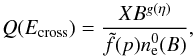 (11)where g(η),
(11)where g(η), 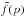 and f(p) are the following functions of η and index p, respectively:
and f(p) are the following functions of η and index p, respectively:
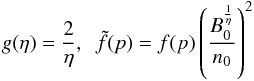 and
and ![\begin{eqnarray} f(p)&=&\frac{A}{C} \frac{(p-1)F(p){\cal B}(\frac{p-3}{2},\frac{4-p}{2})\left[\frac{E_{\rm cross}}{kT}\right]^\frac{1-p}{2}} {(p-2)\xi^{3-p}\left[\frac{m_{\pi^0}c^2}{{\rm GeV}}\right]^{-\alpha_\gamma}} \nonumber \\ &&\times \left[\left(\frac{2E}{m_{\pi^0}c^2}^{}\right)^{\delta\gamma}+\left(\frac{2E}{m_{\pi^0}c^2}\right)^{-\delta\gamma} \right]^{-{\alpha_\gamma}/{\delta_\gamma}},\nonumber \end{eqnarray}](/articles/aa/full_html/2016/12/aa26825-15/aa26825-15-eq147.png) where ℬ it is the beta function,
where ℬ it is the beta function,
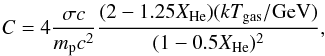 αγ = p−1,
αγ = p−1, 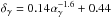 and F(p) is given by Eq. (4).
and F(p) is given by Eq. (4).
 |
Fig. 7 Total gamma-ray fluxes for different thermal plasma densities shown for the field strength B = 2 μG. |
 |
Fig. 8 Profiles of gamma-ray fluxes shown for different thermal plasma densities with the magnetic field strength eliminated via Eq. (8), for η = 1. |
On the other hand, from the observed radio spectrum we have the value of F0, related to B via ne (Eq. (6)), which finally gives
![$$ \kappa=\frac{\sqrt{3}e^3}{m_{\rm e}c^2(p+1)}\Gamma \left(\frac{p}{4}+\frac{19}{12}\right) \Gamma \left(\frac{p}{4}-\frac{1}{12} \right) \left[\frac{2\pi m_{\rm e}c}{3e} \right]^\frac{1-p}{2}\cdot $$](/articles/aa/full_html/2016/12/aa26825-15/aa26825-15-eq159.png) Knowledge of gamma-ray flux for Ecross plus the above formulae allow us to constrain the required variables (for a given Xp), i.e. B and η (or for previously fixed η: B and Xp). Similarly, as in the case of hadron models for radio halos where the combination of radio and gamma-ray data provides a constraint on B, see e.g. Brunetti & Jones (2014), we have here the combination of radio flux and spectral shape of gamma-ray flux. Thus, applying the above procedure, via scaling nth versus B, one obtains an independent limitation on B.
Knowledge of gamma-ray flux for Ecross plus the above formulae allow us to constrain the required variables (for a given Xp), i.e. B and η (or for previously fixed η: B and Xp). Similarly, as in the case of hadron models for radio halos where the combination of radio and gamma-ray data provides a constraint on B, see e.g. Brunetti & Jones (2014), we have here the combination of radio flux and spectral shape of gamma-ray flux. Thus, applying the above procedure, via scaling nth versus B, one obtains an independent limitation on B.
Also Figs. 9 and 10 show a moving point Ecross in the gamma-ray spectrum for other values of the η parameter in the scaling law nth(r) versus B(r).
Another kind of diffusive radio emission especially convenient to compare with the Coma cluster halo is the relic of the A 2256 cluster. Here we have a radio relic whose emission comes from the volume V, which is comparable to the Coma halo volume. The radio fluxes for both diffusive objects are also comparable, as for the halo in Coma Fν ~ 2 Jy, at a frequency of ~400 MHz, while for the relic in A 2256, Fν ~ 1.4 Jy, at a frequency of 350 MHz. In the case of the above relic, the basic observables result from a method that is very different than previous methods; this is briefly described below. We expect that the relic, which occurs at the edge of cluster, provides particularly good conditions for observing the signature in the gamma-ray spectrum discussed above. Essentially, the value of the magnetic field decreases on the edge of the cluster, and because of this, the gamma-ray component due to the IC process acting on a primary population of freshly accelerated electrons becomes relatively bright. The observables necessary to calculate a relevant gamma-ray flux were obtained in the papers quoted below. The approximate value of nth ~ 0.5 × 10-3 cm-3 at the edge of the cluster is taken from Brentjens (2008). The density of proton and electron numbers np ~ 10-11 cm-3, ne ~ 3.6 × 10-12 cm-3 and the value of the magnetic field B ~ 0.05μG were calculated in the paper (Siemieniec-Ozieblo & Pasternak 2011), basing on the knowledge of
-
flux values of synchrotron radiation and non-thermal X-rayemission (IC) and the spectral index characterizing the relic radioemissionα = 0.8; and
-
the postulate of comparable energy density in hadron and lepton fractions of CR, expressed through the value of the parameter K = ρp/ρe ~ 1.
It should be noted that the values of B listed above and 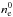 factor ~10-4 cm-3 (in the formula (7) on N(γ); p = 1 + 2α) are comparable with the values of the observables obtained from the method previously mentioned, used in Brentjens (2008). Taking the above into account these values, which result from the two different approaches, seem to be very reliable. In analysing the structure of gamma-ray spectrum for the relic in A 2256, the only “free” parameter, as opposite to the Coma case, is the value nth(r) in the relic. The values for B and
factor ~10-4 cm-3 (in the formula (7) on N(γ); p = 1 + 2α) are comparable with the values of the observables obtained from the method previously mentioned, used in Brentjens (2008). Taking the above into account these values, which result from the two different approaches, seem to be very reliable. In analysing the structure of gamma-ray spectrum for the relic in A 2256, the only “free” parameter, as opposite to the Coma case, is the value nth(r) in the relic. The values for B and 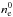 result from solving flux Eqs. (1), (2), in Siemieniec-Ozieblo & Pasternak (2011). Figure 11 shows the same trend in the behaviour of Ecross as in the halo of Coma, implying that the structure within the gamma-ray spectrum depends on nth. As before, with decreasing value of nth (for increasing r) we have an increasing value of Ecross.
result from solving flux Eqs. (1), (2), in Siemieniec-Ozieblo & Pasternak (2011). Figure 11 shows the same trend in the behaviour of Ecross as in the halo of Coma, implying that the structure within the gamma-ray spectrum depends on nth. As before, with decreasing value of nth (for increasing r) we have an increasing value of Ecross.
 |
Fig. 11 Combined gamma-ray emissions for a radio relic at the outskirts of A 2256 galaxy cluster for different values of nth, where the values of ne, np were inferred from radio and HXR observations (Siemieniec-Ozieblo & Pasternak 2011). |
5. Summary
The growing interest in the physics of cluster edges, underlying recent attempts to have a better observational access to them is primarily due to much inadequate knowledge of that virial region that directly links the ICM and the outer intergalactic medium (IGM). The cluster outskirts are particularly important not only because the cluster mass distribution, essential for investigating structure formation evolution, is still unknown to date, but also from the accretion of matter along the filaments, which, on the one hand, leads to effects such as gas clumping and, on the other hand, to the shock occurring there. In fact, the gravitational energy transfer proceeds through the accretion of matter and the associated shocks. The energy is dissipated here to gas, plasma turbulences, magnetic field B, and CR acceleration. The main consequence of shock actions is acceleration/reacceleration of particles, leading to the appearance of non-thermal IGM plasma component. This non-thermal component is crucial not only for the understanding of different radiative mechanisms but also in contributing to non-thermal pressure, which additionally could influence the out-of-equilibrium ICM state that is relevant to this region. The flux of non-thermal radiation significantly depends on the strength of magnetic field frozen in the peripheral plasma. The present knowledge of the B field in the IGM is scanty and its estimated value often depends on the particular method used. In general, many aspects of the B field in clusters are still far from being understood, in particular, its role in the ICM and IGM environments connecting clusters with the large-scale web structure. In this context, any new independent method of estimating the intensity and getting additional information on the IGM magnetic field would be highly desirable. Potentially, this could be achieved by a future detection of gamma-ray spectrum from the edge of the cluster in which a radio relic is observed as well. At present, in some cases, we can also use edge-on radio relics to estimate B (via spectral aging), while this method cannot be applied to face-on relics. So far, only the upper limit on gamma-ray flux was determined by Fermi. Lack of observations constrains the contribution of CRs and thus the CR pressure averaged over the entire cluster. However, there are a number of arguments (e.g. Hong et al. 2014; and Vazza et al. 2012) to suggest that the CR pressure can rise at the cluster edges. Referring to the work of Hong et al. (2014), where protons are accelerated mainly in the outskirts (through infall shocks), in this paper we propose a scenario in which the CR acceleration is due to a double shock, i.e. a shock involving both merger and accretion shocks. Propagating in the direction of accretion shock, the outwards merger shock creates on the edge of the cluster favourable conditions for the appearance of an efficiently accelerated population of electrons. Thus, exactly in this area, we expect an inter-shock gamma-ray emission arising both from the π0 decay and the IC processes. However, since the value of B field is small there, the interaction of electrons with CMB photons is more efficient than their interaction with the field B. Therefore, the contribution to gamma-ray emission from the IC process becomes relatively large and thus comparable with that of π0 decay. Such a combination of both mechanisms should therefore create a gamma-ray spectrum (on the timescale of the radio relic) revealing a characteristic time-dependent structure. As has been shown in the example of two often studied clusters whose observables were derived in previous papers, this feature is located in the photon energy range less than 1 GeV for small values of magnetic field, less than 1 μG. A large-scale simulation of gravitational structure suggests just such a magnetic field in the transition zone from the ICM environment to the IGM filament milieu.
The energy at which the inner structure of the spectrum becomes distinct scales with the value of peripheral magnetic field. Therefore, the knowledge of, for example the thermal gas profile of the cluster and the spectral position of a given gamma-ray feature, could be essential for an independent estimation of magnetic field values at the interface between the ICM and IGM.
Moreover, the potential capability is very promising to see the close neighbourhood of the π0 bump and to find two similar spectral signatures on both sides of this bump in two different energy ranges: at ≲1 GeV via Fermi-LAT and >10 GeV via future CTA instruments (see Fig. 2). The Fermi and CTA overlapping in the extended energy range plus enhanced sensitivity and angular resolution should provide a supplementary tool to constrain the acceleration scenario. These parallel observations will in the future enable us to overcome degeneracy of gamma-ray spectrum, depending both on the magnetic field and relative acceleration efficiency for electrons and protons.
Acknowledgments
We thank the referee for helpful and insightful comments.
References
- Ackermann, M., Ajello, M., Allafort, A., et al. 2010, ApJ, 717, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Afshordi, N., Lin, Y-T., Nagai, D., & Sanderson, A. J. R. 2007, MNRAS, 378, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Arieli, Y., Rephaeli, Y., & Norman, M. L. 2011, ApJ, 738, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Atoyan, A. M., & Völk, H. J. 2000, ApJ, 535, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Bagchi, J., Durret, F., Lima Neto, G. B., & Paul, S. 2006, Science, 314, 791 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bagchi, J., Sirothia, S. K., Werner, N., et al. 2011, ApJ, 736, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Bautz, M. W., Miller, E. D., Sanders, J. S., et al. 2009, PASJ, 61, 1117 [NASA ADS] [Google Scholar]
- Beck, R., & Krause, M. 2005, Astron. Nachr., 326, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Bonafede, A., Feretti, L., Murgia, M., et al. 2010, A&A, 513, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonafede, A., Brüggen, M., van Weeren, R., et al. 2012, MNRAS, 426, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Brentjens, M. A. 2008, A&A, 489, 69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brunetti, G., & Jones, T. W. 2014, Int. J. Mod. Phys. D, 23, 1430007 [Google Scholar]
- Brunetti, G., Mack, K.-H., Prieto, M. A., & Varano, S. 2003, MNRAS, 345, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Burns, J. O., Skillman, S. W., & O’Shea, B. W. 2010, ApJ, 721, 1105 [Google Scholar]
- Clarke, T. E., Kronberg, P. P., & Böhringer, H. 2001, ApJ, 547, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Donnert, J., Dolag, K., Lesch, H., & Müller, E. 2009, MNRAS, 392, 1008 [NASA ADS] [CrossRef] [Google Scholar]
- Donnert, J., Dolag, K., Brunetti, G., Cassano, R., & Bonafede, A. 2010, MNRAS, 401, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Eckert, D., Ettori, S., Molendi, S., Vazza, F., & Paltani, S. 2013, A&A, 551, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- George, M. R., Fabian, A. C., Sanders, J. S., et al. 2009, MNRAS, 395, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Hoeft, M., & Brüggen, M. 2007, MNRAS, 375, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Hong, S. E., Ryu, D., Kang, H., & Cen, R. 2014, ApJ, 785, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Kang, H., Ryu, D., & Jones, T. W. 2012, ApJ, 756, 97 [Google Scholar]
- Kushnir, D., & Waxman, E. 2009, J. Cosmol. Astropart. Phys., 08, 002 [NASA ADS] [CrossRef] [Google Scholar]
- Miniati, F. 2003, MNRAS, 342, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Pfrommer, C., & Ensslin, T. 2004, A&A, 413, 17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinzke, A., & Pfrommer, C. 2010, MNRAS, 409, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Reimer, A., Reimer, O., Schlickeiser, R., & Iyudin, A. 2004, A&A, 424, 773 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reiprich, T. H., Hudson, D. S., Zhang, Y.-Y., et al. 2009, A&A, 501, 899 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sato, T., Sasaki, T., Matsushita, K., et al. 2012, PASJ, 64, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Siemieniec-Ozieblo, G., & Ostrowski, M. 2000, A&A, 355, 51 [NASA ADS] [Google Scholar]
- Siemieniec-Ozieblo, G., & Pasternak, B. M. 2011, Astron. Nachr., 332, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Simionescu, A., Allen, S. W., Mantz, A., et al. 2011, Science, 331, 1576 [NASA ADS] [CrossRef] [Google Scholar]
- Skillman, S. W., Hallman, E. J., O’Shea, B. W., et al. 2011, ApJ, 735, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Thierbach, M., Klein, U., & Wielebinski, R. 2003, A&A, 397, 53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vazza, M., Brüggen, C., Gheller, G., & Brunetti, B. 2012, MNRAS, 421, 3375 [NASA ADS] [CrossRef] [Google Scholar]
- Vazza, F., Eckert, D., Simionescu, A., et al. 2013, MNRAS, 429, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Vink, J., Bleeker, J., van der Heyden, K., et al. 2006, ApJ, 648, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, S. A., Fabian, A. C., Sanders, J. S., et al. 2012, MNRAS, 422, 3503 [NASA ADS] [CrossRef] [Google Scholar]
- van Weeren, R. J., Röttgering, H. J. A., Brüggen, M., & Hoeft, M. 2010, Science, 330, 347 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- van Weeren, R. J., Hoeft, M., Röttgering, H. J. A., et al. 2011, A&A, 528, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Weeren, R. J., Fogarty, K., Jones, C., et al. 2013, ApJ, 769, 101 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Outline of the considered region of radio relic in between the outgoing merger shock and accretion shock for galaxy clusters. |
| In the text | |
 |
Fig. 2 Comparison of Ecross dispersion for two slightly different spectral indices αp, for the IC and π0 fluxes in a wider energy range. |
| In the text | |
 |
Fig. 3 Values of K0 as a function of Ecross, i.e. energy at which qπ flux is equal to qIC flux. |
| In the text | |
 |
Fig. 4 Expected gamma-ray spectrum for thermal plasma density, nth = 10-4 cm |
| In the text | |
 |
Fig. 5 Same as Fig. 4 but fluxes are calculated for thermal density nth = 10-3 cm-3. |
| In the text | |
 |
Fig. 6 Same as Fig. 4 but fluxes are calculated for thermal density nth = 10-2 cm-3. |
| In the text | |
 |
Fig. 7 Total gamma-ray fluxes for different thermal plasma densities shown for the field strength B = 2 μG. |
| In the text | |
 |
Fig. 8 Profiles of gamma-ray fluxes shown for different thermal plasma densities with the magnetic field strength eliminated via Eq. (8), for η = 1. |
| In the text | |
 |
Fig. 9 Same as Fig. 8, fluxes calculated for η = 0.5. |
| In the text | |
 |
Fig. 10 Same as Fig. 8, fluxes calculated for η = 0.1. |
| In the text | |
 |
Fig. 11 Combined gamma-ray emissions for a radio relic at the outskirts of A 2256 galaxy cluster for different values of nth, where the values of ne, np were inferred from radio and HXR observations (Siemieniec-Ozieblo & Pasternak 2011). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.