| Issue |
A&A
Volume 595, November 2016
|
|
|---|---|---|
| Article Number | A12 | |
| Number of page(s) | 14 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201628586 | |
| Published online | 24 October 2016 | |
Magnetic cycles and rotation periods of late-type stars from photometric time series
1 Instituto de Astrofísica de Canarias, 38205 La Laguna, Tenerife, Spain
e-mail: asm@iac.es
2 Universidad de La Laguna, Dpto. Astrofísica, 38206 La Laguna, Tenerife, Spain
3 Consejo Superior de Investigaciones Científicas, 28006 Madrid, Spain
Received: 23 March 2016
Accepted: 11 July 2016
Aims. We investigate the photometric modulation induced by magnetic activity cycles and study the relationship between rotation period and activity cycle(s) in late-type (FGKM) stars.
Methods. We analysed light curves, spanning up to nine years, of 125 nearby stars provided by the All Sky Automated Survey (ASAS). The sample is mainly composed of low-activity, main-sequence late-A to mid-M-type stars. We performed a search for short (days) and long-term (years) periodic variations in the photometry. We modelled the light curves with combinations of sinusoids to measure the properties of these periodic signals. To provide a better statistical interpretation of our results, we complement our new results with results from previous similar works.
Results. We have been able to measure long-term photometric cycles of 47 stars, out of which 39 have been derived with false alarm probabilities (FAP) of less than 0.1 per cent. Rotational modulation was also detected and rotational periods were measured in 36 stars. For 28 stars we have simultaneous measurements of activity cycles and rotational periods, 17 of which are M-type stars. We measured both photometric amplitudes and periods from sinusoidal fits. The measured cycle periods range from 2 to 14 yr with photometric amplitudes in the range of 5−20 mmag. We found that the distribution of cycle lengths for the different spectral types is similar, as the mean cycle is 9.5 yr for F-type stars, 6.7 yr for G-type stars, 8.5 yr for K-type stars, 6.0 yr for early M-type stars, and 7.1 yr for mid-M-type stars. On the other hand, the distribution of rotation periods is completely different, trending to longer periods for later type stars, from a mean rotation of 8.6 days for F-type stars to 85.4 days in mid-M-type stars. The amplitudes induced by magnetic cycles and rotation show a clear correlation. A trend of photometric amplitudes with rotation period is also outlined in the data. The amplitudes of the photometric variability induced by activity cycles of main-sequence GK stars are lower than those of early- and mid-M dwarfs for a given activity index. Using spectroscopic data, we also provide an update in the empirical relationship between the level of chromospheric activity as given by log10R 'HK and the rotation periods.
Key words: stars: low-mass / stars: late-type / stars: rotation / stars: activity / techniques: photometric
© ESO, 2016
1. Introduction
It is widely recognised that starspots in late-type dwarf stars lead to periodic light variations associated with the rotation of the stars Kron (1947). Starspots trace magnetic flux tube emergence and provide valuable information on the forces acting on flux tubes and photospheric motions, both important agents in the dynamo theory (Parker 1955a,b; Steenbeck et al. 1966; Bonanno 2002). Rotation plays a crucial role in the generation of stellar activity (Skumanich 1972). This becomes evident from the strong correlation of magnetic activity indicators with rotation periods (Pallavicini et al. 1981; Walter & Bowyer 1981; Vaughan et al. 1981; Middelkoop et al. 1981; Mekkaden 1985; Vilhu 1984; Simon & Fekel 1987; Drake et al. 1989; Montes et al. 2004; Dumusque et al. 2011, 2012; Suárez Mascareño et al. 2015). Stellar rotation coupled with convective motions generate strong magnetic fields in the stellar interior and produce different magnetic phenomena, including starspots in the photosphere. Big spotted areas consist of groups of small spots whose lifetime is not always easy to estimate, but the main structure can survive for many rotations, causing the coherent brightness variations that we can measure (Hall & Henry 1994). In solar-like main-sequence stars the light modulations associated with rotation are of order a few percent (Dorren & Guinan 1982; Radick et al. 1983), while in young fast rotating stars these modulations can be significantly larger (e.g. Frasca et al. 2011). Starspot induced light modulation was also proposed for M dwarfs decades ago (Chugainov 1971) and more recently investigated by, for example Irwin et al. (2011), Kiraga (2012) and West et al. (2015).
Long-term magnetic activity similar to that of the Sun is also observed on stars with external convection envelopes (Baliunas & Vaughan 1985; Radick et al. 1990; Baliunas et al. 1996; Strassmeier et al. 1997; Lovis et al. 2011; Savanov 2012; Robertson et al. 2013). Photometric and spectroscopic time series observations over decades have revealed stellar cycles similar to the 11 yr sunspot cycle. In some active stars even multiple cycles are often observed (Berdyugina & Tuominen 1998; Berdyugina & Järvinen 2005). It is possible to distinguish between cycles that are responsible for overall oscillation of the global level of the activity (similar to the 11 yr solar cycle) and cycles that are responsible for the spatial rearrangement of the active regions (flip-flop cycles) at a given activity level, such as the 3.7 yr cycle in sunspots (Berdyugina & Usoskin 2003; Moss 2004). The correct understanding of the different types of stellar variability, their relationships, and their link to stellar parameters is a key aspect to properly understand the behaviour of the stellar dynamo and its dependence on stellar mass. While extensive work has been conducted in FGK stars over many decades, M dwarfs have not received so much attention with only a few tens of long-term activity cycles reported in the literature (Robertson et al. 2013; Gomes da Silva et al. 2012).
Understanding the full frame of stellar variability in stars with a low level of activity is also crucial for exoplanet surveys. Modern spectrographs can now reach sub ms-1 precision in the radial velocity measurements (Pepe et al. 2011) and next generation instrumentation is expected to reach a precision of a few cms-1 (Pepe et al. 2013). At such precision level, the stellar activity induced signals in the radial velocity curves become a very important limiting factor in the search for Earth-like planets. Activity induced signals in timescales of days associated with rotation and in timescales of years for magnetic cycles are two of the most prominent sources of radial velocity induced signals (Dumusque et al. 2011). Measuring and understanding this short-term and long-term variability in different types of stars and the associated effects in radial velocity curves, and being able to predict the behaviour of a star, is required to disentangle stellar induced signals from Keplerian signals.
Ground-based automatic photometric telescopes have been running for decades, providing the photometric precision and time coverage to explore rotation periods and activity cycles for sufficiently bright stars with a low activity level. In this work, using All Sky Automated Survey (ASAS) available long-term series of photometric data, we attempt the determination of rotational periods and long-term activity cycles of a sample of G to mid-M stars, with emphasis on the less studied low activity M dwarfs. We investigate the relationships between the level of magnetic activity derived from Ca II H&K, and the rotation and activity cycle periods derived from the photometric series. Several studies have taken advantage of the excellent quality of the Kepler space telescope light curves to determine activity cycles and rotation period, for example Vida et al. (2014), however the limited time span of the observations restricts these studies to cycles of only a few years. Here we investigate the presence of significantly longer activity cycles in our sample of stars.
2. Sample and data
Our sample consists of the stars in the study of rotational modulation of the Ca II lines by Suárez Mascareño et al. (2015) supplemented with a selection of nearby (suitably bright) mostly southern stars with reliable long photometric series in the ASAS public database. We selected the brightest examples of stars in the ASAS database, which offered photometric data in a linear regime. A few young very active fast rotating stars were also included to act as anchor points in the fast-rotating end, high activity range. In total we have analysed photometric data from 125 stars with spectral types from late F to mid-M type with a goal to determine the photometric modulation induced by rotation and long-term activity cycles. Most of the stars in the sample are main-sequence stars.
Figure 1 shows the distribution of spectral types for the total sample of stars originally considered. Table A.1 lists relevant data for only those stars where a reliable determination of photometric modulation was achieved (see below).
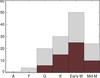 |
Fig. 1 Distribution of spectral types in our sample. M dwarfs were separated in two groups with the fully convective dwarfs (spectral type M3.5 and later) in a separated bin. Filled bins indicate stars in which we were able to retrieve long-term photometric trends and cycles likely caused by stellar activity. |
2.1. Photometric data
The all sky survey ASAS (Pojmanski 1997) in the V and I-bands has been running at Las Campanas Observatory, Chile since 1998. It has a spatial scale of 14′′/pixel and an average accuracy of ~ 0.05 mag per exposure. Best photometric results are achieved for stars with V~ 8−12, but this range can be extended if some additional control on the quality of the data is implemented. ASAS has produced light curves for around 107 stars at Dec < 28°. The catalogue supplies ready-to-use light curves with flags indicating the quality of the data. For this analysis we relied only on good quality data (grade “A” and “B” in the internal flags). Even after this quality control, there are still some high dispersion measurements that cannot be explained by a “regular” stellar behaviour. There are some cases of extreme scatter in stars closer to the magnitude limits of the survey and some stars that show a behaviour compatible with stellar flares. As our data is not well suited for modelling flares, to remove flare affected points, we iteratively rejected all measurements that deviate from the median value more than 2.5 times the root mean square of the full light curve. Iteration was applied until no more measurements where left outside these limits.
2.2. Spectroscopic data
As proxy for the chromospheric activity level of the stars in our sample we rely on the standard chromospheric activiy index  (Noyes et al. 1984). This index was directly adopted from Lovis et al. (2011) and Suárez Mascareño et al. (2015) for the stars in common with these works. For the remaining stars we searched for available spectra of the Ca II H&K lines in the HARPS ESO public data archive and performed our own measurement of the index. HARPS (Mayor et al. 2003) is a fibre-fed high-resolution spectrograph installed at the 3.6 m ESO telescope in La Silla Observatory (Chile). The instrument has a resolving power R ~ 115 000 over a spectral range from 378 to 691 nm. The HARPS pipeline provides extracted and wavelength-calibrated spectra, as well as RV measurements. We used the extracted order-by-order wavelength-calibrated spectra produced by the HARPS pipeline for our analysis. In order to minimise the effects related to atmospheric changes, we created a spectral template for each star by deblazing and co-adding every available spectrum and used the co-added spectrum to correct the order-by-order flux ratios for the individual spectra. We corrected each spectrum for the barycentric radial velocity of the Earth and the radial velocity of the star using the measurements given by the standard pipeline. We finally corrected each spectrum from the flux dispersion and re-binned the spectra into a wavelength-constant step.
(Noyes et al. 1984). This index was directly adopted from Lovis et al. (2011) and Suárez Mascareño et al. (2015) for the stars in common with these works. For the remaining stars we searched for available spectra of the Ca II H&K lines in the HARPS ESO public data archive and performed our own measurement of the index. HARPS (Mayor et al. 2003) is a fibre-fed high-resolution spectrograph installed at the 3.6 m ESO telescope in La Silla Observatory (Chile). The instrument has a resolving power R ~ 115 000 over a spectral range from 378 to 691 nm. The HARPS pipeline provides extracted and wavelength-calibrated spectra, as well as RV measurements. We used the extracted order-by-order wavelength-calibrated spectra produced by the HARPS pipeline for our analysis. In order to minimise the effects related to atmospheric changes, we created a spectral template for each star by deblazing and co-adding every available spectrum and used the co-added spectrum to correct the order-by-order flux ratios for the individual spectra. We corrected each spectrum for the barycentric radial velocity of the Earth and the radial velocity of the star using the measurements given by the standard pipeline. We finally corrected each spectrum from the flux dispersion and re-binned the spectra into a wavelength-constant step.
For the measurement of the  , we followed Suárez Mascareño et al. (2015), where an extension of the index to M-type dwarf stars, which are the majority of our present sample, was proposed.
, we followed Suárez Mascareño et al. (2015), where an extension of the index to M-type dwarf stars, which are the majority of our present sample, was proposed.
We have 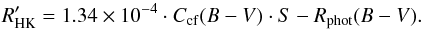 (1)Where S is flux in the Ca II H&K lines, defined as
(1)Where S is flux in the Ca II H&K lines, defined as 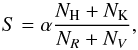 (2)where NH and NK are the fluxes in the core of the lines, NR and NV the fluxes on the nearby continuum, and α a constant equal to 2.3 times 8.
(2)where NH and NK are the fluxes in the core of the lines, NR and NV the fluxes on the nearby continuum, and α a constant equal to 2.3 times 8.
Then we have CCF, the bolometric correction, measured as 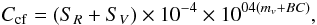 (3)where SR and SV are the mean fluxes in the reference continuum and BC the bolometric correction. This quantity can also be estimated as
(3)where SR and SV are the mean fluxes in the reference continuum and BC the bolometric correction. This quantity can also be estimated as 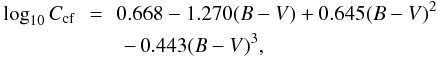 (4)and Rphot is the photospheric contribution to the mean activity level, which we estimate as
(4)and Rphot is the photospheric contribution to the mean activity level, which we estimate as ![\begin{eqnarray} \begin{split} R_{\rm phot}= 1.48 \times 10^{-4} \times \exp [-4.3658 \cdot (B-V)]. \end{split} \end{eqnarray}](/articles/aa/full_html/2016/11/aa28586-16/aa28586-16-eq29.png) (5)
(5)
3. Photometric modulation analysis
We search for periodic photometric variability that is compatible with both stellar rotation and long-term magnetic cycles. We compute the power spectrum using a generalised Lomb-Scargle periodogram (Zechmeister & Kürster 2009) and, if there is any significant periodicity, we fit the detected period using a sinusoidal model with the MPFIT routine (Markwardt 2009). Then we repeat the same process in the residuals of the fit. Typically this allowed us to determine the periodic photometric modulation induced by the magnetic cycle or the stellar rotation and, in some situations, us to measure both. In those cases in which both quantities have been determined, the final parameters come from a simultaneous fit of both signals.
The significance of the periodogram peak is evaluated using the Cumming (2004) modification over the Horne & Baliunas (1986) formula to obtain the spectral density thresholds for a desired false alarm level. Our false alarm probability then is defined as FAP = 1− [1−P(z>z0)] M, where P(z>z0) is the probability of z, the target spectral density, being greater than z0, the measured spectral density, and M is the number of independent frequencies.
As the Nyquist frequency of our data corresponds to a period of two days (Kiraga & Stepien 2007), we limit our high frequency search to that number, except in a few cases where we have hints that a faster rotation might be happening based on previous measurements in the literature. On the low frequency side we limit the search to a period of 10 000 days, which is almost three times longer than the maximum time span of the observations. The determination of incomplete cycles obviously involves large associated uncertainties.
In order to illustrate the method, we describe below the cases of three stars with different spectral types. First, the solar twin HD 2071 for which there are 641 photometric measurements taken over 8.4 yr. Figure 2 shows the periodograms obtained from the raw data and the residuals after removing the long-term variations. Although there is evidence for a long-term cycle, the data do not cover this cycle completely, thus the uncertainty in the determination of the period of the cycle is large. Figures 3 and 4 show the phase fit for both signals. The best-fitting model includes a long-term cycle of 11.3 ± 3.6 yr combined with a rotation period of 29.6 ± 0.1 days, with semi-amplitudes of 4.9 ± 1.3 mmag and 3.1 ± 0.9 mmag, respectively. The measured activity cycle of ~ 11 yr and the rotational period are similar to the corresponding cycle and rotation of the Sun.
 |
Fig. 2 Periodograms for the light curve of the star HD 2071. Top panel: periodogram of the raw data; bottom panel: periodogram of the residuals after fitting the long period signal. |
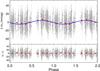 |
Fig. 3 Phase fit for the long-term photometric cycle of HD 2071. For a period of 11.2 ± 3.6 yr with a semi-amplitude of 4.9 ± 1.3 mmag. Grey dots show individual measurements, while red dots show the average measurement of every phase bin. |
For the K-type star HD 224789 there are 489 measurements obtained along 9.0 yr. In Fig. 5 we plot the corresponding periodograms. We find three significant peaks. The shortest period corresponds to the stellar rotation, the longest period is likely induced by the long-term activity cycle, and the middle period is likely an alias of the long-term cycle. This becomes clear when we fit the longest period signal to the light curve and subtract it; the intermediate period signal disappears while the shortest period remains stable. Figures 6 and 7 show the phase fit for the two bona fide signals. The best model includes a long-term cycle of 7.4 ± 0.8 yr combined with a rotation period of 16.6 ± 0.1 days, with photometric semi-amplitudes of 6.7 ± 1.3 mmag and 6.8 ± 1.2 mmag, respectively.
In Figs. 8–10 we show the analysis of the M-type star GJ551 (Proxima Centauri). For this star there are available 991 measurements spanning 8.7 yr. We interpret the two obvious peaks of the periodogram as induced by the rotation and activity cycle, respectively. Even if the short period signal is more significant than the long period signal, we opted to fit the long period signal in the first place. The best results comes from a long-term cycle of 6.8 ± 0.2 yr combined with a rotation period of 83.2 ± 0.1 days, with semi-amplitudes of 15.5 ± 0.9 mmag and 16.5 ± 0.9 mmag, respectively.
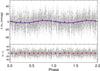 |
Fig. 4 Phase fit for the rotational modulation of HD 2071. The measured period is 29.6 ± 0.1 days with a semi-amplitude of 3.1 ± 0.9 mmag. Grey dots show individual measurements, and red dots show the average measurement of every phase bin. |
 |
Fig. 5 Periodograms for the HD 224789 light curve. Top panel: periodogram of the raw data; bottom pannel: periodogram of the residuals after fitting the long period signal. |
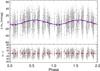 |
Fig. 6 Phase fit for the long-term photometric cycle of HD 224789. For a period of 7.1 ± 0.9 yr with a semi-amplitude of 6.7 ± 1.3 mmag. Grey dots show individual measurements, while red ones the average measurement of every phase bin. |
 |
Fig. 7 Phase fit for the rotational modulation of HD 224789. Measured period is 16.6 ± 0.1 days with a semi-amplitude of 6.8 ± 1.2 mmag. Grey dots show individual measurements, while red ones the average measurement of every phase bin. |
Using this procedure we were able to determine long-term magnetic cycles and/or average rotation periods for 55 stars in the sample. Table A.2 provides the measured cycle and rotation photometric semi-amplitudes and their corresponding periods and false alarm probabilities. The study of variations of the rotational periods across the cycles associated with differential rotation and the changes in the latitude of spots is out of the scope of the present paper and will be addressed in a future work. The reported rotation periods should be considered average values over the reported cycles.
Figure 11 shows the comparison between our measured rotation periods with those previously reported in the literature. We opt to include only those directly measured using periodic photometric or spectroscopic variations and do not consider those estimated from activity-rotation relationships. The plot shows good agreement between the different measurements except in the case of one star, GJ 877, where Suárez Mascareño et al. (2015) found roughly twice the rotation period using the variability of the Ca II index. Further study on this star is needed to clarify the correct measurement of the rotation period. It is important to note that the longer a rotation period the harder it is to determine and the larger the associated uncertainties.
 |
Fig. 8 Periodograms for the GJ551 light curve. Top panel: periodogram of the raw data; bottom panel: periodogram of the residuals after fitting the long period signal. |
 |
Fig. 9 Phase fit for the long-term photometric cycle of GJ551. For a period of 6.8 ± 0.3 yr with a semi-amplitude of 15.5 ± 0.9 mmag. Grey dots show individual measurements, while red dots indicate the average measurement of every phase bin. |
For the remaining 70 stars it was not possible to achieve a determination of rotation periods or activity cycles. In spite of the quality control on the data, some of these stars were so bright that their measurements where frequently in the non-linear regime and thus provided unreliable light curves. In some other stars, the amplitude of the induced photometric variability is below our detection limit or is non-periodic.
3.1. Long-term linear trends
Four of our stars, i.e. HD 82558, HD 45088, HD 215152 and GJ358, showed clear long-term linear trends over the time span of our observations. In the case of HD 45088 and HD 215152, these trends implied the presence of cycles much longer than the time span of the observations. For HD 82558 and GJ358, we also identify long-term trends on top of the ~2.5 yr and ~5 yr cycles that we found for each of these stars. Rotation periods are reported for the four stars.
Some of the measured cycles are longer than the time span of the observations (HD 1388, GJ9482, GJ205, GJ832, GJ382, GJ674, GJ849, and GJ285). While in those cases we have not measured a full cycle yet, we have enough data to give an estimation of the cycle length instead of treating it as a trend.
 |
Fig. 10 Phase fit for the rotational modulation of GJ551. Measured period is 83.2 ± 0.1 days with a semi-amplitude of 16.5 ± 0.9 mmag. Grey dots show individual measurements, while red dots indicate the average measurement of every phase bin. |
 |
Fig. 11 Comparison between our measured photometric periods and those reported in the literature from photometric or spectroscopic time series. Filled dots indicate measurements from Suárez Mascareño et al. (2015), while red empty dots are data taken from Chugainov (1974), Strassmeier et al. (1993), Kiraga & Stepien (2007), Strassmeier (2009), and Wright et al. (2011). The grey dashed line shows the 1:1 relation. |
3.2. Amplitude modulation
Magnetic cycles do not only manifest themselves as changes in the brightness of the stars, but some times in variations of the amplitude of the light curve (Berdyugina & Järvinen 2005). To study this behaviour we regroup the light curve in 30 day bins and use the peak-to-peak magnitude of each bin as a measurement of the amplitude. We then analyse the resulting amplitude curves for all the stars of our sample in the same way as the previous light curves searching for periodicities.
We find that the stars HD 32147 and HD 113538 show clear modulations, with false alarm probabilities smaller than 0.1% and periods of 10.17 ± 2.28 yr and 8.74 ± 1.24 yr respectively. The following stars show less significant modulations: GJ588 shows a periodicity of 1.76 ± 0.09 yr with a FAP of 2.9%; GJ273 shows a periodicity of 8.67 ± 2.41 yr with a FAP of 10.6%; HD 197481 shows a periodicity of 2.77 ± 0.06 yr with a FAP of 16.5%, and GJ382 shows a periodicity of 7.77 ± 1.06 yr with a FAP of 39%. There is also one short period modulation. For the star GJ9482, we find an amplitude periodicity of 133.55 ± 0.75 days with a FAP of 2.5%. The origin of this periodicity is hard to assess. It seems to be too long to be the rotation of the star and too short to be a magnetic cycle.
3.3. Notes on individual stars
HD 10180:Lovis et al. (2011) provides a cycle measurement of 7.4 ± 1.2 yr by studying the variations in the Ca II H&K emission cores. Instead of that we find a 4.1 ± 0.4 yr variation. Using the HARPS-S data, we verified that we detect a ~3.2 yr cycle on top of a ~14 yr variation in the Ca II H&K emission time series. We cannot rule out that we detect a harmonic of the real cycle.
HD 155885: Hempelmann et al. (1995) and Saar & Brandenburg (1999) proposed cycles ranging from 5 to 6 yr, with large associated uncertainty. Our measurement of a 6.2 ± 0.1 yr photometric periodicity supports their previous claims.
HD 63765: while we retrieve a 12.9 ± 4.9 yr cycle in the photometric light curve, Lovis et al. (2011) found a periodicity of 6.1 ± 2.8 yr in the Ca II H&K emission time series. We did not find a 6 yr periodicity, but this measure is compatible with the first harmonic of our measurement.
HD 32147: Baliunas et al. (1995) found a 11.1 ± 0.2 yr cycle studying the Ca II H&K emission time series. Our 5.8 ± 0.5 yr measurement is compatible with the first harmonic of that cycle.
HD 82558: previous studies have reported different cycle lengths for this star, ranging from ~2.5 up to ~12 yr (Oláh et al. 2009). In our data we recover the ~2.5 yr cycle, which might be a flip-flop cycle, and is also evidence for an additional long-term trend.
GJ205:Savanov (2012) finds a 3.7 yr period cycle and some of shorter periods. Our best fit comes from the superposition of two cycles, one of 10.8 ± 1.1 yr and another one of 3.9 ± 0.3 yr cycle. The short period cycle might be a flip-flop cycle.
GJ729: for this star we find two superimposed cycles. One of 7.1 ± 0.1 yr and a shorter cycle of 2.1 ± 0.1 yr. Again the short period cycle might be a flip-flop cycle.
GJ234: this is close binary system composed of two low mass stars with a brightness difference of ΔmK~ 1.6 and a separation of ~1 arcsec (Ward-Duong et al. 2015). Although the photometric light curve is for the unresolved binary, the signal is likely dominated by the primary component given its dominance in the visible range. We ascribe the periodic signals detected in the light curve to the primary.
GJ581: Robertson et al. (2013) detects a 4.5 ± 0.3 yr cycle analysing the Hα time series whereas we detect a 6.2 ± 0.9 yr cycle in the photometry light curve.
GJ551: Cincunegui et al. (2007) claimed a 1.2 yr cycle for which we find no evidence in the photometric light curve. Instead we measure a clear 6.8 ± 0.3 yr cycle. Savanov (2012) found a 7.9 yr cycle.
4. Discussion
The previous analysis of variability in photometric time series provided a collection of magnetic cycles, rotation periods, and chromospheric activity level for 55 stars, out of which 34 are low activity M-type stars, for which only a few tens of magnetic cycles are reported in the literature.
We measured the magnetic cycles for 5 G-type stars for which we found a mean cycle length of 9.0 yr with a dispersion of 4.9 yr. We found a mean cycle length of 6.7 yr with a dispersion of 2 yr for 12 K-type stars. We measured a mean cycle length of 7.4 yr with a dispersion of 3.0 yr for 22 early M-type stars, and we found a mean cycle length of 7.56 yr with a dispersion of 2.6 yr for 9 mid M-type stars. We note that we might be mixing some flip-flop cycles along with the global cycles, but in most cases we do not find multiple cycles making it difficult to distinguish between the two types. Subsequently, we measured the rotation periods for 9 G-type stars with a mean rotation period of 27.9 days and a dispersion of 3.9 days. For 13 K-type stars we measured a typical rotation of 20.3 with a dispersion of 16.4 days. For 20 early M-type stars, we measured an average rotation period of 35.7 days with a dispersion of 23.2 days, and an average rotation period of 78.1 days with a dispersion of 54.8 days for 9 mid M-type stars.
In order to put these results on a broader context we include in the discussion and plots other FGKM stars with known cycles and rotation periods selected from Noyes et al. (1984), Baliunas et al. (1995), Lovis et al. (2011), Robertson et al. (2013), and Suárez Mascareño et al. (2015). In total we deal with more than 150 stars with similar number of G-, K-, and M-type and far fewer F-type stars to study the distribution of cycle lengths and rotation periods for the different spectral types and the activity-rotation relationships.
4.1. Cycle length distribution
Figure 12 shows the distribution histogram of cycles by length and spectral type. We find that, like G-type stars, early M-type stars peak at the 2−4 yr bins, but K-type stars peak at the 6 yr bin. The double peak seen in the distribution might reveal information about peak in global cycles (10 yr) and in flip-flop cycles (6 yr). There are not enough detections to see any particular behaviour for F-type and mid M-type stars. Table 1 shows the main statistics of the typical cycle for each spectral type.
 |
Fig. 12 Distribution of cycle lengths. Grey filled columns show the global distribution while coloured lines the individual distributions. |
Statistics of the length of known cycles.
4.2. Rotation period distribution
Figure 13 shows the distribution of rotation periods and Table 2 lists the typical periods and measured scatter. When looking at the rotation periods we find an upper limit of the distribution growing steadily towards larger periods for later spectral types, and saturating at ~50 days for almost all spectral types (see Fig. 13). M-type stars, especially mid-Ms, show larger scatter going over that saturation limit and reaching periods longer than 150 days.
Many of the M-type stars are extreme slow rotators and that get reflected in their extremely low chromospheric activity levels. Figure 14 shows the distribution of the  against the colour B−V. For solar-type stars the lower envelope of the distribution goes around ~−5.2, but M dwarfs reach level of almost ~−6.
against the colour B−V. For solar-type stars the lower envelope of the distribution goes around ~−5.2, but M dwarfs reach level of almost ~−6.
 |
Fig. 13 Rotation periods vs. B−V colour of stars analysed in this work (filled symbols) and stars from the literature (open symbols). |
Statistics of rotation periods.
4.3. Activity-rotation relation
Suárez Mascareño et al. (2015) proposed a rotation-activity relation for late-F- to mid-M-type main-sequence stars with  ~−4.50 up to ~−5.85. The new measurements presented in Tables A.1 and A.2, and the data from Noyes et al. (1984), Baliunas et al. (1995), and Lovis et al. (2011) serve to extend and better define the relationship. Figure 15 shows the new measurements along with those the literature. These measurements are compatible for almost all spectral types and levels of chromospheric activity, as F-type stars are the only clear outlayers. This speaks of a relation that is more complex than what was proposed. Combining all data we can extend the relationship to faster rotators with levels of chromospheric activity up to
~−4.50 up to ~−5.85. The new measurements presented in Tables A.1 and A.2, and the data from Noyes et al. (1984), Baliunas et al. (1995), and Lovis et al. (2011) serve to extend and better define the relationship. Figure 15 shows the new measurements along with those the literature. These measurements are compatible for almost all spectral types and levels of chromospheric activity, as F-type stars are the only clear outlayers. This speaks of a relation that is more complex than what was proposed. Combining all data we can extend the relationship to faster rotators with levels of chromospheric activity up to  ~−4 and we are able to give an independent relationship for each spectral type. Figure 16 shows the measurements for every individual spectral type.
~−4 and we are able to give an independent relationship for each spectral type. Figure 16 shows the measurements for every individual spectral type.
 |
Fig. 14 Chromospheric activity level |
Assuming a relationship such as 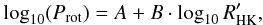 (6)
(6)
 |
Fig. 15 Rotation period vs. chromospheric activity level |
where Prot is in days and the typical residuals of the fit is smaller than 23 per cent of the measured periods for a given level of activity, for stars from G to mid M, and with residuals smaller than 39 per cent in the case of F-type stars. Table 3 shows the coefficients of the best fit for every individual dataset. This relationship provides an estimate of the rotation period of stars with low levels of chromospheric activity.
 |
Fig. 16 Rotation period vs. chromospheric activity level |
The original rotation-activity relationship, which was proposed by Noyes et al. (1984) and updated by Mamajek & Hillenbrand (2008), used as their observable the Rossby number – Ro = PRot/τc, i.e. the rotation period divided by the convective turnover, instead of the rotation period. The use of the convective turnover here raises some problems. The convective turnover can be determined from theoretical models (e.g. Gilman 1980; Gilliland 1985; Rucinski & Vandenberg 1986 or Kim & Demarque 1996) or empirically (Noyes et al. 1984; Stepien 1994; or Pizzolato et al. 2003). While the values of τc are consistent for G-K stars, they diverge badly for M dwarfs. Theoretical models indicate a steep increase of τc with decreasing mass, while purely empirical models indicate that τc increases with decreasing mass down to 0.8 M⊙, but then levels off (Kiraga & Stepien 2007). The behaviour of τc beyond 0.6 M⊙ is uncertain. For the measurement of τc we adopt the definition of Rucinski & Vandenberg (1986) because this definition produces the tightest correlation, i.e.
![\begin{eqnarray} && \log (\tau_{\rm c}) = 1.178 - 1.163 x + 0.279 x^2 - 6.14 x^3 ~(x > 0) \label{eq_tau1} \\[3pt] && \log (\tau_{\rm c}) = 1.178 - 0.941 x + 0.460 x^2 ~(x < 0), \label{eq_tau} \end{eqnarray}](/articles/aa/full_html/2016/11/aa28586-16/aa28586-16-eq95.png) where x = 0.65−(B−V). Figure 17 shows the distribution of the calculated Rossby numbers against the
where x = 0.65−(B−V). Figure 17 shows the distribution of the calculated Rossby numbers against the  . When presenting our results this way we find that, for solar-type stars, the distribution is very similar inside the limits studied in Mamajek & Hillenbrand (2008), but moving towards lower levels of activity increases the scatter. On the other hand, F-type and M-type stars do not follow the same exact relationship, hinting that the mechanism might be more complex than originally assumed or that the estimation of the convective turnover could be less reliable the further we get from the Sun, which was already stated by Noyes et al. (1984) for stars with B−V > 1. Unfortunately there is no reliable calibration for the convective turnover in the case of M-dwarf stars. Even with the bigger scatter the global behaviour of the data remains similar with a change of slope when reaching the very active regime (
. When presenting our results this way we find that, for solar-type stars, the distribution is very similar inside the limits studied in Mamajek & Hillenbrand (2008), but moving towards lower levels of activity increases the scatter. On the other hand, F-type and M-type stars do not follow the same exact relationship, hinting that the mechanism might be more complex than originally assumed or that the estimation of the convective turnover could be less reliable the further we get from the Sun, which was already stated by Noyes et al. (1984) for stars with B−V > 1. Unfortunately there is no reliable calibration for the convective turnover in the case of M-dwarf stars. Even with the bigger scatter the global behaviour of the data remains similar with a change of slope when reaching the very active regime (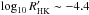 ).
).
Analogous to what we did in Eq. (6), we find that the distribution can be described as 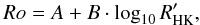 (9)where the typical scatter of the residuals is ~28 per cent of the measured Ro for the very active region and ~19 per cent for the moderately active region. Table 4 shows the parameters of Eq. (9).
(9)where the typical scatter of the residuals is ~28 per cent of the measured Ro for the very active region and ~19 per cent for the moderately active region. Table 4 shows the parameters of Eq. (9).
 |
Fig. 17 Rossby number vs. chromospheric activity level |
4.4. Activity versus photometric cycle amplitude
A relation between the cycle amplitude in Ca IIHK flux variations and the mean activity level of the stars was proposed by Saar & Brandenburg (2002). It was found that stars with a higher mean activity level show also larger cycle amplitudes. We investigate the behaviour of the photometric amplitude of the cycle with the mean activity level as well as with the Rossby number.
Comparing the cycle amplitude with the  we are able to see a weak tendency. Even if there is a large scatter, a trend such that the photometric amplitude of the cycle increases towards higher activity stars is found (see Fig. 18). This agrees with the Saar & Brandenburg (2002) work.
we are able to see a weak tendency. Even if there is a large scatter, a trend such that the photometric amplitude of the cycle increases towards higher activity stars is found (see Fig. 18). This agrees with the Saar & Brandenburg (2002) work.
 |
Fig. 18 Measured cycle photometric amplitude vs. chromospheric activity level |
When comparing the cycle amplitude with the rotation period we found a more clear correlation. While the scatter is large, is clear that the amplitude decreases longer periods (see Fig. 19). This is different to what Saar & Brandenburg (2002) found when studying the Ca II variations, where cycle amplitude saturation may be happening.
 |
Fig. 19 Measured cycle photometric amplitude versus the rotation period. |
4.5. Rotation-cycle relation
The existence of a relationship between the length of the magnetic cycle and rotation period has been studied for a long time. Baliunas et al. (1996) suggested Pcyc/Prot as an observable to study how both quantities relate to each other. It was suggested that the length of the cycle scales as ~Dl, where l is the slope of the relation and D is the dynamo number. Slopes that are different from ~ 1 would imply a correlation between the length of the cycle and rotation period.
Figure 20 shows results on a log-log scale of Pcyc/Prot versus 1 /Prot for all the stars for which we were able to determine both the rotation period and length of the cycle. The slope for our results is 1.01 ± 0.06, meaning no correlation between both quantities. However, we cover from early-G to late-M stars, including main-sequence and pre-main-sequence stars, with rotation periods ranging from ~ 0.2 to more than ~ 160 days. Previous works that found correlations were based on more homogeneous, and thus suitable samples, to study this relationship. For stars with multiple cycles we choose the global cycle (longer cycle), but the possibility of some of the short period cycles being flip-flop cycles cannot be ruled out.
If we restrict our analysis to main-sequence FGK stars, we obtain a slope of 0.89 ± 0.05, meaning that there is a weak correlation between both quantities. The measure is compatible with the result of 0.81 ± 0.05 from Oláh et al. (2009) and implies a weaker correlation than that found by Baliunas et al. (1996) who found a slope of 0.74 when sharing a good part of the sample. This supports the idea that there is a common dynamo behaviour for this group of stars, which does not apply to the M-dwarf stars for which we, as Savanov (2012), do not find a correlation.
 |
Fig. 20 Pcyc/Prot versus 1 /Prot in log-log scale. Filled dots represent main-sequence stars while empty circles stand for pre-main-sequence stars. The dashed line shows the fit to the full dataset. The solid line shows the fit to the main-sequence stars with radiative core. |
In a direct comparison of the length of the cycle with the rotation period, we see an absence of long cycles for extreme slow rotators. Figure 21 shows the distribution of cycle lengths against rotation periods. While the cycle lengths of those stars with rotation periods below the saturation level of ~ 50 days distribute approximately uniformly from ~ 2 to ~ 20 yr, those stars rotating slower than ~ 50 days show only cycles shorter cycles. At this point, it is unclear whether or not this behaviour is real or is related to a selection or observational bias. The number of stars with both rotation and cycle measured in this region is small, and the time span of the observation is shorter than 10 yr. Further investigation is needed to clarify the actual distribution.
 |
Fig. 21 Cycle length versus rotation periods. Filled symbols show the stars analysed in this work. |
Finally, we have also compared the photometric amplitudes induced by the activity cycles and the rotational modulation that seem to show a clear correlation. Both amplitudes increase together with an almost 1:1 relationship, even if with great scatter, and the behaviour seems to be similar for every spectral type (see Fig. 22).
 |
Fig. 22 Measured photometric amplitude of the cycles vs. the photometric amplitude of the rotational modulation as measured in this work. |
5. Summary
We have analysed the photometric variability in long time series for a sample of solar neighbours observable from the southern hemisphere. We analysed the light curves of a sample of 125 late-A to mid-M stars, containing more than 50 000 observations to measure periodic variabilities induced by the rotation and activity cycles.
We have been able to identify analogues of the solar cycle for 47 stars of the solar neighbourhood and 36 rotation periods, where 34 of them are M dwarfs. For 44 stars we have a measurement of the mean activity level ( ) obtained either from the literate or from our own measurements.
) obtained either from the literate or from our own measurements.
The length of the detected magnetic cycles goes from over 2.5 yr to less than 14 yr. No correlation is found between length of cycles and the spectral type. We found some stars that show multiple cycles in which the short-term cycles are possibly flip-flop cycles.
The length of the measured rotation periods goes from a fraction of a day up to more than 150 days. There seems to be a saturation level at ~50 days, only surpassed by M dwarfs, especially fully convective M dwarfs.
Combining our results with previous measurements we refine the activity-rotation relation proposed in Suárez Mascareño et al. (2015) and extend it up to  ~−4. The activity-rotation relationship is more complex than previously stated, having a change of slope for activity levels higher than
~−4. The activity-rotation relationship is more complex than previously stated, having a change of slope for activity levels higher than  ~−4.5 and a completely different behaviour for F-type stars.
~−4.5 and a completely different behaviour for F-type stars.
We find evidence for a correlation between the cycle length and the rotation period for the F, G and K main-sequence stars. For these stars the length of the cycle scales as Dl with l = 0.89.
A weak relationships between the activity level and the amplitude of the sun-like cycles can also be found when analysing photometric light curves of G to mid-M dwarfs. A relation is determined between the amplitudes and the rotation period. We find that the faster a star rotates the larger the amplitude of its cycle.
Acknowledgments
This work has been financed by the Spanish Ministry project MINECO AYA2014-56359-P. J.I.G.H. acknowledges financial support from the Spanish MINECO under the 2013 Ramón y Cajal program MINECO RYC-2013-14875.
References
- Baliunas, S. L., & Vaughan, A. H. 1985, ARA&A, 23, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Baliunas, S. L., Donahue, R. A., Soon, W. H., et al. 1995, ApJ, 438, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Baliunas, S. L., Nesme-Ribes, E., Sokoloff, D., & Soon, W. H. 1996, ApJ, 460, 848 [NASA ADS] [CrossRef] [Google Scholar]
- Berdyugina, S. V., & Järvinen, S. P. 2005, Astron. Nachr., 326, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Berdyugina, S. V., & Tuominen, I. 1998, A&A, 336, L25 [NASA ADS] [Google Scholar]
- Berdyugina, S. V., & Usoskin, I. G. 2003, A&A, 405, 1121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonanno, A., Elstner, D., Rüdiger, G., & Belvedere, G. 2002, A&A, 390, 673 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chugainov, P. F. 1971, Information Bulletin on Variable Stars, 520, 1 [NASA ADS] [Google Scholar]
- Chugainov, P. F. 1974, Izvestiya Ordena Trudovogo Krasnogo Znameni Krymskoj Astrofizicheskoj Observatorii, 52, 3 [NASA ADS] [Google Scholar]
- Cincunegui, C., Díaz, R. F., & Mauas, P. J. D. 2007, A&A, 461, 1107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cousins, A. W. J., & Stoy, R. H. 1962, Royal Greenwich Observatory Bulletins, 64, 103 [Google Scholar]
- Cumming, A. 2004, MNRAS, 354, 1165 [NASA ADS] [CrossRef] [Google Scholar]
- Donahue, R. A., Saar, S. H., & Baliunas, S. L. 1996, ApJ, 466, 384 [NASA ADS] [CrossRef] [Google Scholar]
- Dorren, J. D., & Guinan, E. F. 1982, AJ, 87, 1546 [NASA ADS] [CrossRef] [Google Scholar]
- Drake, S. A., Simon, T., & Linsky, J. L. 1989, ApJS, 71, 905 [NASA ADS] [CrossRef] [Google Scholar]
- Ducati, J. R. 2002, VizieR Online Data Catalog: II/237 [Google Scholar]
- Dumusque, X., Santos, N. C., Udry, S., Lovis, C., & Bonfils, X. 2011, A&A, 527, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dumusque, X., Pepe, F., Lovis, C., et al. 2012, Nature, 491, 207 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Fabricius, C., Høg, E., Makarov, V. V., et al. 2002, A&A, 384, 180 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frasca, A., Fröhlich, H.-E., Bonanno, A., et al. 2011, A&A, 532, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garcés, A., Catalán, S., & Ribas, I. 2011, A&A, 531, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gilliland, R. L. 1985, ApJ, 299, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Gilman, P. A. 1980, in Stellar Turbulence, eds. D. F. Gray, & J. L. Linsky, IAU Colloq., 51, Lect. Notes Phys. (Berlin: Springer Verlag), 114, 19 [Google Scholar]
- Gomes da Silva, J., Santos, N. C., Bonfils, X., et al. 2012, A&A, 541, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hall, D. S., & Henry, G. W. 1994, International Amateur-Professional Photoelectric Photometry Communications, 55, 51 [Google Scholar]
- Hempelmann, A., Schmitt, J. H. M. M., Schultz, M., Ruediger, G., & Stepien, K. 1995, A&A, 294, 515 [NASA ADS] [Google Scholar]
- Høg, E., Fabricius, C., Makarov, V. V., et al. 2000, A&A, 355, L27 [NASA ADS] [Google Scholar]
- Horne, J. H., & Baliunas, S. L. 1986, ApJ, 302, 757 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, J., Berta, Z. K., Burke, C. J., et al. 2011, ApJ, 727, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Jao, W.-C., Henry, T. J., Subasavage, J. P., et al. 2014, AJ, 147, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, J. S., Ramsey, L. W., Jones, H. R. A., et al. 2009, ApJ, 704, 975 [NASA ADS] [CrossRef] [Google Scholar]
- Jetsu, L. 1993, A&A, 276, 345 [NASA ADS] [Google Scholar]
- Kim, Y.-C., & Demarque, P. 1996, ApJ, 457, 340 [NASA ADS] [CrossRef] [Google Scholar]
- Kiraga, M. 2012, Acta Astron., 62, 67 [NASA ADS] [Google Scholar]
- Kiraga, M., & Stepien, K. 2007, Acta Astron., 57, 149 [NASA ADS] [Google Scholar]
- Koen, C., Kilkenny, D., van Wyk, F., & Marang, F. 2010, MNRAS, 403, 1949 [Google Scholar]
- Kron, G. E. 1947, PASP, 59, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Landolt, A. U. 1992, AJ, 104, 340 [NASA ADS] [CrossRef] [Google Scholar]
- Landolt, A. U. 2009, AJ, 137, 4186 [NASA ADS] [CrossRef] [Google Scholar]
- Lovis, C., Dumusque, X., Santos, N. C., et al. 2011, ArXiv e-prints [arXiv:1107.5325] [Google Scholar]
- Mamajek, E. E., & Hillenbrand, L. A. 2008, ApJ, 687, 1264 [NASA ADS] [CrossRef] [Google Scholar]
- Markwardt, C. B. 2009, in Astronomical Data Analysis Software and Systems XVIII, eds. D. A. Bohlender, D. Durand, & P. Dowler, ASP Conf. Ser., 411, 251 [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- Mekkaden, M. V. 1985, Ap&SS, 117, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Mermilliod, J.-C. 1986, Catalogue of Eggen’s UBV data, 0 [Google Scholar]
- Middelkoop, F., Vaughan, A. H., & Preston, G. W. 1981, A&A, 96, 401 [NASA ADS] [Google Scholar]
- Montes, D., Crespo-Chacón, I., Gálvez, M. C., et al. 2004, Lecture Notes and Essays in Astrophysics, 1, 119 [NASA ADS] [Google Scholar]
- Moss, D. 2004, MNRAS, 352, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Noyes, R. W., Hartmann, L. W., Baliunas, S. L., Duncan, D. K., & Vaughan, A. H. 1984, ApJ, 279, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Oláh, K., Kolláth, Z., Granzer, T., et al. 2009, A&A, 501, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Olmedo, M., Chávez, M., Bertone, E., & De la Luz, V. 2013, PASP, 125, 1436 [NASA ADS] [CrossRef] [Google Scholar]
- Pallavicini, R., Golub, L., Rosner, R., et al. 1981, ApJ, 248, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N., 1955a, ApJ, 122, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N., 1955b, ApJ, 121, 491 [NASA ADS] [CrossRef] [Google Scholar]
- Pepe, F., Lovis, C., Ségransan, D., et al. 2011, A&A, 534, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pepe, F., Cristiani, S., Rebolo, R., et al. 2013, The Messenger, 153, 6 [NASA ADS] [Google Scholar]
- Pizzolato, N., Maggio, A., Micela, G., Sciortino, S., & Ventura, P. 2003, A&A, 397, 147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pojmanski, G. 1997, Acta Astron., 47, 467 [NASA ADS] [Google Scholar]
- Radick, R. R., Mihalas, D., Lockwood, G. W., et al. 1983, PASP, 95, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Radick, R. R., Skiff, B. A., & Lockwood, G. W. 1990, ApJ, 353, 524 [NASA ADS] [CrossRef] [Google Scholar]
- Robertson, P., Endl, M., Cochran, W. D., & Dodson-Robinson, S. E. 2013, ApJ, 764, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Robertson, P., Mahadevan, S., Endl, M., & Roy, A. 2014, Science, 345, 440 [NASA ADS] [CrossRef] [Google Scholar]
- Rucinski, S. M., & Vandenberg, D. A. 1986, PASP, 98, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Saar, S. H., & Brandenburg, A. 1999, ApJ, 524, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Saar, S. H., & Brandenburg, A. 2002, Astron. Nachr., 323, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Saar, S. H., & Osten, R. A. 1997, MNRAS, 284, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Savanov, I. S. 2012, Astron. Rep., 56, 716 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, T., & Fekel, Jr. F. C., 1987, ApJ, 316, 434 [NASA ADS] [CrossRef] [Google Scholar]
- Skumanich, A. 1972, ApJ, 171, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Stauffer, J. R. 1984, ApJ, 280, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Steenbeck, M., Krause, F., & Rädler, K.-H. 1966, Z. Naturforschung Teil A, 21, 369 [Google Scholar]
- Stepien, K. 1994, A&A, 292, 191 [NASA ADS] [Google Scholar]
- Strassmeier, K. G. 2009, A&ARv, 17, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Strassmeier, K. G., Hall, D. S., Fekel, F. C., & Scheck, M. 1993, A&AS, 100, 173 [NASA ADS] [Google Scholar]
- Strassmeier, K. G., Bartus, J., Cutispoto, G., & Rodono, M. 1997, A&AS, 125, 11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suárez Mascareño, A., Rebolo, R., González Hernández, J. I., & Esposito, M. 2015, MNRAS, 452, 2745 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, C. A. O., Quast, G. R., da Silva, L., et al. 2006, A&A, 460, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Altena, W. F., Lee, J. T., & Hoffleit, E. D. 1995, The general catalogue of trigonometric [stellar] parallaxes (New Haven, CT: Yale University Observatory) [Google Scholar]
- Vaughan, A. H., Preston, G. W., Baliunas, S. L., et al. 1981, ApJ, 250, 276 [NASA ADS] [CrossRef] [Google Scholar]
- Vida, K., Oláh, K., & Szabó, R. 2014, MNRAS, 441, 2744 [NASA ADS] [CrossRef] [Google Scholar]
- Vilhu, O. 1984, A&A, 133, 117 [NASA ADS] [Google Scholar]
- Walter, F. M., & Bowyer, S. 1981, ApJ, 245, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Ward-Duong, K., Patience, J., De Rosa, R. J., et al. 2015, MNRAS, 449, 2618 [NASA ADS] [CrossRef] [Google Scholar]
- West, A. A., Weisenburger, K. L., Irwin, J., et al. 2015, ApJ, 812, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, N. J., Drake, J. J., Mamajek, E. E., & Henry, G. W. 2011, ApJ, 743, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Zechmeister, M., & Kürster, M. 2009, A&A, 496, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Additional tables
Relevant data for stars in our sample with periodic photometric modulation.
Long-term cycles and rotation periods for the stars in our sample.
continued. Long-term cycles and rotation periods for the analysed stars.
All Tables
All Figures
 |
Fig. 1 Distribution of spectral types in our sample. M dwarfs were separated in two groups with the fully convective dwarfs (spectral type M3.5 and later) in a separated bin. Filled bins indicate stars in which we were able to retrieve long-term photometric trends and cycles likely caused by stellar activity. |
| In the text | |
 |
Fig. 2 Periodograms for the light curve of the star HD 2071. Top panel: periodogram of the raw data; bottom panel: periodogram of the residuals after fitting the long period signal. |
| In the text | |
 |
Fig. 3 Phase fit for the long-term photometric cycle of HD 2071. For a period of 11.2 ± 3.6 yr with a semi-amplitude of 4.9 ± 1.3 mmag. Grey dots show individual measurements, while red dots show the average measurement of every phase bin. |
| In the text | |
 |
Fig. 4 Phase fit for the rotational modulation of HD 2071. The measured period is 29.6 ± 0.1 days with a semi-amplitude of 3.1 ± 0.9 mmag. Grey dots show individual measurements, and red dots show the average measurement of every phase bin. |
| In the text | |
 |
Fig. 5 Periodograms for the HD 224789 light curve. Top panel: periodogram of the raw data; bottom pannel: periodogram of the residuals after fitting the long period signal. |
| In the text | |
 |
Fig. 6 Phase fit for the long-term photometric cycle of HD 224789. For a period of 7.1 ± 0.9 yr with a semi-amplitude of 6.7 ± 1.3 mmag. Grey dots show individual measurements, while red ones the average measurement of every phase bin. |
| In the text | |
 |
Fig. 7 Phase fit for the rotational modulation of HD 224789. Measured period is 16.6 ± 0.1 days with a semi-amplitude of 6.8 ± 1.2 mmag. Grey dots show individual measurements, while red ones the average measurement of every phase bin. |
| In the text | |
 |
Fig. 8 Periodograms for the GJ551 light curve. Top panel: periodogram of the raw data; bottom panel: periodogram of the residuals after fitting the long period signal. |
| In the text | |
 |
Fig. 9 Phase fit for the long-term photometric cycle of GJ551. For a period of 6.8 ± 0.3 yr with a semi-amplitude of 15.5 ± 0.9 mmag. Grey dots show individual measurements, while red dots indicate the average measurement of every phase bin. |
| In the text | |
 |
Fig. 10 Phase fit for the rotational modulation of GJ551. Measured period is 83.2 ± 0.1 days with a semi-amplitude of 16.5 ± 0.9 mmag. Grey dots show individual measurements, while red dots indicate the average measurement of every phase bin. |
| In the text | |
 |
Fig. 11 Comparison between our measured photometric periods and those reported in the literature from photometric or spectroscopic time series. Filled dots indicate measurements from Suárez Mascareño et al. (2015), while red empty dots are data taken from Chugainov (1974), Strassmeier et al. (1993), Kiraga & Stepien (2007), Strassmeier (2009), and Wright et al. (2011). The grey dashed line shows the 1:1 relation. |
| In the text | |
 |
Fig. 12 Distribution of cycle lengths. Grey filled columns show the global distribution while coloured lines the individual distributions. |
| In the text | |
 |
Fig. 13 Rotation periods vs. B−V colour of stars analysed in this work (filled symbols) and stars from the literature (open symbols). |
| In the text | |
 |
Fig. 14 Chromospheric activity level |
| In the text | |
 |
Fig. 15 Rotation period vs. chromospheric activity level |
| In the text | |
 |
Fig. 16 Rotation period vs. chromospheric activity level |
| In the text | |
 |
Fig. 17 Rossby number vs. chromospheric activity level |
| In the text | |
 |
Fig. 18 Measured cycle photometric amplitude vs. chromospheric activity level |
| In the text | |
 |
Fig. 19 Measured cycle photometric amplitude versus the rotation period. |
| In the text | |
 |
Fig. 20 Pcyc/Prot versus 1 /Prot in log-log scale. Filled dots represent main-sequence stars while empty circles stand for pre-main-sequence stars. The dashed line shows the fit to the full dataset. The solid line shows the fit to the main-sequence stars with radiative core. |
| In the text | |
 |
Fig. 21 Cycle length versus rotation periods. Filled symbols show the stars analysed in this work. |
| In the text | |
 |
Fig. 22 Measured photometric amplitude of the cycles vs. the photometric amplitude of the rotational modulation as measured in this work. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


