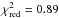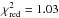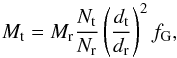| Issue |
A&A
Volume 595, November 2016
|
|
|---|---|---|
| Article Number | A101 | |
| Number of page(s) | 12 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201527840 | |
| Published online | 08 November 2016 | |
ESO 243-49 HLX-1: scaling of X-ray spectral properties and black hole mass determination
1 Dipartimento di FisicaUniversità di Ferrara, via Saragat 1, 44122 Ferrara, Italy
e-mail: titarchuk@fe.infn.it
2 National Research Nuclear University MEPhI (Moscow Engineering Physics Institute), 115409 Moscow, Russia
3 Moscow State University/Sternberg Astronomical Institute, Universitetsky Prospect 13, 119992 Moscow, Russia
e-mail: seif@sai.msu.ru
Received: 26 November 2015
Accepted: 29 August 2016
We report the results of Swift/XRT observations (2008−2015) of a hyper-luminous X-ray source, ESO 243-49 HLX-1. We demonstrate a strong observational evidence that ESO 243-49 HLX-1 undergoes spectral transitions from the low/hard state to the high/soft state during these observations. The spectra of ESO 243-49 HLX-1 are well fitted by the so-called bulk motion Comptonization model for all spectral states. We have established the photon index (Γ) saturation level, Γsat = 3.0 ± 0.1, in the Γ versus mass accretion rate (Ṁ) correlation. This Γ−Ṁ correlation allows us to estimate black hole (BH) mass in ESO 243-49 HLX-1 to be MBH ~ 7 × 104 M⊙ assuming the distance to ESO 243-49 of 95 Mpc. For the BH mass estimate we use the scaling method taking Galactic BHs XTE J1550-564, H 1743-322 and 4U 1630-472, and an extragalactic BH source, M101 ULX-1 as reference sources. The Γ versus Ṁ correlation revealed in ESO 243-49 HLX-1 is similar to those in a number of Galactic and extragalactic BHs and it clearly shows the correlation along with the strong Γ saturation at ≈3. This is a robust observational evidence for the presence of a BH in ESO 243-49 HLX-1. We also find that the seed (disk) photon temperatures are quite low, of order of 50−140 eV which are consistent with high BH mass in ESO 243-49 HLX-1.
Key words: accretion, accretion disks / black hole physics / radiation mechanisms: general / X-rays: individuals: ESO 243-49 HLX-1
© ESO, 2016
1. Introduction
The prominent edge-on galaxy ESO 243-49, located at 95 Mpc away in the constellation Phoenix (see Afonso et al. 2005),hosts a hyper-luminous X-ray source commonly known as HLX-1, which is possibly an intermediate mass black hole (IMBH). This black hole candidate (BHC) was firstly observed in 2004 as a source emitting X-rays in the vicinity of the spiral galaxy ESO 243-49 and it was catalogued as 2XMM J011028.1-460421. Later, in 2008 the field of this X-ray source was deeply re-imaged by a team led by Natalie Webb (the Institut de Recherche en Astrophysique et Planetologie in Toulouse, France).
Farrell et al. (2009) suggested that HLX-1 is an intermediate mass black hole candidate with mass of ~104 M⊙ based on very high X-ray luminosity of HLX-1 (~1042 erg/s in the 0.2–10 keV range) and because its disk blackbody spectrum peaked at kTin ~ 2 keV along with its X-ray spectral variability. X-ray spectral analysis (see Godet et al. 2009, 2012; Servillat et al. 2011; Lasota et al. 2011; Farrell et al. 2009; Davis et al. 2011), optical observations (see Farrell et al. 2012; Wiersema et al. 2010; Soria et al. 2010) and radio observations (see Webb et al. 2012) support the presence of an intermediate-mass BH in ESO 243-49 HLX-1.
Long-term monitoring with the Swift/XRT has shown that X-ray luminosity of HLX-1 changes by a factor of ~50 (Godet et al. 2009; Yan et al. 2015), and its spectral variability is reminiscent of that seen in Galactic stellar-mass BHs (see Servillat et al. 2011). Specifically, the X-ray light curve demonstrates a recurrent “fast rise exponential decay” (FRED) type of pattern in the range of ~370–460 days. This recurrency has been interpreted as an orbital period of the companion star (see Lasota et al. 2011; and Soria 2013). However, the last 2 outbursts have been delayed to be consistent with that explanation. The interval between the last 2 outbursts is almost 3 months longer than the interval between the first two (Soria, priv. comm.).
Recently, Webb et al. (2012), hereafter W12, reported a detection of transient radio emission at the location of HLX-1, which is an agreement with a discrete jet ejection event. These observations also allow W12 to reestimate BH mass to be between ~9 × 103 M⊙ and ~9 × 104 M⊙. In contrast, King & Lasota (2014) suggested that HLX-1 may be a stellar mass binary like SS 433 (see also Lasota et al. 2015), in which the X-ray emission possibly comes from the beamed jet.
HLX-1 is projected in the sky at ~0.8 kpc out of the plane and ~3.3 kpc (≈8′′) of the nucleus of the S0/a galaxy ESO 243-49 (the luminosity distance ~96 Mpc). Galaxy ESO 243-49 is a member of the cluster Abell 2877 (e.g. Malumuth et al. 1992). The association of HLX-1 with ESO 243-49 is confirmed by the redshift measurements of the observed Hα emission line of the counterpart (Soria et al. 2013, hereafter SHP13; Wiersema et al. 2010), although the velocity offset between this and the bulge of ESO 243-49 is ~430 km s-1, close to the escape velocity from the S0 galaxy (SHP13). This fact allows to suggest that HLX-1 can be in a dwarf satellite galaxy or a star cluster near ESO 243-49 rather than in the galaxy itself (SHP13). The HII region in which the HLX is located could be the remnant of a dwarf satellite galaxy that has been accreted (Farrell et al. 2012). The optical counterpart of HLX-1 was detected in various bands, from near infrared to far ultraviolet (FUV, Wiersema et al. 2010; Soria et al. 2010, 2012; Farrell et al. 2012), but its nature remains puzzling.
Note, that Cseh et al. (2015) using radio observations of ESO 243-49 HLX-1 in 2012 based on the Australia Telescope Compact Array (ATCA) and Karl G. Jansky Very Large Array (VLA) esimated BH mass as 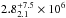 . Yan et al. (2015) have analyzed Swift monitoring observations of ESO 243-49 HLX-1 and compared the HLX-1 outburst properties with those of bright Galactic low-mass X-ray binary transients (LMXBTs). Furthermore, they state that HLX-1 spends progressively smaller time in the succeeding outburst state and much more time in quiescence, but its peak luminosity remains approximately constant. The spectral analysis by Yan et al. strengthen the similarity between the state transitions in HLX-1 and those in Galactic LMXBTs.
. Yan et al. (2015) have analyzed Swift monitoring observations of ESO 243-49 HLX-1 and compared the HLX-1 outburst properties with those of bright Galactic low-mass X-ray binary transients (LMXBTs). Furthermore, they state that HLX-1 spends progressively smaller time in the succeeding outburst state and much more time in quiescence, but its peak luminosity remains approximately constant. The spectral analysis by Yan et al. strengthen the similarity between the state transitions in HLX-1 and those in Galactic LMXBTs.
A very high luminosity of ESO 243-49 HLX-1 is considered as an evidence for the existence of IMBH in HLX-1 (Farrell et al. 2009). However, luminosities up to ~1041 erg/s can be explained by stellar-mass BHs undergoing super-Eddington accretion (see Begelman 2002) and following by beaming. As a result, apparent luminosity can exceed the Eddington limit estimated for isotropic radiation (King 2008; Freeland et al. 2006). In fact, highly collimated sources are not expected to have a disk-blackbody or thermal-dominant spectrum, like we see in HLX-1 in the high/soft state. This is a reason for thinking that HLX-1 is not a strongly beamed source.
Consequently, luminosity above ~1041 erg/s is difficult to explain without considering a massive BH source. Generally, two scenarios for an interpretation of HLX/ULX phenomena have been proposed. First, these sources can be stellar-mass BHs (<100 M⊙) radiating at Eddington or super-Eddington rates ( see e.g. Mukai et al. 2005). Alternatively, they can be intermediate-mass BHs (>100 M⊙) which luminosities are essentially sub-Eddington. The exact origin of such objects yet remains uncertain and there is still no general consensus on what causes the aforementioned poweful outbursts. Recently, Bachetti et al. (2014) discussed another scenario for ULX.
Using the NuSTAR mission(Harrison et al. 2013) they detected pulsations of X-ray emission with an average period 1.37 s modulated by a 2.5-day cycle from ULX-4 located in the nuclear region of the galaxy M82. Bachetti et al. also argue that these pulsations are results of the rotation of a magnetized neutron star, while the modulation arises from its binary orbital motion. Note, that X-ray luminosity of M82 ULX-4 is about LX ~ 2 × 1040 erg s-1 in 0.3–10 keV energy range which suggests luminosity ~100 × LEdd for a 1.4 M⊙ neutron star (NS). Such a source is ten times brighter than any known accreting pulsar. The discovery of M82 ULX-4 and its possible interpretation as a NS can expand possible scenarios for ULXs.
As for ESO 243-49 HLX-1, it is desirable to have an independent BH identification for its central object as well as the mass determination of its BH as an alternative to the abovementioned methods (based on luminosity estimates only). A new method of the BH mass determination was developed by Shaposhnikov & Titarchuk (2009), hereafter ST09, using a correlation scaling between X-ray spectral and timing (or mass accretion rate) properties observed from many Galactic BH binaries during the spectral state transitions. Application of this method has been also extended to a study of another class of X-ray sources, ULXs sources, NGC 5408 X-1 Strohmayer & Mushotzky (2009) and M101 ULX-1 (Titarchuk & Seifina 2015). Note, this method is commonly used for a BH mass determination of supermassive BHs, such as NGC 3227, NGC 5548 NGC 5506 and NGC 3516 (Papadakis et al. 2009; Sobolewska & Papadakis 2009) and NLS1 galaxy Mrk 766 (Giacche et al. 2014), using a sample of Galactic BHC binaries as reference sources. It turns out this scaling method can be applied for BH mass estimates when the conventional dynamical method cannot be used.
 |
Fig. 1 Hardness-intensity diagram for ESO 243-49 HLX-1 using Swift observations (2008–2015) during spectral evolution from the low/hard state to the high/soft states. In the vertical axis, the hardness ratio (HR) is a ratio of the source counts in the two bands: the hard (1.5–10 keV) and soft (0.3–1.5 keV) passbands. The HR decreases with a source brightness in the 0.3–10 keV energy range (horizontal axis). For clarity, we plot only one point with error bars (shown in the bottom right corner) to demonstrate typical uncertainties for the HR and count rate. |
We apply the ST09 method to Swift/XRT data of ESO 243-49 HLX-1. Previously, many properties of HLX-1 were analyzed using Swift/XRT observations (e.g., Soria et al. 2010; Farrell et al. 2013; Webb et al. 2014; Yan et al. 2015). In particular, Soria et al. (2010) assessed Swift (2008–2009) observations by fitting their X-ray spectra. They used a few models, in particular, an additive model of the Blackbody/diskbb plus power-law. They found that in these X-ray spectra the photon index changes from 1.8 to 2.95 but they were unable to find any argument that this source is intermediate-mass BH or foreground NS.
Farinelli & Titarchuk (2011), Seifina et al. (2015), Seifina et al. (2013), Seifina & Titarchuk (2012), Seifina & Titarchuk (2011), hereafter ST11, demonstrate that one can really distinguish BH and NS sources using Γ-Ṁ correlation. ST11 predicted the presence of a BH source in ESO 243-49 HLX-1 and ruled out a quiescent neutron star in this source. In fact, only BH sources demonstrate that the photon index Γ can increase from Γ ~ 1.6 to Γ ~ 3 with mass accretion rate, in contrast to neutron stars for which we usually find the constancy of the photon index around Γ ~ 2 (see e.g. ST11). Furthermore, Wiersema et al. (2010) measured a redshift of z = 0.0223 for HLX-1, which definitely indicates that HLX-1 cannot be a neutron star (NS) source because its luminosity is too high for a NS.
In this Paper we present an analysis of available Swift observations of ESO 243-49 HLX-1 made during 2008–2015 to re-examine our previous conclusions on a BH nature of HLX-1 and to find further indications on intermediate BH mass in HLX-1. In Sect. 2 we present the list of observations used in our data analysis while in Sect. 3 we provide details of the X-ray spectral analysis. We discuss an evolution of the X-ray spectral properties during the high-low state transitions and present the results of the scaling analysis to estimate BH mass of ESO 243-49 HLX-1 in Sect. 4. We have made conclusions on our results in Sect. 5.
 |
Fig. 2 The Chandra/HRC-I (0.1–10 keV) image of the ESO 243-49 HLX-1 field taken on UT 2009 July 4, where yellowsmall circle corresponds to the location of ESO 243-49 HLX-1 and white arrow points correspond to 2XMM J011050.4-460013 source. The large circles (labeled nominal and offset) show the two pointing positions used for the light curve and spectrum extractions in order to minimize contamination of ESO 243–49 HLX–1 by nearby source. |
2. Observations and data reduction
The list of Swift observations of ESO 243-49 HLX-1 used in our analysis.
We used Swift data (Gehrels et al. 2004) of ESO 243-49 HLX-1 carried out from 2008 to 2015. In Table 1 we show the summary of the Swift/XRT (Burrows et al. 2005) observations analyzed in this Paper. In the presented Swift observations, HLX-1 has been detected, at least, at ~2σ significance (see, Evans et al. 2009). The Swift-XRT/PC data (ObsIDs, indicated in the first column of Table 1) were processed using the HEA-SOFT v6.14, the tool XRTPIPELINE v0.12.84 and the calibration files (latest CALDB version is 201507211). The ancillary response files were created using XRTMKARF v0.6.0 and exposure maps generated by XRTEXPOMAP v0.2.7. We fitted the spectrum using the response file SWXPC0TO12S6_20010101v012.RMF. We also applied the online XRT data product generator2 for independent check of light curves and spectra (including background and ancillary response files, see Evans et al. 2007, 2009).Also we made the state identification using the hardness (color) ratio (HR) (see Sect. 3.2) and the Bayesian method developed by Park et al. (2006). Moreover, we apply an effective area option of the Park’s code which includes the count-rate correction factors in their calculations. Our results, adapting above technique, indicate a continuous distribution of the HR with source intensity from high hardness ratio at lower count-rate to low hardness ratio at higher count events (see Fig. 1). Furthermore, the hardness-intensity diagram shows a smooth track. Therefore, we grouped the Swift spectra into seven bands according to count rates (see Sect. 3.1) and fitted the combined spectra of each band using the XSPEC3 package (version 12.8.14, see Arnaud 1996). In addition, all groups of the Swift spectra were binned to a minimum of 20 counts per bin in order to use χ2 statistics for our spectral fitting.
We also employed a Chandra data for more deep image analysis. Specifically, we investigated an observation of HLX-1 for which the HRC-I camera was operated on the board of Chandra with the CIAO v4.1.1 task WAVDETECT.
3. Results
3.1. Images
We made a visual inspection of the source field of view (FOV) image to get rid of a possible contamination from nearby sources. To do this we implement the Chandra image with better resolution than that for Swift image. In Fig. 2 we show adaptively smoothed Chandra/HRC-I (0.1–10 keV) image of the ESO 243-49 HLX-1 field, obtained on 2009 July 4 with an exposure of 1175 s (ObsID: 10919)when ESO 243–49 HLX–1 was in quiescence (see see also blue dashed vertical line in Fig. 3 indicating Chandra/HRC-I observational MJD point in the lightcurve). In fact, two sources were detected in the FOV near HLX–1 position: 2XMM J011050.4-460013 and 2XMM J010953.9-455538. A source related to the position of HLX-1 (Webb et al. 2010) is 2XMM J010953.9-455538 identified as ESO 243-49 HLX-1 (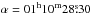 ,
, 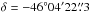 , J2000.0 and indicated by yellow circle in Fig. 2). To separate X-ray emissions from these two sources and minimize contamination of ESO 243–49 HLX–1 by the nearby source we additionally used specific Swift pointing (see dashed circle in Fig. 2), within which only HLX–1 is detected. In Fig. 2 the large circles (labeled nominal and offset) show the two pointing positions used for HLX–1 data extraction for the Swift observations. In this way, we compare the relative contributions of these two sources throughout all Swift observations. For the observations made at the offset pointing positions, the count rates are almost the same as that made at the nominal pointing position. Thus, we conclude that during Swift observations this nearby source remains faint in comparison with the variable HLX–1.
, J2000.0 and indicated by yellow circle in Fig. 2). To separate X-ray emissions from these two sources and minimize contamination of ESO 243–49 HLX–1 by the nearby source we additionally used specific Swift pointing (see dashed circle in Fig. 2), within which only HLX–1 is detected. In Fig. 2 the large circles (labeled nominal and offset) show the two pointing positions used for HLX–1 data extraction for the Swift observations. In this way, we compare the relative contributions of these two sources throughout all Swift observations. For the observations made at the offset pointing positions, the count rates are almost the same as that made at the nominal pointing position. Thus, we conclude that during Swift observations this nearby source remains faint in comparison with the variable HLX–1.
 |
Fig. 3 Swift/XRT light curve of ESO 243-49 HLX-1 in the 0.3−10 keV energy range during 2008–2015. Red points mark the source signal (with 2σ detection level) and green points indicate the background level. Blue dashed line indicatesthe MJD of the Chandra/HRC-I observation presented in Fig. 2. |
3.2. Hardness-intensity diagrams and light curves
Before we proceed withdetails of the spectral fitting we study a hardness ratio (HR). In application to the Swift data we consider the HR is a ratio of the hard and soft counts in the 1.5–10 keV and 0.3–1.5 keV bands, respectively. The HR is evaluated by careful calculation of background counting. In Fig. 1 we demonstrate the hardness-intensity diagram (HID) and thus, we show that different count-rate observations are assocated with different color regimes. Namely, the HR larger values correspond to harder spectra. A Bayesian approach was used to estimate the HR values and their errors (Park et al. 2006)4.
Figure 1 indicates that the HR monotonically reduces with the total count rate (0.3–10 keV). This particular sample is similar to those of most of outbursts of Galactic X-ray binary transients (see Belloni et al. 2006; Homan et al. 2001; Shaposhnikov & Titarchuk 2006; ST09; TS09; Shrader et al. 2010; Muñoz-Darias et al. 2014).
Six recurrent outbursts occurred in HLX-1 during the Swift monitoring (from 2008 up to now). These outbursts were approximately separated by one year apart. We show the Swift/XRT light curve of ESO 243-49 HLX-1 during 2008–2015 for the 0.3–10 keV band in Fig. 3. Red points indicate the source signal and green points correspond to the background level. We found six outbursts of ESO 243-49 HLX-1 peaked at MJD = 55 060, 55 446, 55 791, 56 178, 56 586 and 57 060 with a FRED (“fast rise exponential decay”) profile and rough duration from 70 to 200 days. For the rest of the Swift observations the source remained in the low state. We must admit that individual Swift/XRT observations of ESO 243-49 HLX-1 in photon counting (PC) mode do not have enough counts in order to make statistically significant spectral fits.
We studied the Swift/XRT HID (see Fig. 1) and grouped the observations into seven bands: very low (“A”, HR > 1; “B”, 0.5 < HR < 1), low (“C”, 0.25 < HR < 0.6), intermediate (“D”, 0.13 < HR < 0.25), high (“E”, 0.07 < HR < 0.13; “F”, 0.03 < HR < 0.07) and very high (“G”, HR < 0.03) count rates to resolve this difficult problem. Thus, we have combined the spectra in each related band, regrouping them with the task grppha and then fitted them using the 0.3–10 keV range.
3.3. Spectral analysis
Different spectral models were used in order to test them for all available data for ESO 243-49 HLX-1. We want to establish the low/hard and high/soft state evolution using these spectral models. We investigate the combined Swift spectra to test the following spectral models: power-law, Bbody, BMC and their possible combinations modified by an absorption model. In order to fit all of these spectra we use a neutral column, which is obtained by the best-fit column NH of 5 × 1020 cm-2 (see also Yan et al. 2015; Farrell et al. 2009; Webb et al. 2010, 2012).
 |
Fig. 4 Seven EFE spectral diagrams which are related to different spectral states of ESO 243-49 HLX-1 using the BMC model. The data are taken from XRT/Swift observations related to different hardness ratios: left: HR < 0.03 (black, HSS), 0.03 < HR < 0.07 (bright blue, HSS), 0.5 < HR < 1 (pink, LHS); right: 0.1 < HR < 0.2 (blue, IS), 0.07 < HR < 0.2 (red, HSS), 0.2 < HR < 0.5 (orange, IS), HR > 1 (green, LHS). |
Best-fit parameters of the combined Swift spectra of ESO 243-49 HLX-1 in the 0.3−10 keV range using the following four models†: phabs*power-law, phabs*bbody, phabs*(bbody+power-law) and phabs*bmc.
3.3.1. Choice of the spectral model
We find that the phabs*power-law model well fits the low state data only (e.g., for band-A spectrum, 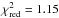 (138 d.o.f.), see the top of Table 2). As we establish this power-law model indicates to very large photon indices (greater than 3, particularly for band-G spectrum, see Fig. 1) and moreover, this model gives unacceptable fit quality, χ2 for all D, E, F and G-spectra of Swift data. Note, for the high state data, the thermal model (Bbody) provides better fits than the power-law model. However, the intermediate state spectra (D-spectra) cannot be fitted by any single-component model. Indeed, a simple power-law model produces a soft excess. These significant positive residuals at low energies, less than 1 keV, suggest the presence of additional emission components in the spectrum. As a result we also test a sum of blackbody and power-law component model. The model parameters are NH = 5 × 1020 cm-2; kTbb = 90−300 eV and Γ = 1.3−2.9 (see more in Table 2). The best fits of the Swift spectra has been found using of the Bulk Motion Comptonization model (BMC XSPEC model, Titarchuk et al. 1997), for which Γ ranges from 1.6 to 3.0 for all observations (see Table 2 and Figs. 4–6). We should emphasize that all these best-fit results are found using the same model for the high and low states.
(138 d.o.f.), see the top of Table 2). As we establish this power-law model indicates to very large photon indices (greater than 3, particularly for band-G spectrum, see Fig. 1) and moreover, this model gives unacceptable fit quality, χ2 for all D, E, F and G-spectra of Swift data. Note, for the high state data, the thermal model (Bbody) provides better fits than the power-law model. However, the intermediate state spectra (D-spectra) cannot be fitted by any single-component model. Indeed, a simple power-law model produces a soft excess. These significant positive residuals at low energies, less than 1 keV, suggest the presence of additional emission components in the spectrum. As a result we also test a sum of blackbody and power-law component model. The model parameters are NH = 5 × 1020 cm-2; kTbb = 90−300 eV and Γ = 1.3−2.9 (see more in Table 2). The best fits of the Swift spectra has been found using of the Bulk Motion Comptonization model (BMC XSPEC model, Titarchuk et al. 1997), for which Γ ranges from 1.6 to 3.0 for all observations (see Table 2 and Figs. 4–6). We should emphasize that all these best-fit results are found using the same model for the high and low states.
3.3.2. Spectral modelling for ESO 243-49 HLX-1
Now, we briefly remind a reader the physical picture described by the BMC model, its key assumptions and parameters. The BMC Comptonization spectrum is a sum of a part of the blackbody (BB) directly visible by the Earth observer (a fraction of 1/(1 + A)) and a fraction of the BB, f = A/ 1 + A, convolved with the Comptonization Green function which is, in the BMC approximation, a broken power-law. It is worthwhile to emphasize that this Comptonization Green function is characterized by the only one parameter, the spectral index α = Γ−1. Thus, as one can see that the BMC model has the main parameters, α, A, the seed blackbody temperature Ts and the BB normalization which is proportional to the seed blackbody luminosity and inverse proportional to d2 where d is a distance to the source (see Fig. 5).
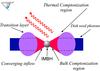 |
Fig. 5 A suggested geometry for ESO 243-49 HLX-1 source. Disk soft photons are upscattered (Comptonized) off relatively hot plasma of the transition layer. |
One can clearly see spectral evolution for the low/hard state-high/soft state (LHS−HSS) transition in Fig. 4. Seven EFE spectral diagrams related to different spectral states in HLX−1 are presented there (see also Sect. 3.2 and Fig. 1).
Thus, the BMC model successfully fits the ESO 243-49 HLX-1 spectra for all spectral states. In particular, the Swift/XRT spectra for band A (red) and band G (blue) fitted using the BMC model are shown in Fig. 6. In Table 2 (at the bottom), we present the results of spectral fitting Swift/XRT data of ESO 243-49 HLX-1 using our main spectral model. phabs*bmc. In particular, the LHS−HS transition is related to the photon index, Γ changes from 1.6 to 3.0 when the relatively low seed photon temperature kTs changes from 50 eV to 140 eV. The BMC normalization, Nbmc varies by a factor of fifteen, in the range of 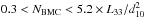 erg s-1 kpc-2. While the Comptonized (illumination) fraction varies in a wide range (−1.2 < log A< 1.1 or f ~ 0.1−1).
erg s-1 kpc-2. While the Comptonized (illumination) fraction varies in a wide range (−1.2 < log A< 1.1 or f ~ 0.1−1).
In Fig. 6 we also demonstrate the spectral evolution of ESO 243-49 HLX-1 in E ∗ F(E) units (top) along with Δχ (bottom). Data are taken from Swift/XRT observations with HR = 1.1 ± 0.1 (red, LHS; Γ = 1.6 ± 0.2, Ts = 54 ± 9 eV, 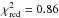 (136 d.o.f.)) and HR = 0.02 ± 0.01 (blue, HSS; Γ = 3.0 ± 0.1, Ts = 130 ± 10 eV,
(136 d.o.f.)) and HR = 0.02 ± 0.01 (blue, HSS; Γ = 3.0 ± 0.1, Ts = 130 ± 10 eV, 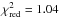 (217 d.o.f.), see also Table 2 for details).
(217 d.o.f.), see also Table 2 for details).
In the fit of the HSS spectrum shown in the third panel of Fig. 6, the BMC model appears to be systematically over-predicting the strength of the thermal emission below 1 keV. This energy range is related to the oxygen and iron line region where absorption features occur at 0.6 keV and 0.9 keV, most likely associated with O VIII Lyα and Fe XVIII–Fe XIX. However, this possible complexity of the model is not well constrained by our data.
As we have already discussed above, the spectral evolution of ESO 243-49 HLX-1 was previously investigated using the Swift data by many authors. In particular, Soria et al. (2010) and Yan et al. (2015) studied the 2008–2009 and 2009–2015 Swift-data sets (see also Table 1) using an additive diskbb plus power-law model and a simple power-law model. These qualitative models describe an evolution of these spectral model parameters throughout state transitions during the outbursts.
Note, we have also found a similar spectral behavior using our model and the full set of the Swift observations. In particular, like in the aforementioned Soria’s and Yan’s et al. papers, we have also revealed that HLX-1 demonstrates monotonic growth of the photon index Γ during the LHS–HSS transition from ~1.6 to 3. In addition, we revealed that Γ tends to saturate at 3 at high values of Nbmc. In other words we found that Γ saturates at high values of mass accretion rate.
In the LHS the seed photons with the lower kTs, related to lower mass accretion rate, are Comptonized more efficiently because the illumination fraction f (or log (A)) is higher. In contrast, in the HSS, these parameters, kTs and log (A) show an opposite behavior, namely log (A) is lower for higher kTs. That means that a relatively small fraction of the seed photons, which temperature is higher because of the higher mass accretion rate in the HSS than that in the LHS, is Comptonized.
Note, our spectral model shows very good performance throughout all data sets. In Table 2 we demonstrate a good performance of the BMC model in application to the Swift data (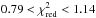 ). The reduced
). The reduced 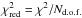 (where Nd.o.f. is the number of degree of freedom) is less or around 1 for all observations.
(where Nd.o.f. is the number of degree of freedom) is less or around 1 for all observations.
We can also estimate a radius of the blackbody emission region. We found the blackbody radius RBB derived using a relation 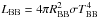 , where LBB is the seed blackbody luminosity and σ is the Stefan-Boltzmann constant. With a distance D to the source of 95 Mpc, we obtain that the region associated with the blackbody has a radius of RBB ~ 5 × 106 km. Such a large BB region should be only around the IMBH and thus, probably ESO 243-49 HLX-1 is the IMBH source. Taking into account that the BMC normalization varies by a factor of 15 and the Bbody (seed) temperature Ts changes by a factor of 2 (see Table 2) we find that the bbody radius is almost constant. Note, RBB is of order of 10−30 km for a Galactic BH of mass around 10 solar masses (see STS14).
, where LBB is the seed blackbody luminosity and σ is the Stefan-Boltzmann constant. With a distance D to the source of 95 Mpc, we obtain that the region associated with the blackbody has a radius of RBB ~ 5 × 106 km. Such a large BB region should be only around the IMBH and thus, probably ESO 243-49 HLX-1 is the IMBH source. Taking into account that the BMC normalization varies by a factor of 15 and the Bbody (seed) temperature Ts changes by a factor of 2 (see Table 2) we find that the bbody radius is almost constant. Note, RBB is of order of 10−30 km for a Galactic BH of mass around 10 solar masses (see STS14).
We have also found that the emergent spectra of ESO 243-49 HLX-1 undergo an evolution from the low/hard state to the high/soft state (see Figs. 1 and 4). In Table 2 we present a change of the seed photon temperature kTs, the BMC normalization and the photon index Γ during 2008−2015 outburst transitions observed with Swift/XRT.
 |
Fig. 6 Examples of E ∗ F(E) spectral diagram of ESO 243–49 HLX–1 during the hard, intermediate and soft state events. The best-fit Swift spectra (top panel) using the BMC model, along with Δχ (bottom panel) for the hard (band-B) state ( |
In particular, we detected a high value of the seed photon temperature kTs = 130 eV in the high/soft state (see Table 2, band-G). On the other hand, the low/hard state of ESO 243-49 HLX-1 is associated with the low kTs ~ 54 eV (see Table 2, band-A).
We also establish that the photon index Γ correlates with the BMC normalization, NBMC (proportional to mass accretion rate Ṁ) and finaly saturates at high values of Ṁ (see Fig. 7). The index Γ monotonically grows from 1.3 to 2.8 with Ṁ and then finally saturates at Γsat = 3.0 ± 0.1 for high values of Ṁ.
4. Discussion
4.1. Saturation of the index as a signature of a BH
Having applied our analysis of the evolution of the photon index Γ in ESO 243-49 HLX-1 we probably find the photon index, Γ saturation with mass accretion rate, Ṁ. In fact, ST09 demonstrates this index saturation is a first indication of the converging flow into a BH.
In the early paper by Titarchuk et al. (1998) it was demonstrated using the equation of motion that the innermost part of the accretion flow (TL), shrinks when Ṁ grows. It is worthwhile to emphasize that for a BH the photon index Γ grows and saturates for high Ṁ. Titarchuk & Zannias (1998), hereafter TZ98, semi-analytically discovered the saturation effect and later Laurent & Titarchuk (1999, 2011), hereafter LT99 and LT11, confirmed this effect making Monte Carlo simulations.
Observations of many Galactic BHs (GBHs) and their X-ray spectral analysis (see ST09, Titarchuk & Seifina 2009; Seifina & Titarchuk 2010, and STS14) demonstrate a confrmation of this TZ98 prediction. For our particular source HLX-1, we also reveal that Γ monotonically increases from 1.6 and then they finally saturates at a value of 3.0 (see Fig. 7).
 |
Fig. 7 Correlation of the photon index Γ (=α + 1) versus the BMC normalization NBMC (proportional to mass accretion rate) in units of |
Using the index-Ṁ correlation found in ESO 243-49 HLX-1 allows us to estimate a BH mass in this source scaling this correlation with those detected in a number of GBHs and M101 ULX-1 (see details below, in Sect. 4.3).
Parameterizations for the reference and target sources.
4.2. X-ray spectra of ULXs
As we have already pointed out above that there are different scenarios for a ULX central source: stellar mass black hole, intermediate mass black hole and neutron star. Possibly, the ULX population is not homogeneous and thus, different ULXs can be related to different origins. In particular, Soria & Kong (2016) find arguments to introduce two sub-classes of ULXs: (i) “hyperluminous” X-ray sources (e.g., ESO 243–49 HLX–1) and “supersoft” ULXs (e.g., M101 ULX–1), but discussion of this classification is outside of this work. However, in spite of these differences and their classifications as ULXs, we can suggest a possible similarity between ESO 243–49 HLX–1 source with M101 ULX–1 and a number of GBHs in terms of their index-mass accretion rate (Γ-Nbmc) correlations.
We note that Yan et al. (2015) did not find any similarity between HLX-1 and GBHBs in terms of the relations of the total radiated energy versus peak luminosity, as well as the total radiated energy vs. e-folding rise/decay timescales (see Figs. 8 and 10, respectively there). On the other hand, we compare the Γ-Nbmc correlations of M101 ULX-1, ESO 243-49 HLX-1 and those found in GBHs, as a result we find they are self-similar and thus, we can apply them to estimate BH mass in ESO 243-49 HLX-1 (see Fig. 8).
4.3. An estimate of BH mass in ESO 243-49 HLX-1 and its comparison with that found in the literature
In order to estimate BH mass, MBH of ESO 243–49 HLX–1, we choose three galactic sources (XTE J1550–564, H 1742–322 (see ST09) and 4U 1630-47 (see STS14)) and an extragalactic source M101 ULX-1 (see TS16), whose BH masses and distances are early estimated (see Table 4), as the reference sources. In particular, BH mass for XTE J1550–564 is estimated by dynamical methods. For a BH mass estimateof ESO 243–49 HLX–1 we also use the BMC normalizations, NBMC of these reference sources. Thus, we scale the index vs. NBMC correlations for these reference sources with that of the target source ESO 243-49 HLX-1 (see Fig. 8). The value of the index saturation is almost the same, Γ ~ 3 for all these target and reference sources. We apply the correlations found in these four reference sources to make a comprehensive cross-check of a BH mass estimate for ESO 243-49 HLX-1.
 |
Fig. 8 Scaling of the photon index, Γ versus the normalization NBMC for ESO 243–49 HLX–1 (black points – target source) using those correlations for the Galactic reference sources, 4U 1630-472, XTE J1550-564 and H1743-322 (pink, blue and green, left panel) and comparison of Γ−NBMC correlations for extragalactic sources, ESO 243-49 HLX–1 and M101 ULX-1 (red points, see right panel). |
As one can see from Fig. 8, the correlations of the target source (ESO 243-49 HLX-1) and the reference sources have similar shapes and index saturation levels. Thus, it allows us to make a reliable scaling of these correlations with that of ESO 243-49 HLX-1. In order to implement the scaling technique we introduce an analytical approximation of the Γ−Nbmc correlation, fitted by a function (see also ST09) ![\begin{equation} F(x)= {\cal A} - ({\cal D}\cdot {\cal B})\ln\{\exp[(1.0 - (x/x_{\rm tr})^{\beta})/{\cal D}] + 1\}, \label{scaling function} \end{equation}](/articles/aa/full_html/2016/11/aa27840-15/aa27840-15-eq129.png) (1)with x = Nbmc. As a result of fitting of the observed correlation by this function F(x) we obtained a set of the best-fit parameters
(1)with x = Nbmc. As a result of fitting of the observed correlation by this function F(x) we obtained a set of the best-fit parameters 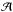 , ℬ,
, ℬ, 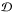 , Ntr, and β. The meaning of these parameters is described in details in our previous paper (Titarchuk & Seifina 2016, hereafter TS16). This function F(x) is widely used for a description of the correlation of Γ versus Nbmc (Sobolewska & Papadakis 2009, ST09; Seifina & Titarchuk 2010; Shrader et al. 2010, STS14; Giacche et al. 2014, and TS16).
, Ntr, and β. The meaning of these parameters is described in details in our previous paper (Titarchuk & Seifina 2016, hereafter TS16). This function F(x) is widely used for a description of the correlation of Γ versus Nbmc (Sobolewska & Papadakis 2009, ST09; Seifina & Titarchuk 2010; Shrader et al. 2010, STS14; Giacche et al. 2014, and TS16).
BH masses and distances.
In order to implement this BH mass estimate for the target source one should rely on the same shape of the Γ−Nbmc correlations for the target source and those for the reference sources. The only difference in values of Nbmc for these four sources is in a ratio of BH mass to the squared distance, MBH/d2. As one can see from Fig. 8 the index saturation value, 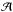 is approximately the same for the target and reference sources (see also the second column in Table 3). For example, as one can see, that the shape of the correlations for ESO 243-49 HLX-1 (black line) and H 1734-322 (green line)] are similar and the only difference of these correlations is in the BMC normalization values (proportional to MBH/d2 ratio).
is approximately the same for the target and reference sources (see also the second column in Table 3). For example, as one can see, that the shape of the correlations for ESO 243-49 HLX-1 (black line) and H 1734-322 (green line)] are similar and the only difference of these correlations is in the BMC normalization values (proportional to MBH/d2 ratio).
To estimate BH mass, Mt of ESO 243-49 HLX-1 (target source) one should shift the reference source correlation along Nbmc-axis to that of the target source (see Fig. 8).
where t and r correspond to the target reference sources, repectively and a geometric factor, fG = (cosθ)r/ (cosθ)t, the inclination angles θr, θt and dr, dt are distances to the reference and target sources respectively (see ST09). One can see values of θ in Table 4) and if some of these θ-values are unavailable then we assume that fG ~ 1.
In Fig. 8 we demonstrate the Γ−Nbmc correlation for ESO 243–49 HLX–1(black points) obtained using the Swift spectra along with the correlations forthree Galactic reference sources (XTE J1550-564 (blue), 4U 1630-47 (pink), and H 1743-322 (green), see left panel) and one extragalactic reference source M101 ULX-1 (red, see right panel). BH masses and distances for each of these target-reference pairs are shown in Table 4.
Note, BH mass, Mt for HLX-1 can be evaluated using a formula (see TS16) 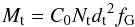 (3)where
(3)where 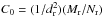 is the scaling coefficient for each of the pairs (target and reference sources), masses Mt and Mr are in solar units and dr is the distance to a particular reference source measured in kpc.
is the scaling coefficient for each of the pairs (target and reference sources), masses Mt and Mr are in solar units and dr is the distance to a particular reference source measured in kpc.
We use values of Mr, Mt, dr, dt, and cos(i) from Table 4 and then we calculate the lowest limit of the mass, using the best fit value of Nt = (4.2 ± 0.1) × 10-6 taken them at the beginning of the index saturation (see Fig. 8) and measured in units of 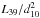 erg s-1 kpc-2 (see Table 3 for values of the parameters of function F(Nt) (see Eq. (1))). Using dr, Mr, Nr (see ST09) we found that C0 ~ 2.0,1.9, 1.72 and 1.83 for M101 ULX-1, XTE J1550-564, H 1723-322 and 4U 1630-472. Finally, we obtain that MHLX ≥ 7.2 × 104M⊙ (MHLX = Mt) assuming dHLX ~95 Mpc (Soria et al. 2010) and fG ~ 1. We summarize all these results in Table 4,
erg s-1 kpc-2 (see Table 3 for values of the parameters of function F(Nt) (see Eq. (1))). Using dr, Mr, Nr (see ST09) we found that C0 ~ 2.0,1.9, 1.72 and 1.83 for M101 ULX-1, XTE J1550-564, H 1723-322 and 4U 1630-472. Finally, we obtain that MHLX ≥ 7.2 × 104M⊙ (MHLX = Mt) assuming dHLX ~95 Mpc (Soria et al. 2010) and fG ~ 1. We summarize all these results in Table 4,
It is worth noting that the inclination of ESO 243-49 HLX-1 may be different from those for the reference Galactic sources (i ~ 60−70°), therefore we take this BH mass estimate for ESO 243-49 HLX-1 as the lowest BH mass value because that MHLX is reciprocal function of cos(iHLX) (see Eq. (3) taking into account that fG = (cosθ)r/ (cosθ)t there). The obtained BH mass estimate is in agreement with a high bolometrical luminosity for ESO 243-49 HLX-1 and kTs value which is in the range of 50−140 eV. A very soft spectrum is consistent with a relatively cold disk for a compact object of high mass. For example, Shakura & Sunyaev (1973; see also Novikov & Thorne 1973) provide an effective temperature of the accretion material of 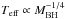 .
.
Yan et al. (2015), suggested that the soft-to-hard state transition luminosity of HLX-1 is at 2% of LEdd based on an analogy to the Galactic BHs, and estimated mass of the accreting compact object as (8 ± 4) × 104 M⊙. It is also important to emphasize that this original mass estimate for the central source in HLX-1, based on a particular X-ray luminosity, is consistent with our scaling BH mass estimate for HLX-1. In addition, our HLX-1 mass estimate is also consistent with IMBH mass of ~104−105 M⊙ derived using a detailed X-ray spectral modelling (Farrell et al. 2010; Davis et al. 2011; Servillat et al. 2011; Godet et al. 2012; Webb et al. 2012)and with the results obtained by Cseh et al. (2014) (MBH< 106 M⊙).
We derived the bolometric luminosity between 3 × 1041 erg/s and 4 × 1042 erg/s based on the normalization of the BMC model. It is evident that this high luminosity is difficult to achieve in a X-ray binary unless the accretor has a mass greater than 103 M⊙ to be consistent with the Eddington limit. Note, our luminosity estimate is in agreement with that previously obtained for HLX-1 with different instruments (see Farrell et al. 2009; Godet et al. 2009; Yan et al. 2015). However, Soria et al. (2013) using optical observations (FORS2 spectrograph on the Very Large Telescope), find that the Hα emission from HLX-1 (LHα ≈ a few times of 1037 erg/s) could be excited by X-ray luminosity of ~1040 erg/s, which is an order of magnitude smaller than the mean luminosity observed over 2009–2012. Soria et al. suggested that the observed Hα emission comes not from the disk surface (it does not have a disk-like profile) but from some material further out, or perhaps from the remnants of previous outflows.
4.4. Possible effects on an estimate of BH mass in ESO 243–49
Now we discuss some potential sources of systematic errors which can affect the validity of our method.
4.4.1. Suggestion on a similarity of Galactic BHs binaries and HLX−1
This similarity is based on comparative analysis of spectral properties for these two classes of objects which are revealed during X-ray outbursts (see Sect. 3.2). In particular, we clearly observe softening of X-ray emission with X-ray outburst flux in HLX–1 (e.g., Fig. 1), which is similar to that in the bright Galactic low-mass X-ray binaries.
Note, that the hardness-intensity diagram shown in Fig. 1 are model independent. We demonstrate that spectra of HLX–1 are poorly fitted by power-law, bbody models and their combination (see Table 2). The detailed modeling of X-ray spectral shape reveals strong rising of the low-energy component (for photon energies less than 1 keV) along with steepening of the higher energy tail during outburst development. This observational effect is a strong confirmation of the converging inflow paradigm in the case of a BH source (see Shaposhnikov & Titarchuk 2009).
4.4.2. Validity of BH mass determination in ESO 243–49 using Galactic BH mass values
In this paper, we used Galactic X-ray binaries to compare their spectral characteristic with those established in ESO 243–49 HLX–1. We use XTE J1550–564 for which the mass of compact object (BH) is evaluated applying “gold standard” dynamical measurements (Orosz 2002). Therefore, BH mass scaling for a pair of ESO 243–49 HLX–1 and XTE J1550–564 provides a reliable BH mass estimate for ESO 243–49 HLX–1. However, the BH mass values of other objects used for scaling procedure, such as 4U 1630–47, H 1743–322, are not based on dynamical measurements and can not be considered as “traditional” BH estimates. It is worth noting that the BH mass value for ESO 243–49 using these BH estimates for 4U 1630–47, H 1743–322 well agrees with that applying BH mass of XTE J1550–564.
4.4.3. Validity of BH mass estimate in ESO 243–49 using scaling with M101 ULX–1
We used the extragalactic source M101 ULX–1 for a BH mass estimate in ESO 243–49. We should point out a wide range of the BH mass estimates for M101 ULX–1 obtained applying X-ray (Kong et al. 2004; Kong & Di Stefano 2005; TS16) and optical data (Liu et al. 2013). In particular, Kong et al. (2004) based on Chandra and XMM-Newton observations of this source during the 2004 July outburst, obtained an estimate for BH mass greater than 2800 M⊙. While, Kong & Di Stefano (2005) suggested that Mm101 is in the range of 1.3 × 103−3 × 104 M⊙. In our recent paper (see TS16) we found, using Swift (2006–2013) and Chandra (2000, 2004, 2005) data, that BH mass in this source is of order of ~104 M⊙ using scaling method (ST09) (which is comparable with the Kong & Di Stefano’s BH values). On the other hand, based on HST optical data of M101 ULX–1 and using the dynamical method, Liu et al. (2013) estimated mass of the compact object as 5–1000 M⊙. Note, that Liu et al. (2013) made this BH mass estimate based on radial velocity analysis adopting a simple two-point mass model for a binary without taking into account a tidal influence and a heating effect to the optical star by the X-ray companion, which can significantly change the resulting BH mass value (Antokhina & Cherepashchuk 1994; Antokhina et al. 2016; Petrov et al. 2016).
Thus, one can see a tendency for smaller values of BH mass, 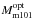 using optical data and bigger ones,
using optical data and bigger ones, 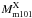 utilizing X-ray data. While we estimate BH mass in ESO 243–49, 3 × 103<MESO< 7 × 104 M⊙ applying scaling technique with “X-ray mass”
utilizing X-ray data. While we estimate BH mass in ESO 243–49, 3 × 103<MESO< 7 × 104 M⊙ applying scaling technique with “X-ray mass” 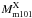 (2.8 × 103−3 × 104 M⊙, see TS16). Note, applying “an optical BH mass” estimate
(2.8 × 103−3 × 104 M⊙, see TS16). Note, applying “an optical BH mass” estimate 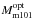 (5−103 M⊙), we find lower masses within a wide interval of from 7 M⊙ to 2 × 103 M⊙ for MESO which is inconsistent with so called “fundamental plane” results 103<MESO< 105 M⊙ (see Davis et al. 2011; and Godet et al. 2011). Thus, one can conclude that our scaling method in application to the pair of BH sources ESO 243–49 and M101 ULX–1 leads to better constraints in the case of “X-ray BH mass”, than that of “optical BH mass”.
(5−103 M⊙), we find lower masses within a wide interval of from 7 M⊙ to 2 × 103 M⊙ for MESO which is inconsistent with so called “fundamental plane” results 103<MESO< 105 M⊙ (see Davis et al. 2011; and Godet et al. 2011). Thus, one can conclude that our scaling method in application to the pair of BH sources ESO 243–49 and M101 ULX–1 leads to better constraints in the case of “X-ray BH mass”, than that of “optical BH mass”.
We should note that found massive BHs in ESO 243–49 and M101 ULX–1 are not in galactic nuclei as it should be in the case of supermassive BHs (SMBHs). As known, the stellar bulge of almost every massive galaxy contains a SMBH (Ferrarese & Ford 2000). When galaxies merge they can form two or more SMBHs with their stellar bulges which are outside of a galactic center. Following a merger, a pair of inspiraling SMBHs can spend for a while in separation before forming a tight binary or finally merge (see Begelman et al. 1980). Similarly, large mass of some IMBHs can be formed as a result of merging of galaxy nuclei. This scenario can be a valid argument for large masses in M101 ULX–1 and ESO 243–49.
Up to now there are still many open quiestions from a theoretical point of view how to explain a formation of massive BHs (such as IMBHs). Recently, Latif & Ferrara (2016) discussed possible formation mechanisms of supermassive BHs. In particular, they suggested that “seed” BHs were formed early on, and grown either due to rapid accretion or BH/galaxy mergers. Latif & Ferrara offered three most popular BH formation scenarios: dynamical evolution of dense nuclear star clusters, a core-collapse of massive stars, and a collapse of a protogalactic metal free gas cloud.
Note, we include M101 ULX–1 in a scaling BH mass sample for ESO 243–49, in spite of the fact that Soria & Kong (2016) presented strong arguments that the observed emission in M101 ULX–1 is not a classic accretion disk. Specifically, Soria & Kong re-examined the X-ray spectral and timing properties of M101 ULX–1 using a series of Chandra and XMM-Newton observations and showed that their model of an optically thick outflow is consistent with the data. They demonstrated that the characteristic radius, RBB of a thermal emitter and its color temperature, kTBB are approximately related to each other as 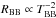 . In addition, they revealed absorption edges fitting the M101 ULX–1 spectra applying thermal plasma models. They interpreted this modeling along with the data as an evidence of a clumpy, multi-temperature outflow around ULX–1, in particularly in the HSS. Soria & Kong highlight that M101 ULX–1 belong to ultraluminous supersoft sources (ULSs) rather than to ULX population. Thus, one can argue that if Soria & Kong are correct then the method of the BH mass determination applied here might not be applicable for M101 ULX–1.
. In addition, they revealed absorption edges fitting the M101 ULX–1 spectra applying thermal plasma models. They interpreted this modeling along with the data as an evidence of a clumpy, multi-temperature outflow around ULX–1, in particularly in the HSS. Soria & Kong highlight that M101 ULX–1 belong to ultraluminous supersoft sources (ULSs) rather than to ULX population. Thus, one can argue that if Soria & Kong are correct then the method of the BH mass determination applied here might not be applicable for M101 ULX–1.
However, our arguments based on the correlation of the photon index with the mass accretion rate in M101 ULX–1 and its resemblance with those in a number of Galactic sources allow us argue that the innermost part of the accretion flow (the disk-Compton cloud-converging flow configuration) is similar in these sources (see TS16 and Fig. 5 here). Moreover, this index-mass accretion rate correlation for M101 ULX-1 is almost identical in terms of the shape for that in ESO 243–49 HLX–1 and those in the chosen Galactic BHs. It is not by chance that we compare all these correlations with each other and find that they are self-similar.
It is worthwhile to point out that Soria & Kong (2016) described the hard tail of the Chandra ULX spectrum of M101 ULX-1 using higher temperatures. They revealed a relatively hard tail in the 0.3–6 keV energy range and apply three mekal components in addition to sample a soft Bbody component. In this case of the high count-rate spectra of three of these mekal components are associated with temperatures of 0.6 keV, 1 keV and ≥2 keV. However, when Soria & Kong replaced this multiple component model by the single Comptt (Titarchuk 1994) component (see Table A3 there), they also obtained a good quality fit with the seed photon temperatures in the range of 90–135 eV.
5. Conclusions
We found the low-high state transitions observed in HLX-1 using the full set of Swift/XRT observations (2008–2015) and we demonstrated a validity of fitting the observed spectra by the BMC model for all observations, independently of the spectral state of the source.
We investigated the X-ray outburst properties of HLX-1 and confirmed the presence of spectral state transitions during the outbursts using of hardness-intensity diagrams (Godet et al. 2009; Servillat et al. 2011) and the index-normalization (or Ṁ) correlation observed in HLX-1, which were similar to those in Galactic BHs. In particular, we find that HLX-1 follows the Γ−Ṁ correlation previously obtained for extragalactic IMBH source M101 ULX-1 and Galactic BHs, 4U 1630-472, XTE J1550-564 and H 1743-322 with taking into account the particular values of the MBH/d2 ratio (Fig. 8). The photon index Γ of ESO 243-49 HLX-1 spectrum is in the range Γ = 1.6−3.0. We also estimate the peak bolometric luminosity, which is about 4 × 1042 erg s-1.
We use the observed index-mass accretion rate correlation to estimate MBH in HLX-1. This scaling method was successfully implemented to find BH masses of Galactic (e.g. ST09, STS13) and extragalactic black holes (TS16; Sobolewska & Papadakis 2009; Giacche et al. 2014). An application of the scaling technique to the X-ray data from XRT/Swift observations of ESO 243-49 HLX-1 allows us to estimate MBH for this particular source. We found values ofMBH ≥ 7.2 × 104M⊙.Furthermore, our BH mass estimate is in an agreement with the previous IMBH mass of ~104−105 M⊙ derived using the detailed X-ray spectral modelling (Farrell et al. 2010; Davis et al. 2011; Servillat et al. 2011; Godet et al. 2012; Webb et al. 2012). Combining all these estimates with the inferred low temperatures of the seed disk photons kTs we can state that the compact object of ESO 243-49 HLX-1 is likely tobe an intermediate-mass black hole with at least MBH> 7.2 × 104M⊙.
A Fortran and C-based program which calculates the ratios using the methods described by Park et al. (2006) (see http://hea-www.harvard.edu/AstroStat/BEHR/).
Acknowledgments
This research was performed using data supplied by the UK Swift Science Data Centre at the University of Leicester. We also acknowledge the interesting remarks and points of the referee.
References
- Afonso, J., Georgakakis, A., Almeida, C., et al. 2005, ApJ, 624, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Antokhina, E. A., & Cherepashchuk, A. M. 1994, Astron. Rep., 38, 367 [NASA ADS] [Google Scholar]
- Antokhina, E. A., Petrov, V. S., & Cherepashchuk, A. M. 2016, Astron. Rep., 93, in press [Google Scholar]
- Arnaud, K. A. 1996, Astronomical Data Analysis Software and Systems V, eds. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [Google Scholar]
- Bachetti, M., Harrison, F. A., Walton, D. J., et al. 2014, Nature, 514, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Begelman, M. C., Blandford, R. D., & Rees, M. J. 1980, Nature, 287, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, D., Hill, J. E., Nousek, J. A., et al. 2005, Sp. Sci. Rev., 120 [Google Scholar]
- Cseh, D., Webb, N. A., Godet, O., et al. 2015, MNRAS, 446, 3268 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, Sh. W., Narayan, R., Zhu, Y., et al. 2011, ApJ, 734, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, P. A., Beardmore, A. P., Page, K. L., et al. 2007, A&A, 469, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, P. A., Beardmore, A. P., Page, K. L., et al. 2009, MNRAS, 397, 1177 [NASA ADS] [CrossRef] [Google Scholar]
- Harrison, F. A., Craig, W. W., Christensen, F. E., et al. 2013, ApJ, 770, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Farrell, S. A., Webb, N. A., Barret, D., Godet, O., & Rodrigues, J. M. 2009, Nature, 460, 73 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Farrell, S. A., Servillat, M., Oates, S. R., et al. 2010, X-ray Astronomy 2009; Present Status, Multi-Wavelength Approach and Future Perspectives, AIP Conf. Proc., 1248, 93 [Google Scholar]
- Farrell, S. A., Servillat, M., Pforr, J., et al. 2012, ApJ, 747, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Freeland, M., Kuncic, Z., Soria, R., & Bicknell, G. V. 2006, MNRAS, 372, 630 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Giacche, S., Gili, R., & Titarchuk, L. 2014, A&A, 562, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Godet, O., Barret, D., Webb, N. A., Farrell, S. A., & Gehrels, N. 2009, ApJ, 705, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Godet, O., Farrell, S. A., Barret, D., Webb, N. A., & Servillat, M. 2011, Atel, 3569 [Google Scholar]
- Godet, O., Plazolles, B., Kawaguchi, T., et al. 2012, ApJ, 752, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Kelson, D. D., Illingworth, G. D., Freedman, W. F., et al. 1996, ApJ, 463, 26 [NASA ADS] [CrossRef] [Google Scholar]
- King, A. R. 2008, MNRAS, 385, L113 [NASA ADS] [CrossRef] [Google Scholar]
- King, A., & Lasota, J.-P. 2014, MNRAS, 444, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Kong, A. K. H., & Di Stefano, R. 2005, ApJ, 632, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Kong, A. K. H., Di Stefano, R., & Yuan, F. 2004, ApJ, 617, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Lasota, J.-P., Alexander, T., Dubus, G., et al. 2011, ApJ, 735, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Lasota, J.-P., King, A. R., & Dubus, G. 2015, ApJ, 801, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Latif, M. A., & Ferrara, A. 2016, PASA, in press [arXiv:1605.07391] [Google Scholar]
- Liu, J., Bregman, J. N., Bai, Y., et al. 2013, Nature, 503, 500 [NASA ADS] [CrossRef] [Google Scholar]
- Laurent, P., & Titarchuk, L. 1999, ApJ, 511, 289 (LT99) [NASA ADS] [CrossRef] [Google Scholar]
- Malumuth, E. M., Kriss, G. A., Dixon, W. V. D., Ferguson, H. C., & Ritchie, C. 1992, AJ, 104, 495 [NASA ADS] [CrossRef] [Google Scholar]
- Mukai, K., Still, M., Corbet, R., Kuntz, K., & Barnard, R. 2005, ApJ, 634, 1085 [NASA ADS] [CrossRef] [Google Scholar]
- Muñoz-Darias, T., Fender, R. P., Motta, S. E., & Belloni, T. M. 2014, MNRAS, 443, 3270 [NASA ADS] [CrossRef] [Google Scholar]
- Novikov, I. D., & Thorne, K. S. 1973, Black holes (Les astres occlus), 343 [Google Scholar]
- Orosz, J. A., Groot, P. J., van der Klis, M., et al. 2002, ApJ, 568, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Papadakis, I. E., Sobolewska, M., Arevalo, P., et al. 2009, A&A, 494, 905 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Park, T., Kashyap, V. L., Siemiginowska, A., et al. 2006, ApJ, 652, 610 [NASA ADS] [CrossRef] [Google Scholar]
- Petri, J. 2008, Ap&SS, 318, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Petrov, V. S., Antokhina, E. A., & Cherepashchuk, A. M. 2016, Astron. Rep., 93, in press [Google Scholar]
- Saǹchez-Fernàndez, C., Castro-Tirado, A. J., Duerbeck, H. W., et al. 1999, A&A, 348, L9 [NASA ADS] [Google Scholar]
- Seifina, E., & Titarchuk, L. 2010, ApJ, 722, 586 (ST10) [NASA ADS] [CrossRef] [Google Scholar]
- Seifina, E., & Titarchuk, L. 2011, ApJ, 738, 128 (ST11) [NASA ADS] [CrossRef] [Google Scholar]
- Seifina, E., & Titarchuk, L. 2012, ApJ, 747, 99 (ST12) [NASA ADS] [CrossRef] [Google Scholar]
- Seifina, E., Titarchuk, L., & Frontera, F. 2013, ApJ, 766, 63 (STF13) [NASA ADS] [CrossRef] [Google Scholar]
- Seifina, E., & Titarchuk, L., & Shaposhnikov, N. 2014, ApJ, 789, 57 (STS14) [NASA ADS] [CrossRef] [Google Scholar]
- Seifina, E., Titarchuk, L., Shraider, Ch., & Shaposhnikov, N. 2015, ApJ, 808, 142 (STSS15) [NASA ADS] [CrossRef] [Google Scholar]
- Servillat, M., Farrell, S. A., Lin, D., Godet, O., Barret, D., & Webb, N. A. 2011, ApJ, 743, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Shaposhnikov, N., & Titarchuk, L. 2006, ApJ, 643, 1098 (ST06) [NASA ADS] [CrossRef] [Google Scholar]
- Shaposhnikov, N., & Titarchuk, L. 2009, ApJ, 699, 453 (ST09) [NASA ADS] [CrossRef] [Google Scholar]
- Sobolewska, M. A., & Papadakis, I. E. 2009, MNRAS, 399, 1997 [Google Scholar]
- Soria, R. 2013, MNRAS, 428, 1944 [NASA ADS] [CrossRef] [Google Scholar]
- Soria, R., & Kong, A. 2016, NMRAS, 456, 1837 [Google Scholar]
- Soria, R., Zampieri, L., Zane, S., et al. 2010, MNRAS, 405, 870 [NASA ADS] [Google Scholar]
- Soria, R., Hakala, P. J., Hau, G. K. T., Gladstone, J. C., & Kong, A. K. H. 2012, MNRAS, 420, 3599 [NASA ADS] [CrossRef] [Google Scholar]
- Shappee, B., & Stanek, K. Z. 2011, ApJ, 733, 12 [Google Scholar]
- Shrader, Ch. R., Titarchuk, L., & Shaposhnikov, N. 2010, ApJ, 718, 488 [NASA ADS] [CrossRef] [Google Scholar]
- Sobczak, G. J., McClintock, J. E., Remillard, R. A., & Bailyn, C. D. 1999, ApJ, 520, 776 [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L. 1994, ApJ, 429, 340 [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L., & Zannias, T. 1998, ApJ, 499, 315 (TZ98) [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L., & Seifina, E. 2009, ApJ, 706, 1463 [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L., & Seifina, E. 2016, A&A, 585, A94 (TS16) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Titarchuk, L., Mastichiadis, A., & Kylafis, N. D. 1997, ApJ, 487, 834 [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L., Lapidus, I. I., & Muslimov, A. 1998, ApJ, 499, 315 (TLM98) [NASA ADS] [CrossRef] [Google Scholar]
- Webb, N. A., Barret, D., Godet, O., et al. 2010, ApJ, 712, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Webb, N., Cseh, D., Lenc, E., et al. 2012, Science, 337, 554 [NASA ADS] [CrossRef] [Google Scholar]
- Wiersema, K., Farrell, S. A., Webb, N. A., et al. 2010, ApJ, 721, L102 [NASA ADS] [CrossRef] [Google Scholar]
- Yan, Z., Wenda, Z., Soria, R., et al. 2015, ApJ, 811, 23 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Best-fit parameters of the combined Swift spectra of ESO 243-49 HLX-1 in the 0.3−10 keV range using the following four models†: phabs*power-law, phabs*bbody, phabs*(bbody+power-law) and phabs*bmc.
All Figures
 |
Fig. 1 Hardness-intensity diagram for ESO 243-49 HLX-1 using Swift observations (2008–2015) during spectral evolution from the low/hard state to the high/soft states. In the vertical axis, the hardness ratio (HR) is a ratio of the source counts in the two bands: the hard (1.5–10 keV) and soft (0.3–1.5 keV) passbands. The HR decreases with a source brightness in the 0.3–10 keV energy range (horizontal axis). For clarity, we plot only one point with error bars (shown in the bottom right corner) to demonstrate typical uncertainties for the HR and count rate. |
| In the text | |
 |
Fig. 2 The Chandra/HRC-I (0.1–10 keV) image of the ESO 243-49 HLX-1 field taken on UT 2009 July 4, where yellowsmall circle corresponds to the location of ESO 243-49 HLX-1 and white arrow points correspond to 2XMM J011050.4-460013 source. The large circles (labeled nominal and offset) show the two pointing positions used for the light curve and spectrum extractions in order to minimize contamination of ESO 243–49 HLX–1 by nearby source. |
| In the text | |
 |
Fig. 3 Swift/XRT light curve of ESO 243-49 HLX-1 in the 0.3−10 keV energy range during 2008–2015. Red points mark the source signal (with 2σ detection level) and green points indicate the background level. Blue dashed line indicatesthe MJD of the Chandra/HRC-I observation presented in Fig. 2. |
| In the text | |
 |
Fig. 4 Seven EFE spectral diagrams which are related to different spectral states of ESO 243-49 HLX-1 using the BMC model. The data are taken from XRT/Swift observations related to different hardness ratios: left: HR < 0.03 (black, HSS), 0.03 < HR < 0.07 (bright blue, HSS), 0.5 < HR < 1 (pink, LHS); right: 0.1 < HR < 0.2 (blue, IS), 0.07 < HR < 0.2 (red, HSS), 0.2 < HR < 0.5 (orange, IS), HR > 1 (green, LHS). |
| In the text | |
 |
Fig. 5 A suggested geometry for ESO 243-49 HLX-1 source. Disk soft photons are upscattered (Comptonized) off relatively hot plasma of the transition layer. |
| In the text | |
 |
Fig. 6 Examples of E ∗ F(E) spectral diagram of ESO 243–49 HLX–1 during the hard, intermediate and soft state events. The best-fit Swift spectra (top panel) using the BMC model, along with Δχ (bottom panel) for the hard (band-B) state ( |
| In the text | |
 |
Fig. 7 Correlation of the photon index Γ (=α + 1) versus the BMC normalization NBMC (proportional to mass accretion rate) in units of |
| In the text | |
 |
Fig. 8 Scaling of the photon index, Γ versus the normalization NBMC for ESO 243–49 HLX–1 (black points – target source) using those correlations for the Galactic reference sources, 4U 1630-472, XTE J1550-564 and H1743-322 (pink, blue and green, left panel) and comparison of Γ−NBMC correlations for extragalactic sources, ESO 243-49 HLX–1 and M101 ULX-1 (red points, see right panel). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.