| Issue |
A&A
Volume 594, October 2016
|
|
|---|---|---|
| Article Number | A89 | |
| Number of page(s) | 9 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201628342 | |
| Published online | 17 October 2016 | |
Stability of multiplanet systems in binaries
Dipartimento di Fisica, University of Padova, via Marzolo 8, 35131 Padova, Italy
e-mail: Francesco.Marzari@pd.infn.it
Received: 19 February 2016
Accepted: 19 July 2016
Context. When exploring the stability of multiplanet systems in binaries, two parameters are normally exploited: the critical semimajor axis ac computed by Holman & Wiegert (1999, AJ, 117, 621) within which planets are stable against the binary perturbations, and the Hill stability limit Δ determining the minimum separation beyond which two planets will avoid mutual close encounters. Both these parameters are derived in different contexts, i.e. Δ is usually adopted for computing the stability limit of two planets around a single star while ac is computed for a single planet in a binary system.
Aims. Our aim is to test whether these two parameters can be safely applied in multiplanet systems in binaries or if their predictions fail for particular binary orbital configurations.
Methods. We have used the frequency map analysis (FMA) to measure the diffusion of orbits in the phase space as an indicator of chaotic behaviour.
Results. First we revisited the reliability of the empirical formula computing ac in the case of single planets in binaries and we find that, in some cases, it underestimates by 10–20% the real outer limit of stability and it does not account for planets trapped in resonance with the companion star well beyond ac. For two-planet systems, the value of Δ is close to that computed for planets around single stars, but the level of chaoticity close to it substantially increases for smaller semimajor axes and higher eccentricities of the binary orbit. In these configurations ac also begins to be unreliable and non-linear secular resonances with the stellar companion lead to chaotic behaviour well within ac, even for single planet systems. For two planet systems, the superposition of mean motion resonances, either mutual or with the binary companion, and non-linear secular resonances may lead to chaotic behaviour in all cases. We have developed a parametric semi-empirical formula determining the minimum value of the binary semimajor axis, for a given eccentricity of the binary orbit, below which stable two planet systems cannot exist.
Conclusions. The superposition of different resonances between two or more planets and the binary companion may prevent the existence of stable dynamical configurations in binaries. As a consequence, care must be devoted when applying the Holman and Wiegert criterion and the Hill stability against mutual close encounters for a multiplanet system in binaries.
Key words: planets and satellites: general / planets and satellites: dynamical evolution and stability
© ESO, 2016
1. Introduction
According to Horch et al. (2014), an estimated fraction of about 40 to 50% of exoplanets are in binary star systems. The dynamical properties of planets in binaries, in terms of eccentricity distribution, do not appear significantly different from those of planets around single stars. It is thus expected that planet-planet scattering is effective in leading to physical collisions between planets, ejection, and eccentricity pumping in binaries as in single stars. Marzari et al. (2005) have shown that there are some statistical differences in the outcome of the chaotic phase which strongly depend on the eccentricity of the binary system for any given value of the binary semimajor axis. For example, in a system of three planets on initially unstable orbits, the number of surviving systems with two planets in a stable configuration at the end of the scattering phase declines with the binary eccentricity.
In this paper we focus on the conditions for the stability/instability of multiplanet systems in binaries. In this study of the dynamics of two planets orbiting the primary star of a binary system we test whether the criterion for the Hill stability, against mutual close approaches, is affected by the presence of the companion star. The initial threshold separation Δ between two planets around a single star granting their long term dynamical stability is given by 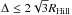 , where Δ = a2 − a1 is the difference between the semimajor axes of the two planets and RHill is the mutual Hill sphere defined as
, where Δ = a2 − a1 is the difference between the semimajor axes of the two planets and RHill is the mutual Hill sphere defined as
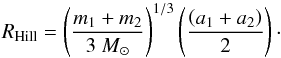 (1)This criterion was derived from Gladman (1993) from the work of Marchal & Bozis (1982) for circular and coplanar orbits and it was numerically confirmed by Chambers et al. (1996). More complex equations are available when the planets are on initially eccentric and inclined orbits (Donnison 2006; Veras & Mustill 2013), but we will concentrate on bodies initially on almost circular orbits approximately lying on the same plane.
(1)This criterion was derived from Gladman (1993) from the work of Marchal & Bozis (1982) for circular and coplanar orbits and it was numerically confirmed by Chambers et al. (1996). More complex equations are available when the planets are on initially eccentric and inclined orbits (Donnison 2006; Veras & Mustill 2013), but we will concentrate on bodies initially on almost circular orbits approximately lying on the same plane.
In this paper we investigate the validity of the above mentioned stability condition in binary systems using the same numerical approach of Marzari (2014) based on the application of the frequency map analysis (FMA). The FMA method (Laskar 1993; Šidlichovský & Nesvorný 1996; Marzari et al. 2003) allows us to outline the stability regions in the phase space with short term numerical integrations by computing the diffusion of the main frequencies of the system. This allows a massive exploration of the region close to the Hill stability separation to test the influence of the binary orbital parameters on its value. Before testing the stability of two planets in binaries we apply the method to the case of a single planet as a test bench. In this way we can compare the outcome of the FMA exploration with the empirical formula of Holman & Wiegert (1999) which defines a critical semimajor axis ac within which the orbit of a planet is assumed to be stable against the binary perturbations. We then concentrate on systems with two planets and test their stability as a function of the binary parameters such as semimajor axis and eccentricity of the stellar pair and their mass ratio.
In Sect. 2 we briefly summarize the numerical model used to explore the stability of planetary systems in binaries. In Sect. 3 we test the method on single planet systems in binaries and compare the results with the semi-empirical formulas of Holman & Wiegert (1999) and Andrade-Ines & Michtchenko (2014). In Sect. 4 we study two-planet systems in binaries and examine the validity of the Hill criterion for different parameters of the binary. In Sect. 5 we exploit a statistical approach to derive a semi-empirical formula predicting the minimum semimajor axis of the binary allowing a significant stability region for two planets as a function of the binary eccentricity, mass ratio and inner planet semimajor axis. We summarize and discuss our findings in Sect. 6.
2. The numerical approach
The FMA is a powerful tool to measure, with short term numerical integrations, the diffusion velocity of a dynamical system in the phase space (Benettin et al. 1976). It can be successfully used to explore the stability of two planets in a binary system since it allows a fine sampling of the phase space with a limited computer load.
We apply the FMA to the non-singular variables h and k, defined as h = e sin(ϖ) and k = e cos(ϖ), of the inner planet. The main frequencies present in the signal are due to the secular perturbations of the companion star and of the second planet. Each dynamical system analysed with the FMA is numerically integrated over 10 Myr, with a sampling period of 5 yr. To perform the analysis, the whole timespan is divided in time-windows extending for 5 × 105. Each window is shifted forward in time by 1 × 105 yr respect to the previous one. On each of these windows the main frequency is computed with the FMFT high precision algorithm described in Laskar (1993) and Šidlichovský & Nesvorný (1996). The chaotic diffusion of the orbit is measured as the logarithm of the relative change of the main frequency of the signal over all the windows, i.e. 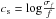 where σf is the standard deviation of the main frequency f. Small values of cs imply a low diffusion rate and then stability over a long timescale. On the contrary, large values are characteristic of systems where the secular frequencies change on a short timescale and are then chaotic. We always test that in all our simulated systems, where different values of the binary and planetary orbital elements are adopted, the secular frequencies complete at least one circulation period over each time-window. This is the minimum interval of time for a reliable determination of the main secular frequency in the spectrum of the h and k variables with the FMA. The computer code halts if this condition is not met. Indeed, in all our models the secular frequencies covered many circulation periods per window allowing an accurate determination of the frequency.
where σf is the standard deviation of the main frequency f. Small values of cs imply a low diffusion rate and then stability over a long timescale. On the contrary, large values are characteristic of systems where the secular frequencies change on a short timescale and are then chaotic. We always test that in all our simulated systems, where different values of the binary and planetary orbital elements are adopted, the secular frequencies complete at least one circulation period over each time-window. This is the minimum interval of time for a reliable determination of the main secular frequency in the spectrum of the h and k variables with the FMA. The computer code halts if this condition is not met. Indeed, in all our models the secular frequencies covered many circulation periods per window allowing an accurate determination of the frequency.
The FMA method could also be applied to the second planet as well and an additional value of cs could be derived from the analysis of its frequencies. However, we found that the cs value for the outer planet is systematically slightly worse, possibly due to the fact that in the power spectrum additional frequencies due to the binary companion are stronger. This leads to a reduction in the strength of the peak we use for the frequency analysis, leading to a degradation in the numerical computation of the frequency. For this reason, we prefer to apply the FMA to the inner planet.
We will consider two different models, the first, used as a test bench, is composed of a single Jupiter-size planet in orbit around a solar type star member of a binary system. The outcome of the FMA in this model is compared to the predictions of the empirical formula of Holman & Wiegert (1999). This formula computes the critical semimajor axis ac of a planet in a binary system beyond which instability is expected. It is the outcome of a fit to the results of numerical integrations where massless particles (elliptical restricted three-body problem) are integrated over 300 binary periods. Those particles which survive till the end of the integration outline the stability limit and then ac. The critical semimajor axis depends on the physical and orbital parameters of the binary as it follows:
![\begin{eqnarray} a_{\rm c}& = &\, [( 0.464 \pm 0.006) + (-0.380 \pm 0.010) \overline{\mu} \\ \nonumber & & + (-0.631 \pm 0.034) e_{\rm B} + (0.586 \pm 0.061) \overline{\mu} e_{\rm B} \\ \nonumber & & + (0.150 \pm 0.041) e_{\rm B}^2 + (-0.198 \pm 0.074) \overline{\mu} e_{\rm B}^2] a_{\rm B}, \label{eq:HW} \end{eqnarray}](/articles/aa/full_html/2016/10/aa28342-16/aa28342-16-eq17.png) (2)where
(2)where 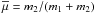 (here we term mass ratio the value of μ = m2/m1), eB and aB are the eccentricity and semimajor axis of the binary, respectively.
(here we term mass ratio the value of μ = m2/m1), eB and aB are the eccentricity and semimajor axis of the binary, respectively.
We have analysed a set of dynamical configurations with a single planet and compared the prediction of the empirical formula of Holman & Wiegert (1999) with the outcome of the FMA analysis. Some differences are expected since not only we integrate the full elliptical three-body problem with a massive planet but we also allow the planet to be on an orbit inclined respect to that of the binary up to a value of 5°. In addition, with the FMA approach we can examine a significantly larger portion of the phase space with a chance of a better definition of the stability limit.
Once performed the test with a single planet, we will finally focus on systems made of two planets having the same size (that of Jupiter) and evolving on progressively more separated orbits. We fix the semimajor axis of the inner planet to a1 = 3 AU and randomly sample the orbit of the second planet. This method is similar to that usually exploited to test the stability against close encounters in multiplanet systems (Chambers et al. 1996; Marzari & Weidenschilling 2002; Chatterjee et al. 2008; Smith & Lissauer 2009, 2010; Marzari 2014; Morrison & Kratter 2016). As shown in Morrison & Kratter (2016) the problem does not easily scale with the mass ratio between the star and the planets. In our case we have the additional problem that the fourth body is a star with a mass comparable to the primary star, so the dynamical system cannot be easily compared to one made of three planets with equal or similar mass. For this reason we have to perform an independent analysis.
As standard model we consider a binary system with two equal stars of solar mass (μ = 1) and two different values of binary eccentricity, i.e. eB = 0 and eB = 0.4. To perform a statistical analysis of the dependence of the stable region for two planets as a function of the binary parameters we consider also systems with different mass ratio ranging from 0.1 to 1, and with sampled values of both aB and eB.
3. Test on single planet systems: evaluation of the critical semimajor axis
In Fig. 1 we show the outcome of the FMA applied to a dynamical system composed of a single planet orbiting the primary star of a binary system with aB = 25 AU and eB = 0. The red dots are all systems stable for at least 10 Myr for which a value of diffusion speed cs has been computed. The black vertical line marks the empirical stability limit of Holman & Wiegert (1999)ac. The green dashed vertical lines indicate the location of the major mean motion resonances with the binary companion. Close to ac, instability begins to grow possibly due to the increasing strength of the resonances with the companion star. The instability is confirmed by the long term integration of a single case, marked by a yellow large filled circle in Fig. 1, where the planet is ejected from the system after about 60 Myr.
However, stable systems are found more than 1 AU beyond ac, out to about a = 8 AU. Thus, it appears that in this dynamical configuration ac underestimates the stability limit. In addition, between 9.5 to 11 AU a limited number of stable systems is also found possibly trapped in mean motion resonances with the binary companion. The numerical integration of two of these systems, marked by large blue filled squares, shows that they are stable over 4 Gyr. They show large regular oscillations in a and e due to the binary perturbations and, since we plot the initial semimajor axis, their location in Fig. 1 may be misleading. The average semimajor axis of these systems is shifted towards smaller values but they are still well beyond 9 AU.
 |
Fig. 1 FMA analysis of a Jupiter-size single planet dynamics in a binary system with aB = 25 AU and eB = 0. The diffusion index cs is drawn vs. the semimajor axis of the planet. Small values of cs means low diffusion, while large values connote chaotic orbits. The yellow filled circle is a case with a large diffusion index which becomes unstable after about 60 Myr. The two filled blue squares are stable cases over 2 Gyr. The green dashed lines show the location of mean motion resonances between the planet and the companion star up to order 10. The black dash-dotted line marks the critical semimajor axis computed from the empirical formula of Holman & Wiegert (1999). |
What is the origin of the discrepancy between our results and the value ac computed from the formula of Holman & Wiegert (1999)? One possible cause is the difference in the dynamical model since we consider the full elliptical three-body problem with a Jupiter-size planet on a slightly inclined orbit while Holman & Wiegert (1999) consider massless particles on planar orbits. To test this hypothesis we repeated the calculations of Fig. 1 setting the mass of the planet to 0 in order to better compare with the outcome of Holman & Wiegert (1999). We find a higher instability in the full three-body model in particular close to the outer stability limit, but the value of this limit is approximately equal in the two models and larger than ac. We then set the inclination of the massless particles to 0, i.e. they all lie on the same plane of the binary but still there are bodies on stable orbits beyond ac as in Fig. 1. A possible alternative explanation to this discrepancy is that we sample a much larger number of dynamical systems compared to Holman & Wiegert (1999) leading to a finer sampling of the phase space. If we compute the number of stable orbits (cs lower than −6) on discrete bins in semimajor axis we can explore the fraction of stable orbits as a function of the planet semimajor axis. In Fig. 2 we plot the number of stable cases n over a range of semimajor axis centered on ac. n is approximately stationary out to 6.5 AU, then it sharply declines till 6.8 AU which is the predicted value of ac according toHolman & Wiegert (1999). However, beyond ac there are additional stable orbits whose frequency is low compared to that within ac. If the sampling of initial configurations is limited in number, the stable region beyond ac can be missed because not densely populated. This is possibly the reason of the difference between our results and those of Holman & Wiegert (1999).
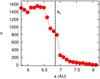 |
Fig. 2 Number of stable orbits (cs lower than −6) computed on equally spaced discrete bins 0.1 AU wide. Close to ac there is a significant drop in number but stable orbits are present also beyond ac even if their number is small. To be found, these orbits require a fine sampling of the phase space which is possible thanks to the use of the FMA analysis. |
To test the dependence of the stability analysis on the eccentricity of the binary we repeated the FMA for a model with eB = 0.4, the most frequent value encountered in binary systems according to Duquennoy & Mayor (1991). In Fig. 3 the FMA outcome is illustrated in this case. Again, the limit of stability is wider compared to that predicted by Holman & Wiegert (1999) since stable configurations are found when the semimajor axis of the planet is around 4.1 AU while ac = 3.67 AU. The most interesting feature is, however, the bimodal distribution of the stability index cs as a function of the semimajor axis. As in Fig. 1, the yellow filled circles are unstable orbits while the blue filled squares are stable ones. The two outer unstable systems have the planet ejected on a hyperbolic trajectory in less than 60 Myr. The inner case with an initial semimajor axis around 3.04 AU takes more time and its evolution is shown in Fig. 4. The orbit shows clear signs of chaotic behaviour from starting, visible only by inspecting the orbit on a short timescale. Finally, the ejection of the planet from the system occurs after about 3.3 Gyr possibly because the path to full instability is long.
To understand the reason of the coexistence of stable and unstable orbits for similar values of semimajor axis we have to explore the frequency space. In Fig. 5 the main frequency of the planet orbit is shown as a function of the initial semimajor axis. There are empty stripes which possibly correspond to the families of unstable orbits identified by Michtchenko & Malhotra (2004) as due to non-linear secular resonances which appear in their generalized numerical secular perturbation theory. These same resonances were retrieved at moderate eccentricities by the order 12 secular theory developed for two coplanar planets by Libert & Henrard (2005). There are significant differences between the configuration explored by Michtchenko & Malhotra (2004) and ours in particular concerning the mass ratio between the two bodies of the system other than the primary star. Michtchenko & Malhotra (2004) consider a mass ratio ranging from 1 to 1/4 between two planets perturbing each other while in our case the ratio between the companion star and the planet is about 1 × 103. However, we may expect that the origin of the instability stripes may be ascribed to similar non-linear resonances which appear only when the companion star is on a highly eccentric orbit (eB = 0.4). In fact, for eB = 0, there is no sign of similar unstable regions in the frequency vs. semimajor axis space and this is in agreement with the findings of Michtchenko & Malhotra (2004) predicting the presence of secular resonances at moderate to large eccentricities.
 |
Fig. 3 Same as Fig. 1 but with aB = 25 AU and eB = 0.4. The larger eccentricity of the binary system induces a higher level of chaoticity. |
 |
Fig. 4 Time evolution of the eccentricity of the system marked by a yellow circle in Fig. 3 whose initial semimajor axis is close to 3.04 AU. The system is chaotic and after about 3.3 Gyr the planet is ejected on a hyperbolic trajectory. The origin of its instability is possibly due to a non-linear secular resonance. |
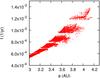 |
Fig. 5 Main frequency of the h and k variables of the planet, as computed by the MFT method within the FMA analysis, vs. the semimajor axis. The empty stripes mark the location of non-linear secular resonances which appear only for high values of the binary eccentricity (eB = 0.4). |
Another way to estimate a stability limit for single planet orbits in binaries is to use the Hill stability criterion described in Marchal & Bozis (1982). We use its formulation as described in Andrade-Ines & Michtchenko (2014) and compute a radius of the stability sphere Rs using their Eqs. (3) and (4). Since the criterion is defined on the radial distance, for applying it to keplerian orbits it is necessary to adopt the following rule: an orbit satisfies the Hill stability criterion if apl(1 + epl) <Rs, in other words the aphelion of the orbit must lie inside Rs. We applied this criterion to the two models with aB = 25 AU and eB = 0 and eB = 0.4, respectively. To compare our sample of orbits with Rs, we select from the whole sample those with cs< − 6, as a conservative choice for stable orbits. For these we compute the maximum value of the aphelion distance over the integration timespan and compare it with Rs. For the case described in Fig. 1, i.e. aB = 25 AU and eB = 0, we find that, all over the sample of stable orbits, the maximum aphelion distance is 9.6 AU which is in good agreement with the prediction of Eq. (4) in Andrade-Ines & Michtchenko (2014) for μ = 1 which gives Rs = 9.8 AU. In the second case illustrated by Fig. 3, i.e. aB = 25 AU and eB = 0.4 the maximum aphelion distance is 4.8 AU against a value of 5.9 AU predicted by the analytical equation. The Hill criterion based on the definition of Rs is assumed to be limited to “short–term” stability, as argued by Andrade-Ines & Michtchenko (2014), however it is interesting that the discrepancy is larger for higher values of eB.
When the semimajor axis of the binary is increased to aB = 50 AU, the stability portraits are very similar to the aB = 25 AU when the eccentricity of the binary is set to 0. When eB = 0.4, the non-linear resonances contribute to the instability also close to the outer border even if the major source of chaos in that region is the mean motion resonance overlap with the binary companion. In Fig. 6 the diffusion map of the planet orbits shows a bimodal distribution only close to the critical semimajor axis ac (black dashed line) but within 5 AU the effects of the non-linear resonances are strongly reduced. In the frequency space the same instability stripes, due to these non-linear resonances, are observed as in Fig. 5.
The test of the FMA method to explore the stability of single planetary systems in binary have shown to be effective and it has lead to new findings that improve the analysis of Holman & Wiegert (1999). In particular, we observe that:
-
The value of ac computed with the empirical equation of Holman & Wiegert (1999) slightly underestimates the stability limit in the case of equal mass binary systems. This is related to the need of a fine sampling of the phase space to outline the stability region.
-
A limited number of stable systems is found well beyond ac and they are possible trapped into stable resonant orbits with the binary companion. Their orbital elements show wide oscillations due to the companion perturbations.
-
When the eccentricity of the binary is set to eB = 0.4, non-linear resonances cause instability for semimajor axis of the planet well within ac as shown in Figs. 3, 5 and 6. In highly eccentric binaries, the stability limit ac is then only indicative and unstable orbits can be found within it.
 |
Fig. 6 Same as Fig. 3 but with aB = 50 AU and eB = 0.4. The non-linear secular resonances are effective in inducing instability only close to the outer stability border and their effect is significantly reduced within a ~ 5 AU. Even in this case, the limit of stability extends beyond the empirical prediction of Holman & Wiegert (1999) (black dashed line). |
We performed additional simulations with aB = 25 and 50 AU and eB = 0. and 0.4 but changing the mass ratio μ from 0.5 to μ = 0.33 (M2 = 0.5 Modot) and μ = 0.17 (M2 = 0.2 Modot). We compared the outer limit derived from the FMA with ac and found that the difference is always in between 10 to 20%. From these results we conclude that on average ac is a good approximation but for a detailed study of a single planetary system a finer sampling of the phase space is needed since ac can be wrong by up to 20%.
4. Stability of two-planet systems
We now apply the FMA method to systems made of two planets in orbit around the primary star of a binary systems. Our goal is to test whether the stability properties outlined by both ac and Δ are preserved or if it is necessary to define limits for their applicability which depend on the binary configuration.
4.1. The circular case (eB = 0)
To explore the stability properties of two planet systems, we start with larger values of the binary separation aB since the semimajor axis of the inner planet is always set at 3 AU. For small values of aB, like aB = 25, there is little room for a stability analysis since the sum of a1 + Δ is larger than ac. For this reason we begin with a binary separation aB = 50 AU with the stars on a circular orbit (eB = 0). In Fig. 7 we show the diffusion portrait of the system as a function of the semimajor axis of the outer planet a2. Within about 7 AU, the mutual secular perturbations of the two planets dominate the evolution of the system while, beyond that limit, the stability properties are determined by the perturbations of the companion star on the outer planet. As in the case with a single planet (Fig. 1), chaotic orbits increase in frequency close to the critical stability limit ac. However, as in the test case with a single planet, stable configurations are found even for a2 as far as ~16 AU confirming that the analytical value of ac computed with the empirical formula of Holman & Wiegert (1999) underestimates the real outer limit. However, it appears that the presence of the inner planet does not significantly affect the stability properties of the second planet close to ac.
An enlarged view of the diffusion map in Fig. 7, limited to a2 ≤ 7 AU, is shown in Fig. 8 (upper panel). It is compared to a similar map without the binary companion (lower panel) to test the influence of the secondary star. This second plot is slightly different respect to that shown in Marzari (2014) in particular close to the 3:2 resonance where stable orbits begin to appear. Even if the implications of the two plots for the long term stability of a two-planet system are the same, in that shown in Marzari (2014) the value of cs appear larger compared to similar configurations in Fig. 8 lower panel. This difference is related to the use of shorter running windows while applying the FMA (5 × 105 yr in this work, 2 Myr in Marzari (2014)) since the binary companion usually leads to faster secular frequencies compared to systems made of two planets only. In addition, our running windows shift by 1 × 105 yr while in Marzari (2014) they were shifted of 1 × 106 yr possibly causing a larger spread of the computed frequency. Two minor sources of differences are related to (1) the numerical integrator used to compute the orbital evolution: in this study it is the 15th order RADAU integrator Everhart (1985) while in Marzari (2014) the symplectic integrator SyMBA (Levison & Duncan 1994; Duncan et al. 1998) was adopted (due to its Hamiltonian splitting structure, SyMBA cannot be used in binary star systems); and (2) to the selection of the FMFT algorithm instead of the MFT endorsed in Marzari (2014).
The comparison between the upper and lower panel of Fig. 8 shows that the presence of the binary companion significantly increases the level of chaoticity close to the Hill stability limit marked by the location of the 3:2 mean motion resonance between the planets. In the case with the binary companion (upper panel), the inner stability limit is populated by a significantly larger number of fast diffusing orbits respect to the same location in the phase space in the lower panel where the companion star has been removed from the system. Additional unstable features appear beyond 5 AU in the upper panel, more marked than in the case with a single star. The higher instability observed in the binary case is possibly due to the superposition of resonances. In addition to the mutual resonances between the planets, resonances with the companion star further perturb the system causing a more complex superposition effect. This is manifest not only close to the stability limit but also in correspondence to the 5:2 resonance between the planets which is markedly wider and chaotic in the binary case. In both panels stable orbits for Trojan planets are observed close to 3 AU. The number of cases is too small to determine in detail the influence of the binary companion on their stability, however it looks like their existence is not jeopardized by the presence of a secondary star. It is noteworthy that the diffusion speed of the orbits in the lower panel, where the binary companion is neglected, is increasing with a2, the semimajor axis of the outer planet. This is not a dynamical effect but it is due to a degradation of the numerical precision in the determination of the secular frequency in each window. Such an effect, observed also in Marzari (2014), is due to the use of a fixed timespan for each running window while computing a frequency which is decreasing for larger a2. At the same time, the forced eccentricity of each planet is smaller for larger values of a2 leading to smaller values of the h, k variables, further increasing the numerical error in the computation of the associated frequencies. This systematic trend does not invalidate the analysis once its origin is known. In addition, in the case of two planets in binaries, both these effects are significantly reduced since the secular frequencies, due to the binary perturbations, are higher and the forced eccentricity grows for larger values of a2.
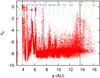 |
Fig. 7 Diffusion map of a two-planet system in a binary with aB = 50 AU and eB = 0. For a2 ≤ 7 AU mean motion resonances between the two planets (blue dashed vertical lines) shape the stability portrait while beyond 7 AU the resonances between the outer planet and the binary (green dashed vertical lines) determine the chaotic diffusion of the orbit. The black dotted line marks the location of ac. |
 |
Fig. 8 Enlarged view of the diffusion portrait shown in Fig. 1 limited to a2 ≤ 7 AU (upper panel). The same diffusion map for a two planet system around a single star is shown as a comparison in the lower panel. The vertical dashed lines mark the locations of mean motion resonances between the two planets. The dynamics in the binary system appears to be more chaotic in particular close to the inner stability border marked by the 3:2 mean motion resonance between the planets and in correspondence to the 5:2 resonance. These effects are due to the gravitational perturbations of the binary companion. |
A similar behaviour is observed also when aB = 100 AU even if the level of chaoticity at the inner stability limit for the two planets is lower. In conclusion, the perturbations of the binary companion do not shift outwards the value of the minimum separation Δ of two planets for stability, but they significantly increase the frequency of chaotic orbits close to the border and even beyond at the major resonances between the planets.
4.2. The eccentric case (eB = 0.4)
When the eccentricity of the binary is increased to eB = 0.4, in the case with aB = 50 a two-planet system is unstable for almost all values of a2 (of course assuming that a1 = 3 AU). The stability portrait in Fig. 9 shows that only a limited number of systems have low diffusion rates compatible with long term survival. The yellow filled circles are planetary systems which are chaotic ending with ejection of at least one planet in less than 1 Gyr. They are located well within ac proving that the outer stability limit computed for systems with only one planet cannot be blindly applied to multiplanet systems. Only for very low values of cs a limited number of systems appear to be stable as those cases marked by a blue filled square which display a quasi-periodic behaviour over 5 Gyr. The mechanism responsible for the instability is again the superposition of mean motion and secular (linear and non-linear) resonances leading to overall instability with few exceptions.
 |
Fig. 9 Diffusion map of a two-planet system in a binary with aB = 50 AU and eB = 0.4. The phase space is mostly chaotic with few exceptions of low diffusion orbits. The yellow filled circles mark systems that become unstable followed by a period of close encounters between the planets. The blue squares are systems which are stable over 10 Gyr. |
If we increase the binary semimajor axis to aB = 100 AU (Fig. 10), the stability range extends out to ac and beyond. However, the region in proximity of the inner stability limit is more chaotic than in the aB = 50 and eB = 0 case (Fig. 8) with non-linear resonances contributing to instability while approaching ac.
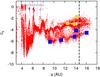 |
Fig. 10 Diffusion portrait for a two-planet system in a binary with aB = 100 AU and eB = 0.4. The inner region, where the mutual planetary resonances dominate, is more chaotic compared to the case with aB = 50 AU and eB = 0. Getting closer to the outer border, stable and unstable orbits coexist as in Figs. 3 and 6. |
From the outcome of the FMA analysis, we can conclude that the eccentricity of the binary eB is more critical than aB in determining the chaotic nature of multiplanet systems. Moreover, the empirical formula of Holman & Wiegert (1999) is a good approximation when a single planet is orbiting the primary star but it may become very inaccurate for multiplanet systems as illustrated in Fig. 9.
5. Statistical analysis
By inspecting Fig. 9, it appears that a system of two planets in binaries is not necessarily stable when both planets have semimajor axes smaller than ac, the critical semimajor axis defined by (Holman & Wiegert 1999). The combination of mean motion resonances between the two planets, between the planets and the binary companion and non-linear secular resonances easily lead to chaotic evolution even within ac. The results shown in the previous section suggest that this may happen in particular for higher values of eB. To grant the presence of a stable region for two-planet systems, for a given value of eB, the semimajor axis of the binary aB must be larger than a critical value. This is confirmed by Fig. 11 where we compare three different cases with the same value of eB = 0.3 but 3 distinct values of aB, i.e. 40, 50 and 60 AU, respectively. For aB = 30 AU there are no stable systems while, by inspecting Fig. 11, it appears that for values of aB larger than 40 AU the stability of two planet systems is slowly restored within the critical value ac computed by Eq. (2). However, the filling of the region a2<ac with stable orbits is not instantaneous but progressive and the fraction of stable orbits within ac increases with aB. This gradual stuffing of the region defined by a2<ac with stable orbits, occurring for increasing aB, is related to two distinct dynamical effects. The first appears close to the inner planet, in between 4 and 6 AU, where there is a reduction of the chaoticity of the orbits marked by lower values of cs related to a weakening of superposition between mean motion resonances between the two planets and resonances between the planets and the binary. At the same time, the stability region stretches also out towards larger values of a2 for increasing values of aB because the overlap of mean motion and secular resonances with the companion become effective in generating chaotic behaviour farther out from the primary star.
 |
Fig. 11 Diffusion portrait for a two-planet system in a binary with eB = 0.3, μ = 1, a1 = 3 AU and for 3 different values of aB, i.e. 40, 50 and 60 AU. A progressive increase in size of the stable region is observed both inside, close to the inner planet, and outside. |
Taking advantage of this simple behaviour, we have tried to to derive a semi-empirical relationship between aB and eB which can be predictive in terms of stability of two-planets systems. Our goal is to compute, for any given value of eB, a critical value of aB, termed 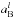 , below which any system of two planets is unstable. On the other hand, for
, below which any system of two planets is unstable. On the other hand, for 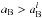 , a significant fraction of stable bi-planet systems can be found with a2<ac. Due to the large number of parameters playing a role in determining the stability properties of two planets in a binary we resorted to a statistical approach for estimating
, a significant fraction of stable bi-planet systems can be found with a2<ac. Due to the large number of parameters playing a role in determining the stability properties of two planets in a binary we resorted to a statistical approach for estimating 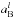 . First of all we sample different values of eB starting from eB = 0.1 and incrementing it with a step Δe = 0.1. For each value of eB we run the FMA analysis for 9 different values of aB ranging from 10 to 100 AU at a pace of 10 AU. Beyond 100 AU the secular evolution of the angles is too slow and an integration time longer than 10 Myr is needed for the FMA analysis. We also consider 3 different values of the mass ratio, i.e. μ = 1,0.5,0.1, and three different values of the semimajor axis of the inner planet a1 = 2,3,4 in order to scale the value of
. First of all we sample different values of eB starting from eB = 0.1 and incrementing it with a step Δe = 0.1. For each value of eB we run the FMA analysis for 9 different values of aB ranging from 10 to 100 AU at a pace of 10 AU. Beyond 100 AU the secular evolution of the angles is too slow and an integration time longer than 10 Myr is needed for the FMA analysis. We also consider 3 different values of the mass ratio, i.e. μ = 1,0.5,0.1, and three different values of the semimajor axis of the inner planet a1 = 2,3,4 in order to scale the value of 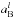 even with these parameters.
even with these parameters.
 |
Fig. 12 Normalized curves showing the number of stable orbits for different values of aB and eB. The sudden step in the number of cases marked the onset of a significant stable zone for that binary parameters. The normalization is performed to the maximum number of stable cases. Since the models run at the same pace, we expect that f measures the size of the stable region which saturates when the rate at which new stable cases are found is constant (i.e. the binary configuration presents a large stable zone for two planets). |
The number of simulations we ran is very large (more than 5 × 105) so we need a simple criterion to determine when a two-planet system has a sufficiently large stable zone for given values of aB and eB. To “measure” the size of the stable zone we resort to a method based on a simple Monte Carlo integration. We assume that the total volume in the phase space where stable two-planet systems can be found, for given aB and eB, is limited by ac, plus 20% to account for the results presented in Sect. 3. We then randomly sample 10 000 systems for each aB,eB for which a2<ac, run the FMA analysis and finally count the number of systems having cs lower than −6 so that they are expected to be stable over a long timescale. The number of cases for which this last condition is fulfilled estimates the area of the stable zone.
In Fig. 12 we show the number of stable cases as a function of both aB and eB. For example, the red curve suggests that for aB< 20 AU no stable two-planet systems can exist. The stable area begins to grow for aB = 30 AU, it has a sudden step marking a consistent widening of the stable zone for aB = 40 AU, and it finally saturates at 60 AU where the stable region is only limited by the value of ac. In this situation the number of stable cases in the 10 000 sample systems is approximately the same even when larger values of aB are considered. By inspecting Fig. 12 we select the value of 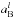 as the one for which the number of stable cases begins to grow. Of course, the resolution with which
as the one for which the number of stable cases begins to grow. Of course, the resolution with which 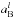 is computed is not very high since we use a step of 10 AU for aB and 0.1 for eB, but we had to make compromises between the CPU load and resolution. The data distribution shown in Fig. 12 indicates that the number of stable orbits scales with the pericenter distance of the companion star, i.e. qB = aB(1 − eB) so we adopt a form of the fitting function reflecting this aspect. In addition, we perform an additional scaling on μ and a1 obtaining the following fitting formula:
is computed is not very high since we use a step of 10 AU for aB and 0.1 for eB, but we had to make compromises between the CPU load and resolution. The data distribution shown in Fig. 12 indicates that the number of stable orbits scales with the pericenter distance of the companion star, i.e. qB = aB(1 − eB) so we adopt a form of the fitting function reflecting this aspect. In addition, we perform an additional scaling on μ and a1 obtaining the following fitting formula: 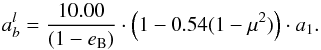 (3)This equation is limited to the range of parameters we have explored, i.e. 0 <eb< 0.6, 10 <aB< 100 AU, 0.1 <μ< 1, and 2 <a1< 4 AU. Adopting values of any of the three variables (eB,μ,a1) far beyond these limits may lead to inaccurate values. For example, when μ reduces to 0.001, which is equivalent to assume that the binary companion is a Jupiter-size planet, the value of
(3)This equation is limited to the range of parameters we have explored, i.e. 0 <eb< 0.6, 10 <aB< 100 AU, 0.1 <μ< 1, and 2 <a1< 4 AU. Adopting values of any of the three variables (eB,μ,a1) far beyond these limits may lead to inaccurate values. For example, when μ reduces to 0.001, which is equivalent to assume that the binary companion is a Jupiter-size planet, the value of 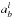 should be about 8 AU, the value predicted by previous studies of the stability of three giant planets around single stars (Marzari & Weidenschilling 2002). The value that is obtained by the previous fit is instead 13.8 AU. However, we should define when a star is small enough to be termed a planet and vice versa. For this reason, we are conservative when we claim that our fit is reliable within the limits given by the numerical simulations.
should be about 8 AU, the value predicted by previous studies of the stability of three giant planets around single stars (Marzari & Weidenschilling 2002). The value that is obtained by the previous fit is instead 13.8 AU. However, we should define when a star is small enough to be termed a planet and vice versa. For this reason, we are conservative when we claim that our fit is reliable within the limits given by the numerical simulations.
6. Discussion and conclusions
Using the FMA, a fast tool to identify chaotic orbits, we have investigated the stability of planetary orbits in binary systems. As a test bench, we have first revisited the Holman & Wiegert (1999) empirical formula which calculates a critical semimajor axis ac beyond which instability occurs for single planets in binaries. We show that this formula underestimates the real stability limit by as much as 20%, depending on the binary orbit. This is due to the low sampling rate used by Holman & Wiegert (1999) which had to explore a wide range of parameters of the binary (aB, eB, and μ) to perform a reliable fit based on these parameters. As a consequence, for each individual set of aB,eB,μ they did not integrate a number of different systems large enough to fully explore the phase space. We have focused on a limited number of binary parameters, but thanks to the FMA we have performed a very dense sampling finding that the stability limit in semimajor axis is larger than that given by the Holman & Wiegert (1999) formula. The fraction of stable orbits decreases quickly beyond ac but they still represent a significant sample of stable configurations. In addition to these orbits, extending just beyond ac, there are additional dynamical systems which are trapped in resonance with the companion star, are stable over 5 Gyr, and have semimajor axis well beyond ac. When applied to the same systems, the Hill stability criterion applied to the binary companion and planet, on the other hand, predicts accurately the stability limit if the eccentricity of the binary is low but it becomes inaccurate for higher values of eB and it significantly overestimates the stability boundary. The use of the FMA has also allowed us to discover unstable systems within ac when the orbit of the companion star is eccentric. These systems densely populate the region with ap<ac and their chaoticity is probably due to the presence of non-linear secular resonances (Michtchenko & Malhotra 2004; Libert & Henrard 2005) induced by the companion star.
When applied to two-planet systems, the FMA method shows that the separation between two planets leading to instability remains close to the Hill stability limit defined by Gladman (1993). However, when aB decreases and eB grows, the perturbations of the companion star progressively make two-planet systems more chaotic. The inner border is populated by an increasing number of unstable systems while the outer border is destabilized by overlap of mean motion and secular (linear and non-linear) resonances. The limiting case is when most planetary systems are chaotic independently of the separation between the two planets as in the case with aB = 50 AU and eB = 0.4 (the inner planet has semimajor axis a1 = 3 AU in all our models). In this configuration mean motion resonances and secular resonances (linear and non-linear) easily superimpose leading to chaos and instability. This implies that the value of ac cannot be carelessly used in multiplanet systems since the combined mutual planetary and binary perturbations may lead to chaotic behaviour well within ac in particular for eccentric binaries.
To derive a semiempirical formula that allows us to compute, at least at a rough approximation level, the value of the binary semimajor axis 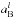 below which two planets cannot coexist around the central star, we have run a series of models with different values of eB,μ,a1 with the goal of finding scaling relationships in these variables. Of course, owing to the huge amount of CPU load required to explore such a large parameter space, our formula is limited. However, it covers a range of parameters which are the most frequently encountered in binary systems, according to Duquennoy & Mayor (1991). It can be used when planning observation strategies while looking for planets in binary systems.
below which two planets cannot coexist around the central star, we have run a series of models with different values of eB,μ,a1 with the goal of finding scaling relationships in these variables. Of course, owing to the huge amount of CPU load required to explore such a large parameter space, our formula is limited. However, it covers a range of parameters which are the most frequently encountered in binary systems, according to Duquennoy & Mayor (1991). It can be used when planning observation strategies while looking for planets in binary systems.
Acknowledgments
We thank an anonymous referee for his/her useful comments and suggestions which helped to improve the paper.
References
- Andrade-Ines, E., & Michtchenko, T. A. 2014, MNRAS, 444, 2167 [NASA ADS] [CrossRef] [Google Scholar]
- Benettin, G., Galgani, L., & Strelcyn, J.-M. 1976, Phys. Rev. A, 14, 2338 [NASA ADS] [CrossRef] [Google Scholar]
- Chambers, J. E., Wetherill, G. W., & Boss, A. P. 1996, Icarus, 119, 261 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Chatterjee, S., Ford, E. B., Matsumura, S., & Rasio, F. A. 2008, ApJ, 686, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Donnison, J. R. 2006, MNRAS, 369, 1267 [NASA ADS] [CrossRef] [Google Scholar]
- Duncan, M. J., Levison, H. F., & Lee, M. H. 1998, AJ, 116, 2067 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duquennoy, A., & Mayor, M. 1991, A&A, 248, 485 [NASA ADS] [Google Scholar]
- Everhart, E. 1985, in Dynamics of Comets: Their Origin and Evolution, Proc. of IAU Colloq., 83, held in Rome, Italy, June 11–15, 1984, eds. A. Carusi & G. B. Valsecchi (Dordrecht: Reidel), Astrophysics and Space Science Library, 115, 185 [Google Scholar]
- Gladman, B. 1993, Icarus, 106, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Holman, M. J., & Wiegert, P. A. 1999, AJ, 117, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Horch, E. P., Howell, S. B., Everett, M. E., & Ciardi, D. R. 2014, ApJ, 795, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Laskar, J. 1993, Physica D, 67, 257 [Google Scholar]
- Levison, H. F., & Duncan, M. J. 1994, Icarus, 108, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Libert, A.-S., & Henrard, J. 2005, Celest. Mech. Dyn. Astron., 93, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Marchal, C., & Bozis, G. 1982, Celest. Mech., 26, 311 [Google Scholar]
- Marzari, F. 2014, MNRAS, 442, 1110 [NASA ADS] [CrossRef] [Google Scholar]
- Marzari, F., & Weidenschilling, S. J. 2002, Icarus, 156, 570 [NASA ADS] [CrossRef] [Google Scholar]
- Marzari, F., Tricarico, P., & Scholl, H. 2003, MNRAS, 345, 1091 [NASA ADS] [CrossRef] [Google Scholar]
- Marzari, F., Weidenschilling, S. J., Barbieri, M., & Granata, V. 2005, ApJ, 618, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Michtchenko, T. A., & Malhotra, R. 2004, Icarus, 168, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Morrison, S. J., & Kratter, K. M. 2016, ApJ, 823, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, A. W., & Lissauer, J. J. 2009, Icarus, 201, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, A. W., & Lissauer, J. J. 2010, Celest. Mech. Dyn. Astron., 107, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Šidlichovský, M., & Nesvorný, D. 1996, Celest. Mech. Dyn. Astron., 65, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Veras, D., & Mustill, A. J. 2013, MNRAS, 434, L11 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 FMA analysis of a Jupiter-size single planet dynamics in a binary system with aB = 25 AU and eB = 0. The diffusion index cs is drawn vs. the semimajor axis of the planet. Small values of cs means low diffusion, while large values connote chaotic orbits. The yellow filled circle is a case with a large diffusion index which becomes unstable after about 60 Myr. The two filled blue squares are stable cases over 2 Gyr. The green dashed lines show the location of mean motion resonances between the planet and the companion star up to order 10. The black dash-dotted line marks the critical semimajor axis computed from the empirical formula of Holman & Wiegert (1999). |
| In the text | |
 |
Fig. 2 Number of stable orbits (cs lower than −6) computed on equally spaced discrete bins 0.1 AU wide. Close to ac there is a significant drop in number but stable orbits are present also beyond ac even if their number is small. To be found, these orbits require a fine sampling of the phase space which is possible thanks to the use of the FMA analysis. |
| In the text | |
 |
Fig. 3 Same as Fig. 1 but with aB = 25 AU and eB = 0.4. The larger eccentricity of the binary system induces a higher level of chaoticity. |
| In the text | |
 |
Fig. 4 Time evolution of the eccentricity of the system marked by a yellow circle in Fig. 3 whose initial semimajor axis is close to 3.04 AU. The system is chaotic and after about 3.3 Gyr the planet is ejected on a hyperbolic trajectory. The origin of its instability is possibly due to a non-linear secular resonance. |
| In the text | |
 |
Fig. 5 Main frequency of the h and k variables of the planet, as computed by the MFT method within the FMA analysis, vs. the semimajor axis. The empty stripes mark the location of non-linear secular resonances which appear only for high values of the binary eccentricity (eB = 0.4). |
| In the text | |
 |
Fig. 6 Same as Fig. 3 but with aB = 50 AU and eB = 0.4. The non-linear secular resonances are effective in inducing instability only close to the outer stability border and their effect is significantly reduced within a ~ 5 AU. Even in this case, the limit of stability extends beyond the empirical prediction of Holman & Wiegert (1999) (black dashed line). |
| In the text | |
 |
Fig. 7 Diffusion map of a two-planet system in a binary with aB = 50 AU and eB = 0. For a2 ≤ 7 AU mean motion resonances between the two planets (blue dashed vertical lines) shape the stability portrait while beyond 7 AU the resonances between the outer planet and the binary (green dashed vertical lines) determine the chaotic diffusion of the orbit. The black dotted line marks the location of ac. |
| In the text | |
 |
Fig. 8 Enlarged view of the diffusion portrait shown in Fig. 1 limited to a2 ≤ 7 AU (upper panel). The same diffusion map for a two planet system around a single star is shown as a comparison in the lower panel. The vertical dashed lines mark the locations of mean motion resonances between the two planets. The dynamics in the binary system appears to be more chaotic in particular close to the inner stability border marked by the 3:2 mean motion resonance between the planets and in correspondence to the 5:2 resonance. These effects are due to the gravitational perturbations of the binary companion. |
| In the text | |
 |
Fig. 9 Diffusion map of a two-planet system in a binary with aB = 50 AU and eB = 0.4. The phase space is mostly chaotic with few exceptions of low diffusion orbits. The yellow filled circles mark systems that become unstable followed by a period of close encounters between the planets. The blue squares are systems which are stable over 10 Gyr. |
| In the text | |
 |
Fig. 10 Diffusion portrait for a two-planet system in a binary with aB = 100 AU and eB = 0.4. The inner region, where the mutual planetary resonances dominate, is more chaotic compared to the case with aB = 50 AU and eB = 0. Getting closer to the outer border, stable and unstable orbits coexist as in Figs. 3 and 6. |
| In the text | |
 |
Fig. 11 Diffusion portrait for a two-planet system in a binary with eB = 0.3, μ = 1, a1 = 3 AU and for 3 different values of aB, i.e. 40, 50 and 60 AU. A progressive increase in size of the stable region is observed both inside, close to the inner planet, and outside. |
| In the text | |
 |
Fig. 12 Normalized curves showing the number of stable orbits for different values of aB and eB. The sudden step in the number of cases marked the onset of a significant stable zone for that binary parameters. The normalization is performed to the maximum number of stable cases. Since the models run at the same pace, we expect that f measures the size of the stable region which saturates when the rate at which new stable cases are found is constant (i.e. the binary configuration presents a large stable zone for two planets). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


