| Issue |
A&A
Volume 593, September 2016
|
|
|---|---|---|
| Article Number | L3 | |
| Number of page(s) | 4 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201629087 | |
| Published online | 30 August 2016 | |
High braking index pulsar PSR J1640-4631: low-mass neutron star with a large inclination angle?
1 School of Physics and Electrical
Information, Shangqiu Normal University, 476000 Shangqiu, PR China
e-mail: chenwc@pku.edu.cn
2 Department of Physics, University of
Oxford, Oxford,
OX1 3RH,
UK
Received:
10
June
2016
Accepted:
24
July
2016
Recent timing observation constrained the braking index of the X-ray pulsar PSR J1640-4631 to be n = 3.15 ± 0.03, which is the highest value of all pulsars with measured braking indices so far. In this Letter, we investigate whether pulsar braking by combined between the magnetic dipole emission and the gravitational radiation might have a braking index greater than three. For conventional neutron star and low mass quark star candidates, the inferred ellipticities derived by the observed braking index are obviously much larger than the theoretical estimated maximum value. If PSR J1640-4631 is a low-mass neutron star with a mass of 0.1 M⊙, the inferred ellipticity can be approximately equal to the theoretical estimated maximum value. Because of the radio-quiet nature of this source, we employ the vacuum gap model developed by Ruderman and Sutherland to constrain the inclination angle to be 87.2 − 90°. Based on this, we propose that a low-mass neutron star with a large inclination angle can interpret the high braking index and the radio-quiet nature of this source. Future observations such as gravitational wave detection and long-term timing for this source are required to confirm or confute our scenario.
Key words: pulsars: individual: PSR J1640-4631 / pulsars: general / stars: formation / gravitational waves
© ESO, 2016
1. Introduction
The source PSR J1640-4631 is an X-ray pulsar discovered by Gotthelf et al. (2014) in a NuSTAR survey of the Norma region in the Galactic plane. Recently, the timing data offer some important parameters of this source such as the spin frequency ν = 4.84 s-1, the frequency derivative 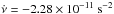 , and the second frequency derivative
, and the second frequency derivative 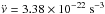 (Archibald et al. 2016). It is generally thought that the rotational kinetic energy of pulsars is converted into radiation energy through magnetic dipole radiation. From the general power-law of pulsar spin-down ν = −Kνn (where K is a constant depending on the momentum of inertia, the magnetic field, and the radius of pulsars), we can obtain the so-called braking index
(Archibald et al. 2016). It is generally thought that the rotational kinetic energy of pulsars is converted into radiation energy through magnetic dipole radiation. From the general power-law of pulsar spin-down ν = −Kνn (where K is a constant depending on the momentum of inertia, the magnetic field, and the radius of pulsars), we can obtain the so-called braking index 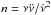 . Based on the timing data, Archibald et al. (2016) derived the braking index of PSR J1640-4631 to be n = 3.15 ± 0.03. The authors performed a series of simulations to identify whether this measurement of the braking index arises from the timing noise. Only 0.01% of these simulations yielded a braking index greater than three. Therefore, Archibald et al. (2016) thought that the timing noise indicates a very low level and is very probably not responsible for the measured high braking index.
. Based on the timing data, Archibald et al. (2016) derived the braking index of PSR J1640-4631 to be n = 3.15 ± 0.03. The authors performed a series of simulations to identify whether this measurement of the braking index arises from the timing noise. Only 0.01% of these simulations yielded a braking index greater than three. Therefore, Archibald et al. (2016) thought that the timing noise indicates a very low level and is very probably not responsible for the measured high braking index.
Until 2015, eight pulsars were known with relatively reliable measurements for the braking indices (Lyne et al. 2015). All of these pulsars have a braking index lower than three, showing that the spin-down mechanism is not pure magnetic dipole radiation. As a new member of the braking indices population, PSR J1640-4631 challenges the radiation and braking mechanisms of pulsars. The magnetic field decay can result in a braking index higher than three (Blandford & Romani 1988; Gourgouliatos & Cumming 2015). The change of inclination angle α between the magnetic axis and the spin axis may also lead to a braking index that is different from three. A long-term observation of the Crab pulsar has revealed that its inclination angle α may be slowly changing at a rate 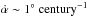 (Lyne et al. 2013). Based on the inclination angle change model, α of PSR J1640-4631 was constrained to be 18.5 ± 3 deg, and is decreasing at a rate of
(Lyne et al. 2013). Based on the inclination angle change model, α of PSR J1640-4631 was constrained to be 18.5 ± 3 deg, and is decreasing at a rate of 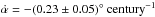 (Ekşi et al. 2016). Recently, Hamil et al. (2016) proposed a two-dipole model of pulsar magnetism, which can explain the inclination angle change. According to the wind braking model, Kou et al. (2016) found that the alignment of the inclination angle can cause the braking index to first increase and then decrease, corresponding to a braking index first higher and then smaller than three. In addition, either a mass quadrupole or a magnetic quadrupole would produce gravitational radiation (Blandford & Romani 1988). The pulsars braking by the magnetic dipole emission and the gravitational radiation could give rise to a braking index of between three to five (Archibald et al. 2016; de Araujo et al. 2016a). Employing the derived ellipticity by the braking index, de Araujo et al. (2016a) concluded that aLIGO would not detect the gravitational wave from PSR J1640-4631, while the planned Einstein Telescope would be able to do so.
(Ekşi et al. 2016). Recently, Hamil et al. (2016) proposed a two-dipole model of pulsar magnetism, which can explain the inclination angle change. According to the wind braking model, Kou et al. (2016) found that the alignment of the inclination angle can cause the braking index to first increase and then decrease, corresponding to a braking index first higher and then smaller than three. In addition, either a mass quadrupole or a magnetic quadrupole would produce gravitational radiation (Blandford & Romani 1988). The pulsars braking by the magnetic dipole emission and the gravitational radiation could give rise to a braking index of between three to five (Archibald et al. 2016; de Araujo et al. 2016a). Employing the derived ellipticity by the braking index, de Araujo et al. (2016a) concluded that aLIGO would not detect the gravitational wave from PSR J1640-4631, while the planned Einstein Telescope would be able to do so.
We here constrain the properties of PSR J1640-4631. In Sect. 2 the braking torques caused by the magnetic dipole emission and the gravitational radiation are applied to investigate the spin-down of this source. In Sect. 3 we constrain the properties of this source by the inferred ellipticity and the vacuum gap model. Finally, we summarize the results with a brief conclusion in Sect. 4.
2. Spin-down of PSR J1640-4631
We assumed the high braking index of PSR J1640-4631 to originate from the gravitational radiation of a compact object with elastic deformation: its spin-down is dominated by the torques originating from the magnetic dipole radiation and the gravitational wave emission. The angular momentum loss rate of the pulsar by magnetic dipole radiation is given by 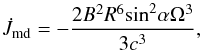 (1)where B,R, and Ω are the surface magnetic field, the radius, and the spin angular velocity of the pulsar, respectively. The pure magnetic dipole radiation predicts a braking index of three (Ostriker & Gunn 1969).
(1)where B,R, and Ω are the surface magnetic field, the radius, and the spin angular velocity of the pulsar, respectively. The pure magnetic dipole radiation predicts a braking index of three (Ostriker & Gunn 1969).
Considering the gravitational radiation of an axisymmetric pulsar with an ellipticity ϵ, the angular momentum loss rate can be written as (Shapiro & Teukolsky 1983) 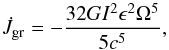 (2)where G is the gravitational constant and I the momentum of inertia of the pulsar. It is clear that a pure gravitational radiation by a mass quadrupole would lead to a braking index of five. Since the change rate of angular momentum of the pulsar is
(2)where G is the gravitational constant and I the momentum of inertia of the pulsar. It is clear that a pure gravitational radiation by a mass quadrupole would lead to a braking index of five. Since the change rate of angular momentum of the pulsar is 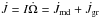 , we can obtain (Palomba 2000)
, we can obtain (Palomba 2000) 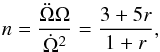 (3)where
(3)where 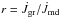 represents the fraction of angular momentum change rate that is due to the gravitational radiation versus the magnetic dipole radiation. In calculation, we ignore the change of the magnetic field, the inclination angle α, the mass, and the radius of the pulsar.
represents the fraction of angular momentum change rate that is due to the gravitational radiation versus the magnetic dipole radiation. In calculation, we ignore the change of the magnetic field, the inclination angle α, the mass, and the radius of the pulsar.
The observed data offer the total angular momentum change rate. We can therefore derive the following formula from Eq. (3): 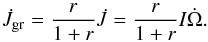 (4)Combining Eqs. (2) to (4), we can derive the ellipticity of the pulsar as follows:
(4)Combining Eqs. (2) to (4), we can derive the ellipticity of the pulsar as follows: 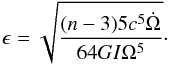 (5)Taking the canonical momentum of inertia I0 = 1045 g cm2 and inserting the observed parameters for PSR J1640-4631, the ellipticity of the pulsar can be constrained to be 4.34−5.31 × 10-3. In Fig. 1 we show the relation between the braking index and the ellipticity for PSR J1640-4631. It is worth noting that only an ellipticity greater than 10-3 can yield a braking index clearly higher than three.
(5)Taking the canonical momentum of inertia I0 = 1045 g cm2 and inserting the observed parameters for PSR J1640-4631, the ellipticity of the pulsar can be constrained to be 4.34−5.31 × 10-3. In Fig. 1 we show the relation between the braking index and the ellipticity for PSR J1640-4631. It is worth noting that only an ellipticity greater than 10-3 can yield a braking index clearly higher than three.
 |
Fig. 1 Braking index as a function of the ellipticity of the pulsar for a conventional neutron star. Two horizontal dashed lines represent the possible range (3.12−3.18) of the measured braking index for PSR J1640-4631. |
3. Constraining the properties of PSR J1640-4631
3.1. Neutron star
A conventional neutron star with a fiducial mass, radius, and breaking strain has a maximum ellipticity ϵmax = 2 × 10-7 (Owen 2005). Therefore, Archibald et al. (2016) proposed that it can be ruled out that the high braking index is caused by the gravitational radiation. However, the empirical formula for the momentum of inertia given by Bejger & Haensel (2002) is invalid for a low-mass neutron star with a mass lower than 0.2 M⊙. Theoretical study shows that the lowest mass of a neutron star with a spin frequency 100 Hz is 0.13 M⊙, and it decreases with decreasing spin frequency (Haensel et al. 2002). Therefore, the lowest mass that might be reached by PSR J1640-4631 at ν = 4.84 Hz is 0.1 M⊙. Observations indicate that low-mass neutron stars may exist in some binary systems such as PSR J1518+4904 (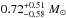 , Janssen et al. 2008), and 4U 1746-37 (
, Janssen et al. 2008), and 4U 1746-37 (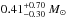 at 99.7% confidence, Li et al. 2015). Recently, the calculation performed by Horowitz (2010) showed that the highest ellipticity of low-mass (M = 0.1 M⊙) neutron stars can reach 5 × 10-3. In principle, we should consider the influence of the momentum of inertia in Eq. (5). According to the mass-radius relation of neutron stars R ∝ M− 1 / 3, a neutron star with 0.1 M⊙ has a radius R ≃ 29 km (we take R = 12 km for M = 1.4 M⊙), which leads to a momentum of inertia I ≃ 0.84 × 1045 g cm2. Inserting the new I into Eq. (5), the pulsar would need have an ellipticity ϵ = 5.3 × 10-3 to yield the high braking index of 3.15. This ellipticity is slightly higher than the theoretical highest ellipticity of a low-mass neutron star. Since the evaluating criterion is not extremely strict, a low-mass neutron star with elastic deformation might be able to produce the strong gravitational radiation and result in the observed braking index.
at 99.7% confidence, Li et al. 2015). Recently, the calculation performed by Horowitz (2010) showed that the highest ellipticity of low-mass (M = 0.1 M⊙) neutron stars can reach 5 × 10-3. In principle, we should consider the influence of the momentum of inertia in Eq. (5). According to the mass-radius relation of neutron stars R ∝ M− 1 / 3, a neutron star with 0.1 M⊙ has a radius R ≃ 29 km (we take R = 12 km for M = 1.4 M⊙), which leads to a momentum of inertia I ≃ 0.84 × 1045 g cm2. Inserting the new I into Eq. (5), the pulsar would need have an ellipticity ϵ = 5.3 × 10-3 to yield the high braking index of 3.15. This ellipticity is slightly higher than the theoretical highest ellipticity of a low-mass neutron star. Since the evaluating criterion is not extremely strict, a low-mass neutron star with elastic deformation might be able to produce the strong gravitational radiation and result in the observed braking index.
3.2. Strange quark star
Some pulsars have been proposed to consist of strange quarks (Bodmer 1971). Compared with a neutron star, a quark star may have a relatively low mass and small radius (Itoh 1970; Alcock et al. 1986). Xu (2005) suggested that the radio-quiet object 1E 1207.4-5209 might be a low-mass bare strange star. Subsequently, Yue et al. (2006) argued that if PSR B0943+10 were a low-mass (0.019 M⊙) quark star with a radius of 2.6 km, the problem about its much smaller polar cap area might be solved naturally. Observations have revealed that the Tev luminosity of the pulsar wind nebula HESS J1640-465 is ~6% of spin-down luminosity of a conventional neutron star (Gotthelf et al. 2014). Based on this, we can constrain the lowest momentum of inertia of the pulsar as I ≃ 0.06I0 = 6 × 1043 g cm2. Because the internal density (ρ) in low-mass quark stars is almost homogeneous, its mass can be approximately written as M = 4πR3ρ/ 3. The density ρ depends on the models of dense matter and is typically a few times the normal nuclear density ρ0 = 2.7 × 1014 g cm-3. Based on the lowest momentum of inertia and for ρ = 2ρ0, the quark star candidate has a mass M ≃ 0.23 M⊙, and the radius of the quark star is R ≃ 5.9 km.
In the framework of strange quark stars, the highest ellipticity can be written as (Owen 2005) 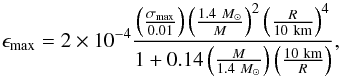 (6)where σmax is the breaking strain of the crust. If we take a typical breaking strain of the crust σmax = 0.01, we derive ϵmax = 8.6 × 10-4 (ϵmax = 2.5 × 10-3 with self-gravity). However, Eq. (5) produces a higher ellipticity ϵ ≃ 0.02 according to the momentum of inertia of this quark star I ≃ 6.0 × 1043 g cm2. The discrepancy is two orders of magnitude between the inferred value from the observation and the theoretical estimated highest value.
(6)where σmax is the breaking strain of the crust. If we take a typical breaking strain of the crust σmax = 0.01, we derive ϵmax = 8.6 × 10-4 (ϵmax = 2.5 × 10-3 with self-gravity). However, Eq. (5) produces a higher ellipticity ϵ ≃ 0.02 according to the momentum of inertia of this quark star I ≃ 6.0 × 1043 g cm2. The discrepancy is two orders of magnitude between the inferred value from the observation and the theoretical estimated highest value.
3.3. Radio-quiet nature
Gotthelf et al. (2014) discovered PSR J1640-4631 as a pulsating X-ray source in a NuSTAR survey. This source is radio quiet (Archibald et al. 2016) and no gamma-ray pulsations have been detected (Gotthelf et al. 2014). The simplest explanation is that the relatively narrow radio beam does not point toward Earth (Brazier & Johnston 1999). However, its characteristic age is 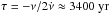 , which means that it is a very young pulsar. Young pulsars tend to have a wide radio radiation beam. For example, PSR J1119-6127 (spin period 407.8 ms, characteristic age 1600 yr, both parameters are very similar to those of PSR J1640-4631) has a beam half-opening angle of ≈30° (Johnston & Weisberg 2006). Another possibility is that this source has already evolved beyond the so-called death line of pulsars (Trümper 2005). In the vacuum gap model, the polar gap surface of the pulsar was thought to be struck by the energetic particles, and is heated and radiates X-rays (Ruderman & Sutherland 1975). The radio emission originates from the particle acceleration by an effective electric force, which is exerted by the potential drop (Φ) between the magnetic axis and the last open field line. If Φ is lower than a critical voltage Φc, the particles cannot be accelerated to an energy high enough to produce sparks. As a result, the pulsar would not give rise to radio emission. The vacuum gap model makes a strong assumption, in which the magnetic axis and the spin axis of the pulsar are aligned. We consider a general case here of an inclination angle α between the magnetic axis and the spin axis. In nonalignment case, the steepest potential drop is given by (Yue et al. 2006)
, which means that it is a very young pulsar. Young pulsars tend to have a wide radio radiation beam. For example, PSR J1119-6127 (spin period 407.8 ms, characteristic age 1600 yr, both parameters are very similar to those of PSR J1640-4631) has a beam half-opening angle of ≈30° (Johnston & Weisberg 2006). Another possibility is that this source has already evolved beyond the so-called death line of pulsars (Trümper 2005). In the vacuum gap model, the polar gap surface of the pulsar was thought to be struck by the energetic particles, and is heated and radiates X-rays (Ruderman & Sutherland 1975). The radio emission originates from the particle acceleration by an effective electric force, which is exerted by the potential drop (Φ) between the magnetic axis and the last open field line. If Φ is lower than a critical voltage Φc, the particles cannot be accelerated to an energy high enough to produce sparks. As a result, the pulsar would not give rise to radio emission. The vacuum gap model makes a strong assumption, in which the magnetic axis and the spin axis of the pulsar are aligned. We consider a general case here of an inclination angle α between the magnetic axis and the spin axis. In nonalignment case, the steepest potential drop is given by (Yue et al. 2006) 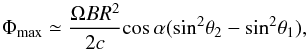 (7)where θ1 = α − θ (when α>θ), 0 (when α ≤ θ), and θ2 = α + θ (when α<π / 2 − θ), π/ 2 (when α ≥ π/ 2 − θ). The angle θ is the opening half-angle of the polar cap, and sin θ = rpc/R, where rpc is the polar cap radius.
(7)where θ1 = α − θ (when α>θ), 0 (when α ≤ θ), and θ2 = α + θ (when α<π / 2 − θ), π/ 2 (when α ≥ π/ 2 − θ). The angle θ is the opening half-angle of the polar cap, and sin θ = rpc/R, where rpc is the polar cap radius.
Main parameters for the three candidates of PSR J1640-4631.
To estimate the polar cap radius, we adopt a formula for an aligned pulsar as follows 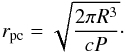 (8)The magnetic field of the pulsar can be calculated by
(8)The magnetic field of the pulsar can be calculated by 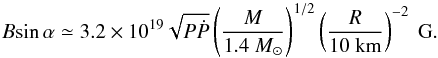 (9)Because r ≈ 0.08 is very low, we assume a pure magnetic dipole radiation in calculating magnetic field. The two cases are different by a factor
(9)Because r ≈ 0.08 is very low, we assume a pure magnetic dipole radiation in calculating magnetic field. The two cases are different by a factor 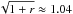 . We consider the influence of inclination angle in calculating magnetic field, while Yue et al. (2006) assumed α = 90°. In addition, the right side of Eq. (9) is different from that in Yue et al. (2006) by a factor of two. This difference originates from different magnetic momentum (μ) formulas: we use μ = BR3, while they took μ = BR3/ 2. To obtain the steepest potential drop, we summarize the related parameters for the candidates of PSR J1640-4631 including conventional neutron star (CNS), low-mass neutron star (LMNS), and low-mass quark star (LMQS) in Table 1.
. We consider the influence of inclination angle in calculating magnetic field, while Yue et al. (2006) assumed α = 90°. In addition, the right side of Eq. (9) is different from that in Yue et al. (2006) by a factor of two. This difference originates from different magnetic momentum (μ) formulas: we use μ = BR3, while they took μ = BR3/ 2. To obtain the steepest potential drop, we summarize the related parameters for the candidates of PSR J1640-4631 including conventional neutron star (CNS), low-mass neutron star (LMNS), and low-mass quark star (LMQS) in Table 1.
 |
Fig. 2 Relation between the steepest potential drops and the inclination angle α. The solid, dashed, and dotted curves denote the cases of CNS, LMNS, and LMQS, respectively. The input parameters in Eq. (7) are those of Table 1. |
According to Eq. (7), we plot the steepest potential drop Φmax vs. the inclination angle α in Fig. 2. The different tendency in the steepest potential drops between our Figs. 2 and 1 of Yue et al. (2006) for small inclination angles is noteworthy. This discrepancy is due to including the influence of inclination angle in this work. Taking a critical voltage Φc = 1012 V, nearly all inclination angles (except for large angles of almost 90°) for CNS, LMNS, and LMQS have a potential drop steeper than Φc. Because it can be ruled out that CNS and LMQS are the candidate of PSR J1640-4631, we can constrain the inclination angle range of LMNS to be α = 87.2−90°.
4. Discussion and summary
Assuming that the gravitational radiation of a pulsar with elastic deformation can be responsible for the high braking index of PSR J1640-4631, we here constrained its properties. To produce the observed high braking index, the ellipticity of the pulsar is ϵ ≈ 5 × 10-3 if the pulsar was a CNS or LMNS. According to the theoretical estimation, it is impossible to possess such a high ellipticity for CNS, while this ellipticity is approximately consistent with the estimated maximum for LMNS. For an LMQS candidate, an ultra-high ellipticity ϵ ≃ 0.2 is required. Based on the vacuum gap model and LMNS candidate, an inclination angle in the range of α = 87.2−90° might account for the radio-quiet nature of this source. Based on the magnetic dipole model with corotating plasma, Ekşi et al. (2016) obtained two possible inclination angles for PSR J1640-4631: 18.5 ± 3° and 56 ± 4°. However, according to the vacuum gap model, CNS can emit in the radio. If their model is correct, the observer is located exactly in the forbidden zone of the radio emission beam. According to the alignment torque equation given by Philippov et al. (2014)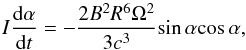 (10)the LMNS model predicts a change rate of the inclination angle
(10)the LMNS model predicts a change rate of the inclination angle 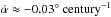 , which is approximately one order of magnitude lower than the value (−0.23 ± 0.05° century-1) predicted by Ekşi et al. (2016). This difference is expected to be explained in the future timing observations.
, which is approximately one order of magnitude lower than the value (−0.23 ± 0.05° century-1) predicted by Ekşi et al. (2016). This difference is expected to be explained in the future timing observations.
Perhaps a serious problem in this work is how to yield such an LMNS. In classical stellar evolution theory, it is impossible to form such an LMNS directly through a supernova explosion. An LMNS might be produced through fragmentation during protoneutron star formation or neutron star collisions (Popov et al. 2007; Horowitz 2010). The deformation of an LMNS should be relatively easy to understand because it experiences a violent event. However, the physical mechanism triggering fragmentation is still a puzzle.
To summarize, PSR J1640-4631 cannot be a CNS or LMQS if the high braking index originates from gravitational radiation. However, it is difficult to confirm that this source is an LMNS. One possibility is to try and detect the gravitational wave signals from this source. The characteristic gravitational wave strain equation reads (Abbott et al. 2007) 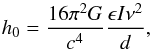 (11)where d is the distance of the source. Insertingly, for the observed parameters and the derived ellipticity of PSR J1640-4631 we have h0 = 4.2 × 10-26. In the gravitational wave frequency νgw = 9.68 Hz, this signal is lower than the strain sensitivity of aLIGO de Araujo et al. (2016a; however, de Araujo et al. 2016b proposed that aLIGO can detect the gravitational wave generated by Vela). Therefore, we expect that the planned Einstein Telescope will investigate this source in the future. According to our scenario, low-mass neutron stars with a braking index greater than three are important gravitational wave sources.
(11)where d is the distance of the source. Insertingly, for the observed parameters and the derived ellipticity of PSR J1640-4631 we have h0 = 4.2 × 10-26. In the gravitational wave frequency νgw = 9.68 Hz, this signal is lower than the strain sensitivity of aLIGO de Araujo et al. (2016a; however, de Araujo et al. 2016b proposed that aLIGO can detect the gravitational wave generated by Vela). Therefore, we expect that the planned Einstein Telescope will investigate this source in the future. According to our scenario, low-mass neutron stars with a braking index greater than three are important gravitational wave sources.
If no gravitational wave from this source is detected, the reasons might be as follows. First, the high braking index of PSR J1640-4631 might be caused by other mechanisms such as the inclination angle change (Ekşi et al. 2016), the quadrupolar field structure (Pétri 2015), and the magnetic field decrease. Second, the high braking index may arise from the contaminant of an anomalous 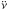 after glitches (Alpar & Baykal 2006). Some pulsars were observed to have an exponential recovery in
after glitches (Alpar & Baykal 2006). Some pulsars were observed to have an exponential recovery in 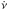 after glitches (see also the panel of PSR J1531-5610 in Fig. 7 of Yu et al. 2013). Such an exponential recovery process in
after glitches (see also the panel of PSR J1531-5610 in Fig. 7 of Yu et al. 2013). Such an exponential recovery process in 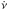 could result in a high measured value of
could result in a high measured value of 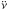 (Johnston & Galloway 1999; Hobbs et al. 2010), which does not originate from a secular braking torque. Such a glitch might naturally produce an anomalous braking index. Therefore, we expect further observations aimed to detect gravitational waves and long-term timing of this source to confirm or confute our scenario.
(Johnston & Galloway 1999; Hobbs et al. 2010), which does not originate from a secular braking torque. Such a glitch might naturally produce an anomalous braking index. Therefore, we expect further observations aimed to detect gravitational waves and long-term timing of this source to confirm or confute our scenario.
Acknowledgments
We are grateful to the anonymous referee for useful suggestions. We also thank Philipp Podsiadlowski, Aris Karastergiou, R.-X. Xu , X.-D. Li, M. Yu, and H. Tong for helpful discussions. This work was partly supported by the National Science Foundation of China (under grant number 11573016), the Program for Innovative Research Team (in Science and Technology) at the University of Henan Province, and the China Scholarship Council.
References
- Abbott, B., Kramer, M., Lyne, A. G., et al. 2007, Phys. Rev. D, 76, 042001 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Alcock, C., Farhi, E., & Olinto, A. 1986, ApJ, 310, 261 [Google Scholar]
- Alpar, M. A., & Baykal, A. 2006, MNRAS, 372, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Archibald, R. F., Gotthelf, E. V., Ferdman, R. D., et al. 2016, ApJ, 819, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Bejger, M., & Haensel, P. 2002, A&A, 396, 917 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blandford, R. D., & Romani, R. W. 1988, MNRAS, 234, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Bodmer, A. R. 1971, Phys. Rev. D, 4, 1601 [NASA ADS] [CrossRef] [Google Scholar]
- Brazier, K. T. S., Johnston, S. 1999, MNRAS, 305, 671 [NASA ADS] [CrossRef] [Google Scholar]
- de Araujo, J. C. N., Coelho, J. G., & Costa, C. A. 2016, J. Cosmil. Astro-Particle Phys., 07, 023 [NASA ADS] [CrossRef] [Google Scholar]
- de Araujo, J. C. N., Coelho, J. G., & Costa, C. A. 2016, Eur. Phys. J. C, submitted [arXiv:1607.05315] [Google Scholar]
- Ekşi, K. Y., Andaç, I. C., Çıkıntoǧlu, S., Gügercinoǧlu, E., Motlagh, A. V., & Kızıltan, B. 2016, ApJ, 823, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Gotthelf, E. V., Tomsick, J. A., Halpern, J. P., et al. 2014, ApJ, 788, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Gourgouliatos, K. N., & Cumming, A. 2015, MNRAS, 446, 1121 [NASA ADS] [CrossRef] [Google Scholar]
- Haensel, P., Zdunik, J. L., & Douchin, F. 2002, A&A, 385, 301 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hamil, Ol. Q., Stone, N. J., Stone, J. R. 2016, ArXiv e-prints [arXiv:1608.01375] [Google Scholar]
- Hobbs, G., Lyne, A. G., & Kramer, M. 2010, MNRAS, 402, 1027 [NASA ADS] [CrossRef] [Google Scholar]
- Horowitz, C. J. 2010, Phys. Rev. D, 81, 103001 [NASA ADS] [CrossRef] [Google Scholar]
- Itoh, N. 1970, Prog. Theor. Phys., 44, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Janssen, G. H., Stappers, B. W., Kramer, M., et al. 2008, A&A, 490, 753 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnston, S., & Galloway, D. 1999, MNRAS, 306, L50 [NASA ADS] [CrossRef] [Google Scholar]
- Johnston, S., & Weisberg, J. M. 2006, MNRAS, 368, 1856 [NASA ADS] [CrossRef] [Google Scholar]
- Kou, F. F., Tong, H., & Wang, N. 2016, MNRAS, submitted [arXiv:1604.01231] [Google Scholar]
- Li, Z., Qu, Z., Chen, L., et al. 2015, ApJ, 798, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Lyne, A., Graham-Smith, F., Weltevrede, P., et al. 2013, Science, 342, 598 [NASA ADS] [CrossRef] [Google Scholar]
- Lyne, A. G., Jordan, C. A., Graham-Smith, F., et al. 2015, MNRAS, 446, 857 [NASA ADS] [CrossRef] [Google Scholar]
- Ostriker, J. P., & Gunn, J. E. 1969, ApJ, 157, 1395 [NASA ADS] [CrossRef] [Google Scholar]
- Owen, B. J. 2005, Phys. Rev. Lett., 95, 211101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Palomba, C. 2000, A&A, 354, 163 [NASA ADS] [Google Scholar]
- Pétri, J. 2015, MNRAS, 450, 714 [NASA ADS] [CrossRef] [Google Scholar]
- Philippov, A., Tchekhovskoy, A., & Li, J. G. 2014, MNRAS, 441, 1879 [NASA ADS] [CrossRef] [Google Scholar]
- Popov, S., Blaschke, D., Grigorian, H., & Prokhorov, M. 2007, Ap&SS, 308, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M., & Sutherland, P. G. 1975, ApJ, 196, 51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shapiro, S. L., & Teukolsky, S. A., 1983, Black holes, white dwarfs, and neutron stars: The physics of compact objects (New York: Wiley-Interscience) [Google Scholar]
- Trümper, J. E. 2005, in The Electromagnetic Spectrum of Neutron Stars, eds. A. Baykal, S. K. Yerli, S. C. Inam, & S. Grebenev, NATO ASIB Proc., 210, 117 [Google Scholar]
- Xu, R. X. 2005, MNRAS, 356, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, M., Manchester, R. N., Hobbs, G., et al. 2013, MNRAS, 429, 688 [NASA ADS] [CrossRef] [Google Scholar]
- Yue, Y. L., Cui, X. H., & Xu, R. X. 2006, ApJ, 649, L95 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Braking index as a function of the ellipticity of the pulsar for a conventional neutron star. Two horizontal dashed lines represent the possible range (3.12−3.18) of the measured braking index for PSR J1640-4631. |
| In the text | |
 |
Fig. 2 Relation between the steepest potential drops and the inclination angle α. The solid, dashed, and dotted curves denote the cases of CNS, LMNS, and LMQS, respectively. The input parameters in Eq. (7) are those of Table 1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


