| Issue |
A&A
Volume 593, September 2016
|
|
|---|---|---|
| Article Number | L18 | |
| Number of page(s) | 4 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201629024 | |
| Published online | 26 September 2016 | |
Pseudomagnitude distances: Application to the Pleiades cluster⋆
1 Laboratoire Lagrange, Univ. Côte d’Azur, Observatoire de la Côte d’Azur, CNRS, Bd de l’Observatoire, 06304 Nice, France
e-mail: Alain.Chelli@oca.eu
2 Univ. Grenoble Alpes, IPAG, 38000 Grenoble, France
3 CNRS, IPAG, 38000 Grenoble, France
Received: 28 May 2016
Accepted: 2 September 2016
The concept of pseudomagnitude has recently been introduced to estimate apparent stellar diameters using a strictly observational methodology. Pseudomagnitudes are distance indicators which have the remarkable property of being reddening free. In this study, we use Hipparcos parallax measurements to compute the mean absolute pseudomagnitudes of solar neighbourhood dwarf stars as a function of their spectral type. To illustrate the use of absolute pseudomagnitudes, we derive the distance moduli of 360 Pleiades stars and find that the centroid of their distribution is 5.715 ± 0.018, corresponding to a distance of 139.0 ± 1.2 pc. We locate the subset of ~50 Pleiades stars observed by Hipparcos at a mean distance of 135.5 ± 3.7 pc, thus confirming the frequently reported anomaly in the Hipparcos measurements of these stars.
Key words: stars: distances / methods: data analysis / methods: observational / techniques: photometric
Table 3 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/593/L18
© ESO, 2016
1. Introduction
In astrophysics, the calculation of interstellar extinction is a complex and recurring problem. For many objects, such as those buried in star-forming regions, dereddening the photometries is a difficult and demanding task. In the case of a star, the calculation of interstellar extinction requires a detailed knowledge of its luminosity class, spectral type, and intrinsic colours, parameters which are not always available and often have uncertain robustness. This leads to the accumulation of errors, and makes it nearly impossible to attempt any massive statistical analysis.
We recently introduced the concept of pseudomagnitude for the calculation of the apparent size of stars, thus avoiding dealing with the problem of visual extinction (Chelli et al. 2014, 2016). This has allowed us to compile a catalogue of 453 000 angular diameters with an accuracy of the order of 1% (2% systematic). Pseudomagnitudes are linear combinations of magnitudes constructed in such a way as to eliminate interstellar extinction1. They are purely observational quantities that are unaffected by reddening effects, and can be applied to any type of object. As in the case of magnitudes, pseudomagnitudes are distance indicators, and absolute pseudomagnitudes measured at a distance of 10 pc are luminosity indicators.
Knowledge of the pseudomagnitudes and absolute pseudomagnitudes of stars allows their distance to be estimated. In the present study, we use the parallax measurements of Hipparcos (ESA 1997; van Leeuwen 2007) to calculate the mean absolute pseudomagnitude of field dwarf stars as a function of their spectral type. As an example, we use this technique to determine the centroid of the distance distribution of 360 stars in the Pleiades cluster.
In Sect. 2, we explain the concept of pseudomagnitudes. In Sect. 3, we use distance filtered parallax measurements to calculate the mean absolute pseudomagnitudes (V,J), (V,H), and (V,Ks) of dwarf stars, and the centroid of the distance distribution of our Pleiades stars is calculated and discussed in Sect. 4.
2. Pseudomagnitudes
We define the pseudomagnitude pm{ i,j } of an astrophysical object as 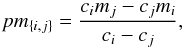 (1)where mi and mj are the magnitudes measured in the photometric bands i and j, ci (resp. cj) is the ratio of the interstellar extinction coefficients Ri and Rv between band i and the visible band. We note that when one of the coefficients ci or cj tends to zero, the pseudomagnitude tends to the magnitude mi or mj. The pseudomagnitude is by construction a reddening free distance indicator. It can be written as
(1)where mi and mj are the magnitudes measured in the photometric bands i and j, ci (resp. cj) is the ratio of the interstellar extinction coefficients Ri and Rv between band i and the visible band. We note that when one of the coefficients ci or cj tends to zero, the pseudomagnitude tends to the magnitude mi or mj. The pseudomagnitude is by construction a reddening free distance indicator. It can be written as 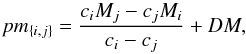 (2)where Mi and Mj are absolute magnitudes and DM is the distance modulus. At this stage, we define the absolute pseudomagnitude PM{ i,j } as
(2)where Mi and Mj are absolute magnitudes and DM is the distance modulus. At this stage, we define the absolute pseudomagnitude PM{ i,j } as 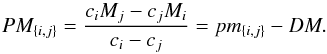 (3)The absolute pseudomagnitude is a reddening free luminosity indicator that can be computed very easily. This requires the knowledge of two magnitudes and a distance. On the other hand, once the mean absolute pseudomagnitude has been calculated for a group of stars sharing the same physical properties, the distance modulus of a star from the same group can be estimated with the knowledge of just two magnitudes.
(3)The absolute pseudomagnitude is a reddening free luminosity indicator that can be computed very easily. This requires the knowledge of two magnitudes and a distance. On the other hand, once the mean absolute pseudomagnitude has been calculated for a group of stars sharing the same physical properties, the distance modulus of a star from the same group can be estimated with the knowledge of just two magnitudes.
3. Absolute pseudomagnitudes of dwarf stars
For our calculations, we use Eqs. (1) and (3), with the second reduction of Hipparcos parallaxes (van Leeuwen 2007); the spectral type; and the magnitude pairs (V,J), (V,H), and (V,Ks) provided by SIMBAD. We adopt the interstellar extinction coefficients determined by Fitzpatrick (1999), thus leading to the following expressions for the pseudomagnitudes: 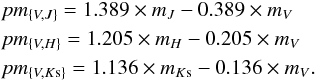 (4)
(4)
3.1. HIPPARCOS data
A priori, the absolute pseudomagnitude of a group of stars with the same spectral type and luminosity class should be constant as a function of distance. Figure 1a plots the pseudomagnitude (V,Ks) of Hipparcos class III and V stars with a spectral type K0 (3747 objects) as a function of their distance modulus. Figure 1b shows the absolute pseudomagnitude (V,Ks); the dwarfs are at the top and the giants at the bottom. For the same class of stars, at first it is constant to within the limits resulting from noise, but beyond a certain distance it then appears to decrease. It is a mere artefact: below 10% noise the inverse of the parallax begins to be numerically biased. In this example, 75% of the dwarfs and only 26% of the giants have a parallax noise smaller than 10%.
 |
Fig. 1 a) (V,Ks) pseudomagnitudes of the 3747 Hipparcos K0 class III and V stars as a function of their distance modulus; b) Absolute (V,Ks) pseudomagnitudes of the same stars, with the dwarfs lying at the top and the giants lying at the bottom of this figure. The decrease of the pseudomagnitudes beyond a certain distance is an artefact due to numerical bias at low signal to noise ratio (see text). |
3.2. Practical absolute pseudomagnitude calculation
In order to calculate the mean absolute pseudomagnitudes of dwarf stars, we proceed as follows: a) we consider all of the stars in the Hipparcos catalogue having the same spectral type, with or without selecting their luminosity class, depending on the possible degree of confusion; b) we place a limit on the distance of the sample in order to minimize the influence of the numerical bias2; c) since we do not control the astrophysical biases (see below), we assume that all of the objects are statistically equivalent, and adjust the fit of the absolute pseudomagnitude distribution to one or – in some cases – two Gaussian functions.
This is a difficult operation because the absolute pseudomagnitude distribution is not always strictly Gaussian. In practice, stars from the same luminosity class and with the same spectral type often have stratified luminosities as a function of their distance. This phenomenon confirms what is already known, i.e. that for any given spectral type and class of luminosity, there are hidden subclasses of stars with distinct physical properties. Although the absolute pseudomagnitudes would permit a detailed investigation of these physical properties, for the time being we do not have sufficient statistical information to implement such an analysis. This will become possible when the measurements provided by Gaia (de Bruijne 2012) become available.
Manual calculations were made for each spectral type, and were repeated several times on various samples of stars. These were based on the analysis of the pseudomagnitudes of approximately 6000 dwarf stars, distributed over 56 spectral subtypes. It corresponds to about 25% of the Hipparcos stars identified as dwarfs. Of the selected data, 90% have a parallax with less than 10% noise, 98% less than 20%. Figure 2 shows the mean absolute pseudomagnitudes (V,Ks) of these dwarf stars as a function of their spectral types, ranging from O9 to M4.
 |
Fig. 2 a) Mean (V,Ks) absolute pseudomagnitudes of field dwarf stars as a function of spectral type; b) open circles: (V,Ks) pseudomagnitudes of 280 Pleiades stars located at less than 0.84 mag (3 times the Gaussian dispersion of Fig. 3) from the Pleiades barycentric distance modulus. Hipparcos stars are identified with larger filled circles, superimposed our main sequence model shifted at the Pleiades distance. |
The median statistical error on the mean absolute pseudomagnitudes is equal to 0.03 mag, which corresponds to an error of 1.5% in terms of distance. For a given group of stars, the observed dispersions can be accounted for by the natural width of the group, which is increased by the influence of multiplicity, errors of magnitude, distance, and classification. To a lesser extent, they also reflect the star’s age or metallicity. We estimate, to within a factor of 2, that the systematic error on a correctly characterised single dwarf star is of the order of 0.05 mag.
Although pseudomagnitudes have many potential applications, the most immediate of these is the determination of the mean distance of a spatially concentrated group of stars, for example in the case of stellar clusters and galaxies. In the following section we calculate the centroid of the distance distribution of 360 stars in the Pleiades cluster, and whenever possible compare our results with those obtained by other authors.
4. Pseudomagnitude distance of the Pleiades
The Pleiades is one of the most commonly observed young open clusters, and the properties of its stars provide a de facto definition of the properties of main sequence stars at age zero. Numerous studies continue to be published regarding the census of this cluster’s coeval stars, and the highest possible accuracy is needed in their distance determinations in order to test the models of stellar structure and evolution. The pseudomagnitude method can be applied to all of the stars in this cluster, for which the spectral type and at least one pair of magnitudes is known. It is perfectly adapted to the calculation of the cluster’s mean distance, and could even be sufficient for the accurate evaluation of the individual distances of these stars (see Sect. 4.3).
Measured distances of Pleiades stars.
4.1. The Pleiades distance controversy
A history of distance estimations of the Pleiades cluster can be found in An et al. (2007) and Melis et al. (2014); Table 1 provides a summary of the measurements published in the last 20 years. Various methods have been used. Excluding Hipparcos, the other direct distance measurements (ground-based and spaceborne parallaxes, binaries, VLBI) have relied on the analysis of a total of ≈30 stars, and position the Pleiades at a distance between 130 and 139 pc. The indirect photometric methods have been applied on a total of ≈120 stars and position the cluster at a distance of 132 pc. In contrast, the mean distance of 54 Pleiades stars of spectral types B, A, and F by Hipparcos (van Leeuwen 2009) lead to the controversial distance of 120.2 ± 1.7 pc, which is indeed markedly lower (by 10%) than all the other measurements.
It should be noted that the Pleiades cluster probably contains more than one thousand stars. When projected onto the sky, it extends over a distance from 10 to 20 pc, and it would be reasonable to assume that the Pleiades has a similar size along its line of sight when viewed from Earth. Under these conditions, the distances measured on a few, or even a few tens of objects, with an accuracy much better than the cluster’s expected size, are only representative distances of these objects. In view of the size of this cluster, it could well be possible to find star concentrations at distances of the order of 15 pc from one another. The controversy does not have as much to do with the so-called distance of the Pleiades cluster3, as with the mean distance of the approximately 54 stars used in the Hipparcos estimate.
It is difficult to compare various distance measurements, as they are based on samples of stars which are generally small and generally disjoint. The Hipparcos sample was not used by other independent distance estimations, it was only reused in new attempts to refine the Hipparcos reduction, first by Makarov (2002), which led to a distance of 129.0 ± 3.3 pc, and then by van Leeuwen (2009), who determined a value of only 120.2 ± 1.7 pc. We note that in view of their uncertainties, these two distance estimations are only marginally (2.4σ) different.
 |
Fig. 3 Distance moduli distribution for 360 Pleiades stars, fitted by a Gaussian distribution plus a second-degree polynomial. The Gaussian dispersion (0.28 mag) is dominated by spectral classifications errors. |
Our absolute pseudomagnitude calibration allows us to evaluate the distance of any sample of stars. In the following section, we calculate the distance of 360 Pleiades stars and of the Hipparcos sample.
4.2. Distance of 360 Pleiades stars
In this section, we assume that Pleiades stars have, at the same spectral types, the same pseudomagnitudes (V,J), (V,H), and (V,Ks) as field dwarfs. Significant differences occur for cool stars somewhere within the M spectral class. Our sample of Pleiades stars was obtained from a total of 3721 stars associated with the “M45” identifier in the Simbad database. After filtering (multiplicity, variability, etc.), a total of 512 stars remained, of which only 360 had the required information for the calculation of their distance. As the Pleiades cluster is very young, in order to increase the size of our sample, we assumed all of the selected stars to be of luminosity class V. As the pseudomagnitude is sensitive to the luminosity class, any non-dwarf star will contribute to the broadening of the distance distribution or will get a distance very different to that of the cluster and will thus be excluded from the analysis. We did not try to perform filtering for membership; non-members will form a diffuse background that is taken into account in our statistical modelling.
The adopted distance modulus of each object is the average of the distance moduli computed from the photometric pairs (V,J), (V,H), and (V,Ks), and its error is the dispersion of the three estimates. The corresponding distances and their errors are given in Table 3. The (V,Ks) pseudomagnitudes of our sample, outliers excluded, are shown in Fig. 2b as a function of the spectral type. It is not a classical colour-magnitude diagram. The observed dispersions per spectral type, 0.2 to 0.4 mag, are not imposed by the physics of the cluster but by errors in spectral classification, which is probably the limiting noise of our present approach. We fit the resulting distance modulus distribution by a Gaussian plus a second-degree polynomial, see Fig. 3. The centre of the Gaussian function provides the barycentre of the distance moduli of the 360 stars studied, i.e. 5.715 ± 0.018, which corresponds to a distance of 139.0 ± 1.2 pc. In view of the small samples used previously, this comparison is somewhat risky; however, our distance calculation is globally in agreement with most estimations, but tends to position the cluster at the high end of measured “distances”.
What of the stars measured by Hipparcos? We have all of the information needed to characterise 44 of the 54 stars given in the list of Makarov (2002). The distribution of their distance moduli exhibits two maxima, at approximately 5.4 and 5.7, a possible indication of subclustering. A Gaussian fit of this distribution leads to a mean distance modulus of 5.66 ± 0.06, i.e. a distance of 135.5 ± 3.7 pc, respectively 1.3σ and 3.8σ above the Makarov (2002) and van Leeuwen (2009) estimates. Our result tends to confirm that on average the Hipparcos distances of these stars are underestimated.
However, the baby should not be thrown out with the bathwater, since all of our distance moduli were obtained using absolute pseudomagnitudes derived from correctly distance-filtered Hipparcos parallax measurements. The fact that we obtain a barycentric distance that is compatible (and probably more accurate in terms of defining the cluster’s centroid, as a consequence of the much greater sample size) with distances measured from the ground, together with the fact that we are able to apparently correct the same controversial Hipparcos measurements, indicates that the Hipparcos parallaxes at large are robust.
4.3. Distance to the VLBI stars
Among recent distance measurements, those of Melis et al. (2014) determined by VLBI are the most accurate. They make it possible to test the robustness of our pseudomagnitude estimations, and we calculate the distance of six of the ten stars scheduled for VLBI observation by Melis et al. (2013) (the remaining four are either not single dwarfs or are lacking spectral type information). Table 2 summarises our predicted distances. For the two stars in common with Melis et al. (2014), the agreement between VLBI and pseudomagnitude distances is remarkable, with relative differences of 1% (0.5σ) and 4% (1.6σ).
5. Conclusion
Pseudomagnitudes are remarkable distance indicators because they are free of interstellar reddening effects. We have calculated the mean absolute pseudomagnitudes of field dwarfs from O9 to M4, based on the Hipparcos parallax measurements of approximately 6000 stars, allowing us to estimate the distance of 360 Pleiades stars. We position the centroid of these stars at 139.0 ± 1.2 pc, and we confirm that the Pleiades stellar distances measured by Hipparcos are on average underestimated by 10%.
Pseudomagnitude distance (PMD) of six Pleiades stars of the Melis et al. (2013) list.
ESA’s recently launched Gaia mission will make it possible to accurately determine the fine structure of absolute pseudomagnitudes, their natural width, and the influence of various parameters such as age and metallicity. It will be possible to calibrate these very accurately in several different optical bands. Our initial results obtained with the Pleiades cluster, together with their comparison with VLBI measurements, are already very encouraging. This technique is purely observational, direct and simple to implement, since it needs the knowledge of only the spectral type, two magnitudes, and the corresponding absolute pseudomagnitude.
Pseudomagnitudes are similar to the Wesenheit quantity (van den Bergh 1975; Madore 1982), based on a linear combination of a magnitude and a colour, and extensively used for the analysis of the period-luminosity relations of Cepheids.
For example, in the case of the K0 stars in Fig. 1b, this limit would be around DM = 4 for dwarves and DM = 7 for giants.
Acknowledgments
We gratefully thank R.I Anderson for pointing out the similarity between the PMs and the Wesenheit quantity, and B.F. Madore and an anonymous referee for their useful comments.
References
- An, D., Terndrup, D. M., Pinsonneault, M. H., et al. 2007, ApJ, 655, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Chelli, A., Bourges, L., Duvert, G., et al. 2014, in Optical and Infrared Interferometry IV, Proc. SPIE, 9146, 91462 [Google Scholar]
- Chelli, A., Duvert, G., Bourgès, L., et al. 2016, A&A, 589, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- David, T. J., Hillenbrand, L. A., Cody, A. M., Carpenter, J. M., & Howard, A. W. 2016, ApJ, 816, 21 [NASA ADS] [CrossRef] [Google Scholar]
- de Bruijne, J. H. J. 2012, Ap&SS, 341, 31 [NASA ADS] [CrossRef] [Google Scholar]
- ESA 1997, The Hipparcos and Tycho Catalogues, ESA SP-1200, 1 [Google Scholar]
- Fitzpatrick, E. L. 1999, PASP, 111, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Gatewood, G., de Jonge, J. K., & Han, I. 2000, ApJ, 533, 938 [NASA ADS] [CrossRef] [Google Scholar]
- Johns-Krull, C. M., & Anderson, J. 2005, in 13th Cambridge Workshop on Cool Stars, Stellar Systems and the Sun, eds. F. Favata, G. A. J. Hussain, & B. Battrick, ESA SP, 560, 683 [Google Scholar]
- Kim, B., An, D., Stauffer, J. R., et al. 2016, ApJS, 222, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Madore, B. F. 1982, ApJ, 253, 575 [NASA ADS] [CrossRef] [Google Scholar]
- Makarov, V. V. 2002, AJ, 124, 3299 [NASA ADS] [CrossRef] [Google Scholar]
- Melis, C., Reid, M. J., Mioduszewski, A. J., Stauffer, J. R., & Bower, G. C. 2013, in Advancing the Physics of Cosmic Distances, ed. R. de Grijs, IAU Symp., 289, 60 [Google Scholar]
- Melis, C., Reid, M. J., Mioduszewski, A. J., Stauffer, J. R., & Bower, G. C. 2014, Science, 345, 1029 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Munari, U., Dallaporta, S., Siviero, A., et al. 2004, A&A, 418, L31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Narayanan, V. K., & Gould, A. 1999, ApJ, 523, 328 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Pan, X., Shao, M., & Kulkarni, S. R. 2004, Nature, 427, 326 [NASA ADS] [CrossRef] [Google Scholar]
- Pinsonneault, M. H., Stauffer, J., Soderblom, D. R., King, J. R., & Hanson, R. B. 1998, ApJ, 504, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Soderblom, D. R., Nelan, E., Benedict, G. F., et al. 2005, AJ, 129, 1616 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J., Maxted, P. F. L., & Smalley, B. 2005, A&A, 429, 645 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stello, D., & Nissen, P. E. 2001, A&A, 374, 105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van den Bergh, S. 1975, in Galaxies and the Universe, eds. A. Sandage, M. Sandage, & J. Kristian (The University of Chicago Press), 509 [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Leeuwen, F. 2009, A&A, 497, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Leeuwen, F., & Evans, D. W. 1998, A&AS, 130, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zwahlen, N., North, P., Debernardi, Y., et al. 2004, A&A, 425, L45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Pseudomagnitude distance (PMD) of six Pleiades stars of the Melis et al. (2013) list.
All Figures
 |
Fig. 1 a) (V,Ks) pseudomagnitudes of the 3747 Hipparcos K0 class III and V stars as a function of their distance modulus; b) Absolute (V,Ks) pseudomagnitudes of the same stars, with the dwarfs lying at the top and the giants lying at the bottom of this figure. The decrease of the pseudomagnitudes beyond a certain distance is an artefact due to numerical bias at low signal to noise ratio (see text). |
| In the text | |
 |
Fig. 2 a) Mean (V,Ks) absolute pseudomagnitudes of field dwarf stars as a function of spectral type; b) open circles: (V,Ks) pseudomagnitudes of 280 Pleiades stars located at less than 0.84 mag (3 times the Gaussian dispersion of Fig. 3) from the Pleiades barycentric distance modulus. Hipparcos stars are identified with larger filled circles, superimposed our main sequence model shifted at the Pleiades distance. |
| In the text | |
 |
Fig. 3 Distance moduli distribution for 360 Pleiades stars, fitted by a Gaussian distribution plus a second-degree polynomial. The Gaussian dispersion (0.28 mag) is dominated by spectral classifications errors. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


