EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 593 (September 2016) A&A, 593 (2016) A54 Full HTML
Free Access
Issue
A&A
Volume 593, September 2016
Article Number A54
Number of page(s) 5
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201628901
Published online 21 September 2016

© ESO, 2016

1. Introduction

Classical novae are prolific dust producers. Infrared and ultraviolet observations have unambiguously revealed a number of dust forming episodes in the ejected shells accompanying nova outbursts (Evans 1990; Evans & Rawlings 2008; Gehrz et al. 1998; Gehrz 2002, 2008; Shore et al. 1994). As first suggested by Stratton & Manning (1939) on the occasion of nova DQ Her, dust formation is revealed by a rise in infrared emission that occurs simultaneously with a decline in the optical lightcurve, several months after peak luminosity.

Such dust forming episodes are driven by the fast decline in temperature and density in the nova outflows, which allows the plasma to recombine and subsequently form molecules. Grain formation (i.e., dust) is a complex process dictated by the local thermodynamical and physicochemical conditions of the environment, requiring moderately low temperatures (below 1500−2000 K) and particle densities (≥108 cm-3). Roughly speaking, it can be qualitatively described as a two-stage process: grain nucleation and growth to macroscopic size (Sedlmayr 1994; Lodders 2003; Andersen 2011). In the former, a handful of molecules assemble into small groups or clusters,which by effect of a suite of chemical processes grow to a critical size. The carbon monoxide (CO) molecule plays an important role in this process. While most heteronuclear, diatomic molecules have dissociation energies around 3–5 eV, the CO molecule is characterized by a striking bond energy of 11.2 eV. Therefore, it is a very stable molecule, and can only be dissociated by high-energy photons. In the absence of intense radiation fields, condensation in an O-rich plasma (i.e., O > C) results in nearly all carbon atoms being locked in the form of the very stable CO molecules. As a result, formation of C-rich grains, such as silicon carbides (SiC), graphites, or nanodiamonds, is unlikely. Conversely, in a C-rich environment (C > O), all oxygen gets trapped in CO molecules and, in principle, oxidized compounds (e.g., corundum, spinel, hibonite, enstatite) cannot form.

Infrared measurements of a number of novae have actually revealed the presence of C-rich dust (Aql 1995, V838 Her 1991, PW Vul 1984), SiC (Aql 1982, V842 Cen 1986), hydrocarbons (V842 Cen 1986, V705 Cas 1993), or SiO2 (V1370 Aql 1982, V705 Cas 1993) in the ejecta. Moreover, sequential formation of all these types of dust has also been reported for some remarkable novae, such as V842 Cen 1986 (Gehrz et al. 1990) and QV Vul 1987 (Gehrz et al. 1998). In fact, it has been suggested that novae may have contributed to the different presolar grain populations isolated from meteorites1 (Clayton & Hoyle 1976; Amari et al. 2001; Amari 2002; Jose et al. 2004; Haenecour et al. 2016). Surprisingly, most theoretical models of nova outbursts (even those that rely on a CO-rich white dwarf as the underlying compact object that hosts the outburst) yield, on average, outflows characterized by O > C, from which only oxidized condensates would be expected2. Equilibrium condensation sequences have suggested, however, that the presence of large amounts of intermediate-mass elements, such as Al, Ca, Mg, or Si, may dramatically alter the condensation process, allowing the formation of C-rich dust even in a slightly O-rich environment (José et al. 2004). Moreover, it is expected that dust condensation in a nova environment proceeds kinetically rather than at equilibrium because of the strong radiation emitted by the underlying white dwarf (see, e.g., Shore & Gehrz 2004). Both effects reduce the significance of the CO molecule in the process of dust formation. But whether the nova ejecta are actually C- or O-rich has not been systematically addressed in the framework of hydrodynamic simulations. Indeed, nova models have traditionally assumed that the composition of the underlying white dwarf star that hosts the outbursts has similar mass fractions of 12C and 16O when low-mass, CO-rich white dwarfs are considered (see, however, Kovetz & Prialnik 1997, for a study of the effect of the white dwarf composition on the basis of pure-C, pure-O, and standard C/O = 1 white dwarf models).

In this paper, a series of nova models are presented, with state-of-the-art chemical profiles based on new evolutionary sequences of intermediate-mass stars that lead to the formation of white dwarfs with outer layers characterized by C > O. An outline of the method of computation and input physics used in this paper is given in Sect. 2. The impact of the abundance profiles of the underlying white dwarf on the nucleosynthesis accompanying classical nova outbursts is presented in Sect. 3. Finally, the most relevant conclusions of this paper are summarized in Sect. 4.

2. Input physics and initial setup

The nova models reported in this paper have been computed with the 1D, implicit, Lagrangian hydrodynamic code SHIVA , extensively used in the modeling of stellar explosions (e.g., classical novae, X-ray bursts). The code solves the standard set of differential equations of stellar evolution: conservation of mass, momentum, and energy, and energy transport by radiation and time-dependent convection. The equation of state includes contributions from the degenerate electron gas, the ion plasma, and radiation. Coulomb corrections to the electron pressure are taken into account. Radiative and conductive opacities are considered. The code is linked to a nuclear reaction network that contains ~120 nuclear species, from H to 48Ti, connected through 630 nuclear interactions, with updated STARLIB rates (Sallaska et al. 2013). Additional details on the SHIVA code can be found in José & Hernanz (1998) and José (2016).

thumbnail Fig. 1

Chemical profiles after a series of thermal pulses following completion of central He-burning for an 8 M⊙ star, computed with the HYADES code.

The nova models computed in this work assume a ~1.0 M⊙ CO white dwarf, resulting from the evolution of an 8 M⊙ progenitor star, self-consistently computed throughout the successive H- and He-burning stages with the HYADES code (see Halabi et al. 2012, and references therein). The database of the Nuclear Astrophysics Compilation of Reaction Rates (hereafter, NACRE; Angulo et al. 1999) was used, in particular for the triple-α and 12C(α, γ) reactions. The chemical structure of the resulting CO-rich white dwarf is shown in Fig. 1. Qualitatively similar chemical profiles have been obtained for the remnants of 6 M⊙ and 7 M⊙ progenitor stars.

Most of the simulations of CO novae (i.e., non-neon novae) performed to date have traditionally assumed that the outer layers of the white dwarf hosting the outburst have equal mass fractions of 12C and 16O (some include a marginal amount of leftover 22Ne, at a level of 1% by mass, but maintaining X(12C)/X(16O) = 1). However, a closeup look at Fig. 1 reveals instead a chemical abundance pattern dominated by the presence of 12C over 16O in the outer white dwarf layers (with the exception of the outermost, unburnt H-rich layers).

In the simulations discussed in Sect. 3, the white dwarf is assumed to accrete solar composition material (Z ~ 0.02) from a low-mass stellar companion at a characteristic mass-accretion rate of Ṁ ~ 2 × 10-10M⊙ yr-1. The accreted material is mixed with material dredged up from the underlying white dwarf (a mixture with 75% solar composition plus 25% outer white dwarf material has been adopted in all the calculations reported in this paper; see Kelly et al. 2013, for a recent reanalysis of mixing fractions in novae supporting a 25% white dwarf contribution; see also Casanova et al. 2010, 2011a,b, for 2D and 3D hydrodynamic simulations of mixing at the core-envelope interface during nova outbursts).

To specifically investigate the role played by the composition of the underlying white dwarf, six different nova models have been evolved. Models 1 to 5 are identical, except for the composition of the substrate with which the solar-like accreted material mixes. To this end, five different locations in the outer white dwarf layers have been considered (see points indicated by arrows in Fig. 1). For comparison, an additional model (Model 6) has been evolved under the traditional assumption of equal mass fractions of 12C and 16O in the outer white dwarfs layers.

3. Results

3.1. Model 1

The importance of the initial C/O ratio in the outer layers of the underlying white dwarf, and specifically, the initial 12C mass fraction in the envelope is described in the framework of the evolution of Model 1. In this particular model, the solar material transferred from the secondary is assumed to mix with a C-rich substrate whose composition is indicated in the upper part of Fig. 1 as point 1 (see also Table 1). The early accretion phase is dominated both by the pp chains (mainly through 1H(p, e+ν)2H) and by the CNO-cycle reaction 12C(p, γ)13N, followed by 13N(β+)13C. When the temperature at the envelope base reaches Tbase = 2.4 × 107 K, the nuclear timescale becomes shorter than the accretion timescale, and accretion is no longer relevant. The rate of nuclear energy generation reaches ~108 erg g-1 s-1 at the innermost envelope shell. The total mass piled on top of the white dwarf at the end of this accretion stage (which lasts ~1.7 × 105 yr) is ~3.9 × 10-5 M⊙ (see Table 2, for details).

Shortly afterwards, degeneracy is lifted at the envelope base, so that pressure becomes sensitive to temperature. Consequently, the envelope begins to expand after achieving a maximum pressure of Pmax,base = 8.6 × 1018 dyn cm-2 and a maximum density of ρmax,base = 3.6 × 103 g cm-3. The beginning of the dynamic stage (i.e., a thermonuclear runaway) is accompanied by the development of superadiabatic gradients at the innermost layers of the envelope. This spawns the onset of convection, which progressively expands throughout the envelope. At Tbase = 5 × 107 K, the nuclear activity is fully dominated by the cold CNO cycle, mainly through 12C(p, γ)13N(β+)13C(p, γ)14N, while no significant activity in the NeNa and MgAl-mass region is noticed. A similar behavior is found at 108 K, when convection has already extended throughout the entire envelope, with a characteristic turnover time of about 1 s. However, the dominant 12C(p, γ)13N(β+)13C(p, γ)14N reactions are now significantly supplemented by 13N(p, γ)14O(β+)14N(p, γ)15O and 16O(p, γ)17F; there is still a marginal contribution from reactions of the NeNa and MgAl mass-regions (mainly, 24Mg(p, γ)25Al). The star has spent about 1.2 × 106 s raising its temperature at the innermost envelope layers from 3 × 107 K to 108 K.

Table 1

Initial composition of the accreted envelopes.

Table 2

Main characteristics of the nova outbursts.

Table 3

Mean composition of the ejecta (CNO-group nuclei).

About 100 s later, when the temperature reaches Tbase = 1.66 × 108 K, the star achieves a maximum rate of nuclear energy generation of 3 × 1016 ergs g-1 s-1. Forty seconds later, the envelope base achieves a peak temperature of Tbase,max = 1.72 × 108 K. At this stage, nuclear energy is mostly released through the hot CNO cycle reactions (HCNO1) 13N(p, γ)14O(β+)14N, supplemented by 12C(p, γ)13N(β+)13C(p, γ)14N(p, γ)15O(β+)15N(p, α)12C and 16O(p, γ)17F(β+)17O(p, α)14N. Secondary nuclear activity involves a series of proton-capture reactions and β+ decays of a handful of species in the NeNa-MgAl mass regions (e.g., 23Na, 24,25,26Mg, 25Al, and both the ground and first isomeric states of 26Al). A small leakage from the MgAl-mass region is driven by proton captures on 27Si and 27Al.

A fraction of the nuclear energy released during the event is transformed into kinetic energy, which powers the ejection of 3.2 × 10-5M⊙ of nuclear-processed material, with a mean velocity of 1540 km s-1. As confirmed by the large concentrations of hydrogen and carbon in the ejecta (see Table 3), the runaway is halted by envelope expansion rather than by fuel consumption.

3.2. Models 2 to 6

As shown by Shara (1981) and Fujimoto (1982), the key parameter that determines the strength of a nova outburst is the pressure achieved at the core-envelope interface, Pbase, a measure of the overall pressure exerted by the layers overlying the ignition shell: 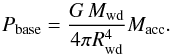(1)In Eq. (1), Mwd and Rwd are the mass and radius of the white dwarf hosting the eplosion, and Macc is the mass of the accreted envelope. To drive mass ejection, pressures in the range Pbase ~ 1019−1020 dyn cm-2 are required at the base of the envelope, the exact value depending on the chemical composition (Fujimoto 1982; MacDonald 1983). For a given pressure, Eq. (1) reveals that the mass of the accreted envelope depends only on the mass of the underlying white dwarf star because of the relationship between stellar mass and radius. As shown in Table 2, the larger the mass of the accreted envelope, the larger the pressure at its base. This translates into a more violent outburst characterized by a larger peak temperature, Tbase,max (Table 2).

The analysis reported for Model 1 reveals that the single most important reaction during the early stages of a nova outburst3 is 12C(p, γ). The rate at which these two species interact per second and per unit volume can, in general, be expressed as (see, e.g., Iliadis 2015, for details) 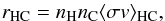(2)where nH and nC denote the number densities of 1H and 12C in the stellar plasma, respectively, and ⟨ σv ⟩ HC is the reaction rate per particle pair. Equation (2) reveals that the rate of interaction is proportional to the mass fractions of the interacting species. Therefore, the most relevant quantity to determine the strength of the outburst is not the amount of 12C, as is frequently stated, but the product [X(1H) ×X(12C)]ini at the beginning of the accretion stage. A reduction in this quantity delays ignition, since fewer nuclear reactions occur and, hence, less energy is released. This translates into a rise in the characteristic timescale for accretion, which subsequently leads to a larger accreted mass, larger pressure at the base, and in the end, a more violent outburst4. Indeed, in the models reported in this work, a reduction in [X(1H) ×X(12C)]ini by a factor of ~80 (see, e.g., Models 1 and 3 in Table 2) translates into an increase by a factor ~2 in the maximum pressure attained at the base of the envelope, and in the amount of mass accreted and ejected (with a smaller effect on the peak temperature achieved in the outburst as well).

3.3. Nucleosynthesis and implications for dust formation

The final, mass-averaged composition of the ejecta accompanying the set of nova outbursts calculated in this work is summarized for CNO-group species in Table 3.

In Model 1, the ejecta is dominated by high concentrations of H (0.498, by mass), 4He (0.240), and 14N (0.106). This is followed by 13C, 16O, 12C, and other CNO-group nuclei. A similar pattern is obtained in Models 2 to 5, except that both 12,13C are individually more abundant than any of the stable O isotopes, 16,17,18O. It is worth noting that Models 1 to 5 yield C-rich ejecta. Model 6, however, presents an important deviation: while H and 4He still present the largest mass fractions in the ejecta, the third most abundant species is now, by far, 16O. In fact, the large concentration of this isotope (X(16O) = 0.117, by mass) results in O-rich ejecta.

While the use of state-of-the-art chemical profiles for CO-rich white dwarfs hosting nova outbursts has a limited impact on the dynamics of the nova outburst (i.e., mass ejected, peak temperature, nucleoynthesis), it has a dramatic effect on the properties of the dust expected to condense in those environments. To date, CO novae have been traditionally ruled out as likely progenitors of C-rich grains, on the basis of the O-rich ejecta obtained when equal mass fractions of 12C and 16O are adopted (see, e.g., José et al. 2004). In sharp contrast, the models reported in this paper show, however, that the implementation of realistic chemical profiles leads to C-rich ejecta, instead. This opens up new possibilities for the contribution of novae to the inventory of presolar grains identified in meteorites, particularly in a number of carbonaceous phases (i.e., nanodiamonds, silicon carbides, and graphites).

4. Discussion

As shown in Sect. 3, the use of state-of-the-art chemical profiles for the white dwarf that hosts a CO nova outburst turns out to be critical for the production of C-rich ejecta. Even though realistic white dwarf models with similar profiles have been reported in the literature (see, e.g., Salaris et al. 1997; Karakas & Lugaro 2016), it is worth analyzing the possible role played by nuclear uncertainties in this regard, both during the previous stages of the evolution of the progenitor and during the nova outburst itself.

4.1. Uncertainties in nova nucleosynthesis

A significant fraction of the nuclear reactions of interest for nova nucleosynthesis that involve stable nuclei (mostly proton-induced reactions) have already been measured directly in the laboratory (José et al. 2006).

For the case of CO novae, in which the main nuclear path does not extend significantly beyond the CNOF mass region, current reaction rate uncertainties (i.e., ≤30%) do not dramatically affect model predictions. Indeed, after a number of improvements on the 17O(p, α) and 17O(p, γ) rates, the main source of uncertainty in this region is mostly dominated by the challenging reaction 18F(p, α), which – under explosive conditions – drives the main nuclear path down to 15O in both hot CNO cycles 2 and 3 (see, e.g., Iliadis 2015; José 2016). It is, however, worth noting that the uncertainty associated with 18F(p, α) has an impact on the expected O yields for ONe novae, but not for CO novae (Iliadis et al. 2002).

All in all, we conclude that the CO nova nucleosynthesis predictions reported in this work are not affected by current reaction-rate uncertainties.

4.2. Uncertainties in the evolution of the progenitor star

The evolution of a star throughout the H- and He-burning stages up to the formation of a CO-rich core may be affected by uncertainties in two key nuclear reaction rates.

The first is the triple-alpha reaction (hereafter, 3α). Models presented in this work rely on chemical profiles for the white dwarf based on stellar evolution computed with the HYADES code, for which the NACRE 3α rate was adopted (Angulo et al. 1999). Since the NACRE compilation, several prescriptions for this rate have been published. Through a measurement of the inverse process, 12C → 3 4He, Fynbo et al. (2005) determined a new 3α rate for temperatures ranging between 107 K and 1010 K. The new rate was found to be higher than the NACRE rate for temperatures below ~5 × 107 K, while much smaller than NACRE above 109 K. The potential effect of the Fynbo et al. 3α rate has been checked by means of new evolutionary sequences of an 8 M⊙ star computed with the HYADES code throughout the He-burning stage. Oxygen becomes higher than carbon in the inner regions of the star, but as in the chemical profiles adopted in this work, the outer layers still remain C-rich. More recently, Ogata et al. (2009) have reported on a new rate based on quantum mechanical calculations of the three-body Schrödinger equation. Around 107 K, the rate exhibited an increase of 20 orders of magnitude over the standard NACRE rate. It is worth noting, however, that this rate has been refuted by more recent calculations, and differences with respect to NACRE at low temperatures are now reduced to less than an order of magnitude (see, e.g., Ishikawa 2013; Akahori et al. 2015, for details).

The second reaction is 12C(α, γ)16O. It is a key reaction determining the final C/O ratio wherever He-burning takes place, and dominates over the triple-α reaction when the helium mass fraction drops below about 0.1. The rate of this reaction is dominated by several subthreshold resonances and still remains uncertain, even though it has been re-evaluated several times since NACRE (e.g., Katsuma et al. 2012; Xu et al. 2013). The Katsuma et al. rate is higher than the NACRE rate for temperatures above ≥3 × 108 K, while the Xu et al. rate exceeds the NACRE rate above ≥5 × 108 K. To estimate the potential effect of the He-burning rates on the results reported in this paper, new evolutionary sequences have been computed with the HYADES code using the Fynbo et al. and the Xu et al. prescriptions for the 3α and 12C(α, γ)16O rates, respectively. The implementation of these rates results in an important increase in the oxygen abundance in the inner layers of the star (up to ~0.75 M⊙ at the end of He-burning); however, the outer layers are still C-rich.

To investigate how our conclusions are affected by the latest He-burning rate determinations, we recomputed an 8 M⊙ model using the Fynbo et al. (2005) rate for the 3α reaction and Xu et al. (2013) for the 12C(α, γ) reaction. We found that the outer core remains C-rich. A 6 M⊙ model by Karakas & Lugaro (2016) using the Fynbo et al. (2005) rate and the Xu et al. (2013) rate for the 3α and the 12C + α reactions, respectively, yields similar conclusions.

A very recent work by Fields et al. (2016), available as a preprint during completion of this manuscript, analyzes the structural and compositional properties of CO white dwarfs in connection with uncertainties in the H- and He-burning rates obtained by a new Monte Carlo sampling procedure. The CO white dwarf remnant of their 3 M⊙ star exhibits a C-rich outer core, which independently shows that our nova nucleosynthesis predictions apply to lower progenitor masses. By evolving a grid of evolutionary models of 1 to 6 M⊙, they find that rate uncertainties, especially those affecting the 3α and 12C(α, γ) reactions, do not have a large impact on the final white dwarf mass distribution, but can significantly affect the central 12C and 16O abundances. Since uncertainty factors are likely temperature-dependant, it is unclear how the C and O profiles in the outer core would be affected, which is the region of interest for nova nucleosynthesis. As a conclusion, current nuclear uncertainties do not significantly affect the formation of C-rich layers in the outer part of CO white dwarfs, and hence, the production of C-rich ejecta in CO nova outbursts.

It is finally worth noting that production of C-rich ejecta in nova outbursts may also account for the origin of C-rich J-type stars. These stars represent 10%−15% of the observed C stars in our Galaxy and in the Large Magellanic Cloud. Indeed, a binary-star formation channel for C-rich J-type stars has been recently proposed in the framework of re-accretion of C-rich nova ejecta onto main sequence companions (Sengupta et al. 2013).

1

See also Pepin et al. (2011) for the possible nova origin of anomalous interplanetary dust particles collected from comets Grigg-Skjellerup and Tempel-Tuttle.

2

See Gehrz et al. (1998), Gehrz (2008), and José & Shore (2008) for examples of O > C ejecta observed in CO novae at different stages of the outburst.

3

Specifically for CO novae. See Shen & Bildsten (2009) for ignition conditions in C-poor envelopes.

4

See José et al. (2007) for a study of nova outbursts in metal-poor, primordial-like binaries.

Acknowledgments

We thank the referee, Robert Gehrz, for very positive feedback on the manuscript. J.J. would like to express his gratitude to the Center of Advanced Mathematical Sciences, American University of Beirut (AUB, Lebanon), for financial support and hospitality during his visit to AUB, where part of this project started. This work has been partially supported by the Spanish MINECO grant AYA2014-59084-P, by the E.U. FEDER funds, and by the AGAUR/Generalitat de Catalunya grant SGR0038/2014 (J.J.). G.H. thanks Christopher Tout and Robert Izzard for helpful discussions, the STFC for funding her postdoctoral research at the Institute of Astronomy, and the FAS at the American University of Beirut where part of the calculations were performed.

References

  1. Akahori, T., Funaki, Y., & Yabana, K. 2015,Phys. Rev. C, 92, 022801 [Google Scholar]
  2. Amari, S. 2002, New Astron. Rev., 46, 519 [Google Scholar]
  3. Amari, S., Gao, X., Nittler, L. R., et al. 2001, ApJ, 551, 1065 [Google Scholar]
  4. Andersen, A. C. 2011, in Why Galaxies Care about AGB Stars II: Shining Examples and Common Inhabitants, eds. F. Kerschbaum, T. Lebzelter, & R. F. Wing (San Francisco: ASP Conf. Ser.), 215 [Google Scholar]
  5. Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [NASA ADS] [CrossRef] [Google Scholar]
  6. Casanova, J., José, J., García-Berro, E., Calder, A., & Shore, S. N. 2010, A&A, 513, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Casanova, J., José, J., García-Berro, E., Calder, A., & Shore, S. N. 2011a, A&A, 527, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Casanova, J., José, J., García–Berro, E., Shore, S. N., & Calder, A. C. 2011b, Nature, 478, 490 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  9. Clayton, D. D., & Hoyle, F. 1976, ApJ, 203, 490 [NASA ADS] [CrossRef] [Google Scholar]
  10. Evans, A. 1990, in Physics of Classical Novae, eds. A. Cassatella, & R. Viotti (Berlin: Springer-Verlag), 253 [Google Scholar]
  11. Evans, A., & Rawlings, M. C. 2008, in Classical Novae, eds. M. F. Bode, & A. Evans, 2nd edn. (Cambridge, UK: Cambridge University Press), 308 [Google Scholar]
  12. Fields, C. E., Farmer, R., Petermann, I., Iliadis, C., & Timmes, F. X. 2016, ApJ, 823, 46 [NASA ADS] [CrossRef] [Google Scholar]
  13. Fujimoto, M. Y. 1982, ApJ, 257, 752 [NASA ADS] [CrossRef] [Google Scholar]
  14. Fynbo, H. O. U., Diget, C. A., Bergmann, U. C., et al. 2005, Nature, 433, 136 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  15. Gehrz, R. D. 1990, in Physics of Classical Novae, eds. A. Cassatella, & R. Viotti (Berlin: Springer-Verlag), 138 [Google Scholar]
  16. Gehrz, R. D. 2002, in Classical Nova Explosions, eds. M. Hernanz, & J. José (Melville: American Inst. Phys.), 198 [Google Scholar]
  17. Gehrz, R. D. 2008, in Classical Novae (2nd Ed.), eds. M. F. Bode, & A. Evans (Cambridge, UK: Cambridge University Press), 167 [Google Scholar]
  18. Gehrz, R. D., Truran, J. W., Williams, R. E., & Starrfield, S. 1998, PASP, 110, 3 [NASA ADS] [CrossRef] [Google Scholar]
  19. Haenecour, P., Floss, C., José, J., et al. 2016, ApJ, 825, 88 [NASA ADS] [CrossRef] [Google Scholar]
  20. Halabi, G. M., El Eid, M. F., & Champagne, A. 2012, ApJ, 761, 10 [NASA ADS] [CrossRef] [Google Scholar]
  21. Iliadis, C. 2015, Nuclear Physics of Stars, 2nd edn. (Weinheim: Wiley-VCH Verlag) [Google Scholar]
  22. Iliadis, C., Champagne, A., José, J., Starrfield, S., & Tupper, P. 2002, ApJS, 142, 105 [Google Scholar]
  23. Ishikawa, S. 2013, Phys. Rev. C, 87, 055804 [NASA ADS] [CrossRef] [Google Scholar]
  24. José, J. 2016, Stellar Explosions: Hydrodynamics and Nucleosynthesis (Boca Raton: CRC/Taylor and Francis) [Google Scholar]
  25. José, J., & Hernanz, M. 1998, ApJ, 494, 680 [NASA ADS] [CrossRef] [Google Scholar]
  26. José, J., & Shore, S. N. 2008, in Classical Novae, eds. M. F. Bode, & A. Evans, 2nd edn. (Cambridge, UK: Cambridge University Press), 121 [Google Scholar]
  27. José, J., Hernanz, M., Amari, S., Lodders, K., & Zinner, E. 2004, ApJ, 612, 414 [NASA ADS] [CrossRef] [Google Scholar]
  28. José, J., Hernanz, M., & Iliadis, C. 2006, Nucl. Phys. A, 777, 550 [NASA ADS] [CrossRef] [Google Scholar]
  29. José, J., García-Berro, E., Hernanz, M., & Gil-Pons, P. 2007, ApJ, 662, L103 [NASA ADS] [CrossRef] [Google Scholar]
  30. Karakas, A., & Lugaro, M. 2016, ApJ, submitted [Google Scholar]
  31. Katsuma, M. 2012, ApJ, 745, 192 [NASA ADS] [CrossRef] [Google Scholar]
  32. Kelly, K. J., Iliadis, C., Downen, L., José, J., & Champagne, A. 2013, ApJ, 777, 130 [Google Scholar]
  33. Kovetz, A., & Prialnik, D. 1997, ApJ, 477, 356 [NASA ADS] [CrossRef] [Google Scholar]
  34. Lodders, K. 2003, ApJ, 591, 1220 [NASA ADS] [CrossRef] [Google Scholar]
  35. MacDonald, J. 1983, ApJ, 267, 732 [NASA ADS] [CrossRef] [Google Scholar]
  36. Ogata, K., Kan, M., & Kamimura, M. 2009, Progr. Theor. Phys., 122, 1055 [Google Scholar]
  37. Pepin, R. O., Palma, R. L., Gehrz, R. D., & Starrfield, S. 2011, ApJ, 742, 86 [NASA ADS] [CrossRef] [Google Scholar]
  38. Sallaska, A. L., Iliadis, C., Champange, A. E., et al. 2013, ApJS, 207, 18 [NASA ADS] [CrossRef] [Google Scholar]
  39. Sedlmayr, E. 1994, in Molecules in the Stellar Environment, ed. U. G. Jorgensen (Berlin: Springer-Verlag), 163 [Google Scholar]
  40. Sengupta, S., Izzard, R. G., & Lau, H. H. B. 2013, A&A, 559, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Shara, M. M. 1981, ApJ, 243, 926 [NASA ADS] [CrossRef] [Google Scholar]
  42. Shen, K., & Bildsten, L. 2009, ApJ, 692, 324 [NASA ADS] [CrossRef] [Google Scholar]
  43. Shore, S. N., & Gehrz, R. D. 2004, A&A, 417, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Shore, S. N., Starrfield, S., Gonzalez-Riestra, R., Hauschildt, P. H., & Sonneborn, G. 1994, Nature, 369, 539 [NASA ADS] [CrossRef] [Google Scholar]
  45. Stratton, F. J. M., & Manning, W. H. 1939, Atlas of Spectra of Nova Herculis 1934 (Cambridge, UK: Solar Physics Observ.) [Google Scholar]
  46. Xu, Y., Takahashi, K., Goriely, S., et al. 2013, Nucl. Phys. A, 918, 61 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Initial composition of the accreted envelopes.

In the text
Table 2

Main characteristics of the nova outbursts.

In the text
Table 3

Mean composition of the ejecta (CNO-group nuclei).

In the text

All Figures

thumbnail Fig. 1

Chemical profiles after a series of thermal pulses following completion of central He-burning for an 8 M⊙ star, computed with the HYADES code.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.