| Issue |
A&A
Volume 593, September 2016
|
|
|---|---|---|
| Article Number | A16 | |
| Number of page(s) | 7 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201628236 | |
| Published online | 30 August 2016 | |
Propeller effect in two brightest transient X-ray pulsars: 4U 0115+63 and V 0332+53
1 Tuorla ObservatoryDepartment of
Physics and Astronomy, University of Turku, Väisäläntie 20, 21500 Piikkiö, Finland
e-mail: sergey.tsygankov@utu.fi
2 Space Research Institute of the
Russian Academy of Sciences, Profsoyuznaya Str. 84/32, 117997
Moscow,
Russia
3 Moscow Institute of Physics and
Technology, Moscow
region, 141700
Dolgoprudnyi,
Russia
4 Institut für Astronomie und
Astrophysik, Universität Tübingen, Sand 1, 72076
Tübingen,
Germany
5 Anton Pannekoek Institute, University
of Amsterdam, Science Park
904, 1098 XH
Amsterdam, The
Netherlands
6 Pulkovo Observatory of the Russian
Academy of Sciences, 196140
Saint Petersburg,
Russia
7 Nordita, KTH Royal Institute of
Technology and Stockholm University, Roslagstullsbacken 23, 10691
Stockholm,
Sweden
Received:
2
February
2016
Accepted:
7
July
2016
Aims. We present the results of the monitoring programmes performed with the Swift/XRT telescope and aimed specifically to detect an abrupt decrease of the observed flux associated with a transition to the propeller regime in two well-known X-ray pulsars 4U 0115+63 and V 0332+53.
Methods. Both sources form binary systems with Be optical companions and undergo so-called giant outbursts every 3−4 years. The current observational campaigns were performed with the Swift/XRT telescope in the soft X-ray band (0.5−10 keV) during the declining phases of the outbursts exhibited by both sources in 2015.
Results. The transitions to the propeller regime were detected at the threshold luminosities of (1.4 ± 0.4) × 1036 erg s-1 and (2.0 ± 0.4) × 1036 erg s-1 for 4U 0115+63 and V 0332+53, respectively. Spectra of the sources are shown to be significantly softer during the low state. In both sources, the accretion at rates close to the aforementioned threshold values briefly resumes during the periastron passage following the transition into the propeller regime. The strength of the dipole component of the magnetic field required to inhibit the accretion agrees well with estimates based on the position of the cyclotron lines in their spectra, thus excluding presence of a strong multipole component of the magnetic field in the vicinity of the neutron star.
Key words: accretion, accretion disks / magnetic fields / X-rays: binaries / stars: individual: 4U 0115+63 / stars: individual: V 0332+53
© ESO, 2016
1. Introduction
Interaction of matter with the magnetosphere of a neutron star determines temporal and spectral properties of X-ray emission from X-ray pulsars (XRPs), accreting millisecond pulsars (AMPs) and recently discovered accreting magnetars. One of the most straightforward manifestations of such an interaction is a transition of the accreting neutron star to the so-called “propeller regime” (Illarionov & Sunyaev 1975), when the accreting matter is stopped by the centrifugal barrier set up by the rotating magnetosphere. Such a transition is expected to occur at the limiting luminosity defined by the dipolar magnetic field strength and rotation rate of the pulsar. Two types of propellers with different properties can be defined as “weak” and “strong” (see e.g. Ustyugova et al. 2006). The strong propeller is characterized by the strong matter outflows and even formation of the collimated jets along the rotational axis of the neutron star. In both cases the transition is accompanied by a dramatic drop of the X-ray flux observed from the source. Confident detection of such a transition provides a completely independent estimate of the magnetic field of the pulsar and in general allows for a better understanding of the interaction of the accretion flow and magnetosphere. However, in spite of clear importance of this effect, so far it has not been systematically studied from observational point of view. One of the reasons is that high sensitivity monitoring X-ray observations required to detect such a transition only became possible recently. Indeed, many accreting pulsars exhibit strong variability, which might be interpreted as a transition into propeller regime. For instance, it was demonstrated by Doroshenko et al. (2011, 2012) that the accretion is not centrifugally inhibited during the so-called “off-states” observed in Vela X-1 and 4U 1907+09, and despite significant luminosity decrease these sources continue to accrete. On the other hand, transition to the propeller regime is expected to inhibit accretion almost completely, and in this case much lower luminosities can be expected in the low state.
In fact, only a few cases of transitions to the propeller regime in X-ray pulsars with known magnetic field strength were mentioned in the literature. Campana et al. (2008) associated the strong variations in the flux from a weakly magnetized (B ~ 3 × 108 G) accreting millisecond pulsar SAX J1808.4−3658 with the onset of the propeller regime at the bolometric limiting luminosity Llim = (5 ± 2) × 1035 erg s-1. Another example is the bursting X-ray pulsar GRO J1744−28 with intermediate magnetic field (B ≈ 5.3 × 1011 G), which exhibited a similar rapid flux drop at the threshold luminosity Llim = (3.0 ± 1.5) × 1037 erg s-1 (Cui 1997). Evidence for the propeller effect was also reported for several weakly magnetized neutron stars in LMXBs (see e.g. Asai et al. 2013; Campana et al. 2014). For a recent review, see Revnivtsev & Mereghetti (2015).
Some hints of the transitions to the propeller regime in 4U 0115+63 and V 0332+53 were reported by Campana et al. (2001) and Stella et al. (1986). The former source was observed exactly during the transition when its luminosity changed by factor of ~250 during only ~15 h, but the limiting luminosity Llim was not measured. However, in the case of V 0332+53 the transition was seen clearly at limiting luminosity Llim = (2.6 ± 0.9) × 1036 erg s-1. Unfortunately, the low sensitivity of EXOSAT did not permit to detect the source in the quiescent state. The most strongly magnetized neutron star (B ~ 1 × 1014 G) that demonstrates the propeller effect is the first pulsating ULX M82 X-2 (Bachetti et al. 2014) in which the centrifugal barrier stops the accretion below the luminosity Llim = 2 × 1040 erg s-1 (Tsygankov et al. 2016). A strong magnetic field scenario is also supported by the detailed analysis of the accretion column presented by Mushtukov et al. (2015a), although other estimates based on the analysis of the accretion torque acting onto the neutron star yield field values in the much wider range of 109 to 1014 G (see e.g. Kluźniak & Lasota 2015; Ekşi et al. 2015).
In this work we present the results of the monitoring programmes performed with the Swift/XRT telescope and aimed specifically to detect the transition to the propeller regime and measurement of the quiescent flux in two well-known X-ray pulsars 4U 0115+63 and V 0332+53. These are characterized by the spin periods of 3.6 s and 4.35 s and magnetic fields of B ≈ 1.3 × 1012 G (White et al. 1983) and 3.0 × 1012 G (Makishima et al. 1990), respectively. Both sources form binary systems with Be optical companions (Be/XRP) and undergo the so-called giant outbursts every 3−4 yrs. The current observational campaigns were performed during the declining phases of their outbursts in 2015 (Nakajima et al. 2015a,b; Doroshenko et al. 2015b).
2. Swift/XRT observations
Swift observatory (Gehrels et al. 2004) permits us to monitor sources of X-ray emission on very different timescales both in soft and hard X-ray ranges. In this work we use observations of two Be/XRPs 4U 0115+63 and V 0332+53 performed with the XRT telescope (Burrows et al. 2005) covering the declining phases of giant outbursts occurred in 2015. In particular, the analysed data on 4U 0115+63 were collected between MJD 57 329 and MJD 57 388 and for V 0332+53 between MJD 57 293 and MJD 57 393.
The XRT observed both pulsars in photon counting (PC) and windowed timing (WT) modes depending on their brightness. Final products (spectrum in each observation) were prepared using the online tools provided by the UK Swift Science Data Centre1 (Evans et al. 2009).
The obtained spectra were grouped to have at least one count per bin and were fitted in XSPEC package using Cash statistics (Cash 1979). To avoid any problems caused by the calibration uncertainties at low energies2, we restricted our spectral analysis to the 0.7−10 keV band.
 |
Fig. 1 Light curve of 4U 0115+63 obtained with the Swift/XRT telescope in the 0.5−10 keV energy range. Luminosity is calculated from the unabsorbed flux under the assumption of the distance d = 7 kpc. The solid grey line shows the best fit of the light curve before the transition to the propeller regime with a Gaussian function. The horizontal dashed line represents the limiting luminosity when the propeller regime sets in. Positions of vertical dashed lines correspond to the times of the periastron passage (Raichur & Paul 2010). Applying the bolometric correction to the observed flux effectively increases the luminosity jump by factor of 2 (see Sect. 4.1). |
 |
Fig. 2 Light curve of V 0332+53 obtained with the Swift/XRT telescope in the 0.5−10 keV energy range. Luminosity is calculated from the unabsorbed flux under assumption of the distance d = 7 kpc. Point near the MJD 57 380 was obtained from averaging of five observations with very low counting statistics. Solid grey line shows the best fit of the light curve before the transition to the propeller regime with a Gaussian function. Horizontal dashed line represents the limiting luminosity when the propeller regime sets in. Positions of vertical dashed lines correspond to the times of the periastron passage (Doroshenko et al. 2016). Applying the bolometric correction to the observed flux effectively increases the luminosity jump by factor of 2 (see Sect. 4.1). |
3. Results
The light curves of 4U 0115+63 and V 0332+53 as observed by Swift/XRT are shown in Figs. 1 and 2, respectively. The fluxes are given in the 0.5−10 keV energy range and were corrected for the absorption. The main feature in both light curves is an abrupt decrease of the observed flux below ~7 × 1035 erg s-1 for 4U 0115+63 and below ~1 × 1036 erg s-1 for V 0332+53 (shown by red horizontal dashed line). We interpret this behaviour as an onset of the propeller regime (see Sect. 4). We assume that the limiting luminosity associated with the transition to the propeller regime corresponds to the dramatic change of the flux time derivative (both figures have a logarithmic flux scale). The transition is well illustrated by comparison of the light curve with the fit to its bright part with a Gaussian function (shown with a solid grey line in Figs. 1 and 2). The transition itself can be fitted with an exponential function with e-folding times of 16.5 h and 6.4 h for 4U 0115+63 and V 0332+53, correspondingly. The bolometric correction increases the luminosity jump by factor of ~2 (see Sect. 4.1) and hence decreases the e-folding times to 14.3 h and 5.6 h. The blue vertical dashed lines represent times of the periastron passage, according to the orbital ephemeris, obtained by Raichur & Paul (2010) for 4U 0115+63 and Doroshenko et al. (2016) for V 0332+53.
We estimated observed luminosities based on the fluxes measured from the spectra, assuming distances to both sources of 7 kpc (Negueruela et al. 1999; Negueruela & Okazaki 2001). We used two simple continuum models for the spectral fitting: the absorbed power-law model (phabs*powerlaw in the XSPEC package) and the absorbed black-body emission model (phabs*bbody). We found that the power-law model approximates spectra of V 0332+53 in the high (accretion) state quite well with the photon index in the range 0.4−0.6 and hydrogen column density NH ≃ (1.0−1.3) × 1022 cm-2. The latter value slightly exceeds the interstellar absorption in the direction of the source derived from the Galactic neutral hydrogen maps, NH ≃ 0.7 × 1022 cm-2 (Kalberla et al. 2005). The counting statistics in an individual observation of V 0332+53 in the low state is not sufficient to determine the absorption independently. Therefore to fit spectra in the low state we fixed it to the average value in the high state of 1.2 × 1022 cm-2.
Also it is not possible to discriminate between different continuum models in a single observation in the low state. To overcome these difficulties we combined all observations with luminosities below 1 × 1034 erg s-1. The resulting spectrum has a much softer shape in comparison to the bright state and can be well fitted (Cstat = 113.7 for 132 d.o.f.) with the absorbed black-body model with the temperature of kT = 0.51 ± 0.03 keV and radius of the emitting area R = 0.6 ± 0.1 km. For comparison, the best-fit approximation with the power-law model gives the photon index Γ = 2.84 ± 0.17 and Cstat = 118.9 for 132 d.o.f. In the subsequent analysis of spectra from all low-luminosity observations, we used a black-body continuum model with the fixed absorption value and free black-body temperature. Analysis of the temperature evolution in the low state is beyond the scope of this work and is presented elsewhere (Wijnands & Degenaar 2016). Here we would like to emphasize the drastic change of the spectral shape due to the onset of the propeller regime and cease of the accretion (Fig. 3).
 |
Fig. 3 Swift/XRT spectra of 4U 0115+63 and V 0332+53 in accretion (red dots) and propeller (blue crosses) regimes. Solid lines represent the best-fit models consisting of an absorbed power law in the high state and the absorbed black body in the low state. |
The observed properties of 4U 0115+63 are quite similar. At higher luminosities its spectrum in the 0.5−10 keV range is well described by a power-law model with the photon index in the range 0.4−0.8 and NH ≃ (0.9−1.2) × 1022 cm-2 (the interstellar value is NH ≃ 0.86 × 1022 cm-2; Kalberla et al. 2005). To describe the average low-state spectrum we used the absorbed black-body model with best-fit temperature of kT = 0.52 ± 0.03 keV, radius of the emitting area R = 0.8 ± 0.1 km, the absorption value fixed at average value of 1.1 × 1022 cm-2, and Cstat = 118.9 for 135 d.o.f. The best-fit approximation with the power-law model gives the photon index Γ = 2.70 ± 0.17 and Cstat = 138.6 for 135 d.o.f. The difference in the source spectra in the high and low states is apparently seen (Fig. 3).
4. Discussion
The sudden drop of the source luminosity in combination with the dramatic spectral change strongly suggests that the accretion ceased in both sources, which we interpret as a transition to the propeller regimes. Below we discuss this effect in detail.
4.1. Spectral changes
As was described in Sect. 3, the luminosity of both sources in low state is a few ×1033 erg s-1 and their spectra are compatible with the black-body model with temperature around 0.5 keV.
Using the Stefan-Boltzmann law we can estimate the area needed to explain the observed flux, 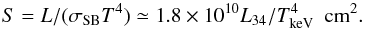 (1)Considering the observed temperature T ≃ 0.5 keV, this gives an area that is comparable with the area of polar caps at the surface of accreting neutron star. Taking into the account that observations took place right after a major outburst, it is natural to associate the observed soft emission with radiation from the cooling polar caps (Wijnands & Degenaar 2016). Indeed, Rutledge et al. (2007) estimate the luminosity of a cooling neutron star at ~0.5% of the average outburst flux, which is fully consistent with observations for both 4U 0115+63 and V 0332+53.
(1)Considering the observed temperature T ≃ 0.5 keV, this gives an area that is comparable with the area of polar caps at the surface of accreting neutron star. Taking into the account that observations took place right after a major outburst, it is natural to associate the observed soft emission with radiation from the cooling polar caps (Wijnands & Degenaar 2016). Indeed, Rutledge et al. (2007) estimate the luminosity of a cooling neutron star at ~0.5% of the average outburst flux, which is fully consistent with observations for both 4U 0115+63 and V 0332+53.
On the other hand, residual accretion also cannot be excluded. Indeed, the typical hard spectrum observed from X-ray pulsars might in principle become significantly softer in quiescence. The hard power-law tail is formed because of the Comptonization of initially thermal X-ray spectrum by electrons in the optically thin atmosphere (Zel’dovich & Shakura 1969) and further in the accretion channel (Lyubarskii & Syunyaev 1982; Becker & Wolff 2007). The spectral changes in the atmosphere are comparatively small in the case of low mass accretion rates (Zel’dovich & Shakura 1969). The Thomson optical thickness across the accretion channel 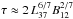 (Mushtukov et al. 2015b) is well below unity for accretion luminosity ~1034−1035 erg s-1. Therefore, at low accretion rates Comptonization in the accretion channel is not expected to significantly affect the initial spectrum as well, so it is likely to remain relatively soft. The variations of spectral hardness and its correlation with the mass accretion rate for XRPs were discussed recently by Postnov et al. (2015) in context of a reflection model (see Poutanen et al. 2013).
(Mushtukov et al. 2015b) is well below unity for accretion luminosity ~1034−1035 erg s-1. Therefore, at low accretion rates Comptonization in the accretion channel is not expected to significantly affect the initial spectrum as well, so it is likely to remain relatively soft. The variations of spectral hardness and its correlation with the mass accretion rate for XRPs were discussed recently by Postnov et al. (2015) in context of a reflection model (see Poutanen et al. 2013).
Regardless of the origin of the emission in the low (propeller) state, we can use our spectral fits to estimate the bolometric corrections for both intensity states, which is important to constrain the bolometric transitional luminosity and thus accretion rate. For this purpose we used the results of our spectral analysis of the emission of the sources in a wide energy range, obtained during previous outbursts with the RXTE and INTEGRAL observatories (Tsygankov et al. 2006, 2007). It was found that the source flux in the 0.5−10 keV energy was ~50% from the bolometric (i.e. flux in the 0.5−100 keV energy range). Based on these results, in the subsequent calculations we used the coefficient 2 for the conversion of fluxes for both sources in the bright (accretion) state. In the propeller state, Swift/XRT energy coverage is sufficient to detect most of the emergent flux and no additional bolometric correction is needed. Indeed, this conclusion is valid both for the black body and power-law models due to the low temperatures (kT ≃ 0.5 keV) or steep photon indexes (Γ ≃ 2.7−2.8).
The bolometric correction may introduce additional uncertainty because of our ignorance of the broadband source spectrum at luminosities around the transition. We estimated this uncertainty at the level of 10−20% and added it to the final uncertainty for the limiting luminosity. Taking all uncertainties into account, we estimate the bolometric limiting luminosities for the onset of the propeller regime at (1.4 ± 0.4) × 1036 erg s-1 and (2.0 ± 0.4) × 1036 erg s-1 for 4U 0115+63 and V 0332+53, respectively.
 |
Fig. 4 Observed correlation between a combination of the propeller limiting luminosity and the period, LlimP7 / 3, and independently determined magnetic field strength B for five pulsars and one accreting magnetar (M82 X-2) is shown with circles with error bars (Tsygankov et al. 2016). The dashed and dash-dotted lines represent the theoretical dependence from Eq. (2), assuming NS standard parameters (M = 1.4 M⊙, R = 10 km) and k = 0.5 and k = 0.7, respectively. The red star and open box indicate the positions of 4U 0115+63 and V 0332+53 obtained in this work, respectively. |
4.2. “Propeller” effect
The “propeller effect” (Illarionov & Sunyaev 1975) is caused by a substantial centrifugal barrier produced by the rotating magnetosphere of the neutron star. The matter stopped at the magnetospheric radius can only penetrate the magnetosphere if the velocity of the field lines is lower than the local Keplerian velocity. In other words, the matter will be accreted only in the case when the magnetospheric radius (Rm) is smaller than the corotation radius (Rc). The magnetospheric radius depends on the mass accretion rate, and, therefore, one can estimate the limiting luminosity corresponding to the onset of the propeller regime by equating the corotation and magnetospheric radii (see e.g. Campana et al. 2002) 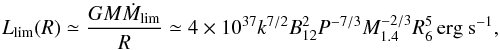 (2)where M1.4 is the neutron star mass in units of 1.4 M⊙, R6 is neutron star radius in units of 106 cm, P its rotational period in seconds, B12 is the magnetic field strength in units of 1012 G, and Ṁ is the mass accretion rate onto the neutron star. Factor k relates the magnetospheric radius for disc accretion to the Alfvén radius calculated for spherical accretion and is usually assumed to be k = 0.5 (Ghosh & Lamb 1978).
(2)where M1.4 is the neutron star mass in units of 1.4 M⊙, R6 is neutron star radius in units of 106 cm, P its rotational period in seconds, B12 is the magnetic field strength in units of 1012 G, and Ṁ is the mass accretion rate onto the neutron star. Factor k relates the magnetospheric radius for disc accretion to the Alfvén radius calculated for spherical accretion and is usually assumed to be k = 0.5 (Ghosh & Lamb 1978).
Because the accretion efficiency in the propeller regime is much lower, the decrease of the accretion rate below Ṁlim leads to the drop in the luminosity to the value expected for the so-called “magnetospheric accretion” case (Corbet 1996) 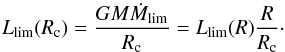 (3)Therefore, in the absence of other sources of emission in the low (propeller) state we can expect a very large drop of the observed luminosity
(3)Therefore, in the absence of other sources of emission in the low (propeller) state we can expect a very large drop of the observed luminosity 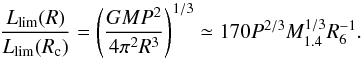 (4)Substituting spin periods of 4U 0115+63 and V 0332+53 to Eq. (4), we get the expected drop in luminosities of ~400 and ~450, respectively. However, these estimates do not take into account a substantial shift of the spectral distribution in the case of magnetospheric accretion. Indeed, the temperature of the accretion disc at the magnetospheric radius is
(4)Substituting spin periods of 4U 0115+63 and V 0332+53 to Eq. (4), we get the expected drop in luminosities of ~400 and ~450, respectively. However, these estimates do not take into account a substantial shift of the spectral distribution in the case of magnetospheric accretion. Indeed, the temperature of the accretion disc at the magnetospheric radius is 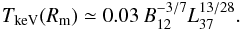 (5)For the mass accretion rate corresponding to the transition to the propeller regime for both pulsars, (about 1016 g / s) the disc temperature at Rm is ~10 eV ≈ 105 K, which corresponds to emission in the UV band for the magnetospheric accretion (Stella et al. 1994).
(5)For the mass accretion rate corresponding to the transition to the propeller regime for both pulsars, (about 1016 g / s) the disc temperature at Rm is ~10 eV ≈ 105 K, which corresponds to emission in the UV band for the magnetospheric accretion (Stella et al. 1994).
Therefore, the drop in X-ray luminosity that is calculated using Eq. (4) should only be considered as a lower limit. On the other hand, additional emission might come directly from the neutron star either owing to the leakage of matter through the centrifugal barrier or thermal emission of the cooling NS surface (Sect. 4.1). Taking into the account that interaction of the accretion disc with the magnetosphere is not fully understood, and the likely additional contribution to the flux in the low state, we consider the observed drops in the luminosity (200 ± 50 and 250 ± 50 for 4U 0115+63 and V 0332+53, respectively) to be in reasonable agreement with theory.
Another expected consequence of the onset of the propeller regime is a substantial decrease of the pulsed fraction owing to partial or even complete blocking of the accretion along magnetic field lines. Unfortunately, we were unable to verify this assumption because of the insufficient temporal resolution of XRT telescope in the PC mode (2.5 s) and, more importantly, extremely low flux from both sources in the propeller state resulting in a count rate about 10-2 cnt s-1 or less.
Figure 4 shows the correlation between the independently measured magnetic field strength and combination of the propeller limiting luminosity and the period, LlimP7 / 3, for four sources exhibiting transitions to the propeller regime. Measurements taken from the literature (for details see Tsygankov et al. 2016) are shown with circles with error bars (from Ibragimov & Poutanen 2009, for SAX J1808.4−3658; D’Aì et al. 2015 and Doroshenko et al. 2015a, for GRO J1744−28; White et al. 1983, for 4U 0115+63; Makishima et al. 1990, for V 0332+53; Mushtukov et al. 2015a, for M82 X-2). The dashed line represents the theoretical dependence from Eq. (2) assuming the standard parameters M = 1.4 M⊙, R = 10 km, k = 0.5. The star and open box indicate the positions of 4U 0115+63 and V 0332+53 obtained in this work, respectively. Good agreement with the theoretical prediction can be clearly seen. Taking into account the strong dependence of the limiting luminosity Llim on the parameter k, we can roughly restrict the range of its values between 0.5 and 0.7 (shown by dashed and dash-dotted lines, respectively).
4.3. Episodes of resumed accretion
Light curves of 4U 0115+63 and V 0332+53, in addition to the main propeller transition, exhibit another interesting feature: in both cases a sudden increase of the bolometric flux is observed (on MJD 57 354 up to 1 × 1036 erg s-1 and on MJD 57 358 up to 2 × 1036 erg s-1 , respectively). The corresponding luminosities are within the error consistent with the limiting luminosities for the propeller regime in 4U 0115+63 (Llim = (1.4 ± 0.4) × 1036 erg s-1) and V 0332+53 (Llim = (2.0 ± 0.4) × 1036 erg s-1). We interpret this brightening as a temporary transition back to the accretor regime due to increased mass accretion rate.
Indeed, in both cases the re-brightening occurred close to the periastron passage (see Figs. 1 and 2); such episodes of intermittent accretion are expected for the case of steady low-level mass accretion (see e.g. D’Angelo & Spruit 2010, 2012; Zanni & Ferreira 2013).
Spectra of both sources significantly harden during the resumed accretion episodes becoming consistent with the spectrum right before the first transition to the propeller. We note that the regular transitions from the accretor to propeller and back are observed in another X-ray pulsar − the accreting magnetar M82 X-2 (Tsygankov et al. 2016).
4.4. Accretion disc instability
Exponential decay of the outbursts is not a unique property of X-ray pulsar giant II-type outburst. Many other classes of outbursting astrophysical objects, such as dwarf novae and soft X-ray transients, show similar flux decay in the end of the bursts. Current interpretation is that the accretion disc instability arising from partial ionization of the hydrogen (so-called thermal-viscosity instability) governs the observed outburst dynamics (Meyer & Meyer-Hofmeister 1984; Smak 1984; Mineshige et al. 1993; Cheng et al. 1992; Chen et al. 1997). Here we discuss whether disc instability can be responsible for the observed behaviour of 4U 0115+63 and V 0332+53.
Ionization of disc plasma implies significant changes of the opacity and gas equation of state, and, therefore, α-viscosity (see e.g. the review by Lasota 2001). This leads to a drastic change in the accretion rate and defines a general picture of a dwarf nova outbursts.
There are two different states of the accretion disc: the cold state with mainly atomic hydrogen and low viscosity, when the accreted matter from the secondary accumulated in the disc, and the hot state with mainly ionized hydrogen and high viscosity, when all the accumulated matter rapidly accretes on the central object (white dwarf in the case of dwarf nova). The transition between the states occurs at the local effective temperature of ~6500 K. The accretion process is stable if the temperature is below the critical value over the entire disc, i.e. at the sufficiently low mass accretion rate (Lasota 1997), 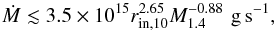 (6)or if the temperature is higher than the critical temperature over the entire disc. This corresponds to the situation when mass accretion rate is high enough,
(6)or if the temperature is higher than the critical temperature over the entire disc. This corresponds to the situation when mass accretion rate is high enough, 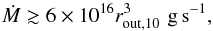 (7)where rin,10 = rin/ 1010 cm is the inner disc radius and rout,10 = rout/ 1010 cm is the outer disc radius. Intermediate mass accretion rate leads to developing the instability.
(7)where rin,10 = rin/ 1010 cm is the inner disc radius and rout,10 = rout/ 1010 cm is the outer disc radius. Intermediate mass accretion rate leads to developing the instability.
Initial transition from the cold to hot state occurs at the inner or outer part of the disc (Smak 1984). The transition is triggered by a heating wave propagating through the disc. The transition wave velocity vtr ~ αcs(H/r)0.5 (Vishniac & Wheeler 1996) is a few times higher than the radial velocity of the matter in the disc vR ~ αcsH/r, where cs ≈ 106 (T/ 104 K)1 / 2 cm s-1 is the local sound speed, α ~ 0.01−0.1 is a viscosity parameter, and H is a local disc half thickness. We assume α = 0.1 for all subsequent estimates. The reverse transition to the cold state happens when the disc temperature drops back to the critical temperature at some radius. At this stage the cooling front arises and propagates inwards from larger to smaller radii. Assuming dimensionless viscosity α ∝ (H/r)n with n ≃ 1.5 the velocity of the cooling front vtr ∝ r (Cannizzo et al. 1995; Vishniac & Wheeler 1996). As a consequence the hot inner parts lose angular momentum and the mass transfer rate decays exponentially at any radii (including the inner disc radius). The accretion rate thus decays exponentially on timescales that are sufficient for the cooling front to reach the inner disc radius.
The disc viscosity diffusion time ~rout/vR(rout) determines the outburst duration, whereas the timescales for rising and declining phases are determined by the transition wave velocity ~rout/vtr(rout). Observed rising and declining times can be shorter because the accretion luminosity is determined by processes that are near the inner disc radius.
Dwarf novae are, as a rule, compact systems with orbital periods Porb of roughly a few hours, and their discs are also compact with rout ~ 1010 cm. As a result, their outbursts are relatively short (~10−20 days) with the rising and declining time lasting roughly a few days (Warner 2003). Because of the relatively small size of the accretion discs, the averaged mass transfer rate can be high enough to keep entire disc in a hot state. Such systems in the permanent outburst are known as nova-like variables (Warner 2003).
The binary system consisting of V 0332+53 and its optical companion BQ Cam is not compact: the orbital period is Porb ≈ 34 days and the distance between companions varies from 6.3 × 1012 to 8.5 × 1012 cm (Negueruela et al. 1999) because of the neutron star orbit eccentricity. The tidal radius of the neutron stars Roche lobe is ~1012 cm and the effective temperature at this radius is less than 1000 K even for the maximum mass accretion rate Ṁ ~ 1018 g s-1 at the peak of the outburst. Therefore, it is probable that the disc instability takes place in the system.
The total mass of the steady-state disc in outburst can be estimated by integrating the surface density Σ(R) from the corotation radius, which is ~4.6 × 108 cm, up to the radius where the effective temperature reaches critical temperature of 6500 K, which is ~7 × 1010 cm for the mass accretion rate Ṁ = 1018 g s-1 and the neutron star mass 1.5 M⊙, 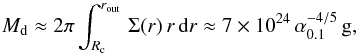 (8)where α0.1 ≡ α/ 0.1. This is the lower limit of the total disc mass because a larger part of the disc can be involved in the outburst due to irradiation. Here we use the steady-state α-disc model (Shakura & Sunyaev 1973) without irradiation, using the analytic solution for zone C, which is presented by Suleimanov et al. (2007).
(8)where α0.1 ≡ α/ 0.1. This is the lower limit of the total disc mass because a larger part of the disc can be involved in the outburst due to irradiation. Here we use the steady-state α-disc model (Shakura & Sunyaev 1973) without irradiation, using the analytic solution for zone C, which is presented by Suleimanov et al. (2007).
On the other hand, total fluence of the current outburst was Efl ≈ 1045 erg and, therefore, the total accreted mass is ΔM = Efl/ (0.1c2) ≈ 1025 g. This value is close to the estimated total mass of the disc suggesting that most of the disc was, in fact, accreted during the outburst. The typical viscous time, rout/vR ~ 1011/ 104 ≈ 107 s, is also comparable to an order of magnitude with the observed outburst decay timescale. The outburst evolution is, therefore, indeed quite similar to that observed in dwarf novae.
The situation is more complicated, however, for a magnetized neutron star. If the magnetospheric radius during the quiescence remains smaller than the corotation radius, the flux decay is caused by the disc transition into a cold state, which is similar to the outburst declining in non-magnetized systems. This case is demonstrated by dwarf nova GK Per with a magnetized white dwarf as a main star (Suleimanov et al. 2016). If this is not the case, however, the accretion might be inhibited before the transition cooling wave reaches the corotation radius.
One can estimate typical timescales for mass accretion rate decay in both cases. The fast transition to the quiescence occurs at the luminosity of about 1036 erg s-1 for V 0332+53. The corresponding outer disc radius, where the effective temperature equals 6500 K, is ~1.5 × 1010 cm and H/r ≈ 0.04. Therefore, the transition wave velocity is ~104 cm s-1 and the typical decay time from the disc instability has to be ~106 s, i.e. ~10 days. On the other hand, the accretion quenching due to the propeller effect has to be realized near the corotation radius with a typical diffusion velocity, which is, in this case about 1.5 × 104 cm s-1. The corresponding timescale is then ~3 × 104 s, or ~8 h. As it was shown before, the typical fast decay time is ~7 h for V 0332+53. Therefore, we conclude that the propeller effect is more probable cause for the accretion quenching in this case. The main conclusions would be the same for our second object, 4U 0115+63.
The accretion disc irradiation is significant during the outburst. It can potentially affect the outer disc properties and keep the disc in a hot stable state longer (see e.g. van Paradijs 1996; King & Ritter 1998). The irradiation also makes the typical timescales of disc instability evolution even longer. In this sense the main conclusion about the nature of observed luminosity decay remains the same.
5. Conclusion
In this work we presented the results of the monitoring programmes dedicated to detecting the transitions to the propeller regime in two bright transient X-ray pulsars, 4U 0115+63 and V 0332+53, during their recent giant outbursts in 2015. In both sources such transitions were detected with confidence for the first time. The threshold luminosities for the propeller regime onset are Llim = (1.4 ± 0.4) × 1036 erg s-1 and Llim = (2.0 ± 0.4) × 1036 erg s-1 for 4U 0115+63 and V 0332+53, respectively. The luminosity drop by a factor of ~200 and ~250 is somewhat lower than expected (~400 and ~450), which suggests the existence of some additional source of emission in the low (propeller) states in both sources. The most probable source of this emission is the cooling of the neutron star surface heated during the outbursts. The observed substantial softening of the source spectrum in the low state in combination with the estimated emitting area support this supposition.
Both sources exhibit brief episodes of resumed accretion as the quiescent neutron star approaches the periastron. Interestingly, the luminosity during these episodes coincides with the limiting luminosity for the propeller transition. The spectrum also becomes hard again suggesting the revival of the accretion onto the neutron star surface. Similar transitions are observed regularly in the first pulsating ULX M82 X-2, which was recently associated with an accreting magnetar.
The strength of the dipole component of the magnetic field for both sources obtained in our work are fully compatible with estimates based on the observations of the cyclotron lines in their spectra, thus excluding an existence of a strong multipole component of the magnetic field in the vicinity of the neutron star. The strong dependence of the limiting luminosity on the parameter k, relating the magnetospheric and Alfvén radii, may permit us to estimate the range of its possible values and compare it with the theoretical predictions once the sample of sources increases (see e.g. Parfrey et al. 2016, and references therein).
We also discussed the possibility that the disc instability (Lasota 2001) is a cause of the observed drop of the luminosity in 4U 0115+63 and V 0332+53. We find that while the observed outburst duration and rise timescale in the bright state are fully consistent with this mechanism, the significantly longer expected decay timescale suggests that the rapid drop in the declining phase of the outburst cannot be explained with it.
Acknowledgments
We are grateful to the Swift team for the execution of our ToO request. This work was supported by the Russian Science Foundation grant 14-12-01287 (S.S.T., A.A.L., A.A.M.) and the Academy of Finland grant 268740 (J.P.). V.D. thank the Deutsches Zentrums for Luft- und Raumfahrt (DLR) and Deutsche Forschungsgemeinschaft (DFG) for financial support (grant DLR 50 OR 0702). We also acknowledge the support from the COST Action MP1304.
References
- Asai, K., Matsuoka, M., Mihara, T., et al. 2013, ApJ, 773, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Bachetti, M., Harrison, F. A., Walton, D. J., et al. 2014, Nature, 514, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, P. A., & Wolff, M. T. 2007, ApJ, 654, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, D. N., Hill, J. E., Nousek, J. A., et al. 2005, Space Sci. Rev., 120, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Campana, S., Gastaldello, F., Stella, L., et al. 2001, ApJ, 561, 924 [NASA ADS] [CrossRef] [Google Scholar]
- Campana, S., Stella, L., Israel, G. L., et al. 2002, ApJ, 580, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Campana, S., Stella, L., & Kennea, J. A. 2008, ApJ, 684, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Campana, S., Brivio, F., Degenaar, N., et al. 2014, MNRAS, 441, 1984 [NASA ADS] [CrossRef] [Google Scholar]
- Cannizzo, J. K., Chen, W., & Livio, M. 1995, ApJ, 454, 880 [NASA ADS] [CrossRef] [Google Scholar]
- Cash, W. 1979, ApJ, 228, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, W., Shrader, C. R., & Livio, M. 1997, ApJ, 491, 312 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, F. H., Horne, K., Panagia, N., et al. 1992, ApJ, 397, 664 [NASA ADS] [CrossRef] [Google Scholar]
- Corbet, R. H. D. 1996, ApJ, 457, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Cui, W. 1997, ApJ, 482, L163 [NASA ADS] [CrossRef] [Google Scholar]
- D’Aì, A., Di Salvo, T., Iaria, R., et al. 2015, MNRAS, 449, 4288 [NASA ADS] [CrossRef] [Google Scholar]
- D’Angelo, C. R., & Spruit, H. C. 2010, MNRAS, 406, 1208 [NASA ADS] [Google Scholar]
- D’Angelo, C. R., & Spruit, H. C. 2012, MNRAS, 420, 416 [NASA ADS] [CrossRef] [Google Scholar]
- Doroshenko, V., Santangelo, A., & Suleimanov, V. 2011, A&A, 529, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Doroshenko, V., Santangelo, A., Ducci, L., & Klochkov, D. 2012, A&A, 548, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Doroshenko, R., Santangelo, A., Doroshenko, V., Suleimanov, V., & Piraino, S. 2015a, MNRAS, 452, 2490 [NASA ADS] [CrossRef] [Google Scholar]
- Doroshenko, V., Tsygankov, S., Ferrigno, C., et al. 2015b, ATel, 7822 [Google Scholar]
- Doroshenko, V., Tsygankov, S., & Santangelo, A. 2016, A&A, 589, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ekşi, K. Y., Andaç, İ. C., Çıkıntoğlu, S., et al. 2015, MNRAS, 448, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, P. A., Beardmore, A. P., Page, K. L., et al. 2009, MNRAS, 397, 1177 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Ghosh, P., & Lamb, F. K. 1978, ApJ, 223, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Ibragimov, A., & Poutanen, J. 2009, MNRAS, 400, 492 [NASA ADS] [CrossRef] [Google Scholar]
- Illarionov, A. F., & Sunyaev, R. A. 1975, A&A, 39, 185 [NASA ADS] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- King, A. R., & Ritter, H. 1998, MNRAS, 293, L42 [NASA ADS] [CrossRef] [Google Scholar]
- Kluźniak, W., & Lasota, J.-P. 2015, MNRAS, 448, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Lasota, J. P. 1997, in IAU Colloq. 163: Accretion Phenomena and Related Outflows, eds. D. T. Wickramasinghe, G. V. Bicknell, & L. Ferrario, ASP Conf. Ser., 121, 351 [Google Scholar]
- Lasota, J.-P. 2001, New Astron., 45, 449 [Google Scholar]
- Lyubarskii, Y. E., & Syunyaev, R. A. 1982, Sov. Astron. Lett., 8, 330 [NASA ADS] [Google Scholar]
- Makishima, K., Mihara, T., Ishida, M., et al. 1990, ApJ, 365, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, F., & Meyer-Hofmeister, E. 1984, A&A, 132, 143 [NASA ADS] [Google Scholar]
- Mineshige, S., Yamasaki, T., & Ishizaka, C. 1993, PASJ, 45, 707 [NASA ADS] [Google Scholar]
- Mushtukov, A. A., Suleimanov, V. F., Tsygankov, S. S., & Poutanen, J. 2015a, MNRAS, 454, 2539 [Google Scholar]
- Mushtukov, A. A., Suleimanov, V. F., Tsygankov, S. S., & Poutanen, J. 2015b, MNRAS, 447, 1847 [NASA ADS] [CrossRef] [Google Scholar]
- Nakajima, M., Masumitsu, T., Negoro, H., et al. 2015a, ATel, 8179 [Google Scholar]
- Nakajima, M., Mihara, T., Negoro, H., et al. 2015b, ATel, 7685 [Google Scholar]
- Negueruela, I., & Okazaki, A. T. 2001, A&A, 369, 108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Negueruela, I., Roche, P., Fabregat, J., & Coe, M. J. 1999, MNRAS, 307, 695 [NASA ADS] [CrossRef] [Google Scholar]
- Parfrey, K., Spitkovsky, A., & Beloborodov, A. M. 2016, ApJ, 822, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Postnov, K. A., Gornostaev, M. I., Klochkov, D., et al. 2015, MNRAS, 452, 1601 [NASA ADS] [CrossRef] [Google Scholar]
- Poutanen, J., Mushtukov, A. A., Suleimanov, V. F., et al. 2013, ApJ, 777, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Raichur, H., & Paul, B. 2010, MNRAS, 406, 2663 [NASA ADS] [CrossRef] [Google Scholar]
- Revnivtsev, M., & Mereghetti, S. 2015, Space Sci. Rev., 191, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Rutledge, R. E., Bildsten, L., Brown, E. F., et al. 2007, ApJ, 658, 514 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Smak, J. 1984, Acta Astron., 34, 161 [NASA ADS] [Google Scholar]
- Stella, L., White, N. E., & Rosner, R. 1986, ApJ, 308, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Stella, L., Campana, S., Colpi, M., Mereghetti, S., & Tavani, M. 1994, ApJ, 423, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Suleimanov, V. F., Lipunova, G. V., & Shakura, N. I. 2007, Astron. Rep., 51, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Suleimanov, V., Doroshenko, V., Ducci, L., Zhukov, G. V., & Werner, K. 2016, A&A, 591, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tsygankov, S. S., Lutovinov, A. A., Churazov, E. M., & Sunyaev, R. A. 2006, MNRAS, 371, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Tsygankov, S. S., Lutovinov, A. A., Churazov, E. M., & Sunyaev, R. A. 2007, Astron. Lett., 33, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Tsygankov, S. S., Mushtukov, A. A., Suleimanov, V. F., & Poutanen, J. 2016, MNRAS, 457, 1101 [NASA ADS] [CrossRef] [Google Scholar]
- Ustyugova, G. V., Koldoba, A. V., Romanova, M. M., & Lovelace, R. V. E. 2006, ApJ, 646, 304 [NASA ADS] [CrossRef] [Google Scholar]
- van Paradijs, J. 1996, ApJ, 464, L139 [NASA ADS] [CrossRef] [Google Scholar]
- Vishniac, E. T., & Wheeler, J. C. 1996, ApJ, 471, 921 [NASA ADS] [CrossRef] [Google Scholar]
- Warner, B. 2003, in Cataclysmic Variable Stars (Cambridge University Press), 592 [Google Scholar]
- White, N. E., Swank, J. H., & Holt, S. S. 1983, ApJ, 270, 711 [NASA ADS] [CrossRef] [Google Scholar]
- Wijnands, R., & Degenaar, N. 2016, MNRAS, submitted [arXiv:1602.02275] [Google Scholar]
- Zanni, C., & Ferreira, J. 2013, A&A, 550, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zel’dovich, Y. B., & Shakura, N. I. 1969, Sov. Astron., 13, 175 [NASA ADS] [Google Scholar]
All Figures
 |
Fig. 1 Light curve of 4U 0115+63 obtained with the Swift/XRT telescope in the 0.5−10 keV energy range. Luminosity is calculated from the unabsorbed flux under the assumption of the distance d = 7 kpc. The solid grey line shows the best fit of the light curve before the transition to the propeller regime with a Gaussian function. The horizontal dashed line represents the limiting luminosity when the propeller regime sets in. Positions of vertical dashed lines correspond to the times of the periastron passage (Raichur & Paul 2010). Applying the bolometric correction to the observed flux effectively increases the luminosity jump by factor of 2 (see Sect. 4.1). |
| In the text | |
 |
Fig. 2 Light curve of V 0332+53 obtained with the Swift/XRT telescope in the 0.5−10 keV energy range. Luminosity is calculated from the unabsorbed flux under assumption of the distance d = 7 kpc. Point near the MJD 57 380 was obtained from averaging of five observations with very low counting statistics. Solid grey line shows the best fit of the light curve before the transition to the propeller regime with a Gaussian function. Horizontal dashed line represents the limiting luminosity when the propeller regime sets in. Positions of vertical dashed lines correspond to the times of the periastron passage (Doroshenko et al. 2016). Applying the bolometric correction to the observed flux effectively increases the luminosity jump by factor of 2 (see Sect. 4.1). |
| In the text | |
 |
Fig. 3 Swift/XRT spectra of 4U 0115+63 and V 0332+53 in accretion (red dots) and propeller (blue crosses) regimes. Solid lines represent the best-fit models consisting of an absorbed power law in the high state and the absorbed black body in the low state. |
| In the text | |
 |
Fig. 4 Observed correlation between a combination of the propeller limiting luminosity and the period, LlimP7 / 3, and independently determined magnetic field strength B for five pulsars and one accreting magnetar (M82 X-2) is shown with circles with error bars (Tsygankov et al. 2016). The dashed and dash-dotted lines represent the theoretical dependence from Eq. (2), assuming NS standard parameters (M = 1.4 M⊙, R = 10 km) and k = 0.5 and k = 0.7, respectively. The red star and open box indicate the positions of 4U 0115+63 and V 0332+53 obtained in this work, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


