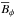| Issue |
A&A
Volume 593, September 2016
|
|
|---|---|---|
| Article Number | A134 | |
| Number of page(s) | 9 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201628165 | |
| Published online | 05 October 2016 | |
Robustness of oscillatory α2 dynamos in spherical wedges
1 Department of Physics, Gustaf Hällströmin katu 2a, PO Box 64, University of Helsinki, 00014 Helsinki, Finland
e-mail: lizmcole@gmail.com
2 Nordita, KTH Royal Institute of Technology and Stockholm University, Roslagstullsbacken 23, 10691 Stockholm, Sweden
3 Department of Astronomy, AlbaNova University Center, Stockholm University, 10691 Stockholm, Sweden
4 JILA and Department of Astrophysical and Planetary Sciences, Box 440, University of Colorado, Boulder, CO 80303, USA
5 Laboratory for Atmospheric and Space Physics, 3665 Discovery Drive, Boulder, CO 80303, USA
6 ReSoLVE Centre of Excellence, Department of Computer Science, Aalto University, PO Box 15400, 00076 Aalto, Finland
7 Max-Planck-Institut für Sonnensystemforschung, Justus-von-Liebig-Weg 3, 37077 Göttingen, Germany
Received: 20 January 2016
Accepted: 6 July 2016
Context. Large-scale dynamo simulations are sometimes confined to spherical wedge geometries by imposing artificial boundary conditions at high latitudes. This may lead to spatio-temporal behaviours that are not representative of those in full spherical shells.
Aims. We study the connection between spherical wedge and full spherical shell geometries using simple mean-field dynamos.
Methods. We solve the equations for one-dimensional time-dependent α2 and α2Ω mean-field dynamos with only latitudinal extent to examine the effects of varying the polar angle θ0 between the latitudinal boundaries and the poles in spherical coordinates.
Results. In the case of constant α and ηt profiles, we find oscillatory solutions only with the commonly used perfect conductor boundary condition in a wedge geometry, while for full spheres all boundary conditions produce stationary solutions, indicating that perfect conductor conditions lead to unphysical solutions in such a wedge setup. To search for configurations in which this problem can be alleviated we choose a profile of the turbulent magnetic diffusivity that decreases toward the poles, corresponding to high conductivity there. Oscillatory solutions are now achieved with models extending to the poles, but the magnetic field is strongly concentrated near the poles and the oscillation period is very long. By changing both the turbulent magnetic diffusivity and α profiles so that both effects are more concentrated toward the equator, we see oscillatory dynamos with equatorward drift, shorter cycles, and magnetic fields distributed over a wider range of latitudes. Those profiles thus remove the sensitive and unphysical dependence on θ0. When introducing radial shear, we again see oscillatory dynamos, and the direction of drift follows the Parker-Yoshimura rule.
Conclusions. A reduced α effect near the poles with a turbulent diffusivity concentrated toward the equator yields oscillatory dynamos with equatorward migration and reproduces best the solutions in spherical wedges. For weak shear, oscillatory solutions are obtained only for perfect conductor field conditions and negative shear. Oscillatory solutions become preferred at sufficiently strong shear. Recent three-dimensional dynamo simulations producing solar-like magnetic activity are expected to lie in this range.
Key words: turbulence / magnetohydrodynamics (MHD) / hydrodynamics
© ESO, 2016
1. Introduction
The Sun’s magnetic field is generally believed to be the result of a turbulent αΩ dynamo in which differential rotation plays an important role. This is referred to as the Ω effect, and it has long been identified as a robust mechanism for amplifying the azimuthal magnetic field of the Sun by winding up the poloidal field (Babcock 1961; Ulrich & Boyden 2005; Brown et al. 2010). The production of poloidal field, on the other hand, is more complicated and harder to verify in computer simulations, but it is thought to be associated with helical motions in the rotating, density stratified convection zone (Parker 1955; Steenbeck et al. 1966). This process is commonly parametrised by an α effect. Although there remain substantial uncertainties regarding the α effect as an important ingredient at large magnetic Reynolds numbers (Cattaneo & Hughes 2006), simulations of turbulence and rotating convection have subsequently confirmed that conventional estimates of α and turbulent diffusivity ηt are reasonably accurate up to moderate values of the magnetic Reynolds number (Sur et al. 2008; Käpylä et al. 2009).
Simulations also demonstrate the generation of differential rotation from anisotropic rotating convection, which amounts to a relative value of 20−30% in latitude (e.g. Miesch et al. 2000; Käpylä et al. 2011). However, whether or not this is enough to drive an αΩ dynamo as opposed to an α2 dynamo, in which the Ω effect would be subdominant, can only be decided on the basis of quantitative calculations. Furthermore, in reality, α and ηt are tensors and additional mean-field effects such as turbulent pumping and Ω × J effect are likely to contribute to dynamo solutions in stars (e.g Rädler 1980; Warnecke et al. 2016).
In the absence of a conclusive answer, one tends to resort to qualitative arguments. One is related to the clear east-west orientation of bipolar regions in the Sun, which suggests that the azimuthal field must be much stronger than the poloidal field. Another argument is that αΩ dynamos are usually cyclic and can display equatorward migration of magnetic field either through suitable radial differential rotation (Parker 1955; Steenbeck & Krause 1969a) or through sufficiently strong meridional circulation in the presence of an α effect that operates only in the surface layers (Choudhuri et al. 1995). However, both arguments are problematic. Although it is probably true that the azimuthal field is stronger than the poloidal, their ratio may not be large enough to justify the dominance of the Ω effect. Furthermore, α2 dynamos may well be oscillatory (e.g. Käpylä et al. 2013a; Masada & Sano 2014) and can display equatorward migration under suitable conditions (Mitra et al. 2010). A completely different argument that motivates the study of oscillatory α2 dynamos are recent simulations of convective dynamos in spherical wedges and full shells that also show equatorward migration (Käpylä et al. 2012, 2013b; Warnecke et al. 2013; Augustson et al. 2015). It is now believed that the equatorward migration in the simulations is facilitated by a region of negative shear and positive (negative) α effect in the northern (southern) hemisphere – in accordance with the Parker-Yoshimura rule (Warnecke et al. 2014). Recently an alternative scenario was reported by Duarte et al. (2016), who found that the sign of the α effect can be inverted in certain parameter ranges allowing equatorward migration also with positive radial shear. Although it is unclear to what extent those simulations represent stellar magnetic fields, it might be helpful to understand first the mechanism operating in those simulations before trying to understand real stars.
The idea of simulating solar or stellar magnetic fields in spherical wedge-shaped geometries with perfectly conducting latitudinal boundaries goes back to an early paper by Jennings et al. (1990). These authors found that such solutions give a faithful representation of systems in full spherical shells. However, they only considered αΩ dynamos. There are now concerns that this conclusion might not carry over to α2 dynamos. Indeed, while the explanation of equatorward migration through α2 dynamo action might work in spherical wedge simulations, there is the problem that such solutions have never been seen in full-shell simulations that extend not just to high latitudes, but go all the way to the poles. Indeed, α2 dynamos in full spherical shells are known to be steady (Steenbeck & Krause 1969b). Exceptions are dynamos with an anisotropic α tensor (Rüdiger et al. 2003) and the non-axisymmetric oscillatory solutions found by Jiang & Wang (2006), but for an isotropic α effect, oscillatory axisymmetric α2 dynamos seem to be an artefact of having imposed a boundary condition at high latitudes. One could choose another boundary condition; a normal-field (pseudo-vacuum) boundary condition might be an obvious choice, but from corresponding Cartesian simulations we know that this would again lead to oscillatory solutions, but with poleward migration (Brandenburg et al. 2009).
Although the mean-field description of oscillatory α2 dynamos seems to face an internal inconsistency regarding the limit to full spherical shells, there remains the question whether certain plausible changes in the setup of the full spherical shell model could lead to oscillatory solutions that are internally consistent and otherwise similar to the solutions in spherical wedges. There is a priori no physical motivation for this, but from a mathematical point of view, this is a natural choice when trying to reproduce the conditions encountered previously with a perfect conductor boundary condition. One possibility is a suitable latitudinal ηt profile with a larger conductivity (weaker magnetic diffusion) at high latitudes to simulate the behaviour of perfect conductor boundary conditions used in spherical wedges.
In each of those cases, it is important to assess how much shear would be needed to change the dynamo mode into an αΩ type mode. To keep things simple, we employ a one-dimensional model with only latitudinal extent. However, in its standard formulation, with radial derivatives simply being dropped, the first excited mode of such an αΩ dynamo is non-oscillatory (Jennings et al. 1990). This is an artefact that is easily removed by substituting radial derivatives with a damping term (Kuzanyan & Sokoloff 1995; Moss et al. 2004), instead of setting them to zero.
We begin by describing our model in detail, next, we focus on the analysis of spherical wedges of different extent and turn then to full spherical shells with variable latitudinal ηt profiles. In view of the aforementioned complications regarding the possibility of oscillatory behaviour in the corresponding αΩ dynamos, we also discuss the sensitivity of our solutions with respect to an additional damping term that mimics the otherwise neglected radial derivative terms.
2. Model
We consider the mean-field dynamo equation for the mean magnetic field 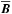 with a given mean electromotive force
with a given mean electromotive force 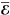 in the form
in the form 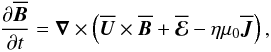 (1)where
(1)where 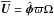 is the mean flow from angular velocity with ϖ = rsinθ being the distance from the axis, Ω(r,θ) is the internal angular velocity,
is the mean flow from angular velocity with ϖ = rsinθ being the distance from the axis, Ω(r,θ) is the internal angular velocity, 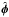 is the unit vector in the azimuthal direction,
is the unit vector in the azimuthal direction, 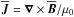 is the mean current density, μ0 is the vacuum permeability, and η is the non-turbulent magnetic diffusion coefficient. In the absence of a memory effect, and under the assumption of isotropic α effect and turbulent magnetic diffusivity ηt, the mean electromotive force is given by
is the mean current density, μ0 is the vacuum permeability, and η is the non-turbulent magnetic diffusion coefficient. In the absence of a memory effect, and under the assumption of isotropic α effect and turbulent magnetic diffusivity ηt, the mean electromotive force is given by 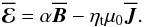 (2)We solve Eqs. (1) and (2) numerically using sixth-order finite differences in space and a third-order accurate time-stepping scheme. We employ the Pencil Code1, which solves the governing equations in terms of the mean magnetic vector potential
(2)We solve Eqs. (1) and (2) numerically using sixth-order finite differences in space and a third-order accurate time-stepping scheme. We employ the Pencil Code1, which solves the governing equations in terms of the mean magnetic vector potential 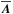 , such that
, such that  . It is convenient to use the advective gauge (Brandenburg et al. 1995; Candelaresi et al. 2011), in which the electrostatic potential has a contribution
. It is convenient to use the advective gauge (Brandenburg et al. 1995; Candelaresi et al. 2011), in which the electrostatic potential has a contribution 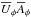 , so that
, so that 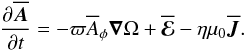 (3)To allow for the use of a one-dimensional model with
(3)To allow for the use of a one-dimensional model with 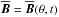 , we restrict ourselves to an angular velocity profile that varies linearly in r, specifically, Ω(r,θ) = rS(θ), so the angular velocity gradient becomes ∇Ω = (S,∂θS,0). The mean current density is then
, we restrict ourselves to an angular velocity profile that varies linearly in r, specifically, Ω(r,θ) = rS(θ), so the angular velocity gradient becomes ∇Ω = (S,∂θS,0). The mean current density is then 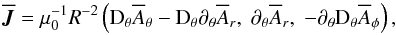 (4)where Dθ = cotθ + ∂θ is a modified θ derivative. To account for the neglect of r derivatives, we add in Eq. (3) a damping term of the form
(4)where Dθ = cotθ + ∂θ is a modified θ derivative. To account for the neglect of r derivatives, we add in Eq. (3) a damping term of the form 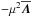 , that is, we have
, that is, we have 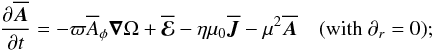 (5)see Moss et al. (2004) for a survey of solutions for different values of μ. For α and ηt we use latitudinal profile functions of the form
(5)see Moss et al. (2004) for a survey of solutions for different values of μ. For α and ηt we use latitudinal profile functions of the form 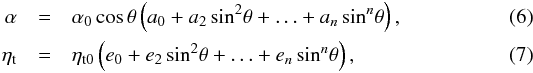 where ai and ei are coefficients denoted by the vectors a = (a0,a2,a4,...,an) and e = (e0,e2,e4,...,en), respectively. However, we often refer to only the three first components as a = (a0,a2,a4) and e = (e0,e2,e4). These expansions can also be expressed in terms of Legendre polynomials, which are orthonormal functions that obey regularity at the poles. The occurrence of higher order terms in α has been associated with higher orders terms in g·Ω, which are normally omitted in theoretical calculations (Rüdiger & Brandenburg 1995).
where ai and ei are coefficients denoted by the vectors a = (a0,a2,a4,...,an) and e = (e0,e2,e4,...,en), respectively. However, we often refer to only the three first components as a = (a0,a2,a4) and e = (e0,e2,e4). These expansions can also be expressed in terms of Legendre polynomials, which are orthonormal functions that obey regularity at the poles. The occurrence of higher order terms in α has been associated with higher orders terms in g·Ω, which are normally omitted in theoretical calculations (Rüdiger & Brandenburg 1995).
As usual, the problem is governed by two dynamo numbers, 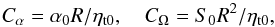 (8)where S(θ) = S0 is now a constant. We consider the following sets of boundary conditions:
(8)where S(θ) = S0 is now a constant. We consider the following sets of boundary conditions:
 where the sequence of letters S and A refer respectively to symmetric (∂θ = 0) and antisymmetric (vanishing function value) of
where the sequence of letters S and A refer respectively to symmetric (∂θ = 0) and antisymmetric (vanishing function value) of 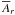 ,
, 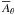 , and
, and 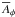 across the boundary. The same conditions are also applied on the corresponding boundary in the southern hemisphere where π−θ = θ0. In this work, no symmetry condition on the equator is applied, so the parity of the solution is not constrained.
across the boundary. The same conditions are also applied on the corresponding boundary in the southern hemisphere where π−θ = θ0. In this work, no symmetry condition on the equator is applied, so the parity of the solution is not constrained.
As initial conditions, we assume a seed magnetic field consisting of low-amplitude Gaussian noise. Such a field is sufficiently complex so that the fastest growing eigenmode of either parity tends to emerge after a short time. We note that mixed parity solutions are only possible in the nonlinear regime (Brandenburg et al. 1989), but this will not be considered here. In this work, we adjust the values of Cα and CΩ such that the solutions are marginally excited, in other words, the field neither grows nor decays.
3. Results
We consider separately the cases where the dynamo is driven either solely by the α effect (α2 dynamos) or by the combined action of the α effect and large-scale shear (α2Ω dynamos).
3.1. α2 dynamos
3.1.1. Varying θ0
We begin by considering the simplest case with a = (1,0,0) and e = (1,0,0), resulting in a spatially constant turbulent diffusivity and a cosθ profile for α. We have calculated the critical value of Cα, hereafter  , for an α2 dynamo where CΩ = 0. We used the boundary conditions SAA, ASA, and SAS for selected values of θ0.
, for an α2 dynamo where CΩ = 0. We used the boundary conditions SAA, ASA, and SAS for selected values of θ0.
It turns out that  decreases as we approach the pole (θ0 → 0°); see Fig. 1. The SAA and SAS boundary conditions result in very similar non-oscillatory solutions with a
decreases as we approach the pole (θ0 → 0°); see Fig. 1. The SAA and SAS boundary conditions result in very similar non-oscillatory solutions with a  of only approximately 40% of that
of only approximately 40% of that  obtained for the ASA boundary condition. Oscillatory solutions show travelling waves that propagate equatorward; see Fig. 2. The boundary condition with the greatest variation of
obtained for the ASA boundary condition. Oscillatory solutions show travelling waves that propagate equatorward; see Fig. 2. The boundary condition with the greatest variation of  with θ0 is the perfect conductor, ASA. We also find that the most easily excited dynamo mode changes from stationary to oscillatory as θ0 increases from zero to one degree in that case. For the case where θ0 = 1° we find both stationary and oscillatory solutions, depending on the initial conditions. The critical dynamo number is slightly higher for the oscillatory mode than for the corresponding stationary solution.
with θ0 is the perfect conductor, ASA. We also find that the most easily excited dynamo mode changes from stationary to oscillatory as θ0 increases from zero to one degree in that case. For the case where θ0 = 1° we find both stationary and oscillatory solutions, depending on the initial conditions. The critical dynamo number is slightly higher for the oscillatory mode than for the corresponding stationary solution.
These results suggest that we cannot regard the limit θ0 → 0° with the isotropic α effect and turbulent diffusivity using perfect conductor boundaries as an approximation to the full spherical shell model when searching for oscillatory solutions. Thus, the limit θ0 → 0° is singular in this sense. Extending the model to the poles with the ASA boundary condition changes the resulting dynamo from oscillatory to stationary. The SAA and SAS boundary conditions give stationary solutions with relatively similar values for  , but the ASA boundary condition near the poles gives both oscillatory and stationary solutions, depending on the initial conditions of the seed magnetic field. While no stationary solutions were found for θ0> 1°, their existence is not ruled out by our models.
, but the ASA boundary condition near the poles gives both oscillatory and stationary solutions, depending on the initial conditions of the seed magnetic field. While no stationary solutions were found for θ0> 1°, their existence is not ruled out by our models.
 |
Fig. 1 Dependence of |
 |
Fig. 2 Azimuthal magnetic field |
3.1.2. Varying latitudinal ηt profile
Given that we have found the limit θ0 → 0° in the case of the perfect conductor boundary condition not to be an approximation to a full spherical shell model, we now investigate whether physically motivated alterations of the full spherical shell model with the SAA boundary condition could produce oscillatory, equatorward solutions similar to those found for θ0 ≠ 0° with the ASA boundary condition. An obvious possibility is the use of an ηt profile that corresponds to high conductivity near the pole. Such a profile could correspond to the possible effect of rotation on the magnetic diffusivity (Kitchatinov et al. 1994) at various latitudes.
 for pure α2 dynamos with varied magnetic diffusivity and α profiles and the corresponding oscillations frequencies in units of ηt0/R2.
for pure α2 dynamos with varied magnetic diffusivity and α profiles and the corresponding oscillations frequencies in units of ηt0/R2.
One possible alteration to the diffusivity profile is to use higher order terms for ηt. In particular, we examine solutions where the orders n = 2, 4, 6, and 8 are used for en; see Eq. (7). Solutions are examined for e0 = η/ηt0 = 0.01 and 0.05. A non-zero uniform value of η is needed to ensure the stability of the solutions in the cases where the turbulent magnetic diffusivity is zero at the poles due to the profiles being proportional to powers of sinθ, which vanishes at the poles. We have verified that neither value of η used here leads to spurious growth in the absence of an α-effect. Furthermore, we calculate the oscillation frequency as ω = 2π/T where T is the period of oscillation for the large-scale magnetic field.
Values for  are indicated in Table 1 for cases where the turbulent diffusivity and α effect profiles are expanded up to orders e8 and a4, respectively. We find that for a = (1,0,0), the e0 = 0.05 case produces only stationary solutions, but at e0 = 0.01, only solutions for n = 2 are stationary and all higher orders oscillate; see Table 1. Some solutions initially show rapidly oscillating behaviour, exhibiting antisymmetry with respect to the equator, but these disappear later and only a slower, persistent oscillatory mode remains; see Fig. 3a. These low-frequency oscillations have neither equatorward nor poleward migration and are symmetric about the equator.
are indicated in Table 1 for cases where the turbulent diffusivity and α effect profiles are expanded up to orders e8 and a4, respectively. We find that for a = (1,0,0), the e0 = 0.05 case produces only stationary solutions, but at e0 = 0.01, only solutions for n = 2 are stationary and all higher orders oscillate; see Table 1. Some solutions initially show rapidly oscillating behaviour, exhibiting antisymmetry with respect to the equator, but these disappear later and only a slower, persistent oscillatory mode remains; see Fig. 3a. These low-frequency oscillations have neither equatorward nor poleward migration and are symmetric about the equator.  increases with e0, and decreases as n increases for en, in accordance with the total diffusivity increasing and decreasing, respectively. The frequency of the oscillatory modes found for e0 = 0.01 decreases as n increases. This is also consistent with mean-field theory where the oscillation frequency is proportional to the magnetic diffusion coefficient. The magnetic field is antisymmetric with respect to the equator in all cases, except for a = (1,0,0) and e0 = 0.01; see Fig. 3a.
increases with e0, and decreases as n increases for en, in accordance with the total diffusivity increasing and decreasing, respectively. The frequency of the oscillatory modes found for e0 = 0.01 decreases as n increases. This is also consistent with mean-field theory where the oscillation frequency is proportional to the magnetic diffusion coefficient. The magnetic field is antisymmetric with respect to the equator in all cases, except for a = (1,0,0) and e0 = 0.01; see Fig. 3a.
The azimuthal magnetic field is strongly concentrated toward the poles when the α effect has only the cosθ variation in latitude; see the top panels of Figs. 3 and 4. In view of the equatorial magnetic field concentration in the Sun and in three-dimensional solar dynamo simulations, where the kinetic helicity is known to be strongly concentrated toward the equator (Käpylä et al. 2012), it is of interest to consider models with a = (0,1,0) and a = (0,0,1), so that the α effect is more concentrated toward lower latitudes. Indications for α being stronger at lower latitudes have been observed, for example, in models of rapidly rotating convection (Käpylä et al. 2006). The values for  are given in Table 1, columns for a = (0,1,0) and a = (0,0,1). A similar trend as for the case where a = (1,0,0) is seen, where higher orders of en result in lower values for
are given in Table 1, columns for a = (0,1,0) and a = (0,0,1). A similar trend as for the case where a = (1,0,0) is seen, where higher orders of en result in lower values for  , in accordance with lower total diffusion. Changes in the α profile have a larger effect on
, in accordance with lower total diffusion. Changes in the α profile have a larger effect on  than changes in the diffusivity profile. However, this is simply because, owing to the presence of the cosθ factor in the α profile, its maximum value diminishes as higher powers of sinθ are used, while the maximum value of ηt is always unity, irrespective of the profile. The oscillation frequencies of the solutions for a = (0,1,0) and a = (0,0,1) are two orders of magnitude higher than the low-frequency mode seen for a = (1,0,0). It turns out that the magnetic field is then more uniformly distributed over all latitudes; see Figs. 3 and 4. For e0 = 0.01, this distribution is largely uniform with very slight equatorward drift (Figs. 3b and c), and when e0 = 0.05, the equatorward drift becomes more pronounced and extends to lower latitudes (Figs. 4b and c).
than changes in the diffusivity profile. However, this is simply because, owing to the presence of the cosθ factor in the α profile, its maximum value diminishes as higher powers of sinθ are used, while the maximum value of ηt is always unity, irrespective of the profile. The oscillation frequencies of the solutions for a = (0,1,0) and a = (0,0,1) are two orders of magnitude higher than the low-frequency mode seen for a = (1,0,0). It turns out that the magnetic field is then more uniformly distributed over all latitudes; see Figs. 3 and 4. For e0 = 0.01, this distribution is largely uniform with very slight equatorward drift (Figs. 3b and c), and when e0 = 0.05, the equatorward drift becomes more pronounced and extends to lower latitudes (Figs. 4b and c).
In summary, extending the model all the way to the poles and including an ηt profile concentrated toward the equator results in oscillatory behaviour with long cycles but no equatorward migration. Including an α-effect also concentrated at lower latitudes produces equatorward cycles with shorter cycle periods with the strongest magnetic fields appearing at lower latitudes. These results are in qualitative agreement with direct and large-eddy simulations (Käpylä et al. 2012, 2013b; Augustson et al. 2015; Duarte et al. 2016).
 |
Fig. 5 Dependence of |
 |
Fig. 6 Azimuthal magnetic field for θ0 = 5°, a = (0,0,1), e4, e0 = 0.05, and the SAA (a) and ASA (b) boundary conditions. |
We examine the impact of changing θ0 on the resulting magnetic field using the same a and e in Fig. 4c. As θ0 approaches zero,  changes in a continuous fashion both for the ASA and SAA boundary conditions; see Fig. 5. Thus, the limit θ0 → 0° is now no longer singular. If the azimuthal fields are compared for the oscillatory solutions (Figs. 6 and 4c), solutions are equatorward and the only significant difference is that the ASA boundary condition produces fields strongest at the boundary, whereas the SAA boundary condition concentrates the field at lower latitudes.
changes in a continuous fashion both for the ASA and SAA boundary conditions; see Fig. 5. Thus, the limit θ0 → 0° is now no longer singular. If the azimuthal fields are compared for the oscillatory solutions (Figs. 6 and 4c), solutions are equatorward and the only significant difference is that the ASA boundary condition produces fields strongest at the boundary, whereas the SAA boundary condition concentrates the field at lower latitudes.
3.2. α2Ω dynamos
Given that the commonly used ASA boundary condition was previously found to yield non-singular behaviour – even for a uniform ηt profile (Jennings et al. 1990), it is now of interest to re-address this problem in the context of the present model.
 |
Fig. 7 Values for |
 |
Fig. 8 Dependence of ω on CΩ for θ0 = 1° (blue) and θ0 = 0° (red) for |
3.2.1. Overall behaviour of dynamo solutions
We now add large-scale radial shear and a damping term given by μR2/ηt and use 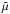 to denote μR2/ηt0. We first explore the dynamo regimes and the dependency on
to denote μR2/ηt0. We first explore the dynamo regimes and the dependency on 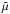 by setting θ0 = 1° and once again use a = (1,0,0) and e = (1,0,0). The critical value
by setting θ0 = 1° and once again use a = (1,0,0) and e = (1,0,0). The critical value  now depends on the value of
now depends on the value of 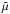 ; see Fig. 7. We now concentrate on studying the dynamo modes that are excited in the system for values of
; see Fig. 7. We now concentrate on studying the dynamo modes that are excited in the system for values of 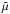 between 0 and 4 and various values of CΩ.
between 0 and 4 and various values of CΩ.
When 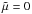 , all resulting dynamos are stationary, with the exception of the case where CΩ = 0 where oscillations depend on initial conditions, and
, all resulting dynamos are stationary, with the exception of the case where CΩ = 0 where oscillations depend on initial conditions, and  decreases as CΩ increases. For solutions pertaining to
decreases as CΩ increases. For solutions pertaining to  , two solutions exist in the regime CΩ ≳ 33.5 with either oscillatory or stationary magnetic fields. When CΩ is less than this value, we find only stationary solutions. Near this limit, the frequency of oscillations is sensitive to both
, two solutions exist in the regime CΩ ≳ 33.5 with either oscillatory or stationary magnetic fields. When CΩ is less than this value, we find only stationary solutions. Near this limit, the frequency of oscillations is sensitive to both  and CΩ and even small changes can double the frequency. The
and CΩ and even small changes can double the frequency. The  for stationary dynamos is significantly less than for oscillating solutions. It is possible that for
for stationary dynamos is significantly less than for oscillating solutions. It is possible that for 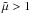 a similar bifurcation also exists, as there always appears a change in the dependence of cycle frequency on
a similar bifurcation also exists, as there always appears a change in the dependence of cycle frequency on  as the dynamo mode changes from stationary to oscillatory. However, at least in the case with
as the dynamo mode changes from stationary to oscillatory. However, at least in the case with 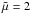 , the stationary solutions were found to disappear. For cases where
, the stationary solutions were found to disappear. For cases where 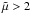 ,
,  decreases with CΩ, and oscillations only occur above certain critical values for CΩ. In the regime of negative shear (CΩ< 0), all solutions found were oscillatory.
decreases with CΩ, and oscillations only occur above certain critical values for CΩ. In the regime of negative shear (CΩ< 0), all solutions found were oscillatory.
 |
Fig. 9 Azimuthal magnetic field for θ0 = 1° with the ASA boundary condition; α2Ω dynamo with |
We calculate the frequency ω of oscillatory solutions as in the previous section and show the results in Fig. 8. It can be seen that for positive shear, ω approaches 0 as CΩ → 33.55. There also exists a jump in frequency around CΩ ~ 70, corresponding to a change in the symmetry of the azimuthal field. This is demonstrated in Fig. 9 where time-latitude diagrams of the azimuthal magnetic fields are shown for a representative selection of CΩ values for models with θ0 = 1°. The symmetry change corresponding to the frequency jump in Fig. 8 can be seen in the change from antisymmetric about the equator (Fig. 9c, CΩ = 40) to symmetric (Fig. 9d, CΩ = 80). The magnetic field is also symmetric in the oscillatory solution found for CΩ = 0.
All oscillatory solutions with positive (negative) shear show poleward (equatorward) migration in accordance with the Parker-Yoshimura rule (Parker 1955; Yoshimura 1975), compare Figs. 9c and e, respectively, for representative results. The frequency of the oscillations increases with greater CΩ in accordance with linear theory of αΩ dynamos, except that there 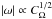 (e.g. Brandenburg & Subramanian 2005). Most of the magnetic field is concentrated at high latitudes above | 90°−θ | > 60° for cases where CΩ is positive, Figs. 9b–d. When CΩ ≤ 0, the field is even more concentrated close to boundaries; see Fig. 9e.
(e.g. Brandenburg & Subramanian 2005). Most of the magnetic field is concentrated at high latitudes above | 90°−θ | > 60° for cases where CΩ is positive, Figs. 9b–d. When CΩ ≤ 0, the field is even more concentrated close to boundaries; see Fig. 9e.
3.2.2. Comparison between θ0 = 0° and θ0 = 1° cases
The model is now extended to the poles to study the differences between wedges and full spheres. The boundary condition on θ0 = 0° is changed to comply with the regularity requirement (SAA). We focus on the case where  . We consider a few models with
. We consider a few models with 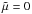 and 2 to probe whether the behaviour is similar to the θ0 = 1° case. We find that the values of
and 2 to probe whether the behaviour is similar to the θ0 = 1° case. We find that the values of  are fairly close to those obtained for the corresponding θ0 = 1° models; see Fig. 7. Similarly as in the θ0 = 1° case, a bifurcation into stationary and oscillatory solutions exists in the positive CΩ regime with a cut-off point at CΩ ≈ 33.2, which is slightly lower than in the θ0 = 1° case. For negative shear, unlike for θ0 = 1° where all values produce oscillatory dynamos, the regime for oscillations is found only for CΩ ≲ −21. The oscillatory mode gradually disappears and only a stationary mode persists.
are fairly close to those obtained for the corresponding θ0 = 1° models; see Fig. 7. Similarly as in the θ0 = 1° case, a bifurcation into stationary and oscillatory solutions exists in the positive CΩ regime with a cut-off point at CΩ ≈ 33.2, which is slightly lower than in the θ0 = 1° case. For negative shear, unlike for θ0 = 1° where all values produce oscillatory dynamos, the regime for oscillations is found only for CΩ ≲ −21. The oscillatory mode gradually disappears and only a stationary mode persists.
 |
Fig. 10 Azimuthal magnetic field for θ0 = 0° with the SAA boundary condition; α2Ω dynamo with |
The oscillation frequencies (Fig. 8) are similar to those in the case of positive shear. Similarly to the θ0 = 1° case, a jump in frequency is observed when the azimuthal field changes symmetry with respect to the equator, as shown in Figs. 10c and d for antisymmetric (CΩ = 40) and symmetric (CΩ = 80) field configurations, respectively. In the antisymmetric regime, the azimuthal field is concentrated at approximately the same latitudes as for the case θ0 = 1°. In the symmetric regime where CΩ ≳ 70, the azimuthal field extends to lower latitudes, | 90°−θ | > 30°; see Fig. 10d. The main difference occurs at the boundary itself such that for θ0 = 1° (ASA) the magnetic field peaks at the boundary whereas it vanishes at the pole for θ0 = 0° (SAA). When shear is negative, the field instead becomes concentrated and symmetric around the equator, and in accordance with the Parker-Yoshimura rule, the dynamo has an equatorward drift. The case of negative shear results in a dramatically different concentration of the azimuthal field when compared with the θ0 = 1° counterpart; see Figs. 9e and 10e for runs with CΩ = −40 for the two cases. Even though the values for  are similar for θ0 = 0° and 1°, the frequency of oscillations is less by about a factor of two in the former case; see Fig. 8.
are similar for θ0 = 0° and 1°, the frequency of oscillations is less by about a factor of two in the former case; see Fig. 8.
Finally, we examine the effect that θ0 has on the results by holding CΩ constant and determining  . The results are given in Table 2. We find that there is a dependency on θ0, but the behaviour is consistent if one goes to the poles and changes the boundary condition; see Table 2 where the change between θ0 = 5° and 1° is comparable to the difference between 1° and 0°. All solutions are oscillatory with poleward migration.
. The results are given in Table 2. We find that there is a dependency on θ0, but the behaviour is consistent if one goes to the poles and changes the boundary condition; see Table 2 where the change between θ0 = 5° and 1° is comparable to the difference between 1° and 0°. All solutions are oscillatory with poleward migration.
 for runs with θ0 = 0°, 1°, 5°, and 15° with a = (1,0,0) and e = (1,0,0) and
for runs with θ0 = 0°, 1°, 5°, and 15° with a = (1,0,0) and e = (1,0,0) and 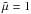 .
.
Our results suggest that, at least in the cases where CΩ> 0, a setup with θ0 = 1° and the perfect conductor boundary condition (ASA) gives similar results as full sphere models with θ0 = 0° and the regularity (SAA) condition. Furthermore, solutions for 33.4 <CΩ< 75 are also fairly similar. This indicates that the wedges are a fair approximation of full spheres in this parameter regime. If the shear is negative, there is a qualitative change in the results between θ0 = 1° and θ0 = 0° cases. It appears that for weak negative shear, oscillatory solutions are obtained only for the ASA boundary condition.
3.2.3. Varying the α and ηt profiles
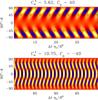 |
Fig. 11 Azimuthal magnetic field for θ0 = 0° with e0 = 0.05, |
Finally, we consider changes to the turbulent magnetic diffusivity profile. We do not perform a thorough parameter study but consider a pair of cases corresponding to CΩ = ± 40, a = e = (0,0,1), e0 = 0.05, 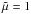 , and θ0 = 0° with regularity conditions for the magnetic field. We show the time–latitude diagrams of the azimuthal field from these models in Fig. 11.
, and θ0 = 0° with regularity conditions for the magnetic field. We show the time–latitude diagrams of the azimuthal field from these models in Fig. 11.
In the case of positive shear, the combination of shear, α and ηt profiles, creates a steady migration poleward at latitudes above ± 45°. Comparing this to an α2 dynamo with the same profiles of α and ηt (Fig. 4c), and to an α2Ω run with no sin2nθ contributions in the profiles but the same value of CΩ (Fig. 10c), shows that the migration direction is reversed in comparison to the α2 run and that the poleward drift is more coherent than in the α2Ω model. These results indicate that the shear determines the direction of the dynamo wave in this parameter regime. The azimuthal field in both of the comparison cases is antisymmetric, and this result also carries over to the case when shear is included with the same α and ηt profiles. The frequency of the oscillations is ω = 5.54, and the critical dynamo parameter is 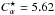 . These values are somewhat close to the values (ω = 3.90 and
. These values are somewhat close to the values (ω = 3.90 and 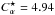 ) obtained in Sect. 3.2.1 in the case with more uniform profiles of the turbulent transport coefficients.
) obtained in Sect. 3.2.1 in the case with more uniform profiles of the turbulent transport coefficients.
We found earlier that in the case of negative shear, the azimuthal field was symmetric about the equator; see Fig. 10e. With more equatorially concentrated turbulent diffusivity and α profiles we also find solutions with equatorial symmetry, see the bottom panel of Fig. 11. Furthermore, the magnetic field now has a minimum around latitudes ± 25°. The Parker-Yoshimura rule still holds true, and the migration is equatorward. However,  has almost doubled from 5.62 to 10.75, and the frequency of oscillations is much larger, ω = 14.56 in comparison to 5.54. The main effect from the more concentrated profiles for α and ηt in the case of α2Ω dynamos is seen in the latitudinal profile of the resulting magnetic fields, but the qualitative character of the solutions remains unchanged in comparison to models with simpler latitude dependence of the turbulent transport coefficients.
has almost doubled from 5.62 to 10.75, and the frequency of oscillations is much larger, ω = 14.56 in comparison to 5.54. The main effect from the more concentrated profiles for α and ηt in the case of α2Ω dynamos is seen in the latitudinal profile of the resulting magnetic fields, but the qualitative character of the solutions remains unchanged in comparison to models with simpler latitude dependence of the turbulent transport coefficients.
Concerning the earlier work of Jennings et al. (1990), we can now conclude that they have been lucky, because in their case, although they used negative shear, they found similar solution in a wedge and a full spherical shell. This could have been because in their case θ0 = 45°. As we now know, the solutions for θ0 = 0° and 1° are quantitatively different, although qualitatively similar; see Fig. 8.
4. Conclusions
Motivated by earlier results of global simulations in wedge geometry, we have studied the robustness of oscillatory solutions in α2 dynamos in simple one-dimensional mean-field dynamo models. We found that the latitudinal boundary conditions play a major role in the realised solutions for α2 dynamos with a simple cosθ profile for α and constant turbulent diffusivity. Imposing the perfect conductor boundary condition creates oscillating solutions only for cases where θ0 ≳ 1°. For θ0 = 1°, both oscillatory and stationary solutions were found to appear with slightly differing critical dynamo numbers. We found no oscillatory solutions for the normal field (SAS) or regularity conditions (SAA). On the one hand, this motivates future experiments with SAS or SAA conditions in global simulations in wedge geometry. On the other hand, the oscillatory solutions found in global simulations in wedge geometry might still be physical and not an artefact of using a perfect conductor boundary condition on the latitudinal boundaries. Some global simulations in wedge geometry with the SAS condition have already been performed (Käpylä et al. 2016b), but their cases were in a regime where no oscillations occur.
Keeping a simple cosθ profile for the α effect and varying the ηt profile creates oscillating solutions with a low frequency and no clear migration or stationary solutions, depending on the value of the underlying (constant) magnetic diffusivity. The magnetic field is largely concentrated near the poles. If the α profile is changed to be concentrated near the equator, similar to profiles observed in rapidly rotating turbulent convection, the magnetic field becomes more evenly distributed towards the equator. The magnetic field also exhibits clear equatorward migration and antisymmetry with respect to the equator. The overall conclusion is that α2 dynamos can produce solar-like magnetic activity if the α effect and turbulent diffusivity have latitudinal profiles that are sufficiently concentrated toward the equator. One may speculate that this could actually be the case in the spherical wedge simulations of Käpylä et al. (2012), where most of the magnetic activity and most of the magnetic helicity were found to occur away from the axis, outside the inner tangent cylinder.
We then added positive shear to study α2Ω dynamos and how they connect to the pure α2 solutions in the same wedge geometry with θ0 = 1°. For weak shear the azimuthal magnetic field is concentrated at the poles and shifts equatorward. Over a certain interval in CΩ, which depends on the added local friction 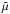 , oscillatory solutions are found and the field is more concentrated across all upper latitudes. For
, oscillatory solutions are found and the field is more concentrated across all upper latitudes. For 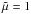 , we found that both stationary and oscillatory solutions exist with the oscillatory one having a substantially higher critical dynamo number. Going to a full sphere with θ0 = 0° and changing the boundary condition to SAA produced qualitatively and quantitatively similar results when the shear was positive. Results are less similar if negative shear is introduced. When θ0 = 1°, all solutions with CΩ< 0 were found to oscillate. However, when θ0 = 0°, shear had to exceed a critical value, CΩ< −21, for solutions to oscillate. Furthermore, the structure of the azimuthal field over time was significantly different, showing symmetry about the equator and concentration at the equator. In all cases with shear, the Parker-Yoshimura rule was found to be obeyed where oscillatory solutions with negative shear migrated equatorward and positive shear, poleward. When combining the ηt profile with shear, the direction of migration was determined by the sign of CΩ. The frequency increased in the case of negative shear when using an ηt and α profile with higher order terms.
, we found that both stationary and oscillatory solutions exist with the oscillatory one having a substantially higher critical dynamo number. Going to a full sphere with θ0 = 0° and changing the boundary condition to SAA produced qualitatively and quantitatively similar results when the shear was positive. Results are less similar if negative shear is introduced. When θ0 = 1°, all solutions with CΩ< 0 were found to oscillate. However, when θ0 = 0°, shear had to exceed a critical value, CΩ< −21, for solutions to oscillate. Furthermore, the structure of the azimuthal field over time was significantly different, showing symmetry about the equator and concentration at the equator. In all cases with shear, the Parker-Yoshimura rule was found to be obeyed where oscillatory solutions with negative shear migrated equatorward and positive shear, poleward. When combining the ηt profile with shear, the direction of migration was determined by the sign of CΩ. The frequency increased in the case of negative shear when using an ηt and α profile with higher order terms.
In summary, we may conclude that large-scale dynamo action in spherical domains can, under certain conditions, be approximated by solutions in wedge-shaped geometries. This may well be the case for the simulations of Käpylä et al. (2012, 2016a). At least in the outer parts, close to the surface, those solutions exhibit a phase relation between poloidal and toroidal fields that is only seen in α2 dynamos of the type presented in Sect. 3.1; see Sect. 3.6 of Käpylä et al. (2013b). A subsequent study by Warnecke et al. (2014) showed, however, that the equatorward migration is the result of a standard α2Ω dynamo operating in deeper layers; see their Figs. 5c and d.
The angular velocities used in the simulations of Käpylä et al. (2013b) were probably too large to represent the Sun. The solar dynamo may therefore still be of α2 type. However, as we have seen, those dynamos would only be oscillatory if the polar regions can be regarded as highly conducting; see Sect. 3.1.1. There may be alternative possibilities for obtaining oscillatory solutions to the α2 dynamo. One possibility is to study the effect of decreasing the (microphysical) magnetic diffusivity even further. Another possibility is to study the memory effect, which has recently been identified as a means to facilitate oscillatory behaviour (Rheinhardt & Brandenburg 2012), although so far only decaying solutions have been found to be modified in that way (Devlen et al. 2013). However, under suitable conditions such solutions can indeed become oscillatory (Rheinhardt et al. 2014) and may present a possible solution to the problem where equatorward motion obtained via varying the α profile with a = (0,0,1), for example, is limited to certain latitudes.
Acknowledgments
The authors thank Nordita for hospitality during their visits. Financial support from the Vilho, Yrjö and Kalle Väisälä Foundation (EC), the Academy of Finland grants No. 136189, 140970 (P.J.K.) and the Academy of Finland Centre of Excellence ReSoLVE (272157; M.J.K. and P.J.K.), as well as the Swedish Research Council grants 621-2011-5076 and 2012-5797, and the European Research Council under the AstroDyn Research Project 227952 are acknowledged. We acknowledge CSC – IT Center for Science Ltd., who are administered by the Finnish Ministry of Education, for the allocation of computational resources.
References
- Augustson, K., Brun, A. S., Miesch, M. S., & Toomre, J. 2015, ApJ, 809, 149 [Google Scholar]
- Babcock, H. W. 1961, ApJ, 133, 572 [Google Scholar]
- Brandenburg, A., & Subramanian, K. 2005, Phys. Rev., 417, 1 [Google Scholar]
- Brandenburg, A., Krause, F., Meinel, R., Moss, D., & Tuominen, I. 1989, MNRAS, 213, 411 [Google Scholar]
- Brandenburg, A., Nordlund, Å., Stein, R. F., & Torkelsson, U. 1995, A&A, 446, 741 [Google Scholar]
- Brandenburg, A., Candelaresi, S., & Chatterjee, P. 2009, ApJ, 398, 1414 [Google Scholar]
- Brown, B. P., Browning, M. K., Brun, A. S., Miesch, M. S., & Toomre, J. 2010, ApJ, 711, 424 [Google Scholar]
- Candelaresi, S., Hubbard, A., Brandenburg, A., & Mitra, D. 2011, Phys. Plasmas, 18, 012903 [NASA ADS] [CrossRef] [Google Scholar]
- Cattaneo, F., & Hughes, D. W. 2006, J. Fluid. Mech., 553, 401 [Google Scholar]
- Choudhuri, A. R., Schüssler, M., & Dikpati, M. 1995, A&A, 303, L29 [NASA ADS] [Google Scholar]
- Devlen, E., Brandenburg, A., & Mitra, D. 2013, MNRAS, 432, 1651 [NASA ADS] [CrossRef] [Google Scholar]
- Duarte, L. D. V., Wicht, J., Browning, M. K., & Gastine, T. 2016, MNRAS, 456, 1708 [NASA ADS] [CrossRef] [Google Scholar]
- Jennings, R., Brandenburg, A., Moss, D., & Tuominen, I. 1990, A&A, 230, 463 [NASA ADS] [Google Scholar]
- Jiang, J., & Wang, J.-X. 2006, Chin. J. Astron. Astrophys., 2, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Käpylä, P. J., Korpi, M. J., Ossendrijver, M., & Stix, M. 2006, A&A, 455, 401 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Käpylä, P. J., Korpi, M. J., & Brandenburg, A. 2009, A&A, 500, 633 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Käpylä, P. J., Mantere, M. J., Guerrero, G., Brandenburg, A., & Chatterjee, P. 2011, A&A, 531, A162 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Käpylä, P. J., Mantere, M. J., & Brandenburg, A. 2012, ApJ, 755, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Käpylä, P. J., Mantere, M. J., & Brandenburg, A. 2013a, Geophys. Astrophys. Fluid Dyn., 107, 244 [Google Scholar]
- Käpylä, P. J., Mantere, M. J., Cole, E., Warnecke, J., & Brandenburg, A. 2013b, ApJ, 778, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Käpylä, M. J., Käpylä, P. J., Olspert, N., et al. 2016a, A&A, 589, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Käpylä, P. J., Käpylä, M. J., Olspert, N., Warnecke, J., & Brandenburg, A. 2016b, A&A, submitted [arXiv:1605.05885] [Google Scholar]
- Kitchatinov, L. L., Rüdiger, G., & Pipin, V. V. 1994, Astron. Nachr., 315, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Kuzanyan, K. M., & Sokoloff, D. D. 1995, Geophys. Astrophys. Fluid Dyn., 81, 113 [Google Scholar]
- Masada, Y., & Sano, T. 2014, ApJ, 794, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Miesch, M. S., Elliott, J. R., Toomre, J., et al. 2000, ApJ, 532, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Mitra, D., Tavakol, R., Käpylä, P. J., & Brandenburg, A. 2010, ApJ, 719, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Moss, D., Sokoloff, D., Kuzanyan, K., & Petrov, A. 2004, Geophys. Astrophys. Fluid Dyn., 98, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1955, ApJ, 122, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Rädler, K.-H. 1980, ApJ, 301, 101 [Google Scholar]
- Rheinhardt, M., & Brandenburg, A. 2012, Astron. Nachr., 333, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Rheinhardt, M., Devlen, E., Rädler, K.-H., & Brandenburg, A. 2014, MNRAS, 441, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Rüdiger, G., & Brandenburg, A. 1995, A&A, 296, 557 [NASA ADS] [Google Scholar]
- Rüdiger, G., Elstner, D., & Ossendrijver, M. 2003, A&A, 406, 15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Steenbeck, M., & Krause, F. 1969a, Astron. Nachr., 291, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Steenbeck, M., & Krause, F. 1969b, Astron. Nachr., 291, 271 [Google Scholar]
- Steenbeck, M., Krause, F., & Rädler, K.-H. 1966, Z. Naturforsch. A, 21, 369 [NASA ADS] [Google Scholar]
- Sur, S., Brandenburg, A., & Subramanian, K. 2008, MNRAS, 385, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Ulrich, R. K., & Boyden, J. E. 2005, ApJ, 620, L123 [NASA ADS] [CrossRef] [Google Scholar]
- Warnecke, J., Käpylä, P. J., Mantere, M. J., & Brandenburg, A. 2013, ApJ, 778, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Warnecke, J., Käpylä, P. J., Käpylä, M. J., & Brandenburg, A. 2014, ApJ, 796, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Warnecke, J., Rheinhardt, M., Käpylä, P. J., Käpylä, M. J., & Brandenburg, A. 2016, A&A, submitted [arXiv:1601.03730] [Google Scholar]
- Yoshimura, H. 1975, ApJ, 201, 740 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
 for pure α2 dynamos with varied magnetic diffusivity and α profiles and the corresponding oscillations frequencies in units of ηt0/R2.
for pure α2 dynamos with varied magnetic diffusivity and α profiles and the corresponding oscillations frequencies in units of ηt0/R2.
All Figures
 |
Fig. 1 Dependence of |
| In the text | |
 |
Fig. 2 Azimuthal magnetic field |
| In the text | |
 |
Fig. 3 Azimuthal magnetic field for e4, e0 = 0.01 in Table 1 with θ0 = 0° and the SAA condition. |
| In the text | |
 |
Fig. 4 Azimuthal magnetic field for e4, e0 = 0.05 in Table 1 with θ0 = 0° and the SAA condition. |
| In the text | |
 |
Fig. 5 Dependence of |
| In the text | |
 |
Fig. 6 Azimuthal magnetic field for θ0 = 5°, a = (0,0,1), e4, e0 = 0.05, and the SAA (a) and ASA (b) boundary conditions. |
| In the text | |
 |
Fig. 7 Values for |
| In the text | |
 |
Fig. 8 Dependence of ω on CΩ for θ0 = 1° (blue) and θ0 = 0° (red) for |
| In the text | |
 |
Fig. 9 Azimuthal magnetic field for θ0 = 1° with the ASA boundary condition; α2Ω dynamo with |
| In the text | |
 |
Fig. 10 Azimuthal magnetic field for θ0 = 0° with the SAA boundary condition; α2Ω dynamo with |
| In the text | |
 |
Fig. 11 Azimuthal magnetic field for θ0 = 0° with e0 = 0.05, |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.