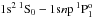| Issue |
A&A
Volume 592, August 2016
|
|
|---|---|---|
| Article Number | A135 | |
| Number of page(s) | 9 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201628484 | |
| Published online | 15 August 2016 | |
Scaling of collision strengths for highly-excited states of ions of the H- and He-like sequences⋆
1 Department of Physics, University of Strathclyde, Glasgow G4 0NG, UK
e-mail: luis.fernandez-menchero@drake.edu
2 Present address: Department of Physics and Astronomy, Drake University, 2507 University Avenue Des Moines, IA 50311, USA
3 Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Cambridge CB3 0WA, UK
Received: 10 March 2016
Accepted: 6 June 2016
Emission lines from highly-excited states (n ≥ 5) of H- and He-like ions have been detected in astrophysical sources and fusion plasmas. For such excited states, R-matrix or distorted wave calculations for electron-impact excitation are very limited, due to the large size of the atomic basis set needed to describe them. Calculations for n ≥ 6 are also not generally available. We study the behaviour of the electron-impact excitation collision strengths and effective collision strengths for the most important transitions used to model electron collision dominated astrophysical plasmas, solar, for example. We investigate the dependence on the relevant parameters: the principal quantum number n or the nuclear charge Z. We also estimate the importance of coupling to highly-excited states and the continuum by comparing the results of different sized calculations. We provide analytic formulae to calculate the electron-impact excitation collision strengths and effective collision strengths to highly-excited states (n ≥ 8) of H- and He-like ions. These extrapolated effective collision strengths can be used to interpret astrophysical and fusion plasma via collisional-radiative modelling.
Key words: atomic data / Sun: corona / techniques: spectroscopic
Tables of atomic data for Si xiii and S xv are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/592/A135
© ESO, 2016
1. Introduction
Spectral emission lines of H- and He-like ions have been used for diagnostics of both fusion and astrophysical plasmas for decades. Perhaps the most famous examples are the temperature and density diagnostics of the He-like ions in the X-rays, described by Gabriel & Jordan (1969). However, the status of the atomic data for these ions still requires improvement. As described below, atomic data for ions in these sequences are generally only available up to the principal quantum number n = 5. Atomic data for highly-excited levels are needed for a variety of reasons. First, lines from these levels (up to n = 10) have been observed in laboratory plasma (see, e.g. the compilations in the NIST database Kramida et al. 2013) and recently also in X-ray spectra of solar flares (see, e.g. Kepa et al. 2006). Second, transitions between highly-excited levels should be included for any appropriate collisional-radiative modelling of these ions. Third, even if in most astrophysical spectra lines from these levels are not readily visible, they do contribute to the X-ray pseudo-continuum, so they should be included in any spectral modelling.
Calculating atomic data for highly-excited levels is not a trivial task and has various limitations, since it requires a significant increase in the size of the atomic basis set. In Sect. 2 we review previous calculations for the electron-impact excitation of He- and H-like ions, and present the results of test calculations made with larger basis sets. These calculations are performed to see how well the extrapolated data agree with the calculated ones for higher n. In Sect. 3 we study the behaviour of the electron-impact excitation collision strengths and effective collision strengths for several kinds of transitions. These are the most common transitions that decay producing the lines observed in astrophysics. We also estimate the importance of coupling to highly-excited states and the continuum by comparing the results of differently sized distorted wave and R-matrix calculations. We then provide analytic formulae to calculate electron-impact excitation collision strengths to highly-excited states (n ≥ 8) of H- and He-like ions. This is done by extrapolating the results obtained with the R-matrix or distorted wave methods. Potentially, the method provides results up to n = ∞, although accuracy reduces as n increases. In Sect. 4 we compare the solar flare line intensities with those predicted by applying the extrapolation rules to the effective collision strengths. Finally, in Sect. 5 we summarise the main conclusions.
2. Atomic data
A number of calculations for the electron-impact excitation of ions of the H- and He-like sequences can be found in the literature. Authors have used a number of different methodologies and different configuration interaction (CI) and close coupling (CC) basis sets.
Whiteford et al. (2001) calculated electron-impact excitation effective collision strengths for He-like ions. Whiteford et al. (2001) included in the CI/CC basis set all the single-electron excitations up to principal quantum number n = 5 (49 fine-structure levels) and used the radiation-damped intermediate coupling frame transformation ICFT R-matrix method (Griffin et al. 1998). These data are the most rigorous and complete to date. They can be found in the UK APAP network database1, as well as in OPEN-ADAS2 and in the most recent version 8 (Del Zanna et al. 2015) of the CHIANTI database3.
There are other studies in the literature. Aggarwal & Keenan (2005) calculated electron-impact effective collision strengths for Ar16 + up to n = 5 using the Dirac R-matrix method (Norrington & Grant 1987). Chen et al. (2006) calculated Dirac R-matrix electron-impact excitation effective collision strengths for Ne8 + up to n = 5. Kimura et al. (2000) performed Dirac R-matrix calculations for the He-like ions S14 +, Ca18 + and Fe24 + up to n = 4.
In the H-like sequence, Ballance et al. (2003) performed a detailed study of hydrogenic ions from He+ to Ne9 + plus Fe25 +. Ballance et al. (2003) used a quite extensive basis set, including pseudostates. The basis set included all the spectroscopic terms up to n = 5 for all the ions except Ne9 +. For Ne9 + the basis set was extended up to n = 6. The pseudo-state terms included in the calculations varied for each ion.
Even though the above calculations are quite extensive, they are still insufficient for the modelling of highly-excited shells (n > 5), as noted in the introduction.
In the present work we have performed some test calculations with an extensive basis set up to n = 8. The calculations are focused on checking the validity of the extrapolation methods that we have developed, and discuss in the next section. As such, we do not include radiation damping of resonances. The target basis set includes all the possible l values for n = 1 − 6, and then up to 7g and 8f. We have performed both R-matrix and distorted wave calculations with the same basis set. The R-matrix suite of codes are described in Hummer et al. (1993) and Berrington et al. (1995). The calculation in the inner region was in LS coupling and included mass and Darwin relativistic energy corrections. The outer region calculation used the ICFT method (Griffin et al. 1998). The distorted wave calculations were carried-out using the autostructure program (Badnell 2011). The ICFT R-matrix and distorted wave calculations were carried out with the same atomic structure to estimate the effects of the resonances and coupling in general.
To estimate the collision strengths for higher shells (n = 8 − 12) we performed a different distorted wave calculation. In this second calculation we used a configuration basis set consisting of 1s2 and 1snl for n = 8 − 12 and l up to 8h, 9h, 10g, 11f and 12d, that is, we neglect configurations with n = 2 − 7. Thus, although we automatically have CI between these more highly-excited n-shells, there is no mixing with lower ones, save for the ground. The atomic structure is oversimplified in order to get a description of the highly-excited states which becomes increasingly demanding when retaining the full CI expansion. This calculation has a poorer atomic structure so it is expected that these results will not be of such high accuracy. It has been performed only to check if such an oversimplified atomic structure can give results for the effective collision strengths with an error which is acceptable for plasma modelling, and to compare that error with the one arising from the extrapolation of results obtained using the (smaller) full-CI expansion.
3. Extrapolation rules
The scattering calculations provide the collision strengths Ω as a function of the incident electron energy. The collision strengths are extended to high energies by interpolation using the appropriate high-energy limits in the Burgess & Tully (1992) scaled domain. The infinite energy limit points are calculated with autostructure. The temperature-dependent effective collisions strength Υ are calculated by convoluting these collision strengths with a Maxwellian electron velocity distribution.
The behaviour of the collision strengths Ω and effective collision strengths Υ for highly-excited levels follows the semi-empirical formula: 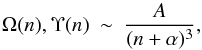 (1)where n is the principal quantum number and A and α are parameters to be determined. Usually α is small and can be set to zero. The formula 1 is usually a good description for highly-excited states, where the atom can be considered as a Rydberg one, meaning that for n at least two units more than the last atomic shell occupied by any inactive core electrons of the ion.
(1)where n is the principal quantum number and A and α are parameters to be determined. Usually α is small and can be set to zero. The formula 1 is usually a good description for highly-excited states, where the atom can be considered as a Rydberg one, meaning that for n at least two units more than the last atomic shell occupied by any inactive core electrons of the ion.
We used three models to determine the parameters of the formula 1:
-
Model 1:
least-squares fit, including all the calculated values ofΩ and n.
-
Model 2:
two point extrapolation, calculate A and α from the values of Ω and n of the last two points calculated.
-
Model 3:
one point extrapolation, fix α = 0 and calculate A from the value of Ω and n of the last point calculated.
We have compared the results of these extrapolation Models with those obtained from explicit R-matrix and distorted wave test calculations which we have performed. In the following sections we discuss the different cases.
3.1. Dipole-allowed transitions
These transitions are between states with opposite parity and with changes in total angular momenta ΔJ = 0,1 (and J = 0 → 0 forbidden) that is to say, electric dipole. The collision strength diverges logarithmically as the collision energy tends to infinity. (Burgess & Tully 1992). In general, the contribution from resonances will be small compared to the background, so distorted wave and R-matrix methods produce similar results for the effective collision strengths.
Figure 1 shows the calculated collision strengths for the electric dipole transitions 1s21S0 − 1snp 1P1 of the moderately-charged Si12 + and the highly-charged Fe24 + ions. We plot both the results of the R-matrix and distorted wave methods. Both calculations were carried out with the same atomic structure, with a somewhat large CI/CC expansion, up to the atomic shell n = 8.
 |
Fig. 1 Electron-impact excitation collision strengths for the electric dipole transition 1s21S0 − 1snp 1P1 of the ions Si12 + and Fe24 +. Curved lines: R-matrix; ⋄: distorted wave calculation. |
At low temperatures, the effects of the resonances is not significant. This is expected for strong dipole transitions, where the background is large in comparison. As we pointed out in Fernández-Menchero et al. (2015), the R-matrix calculations can not guarantee accuracy at very low temperatures, of the order of the energy of the first excited level. In fact, uncertainties associated with the position of the resonances can reach 100% for such low temperatures. However, for electron collision dominated plasmas, for example solar, the ions are mainly formed near the peak abundance temperature (vertical lines in the plots in Fig. 2), and at these temperatures the position of the resonances has a negligible effect on the effective collision strength.
 |
Fig. 2 Electron-impact excitation effective collision strengths for the electric dipole transition 1s21S0 − 1snp 1P1 of the ions Si12 + and Fe24 +. Curved lines: R-matrix; ⋄: distorted wave calculation basis n = 1 − 8; °: distorted wave calculation basis n = 8 − 12; vertical line: peak abundance temperature for electron collisional plasmas (Mazzotta et al. 1998). |
Figure 2 shows the Maxwell-integrated effective collision strengths for the same transitions and ions. The difference in the Υ between both calculations for the transition from the ground level to 8p is around 15%.
 |
Fig. 3 Electron-impact excitation effective collision strengths (× n3) for the electric dipole transition 1s21S0 − 1snp 1P1 of the ions Si12 + and Fe24 + versus the principal quantum number n around peak abundance temperature. ×: R-matrix results; ⋄: distorted wave results with basis set n = 1 − 8; °: distorted wave results with basis set n = 8 − 12; solid line: least-squares fit using points n = 2 − 5; dashed line: extrapolation using the last two points; dotted line: extrapolation using the last point; see text. |
Figure 3 shows the behaviour of the effective collision strengths Υ with respect to the principal quantum number n at the peak abundance temperature. We compare the extrapolations from n = 5 with the calculated values for the three models. For the lower-charged ion, Si12 +, the disagreement between the R-matrix and distorted wave results increases more rapidly for higher n, reaching 20% at n = 8. This is due to stronger coupling between the more highly-excited states included in the close-coupling expansion. However, we note that the R-matrix calculation cannot accurately describe transitions to the highest states included in the CI/CC expansion (Fernández-Menchero et al. 2015). For Fe24 +, the R-matrix and distorted wave results agree better with each other, to 10% at n = 8, as coupling decreases with increasing charge.
Table 1 shows the different extrapolation parameters calculated with the three methods for Si12 +, and choosing different reference points n0 for the extrapolation. The linear fit is performed taking into account all the points between n = 2 and n0. The two-point model takes the values of Υ(n) for n = n0 − 1 and n0 and calculates the parameters A and α through a two-equation and two-unknown system (1). Finally, the one-point model uses Υ(n0) to calculate A and sets α = 0. Figure 4 displays the calculated analytic functions corresponding to each of the three models. The predicted extrapolation curves with the two-point model vary considerably in terms of the reference point n0, by more than 30%. They are influenced too much by the smaller values of n, which have yet to reach their asymptotic form. We see a similar variation in the two-point model. On the other hand, the one-point extrapolation gives more stable results. The predicted value of A changes by just 10% with the different choices of n0.
With the linear fit it is necessary to include many points to obtain acceptable statistics and to reduce the associated error of kind β. In a linear least-squares fit, an acceptable number of points is around twelve to get a β error under 20%. The computation cost of the linear fit is also larger. For such a small set of points, the linear fit is not an appropriate model. Thus, for strong dipole electric transitions we recommend use of the one-point extrapolation.
The last calculated n-shell (n = 8) is not a good reference point for the extrapolation due to the lack of convergence of the CI and CC expansions, compared to n ≤ 7. The parameters A and α calculated with the two-point model are very similar using the second and the third last point as reference, and they are also with α closest to zero. These two curves for n0 = 6 and n0 = 7 shown in Fig. 4 are the best extrapolation models for this type of transition, if such data is available. If not, for smaller values of n0, the one-point extrapolation is the best model.
Fitting parameters for the extrapolation of the Υ at high-n for the dipole electric transition of Si12 +1s21S0 − 1snp 1P1 at a temperature of T = 3.4 × 106 K, for different extrapolation reference points n0.
 |
Fig. 4 Extrapolation curves for the Υ × n3 displayed in Fig. 3, taking different extrapolation points n0. ×: R-matrix results; ⋄: distorted wave results. |
3.2. Born-allowed transitions
For non-dipole Born-allowed transitions the collision strength tends to a constant value as the collision energy tends to infinity, given by the plane-wave Born 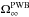 (Burgess & Tully 1992). The
(Burgess & Tully 1992). The 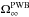 is zero for double-electron jumps and spin-change transitions, in the absence of mixing. In the intermediate coupling scheme (IC), most transitions will be Born-allowed or dipole-allowed through configuration and/or spin-orbit mixing.
is zero for double-electron jumps and spin-change transitions, in the absence of mixing. In the intermediate coupling scheme (IC), most transitions will be Born-allowed or dipole-allowed through configuration and/or spin-orbit mixing.
Figure 5 shows the effective collision strengths for the one-photon optically forbidden transitions 1s21S0 − 1sns 1S0 for the ions Si12 + and Fe24 +. This kind of transition has a very weak background collision strength at all energies, so the enhancement due to resonances is large. This effect is largest at low temperatures; the Υ calculated using the distorted wave method are a considerable underestimate compared to those obtained with the R-matrix method. The underestimation for the lowest temperatures (~105 K) and lowest excited states can reach a factor of between two and ten. This effect is reduced progressively at higher temperatures and for more highly excited states. At the peak abundance temperature, the resonance enhancement is reasonably small, reduced to 10% for a moderately-charged or a highly-charged ion, see Fig. 5.
 |
Fig. 5 Electron-impact excitation effective collision strengths for the Born transition 1s21S0 − 1sns 1S0 of the ions Si12 + and Fe24 +. Curved line: R-matrix; ⋄: distorted wave calculation basis n = 1 − 8; °: distorted wave calculation basis n = 8 − 12; vertical line: peak abundance temperature for electron collisional plasmas (Mazzotta et al. 1998). |
Figure 6 shows the comparison between the Υ calculated with the R-matrix method, with the distorted wave method using both basis sets, and for the three extrapolation models, all at the peak abundance temperature. For n ≥ 4, the R-matrix and distorted wave results agree below 10%.
 |
Fig. 6 Electron-impact excitation effective collision strengths (× n3) for the Born transition 1s21S0 − 1sns 1S0 of the ions Si12 + and Fe24 + versus the principal quantum number n around peak abundance temperature. ×: R-matrix results; ⋄: distorted wave results with basis set n = 1 − 8; °: distorted wave results with basis set n = 8 − 12; solid line: least-squares fit using points n = 2 − 5; dashed line: extrapolation using the last two points; dotted line: extrapolation using the last point; see text. |
To test the validity of the extrapolation rules for this type of transition we show again in Table 2 the calculated parameters for the three methods with different reference points n0 for Si12 +. Fig. 7 shows the analytic curves.
Fitting parameters for the extrapolation of the Υ at high-n for the dipole electric transition of Si12 +1s21S0 − 1sns 1S0 at a temperature of T = 3.4 × 106 K, for different extrapolation reference points n0.
 |
Fig. 7 Extrapolation curves for the Υ × n3 displayed in Fig. 6, taking different extrapolation points n0. ×: R-matrix results; ⋄: distorted wave results. |
For this transition the two-point model gives very similar results for extrapolation with n0 = 5,6,7. The two-point model with n0 = 8 is slightly different, but the last point of the calculation should not be considered a good reference for the extrapolation. The error of the two-point model extrapolation from n0 = 5,6,7 with respect to the calculated R-matrix data is less than 10%. For Born-allowed transitions, we recommend a two-point extrapolation model as the most accurate. The α parameters calculated with the two-point model are also close to zero for n0 = 6,7, and so here the one-point extrapolation also gives accurate results.
In general, the calculations with the oversimplified atomic structure give worse results than the extrapolated ones. We do not recommend such simplifications at all for estimation purposes.
3.3. Forbidden transitions
These transitions are characterised by zero limit points, electric dipole and plane-wave Born (Burgess & Tully 1992). They can arise for spin-changing and/or multiple-electron jump transitions. They are infrequent because of configuration and spin-orbit mixing. For high impact energies, the collision strength decays with a power law Ω ~ E− γ, with γ close to two. This rapid decay makes the resonance enhancement large, particularly at low temperatures.
Figure 8 shows the effective collision strengths for the pure spin-change transition 1s21S0 − 1snp 3P0 for the ions Si12 + and Fe24 +. As expected, at low temperatures there are differences up to a factor of two between distorted wave and R-matrix due to the resonances.
 |
Fig. 8 Electron-impact excitation effective collision strengths for the forbidden transition 1s21S0 − 1snp 3P0 of the ions Si12 + and Fe24 +. Curved lines: R-matrix; ⋄: distorted wave calculation basis n = 1 − 8; °: distorted wave calculation basis n = 8 − 12; vertical line: peak abundance temperature for electron collisional plasmas (Mazzotta et al. 1998). |
Figure 9 shows the comparison between the Υ calculated with the R-matrix method, the distorted wave methods with both basis sets, and the three extrapolation models, at the peak abundance temperature. In this case, the models fit quite well the data for n = 6 − 8. For these transitions, the value of the parameter α is quite large, and the results of models type 2 and 3 differ significantly. The calculations with the simplified atomic structure again poorly reproduce the data.
 |
Fig. 9 Electron-impact excitation effective collision strengths (× n3) for the forbidden transition 1s21S0 − 1snp 3P0 of the ions Si12 + and Fe24 + versus the principal quantum number n around peak abundance temperature. ×: R-matrix results; ⋄: distorted wave results with basis set n = 1 − 8; °: distorted wave results with basis set n = 8 − 12; solid line: least-squares fit using points n = 2 − 5; dashed line: extrapolation using the last two points; dotted line: extrapolation using the last point; see text. |
We show again in Table 3 the different extrapolation parameters calculated with the three methods and different reference point n0. Figure 9 shows the extrapolation curves. Calculated values for the parameters A and α are quite similar for the different reference points n0 = 5,6,7 if the same model is used, one or two-point. On the other hand, if we compare the results obtained with same n0 but different models, they are quite different. The one-point model does not correctly reproduce the behaviour of the R-matrix results for high-n. For this type of transition we recommend a two-point model.
Fitting parameters for the extrapolation of the Υ at high-n for the dipole electric transition of Si12 +1s21S0 − 1snp 3P0 at a temperature of T = 3.4 × 106 K, for different extrapolation reference points n0.
 |
Fig. 10 Extrapolation curves for the Υ displayed in Fig. 9, taking different extrapolation points n0. ×: R-matrix results. |
3.4. Low-charged ions
The n-3 behaviour of the collision strengths is fulfilled if we are in the limit of Rydberg atom, that is when the interaction of the core with the active electron can be considered a one-body Coulomb one. For lower-charged atoms the electron-electron interaction is of the same order as the nucleus-electron one. For such ions this Rydberg atom limit is reached at a higher value of the principal quantum number n. In principle, the above extrapolation rules should work in a lower-charged ion, but the reference point n0 should be high enough for it to be considered a Rydberg atom. This means that reference data for extrapolation are required up to n ≈ 8 − 10. This is a rather large R-matrix calculation, because of the large box-size. In addition, the coupling with the continuum increases as the charge decreases. So a good quality calculation for high-n for a low-charged ion must include pseudostates in the CI/CC expansions.
Figure 11 shows the effective collision strengths for dipole and Born allowed transitions of C4 +. The background collision strength falls off as z-2 while, initially, the resonance strength is independent of z, although at sufficiently high charge radiation damping usually starts to reduce the resonance contribution. So in C4 + the resonance enhancement of the effective collision strengths at low temperatures is seen to be relatively smaller than for Si12 + and Fe24 +.
 |
Fig. 11 Electron-impact excitation effective collision strengths for dipole allowed and Born transitions |
The effective collision strengths for the last n-shells included in the basis set show irregular behaviour. This is caused by the loss of quality for the description of the highest excited states. In low-charged ions the inaccuracy in the description of the atomic structure is larger due to stronger coupling with more highly-excited bound states and the continuum, which we neglect. For the present test calculations we did not include pseudostates in the description of C4 + atomic structure or the close-coupling expansion. Thus, we do not recommend using this data in preference to R-matrix with pseudo-states data, rather it is a guide to extrapolating data in low-charge ions. The uncertainty associated with an inaccurate atomic structure due to, for example, the lack of pseudostates in the case of a low-charged ion, generates a much larger error than that associated with the use of an extrapolation formula.
Experimental and theoretical ratios (erg) for Si xiii.
Experimental and theoretical ratios (erg) for S xv.
3.5. Other sequences
As explained above, the behaviour of the collision strengths with respect to the quantum number tends to the form given by (1) when the active electron is highly enough excited, so the ion can be considered a Rydberg one. We need to consider transitions between Rydberg states with a difference in n-values between the active electron and the highest core-electron of at least two. For low-charged ions, this difference in n may be necessary to be increased to up to four. In H- and He-like sequences the ~n-3 behaviour applies starting from n = 5, as shown before. For the Li- and Be-like sequences the starting shell is n = 6 and for Na- and K-like the n = 7.
As the number of electrons increases, the size of the basis set required to obtain accurate results for the excited shells increases significantly. The complication of the core calculations increases and the application of the extrapolation rules becomes impossible. The present extrapolations provide good estimates only for the H- and He-like sequences. For other sequences they may not be valid, and cannot be easily tested.
4. Comparisons with observations
In Tables 4 and 5 we show a comparison of the line ratios calculated with the extrapolation rules of the present work with the observed ones of Kepa et al. (2006) for the soft X-rays detected by RESIK coming from highly-excited states of Si xiii and S xv in solar flares. The transitions involved in the line ratios are dipole allowed.
We have used as our starting point for the extrapolation calculations the n = 5R-matrix data of Whiteford et al. (2001). We have used a two-point extrapolation model and a reference point n0 = 5, and we have obtained extrapolated Υ from the ground state up to n = 10 the extrapolated values of energies, radiative parameters gf, and electron-impact excitation effective collision strengths Υ obtained with the extrapolation rules described here are available at the CDS. The modelling has been carried out by converting these data into CHIANTI Del Zanna et al. (2015) format and using the CHIANTI population solver to obtain the level populations.
Our theoretical line ratios are quite close (within 10% for most cases) with those estimated by Kepa et al. (2006). Regarding the observed values, Kepa et al. (2006) report a range. The lower values correspond to the peak and gradual phase of the flares. They are within the theoretical values in the 5 − 10 MK range. The higher values, instead, correspond to the early impulsive phase, and are in most cases outside the range of the theoretical values.
5. Discussion and conclusions
We carried out several new calculations, both R-matix and distorted wave, for the electron-impact excitation of H- and He-like ions. We have shown the dependence of the effective collision strengths Υ with respect to the principal quantum number n for several transition types of some benchmark ions of the He-like isoelectronic sequence. We tested three models to reproduce the behaviour of the Υ(n) and extrapolate them to more highly-excited states.
In general, the extrapolation rules do not give such accurate values for the effective collision strengths as explicit calculations do; instead, they give an approximation that can be used for estimation purposes in modelling. Clearly, it is first necessary to have a good starting calculation before applying the extrapolations to the data. We note that R-matrix results become increasingly uncertain for the highest energy states included in the CI and CC expansions of the target, due to their lack of convergence (Fernández-Menchero et al. 2015). The description of the atomic structure, energy levels and radiative data, and the corresponding effective collision strengths, increasingly lose accuracy as we approach the last states included in the basis expansions. The same happens with the distorted wave calculations. Even when the distorted wave results are not affected by the coupling or resonances, which are included in the R-matrix ones, the description of the atomic structure is its main limitation. In consequence, such calculations may not give more accurate results for high-n than the extrapolation rules combined with accurate calculations for lower, but sufficiently excited, states.
Among the three extrapolation models considered, we recommend the second one. The Model 2 two-point extrapolation provides results that are closer to the R-matrix data, and reproduces the behaviour at high-n. Nevertheless it is not a completely general rule, and each particular transition type should be analysed to check which is the most accurate extrapolation method for the ion. We do not recommend Model 1 the least-squares fitting for several reasons. First, having just four points is not enough for a good-quality fitting. Second, the first data points n = 2,3 have not yet reached the required n-3 behaviour. This occurs because they can not be considered Rydberg levels: they interact more strongly with the core and resonances play a larger role for excitation to these shells. Finally, the fitting method requires a considerably larger computational effort to obtain a result that may be worse than the simpler methods.
The Model 3 one-point extrapolation gives, in general, a poorer estimate than the two-point one, and the computational work is not substantially reduced. On the other hand, sometimes the parameters estimated with the one-point rule are more stable with respect to the reference point n0 than the two-point one, for example, the dipole transitions shown here.
Due to the inherent uncertainty in data for the most highly-excited states, we do not recommend extrapolating the Υ from the last n-shell, but suggest dropping form the extrapolation the last one or two n-values. Also, the n-3 behaviour applies only from a certain excited shell. The extrapolation has to start from a level when the atom can be considered as a Rydberg one. That is at least approximately two shells higher than the last occupied one (n = 3 for H- and He-like sequences).
We also do not recommend the use of models with an oversimplified atomic structure so as to reach high-n shells. The extrapolation from an accurate calculation to lower-n provides in general a better estimate than a larger explicit calculation with a poorer atomic structure.
As an example application, we have compared lines ratios obtained with the presented extrapolation-rule Model 2 with observations of X-rays by RESIK. We obtain good agreement with the observed Si xiii and S xv ratios during the peak phase of solar flares, but the values during the impulsive phase are still outside the theoretical range. It is expected that during the impulsive phase non-equilibrium effects are present. We investigated whether a non-Maxwellian distribution such as a κ-distribution was able to increase the ratios, but did not find significant increases. We are currently investigating other possible causes.
For photoionised plasmas the ions exist at temperatures lower than the peak abundance in an electron collision
dominated plasma. At these lower temperatures, the Υ are affected more by resonance enhancement, and perhaps radiation damping thereof, and can depend greatly on the position of these resonances, which are determined by the atomic structure.
Resonance effects can cause the Υ to deviate from the n-3 rule. The extrapolation rules should therefore only be applied starting from a higher excited shell, so these effects are minimised. This occurs even if the calculations are perfectly accurate at low temperatures. In these case, we suggest to start the extrapolation at least from four shells above the last occupied (n = 5 for H- and He-like sequences).
We estimate that the accuracy of the extrapolation Model 2 is approximately 20% for all transition types of moderately- and highly-charged ions, and approximately 50% for low-charged ions. This estimate considers the core calculations to be perfect and the extrapolation carried out from a shell where the ion can be considered as Rydberg. The inaccuracies in the core calculations could lead to larger errors in some cases, especially for low-charged ions and/or low temperatures.
Acknowledgments
This work was funded by STFC (UK) through the University of Strathclyde UK APAP network grant ST/J000892/1 and the University of Cambridge DAMTP astrophysics consolidated grant. Luis Fernández-Menchero thanks the National Science Foundation (USA) for the grant PHY-1520970.
References
- Aggarwal, K. M., & Keenan, F. P. 2005, A&A, 441, 831 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Badnell, N. R. 2011, Comput. Phys. Commun., 182, 1528 [NASA ADS] [CrossRef] [Google Scholar]
- Ballance, C. P., Badnell, N. R., & Smyth, E. S. 2003, J. Phys. B, 36, 3707 [Google Scholar]
- Berrington, K. A., Eissner, W. B., & Norrington, P. H. 1995, Comput. Phys. Commun., 92, 290 [NASA ADS] [CrossRef] [Google Scholar]
- Burgess, A., & Tully, J. A. 1992, A&A, 254, 436 [NASA ADS] [Google Scholar]
- Chen, G. X., Smith, R. K., Kirby, K., Brickhouse, N. S., & Wargelin, B. J. 2006, Phys. Rev. A, 74, 042709 [NASA ADS] [CrossRef] [Google Scholar]
- Del Zanna, G., Dere, K. P., Young, P. R., Landi, E., & Mason, H. E. 2015, A&A, 582, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fernández-Menchero, L., Del Zanna, G., & Badnell, N. R. 2015, MNRAS, 450, 4174 [NASA ADS] [CrossRef] [Google Scholar]
- Gabriel, A. H., & Jordan, C. 1969, MNRAS, 145, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Griffin, D. C., Badnell, N. R., & Pindzola, M. S. 1998, J. Phys. B, 31, 3713 [Google Scholar]
- Hummer, D. G., Berrington, K. A., Eissner, W., et al. 1993, A&A, 279, 298 [NASA ADS] [Google Scholar]
- Kepa, A., Sylwester, J., Sylwester, B., et al. 2006, Adv. Space Res., 38, 1538 [Google Scholar]
- Kimura, E., Nakazaki, S., Berrington, K. A., & Norrington, P. H. 2000, J. Phys B, 33, 3449 [Google Scholar]
- Kramida, A., Yu. Ralchenko, Reader, J., & and NIST ASD Team 2013, NIST Atomic Spectra Database (ver. 5.1), http://physics.nist.gov/asd [2014, July 30] [Google Scholar]
- Mazzotta, P., Mazzitelli, G., Colafrancesco, S., & Vittorio, N. 1998, A&AS, 133, 403 [Google Scholar]
- Norrington, P. H., & Grant, I. P. 1987, J. Phys. B, 20, 4869 [NASA ADS] [CrossRef] [Google Scholar]
- Whiteford, A. D., Badnell, N. R., Ballance, C. P., et al. 2001, J. Phys. B, 34, 3179 [Google Scholar]
All Tables
Fitting parameters for the extrapolation of the Υ at high-n for the dipole electric transition of Si12 +1s21S0 − 1snp 1P1 at a temperature of T = 3.4 × 106 K, for different extrapolation reference points n0.
Fitting parameters for the extrapolation of the Υ at high-n for the dipole electric transition of Si12 +1s21S0 − 1sns 1S0 at a temperature of T = 3.4 × 106 K, for different extrapolation reference points n0.
Fitting parameters for the extrapolation of the Υ at high-n for the dipole electric transition of Si12 +1s21S0 − 1snp 3P0 at a temperature of T = 3.4 × 106 K, for different extrapolation reference points n0.
All Figures
 |
Fig. 1 Electron-impact excitation collision strengths for the electric dipole transition 1s21S0 − 1snp 1P1 of the ions Si12 + and Fe24 +. Curved lines: R-matrix; ⋄: distorted wave calculation. |
| In the text | |
 |
Fig. 2 Electron-impact excitation effective collision strengths for the electric dipole transition 1s21S0 − 1snp 1P1 of the ions Si12 + and Fe24 +. Curved lines: R-matrix; ⋄: distorted wave calculation basis n = 1 − 8; °: distorted wave calculation basis n = 8 − 12; vertical line: peak abundance temperature for electron collisional plasmas (Mazzotta et al. 1998). |
| In the text | |
 |
Fig. 3 Electron-impact excitation effective collision strengths (× n3) for the electric dipole transition 1s21S0 − 1snp 1P1 of the ions Si12 + and Fe24 + versus the principal quantum number n around peak abundance temperature. ×: R-matrix results; ⋄: distorted wave results with basis set n = 1 − 8; °: distorted wave results with basis set n = 8 − 12; solid line: least-squares fit using points n = 2 − 5; dashed line: extrapolation using the last two points; dotted line: extrapolation using the last point; see text. |
| In the text | |
 |
Fig. 4 Extrapolation curves for the Υ × n3 displayed in Fig. 3, taking different extrapolation points n0. ×: R-matrix results; ⋄: distorted wave results. |
| In the text | |
 |
Fig. 5 Electron-impact excitation effective collision strengths for the Born transition 1s21S0 − 1sns 1S0 of the ions Si12 + and Fe24 +. Curved line: R-matrix; ⋄: distorted wave calculation basis n = 1 − 8; °: distorted wave calculation basis n = 8 − 12; vertical line: peak abundance temperature for electron collisional plasmas (Mazzotta et al. 1998). |
| In the text | |
 |
Fig. 6 Electron-impact excitation effective collision strengths (× n3) for the Born transition 1s21S0 − 1sns 1S0 of the ions Si12 + and Fe24 + versus the principal quantum number n around peak abundance temperature. ×: R-matrix results; ⋄: distorted wave results with basis set n = 1 − 8; °: distorted wave results with basis set n = 8 − 12; solid line: least-squares fit using points n = 2 − 5; dashed line: extrapolation using the last two points; dotted line: extrapolation using the last point; see text. |
| In the text | |
 |
Fig. 7 Extrapolation curves for the Υ × n3 displayed in Fig. 6, taking different extrapolation points n0. ×: R-matrix results; ⋄: distorted wave results. |
| In the text | |
 |
Fig. 8 Electron-impact excitation effective collision strengths for the forbidden transition 1s21S0 − 1snp 3P0 of the ions Si12 + and Fe24 +. Curved lines: R-matrix; ⋄: distorted wave calculation basis n = 1 − 8; °: distorted wave calculation basis n = 8 − 12; vertical line: peak abundance temperature for electron collisional plasmas (Mazzotta et al. 1998). |
| In the text | |
 |
Fig. 9 Electron-impact excitation effective collision strengths (× n3) for the forbidden transition 1s21S0 − 1snp 3P0 of the ions Si12 + and Fe24 + versus the principal quantum number n around peak abundance temperature. ×: R-matrix results; ⋄: distorted wave results with basis set n = 1 − 8; °: distorted wave results with basis set n = 8 − 12; solid line: least-squares fit using points n = 2 − 5; dashed line: extrapolation using the last two points; dotted line: extrapolation using the last point; see text. |
| In the text | |
 |
Fig. 10 Extrapolation curves for the Υ displayed in Fig. 9, taking different extrapolation points n0. ×: R-matrix results. |
| In the text | |
 |
Fig. 11 Electron-impact excitation effective collision strengths for dipole allowed and Born transitions |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.