| Issue |
A&A
Volume 592, August 2016
|
|
|---|---|---|
| Article Number | A47 | |
| Number of page(s) | 10 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201527819 | |
| Published online | 20 July 2016 | |
Constraining the escape fraction of ionizing photons from H ii regions within NGC 300: A concept paper⋆,⋆⋆
1 Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA
e-mail: fniederhofer@stsci.edu
2 Universitäts-Sternwarte München, Scheinerstraße 1, 81679 München, Germany
3 Excellence Cluster Origin and Structure of the Universe, Boltzmannstr. 2, 85748 Garching bei München, Germany
4 European Southern Observatory, Karl-Schwarzschild-Straße 2, 85748 Garching bei München, Germany
5 Astrophysics Research Institute, Liverpool John Moores University, 146 Brownlow Hill, Liverpool L3 5RF, UK
Received: 24 November 2015
Accepted: 31 May 2016
Using broadband photometry from the Hubble Space Telescope in combination with Very Large Telescope narrowband Hα observations of the nearby spiral galaxy NGC 300, we explore a method for estimating the escape fractions of hydrogen-ionizing photons from H ii regions within this galaxy. Our goal in this concept study is to evaluate the spectral types of the most massive stars using the broadband data and estimating their ionizing photon output with the help of stellar atmosphere models. A comparison with the Hα flux that gives the amount of ionized gas in the H ii region provides a measure of the escape fraction of ionizing photons from that region. We performed some tests with a number of synthetic young clusters with varying parameters to assess the reliability of the method. However, we found that the derived stellar spectral types and consequently the expected ionizing photon luminosity of a region is highly uncertain. The tests also show that on one hand we tended to overestimate the integrated photon output of a region for young ages and low numbers of stars, and on the other hand we mostly underestimated the combined ionizing luminosity for a large stellar number and older cluster ages. We conclude that the proposed method of using stellar broadband photometry to infer the leakage of ionizing photons from H ii regions is highly uncertain and dominated by the errors of the resulting stellar spectral types. Therefore this method is not suitable. Stellar spectra are needed to reliably determine the stellar types and escape fractions. Studies to this end have been carried out for the Magellanic Clouds.
Key words: stars: massive / HII regions / galaxies: individual: NGC 300 / galaxies: ISM
Based on observations made with the NASA/ESA Hubble Space Telescope, and obtained from the Hubble Legacy Archive, which is a collaboration between the Space Telescope Science Institute (STScI/NASA), the Space Telescope European Coordinating Facility (ST-ECF/ESA) and the Canadian Astronomy Data Centre (CADC/NRC/CSA).
© ESO, 2016
1. Introduction
Massive stars are the main source of radiation with energies high enough to ionize neutral H atoms. Most of this Lyman-continuum (LyC) emission is absorbed very quickly by neutral gas, thereby heating the surrounding interstellar medium (ISM). However, some parts of the created H ii region might be optically thin, and a certain fraction of the ionizing radiation eventually escapes into the diffuse medium of the galaxy or into the intergalactic medium (IGM). The escape fraction of ionizing photons, fesc, affects the energy budget of the ISM as well as the evolution of a galaxy.
It is not possible to directly determine fesc because any LyC radiation that is able to escape its parent system will be absorbed by the ISM of the Milky Way disk. For this reason, several observational studies used various methods and techniques to estimate the escape fraction of H ii regions or entire galaxies. Leitherer et al. (1995) measured the redshifted LyC flux of a sample of starburst galaxies (z > 0.015) that is not absorbed by our Galaxy to infer fesc. They found that the leakage of ionizing photons from these galaxies is below 3%. Similar results for moderate redshifts (z < 1.5) are found, for example, by Siana et al. (2010), Leitet et al. (2013) and, very recently, Rutkowsky et al. (2016).
Pellegrini et al. (2012) used the method of ionization-parameter mapping to determine the optical depth of H ii regions in the Large and Small Magellanic Cloud (LMC and SMC). Radiation-bound regions are characterized by transition regions in their ionization structure and can be measured by emission line ratios. Pellegrini et al. (2012) used the [S ii] to [O iii] ratio for their analysis. They found that the most luminous H ii regions are optically thin to LyC radiation and that regions with low gas column density and irregular shape tend to have higher escape fractions. The global fraction of ionizing photons that are leaving the Magellanic Clouds are determined to be between 10 and 20%. Zastrow et al. (2013) mapped the ionization structure of nearby dwarf starburst galaxies to analyze their amount of escaping ionizing radiation. Some galaxies in their sample show evidence for LyC photons leaking in a preferred limited direction.
Another method for inferring the escape fraction of H ii regions in nearby galaxies includes the analysis of the high-mass stars within the regions. With the knowledge of the spectral types of the stars responsible for the ionizing radiation, it is possible to estimate the expected total ionizing photon output Q0 of these stars using theoretical atmosphere grids. A comparison with the total amount of the ionized gas (NH ii) in the surrounding regions of these stars, using Hα imaging, for example, then allows for an estimate of fesc. Oey & Kennicutt (1997) applied this method to H ii regions within the LMC using available spectral classifications of O-type stars. Their analysis shows that a considerable fraction of the studied regions is optically thin to ionizing radiation with escape fractions of up to 50%. This work has been revised by Voges et al. (2008). Using newer stellar atmosphere models (e.g., from Smith et al. 2002), they found, in contrast to Oey & Kennicutt (1997), that the majority of the H ii regions in the LMC is radiation bounded. In a similar work, Doran et al. (2013) estimated the escape fraction of 30 Doradus to be between 0 and 60%.
In this paper, we examine a similar approach to constrain the escape fraction from individual H ii regions within the nearly face-on spiral galaxy NGC 300. Our method is based on inferring the parameters of the hottest stars within the emission nebulae with the help of broadband photometric data to determine whether photometric classification is accurate enough. The implication is that if this is the case, the method can be applied to many nearby galaxies without the need of time-consuming spectroscopic observations. It is expected that the escape fraction from Hii regions varies within galaxies. As the gas densities increase toward the centers, regions in the inner parts of galaxies may have lower escape fractions locally than regions in the outer parts. Similarly, in the outskirts the chances are highest that ionizing photons can escape the galaxy, so that young clusters away from the central regions may preferentially contribute to the photons ionizing the intergalactic medium. Conroy & Kratter (2012) adopted a similar idea and proposed massive runaway stars which escape the high-density regions and enhance fesc from galaxies in the early Universe.
For the method described in this paper, we used archival photometric data from the Hubble Space Telescope (HST) in the filters F475W, F606W, and F814W, taken with the Advanced Camera for Surveys (Dalcanton et al. 2009; Gogarten et al. 2010). Additionally, we used narrowband Hα images observed at the Very Large Telescope (VLT) with the FORS2 instrument (Bresolin et al. 2009) to estimate the amount of ionized gas.
The structure of the paper is the following: in Sect. 2 we describe the observations and the data reduction procedure. The method used to derive the escape fractions and the results are explained in Sect. 3. The discussion and final conclusions are presented in Sect. 4.
2. Observations and data reduction
In this section we describe the data sets that we used to determine the escape fraction of a sample of H ii regions within NGC 300. The first set comprises photometric broadband data in three filters taken with HST. We used this photometry to obtain the temperatures and ionizing fluxes Q0 of the stars in the H ii regions. The second data set consists of narrowband Hα images taken with the VLT/FORS2 instrument. The Balmer line flux is a measure of the amount of ionizing stellar photons that are absorbed by the surrounding material.
2.1. Hubble dataset
The broadband photometric data of NGC 300 were taken with the Advanced Camera for Surveys (ACS) onboard the HST. The galaxy was observed November 08−11 2006 as part of the ACS Nearby Galaxy Survey Treasury (ANGST) program (Dalcanton et al. 2009). Three filters were used to observe NGC 300: F475W, F606W, and F815W. We used three slightly overlapping fields that cover a radial strip of NGC 300 extending from the northwest to the center of the galaxy (see Figs. 1 and 2 in Gogarten et al. 2010). Each of these fields covers an area of ~3 8 × 3
8 × 3 8. They are referred to as Wide 1, Wide 2, and Wide 3 (going from the outskirts to the center). The pixel scale of the ACS is 0
8. They are referred to as Wide 1, Wide 2, and Wide 3 (going from the outskirts to the center). The pixel scale of the ACS is 0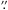 05 per pixel, corresponding to ~0.47 pc at the distance of NGC 300. We assumed a distance of 1.93 Mpc (Bresolin et al. 2005). For details of the data reduction see Dalcanton et al. (2009), and Gogarten et al. (2010) for a description of the photometry and its use in constraining the star formation history (SFH) of NGC 300. We used the fully reduced photometric tables that are available for the public on the ANGST website1.
05 per pixel, corresponding to ~0.47 pc at the distance of NGC 300. We assumed a distance of 1.93 Mpc (Bresolin et al. 2005). For details of the data reduction see Dalcanton et al. (2009), and Gogarten et al. (2010) for a description of the photometry and its use in constraining the star formation history (SFH) of NGC 300. We used the fully reduced photometric tables that are available for the public on the ANGST website1.
2.2. VLT/FORS2 dataset
Our second dataset consists of archival narrowband Hα images of NGC 300 (Bresolin et al. 2009, under the program 077.B-0269(A)). The data have been observed in 2006, June 22 and July 1 with the FORS2 instrument mounted at ESO’s (European Southern Observatory) VLT on Cerro Paranal. The images consist of three different pointings and cover the northwestern, central, and eastern part of the galaxy. The seeing during the first night of observations was between ~0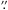 7 and 0
7 and 0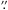 9, thus corresponding to ~7.5−8.4 pc at the assumed distance to NGC 300. In the second night the seeing was worse with values between ~1
9, thus corresponding to ~7.5−8.4 pc at the assumed distance to NGC 300. In the second night the seeing was worse with values between ~1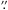 0 and 1
0 and 1 6, corresponding to ~9.4−15.0 pc. The Hα filter used in combination with the SR collimator has a central wavelength of 656.3 nm.
6, corresponding to ~9.4−15.0 pc. The Hα filter used in combination with the SR collimator has a central wavelength of 656.3 nm.
The flat-field correction and the bias subtraction were made using the standard ESO pipeline EsoRex. For the further processing of the data we used IRAF2. Cosmic rays were removed with the task L.A.Cos (van Dokkum 2001). After this, the images of the same fields were transformed to the same reference point using geomap and gregister and averaged together with the task imcombine, thereby blurring the images from the first night to the resolution of the images from the second night using the IRAF task gauss. As the Hα image does not only contain flux from the Hα line but also emission from the stellar continuum, this stellar component had to be removed from the science data. The stellar continuum was subtracted with the help of the narrowband filter Hα/4500, which is centered off the Hα emission line at 666.5 nm. The data in this filter were taken in the second observation night and were processed in the same way as the actual science data. As a first step in the continuum subtraction, the Hα image was blurred using the IRAF task gauss to fit the resolution of the image in the Hα/4500 filter because these observations were taken at systematically larger seeings. Next, all stars in both images were identified with the task daofind of the DAOPHOT package (Stetson 1987), and an aperture photometry was performed on them using phot. The tables of the stars were cross correlated to find stars that were detected in both images. After this, we plotted the counts of the stars in the Hα image versus the stellar counts in the Hα/4500 image. The slope of the least-squares-fitted line to the data points yields the scaling factor between the images in the two filters. Finally, we subtracted the scaled Hα/4500 image from the science data to remove the stellar continuum.
For an absolute flux calibration the star Feige 110 served as the photometric standard (Oke 1990). The conversion from instrumental counts into physical units (erg s-1 cm-2) was made as described in Jacoby et al. (1987). The conversion factor S is given by 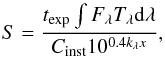 (1)where texp is the exposure time, Fλ the theoretical flux of the standard star, Tλ the transmission curve of the filter, Cinst the counts in the image, kλ the extinction coefficient, and x the airmass. To convert the counts into the actual Hα flux that arrives at the telescope, the transmission curve of the used filter has to be taken into account and the exact shape of the emission line spectrum must be known. As a good approximation, we here assumed that the Hα line spectrum is a δ peak that is redshifted by 145 km s-1 (the heliocentric radial velocity of NGC 300) with respect to the rest frequency. Therefore, the conversion between the observed counts and the flux of the emission using the conversion factor S from Eq. (1) is given by
(1)where texp is the exposure time, Fλ the theoretical flux of the standard star, Tλ the transmission curve of the filter, Cinst the counts in the image, kλ the extinction coefficient, and x the airmass. To convert the counts into the actual Hα flux that arrives at the telescope, the transmission curve of the used filter has to be taken into account and the exact shape of the emission line spectrum must be known. As a good approximation, we here assumed that the Hα line spectrum is a δ peak that is redshifted by 145 km s-1 (the heliocentric radial velocity of NGC 300) with respect to the rest frequency. Therefore, the conversion between the observed counts and the flux of the emission using the conversion factor S from Eq. (1) is given by 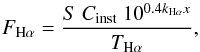 (2)where THα is the filter transmission at the position of the Hα line.
(2)where THα is the filter transmission at the position of the Hα line.
However, the narrowband Hα filter contains not only the Hα line, but also the nearby [N ii] λ6548 and λ6583 lines. As the [N ii]/Hα ratio is not known for all the regions, it is not possible to correct for the additional transmitted [N ii] lines for each region individually. Instead we assumed that the [N ii] emission is 0.1 of the total Hα+[N ii] emission, as was done by Roussel et al. (2005) for NGC 300 H ii regions, and in this way removed the blending flux. Typically, we expect a scatter of ±0.04 for this ratio (cf. Bresolin et al. 2009).
3. Methods and results
NGC 300 parameters.
3.1. Basic steps
We used broadband HST images together with narrowband Hα data taken at the VLT with the FORS2 instrument to examine the escape fraction fesc of H ii regions across the nearby Sculptor group spiral galaxy NGC 300. The parameters of this galaxy are summarized in Table 1. The Hα flux of H ii regions is a measure of how much of the ionizing flux of the hot stars located inside the region is absorbed by the surrounding medium. Comparing this quantity with the actual integrated ionizing photon emission rate Q0 of all stars inside the H ii region yields the escape fraction of that region. Assuming Case B recombination and a typical electron temperature of 10 000 K, the LyC to Hα photon emission rate conversion factor is 2.2 (Hummer & Storey 1987), which translates into a conversion of Hα luminosity to LyC photons Q(Hα) of Q(Hα) = 7.31 × 1011L(Hα)s-1 (Kennicutt et al. 1995; Kennicutt 1998). Q(Hα) gives the number of LyC photons emitted by the stars that are absorbed and create the observed Hα luminosity L(Hα). The escape fraction is therefore given by 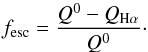 (3)We determined the escape fraction of individual H ii regions in three basic steps:
(3)We determined the escape fraction of individual H ii regions in three basic steps:
-
1.
Measure the Hα flux of individual H ii regions from the FORS2 data set as described in Sects. 2.2 and 3.2.
-
2.
Estimate the integrated ionizing photon flux Q0 of a region by converting the magnitudes and colors from stellar photometry described in Sect. 2.1 into the stellar effective temperatures Teff and surface gravity log G and the visual extinction AV.
-
3.
Calculate the escape fraction by using Eq. (3).
More details about the methods employed are given below.
3.2. Measure of the Hα flux
To determine the integrated flux of the H ii regions in the Hα image, we made use of the CASAviewer of the common astronomy software applications (CASA) package, which is originally designed to analyze astronomical radio data-cubes. For each region we first determined the local sky background and its standard deviation σ in a polygonal area with no flux around the region. We then summed the counts inside the isophotal contour that is at 4σ above the sky background and converted the integrated and background-subtracted counts into actual flux using Eq. (2) and considering the additional [Nii] component. Finally we corrected the flux for extinction, which is determined in the next step. To correct the Hα flux, we took into account that the typical ratio of Hα to stellar extinction at 656.3 nm equals 1.5 (Calzetti 2001).
3.3. Determination of the stellar parameters
Based on the three-filter broadband photometry, we determined Teff and log G of the hot stars inside our H ii sample plus the visual extinction AV. This was done in two steps. We assumed that all the hot stars inside a single H ii region have the same age and that all stars in one H ii region have the same extinction and a Cardelli extinction law (Cardelli et al. 1989) with an RV of 3.1. Using these constraints, we fit a single theoretical isochrone to the color-magnitude diagram (CMD) of each stellar population in an H ii region. Our method of fitting the isochrone was to minimize the geometrical distance in the CMD of an isochrone of given age and extinction to each star. To account for different numbers of stars in different parts of the CMD, we weighted each distance by the inverse number of stars in a 0.5 mag bin. For the fit we used all stars that form the main sequence (MS) down to a magnitude of ~25−26. We then excluded from the fit stars that clearly deviated from the MS. The theoretical isochrones are from the Padova isochrone set (Marigo et al. 2008). As a distance to NGC 300 we adopted 1.93 Mpc (Bresolin et al. 2005), which translates into a distance modulus of 26.43 mag. For the metallicities of the stars we used the values give by Gogarten et al. (2010), which extend between [M/H] = −0.47 in the range 2.7 kpc <r< 3.6 kpc and [M/H] = −0.24 in the central region for the youngest stars. In the second step we fit the stellar effective temperature and surface gravity using the tool for astrophysical data analysis TA-DA (Da Rio & Massimo 2012). In TA-DA we used the model grid from Marigo et al. (2008) as the evolutionary model and the BT-Settl2010 grid (Allard et al. 2011) for the synthetic spectra.
With the stellar parameters in hand, we calculated the ionizing photon output rate of the stars. For the sake of consistency, we used the BT-Settl2010 atmosphere model grid to calculate Q0. For this we downloaded a grid of stellar spectra at various temperatures, surface gravities, and metallicities from the BT-Settl web page3. To derive the ionizing photon flux of the model stars, we integrated the theoretical spectra up to the Lyman limit of 912 Å thereby dividing each spectral bin by the photon energy at the respective wavelength. We then calculated the ionizing photon fluxes of the stars in the H ii regions by interpolating the created grid of fluxes in temperature, surface gravity, and metallicity. Finally, we multiplied the resulting photon flux by the fitted surface of each star (also from TA-DA) to obtain the total ionizing photon luminosity. As an example, Fig. 1 shows the rate of emitted LyC photons as a function of stellar temperature and surface gravity for a metallicity Z = 0.006. The black dots indicate the positions of the calculated values from the BT-Settl2010 models, while the different colors are the interpolated values.
 |
Fig. 1 Ionizing photon flux as a function of the stellar effective temperature and surface gravity log G from the BT-Settl2010 models for a metallicity of Z = 0.006. The black dots show the positions of the individual calculated model points, while the colors represent the interpolated values. The color scale is in logarithmic units. |
H ii region sample.
 |
Fig. 2 HST images of the three Wide fields with overplotted contours of Hα emission (VLT/FORS2; Bresolin et al. 2009). Top: Wide 1, middle: Wide 2, bottom: Wide 3. |
3.4. Analysis and results
We analyzed a sample of 20 H ii regions of different sizes and shapes at various distances from the center of the galaxy (see Fig. 2) with this method. Table 2 lists all the regions. We selected all objects that were classified as stars (object type ≤2) in the Dalcanton et al. (2009) catalog that are located inside the compact regions of the H ii regions because these stars are considered to be responsible for the ionization of their surrounding gas. We fit the parameters of all stars that lay inside pre-defined color (F475W−F814W colors between −1 and 0.5) and magnitude (brighter than 25th magnitude in the F814W filter) cuts. This cuts restrict our fits to main-sequence stars hotter than ~25 000 K and massive evolved stars. Given the logarithmic dependence of Q0 on the temperature, the contribution of stars with temperatures ≤25 000 K is negligible. Unfortunately, many of the regions in our H ii region sample are sparsely sampled in the upper parts of the CMD, and therefore fitting of an isochrone to it is ambiguous. For the further examination of our method, we selected a subsample of nine regions that are better sampled (see Fig. 4). Table 3 lists the results of the calculated escape fractions of the shortlisted regions. On the one hand, we found for half of the regions “negative” escape fractions. These values result from the fact that we measured more Hα photons than can be explained by the integrated LyC luminosity of the stars within the H ii region. This indicates that our fit underestimated the Q0 flux, down to a factor of ~10. On the other hand, we also obtained a quite high value for fesc of more than 60%. These values are probably also very uncertain. As we discuss in the next section, our tests show that Q0 can be overestimated by factors of more than four. In regions with negative values for fesc, much younger ages must be assumed to bring the integrated ionizing photon flux from the stars and the observed Hα flux in agreement. In clusters where the upper parts of the CMDs are not populated, such as regions 4 or 13, younger ages would still be in agreement with the observations. In regions 2 or 3, however, the ages needed to explain the Hα luminosity miss the bright evolved stars and therefore seem to disagree with the observations.
It is clear that our results are contaminated by uncertainties. To identify these errors and improve on the method, we performed additional tests, as described in the next section.
 |
Fig. 3 Detailed view of the shortlisted H ii regions. The red contours indicate the isophote 4σ above the local background inside which the Hα flux was measured. |
H ii region parameters.
 |
Fig. 4 CMDs of the shortlisted H ii regions with isochrones that fit the data best. The age of the isochrone is indicated in upper left corner of each panel. The stars for which we fit the parameters using TA-DA are color-coded by their fitted temperature. In the upper left panel, the black crosses indicate the typical photometric errors in color and magnitude as a function of the F814W magnitude. |
3.5. Test of the method
To check how reliable our method of fitting stellar parameters is, we carried out additional tests with artificial star clusters. We also checked whether we would benefit from adding a supplementary filter and performed the tests using B,V and I photometry on the one hand, which corresponds approximately to the used HST filter combination, and on the other hand using the U,B,V and I photometry because the U filter is more sensitive to the emission peak of hot stars. We created synthetic photometry of 19 stellar clusters based on the theoretical Padova isochrone set (Marigo et al. 2008). The clusters contain a random number of stars between 30 and 120. The stars themselves were chosen to have masses of between 15 and 100 M⊙ with an underlying Salpeter logarithmic initial mass function (IMF) with an index α of −2.35 (Salpeter 1955). Extrapolated to a lower mass of 1 M⊙ using the same IMF, the clusters have masses of between 3.7 × 103 and 1.1 × 104M⊙. Each cluster has a random mean age of between 4 and 10 Myr with an allowed Gaussian scatter between 0.1 and 0.5 Myr around it. To the stellar magnitudes of each cluster we added a Gaussian noise of 0.01 mag as well as an extinction value that consists of an mean foreground extinction plus an additional lognormal scatter.
We fit the parameters of the created stellar associations in three different ways:
-
1.
Without any a priori constraints on the age of the stars and with anextinction AV ranging from 0.0 to 0.7 mag, so that we cover the range of mean extinction values of our created clusters and to allow higher values as well.
-
2.
Constraining the stellar ages and extinction values to the real mean values of the cluster.
-
3.
Fitting of theoretical isochrones to the CMDs of the clusters, as we did for the H ii regions of NGC 300.
After the fitting we computed the ionizing photon emission rates of the synthetic clusters for each of the three different fits and compared it to the true value using the BT-Settl2010 model atmosphere grids to test the reliability of the three different methods. Fitting without a priori assumptions is a highly degenerate problem and the results are therefore very uncertain, both for the UBVI and the BVI filter set (see Fig. 5). However, for the UBVI filter set, the results show a systematic offset. Even if we set our fitting tool with pre-defined age and extinction values, the final results show clear discrepancies between the fit and true Q0 values for both the mean real ages and extinctions and those determined by isochrone fitting to the CMD (see Figs. 6 and 7). The error bars in all figures represent the maximum errors resulting from the uncertainties in the fitted stellar temperatures as given by TA-DA. For most of the clusters, the parameters of the fitted isochrone agree well with the real mean ones, which explains the comparable scatter around the one-to-one relation for both methods. For the UBVI (BVI) filter photometry, 14 (15) out of 19 clusters have fitted ages that are within ±15% of the real mean value. The fitting of the mean extinction was less accurate. For the UBVI (BVI) filter combination, only 6 (7) clusters are within ±15% of the real mean value and 12 (13) within ±30%. Surprisingly, the usage of the additional U filter does not improve the result of Q0 for all of the three methods (see Fig. 6).
The results of the fitting might depend on the cluster properties. Therefore, we correlated the relative errors of the ionizing photon flux with the parameters of the test clusters and searched for any trends. Figure 8 shows the relative error of the fitted Q0 value as a function of the fitted age of the cluster. For young ages (≲5 Myr) we are more likely to overestimate the ionizing photon output of the cluster, while for older fitted ages we obtain Q0 that is lower than the real values. This is also evident in Fig. 9, where we plot the relative error in Q0 as a function of the relative error in the fitted age of the cluster. The greater the number of hot stars in the cluster, the smaller the scatter in the relative error of Q0 (Fig. 10). This is as expected because the greater the number of stars, the smaller the contribution of a single star. In clusters with fewer than 50 stars, the relative error in Q0 is between 0.4 and 4.8. We note, however, that in clusters with more than 50 stars we systematically underestimate the ionizing photon flux. There, our fitting yields between 0.3 and 1.0 times the real value of Q0.
 |
Fig. 5 Fitted ionizing photon flux as a function of the real ionizing photon emission rate without any a priori assumptions about the ages and extinction. The blue solid line is the one-to-one relation. Top: for UBVI photometry, bottom: for BVI photometry. |
 |
Fig. 6 Fitted ionizing photon flux as a function of the real ionizing photon emission rate. Before fitting with TA-DA, we fit a single isochrone to the CMD to constrain the age and extinction of the synthetic cluster. The blue solid line is the one-to-one relation. Top: for UBVI photometry; bottom: for BVI photometry. |
 |
Fig. 7 Fitted ionizing photon flux as a function of the real ionizing photon emission rate using the mean real ages and extinctions of the clusters. The blue solid line is the one-to-one relation. Top: for UBVI photometry; bottom: for BVI photometry. |
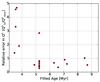 |
Fig. 8 Relative error in the fitted value of Q0 as a function of the fitted age of the cluster using BVI photometry. |
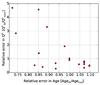 |
Fig. 9 Relative error of Q0 as a function of the relative error of the fitted cluster age using BVI photometry. |
 |
Fig. 10 Relative error of Q0 as a function of the number of stars in the cluster using BVI photometry. |
4. Discussion and conclusions
We examined the feasibility of inferring the escape fraction of LyC photons from individual H ii regions within the nearby spiral galaxy NGC 300 using broadband and narrowband photometric data. Our approach was to determine the integrated Q0 value of the stars within the young clusters from broadband photometry and stellar model atmospheres. However, we have shown here that the uncertainties inherent to spectral typing using broadband data completely dominate the results. Our tests using artificial clusters showed that we are unable to correctly reconstruct the stellar parameters from photometric data in three or four bands even under idealized conditions. The tests assumed that the young clusters consist of a coeval population, which may not necessarily be true. There might also be a variable amount of reddening throughout the region because the young clusters are probably located within a patchy cloud. We accounted for these facts and allowed a small scatter in age and extinction within the clusters in our tests. As a result of these uncertainties, stars are fit to an incorrect isochrone, leading to incorrect stellar parameters. As some regions are also sparsely sampled in the upper parts of the CMD, an accurate fitting of the mean age and extinction is not possible, which increases the errors in the integrated Q0 even more. In our analysis and tests, we ignored other factors that also influence the determination of the stellar spectral types, such as photometric crowding and unresolved binary stars.
In our tests with artificial star clusters we found that we tend to underestimate the LyC luminosity for fitted ages older than about 5 Myr. This is reflected in the results of fesc of the real H ii regions. All regions fit to be older than about 5.5 Myr have “negative” escape fractions, confirming that the inferred Q0 values are too low. All regions with younger ages are found to leak ionizing photons with escape fractions of up to ~66%. The reason is that at younger ages the Q0 is generally overestimated by large factors. This apparent trend is against the expectations, as the escape fraction should increase with increasing age of the cluster (e.g., Dale et al. 2013).
In our simplified analysis we have assumed that all stars within a single H ii region have the same age and are equally affected by extinction. However, this is not necessarily true because most of the clusters in our sample show a broadened main sequence or even a second sequence at redder colors, which disagrees with photometric errors (see Fig. 4). This broadening can be caused by stellar blending or crowding, unresolved stellar binaries, or differential extinction, or a combination of several effects. To explain the stars that are scattered to the red side of the main sequence, age spreads of about 30 Myr or more must be assumed, which is unreasonable. Therefore age spreads seem to be an unlikely explanation. From our data set we are not able to tell which other effects might cause this broadening. If a varying reddening throughout the H ii region is responsible for it, then a difference in extinction ΔAV of up to 1.25 mag is required to explain the spread. If we allow a varying extinction to cover the width of the main sequence, then our estimates of the stellar temperatures and surface gravities, and thus of Q0, are very different from the previous ones with a fixed value for extinction. In three clusters, the LyC flux calculated in this way would be approximately half of the original, while in two clusters we would obtain approximately twice the flux. Only in four H ii regions would the ionizing photon output of the cluster be within 20% of the previous one.
Another source of uncertainty in determining the escape fraction comes from the accuracy of the predicted ionizing photon fluxes from various theoretical stellar atmosphere models. This has been demonstrated by Oey & Kennicutt (1997) and Voges et al. (2008), who determined the escape fraction from H ii regions within the LMC using the same set of data, but various sets of atmosphere models. While Oey & Kennicutt (1997) concluded that most of the regions are density bound, Voges et al. (2008) determined the regions to be radiation bound using newer sets of atmosphere models. They also compared the ionizing photon output as a function of stellar spectral types for different sets of models in their Fig. 1. We used the BT-Settl2010 grid from Allard et al. (2011) to estimate the Q0 value of the stars to obtain consistent results because TA-DA also uses these models to fit the stellar parameters. Additionally, we tested how the outcome of our estimates of the ionizing photon fluxes depends on the used stellar models. For this, we used the hot-star atmosphere model grids of Smith et al. (2002), which are based on models calculated with the WM-Basic code (Pauldrach et al. 2001). The model atmosphere grids are calculated for the luminosity classes V and I for 5 different metallicities. Giant star models were not calculated explicitly and are just interpolations between the dwarf and supergiant models. We found that in all but two cases, the integrated LyC flux is higher when using the Smith et al. (2002) models, by a medium factor of two. Only in the H ii regions 17 and 19, which in our fitting are dominated by very hot stars (Teff> 50 000 K), is the ionizing photon flux about the same (within 5%).
In conclusion we can state that the examined approach is dominated by uncertainties in determining the spectral types of the stars within the H ii regions and the photometric classification is not accurate enough. There are too many unknown or not precisely known parameters, such as the age of the stars, the extinction toward the stars, and the metallicity, to obtain a reasonable fit for the temperature and the surface gravity of the stars. These are crucial to accurately determine their Q0 values with broadband data alone, however. In a following project, the method introduced by Pellegrini et al. (2012) might be employed to determine the leakage of ionizing photons from the objects studied here. Already existing narrowband data of NGC 300 in [O iii] and [S ii] emission lines taken with the Wide Field Imager (WFI) instrument at the MPG/ESO telescope can be used as a starting point. Alternatively, stellar spectra can be used for a more accurate stellar classification, as has already been done for the Magellanic Clouds (e.g., Oey & Kennicutt 1997; Voges et al. 2008; Doran et al. 2013). It should be possible to obtain a reasonable estimate of the escape fraction of regions with low stellar densities by spectroscopically determining the temperatures of the hottest four to five stars within them because these dominate the total ionizing photon output.
Acknowledgments
We thank the anonymous referee for useful comments and suggestions that helped improve the manuscript This research was supported by the DFG cluster of excellence “Origin and Structure of the Universe”. N.B. is partially funded by a Royal Society University Research Fellowship.
References
- Allard, F., Homeier, D., & Freytag, B. 2011, in 16th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun, eds. C. M. Johns-Krull, M. K. Browning, & A. A. West (San Francisco, CA: ASP), ASP Conf. Ser., 448, 91 [Google Scholar]
- Bresolin, F., Pietrzyński, G., Gieren, W., & Kudritzki, R.-P. 2005, ApJ, 634, 1020 [NASA ADS] [CrossRef] [Google Scholar]
- Bresolin, F., Gieren, W., Kudritzki, R.-P., et al. 2009, ApJ, 700, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D. 2001, PASP, 113, 1449 [NASA ADS] [CrossRef] [Google Scholar]
- Conroy, C., & Kratter, K. M. 2012, ApJ, 755, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Dalcanton, J. J., Williams, B. F., Seth, A. C., et al. 2009, ApJS, 183, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, J. E., Ercolano, B., & Bonnell, I. A. 2013, MNRAS, 430, 234 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Da Rio, N., & Robberto, M. 2012, AJ, 144, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Deharveng, L., Caplan, J., Lequeux, J., et al. 1988, A&AS, 73, 407 [NASA ADS] [Google Scholar]
- Doran, E. I., Crowther, P. A., de Koter, A., et al. 2013, A&A, 558, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gogarten, S. M., Dalcanton, J. J., Williams, B. F., et al. 2010, ApJ, 712, 858 [NASA ADS] [CrossRef] [Google Scholar]
- Hummer, D. G., & Storey, P. J. 1987, MNRAS, 224, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Jacoby, G. H., Africano, J. L., & Quigley, R. J. 1987, PASP, 99, 672 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C. 1998, ARA&A, 36, 189 [Google Scholar]
- Kennicutt, R. C., Jr., Bresolin, F., Bomans, D. J., Bothun, G. D., & Thompson, I. B. 1995, AJ, 109, 594 [NASA ADS] [CrossRef] [Google Scholar]
- Leitet, E., Bergvall, N., Hayes, M., Linne, S., & Zackrisson, E. 2013, A&A, 553, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leitherer, C., Ferguson, H. C., Heckman, T. M., & Lowenthal, J. D. 1995, ApJ, 454, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Marigo, P., Girardi, L., Bressan, A., et al. 2008, A&A, 482, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oey, M. S., & Kennicutt, Jr., R. C. 1997, MNRAS, 291, 827 [NASA ADS] [CrossRef] [Google Scholar]
- Oke, J. B. 1990, AJ, 99, 1621 [NASA ADS] [CrossRef] [Google Scholar]
- Paturel, G., Petit, C., Prugniel, P., et al. 2003, A&A, 412, 45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pauldrach, A. W. A., Hoffmann, T. L., & Lennon, M. 2001, A&A, 375, 161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pellegrini, E. W., Oey, M. S., Winkler, P. F., et al. 2012, ApJ, 755, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Roussel, H., Gil de Paz, A., Seibert, M., et al. 2005, ApJ, 632, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Rutkowski, M. J., Scarlata, C., Haardt, F., et al. 2016, ApJ, 819, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Siana, B., Teplitz, H. I., Ferguson, H. C., et al. 2010, ApJ, 723, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, L. J., Norris, R. P. F., & Crowther, P. A. 2002, MNRAS, 337, 1309 [NASA ADS] [CrossRef] [Google Scholar]
- Stetson, P. B. 1987, PASP, 99, 191 [NASA ADS] [CrossRef] [Google Scholar]
- van Dokkum, P. G. 2001, PASP, 113, 1420 [NASA ADS] [CrossRef] [Google Scholar]
- Voges, E. S., Oey, M. S., Walterbos, R. A. M., & Wilkinson, T. M. 2008, AJ, 135, 1291 [NASA ADS] [CrossRef] [Google Scholar]
- Zastrow, J., Oey, M. S., Veilleux, S., & McDonald, M. 2013, ApJ, 779, 76 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Ionizing photon flux as a function of the stellar effective temperature and surface gravity log G from the BT-Settl2010 models for a metallicity of Z = 0.006. The black dots show the positions of the individual calculated model points, while the colors represent the interpolated values. The color scale is in logarithmic units. |
| In the text | |
 |
Fig. 2 HST images of the three Wide fields with overplotted contours of Hα emission (VLT/FORS2; Bresolin et al. 2009). Top: Wide 1, middle: Wide 2, bottom: Wide 3. |
| In the text | |
 |
Fig. 3 Detailed view of the shortlisted H ii regions. The red contours indicate the isophote 4σ above the local background inside which the Hα flux was measured. |
| In the text | |
 |
Fig. 4 CMDs of the shortlisted H ii regions with isochrones that fit the data best. The age of the isochrone is indicated in upper left corner of each panel. The stars for which we fit the parameters using TA-DA are color-coded by their fitted temperature. In the upper left panel, the black crosses indicate the typical photometric errors in color and magnitude as a function of the F814W magnitude. |
| In the text | |
 |
Fig. 5 Fitted ionizing photon flux as a function of the real ionizing photon emission rate without any a priori assumptions about the ages and extinction. The blue solid line is the one-to-one relation. Top: for UBVI photometry, bottom: for BVI photometry. |
| In the text | |
 |
Fig. 6 Fitted ionizing photon flux as a function of the real ionizing photon emission rate. Before fitting with TA-DA, we fit a single isochrone to the CMD to constrain the age and extinction of the synthetic cluster. The blue solid line is the one-to-one relation. Top: for UBVI photometry; bottom: for BVI photometry. |
| In the text | |
 |
Fig. 7 Fitted ionizing photon flux as a function of the real ionizing photon emission rate using the mean real ages and extinctions of the clusters. The blue solid line is the one-to-one relation. Top: for UBVI photometry; bottom: for BVI photometry. |
| In the text | |
 |
Fig. 8 Relative error in the fitted value of Q0 as a function of the fitted age of the cluster using BVI photometry. |
| In the text | |
 |
Fig. 9 Relative error of Q0 as a function of the relative error of the fitted cluster age using BVI photometry. |
| In the text | |
 |
Fig. 10 Relative error of Q0 as a function of the number of stars in the cluster using BVI photometry. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


