| Issue |
A&A
Volume 592, August 2016
|
|
|---|---|---|
| Article Number | A60 | |
| Number of page(s) | 10 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201527704 | |
| Published online | 25 July 2016 | |
Properties of the prominence magnetic field and plasma distributions as obtained from 3D whole-prominence fine structure modeling
1 Astronomical Institute, The Czech Academy of Sciences, 25165 Ondřejov, Czech Republic
e-mail: stanislav.gunar@asu.cas.cz
2 School of Mathematics and Statistics, University of St Andrews, North Haugh, St Andrews, KY16 9SS, UK
e-mail: dhm@st-andrews.ac.uk
Received: 5 November 2015
Accepted: 25 May 2016
Aims. We analyze distributions of the magnetic field strength and prominence plasma (temperature, pressure, plasma β, and mass) using the 3D whole-prominence fine structure model.
Methods. The model combines a 3D magnetic field configuration of an entire prominence, obtained from non-linear force-free field simulations, with a detailed semi-empirically derived description of the prominence plasma. The plasma is located in magnetic dips in hydrostatic equilibrium and is distributed along multiple fine structures within the 3D magnetic model.
Results. We show that in the modeled prominence, the variations of the magnetic field strength and its orientation are insignificant on scales comparable to the smallest dimensions of the observed prominence fine structures. We also show the ability of the 3D whole-prominence fine structure model to reveal the distribution of the prominence plasma with respect to its temperature within the prominence volume. This provides new insights into the composition of the prominence-corona transition region. We further demonstrate that the values of the plasma β are small throughout the majority of the modeled prominences when realistic photospheric magnetic flux distributions and prominence plasma parameters are assumed. While this is generally true, we also find that in the region with the deepest magnetic dips, the plasma β may increase towards unity. Finally, we show that the mass of the modeled prominence plasma is in good agreement with the mass of observed non-eruptive prominences.
Key words: Sun: filaments, prominences / Sun: magnetic fields / plasmas / methods: numerical
© ESO, 2016
1. Introduction
In this paper, we analyze the basic physical properties of prominences, using the 3D whole-prominence fine structure (WPFS) model developed by Gunár & Mackay (2015a, hereafter Paper. The WPFS model combines 3D prominence magnetic field simulations with detailed semi-empirically derived information on the prominence plasma properties. This allows us to comprehensively analyze the 3D distribution of the magnetic field strength within the prominence, together with the variations of the temperature and pressure of the prominence plasma. We also study the variation of the plasma β parameter and analyze the mass of the prominence plasma along with its variation during the evolution of the modeled magnetic field configuration. We follow the evolution of the modeled prominence through the series of time steps (snapshots) considered in Gunár & Mackay (2015b, hereafter Paper II).
Over the last two decades, the structure of prominence magnetic fields has been studied by many authors employing numerous 3D simulations. These simulations have mainly dealt with the entire magnetic field configuration of the prominence. For more details of these simulations we refer the reader to the reviews of Mackay et al. (2010), van Ballegooijen & Su (2014), or Gunár (2014). Reviews of prominence plasma properties can be found in e.g., Labrosse et al. (2010) or Parenti (2014). A comprehensive review of the properties of solar prominences is presented in the new book by Vial & Engvold (2015). For more details of the WPFS model and its relation to previous studies see Papers I and II.
The 3D WPFS model developed in Paper I allows us to not only study the prominence magnetic field configuration, but also to relate its internal structure to the distribution of the prominence plasma. This is achieved by filling the magnetic dips produced by the 3D non-linear force-free field (NLFF) simulations of Mackay & van Ballegooijen (2009) with prominence plasma in hydrostatic equilibrium. The process of filling the dips is achieved through the iterative method developed by Gunár et al. (2013). This method produces individual prominence fine structures whose plasma distribution depends on the local configuration of the magnetic field. The plasma temperature distribution is specified semi-empirically, taking into account two distinct forms of the prominence-corona transition region (PCTR). The first is a narrow region with a steep temperature gradient in the direction perpendicular to the magnetic field, and the second is a more extended region in the direction parallel to the magnetic field with a gradual increase of the temperature from the central cool part. While we do not consider the origin of the prominence plasma and of the PCTR we chose a shape of the PCTR that has been shown to produce synthetic hydrogen Lyman spectra in good agreement with observations (see, e.g., Gunár et al. 2008, 2010). For studies that consider the origin of the prominence plasma, see Sect. 3 of Mackay et al. (2010) for a review.
The combined information of the magnetic field and plasma distribution within the modeled prominence volume allows us to study the distribution of the plasma β within the modeled prominences. Plasma β provides information on the relative importance of forces (plasma pressure vs. magnetic pressure) and is thus a critical parameter for understanding the stability, dynamics, and small-scale structure of prominences. In most 3D prominence magnetic field simulations, the plasma β is generally assumed to be small (β ≪ 1, force-free field assumption). On the other hand, several prominence fine structure models such as those of Heinzel & Anzer (2001) assume that the prominence plasma produces the magnetic dips by its weight (gravity-induced dips) and therefore assumes large values of the plasma β (see also Hillier & van Ballegooijen 2013).
One important aspect of the WPFS model is that it allows us to derive the mass of the prominence plasma and to study its distribution with temperature and its variation during the prominence evolution. The total prominence mass represents another critical parameter influencing the stability of prominences. Moreover, in the case where prominences become unstable and produce coronal mass ejections, prominence material may represent a large portion of the mass budget of the ejected plasma. Therefore, information about the prominence mass can have direct implications for space weather studies. As the mass of prominences can also be derived from observations (see, e.g., Gilbert et al. 2006, 2011 or Schwartz et al. 2015b), it provides a useful comparison for the model.
In the present paper, we present a study of the distribution of the prominence magnetic field strength, prominence plasma temperature, and pressure. In addition, we consider the plasma β distribution and the prominence mass from the WPFS modeling (Sects. 2−5). In Sect. 6 we provide the discussion and in Sect. 7 we present our conclusions.
2. Magnetic field strength distribution
We use the 3D NLFF simulations of Mackay & van Ballegooijen (2009) to prescribe the whole prominence magnetic field configuration used in this paper. These simulations were also employed in Papers I and II. In the following paragraph, we briefly summarize their key features. Full details of the simulations can be found in Mackay & van Ballegooijen (2009) and a description of their implementation into the 3D WPFS model is given in Sect. 2.1 of Paper I.
The simulations of Mackay & van Ballegooijen (2009) construct an initial 3D linear force-free field configuration (α is fixed at − 1.477 × 10-8 m-1) from a basic photospheric flux distribution. The photospheric flux distribution represents a magnetic arcade that produces the basic dipped magnetic field configuration (main body) of a prominence. As a bipole is inserted and its minority polarity advected towards the main body of the filament, the initial magnetic field configuration is perturbed and evolves through a series of quasi-static NLFF states, as described by the magneto-frictional technique of van Ballegooijen et al. (2000) and Mackay & van Ballegooijen (2006). The photospheric flux distribution containing the magnetic arcade and the bipole are chosen to represent the flux of a decaying active region and an ephemeral region, respectively. The ratio of bipole flux (Fb) to arcade flux (Fa) is Fb/Fa = 0.0084, while the ratio of bipole to filament flux (Ff) is Fb/Ff = 2.7. These values correspond to the typical size of regions and are set to represent the middle range of the observationally constrained photospheric flux values. The photospheric flux distribution can be seen in Fig. 1, where white represents positive flux and black negative flux. In this figure we also show the representative dipped (purple) and non-dipped (blue) lines relative to the photospheric flux distribution. This demonstrates the full connectivity of the 3D magnetic field of the modeled prominence. In particular, the position and connectivity of the field can be seen relative to the small ephemeral region. A further discussion of the photospheric flux distribution can be found in Sect 2.1 of Paper II.
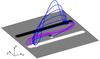 |
Fig. 1 Photospheric flux distribution of the modeled prominence is shown, together with the representative dipped (purple) and non-dipped (blue) field lines. For the flux distribution white/black represents possitive/negative flux. |
In this paper, we consider the distribution of the magnetic field strength that occurs inside the modeled prominence as a consequence of the photospheric flux distribution described above. However, the amount of photospheric flux is a free parameter and can be scaled up or down without altering the resulting prominence magnetic field configuration. The strength of the prominence magnetic field scales linearly with the photospheric flux values, while the spatial distribution and the geometrical structure of the dips, including their depths, remains the same. For example, by increasing the photospheric flux by a factor of five the field strength inside the magnetic dips becomes five times larger; however, the dips have the same depth. With the applied plasma model such an increase in the magnetic field strength does not have any influence on the temperature and pressure variations, or on the Hα visibility of the prominence plasma – assuming that force-free field assumption is upheld – because the pressure depends only on the depth of the dips. However, higher field strength values have an impact on the distribution of the plasma β within the modeled prominence.
 |
Fig. 2 Dipped portions of the magnetic field lines from Snapshot 10 plotted in the top view (x-y plane) and the side view (x-z plane). Colors represent the magnetic field strength in G. The position of the positive polarity (solid blue lines) and negative polarity (dashed blue lines) of the inserted bipole is marked by contours corresponding to Bz values ±1, ±2, ±3, and ±4 G. The dashed box marks the area shown enlarged in Fig. 3. |
We now describe the distribution of the magnetic field strength in the WPFS model used in Paper I and identified in Paper II as Snapshot 10. In Fig. 2 we show the dipped portions of the magnetic field lines for the entire modeled prominence, plotted from above (x-y plane) and from the side (x-z plane). In Fig. 3 we also show an enlarged view of the dipped magnetic field lines from the dashed box area marked in Fig. 2. The z-axis in Fig. 3 is enlarged five times to emphasize the depth of the dips. In both figures, colors represent the magnetic field strength.
Figures 2 and 3 show that the spatial variation of the magnetic field strength throughout the modeled prominence volume is insignificant on scales comparable with the typical observed widths of the prominence fine structures (around 1000 km or lower). Although the difference between the lowest and highest field strength values is nearly 50%, this change occurs gradually within the prominence volume. Regions of both the weakest and the strongest field lie above the negative polarity of the inserted bipole. The lowest field strength values occur in the bottom portions of deep dips, while the strongest values occur near the dip shoulders. We note that while in this paper we focus on Snapshot 10, similar regions of weak and strong fields occur in all snapshots considered in Paper II. The minimum and maximum field strength values in each snapshot are listed in Table 1.
 |
Fig. 3 Enlarged view of the x-z plane showing the dipped magnetic field lines. The z-axis dimension is enlarged five times to emphasize the depth of the dips. Colors represent the magnetic field strength in G. This view corresponds to the area marked by the dashed box in Fig. 2. |
List of the minimum and maximum values of the magnetic field strength (in G), maximum gas pressure (in dyn cm-2), and the maximum values of the plasma β in all snapshots.
3. Temperature and pressure distribution
 |
Fig. 4 Distribution of temperature (left) and gas pressure (right) in a single 3D prominence fine structure along a single dipped field line. Panels b) and d) show cross-sectional cuts. We note that every cut showing the temperature in panel b) is surrounded by a very narrow red ring that represents the PCTR temperatures. The invisibility of these rings in some cuts is solely due to the visualization procedure. |
The semi-empirical iterative method of Gunár et al. (2013) for filling individual magnetic dips with hydrostatic plasma produces a realistic distribution of the prominence plasma pressure and temperature, including the PCTR. We note that while it produces a realistic distributions of plasma, the model does not describe the origin or dynamics of the prominence plasma. The local properties of the plasma in each dip depend on the depth and the shape of the individual magnetic dips, but not on the magnetic field strength of the dip. This, in combination with a set of global input parameters that are common to all the fine structures in the modeled prominence, produces a set of unique prominence fine structures. The global parameters describe the semi-empirical temperature structure of the PCTR and fix the gas pressure at the boundary. They also prescribe the maximum column mass along the magnetic field lines, together with its variation within the fine structure cross-section. A full list of these parameters, along with a discussion of their choice can be found in Paper I. These global parameters are chosen such that they produce profiles of Lyman lines comparable with observations.
 |
Fig. 5 Temperature and gas pressure distribution in all prominence fine structures from Snapshot 10. Panel a) shows temperature between 7000 and 14 000 K (T< 14), panel b) temperature between 14 000 and 30 000 K ( |
In Fig. 4 we show the 3D distribution of the temperature and gas pressure inside a typical modeled fine structure. It has an elongated form, following the shape of its respective dipped magnetic field line. In addition to being curved (dipped) in the vertical direction (z-axis), it is also curved within the horizontal x-y plane. The temperature rises gradually along the length of the fine structure from its minimum, which is located at the bottom (center) of the dip, to the maximum temperature at each end. Since the dip is asymmetric, the temperature and pressure distribution is also asymmetric. This gradual temperature rise represents the extended part of the PCTR spreading along the magnetic field line (see Eq. (2) in Paper I). On the other hand, a narrow PCTR extends across the magnetic field lines and is represented by the steep temperature gradient (Eq. (6) in Paper I) within the fine structure cross-section. We note that this narrow region may be difficult to spot in panel b where it is represented by very narrow red rings (corresponding to the highest temperature) surrounding each cross-sectional cut. The narrow PCTR region perpendicular to the magnetic field is present in all of the displayed cuts. However, owing to visualization problems it is sometimes difficult to see. The gas pressure, determined by assuming hydrostatic equilibrium (see Gunár et al. 2013) decreases from its maximum value at the bottom (center) of the dip towards the edges. However, owing to asymmetric shapes of individual magnetic dips, the method of Gunár et al. (2013) produces pressure imbalances in the modeled prominence fine structures. These imbalances are represented by different values of the pressure at the dip ends, as can be seen in Fig. 4c or Figs. 6 and 7 in Gunár et al. (2013). In the present paper, we do not consider any dynamical response of the prominence plasma to such imbalances. However, flows caused by these pressure differences could contribute to the overall dynamics of the prominence fine structure plasma. We will consider such flows in future work, together with other important sources of the dynamics of prominence plasma.
The WPFS model considered in this paper is composed of a large number of these prominence fine structures, each of which has unique properties of temperature and pressure depending on the shape of each magnetic dip. To better visualize the 3D distribution of the temperature in such complex models, we divide the entire temperature range into three temperature intervals. The first (T < 14) covers the range between the minimum central temperature T0, set as a global parameter (in this paper we assume a value of 7000 K) and 14 000 K. This interval approximately covers the cool prominence plasma observable in the Hα line. It is also consistent with the range of temperatures considered in the Hα visualization method of Heinzel et al. (2015). The second interval (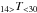 ) covers the temperatures between 14 000 and 30 000 K. Its upper limit approximately corresponds to the temperature above which hydrogen plasma becomes fully ionized. The third interval (T > 30) covers the temperatures between 30 000 K and the maximum boundary temperature Ttr set again as a global parameter. In this paper we assume a value of 100 000 K. This range covers the cooler part of the PCTR. The semi-empirical temperature distribution forming the elongated part of the PCTR aligned with the magnetic field is based on the 2D non-LTE radiative transfer models of Heinzel & Anzer (2001); see also Heinzel et al. (2005) and Gunár et al. (2007). Such a distribution is not necessarily in thermal equilibrium (we do not consider any energy balance computations in this work). However, PCTR regions with a similar geometrical extent of several tens of thousands of kilometers along the magnetic field are required to produce synthetic Lyman spectra with good profile-to-profile and statistical agreement with observations (Gunár et al. 2010; Schwartz et al. 2015a). Moreover, the 2D prominence fine structure models, with extended PCTR along the magnetic field and very narrow PCTR across the field lines, also produce synthetic differential emission measure curves in good agreement with observations (see Gunár et al. 2011a,b). The applied model produces a good agreement with observations and so we chose to use it, even though it is probably not in thermal equilibrium. In the future we will focus on studies of energy balance within the individual 3D prominence fine structures that make up the 3D WPFS model. In addition, we will consider a higher upper temperature limit to reach hot PCTR temperatures.
) covers the temperatures between 14 000 and 30 000 K. Its upper limit approximately corresponds to the temperature above which hydrogen plasma becomes fully ionized. The third interval (T > 30) covers the temperatures between 30 000 K and the maximum boundary temperature Ttr set again as a global parameter. In this paper we assume a value of 100 000 K. This range covers the cooler part of the PCTR. The semi-empirical temperature distribution forming the elongated part of the PCTR aligned with the magnetic field is based on the 2D non-LTE radiative transfer models of Heinzel & Anzer (2001); see also Heinzel et al. (2005) and Gunár et al. (2007). Such a distribution is not necessarily in thermal equilibrium (we do not consider any energy balance computations in this work). However, PCTR regions with a similar geometrical extent of several tens of thousands of kilometers along the magnetic field are required to produce synthetic Lyman spectra with good profile-to-profile and statistical agreement with observations (Gunár et al. 2010; Schwartz et al. 2015a). Moreover, the 2D prominence fine structure models, with extended PCTR along the magnetic field and very narrow PCTR across the field lines, also produce synthetic differential emission measure curves in good agreement with observations (see Gunár et al. 2011a,b). The applied model produces a good agreement with observations and so we chose to use it, even though it is probably not in thermal equilibrium. In the future we will focus on studies of energy balance within the individual 3D prominence fine structures that make up the 3D WPFS model. In addition, we will consider a higher upper temperature limit to reach hot PCTR temperatures.
In Fig. 5 we show the 3D distribution of the temperature and gas pressure for the entire modeled prominence. We again focus here on Snapshot 10, but the obtained distributions are generally similar in all snapshots considered in Paper II. In panels a−c we display the temperature distribution in temperature intervals T < 14, 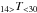 , and T > 30, respectively. These panels demonstrate that the plasma at different temperatures tends to occupy distinct volumes of the modeled prominence. The cool plasma that can be visible in the Hα line forms a relatively compact structure clustered in the middle part of the modeled prominence volume. While we acknowledge that it is complicated to relate the 3D view of the temperature distribution in Fig. 5a with the synthetic Hα images, these clusters correspond to the main features visible in the synthetic Hα images shown in Figs. 5 and 6 in Paper I. The plasma with higher temperatures occupies a large volume that envelops the cool plasma. Although the hotter plasma also forms a narrow PCTR layer surrounding each fine structure in the direction across the magnetic field lines, the bulk of the PCTR plasma is located in the wide areas expanding along the magnetic field line towards the ends of each fine structure. The temperature distribution over the entire temperature range is shown in panel d. Panel d also indicates the positions of the vertical cuts shown in panels e and f. Panels e and f demonstrate that the locations of highest pressure coincide with the locations of lowest temperature. However, not all regions of the cool plasma necessarily correspond to the high pressure areas.
, and T > 30, respectively. These panels demonstrate that the plasma at different temperatures tends to occupy distinct volumes of the modeled prominence. The cool plasma that can be visible in the Hα line forms a relatively compact structure clustered in the middle part of the modeled prominence volume. While we acknowledge that it is complicated to relate the 3D view of the temperature distribution in Fig. 5a with the synthetic Hα images, these clusters correspond to the main features visible in the synthetic Hα images shown in Figs. 5 and 6 in Paper I. The plasma with higher temperatures occupies a large volume that envelops the cool plasma. Although the hotter plasma also forms a narrow PCTR layer surrounding each fine structure in the direction across the magnetic field lines, the bulk of the PCTR plasma is located in the wide areas expanding along the magnetic field line towards the ends of each fine structure. The temperature distribution over the entire temperature range is shown in panel d. Panel d also indicates the positions of the vertical cuts shown in panels e and f. Panels e and f demonstrate that the locations of highest pressure coincide with the locations of lowest temperature. However, not all regions of the cool plasma necessarily correspond to the high pressure areas.
 |
Fig. 6 Dipped portions of the magnetic field lines from Snapshot 10 plotted in the top view (x-y plane) and the side view (x-z plane). Colors represent the plasma β values. The position of the positive polarity (solid blue contours) and negative polarity (dashed blue contours) of the inserted bipole is marked by contours corresponding to Bz values ±1, ±2, ±3, and ±4 G. The dashed box marks the area shown enlarged in Fig. 7. |
4. Plasma β distribution
The 3D WPFS model provides us with detailed information about the magnetic field strength and the plasma properties of the modeled prominence. This allows us to compute the value of the plasma β in the whole prominence volume. The plasma β is defined as the ratio of the gas pressure to the magnetic pressure. The magnetic pressure is defined as pmag = B2/ 8π, where B is the magnetic field strength in G. The plasma β is then given as 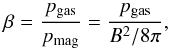 (1)where the gas pressure pgas is in units of dyn cm-2. For the case where the value of the plasma β is well below unity, the magnetic field is dominant and plasma does not deform the magnetic field configuration in which it is located. In contrast, if the value of the plasma β approaches or exceeds unity, the plasma has an influence on the magnetic field configuration and can change the shape of the field lines.
(1)where the gas pressure pgas is in units of dyn cm-2. For the case where the value of the plasma β is well below unity, the magnetic field is dominant and plasma does not deform the magnetic field configuration in which it is located. In contrast, if the value of the plasma β approaches or exceeds unity, the plasma has an influence on the magnetic field configuration and can change the shape of the field lines.
In Fig. 6 we show the dipped portions of the magnetic field lines of the modeled prominence in the same view as in Fig. 2, but now the colors represent the values of the plasma β. Figure 7 shows an enlarged view of the area marked in Fig. 6. From these figures it is clear that the modeled prominence consists mostly of very low-β plasma. However, a noticeable portion of field lines with plasma β values approaching unity is located above the negative polarity of the inserted bipole. We again focus here on Snapshot 10, but similar distributions of plasma β are exhibited in all snapshots considered in Paper II. The highest plasma β values occur in the bottom parts of the deep magnetic dips. These correspond to the location of the weakest magnetic field as shown in Figs. 2 and 3. These represent the prominence barb, not its main body. These deep dips also contain the highest pressure plasma. We list the maximum values of the plasma β and the gas pressure for all snapshots in Table 1. The minimum plasma β value over all snapshots is less than 0.05.
 |
Fig. 7 Enlarged view of the x-z plane showing the dipped magnetic field lines. The z-axis dimension is enlarged five times to emphasize the depth of the dips. Colors represent the plasma β values. This view corresponds to the area marked by the dashed box in Fig. 6. |
5. Mass of the prominence plasma
From the detailed 3D temperature and gas pressure distributions of the prominence plasma, as provided by the WPFS model, we can also calculate the total mass of the prominence. To do this we first derive the plasma density by assuming the local hydrogen ionization degree i(x,y,z) of the form ![\begin{equation} \label{Eq:i_loc} i(x,y,z)=1-(1-i_{\rm min})\left[\frac{T_{\rm tr}-T(x,y,z)}{T_{\rm tr}-T_{0}}\right]^2 \end{equation}](/articles/aa/full_html/2016/08/aa27704-15/aa27704-15-eq30.png) (2)adapted from Eq. (3) in Paper I. Here imin = 0.3 is the estimated minimum value of the ionization degree, T0 and Ttr are the minimum and maximum temperatures, and T(x,y,z) represents the local temperature. We note that it is possible to obtain a more realistic estimate of the local ionization degree as carried out in the Hα visualization method of Heinzel et al. (2015). However, this can only be done for temperatures below 14 000 K. Therefore, to maintain the consistency over the whole temperature range considered here, we use Eq. (2) for all temperatures.
(2)adapted from Eq. (3) in Paper I. Here imin = 0.3 is the estimated minimum value of the ionization degree, T0 and Ttr are the minimum and maximum temperatures, and T(x,y,z) represents the local temperature. We note that it is possible to obtain a more realistic estimate of the local ionization degree as carried out in the Hα visualization method of Heinzel et al. (2015). However, this can only be done for temperatures below 14 000 K. Therefore, to maintain the consistency over the whole temperature range considered here, we use Eq. (2) for all temperatures.
For the local value of the mean molecular mass μ(x,y,z) of the hydrogen-helium plasma we take 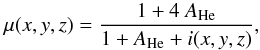 (3)where AHe = 0.1 is the helium-to-hydrogen abundance ratio. The density is then given by
(3)where AHe = 0.1 is the helium-to-hydrogen abundance ratio. The density is then given by 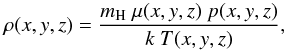 (4)where mH is the mass of the hydrogen atom, k is the Boltzmann constant, and p(x,y,z) represents the local value of the gas pressure. If we further assume that the volume of one grid cell has a uniform density, we can compute the mass of each grid cell and sum up all incremental masses to derive the total mass of the modeled prominence.
(4)where mH is the mass of the hydrogen atom, k is the Boltzmann constant, and p(x,y,z) represents the local value of the gas pressure. If we further assume that the volume of one grid cell has a uniform density, we can compute the mass of each grid cell and sum up all incremental masses to derive the total mass of the modeled prominence.
In Table 2 we list the values of the prominence mass for all snapshots considered in Paper II. We separate the listed mass into three temperature intervals – T < 14, 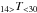 , and T > 30. The mass of the plasma in a given interval and the total mass vary significantly between individual snapshots. For example, the total mass of Snapshot 1 (10.3 × 1013 g) is three times lower than that of Snapshot 16 (31.1 × 1013 g). On the other hand, ratios of the mass in individual temperature intervals to the total mass vary only slightly between snapshots. On average the mass in the T< 14 interval represents around 70% of the total mass. The mass in the intervals
, and T > 30. The mass of the plasma in a given interval and the total mass vary significantly between individual snapshots. For example, the total mass of Snapshot 1 (10.3 × 1013 g) is three times lower than that of Snapshot 16 (31.1 × 1013 g). On the other hand, ratios of the mass in individual temperature intervals to the total mass vary only slightly between snapshots. On average the mass in the T< 14 interval represents around 70% of the total mass. The mass in the intervals 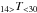 and T> 30 represent approximately 19% and 11% of the total mass, respectively. The total mass of the prominence plasma for each of the snapshots is in good agreement with the values obtained from observations (see Gilbert et al. 2006, 2011; Schwartz et al. 2015b).
and T> 30 represent approximately 19% and 11% of the total mass, respectively. The total mass of the prominence plasma for each of the snapshots is in good agreement with the values obtained from observations (see Gilbert et al. 2006, 2011; Schwartz et al. 2015b).
Mass of the prominence plasma in all snapshots divided into three temperature intervals – T < 14, 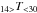 , and T > 30.
, and T > 30.
6. Discussion
It can be argued that the overall level of the magnetic field strength found in the modeled prominence presented in Sect. 2 is rather low, especially for prominences associated with active regions. The field strength values presented in Figs. 2 and 3 are, in fact, at the limit of present capabilities of current observational techniques (see, e.g., Casini et al. 2009; Orozco Suárez et al. 2014). However, the distribution of the photospheric magnetic flux used in this paper represents the typical flux of a decaying active region and ephemeral region. While it is possible to increase the amount of the magnetic flux within the photospheric flux distribution and thus increase the field strength in the modeled prominence, the values of the photospheric flux used lie in the middle of the observationally constrained range. Therefore, a weaker magnetic flux can also be realistically considered, which would lead to an even weaker field inside the modeled prominence. This suggests that such low values of the magnetic field strength might be possible in both the quiescent (see, e.g., Casini et al. 2003; Orozco Suárez et al. 2014) and the active region non-erupting prominences. We note that the scope for scaling the amount of photospheric flux up or down in the modeled prominence is limited to a factor of 2−5.
The spatial distribution of the magnetic field strength and its orientation in the modeled prominence, is mostly uniform and smooth (Figs. 2 and 3). This is especially true when compared to the typical observed widths of prominence fine structures (around 1000 km or lower). It means that the variation of both the field strength and its orientation along any line of sight (LOS) through the modeled prominence would be minimal.
If real prominences behave in this manner, this might contribute to the reliability of the techniques used to infer the properties of the magnetic field from prominence polarimetric observations. These techniques use inversion methods relying on simplified prominence models and provide line-of-sight-averaged information about the magnetic field strength and orientation (see, e.g., López Ariste 2015, for a review). Therefore, if the magnetic field does not vary significantly along a given LOS, values inferred from observations would better represent reality. However, even for the case of the relatively simple photospheric flux distribution used in this modeled prominence, it is possible to encounter field strength variations of up to 50% along some lines of sight. Even more significant LOS variations would be expected in some parts of observed prominences, especially those produced from complex photospheric flux distributions. Nevertheless, even in cases where the absolute difference of the field strength values along a given LOS are large, the spatial variation on the scale of a thousand kilometers is minimal.
In the WPFS model, the plasma variation in the direction perpendicular to the magnetic field lines is not determined by variations in the magnetic field that occur in the same direction. Instead, we use an empirically prescribed plasma variation (see Paper I) to produce the plasma fine structures with cross-sectional dimensions of 1000 km. We now consider how these structures may arise. The first possible scenario is that there is a local mass loading procedure. This procedure would have to preferentially load mass on selected field lines, such that the width of the plasma across the field would produce the observed cross-field structure (with dimensions as low as a few hundreds kilometers; see, e.g., Lin et al. 2005). Such a local mass loading procedure is required for the prominence modeled here, as the magnetic field configuration used does not vary significantly in the direction perpendicular to the magnetic field lines. This means that very few isolated, dipped magnetic structures with a cross-field dimension on the scale of a thousand kilometers are produced. Rather, the dipped regions extend across the whole width of the prominence with varying depth of the local magnetic dips. Thus, to avoid loading such a large-scale dipped region with mass and producing a single continuous plasma slab of width on the order of 10 000 km extent, we require a localized mass loading procedure. As yet this mass loading procedure has not been identified. One of the possible mechanisms of prominence formation-the thermal non-equilibrium evaporation-condensation model-was developed by Antiochos et al. (1999) and has been further explored by e.g., Karpen et al. (2006), Luna et al. (2012), Xia & Keppens (2016), see also Karpen (2015). This mechanism produces a deposition of the prominence plasma onto individual field lines or small-scale bundles of them. Such locally deposited plasma would be unable to move across the field lines, which in principle could result in very fine plasma structures. In this case, the cross-field dimensions of the resulting plasma fine structures would be dependent on the geometrical extent of the heating process causing the evaporation.
In contrast, it is possible that the physical process of loading mass into the prominence works on a larger scale and uniformly deposits plasma into the magnetic field. In order to avoid producing a large-scale single slab plasma structure, the prominence magnetic field would need to have large variations on scales below 1000 km. Such large variations would create small-scale magnetic field structures, where the depth of the magnetic dips on neighboring field lines would change significantly from dipped to non-dipped on scales smaller than 1000 km. Such small-scale magnetic structures can be produced for example as gravity-induced dips in the models of Heinzel & Anzer (2001, see Fig. 4 therein). A possible way of introducing more cross-field structure into the magnetic field of the modeled prominence, and removing the uniformity, is to include a much more complicated distribution of the photospheric field. This could be done by including a full magnetic carpet description rather than just a single magnetic bipole. It is, however, not clear that such a complicated photospheric field would produce variations in the corona at the required scales because magnetic field simulations that use extrapolations of the observed photospheric flux distributions to produce 3D configurations of the prominence magnetic field have not yet produced such small-scale variations (see, e.g., Dudík et al. 2008; Su & van Ballegooijen 2012).
Small-scale plasma structures may also be caused by dynamic processes, such as small-scale mass flows along bundles of field lines (see, e.g., Schmieder et al. 2010), prominence fine structure oscillations (see, e.g., Ballester 2014) or turbulent upflows (as reported by Berger et al. 2010, 2011 and studied by e.g., Hillier et al. 2012). Such dynamical processes may lead to either a break-up of the large-scale plasma structures or to an increase in the spatial variation of the prominence magnetic field, thus creating small-scale magnetic structures. Another possible physical process producing small-scale plasma structures is the deformation of the magnetic field due to the loss of the force-free field condition (see, e.g., Hillier & van Ballegooijen 2013).
Although not considered in the present study, the deformation of magnetic dips due to the presence of high-pressure prominence plasma is, in principle, possible for the modeled prominence presented here. In Sect. 4 we show that when we assume a typical photospheric flux for a decaying active region and an ephemeral region, along with a realistic prominence plasma, we obtain a relatively large plasma β value in the small part of the prominence that has the deepest dips. Plasma with a relatively large β value is located at the bottom of the deep magnetic dips (see Figs. 6 and 7) where the prominence plasma has the highest pressure. The maximum values found for the plasma β are generally below unity, but approach it (see Table 1) in all snapshots apart from Snapshot 1 where the value is much higher. The large plasma β value found in Snapshot 1 is a consequence of numerical effects occurring shortly after the bipole is inserted. It is interesting to note that the large plasma β values occur in deep dips accommodating high pressure plasma, which have higher Hα visibility and so would be easier to observe.
The WPFS model provides us with a technique to obtain information about the distribution of the prominence plasma from magnetic field models. Therefore, we studied the variation of the plasma temperature and pressure within the volume of the modeled prominence. However, our semi-empirical technique cannot address either the dynamics or the origin of the prominence material. To study the dynamics, time-dependent non-linear simulations are necessary. In Fig. 5a we show the extent of the cool prominence plasma (T< 14) that may be visible in the Hα line, although its actual visibility also depends on the gas pressure. In comparison, panel c) shows the hotter plasma (T> 30) that may be visible in spectral lines with a higher formation temperature, for example the He ii 304 Å line. By comparing these two panels we can show that the modeled prominence has a significantly more extended shape in the hotter spectral lines than in the cooler lines, such as Hα. This offers an explanation for the observed differences of shapes and extents of solar prominences when simultaneously observed in different spectral lines. Such variations of the prominence plasma temperature distribution could be studied using differential emission measure curves. These curves have been obtained from observed prominences by e.g., Cirigliano et al. (2004) and Parenti & Vial (2007), and from the 2D prominence fine structure models by Gunár et al. (2011a,b). We will investigate the synthetic differential emission measure curves from the prominence plasma distributions provided by the 3D WPFS model in future studies.
Another physical property that we have studied is the prominence mass. The total mass of the prominence plasma in the entire temperature range in all snapshots (see Table 2) lies comfortably within the range of masses found from observations for non-eruptive prominences. For example, the results of Gilbert et al. (2006) show the median mass of quiescent prominences to be between 10 and 29 × 1013 g when derived in the 195 Å channel. Gilbert et al. (2011) give masses of several prominences between 1 and 8 × 1013 g when derived in the 368 Å and 625 Å channels, and between 7 and 21 × 1013 g when derived in 171 Å and 195 Å channels. The results of Schwartz et al. (2015b) show the median values of the prominence mass to be between 18 and 42 × 1013 g with some prominences with mass in excess of 100 × 1013 g. These results are in good agreement with, for example, the total mass of Snapshot 10, which is equal to 25.7 × 1013 g. The mass of the cool prominence plasma (T < 14) in this snapshot is 18.2 × 1013 g.
The distribution of the prominence mass between individual temperature intervals (T< 14, 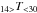 , and T> 30) shows that around 30% of the plasma in all snapshots has temperatures higher than 14 000 K and thus would not be visible in the Hα line. Such large differences suggest that the values of the prominence mass obtained from observations could depend significantly on the spectral lines used. This is in line with the results obtained by Gilbert et al. (2011) and Schwartz et al. (2015b), who show large differences between the prominence mass values obtained from different spectral channels.
, and T> 30) shows that around 30% of the plasma in all snapshots has temperatures higher than 14 000 K and thus would not be visible in the Hα line. Such large differences suggest that the values of the prominence mass obtained from observations could depend significantly on the spectral lines used. This is in line with the results obtained by Gilbert et al. (2011) and Schwartz et al. (2015b), who show large differences between the prominence mass values obtained from different spectral channels.
We note that the values listed in Table 2 represent the upper limit of the modeled prominence mass. This is a consequence of assuming a 100% filling of the independent prominence fine structures (for more details see Gunár & Mackay 2015a). However, the 100% filling of the independent prominence fine structures does not correspond to a filling factor of 1. The entire volume of the modeled prominence is not filled with prominence plasma (for illustration see Fig. 5, panels e and f). The 100% filling of all independent fine structures means that we fill all fine structures that are not overlapping with other fine structures.
An empirical estimate of the lower limit for the filling of the modeled prominences could be provided by their appearance in the synthetic Hα images. In the case where we fill only 25% of the independent structures, the modeled prominence loses its vertical features apparent in the synthetic Hα images and starts to appear as a collection of isolated horizontal threads (see Fig. 5 in Gunár & Mackay 2015a). Such a prominence structure does not correspond to the properties of the most observed prominences. Therefore, a filling of about a quarter of the independent prominence fine structures could be empirically assumed to represent the lower mass-loading limit for the modeled prominence. This would provide us with the lower limit for the prominence masses that would correspond to a factor of 1/4 of the values listed in Table 2.
A theoretical estimate for the amount of filling in modeled prominences can be obtained, for example, from the criterion described by Karpen et al. (2003). This criterion provides an estimate for a critical value of the ratio between the depth and the half-length of the magnetic dips above which the prominence plasma condensations will remain inside the dips. For the case of a steady asymmetrical foot-point heating and a symmetrical shape of the magnetic dips, the estimated value of this ratio is approximately 9%. This translates into a ratio of the dip depth to its full length of around 4.5%. In Fig. 8 we show a scatter plot of the depth and the length of all magnetic dips from Snapshot 10 along with the Karpen et al. (2003) criterion. This indicates that many of the dips from Snapshot 10 would be too shallow to accommodate the prominence plasma condensations if the mass loading model from Karpen et al. (2003) were assumed. However, the magnetic dips from the 3D WPFS models are, in general, asymmetrical. This means that the slope of the dips can be different on each side of the dip. This will result in different values of the critical ratio of the depth to the half-length for individual dips, depending on the assumed asymmetry of the foot-point heating. Therefore, the criterion displayed in Fig. 8 can provide only a rough estimate of the number of filled dips, all of which is based on the evaporation-condensation mass loading model of Karpen et al. (2006). However, there are other models of mass loading that do not depend on field line geometry (see Sect. 3 of Mackay et al. 2010). Moreover, even those dips with the depth below the Karpen et al. (2003) criterion could contain dynamic cool plasma for a shorter time. A more detailed study of such a theoretical mass-loading estimate will be needed in the future.
 |
Fig. 8 Depth and the length of all magnetic dips from Snapshot 10. The blue solid line indicates the critical ratio (4.5%) of the dip depth to its full length derived from the Karpen et al. (2003) criterion. |
7. Conclusions
We use the 3D WPFS model developed in Paper I to analyze the distribution of the magnetic field strength, prominence plasma temperature, pressure, and plasma β. We also compute the mass of the prominence plasma. In the present paper we mainly focus on a single snapshot of the magnetic field from the NLFF simulations of Mackay & van Ballegooijen (2009) identified in Paper II as Snapshot 10. In addition to considering Snapshot 10, we also follow the variation of the analyzed quantities during the evolution of the modeled prominence.
We do not attempt to relate the results of this analysis to any particular observed prominence. Our aim is to showcase the abilities of the 3D WPFS model and highlight the areas where this new class of prominence model can help us to further our understanding of solar prominences. The WPFS model provides information about the 3D magnetic field configuration and the local prominence plasma distributed along numerous fine structures. This unique combination allows us for the first time to study the basic physical properties of prominences in great detail and to relate the 3D distributions of various physical quantities to each other.
Our analysis of the magnetic field configuration of the modeled prominence shows that the magnetic field strength and its orientation do not vary significantly on scales of a thousand kilometers. This finding might contribute to the reliability of the inversion techniques used to infer the magnetic field from spectropolarimetric observations. More importantly, the fact that the prominence magnetic field does not contain small-scale magnetic structures in which the depth of the magnetic dips on neighboring field lines changes significantly means that a large-scale uniform mass-loading process could not lead to the production of prominence plasma fine structures comparable with observations. To produce such small-scale plasma structures we need either a localized mass-loading process or a magnetohydrodynamical evolution process that breaks up the initial large-scale prominence magnetic field structures.
The combined information on the magnetic field and plasma distributions within the modeled prominence allows us to study the plasma β distribution within the whole prominence volume. We show that, when a typical photospheric magnetic flux distribution and realistic prominence plasma parameters are assumed, the plasma β is small in most of the modeled prominence. However, we also find that the plasma β in the region with the deepest magnetic dips may increase towards unity. This may lead to the deformation of the prominence magnetic field configuration.
The 3D WPFS model also represents a unique tool for the study of the spatial distribution of the prominence plasma with respect to its temperature. We are able to distinguish the volumes occupied by the plasma at different temperatures, which provides us with an insight into the shape and extent of the PCTR – the region important for the formation of the various spectral lines used for prominence observations. This investigation demonstrates that the 3D WPFS model may offer an explanation for the significant differences in the shape of the observed prominences when different spectral lines are used.
Moreover, the detailed information available about the distribution of the plasma in the modeled prominence, allows us to compute its mass. The WPFS model also enables us to study the distribution of the prominence mass at different plasma temperatures and follow its variation during the evolution of the modeled prominence. The computed prominence mass values sit within the middle of the range of observed values. This shows that the WPFS model considered in this paper might serve as a good representation for non-eruptive prominences.
Acknowledgments
S.G. acknowledges support from the grant 16-17586S of the Czech Science Foundation (GA ČR). S.G. acknowledges support from the European Commission via the Marie Curie Actions – Intra-European Fellowships Project No. 328138. DHM acknowledges financial support from the STFC, the Leverhulme Trust, and NASA. We thank the referee for constructive comments that added greater depth to this paper. CloudCompare – 3D point cloud and mesh processing open source software – and Coyote’s IDL routines were used for the visualization of the results presented in this paper.
References
- Antiochos, S. K., MacNeice, P. J., Spicer, D. S., & Klimchuk, J. A. 1999, ApJ, 512, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Ballester, J. L. 2014, in IAU Symp. 300, eds. B. Schmieder, J.-M. Malherbe, & S. T. Wu, 30 [Google Scholar]
- Berger, T., Testa, P., Hillier, A., et al. 2011, Nature, 472, 197 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Berger, T. E., Slater, G., Hurlburt, N., et al. 2010, ApJ, 716, 1288 [NASA ADS] [CrossRef] [Google Scholar]
- Casini, R., López Ariste, A., Tomczyk, S., & Lites, B. W. 2003, ApJ, 598, L67 [NASA ADS] [CrossRef] [Google Scholar]
- Casini, R., López Ariste, A., Paletou, F., & Léger, L. 2009, ApJ, 703, 114 [Google Scholar]
- Cirigliano, D., Vial, J., & Rovira, M. 2004, Sol. Phys., 223, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Dudík, J., Aulanier, G., Schmieder, B., Bommier, V., & Roudier, T. 2008, Sol. Phys., 248, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Gilbert, H. R., Falco, L. E., Holzer, T. E., & MacQueen, R. M. 2006, ApJ, 641, 606 [NASA ADS] [CrossRef] [Google Scholar]
- Gilbert, H., Kilper, G., Alexander, D., & Kucera, T. 2011, ApJ, 727, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Gunár, S. 2014, in IAU Symp. 300, eds. B. Schmieder, J.-M. Malherbe, & S. T. Wu, 59 [Google Scholar]
- Gunár, S., & Mackay, D. H. 2015a, ApJ, 803, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Gunár, S., & Mackay, D. H. 2015b, ApJ, 812, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Gunár, S., Heinzel, P., Schmieder, B., Schwartz, P., & Anzer, U. 2007, A&A, 472, 929 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gunár, S., Heinzel, P., Anzer, U., & Schmieder, B. 2008, A&A, 490, 307 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gunár, S., Schwartz, P., Schmieder, B., Heinzel, P., & Anzer, U. 2010, A&A, 514, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gunár, S., Heinzel, P., & Anzer, U. 2011a, A&A, 528, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gunár, S., Parenti, S., Anzer, U., Heinzel, P., & Vial, J.-C. 2011b, A&A, 535, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gunár, S., Mackay, D. H., Anzer, U., & Heinzel, P. 2013, A&A, 551, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heinzel, P., & Anzer, U. 2001, A&A, 375, 1082 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heinzel, P., Anzer, U., & Gunár, S. 2005, A&A, 442, 331 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heinzel, P., Gunár, S., & Anzer, U. 2015, A&A, 579, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hillier, A., & van Ballegooijen, A. 2013, ApJ, 766, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Hillier, A., Berger, T., Isobe, H., & Shibata, K. 2012, ApJ, 746, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Karpen, J. T. 2015, in Solar Prominences, eds. J.-C. Vial, & O. Engvold, Astrophys. Space Sci. Library, 415, 237 [Google Scholar]
- Karpen, J. T., Antiochos, S. K., Klimchuk, J. A., & MacNeice, P. J. 2003, ApJ, 593, 1187 [NASA ADS] [CrossRef] [Google Scholar]
- Karpen, J. T., Antiochos, S. K., & Klimchuk, J. A. 2006, ApJ, 637, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Labrosse, N., Heinzel, P., Vial, J., et al. 2010, Space Sci. Rev., 151, 243 [Google Scholar]
- Lin, Y., Engvold, O., Rouppe van der Voort, L., Wiik, J. E., & Berger, T. E. 2005, Sol. Phys., 226, 239 [NASA ADS] [CrossRef] [Google Scholar]
- López Ariste, A. 2015, in Astrophys. Space Sci. Library 415, eds. J.-C. Vial, & O. Engvold, 179 [Google Scholar]
- Luna, M., Karpen, J. T., & DeVore, C. R. 2012, ApJ, 746, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Mackay, D. H., Karpen, J. T., Ballester, J. L., Schmieder, B., & Aulanier, G. 2010, Space Sci. Rev., 151, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Mackay, D. H., & van Ballegooijen, A. A. 2006, ApJ, 641, 577 [NASA ADS] [CrossRef] [Google Scholar]
- Mackay, D. H., & van Ballegooijen, A. A. 2009, Sol. Phys., 260, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Orozco Suárez, D., Asensio Ramos, A., & Trujillo Bueno, J. 2014, A&A, 566, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parenti, S. 2014, Liv. Rev. Sol. Phys., 11, 1 [Google Scholar]
- Parenti, S., & Vial, J.-C. 2007, A&A, 469, 1109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmieder, B., Chandra, R., Berlicki, A., & Mein, P. 2010, A&A, 514, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schwartz, P., Gunár, S., & Curdt, W. 2015a, A&A, 577, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schwartz, P., Heinzel, P., Kotrč, P., et al. 2015b, A&A, 574, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Su, Y., & van Ballegooijen, A. 2012, ApJ, 757, 168 [NASA ADS] [CrossRef] [Google Scholar]
- van Ballegooijen, A. A., & Su, Y. 2014, in IAU Symp. 300, eds. B. Schmieder, J.-M. Malherbe, & S. T. Wu, 127 [Google Scholar]
- van Ballegooijen, A. A., Priest, E. R., & Mackay, D. H. 2000, ApJ, 539, 983 [NASA ADS] [CrossRef] [Google Scholar]
- Vial, J.-C., & Engvold, O. 2015, in Solar Prominences, Astrophys. Space Sci. Libr., 415 [Google Scholar]
- Xia, C., & Keppens, R. 2016, ApJ, 823, 22 [Google Scholar]
All Tables
List of the minimum and maximum values of the magnetic field strength (in G), maximum gas pressure (in dyn cm-2), and the maximum values of the plasma β in all snapshots.
Mass of the prominence plasma in all snapshots divided into three temperature intervals – T < 14, 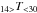 , and T > 30.
, and T > 30.
All Figures
 |
Fig. 1 Photospheric flux distribution of the modeled prominence is shown, together with the representative dipped (purple) and non-dipped (blue) field lines. For the flux distribution white/black represents possitive/negative flux. |
| In the text | |
 |
Fig. 2 Dipped portions of the magnetic field lines from Snapshot 10 plotted in the top view (x-y plane) and the side view (x-z plane). Colors represent the magnetic field strength in G. The position of the positive polarity (solid blue lines) and negative polarity (dashed blue lines) of the inserted bipole is marked by contours corresponding to Bz values ±1, ±2, ±3, and ±4 G. The dashed box marks the area shown enlarged in Fig. 3. |
| In the text | |
 |
Fig. 3 Enlarged view of the x-z plane showing the dipped magnetic field lines. The z-axis dimension is enlarged five times to emphasize the depth of the dips. Colors represent the magnetic field strength in G. This view corresponds to the area marked by the dashed box in Fig. 2. |
| In the text | |
 |
Fig. 4 Distribution of temperature (left) and gas pressure (right) in a single 3D prominence fine structure along a single dipped field line. Panels b) and d) show cross-sectional cuts. We note that every cut showing the temperature in panel b) is surrounded by a very narrow red ring that represents the PCTR temperatures. The invisibility of these rings in some cuts is solely due to the visualization procedure. |
| In the text | |
 |
Fig. 5 Temperature and gas pressure distribution in all prominence fine structures from Snapshot 10. Panel a) shows temperature between 7000 and 14 000 K (T< 14), panel b) temperature between 14 000 and 30 000 K ( |
| In the text | |
 |
Fig. 6 Dipped portions of the magnetic field lines from Snapshot 10 plotted in the top view (x-y plane) and the side view (x-z plane). Colors represent the plasma β values. The position of the positive polarity (solid blue contours) and negative polarity (dashed blue contours) of the inserted bipole is marked by contours corresponding to Bz values ±1, ±2, ±3, and ±4 G. The dashed box marks the area shown enlarged in Fig. 7. |
| In the text | |
 |
Fig. 7 Enlarged view of the x-z plane showing the dipped magnetic field lines. The z-axis dimension is enlarged five times to emphasize the depth of the dips. Colors represent the plasma β values. This view corresponds to the area marked by the dashed box in Fig. 6. |
| In the text | |
 |
Fig. 8 Depth and the length of all magnetic dips from Snapshot 10. The blue solid line indicates the critical ratio (4.5%) of the dip depth to its full length derived from the Karpen et al. (2003) criterion. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


