| Issue |
A&A
Volume 592, August 2016
|
|
|---|---|---|
| Article Number | A139 | |
| Number of page(s) | 13 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201526672 | |
| Published online | 15 August 2016 | |
Possibility for albedo estimation of exomoons: Why should we care about M dwarfs?
1 Konkoly Thege Miklós Astronomical Institute, Research Centre for Astronomy and Earth Sciences, Hungarian Academy of Sciences, 1121 Konkoly Thege Miklós út 15-17, Budapest, Hungary
e-mail: dobos@konkoly.hu
2 Sydney Institute for Astronomy, School of Physics A28, University of Sydney, NSW 2006, Australia
Received: 4 June 2015
Accepted: 4 June 2016
Occultation light curves of exomoons may give information on the exomoons’ albedo and hence indicate the presence of ice cover on the surface. Icy moons might have subsurface oceans, and thus may potentially be habitable. The objective of our paper is to determine whether next generation telescopes will be capable of albedo estimations for icy exomoons using their occultation light curves. The success of the measurements depends on the depth of the moon’s occultation in the light curve and on the sensitivity of the used instruments. We applied simple calculations for different stellar masses in the V and J photometric bands, and compared the flux drop caused by the moon’s occultation and the estimated photon noise of next generation missions with 5σ confidence. We found that albedo estimation by this method is not feasible for moons of solar-like stars, but small M dwarfs are better candidates for such measurements. Our calculations in the J photometric band show that E-ELT MICADO’s photon noise is just about 4 ppm greater than the flux difference caused by an icy satellite twice the Earth’s radius in a circular orbit at the snowline of an 0.1 stellar mass star. However, considering only photon noise underestimates the real expected noise, because other noise sources, such as CCD read-out and dark signal become significant in the near-infrared measurements. Hence we conclude that occultation measurements with next generation missions are far too challenging, even in the case of large, icy moons at the snowline of small M dwarfs. We also discuss the role of the parameters that were neglected in the calculations, for example inclination, eccentricity, orbiting direction of the moon. We predict that the first albedo estimations of exomoons will probably be made for large icy moons around the snowline of M4 – M9 type main sequence stars.
Key words: planets and satellites: surfaces / methods: numerical / planets and satellites: detection / occultations
© ESO, 2016
1. Introduction
The solar system provides useful analogues to extrapolate extrasolar satellite properties. The satellites of the giant planets hold substantial masses of water ice that is often located on the surface (Brown & Cruikshank 1997; Verbiscer et al. 1990). Although there could be differences between satellite systems, the icy surface, including water ice, is abundant on them (Stevenson 1985; Sasaki et al. 2010). Analysing the optical properties of the solar system satellites, it can be seen that the high albedo in general indicates water ice. Non-ice covered satellites usually show low geometric albedo values between 0.04 and 0.15, while ice-covered satellites show higher values, although different ingredients (mostly silicate grains) could decrease the albedo if they are embedded in the ice, or the ice is old and strongly irradiated/solar gardened (Grundy & Stansberry 2000; Sheppard et al. 2005). These satellites show moderate geometric albedo between 0.21 for Umbriel and 0.99 for Dione (Veverka et al. 1991; Verbiscer et al. 2013). Beside water ice, nitrogen ice is also a strong reflector, producing albedo around 0.76 on Triton (Hicks & Buratti 2004). On this satellite the bright surface can partly be explained by its relatively young, 6−10 Myr old age. (Schenk & Zahnle 2007). The most important analogues for high albedo in the solar system could be Europa with 1.02 and Enceladus with 1.38 geometric albedo (Verbiscer et al. 2013). In the case of Europa the relatively young (about 50 million year old) surface is accompanied by clean and bright ice, while on Enceladus freshly fallen ice crystals increase the albedo significantly (Pappalardo et al. 1999; Porco et al. 2006). Based on these observations, we assume that geometric albedo above around 0.7 indicates some ice, often water ice, with relatively young surface, and higher albedo might suggest freshly fallen water ice crystals. In this work we are analysing exomoons with such high albedo, as it might give insight into their surface properties.
For exomoon detection, current techniques mostly focus on light curve analysis (Kipping 2009a,b; Kipping et al. 2009, and references therein). The concept is that the exomoon alters the light curve in a specific and identifiable way (Szabó et al. 2006; Simon et al. 2007). Other methods also have been proposed, such as direct imaging (Peters & Turner 2013), radial velocity measurements (Simon et al. 2010), microlensing (Liebig & Wambsganss 2010; Bennett et al. 2014), or pulsar timing (Lewis et al. 2008). In this work we discuss how the light curves of occultations can provide insights for albedo estimation.
Habitability is also a focus for research on exomoons. Heller & Barnes (2013) developed a model for calculating the incident flux on an exomoon arriving from stellar irradiation, reflective light from the planet, thermal radiation of the planet and from tidal heating of the moon. They also considered eclipses as possible energy sinks. Too much incident flux on a moon can trigger the runaway greenhouse effect, which leads to the loss of water reservoirs on the body, hence making it uninhabitable (Kasting 1988). Forgan & Kipping (2013) developed a climate model for exomoons to investigate the energy balance of satellites. This model combined with eclipses and the ice-albedo feedback is capable of predicting the orbital parameters of a moon that will result in a snowball state, defining an outer limit for the exomoon habitable zone (Forgan & Yotov 2014; Forgan & Dobos 2016).
M dwarfs could have specific characteristics regarding the exomoon identification and analysis. Although most search projects focus on solar-like stars, M dwarfs as targets should also be considered, because of more than 70% of the stars are of M spectral type. In theory it is possible that no large exomoons are present around M dwarfs, as their smaller stellar mass allow the formation of only smaller exoplanets and exomoons than in the solar system. But based on the discovered exoplanets currently 68 M dwarfs are known to have 96 exoplanets, from which the heaviest planet’s mass is 62 MJ, 20 other exoplanets have at least 10 Jupiter-masses, and there are 13 other planets that are heavier than 1 MJ (source: exoplanet.eu, January 2016). The average mass of the exoplanets of the 68 M dwarfs is 4.8 MJ.
The mass of a moon is limited by the mass of its host planet (Crida & Charnoz 2012) and the mass of satellite systems is usually proportional to the mass of their host planet. Canup & Ward (2006) showed that this might be the case for extrasolar satellite systems as well, giving an upper limit for the mass ratio at around 10. Thus ten Jupiter-mass planets may have 0.3 Earth-mass satellites. However, if the moon did not originate from the circumplanetary disk, but from collision, as in the case of the Earth’s Moon, then even larger satellites might exist.
Moons are more likely to form by ejection around Neptune than around Jupiter-like giants because Jupiter-like gas giants are composed of mostly liquid and gaseous hydrogen at their outer layers, thus the ejected satellite-forming material might be H2O poor, composed mostly of gaseous H2 and could easily escape. But if this event happens before the dispersion of the circumplanetary disk, the co-accreted ice in the disk could lead to an icy surface for such satellite. Neptune-like planets seem to be better candidates. They are mainly composed of H2O, and the ejected satellite, too. The occurrence of impacts at giant planets are favoured by certain theories, as a contributor to the continuous gas accretion (Broeg & Benz 2012), increasing the probability of impact-ejected icy satellites.
Besides ejection, capture could also produce a large moon. In the so-called binary-exchange captures, a terrestrial-sized moon can be captured by a planet five times Jupiter’s radius around an M dwarf, if the planetary encounter is close enough (Williams 2013). For Neptune-mass planets the capture is easier than for Jupiter-mass planets, because generally the encounter speeds are lower. The capturing is much more difficult at small stellar distances, but if it occurs before or during the planetary migration, then it is possible that such a planet-moon pair will orbit an M dwarf at a close distance (around the snowline). In the solar system, Triton may be an example for such binary-exchange capture (Agnor & Hamilton 2006). For these reasons we consider the existence of large exomoons (up to a few Earth-masses) of Neptune-mass planets around M dwarfs.
The aim of this work is to propose a new method to identify elevated albedo and thus the possibility of water ice on the surface of an exomoon using photometric measurements during occultations. We also discuss the role of different orbital and physical parameters that may influence the observed data. As in the case of exomoons, surface ice cover might be more frequent than for exoplanets, based on examples of the solar system and theoretical argumentation. Although the photometric signal would be small, it is worth considering the possibility and potential results of such measurements, because of the following reasons: the findings might orient the instrumental development, and search programmes to focus on given stellar type, and also give a hint about surface properties of exomoons, or provide information on their habitability. Analysing different configurations helps to see the best possibility to estimate exomoons’ albedo. We also aim to compare the scale and possible role of such configurations of exomoons that are realistic but not present in the solar system. Just as in the case of exoplanets, unusual situations could be present and occasionally dominate because of observational selection effects (see for example the case of many hot Jupiters during the first decade of exoplanet discoveries). In this work we analyse these possibilities, indicating the difficulties, possible ways and best conditions for such estimation.
Although such precise measurements are difficult to make, the method could be used to differentiate among exomoon surface properties. Despite no exomoon having been discovered yet, they are probably numerous in other planetary systems, and will play an important role in astrobiology research in the future (Kaltenegger 2010; Heller & Barnes 2013) providing a rationale to elucidate the potential method outlined here. Because of the large number of possible configurations and different parameters of exomoon systems, specific cases are considered in this paper with the aim of giving general insights about the factors that are important for albedo estimation. We also consider such possible conditions that are not present in the solar system but could be observed in certain exomoons, for example large exomoons, and objects on eccentric, inclined, or retrograde orbits (Sect. 4.2).
The structure of this paper is as follows. In Sect. 2 we describe the numerical treatment to determine the albedo of an exomoon and the photon noise level of different instruments. In Sect. 3 we present the results and consider both solar system objects and hypothetical moons to imply our calculations. In Sect. 4 we discuss the rationality and limitations of this method, followed by conclusions in Sect. 5.
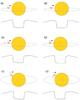 |
Fig. 1 Schematic light curve during an occultation with an exomoon orbiting its exoplanet with some different basic conditions: a1) exomoon occults after the exoplanet; a2) exomoon occults before the exoplanet; b1) observationally favourable case of large eccentricity increasing the plateau duration; b2) unfavourable case of large eccentricity decreases the plateau duration; c1) favourable case of large inclination (relative to the plane perpendicular to the line of sight); c2) unfavourable case of large inclination. The sizes of the objects are not to scale. |
2. Methods
In this section we present the background of albedo calculations from occultation light curve. Because of the wide range of possible conditions (distance of the moon from its host planet and host star, orbital elements, size, albedo etc.) only general and simple cases are used here. With this approach we obtain insight into the most important parameters without analysing all possibilities. The potential significance of those parameters that are not used in this model are discussed in Sect. 4.2.
Three different configurations are possible just before and after any occultation:
-
1.
the exomoon is behind the planet (both the planet and the moonare in the same line of sight);
-
2.
the exomoon is in front of the planet (both the planet and the moon are in the same line of sight);
-
3.
the exomoon and the planet are separately visible (although spatially not resolved).
It can be generally assumed that the configuration does not change much in most cases during the occultation. The reason is that the time duration of the occultation varies over a couple of hours time scale, while the orbital period of the exomoon is assumed to be longer (Cabrera & Schneider 2007). A reverse scenario is unlikely, but also discussed by Simon et al. (2010) and Sato & Asada (2010).
From the three possible configurations, the third (3) is the one which favours the identification of the exomoon, since in the other cases the moon’s presence does not change the shape of the light curve (although the depth of the flux minimum can be different). The third configuration is also the most probable of all, based on geometric considerations (Heller 2014). Apart from a few special cases, the moon spends just a small fraction of its orbital time in front of or behind the planet (Heller 2012). In this (third) case two sub-configurations are possible: the planet occults before the moon (a1 in Fig. 1), or the moon occults before the planet (a2 in Fig. 1). These cases can be seen in Fig. 1. along with schematic light curves. Note that unlike at transits, stellar limb darkening does not affect the light curve at occultations.
2.1. Albedo
We use simple formulae for the calculations, because this is a basic phenomenon of exomoons that has not been analysed before. Simplified cases are considered because of the large number of possibilities and also to see the big picture without being lost in the details.
For the albedo calculation we considered the following formulae and configuration. Figure 2 shows a schematic light curve of an occultation, assuming that first the planet moves behind the star, followed by the moon (case a1 in Fig. 1). The light curve has its maximum at y1 and the minimum of the occultation is at y4. The latter corresponds to the stellar flux (the planet and the moon are behind the star), denoted by F⋆ which is normalised so that F⋆ = 1. Reflected stellar light from the planet and from the moon give contributions to the observed flux. Values of y3 and y2 refer to the measured flux before the occultation of the moon and after the occultation of the planet (the moon is still occulting), respectively. Measuring both y1−y2 and y3−y4 can be used to refine their value (which should be equal in theory), assuming that the apparent configuration of the system does not significantly change during the occultation. The accuracy of this value is very important, because it plays a key role in calculating the moon’s albedo.
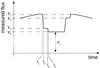 |
Fig. 2 Schematic representation of the light curve (case a1 in Fig. 1) during the occultation of an exoplanet with an exomoon. |
For the difference of the measured fluxes 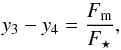 (1)where Fm/F⋆ is the relative flux contribution of the moon normalised to the stellar flux. The flux contribution of the planet is irrelevant for our study. We call the y3−y4 difference moon occultation (MO) depth. Adapting Eq. (2) from Rowe et al. (2008) to this case, the ratio of the fluxes can also be written as
(1)where Fm/F⋆ is the relative flux contribution of the moon normalised to the stellar flux. The flux contribution of the planet is irrelevant for our study. We call the y3−y4 difference moon occultation (MO) depth. Adapting Eq. (2) from Rowe et al. (2008) to this case, the ratio of the fluxes can also be written as 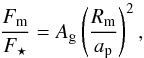 (2)where Ag is the geometric albedo, Rm is the radius and ap is the distance of the exomoon from its host star, which is approximated by the semi-major axis of the planet. The radius of the moon is assumed to be already known from previous transit observations. The geometric albedo is the ratio of brightness at zero phase angle compared to an idealised, flat, fully reflecting, diffusively scattering disk. The Bond albedo on the other hand, is the reflectivity at all phase angles. The value of the Bond albedo is restricted between zero and one. The geometric albedo on the other hand, can occasionally be higher than one, especially for atmosphereless bodies with icy surface (e.g. Enceladus, Tethys) because of the strong backscattering and opposition effect (Verbiscer et al. 2007). Because of the coherent backscatter opposition effect (CBOE), the phase difference of the lightwaves in the exact backscatter direction will be zero and the amplitudes add coherently as they interfere with each other, resulting in higher intensity up to a factor of two (Hapke 2012; Verbiscer et al. 2013).
(2)where Ag is the geometric albedo, Rm is the radius and ap is the distance of the exomoon from its host star, which is approximated by the semi-major axis of the planet. The radius of the moon is assumed to be already known from previous transit observations. The geometric albedo is the ratio of brightness at zero phase angle compared to an idealised, flat, fully reflecting, diffusively scattering disk. The Bond albedo on the other hand, is the reflectivity at all phase angles. The value of the Bond albedo is restricted between zero and one. The geometric albedo on the other hand, can occasionally be higher than one, especially for atmosphereless bodies with icy surface (e.g. Enceladus, Tethys) because of the strong backscattering and opposition effect (Verbiscer et al. 2007). Because of the coherent backscatter opposition effect (CBOE), the phase difference of the lightwaves in the exact backscatter direction will be zero and the amplitudes add coherently as they interfere with each other, resulting in higher intensity up to a factor of two (Hapke 2012; Verbiscer et al. 2013).
From Eqs. (1) and (2) we obtain 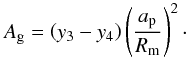 (3)The geometric albedo of an exomoon can be calculated by obtaining the MO depth from observations during occultation, and by using Eq. (3). However, very precise measurements are required, hence it is reasonable to consider the MO depth as an upper limit (Rowe et al. 2006). Several observations are needed for a phase-folded light curve that show the presence of the exomoon because of the photometric orbital sampling effect (Heller 2014).
(3)The geometric albedo of an exomoon can be calculated by obtaining the MO depth from observations during occultation, and by using Eq. (3). However, very precise measurements are required, hence it is reasonable to consider the MO depth as an upper limit (Rowe et al. 2006). Several observations are needed for a phase-folded light curve that show the presence of the exomoon because of the photometric orbital sampling effect (Heller 2014).
Using Eq. (3) we calculated the MO depth values for different bodies, in order to investigate the required precision of future observations. These photometric measurements may allow us to obtain the albedo of an exomoon using of the described method.
2.2. Calculation of “plateau duration” and “MO duration”
In order to achieve the detection of small flux differences, long enough detector integration time is required. An important limiting factor for detection is the duration while the exomoon is visible alone and the exoplanet is behind the star (the time interval t3−t2 in Fig. 2), or when only the exoplanet is visible without the moon. We call this phase plateau duration, because it causes a plateau in the light curve.
The plateau duration is calculated for ideal cases, when the exomoon is located at its maximum elongation from the exoplanet (where it has only radial velocity component). Circular orbits were assumed both for the planet and for the moon. This is a crude simplification, but in case of captured or impact-ejected moons (like Triton around Neptune or the Moon around the Earth) tidal interactions can strongly reduce the satellite’s eccentricity, almost circularising the orbit. With this simplified model the plateau duration can easily be calculated by using the speed of the planet-moon pair around the central star: 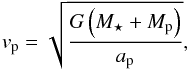 (4)where vp is the orbital speed of the planet, G is the gravitational constant, M⋆ and Mp are the masses of the star and the planet, respectively. Since circular orbits are considered, ap indicates the planet’s orbital distance. In most cases the apparent location of the moon does not change significantly during the occultation. For this reason the plateau duration can be estimated from the orbital speed of the planet, if the orbital distance of the moon (am) is known (this is the distance that the moon needs to travel after the planet disappears behind the star). If the moon was not in its maximal elongation, then the distance (and hence the plateau duration) would be shorter.
(4)where vp is the orbital speed of the planet, G is the gravitational constant, M⋆ and Mp are the masses of the star and the planet, respectively. Since circular orbits are considered, ap indicates the planet’s orbital distance. In most cases the apparent location of the moon does not change significantly during the occultation. For this reason the plateau duration can be estimated from the orbital speed of the planet, if the orbital distance of the moon (am) is known (this is the distance that the moon needs to travel after the planet disappears behind the star). If the moon was not in its maximal elongation, then the distance (and hence the plateau duration) would be shorter.
However, the moon can be fast enough on its own orbit around the planet to influence the plateau duration. In case the moon passes 25% of its orbit (starting from its maximal elongation) then we terminate the plateau duration, because the moon must be in front of or behind the planet. These cases were taken into account as well. The orbital speed of the moon (vm) was calculated by 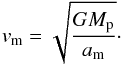 (5)Both time intervals were calculated: ta = am/vp and t25 = 0.25(2amπ)/vm, and the shorter was considered as the plateau duration (Tevent) in each case.
(5)Both time intervals were calculated: ta = am/vp and t25 = 0.25(2amπ)/vm, and the shorter was considered as the plateau duration (Tevent) in each case.
The plateau duration was calculated for host planets of different mass. It can be shown that having 1, 5, or 10 MJ mass planets (MJ denotes the mass of Jupiter) does not change the order of magnitude of the results. Table 1 shows such cases for two moons. The stellar distance is 3 AU in each case, and a Sun-like star was used in the calculations. For the calculation, the radius of the planet was calculated from the mean density (1326 kg/m) and original radius (71 492 km) of Jupiter in each case. For the orbital distance of the two moons the real semi-major axes were used.
Plateau duration for different planetary masses at 3 AU distance from a Sun-like star.
The plateau duration depends on many factors, including the exomoon’s apparent distance from its host planet, its orbital velocity and the size of the host star. Larger stellar disk, lower velocity and larger planetary distance of the moon increase the length of the plateau duration. If the apparent planet-moon distance is larger than the diameter of the star, then the plateau will not appear in the light curve, because the planet and the moon will occult separately, making two separate drops in the light curve (i.e. the planet’s occultation ends before the moon’s occultation starts or the moon’s occultation ends before the planet’s starts). In other words the occultations of the moon and the planet will not overlap in time. In this case the plateau duration is replaced by the duration of the moon’s occultation. We call it moon occultation duration, or MO duration.
In these cases, when the size of the star limits the MO duration, the following simple calculation was used. The velocity of the moon is already known from previous calculations, and the distance that the moon travels during the MO duration is approximately equal to the diameter of the star. Since it is assumed that the impact parameter of the moon and the inclination of both the planet and the moon are zeros, the related time can be calculated from tMO = 2R⋆/vp. If tMO<ta, then tMO will be considered as the MO duration (Tevent).
 |
Fig. 3 The so-called plateau duration for different stellar and planetary distances. The masses of the star and the planet are 1 solar mass and 1MJ, respectively, for all cases. Black and white colours indicate the longest (41 h) and the shortest (6 min) plateau durations, respectively. The dashed grey line separates those cases where the moon’s orbital velocity is high enough to reach 25% of its orbit before the plateau duration ends (in the bottom right corner). The solid horizontal white line at about 1 393 000 km (2 R⋆) indicates that the plateau duration is constant above this planetary distance. Examples from the solar system are plotted for comparison. |
The phase space of different stellar and planetary distances of a hypothetical moon was mapped. The plateau duration for different stellar and planetary distances can be seen in Fig. 3. Below the dashed grey line the plateau duration is terminated, because the moon reaches 25% of its orbit. It mainly occurs for higher stellar distances, which produces lower orbital velocity around the star. Because of this lower velocity t25 will be smaller than ta. The growing semi-major axis of the moon results in larger ta, but at the horizontal white line ta = tMO, or in other words, above this planetary distance the planet and the moon occults separately (the MO duration takes the place of the plateau duration).
2.3. Calculating the photon noise level of different instruments
Let us assume that the star emits perfect black-body radiation. This is a good assumption if we intend to estimate the photon noise level for a given instrument. The star is characterised by its radius R⋆ and T⋆, the effective temperature of the stellar surface. According to Planck’s law, the power density on unit surface and unit solid angle as the function of the wavelength λ can be written as 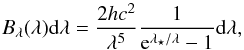 (6)where
(6)where 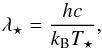 (7)
(7)
which is proportional to the location of the peak of the spectral energy distribution. The constants are the following: kB is the Boltzmann constant, h is the Planck constant and c is the speed of light. The integral over the stellar surface 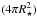 as well as on the irradiated hemisphere according to Lambert’s cosine law yields a total power output at a certain wavelength which can be computed as
as well as on the irradiated hemisphere according to Lambert’s cosine law yields a total power output at a certain wavelength which can be computed as 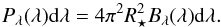 (8)The number of photons emitted at a certain wavelength can then be computed by dividing the power Pλ(λ) by the photon energy hc/λ. The total number of photons detected by a detector having a gross quantum efficiency of Q(λ) at unit time is then
(8)The number of photons emitted at a certain wavelength can then be computed by dividing the power Pλ(λ) by the photon energy hc/λ. The total number of photons detected by a detector having a gross quantum efficiency of Q(λ) at unit time is then 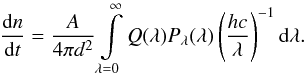 (9)Here A is the area of the entrance aperture on the telescope (on which the detector is mounted) and d is the distance to the star. In practical applications, Q(λ) is the product of the transparencies of various filters, lens and reflective elements forming the telescope optics and the quantum efficiency of the detector itself. In order to simplify our calculations, Q(λ) can be written as a characteristic function having a constant value of Q within an interval of [λmin,λmax] (and it is zero outside this interval). Let us define Δλ as the effective bandwidth of the filter as Δλ = λmax−λmin and the central wavelength as λf = (λmin + λmax) / 2.
(9)Here A is the area of the entrance aperture on the telescope (on which the detector is mounted) and d is the distance to the star. In practical applications, Q(λ) is the product of the transparencies of various filters, lens and reflective elements forming the telescope optics and the quantum efficiency of the detector itself. In order to simplify our calculations, Q(λ) can be written as a characteristic function having a constant value of Q within an interval of [λmin,λmax] (and it is zero outside this interval). Let us define Δλ as the effective bandwidth of the filter as Δλ = λmax−λmin and the central wavelength as λf = (λmin + λmax) / 2.
Using the assumption above, the total number of photons received at unit time can be written as 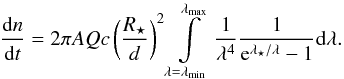 (10)
(10)
By introducing the variable x = λ⋆/λ and applying the respective measure of dλ = (λ⋆/x2)dx, we can write 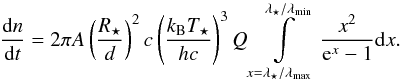 (11)If the bandwidth of the filter is narrow, that is Δλ ≪ λf, the integral above can further be simplified by assuming the expression x2(ex−1)-1 to be constant in the interval of [λ⋆/λmax,λ⋆/λmin]. In this case, Δx = xmax−xmin can be approximated as
(11)If the bandwidth of the filter is narrow, that is Δλ ≪ λf, the integral above can further be simplified by assuming the expression x2(ex−1)-1 to be constant in the interval of [λ⋆/λmax,λ⋆/λmin]. In this case, Δx = xmax−xmin can be approximated as 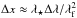 and hence the photon flow is
and hence the photon flow is 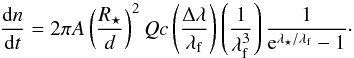 (12)Once the photon flow, that is the number of photons received by the detector is known, the photon noise of the instrument can be computed for any exposure time (T) as
(12)Once the photon flow, that is the number of photons received by the detector is known, the photon noise of the instrument can be computed for any exposure time (T) as 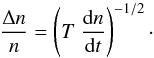 (13)If the filter bandwidth is comparable to the central wavelength, the integral in Eq. (11) can be computed numerically. Since the integrand is a well-behaved function, even a few steps using Simpson’s rule can be an efficient numerical method for this computation. We note that in the case of Kepler or TESS or PLATO 2.0, where CCDs are used without any filters, the bandwidth of the quantum efficiency curve is comparable to its central wavelength, so this numerical computation is more accurate. However, the error in the accuracy introduced by this simplification is comparable to the discretisation of the Q(λ) function (i.e. it is in the range of 10−20% in total, depending on the actual values of λ⋆, λf and Δλ).
(13)If the filter bandwidth is comparable to the central wavelength, the integral in Eq. (11) can be computed numerically. Since the integrand is a well-behaved function, even a few steps using Simpson’s rule can be an efficient numerical method for this computation. We note that in the case of Kepler or TESS or PLATO 2.0, where CCDs are used without any filters, the bandwidth of the quantum efficiency curve is comparable to its central wavelength, so this numerical computation is more accurate. However, the error in the accuracy introduced by this simplification is comparable to the discretisation of the Q(λ) function (i.e. it is in the range of 10−20% in total, depending on the actual values of λ⋆, λf and Δλ).
In order to apply Eq. (12) in practice, it is worth converting R⋆, d, λf and λ⋆ into astronomically relevant units (such as solar radius, parsec and microns) instead of SI units. After these substitutions, we can write the approximation 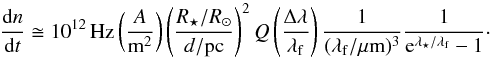 (14)This approximation is accurate within a few percents w.r.t. Eq. (12). In the constant 1012 Hz we included both the dimension conversions (solar radius, parsec, microns) as well as the other constants such as 2π and the speed of light.
(14)This approximation is accurate within a few percents w.r.t. Eq. (12). In the constant 1012 Hz we included both the dimension conversions (solar radius, parsec, microns) as well as the other constants such as 2π and the speed of light.
If we intend to detect a signal S over the (cumulative) time T, the corresponding signal-to-noise ratio is going to be 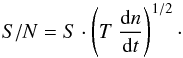 (15)The integration time is calculated as the product of the MO duration (or plateau duration) and the number of events (occultations): T = Tevent·Nevent. For observatories, 30 events are assumed for the measurements, and for survey missions the number of events is calculated from the length of the mission campaign and the orbital period of the planet: Nevent = Tcampaign/Pp.
(15)The integration time is calculated as the product of the MO duration (or plateau duration) and the number of events (occultations): T = Tevent·Nevent. For observatories, 30 events are assumed for the measurements, and for survey missions the number of events is calculated from the length of the mission campaign and the orbital period of the planet: Nevent = Tcampaign/Pp.
For all the calculations presented in this work, d = 50 pc and S/N = 5 is used, the latter corresponds to 5σ detection. In some cases (see Table 4 for specific cases), instead of the Q quantum efficiency, the system throughput was used, which contains Q and other optical attenuations as well. In order to make these different cases comparable, either the system throughputs, or 80 percent of the quantum efficiency (0.8Q) was used in the calculations.
2.4. Orbital distances around M dwarfs
Beside solar-like stars, the calculations are applied to a range of small M dwarfs. The orbital distances of the planet and the moon are calculated as functions of the stellar mass. In the case of M dwarf host stars, the planet-moon pair is set to the snowline. Icy exomoons are expected to form beyond or around the so-called snowline, which is the distance where water ice condenses in the protoplanetary disk, supporting the formation of large mass planetesimals that finally evolve toward gravitationally collected gas giants (Ida & Lin 2008; Qi et al. 2013).
The location of the snowline is calculated from the equilibrium temperature at the planet’s sub-stellar point (T0) (Cowan & Agol 2011): 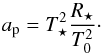 (16)T0 is assumed to be approximately 230 K at the ice condensation boundary. To obtain R⋆ and T⋆ from the stellar mass (M⋆), a parabolic equation was fitted to the effective temperature and radius values given by Kaltenegger & Traub (2009, Table 1). Only M4 – M9 stars were used for the fitting. The obtained equations are:
(16)T0 is assumed to be approximately 230 K at the ice condensation boundary. To obtain R⋆ and T⋆ from the stellar mass (M⋆), a parabolic equation was fitted to the effective temperature and radius values given by Kaltenegger & Traub (2009, Table 1). Only M4 – M9 stars were used for the fitting. The obtained equations are: 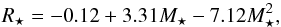 (17)and
(17)and 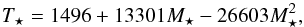 (18)that can be used if 0.075 <M⋆< 0.2.
(18)that can be used if 0.075 <M⋆< 0.2.
The moon’s orbital distance is set to 0.45 Hill radius (RH), hence it also depends on the stellar mass. It was calculated from the following formula:  (19)We chose this distance to avoid orbital instability, since Domingos et al. (2006) and Donnison (2010) showed that beyond approximately half of the Hill radius, the orbit of a direct orbiting exomoon becomes unstable.
(19)We chose this distance to avoid orbital instability, since Domingos et al. (2006) and Donnison (2010) showed that beyond approximately half of the Hill radius, the orbit of a direct orbiting exomoon becomes unstable.
3. Results
The basic idea behind this work is that the exomoons’ albedo could be estimated from the flux change during occultation. High albedo values might suggest water ice on the surface (Verbiscer et al. 2013). With the analysis of periodic changes in the transit time and its duration (Kipping 2009a,b), the mass of the moon can be calculated, from which the bulk density could also be estimated. The density of the moon helps in determining whether or not the moon contains significant amount of ice. For the albedo calculations solar system moons and hypothetical bodies were considered as exomoons, in order to determine their observability during the occultation. The possible usage, problems and uncertainties of this method are described in the Sect. 4.
3.1. Solar-type stars
First, the flux change caused by the presence of different hypothetical exomoons was calculated using Eq. (3). As there might be a great variety of sizes, orbital distances and stellar luminosities, we restricted our analysis to certain number of example cases. For stellar distance 3 AU was used, which is the approximate location of the snowline in the solar system. In the following calculations the Sun was used as central object, because future surveys and monitoring programmes will probably focus on Sun-like stars to search for Earth-like exomoons (Kaltenegger 2010; Peters & Turner 2013). Beside solar-type stars we also calculated some example cases for M dwarfs (see Sect. 3.2.2), as they came into the focus of exoplanet related research recently (see the MEarth project, Berta et al. 2013).
A few parameters of interesting examples are shown in Table 2. Beside solar system bodies (Earth, Europa, Enceladus, Io), “icy Earth” is introduced as a hypothetical moon. Icy Earth is considered to reflect as much light as Enceladus (almost 100% of the incident light) and its radius equals to that of the Earth. It is important to note that Europa and Enceladus have no relevant atmospheres and thus we also consider the hypothetical icy Earth to satisfy this criterion as well. Io does not contain water ice on its surface, but still has moderately elevated albedo because of fresh-sulphur containing material. Although there is no Earth-sized moon in the solar system, a natural satellite with this size might be considered realistic, and can serve as a useful for comparison to other objects (Ogihara & Ida 2012). As can be seen from Table 2, the required photometric precision is many orders of magnitude beyond the capability of current technology and such measurements will not be feasible in the foreseeable future.
Calculated values of the MO depth for different bodies around a Sun-like star.
3.2. Moons in systems of M dwarfs
3.2.1. Different wavelengths
It is well known that M stars are much brighter in the infrared than in the visible spectrum. For this reason it seems obvious to measure the flux at longer wavelengths, however, water ice is most reflective in the visible. In this section we discuss which wavelengths are optimal to use for successful measurements of icy moons.
Beside water ice, methane ice is also very reflective and such bodies are also known in the solar system that are covered at least partially with methane ice. For this reason, if the estimated albedo is high, it may be challenging to decide whether water ice or methane ice is present on the surface. To make the distinction easier, see the differences in the spectra of Enceladus and Eris in the bottom panel of Fig. 4 (the spectra are from Verbiscer et al. 2006 and Alvarez-Candal et al. 2011). Eris is a good example for a small body covered by methane ice, and Enceladus is used as a representation of a moon with water ice on the surface. The spectra are normalised, but these normalised values must be in good correspondence with the geometrical albedo for both bodies: the spectra of Enceladus are normalised at 0.889 μm where the geometric albedo (at phase angle ≈ 3°) of the leading and the trailing hemispheres are 1.02 and 1.06, respectively (Buratti et al. 1998), and the reflectance of Eris is normalised at 0.6 μm (Alvarez-Candal et al. 2011), and its geometric albedo in the V band is 0.96 (Verbiscer et al. 2013) which is very close to one. From their spectra, the albedo values at different photometric bands are estimated and presented in Table 3. All values in the table are rough estimations, which can differ for various exomoons. The albedo of Enceladus (water ice case in the table) in the V band is from Verbiscer et al. (2007).
 |
Fig. 4 Top panel: spectrum of water clouds on Earth. Bottom panel: spectra of Enceladus (both the leading and the trailing hemispheres are indicated with blue and red colours, respectively) and Eris (black) from Verbiscer et al. (2006) and Alvarez-Candal et al. (2011), respectively. The visible spectrum of Enceladus is not shown, but the geometric albedo is known to be 1.375 (Verbiscer et al. 2007). Yellow vertical bands indicate the full widths at half maximum of the V, R, I, J, H and K photometric bands. The green vertical band indicates the F140M filter band where the cloud spectrum is low but the water ice spectrum is relatively high. |
Estimated albedo values at different photometric bands, based on the spectrum of Enceladus (water ice surface, Verbiscer et al. 2006, 2007) and Eris (methane ice surface, Alvarez-Candal et al. 2011).
To see the albedo variations with respect to wavelength, it is best to measure the flux in all photometric bands indicated in Table 3, but it seems that the V and the J bands are the most relevant. Measuring in these two bands provide useful data, partly because of the apparent difference in the albedo for the two kinds of ice, which helps determining whether water or methane ice is present on the surface. Another reason for the V band is the maximum reflectance of water ice, and for the J band is the maximum spectral radiance of low-mass M dwarfs. The radiance of an M6 – M7 main-sequence star in the J band is about 5 times stronger than in the V band. Because of the larger number of photons that arrive to the detector, it is easier to observe the occultation in the J band, where the albedo of water ice is still relatively high. However, the shape of the light curve will not change in different bands.
Clouds are also very reflective and for this reason it may be challenging to determine whether we see an icy surface or clouds in the atmosphere. Since water is very abundant in the Universe, we assume that clouds form from H2O. The upper panel of Fig. 4 shows the intensity of water cloud on Earth (Gottwald et al. 2006, Chap. 7). In the F140M filter band (indicated by a green vertical band in the figure) the intensity of the clouds are very low while the reflectance of water ice is moderately high (see the Enceladus’ spectrum in the bottom panel). This photometric band gives opportunity to separate clouds from ice.
3.2.2. Next generation telescopes and the occultation of exomoons
It seems easier to estimate the albedo of satellites around M dwarfs than around larger stars. This is because the fact that the lower mass the star has, the closer the snowline is located. It means that the planet-moon system can be closer to the central star without the sublimation and/or melting of the ice on the surface. If the moon is closer to the star, then the light drop caused by its presence will be more significant in the light curve. This effect favours detection. In other words, it may be easier to observe icy moons around lower mass stars in occultation, than around more massive stars. It also means, that smaller moons may also be detected in occultation around late-type stars.
The capabilities of next generation telescopes are of fundamental importance in successful albedo estimations. Beside Kepler, the most relevant missions for exomoon detection are the CHaracterising ExOPlanets Satellite (CHEOPS, Broeg et al. 2013), the Transiting Exoplanet Survey Satellite (TESS, Ricker et al. 2010, 2014), the James Webb Space Telescope (JWST, Clanton et al. 2012), the PLAnetary Transit and Oscillations of stars (PLATO 2.0, Rauer et al. 2011, 2014) and the European Extremely Large Telescope (E-ELT, Ramsay et al. 2014). The photon noise levels of these instruments were calculated as described in Sect. 2.3. The data used for the calculations for each instrument are shown in Table 4. All these numbers are subject to change, since most of these missions are in the planning and testing phase. The numbers in the last column indicate references as explained in the footnote1.
Instrument parameters for calculating the photon noise level.
Figures 5 and 6 show the relation between the MO depth of icy moons and the mass of the host star in the V and J photometric bands, respectively. The objects covered in this figure are low-mass M dwarfs: M9−M5 according to Kaltenegger & Traub (2009). The MO depth is in logarithmic scale. The radius of the moon indicated by black curves was calculated for all stellar mass and MO depth pairs. For this calculation Eq. (3) was used and the albedo was fixed to that of Enceladus in each case, i.e. 1.38 for Fig. 5 and 0.84 for Fig. 6. The distance from the star was set to the snowline, which was calculated from Eq. (16), and is indicated in the upper axis. This is the minimum stellar distance that is required in order to prevent the melting of the surface ice. It also means that our calculation is an optimistic approach: the minimum distance and the approximately minimum moon radius are determined for a succesful detection. The vertical grey lines indicate the 60, 90 and 120 min MO durations. In all investigated cases, the moon and the planet occults separately. For larger stellar masses the MO duration is longer, because of the larger stellar distance. The expected noise levels for the telescopes are indicated by coloured curves. Those instruments that measure in or near the J photometric band (HST WFC3 IR, JWST NIRCam and E-ELT MICADO) are shown in Fig. 6, all the others are in Fig. 5, however, because of their limited capabilities, TESS, and CoRoT do not appear in Fig. 5.
 |
Fig. 5 Radius of icy moons around different late-type stars with a given MO depth. The moon’s geometric albedo was set to Ag = 1.38 in each case (according to the reflectance of ice in the V photometric band), and the distance from the star is at the snowline, that is calculated from Eq. (16), and indicated in the top axis, too. Brown, blue, green and purple curves indicate the estimated photon noise levels with 5σ confidence of PLATO 2.0, CHEOPS, HST and Kepler, respectively. The dashed curves for PLATO 2.0 and Kepler indicate that these are survey missions in contrast with the HST and CHEOPS observatories. Grey vertical lines indicate the 60, 90 and 120 min MO duration contours for a moon in circular orbit around a Neptune-mass planet. |
 |
Fig. 6 Radius of icy moons around different late-type stars with a given MO depth. The moon’s geometric albedo was set to Ag = 0.84 in each case (according to the reflectance of ice in the J photometric band), and the distance from the star is at the snowline, that is calculated from Eq. (16), and indicated in the top axis, too. Green and light blue coloured curves indicate the estimated photon noise levels with 5σ confidence of HST and E-ELT, respectively. Orange and red curves depict the same for JWST but with two different filters (F140N and F115W, respectively). Grey vertical lines indicate the 60, 90 and 120 min MO duration contours for a moon in circular orbit around a Neptune-mass planet. |
The highest radius that is shown in Figs. 5 and 6 is 2.5 Earth-radii (for comparison, the radius of Neptune is 3.9 Earth-radii). We choose this 2.5 Earth-radii as an upper limit for a rocky moon with surface ice to guarantee that its mass is not greater than five Earth-masses. (The radius of a body with the density of Enceladus and with a mass of five Earth-masses is 2.58 Earth-radii.) Such large body around a Neptune-mass planet could also be called a binary planet, which would probably be a different system than the Saturn-Enceladus planet-moon pair. For simplicity, and also because we use this 2.5 Earth-radii as an upper limit, we still call them moons in the rest of the paper.
In the visible spectrum, the photon noise of the telescopes is much higher than the required precision for detecting large, rocky moons in occultation. However, in the J photometric band (see Fig. 6) the E-ELT’s photon noise is just a few ppm greater than the MO depth of large icy exomoons. (Note that the MO depth is shown in a logarithmic scale.) For example, for a 2.5 Earth-radii moon around an 0.11 stellar mass star, the difference is about 3−4 ppms, and for a 1.5 Earth-radii moon at an 0.085 stellar mass star, it’s about 7 ppms. The accuracy of the measurements and additional parameters that can influence the success of the observations are discussed thoroughly in the next section.
4. Discussion
The findings on the observability of different exomoons, the estimation of their surface albedo, and other related considerations are summarised below.
-
Smaller stellar distance: the depth of the flux drop caused by themoon in occultation as well as its observability increases withdecreasing stellar distance. In case of smaller stars, the surfaceof the moon can keep its icy composition even for small stellardistances, because the star’s luminosity is low. Small stellar dis-tances (such as 0.01–0.1 AU in our calculations) are importantregarding the long term stability of a planet-moon system, too.According to migration theories and perturbation effects, numer-ous criteria have to be satisfied in order to support the presence ofan exomoon that survived a certain time period after it got close tothe central star (Barnes & O’Brien 2002). Duringthis process they might be able to keep their satellite system pro-tected against perturbations by the central star and other planetaryobjects (Mosqueira & Estrada 2003). However,the migration is not relevant if the moon is captured or impact-ejected (which seems more likely for large satellites) after theplanet’s migration phase.
-
Larger size: among the analysed cases, the best possibility for determine the albedo is of Earth-sized, or even larger exomoons, because the reflecting surface is larger.
-
Higher albedo: the higher the albedo that an exomoon has, the more stellar light it reflects, and the flux difference in the light curve is larger during the occultation. Extremely high geometric albedos (for example 1.375 in the case of Enceladus in the solar system) are indicators of the presence of relatively young and fresh water ice since this is the only known material that could reflect such high percentage of light. The presence of water ice on the surface may imply astrobiological importance. Considering strongly reflecting atmospheric clouds, their presence also could cause high albedo. The separation of cloud and ice reflection with optical methods could be difficult, but in case of succesful measurements with an F140M filter, it may be feasible, as discussed in Sect. 3.2.1. However, our results show that such measurements will not be achievable with the instruments presented in Sect. 3.2.2, meaning that next generation telescopes will still not be able to separate atmospheric clouds from surface ice on exoplanetary bodies.
Beside the challenge in observation of the small flux contribution of the exomoon, analysing the measured data will also be difficult, as to fit a realistic model, because many possible configurations are needed to consider. To see the possible roles of these factors, and in order to help to plan and target future observations, in the following sections we evaluate how several basic parameters affect the observation and analysis.
4.1. Accuracy
For an adequate result from the light curve measurements, repeated observations are needed. It is not necessary that the moon is positioned exactly at the same apparent position every time when the occultation occurs. For this reason the small flux drop caused by the moon may be shorter or longer, and may not be seen at every observation. Simon et al. (2012) propose using an averaged light curve of several observations to deal with the scattered position of the flux change caused by the presence of the moon. They also present a four-step detection strategy for discovering exomoons by transit method. Occultation events with the same apparent positions of the moon and the planet might be rare, but in tidally locked situations, a given configuration during subsequent occultations could be frequent or regular and repeated at every revolution of the exoplanet, and the exomoon might be at the same position viewed from our line of sight.
Variable surface features of the host star, such as granules and micro-flares could influence the result, producing small flux fluctuations. Such variability is expected especially in the late-type stellar atmospheres related to convective motion (Ludwig 2006). From the moon’s transit measurements and from the occultation of the host planet, the expected time of the moon’s occultation can be estimated, which may help in distinguishing the MO signal from the stellar surface fluctuations, especially because the occultation will cause a periodic change in the light curve.
Beside the uncertainties in flux measurements, the accuracy of albedo estimation also depends on the accuracy of the exomoon’s size and the stellar distance. In our work both are assumed to be already known from transit detections, and determining their accuracy was already discussed by several authors (see e.g. Pál 2008; Carter et al. 2008). However, the errors from transit measurements propagate into the determination of the geometric albedo. The total error of the albedo can be obtained from 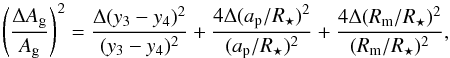 (20)where the three terms of the right side of the equation can safely be considered to be independent from each-other. The first term is (1 / 5)2 since we set the measurements to 5σ. The second term is typically around (1−5%)2 (Pál 2008). Assuming that am/R⋆ ≥ 1 (i.e. the moon and the planet occult separately, which was true in all cases described in Sect. 3.2.2), and that the same number of occultations are detected for the moon as for the planet, and that these measurements were made with the same instrument, the third term can be expressed as
(20)where the three terms of the right side of the equation can safely be considered to be independent from each-other. The first term is (1 / 5)2 since we set the measurements to 5σ. The second term is typically around (1−5%)2 (Pál 2008). Assuming that am/R⋆ ≥ 1 (i.e. the moon and the planet occult separately, which was true in all cases described in Sect. 3.2.2), and that the same number of occultations are detected for the moon as for the planet, and that these measurements were made with the same instrument, the third term can be expressed as 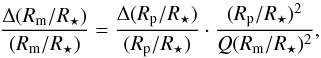 (21)where Q is the quantum efficiency. This error can be calculated for given geometric configurations. In any case, the last term must be smaller than the first one in Eq. (20), because the S/N ratio is much larger for transits than for occultations, hence transit measurements are much more precise. See for example the case of CoRot-1b which was measured in transit and occultation, as well (Snellen et al. 2009). The same effect is true for exomoons. It means that the first term of Eq. (20) is dominating in the error of the albedo estimation.
(21)where Q is the quantum efficiency. This error can be calculated for given geometric configurations. In any case, the last term must be smaller than the first one in Eq. (20), because the S/N ratio is much larger for transits than for occultations, hence transit measurements are much more precise. See for example the case of CoRot-1b which was measured in transit and occultation, as well (Snellen et al. 2009). The same effect is true for exomoons. It means that the first term of Eq. (20) is dominating in the error of the albedo estimation.
In the calculations shown in Sect. 3.2.2 only photon noise was considered based on the quantum efficiency or on the system throughput. However, additional noise sources can also be significant, including both random noises (such as detector readout, dark current, zodiac light or airglow) and systematic noises (sky variations, tracking jitters, subpixel structure, etc.). These noise sources could even be larger in the near-infrared regime and can be comparable to the photon noise itself for faint(er) targets. However, for brighter objects, the photometric precision is mostly limited by the photon noise and the accuracy is limited by the systematic variations. The system throughput that was considered in the calculations (even when the quantum efficiency was used, since in these cases the quantum efficiency was multiplied by 0.8) already contains some of these extra noise sources, but in future missions these are subject to change, since their precise values will be known only after the commissioning of the instruments. In addition, we assumed 30 occultation detections for observatories that would require at least five years for E-ELT because the orbital period of the planet at the snowline is approximately 31 days, and the occultation can only be measured at nights. Considering that not all noise sources were included in our estimations, and that measuring 30 occultations may be unrealistic in most cases, it can be concluded that our calculations are too optimistic, and the real noise level of the instruments will be higher than presented.
According to Simon et al. (2007), measuring the photometric transit timing variations (TTVp) leads to the estimation of the size of the exomoon. By analysing transit duration variations (TDVs) as well, rough mass estimation is also possible under favourable conditions (Kipping 2009a,b). Using the derived mass and radius together, information on bulk density could be gained, and putting together this value with the presence of surface ice gives strong hint on the possible existence and ratio of water ice in the interior.
Summary of various factors that influence the successful albedo estimation for an exomoon.
4.2. Considering different parameters
In the following we categorize parameters by their importance in influencing the results of the observations. Specific cases that might be relevant for certain exomoons, but are not usual in our solar system are discussed below.
-
Eccentricity: for the analysed, relatively large exomoons we donot expect highly eccentric orbits as the large satellites in the solarsystem (even the captured ones) have low eccentricity. However,perturbations might elongate the orbit, or resonances with othermoons may maintain a higher eccentricity. The variable orbitalvelocity around the host planet influences the apparent speedof the exomoon perpendicular to our line of sight. The chang-ing velocity influences the length of the plateau/occultationduration. Shorter plateau/MO duration means less integrationtime for the telescope which results in larger photon noise. Themoon-star distance periodically change with the orbital phase ofthe moon, influencing its brightness, but this effect is very small.Eccentricity of the moon may enhance this phenomenon. It couldbe substantial in cases when the ratio between the stellar distanceand the exomoon’s semi-major axis is relatively small. Sato &Asada (2010) described the effect of the satel-lite’s eccentricity on the transit light curve in details, which cansimilarly be used to occultations with some changes.
-
Inclination: large tilt of the orbital plane of the exomoon relatively to the planet’s orbital plane around the host star could also influence the plateau/occultation duration, especially when the exoplanet orbits at large distances from the host star. In case of large inclinations, instead of occulting, the moon may pass beside the star. The length of the plateau/occultation duration also depends on the inclination and the ratio of the exomoon’s apparent distance from its host planet and the diameter of the host star. Larger stellar disk and smaller orbital distance increase the influencing effect of higher inclinations, however if the stellar disk is smaller, then the moon will not occult for high inclinations. For transits the effect of the exomoon’s inclination is discussed by Sato & Asada (2010).
-
Reflected light from planet: in ideal cases the exomoon’s brightness might be elevated by reflected light from its host planet. The strongest reflected light flux reaches the exomoon during the new moon phase (watching from the exoplanet). In different configurations mutual transits and mutual shadows affect the shape of the light curve (Cabrera & Schneider 2007). In the albedo estimation this effect of the reflected light from the planet is not significant, as the exomoon shows almost full moon phase during the occultation (looking from the Earth). This reflected light flux is negligibly small comparing to the stellar irradiation (Hinkel & Kane 2013). The illumination from the planet with other light sources is thoroughly discussed by Heller & Barnes (2013).
-
Orbital direction: retrograde orbits affect the plateau/occultation duration as stellar eclipses by the host planet are more frequent, than with a prograde orbit and can be prolonged because of the large size of giant planets (Forgan & Kipping 2013). Such eclipses may occur just before or after the occultation with the star, changing the shape of the light curve. Using the phase-folded light curve of several observations may help in filtering out such cases. Beside eclipses, it does not influence the observability whether the exomoon is approaching to or receding from the host star viewing from the Earth.
-
Effect of hemispherical asymmetry: an exomoon that faces with different sides toward the star (and the toward the Earth) might have different brightness at different occultations, if significant albedo difference exists between the two hemispheres. Calculating with a solar system analogy, Iapetus shows huge difference in its Bond albedo with ~0.31 at the trailing, and maximum 0.1 at the leading hemisphere (Howett et al. 2010). The difference between the observations of the two hemispheres produces such brightness difference that can not be neglected. This effect may influence the result of the albedo estimation, but using the phase-folded light curve such flux changes may be noticed, and from the average light curve the average albedo can be estimated.
Based on this subsection, different parameters are categorised by their importance in occultation observations. The results can be seen in Table 5. The most relevant factors influencing the observation are: 1. close stellar distance that is observationally favourable especially at small main sequence stars; 2. star/planet diameter ratio: the larger the ratio is the longer MO duration could be observed which helps in reaching smaller photon noise for the measurement (only relevant at small stars); 3. larger exomoons are easier targets, and are favourable to form by impact ejection or by capture; 4. larger planetary distance of the moon can increase the length of the plateau duration; 5. higher albedo means that the satellite is brighter, hence makes observation easier.
4.3. Importance of ice
Icy moons with subsurface oceans might hold large volumes of liquid water for geologic time-scales and thus may potentially be habitable or at least could be considered as favourable environments for life. In the solar system such subsurface oceans exist in Europa, Titan, Enceladus, and possibly also in Ganymede and Callisto. The liquid phase state of these oceans are maintained by tidal heat production, freezing point depressing solved ingredients, and/or internal heat due to accretional energy conservation and radiogenic heat (Carr et al. 1998; Khurana et al. 1998; Kargel et al. 2000; Zimmer et al. 2000; McCord et al. 2001; Schenk 2002; Collins & Goodman 2007; Roberts & Nimmo 2008; Lorenz et al. 2008; Postberg et al. 2009; Iess et al. 2014; Dobos & Turner 2015). Having information on the existence of surface ice, using mass estimation from TTV and TDV might increase the probability of identifying exomoons that are likely to have subsurface oceans.
The brightness of the ice could point to relatively young surface and active resurfacing processes. In the case of Europa the ocean gives possibility for active resurfacing thus for the existence of clean and bright ice there, although locations with non-ice ingredients can also be found on Europa, while on Enceladus the subsurface liquid water contributes to the geyser-like eruptions, and to the increase of surface albedo caused by fresh water ice crystals that fall back to the surface (Kadel et al. 2000; Fagents 2003; Porco et al. 2006; Spencer et al. 2006; Verbiscer et al. 2007; Howett et al. 2011). Although there may be other reasons for elevated albedo, the very high albedo is still a strong indication of the water ice on the surface, and even of a liquid subsurface ocean.
Estimation of moons’ albedo is much easier at M-type stars, if the planet and the moon are close to the snowline. However, strong, regular flares and coronal mass ejections are expected, that potentially make the orbiting rocky bodies uninhabitable, because of high UV irradiation and loss of the atmosphere (Scalo et al. 2007). Exomoons still might be habitable because the ice cover attenuate UV radiation, and serve as a physical screening mechanism (Cockell 1998; Cockell et al. 2000). The loss of the atmosphere could also easily happen at small stellar distance, but does not influence directly the oceans beneath ice sheets.
5. Conclusions
In this work we proposed a method for the first time that suggests the surface albedo of an exomoon and thus might indicate the existence of water ice. The argumentation presented in this work can be useful to orient future research and to identify the best candidate systems for such observations. First we presented methods and the results of our calculations, then we listed those parameters which substantially influence such measurements and also those that are not relevant – as such information is useful in planning and targeting observations.
Moons of smaller stars seem to be easier to detect, if their stellar distance is smaller. In addition, the smaller the star, the closer the snowline located, meaning that rocky bodies can stay icy even if they are orbiting the star in a closer orbit (but still outside the snowline). The vicinity to the star makes the body brighter, thus an icy exomoon is easier to detect in occultation close to the snowline of an M dwarf, than at the snowline of a solar-like star. The largest flux difference is expected from large, ~2.5 Earth-radii icy moons (about five Earth-mass body with similar density of Enceladus) orbiting small M dwarfs (~0.07−0.13 solar masses) close to the snowline. We have found that such moons cannot be observed in occultation with next generation space missions in the visual spectrum, because the instruments’ photon noise is far greater than the flux drop caused by the moon. However, in the near infrared (J band), the E-ELT’s photon noise is just about 5−6 ppm greater than the MO depth, despite the lower albedo of ice. This result, however, is too optimistic, because it does not take into account other noise sources, such as CCD read-out and dark signal, which become significant in the near infrared measurements. Considering that not all noise sources were included in our estimations, and that measuring 30 occultations may be unrealistic in most cases, since it would require years to achieve, it can be concluded that the real noise level of the instruments in the near infrared wavelengths will be higher than that presented in Sect. 3.2.2. Flux fluctuations caused by stellar activity makes the measurements even more difficult. We conclude that occultation measurements with next generation missions are far too challenging, even in the case of large, icy moons at the snowline of small M dwarfs. However, we expect that as future missions will further develop in the next decades, resulting in even better precisions, their noise level will be lower, hence occultations may be detected for exomoons around small M dwarfs.
We outlined the parameters that can influence the detection. Based on assumptions, the orbital and physical parameters of exomoons might be highly diverse, thus we evaluated a range in the space of several parameters. We categorised these parameters by their influence on the success of MO detections (see Table 5).
We also discussed the possible properties of the most suitable exomoons for characterisation which may be useful once the instrumentation is available. Exomoons around Neptune-sized exoplanets of small stars seem to be the best targets for occultation-based albedo estimation opposite to Jupiter-like exoplanets, if the satellites, formed by impact ejection or capturing, are large enough. In case of such satellites the surface ice cover might be co-accreted if the ejection happened before the clearing up of the circumplanetary disk, or formed by ejection from planets composed mostly of water ice, like Neptune and not of hydrogen, like Jupiter. Binary-exchange capture is also a possibility for a giant planet to have a large icy satellite (Neptunes are better candidates for this process than Jupiters).
Based on our work, the first albedo estimations of exomoons from occultations are expected around low mass M dwarfs at small stellar distances. These moons will probably be large, and have high albedo which may imply the presence of ice on the surface.
1: Ricker et al. (2014), 2: Auvergne et al. (2009); 3: Broeg et al. (2013); 4: The CHEOPS Study Team (2013); 5: Rauer et al. (2014); 6: Van Cleve & Caldwell (2009); 7: Avila (2016); 8: Dressel (2016); 9: JWST webpage: http://www.stsci.edu/jwst/instruments/nircam/instrumentdesign/filters/; 10: Davies et al. (2010).
Acknowledgments
We thank the useful comments for the anonymous referee who helped in substantially improving the manuscript. We also thank René Heller for the helpful discussion. V.D. has been supported by the Hungarian OTKA Grant K104607, the Hungarian National Research, Development and Innovation Office (NKFIH) grant K-115709, the Lendület-2009 Young Researchers Program of the Hungarian Academy of Sciences, the TÉT-14FR-1-2015-0012 project, and the ESA PECS Contract No. 4000110889/14/NL/NDe. Á.K. has been supported by the Astrophysical and Geochemical Laboratory and the COST TD 1308 project. P.A. has been supported by the LP2012-31 project.
References
- Agnor, C. B., & Hamilton, D. P. 2006, Nature, 441, 192 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Alvarez-Candal, A., Pinilla-Alonso, N., Licandro, J., et al. 2011, A&A, 532, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Auvergne, M., Bodin, P., Boisnard, L., et al. 2009, A&A, 506, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Avila, R., et al. 2016, ACS Instrument Handbook, Version 15.0 (Baltimore: STScI) [Google Scholar]
- Barnes, J. W., & O’Brien, D. P. 2002, ApJ, 575, 1087 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, D. P., Batista, V., Bond, I. A., et al. 2014, ApJ, 785, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Berta, Z. K., Irwin, J., & Charbonneau, D. 2013, ApJ, 775, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Broeg, C. H., & Benz, W. 2012, A&A, 538, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Broeg, C., Fortier, A., Ehrenreich, D., et al. 2013, in Eur. Phys. J. Web Conf. 47, 3005 [Google Scholar]
- Brown, R. H., & Cruikshank, D. P. 1997, Ann. Rev. Earth Planet. Sci., 25, 243 [Google Scholar]
- Buratti, B. J., Mosher, J. A., Nicholson, P. D., McGhee, C. A., & French, R. G. 1998, Icarus, 136, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Cabrera, J., & Schneider, J. 2007, A&A, 464, 1133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Canup, R. M., & Ward, W. R. 2006, Nature, 441, 834 [NASA ADS] [CrossRef] [Google Scholar]
- Carr, M. H., Belton, M. J. S., Chapman, C. R., et al. 1998, Nature, 391, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Carter, J. A., Yee, J. C., Eastman, J., Gaudi, B. S., & Winn, J. N. 2008, ApJ, 689, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Clanton, C., Beichman, C., Vasisht, G., Smith, R., & Gaudi, B. S. 2012, PASP, 124, 700 [NASA ADS] [CrossRef] [Google Scholar]
- Cockell, C. S. 1998, J. Theor. Biol., 193, 717 [CrossRef] [Google Scholar]
- Cockell, C. S., Catling, D. C., Davis, W. L., et al. 2000, Icarus, 146, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Collins, G. C., & Goodman, J. C. 2007, Icarus, 189, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Cowan, N. B., & Agol, E. 2011, ApJ, 729, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Crida, A., & Charnoz, S. 2012, Science, 338, 1196 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, R., Ageorges, N., Barl, L., et al. 2010, in Ground-based and Airborne Instrumentation for Astronomy III, SPIE Conf. Ser., 7735, 77352A [Google Scholar]
- Dobos, V., & Turner, E. L. 2015, ApJ, 804, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Domingos, R. C., Winter, O. C., & Yokoyama, T. 2006, MNRAS, 373, 1227 [NASA ADS] [CrossRef] [Google Scholar]
- Donnison, J. R. 2010, MNRAS, 406, 1918 [NASA ADS] [Google Scholar]
- Dressel, L. 2016, Wide Field Camera 3 Instrument Handbook, Version 8.0 (Baltimore: STScI) [Google Scholar]
- Fagents, S. A. 2003, J. Geophys. Res., 108, 5139 [CrossRef] [Google Scholar]
- Forgan, D., & Dobos, V. 2016, MNRAS, 457, 1233 [NASA ADS] [CrossRef] [Google Scholar]
- Forgan, D., & Kipping, D. 2013, MNRAS, 432, 2994 [NASA ADS] [CrossRef] [Google Scholar]
- Forgan, D., & Yotov, V. 2014, MNRAS, 441, 3513 [NASA ADS] [CrossRef] [Google Scholar]
- Gottwald, M., Bovensmann, H., G. Lichtenberg, Noel, S., et al. 2006, SCIAMACHY, Monitoring the Changing Earth’s Atmosphere (DLR) [Google Scholar]
- Grundy, W. M., & Stansberry, J. A. 2000, Icarus, 148, 340 [NASA ADS] [CrossRef] [Google Scholar]
- Hapke, B. 2012, in Theory of Reflectance and Emittance Spectroscopy (Cambridge University Press), 221 [Google Scholar]
- Heller, R. 2012, A&A, 545, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heller, R. 2014, ApJ, 787, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Heller, R., & Barnes, R. 2013, Astrobiology, 13, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Hicks, M. D., & Buratti, B. J. 2004, Icarus, 171, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Hinkel, N. R., & Kane, S. R. 2013, ApJ, 774, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Howett, C. J. A., Spencer, J. R., Pearl, J., & Segura, M. 2010, Icarus, 206, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Howett, C. J. A., Spencer, J. R., Pearl, J., & Segura, M. 2011, J. Geophys. Res., 116, 3003 [CrossRef] [Google Scholar]
- Ida, S., & Lin, D. N. C. 2008, ApJ, 685, 584 [NASA ADS] [CrossRef] [Google Scholar]
- Iess, L., Stevenson, D. J., Parisi, M., et al. 2014, Science, 344, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Kadel, S. D., Chuang, F. C., Greeley, R., Moore, J. M., & Galileo SSI Team. 2000, J. Geophys. Res., 105, 22657 [NASA ADS] [CrossRef] [Google Scholar]
- Kaltenegger, L. 2010, ApJ, 712, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Kaltenegger, L., & Traub, W. A. 2009, ApJ, 698, 519 [NASA ADS] [CrossRef] [Google Scholar]
- Kargel, J. S., Kaye, J. Z., Head, J. W., et al. 2000, Icarus, 148, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Kasting, J. F. 1988, Icarus, 74, 472 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Khurana, K. K., Kivelson, M. G., Stevenson, D. J., et al. 1998, Nature, 395, 777 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kipping, D. M. 2009a, MNRAS, 392, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M. 2009b, MNRAS, 396, 1797 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M., Fossey, S. J., & Campanella, G. 2009, MNRAS, 400, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, K. M., Sackett, P. D., & Mardling, R. A. 2008, ApJ, 685, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Liebig, C., & Wambsganss, J. 2010, A&A, 520, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lorenz, R. D., Stiles, B. W., Kirk, R. L., et al. 2008, Science, 319, 1649 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ludwig, H.-G. 2006, A&A, 445, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McCord, T. B., Hansen, G. B., & Hibbitts, C. A. 2001, Science, 292, 1523 [NASA ADS] [CrossRef] [Google Scholar]
- Mosqueira, I., & Estrada, P. R. 2003, Icarus, 163, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Ogihara, M., & Ida, S. 2012, ApJ, 753, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Pál, A. 2008, MNRAS, 390, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Pang, K. D., Lumme, K. A., & Bowell, E. 1981, in Lun. Planet. Sci. Conf., 12, 1543 [Google Scholar]
- Pappalardo, R. T., Belton, M. J. S., Breneman, H. H., et al. 1999, J. Geophys. Res., 104, 24015 [NASA ADS] [CrossRef] [Google Scholar]
- Peters, M. A., & Turner, E. L. 2013, ApJ, 769, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Porco, C. C., Helfenstein, P., Thomas, P. C., et al. 2006, Science, 311, 1393 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Postberg, F., Kempf, S., Schmidt, J., et al. 2009, Nature, 459, 1098 [NASA ADS] [CrossRef] [Google Scholar]
- Qi, C., Öberg, K. I., Wilner, D. J., et al. 2013, Science, 341, 630 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ramsay, S. K., Casali, M. M., González, J. C., & Hubin, N. 2014, in SPIE Conf. Ser., 9147, 91471 [Google Scholar]
- Rauer, H., Gebauer, S., Paris, P. V., et al. 2011, A&A, 529, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rauer, H., Catala, C., Aerts, C., et al. 2014, Exp. Astron., 38, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Ricker, G. R., Latham, D. W., Vanderspek, R. K., et al. 2010, in BAAS, 42, 215 [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2014, in SPIE Conf. Ser., 9143, 20 [Google Scholar]
- Roberts, J. H., & Nimmo, F. 2008, Icarus, 194, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Rowe, J. F., Matthews, J. M., Seager, S., et al. 2006, ApJ, 646, 1241 [NASA ADS] [CrossRef] [Google Scholar]
- Rowe, J. F., Matthews, J. M., Seager, S., et al. 2008, ApJ, 689, 1345 [NASA ADS] [CrossRef] [Google Scholar]
- Sasaki, T., Stewart, G. R., & Ida, S. 2010, ApJ, 714, 1052 [NASA ADS] [CrossRef] [Google Scholar]
- Sato, M., & Asada, H. 2010, PASJ, 62, 1203 [NASA ADS] [CrossRef] [Google Scholar]
- Scalo, J., Kaltenegger, L., Segura, A. G., et al. 2007, Astrobiology, 7, 85 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Schenk, P. M. 2002, Nature, 417, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Schenk, P. M., & Zahnle, K. 2007, Icarus, 192, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Sheppard, S. S., Jewitt, D., & Kleyna, J. 2005, AJ, 129, 518 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, A., Szatmáry, K., & Szabó, G. M. 2007, A&A, 470, 727 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simon, A. E., Szabó, G. M., Szatmáry, K., & Kiss, L. L. 2010, MNRAS, 406, 2038 [NASA ADS] [Google Scholar]
- Simon, A. E., Szabó, G. M., Kiss, L. L., & Szatmáry, K. 2012, MNRAS, 419, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Snellen, I. A. G., de Mooij, E. J. W., & Albrecht, S. 2009, Nature, 459, 543 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Spencer, J. R., Pearl, J. C., Segura, M., et al. 2006, Science, 311, 1401 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Stevenson, D. J. 1985, Icarus, 62, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Szabó, G. M., Szatmáry, K., Divéki, Z., & Simon, A. 2006, A&A, 450, 395 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- The CHEOPS Study Team 2013, CHEOPS Definition Study Report (Red Book) [Google Scholar]
- Van Cleve, J., & Caldwell, D. A. 2009, Kepler Instrument Handbook, KSCI 19033-001 (NASA Ames Research Center) [Google Scholar]
- Verbiscer, A., Helfenstein, P., & Veverka, J. 1990, Nature, 347, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Verbiscer, A. J., Peterson, D. E., Skrutskie, M. F., et al. 2006, Icarus, 182, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Verbiscer, A., French, R., Showalter, M., & Helfenstein, P. 2007, Science, 315, 815 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Verbiscer, A. J., Helfenstein, P., & Buratti, B. J. 2013, in Photometric Properties of Solar System Ices, eds. M. S. Gudipati, & J. Castillo-Rogez (Springer), 47 [Google Scholar]
- Veverka, J., Brown, R. H., & Bell, J. F. 1991, in Uranus satellites − Surface properties, eds. J. T. Bergstralh, E. D. Miner, & M. S. Matthews (University of Arizona Press), 528 [Google Scholar]
- Williams, D. M. 2013, Astrobiology, 13, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Zimmer, C., Khurana, K. K., & Kivelson, M. G. 2000, Icarus, 147, 329 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Plateau duration for different planetary masses at 3 AU distance from a Sun-like star.
Estimated albedo values at different photometric bands, based on the spectrum of Enceladus (water ice surface, Verbiscer et al. 2006, 2007) and Eris (methane ice surface, Alvarez-Candal et al. 2011).
Summary of various factors that influence the successful albedo estimation for an exomoon.
All Figures
 |
Fig. 1 Schematic light curve during an occultation with an exomoon orbiting its exoplanet with some different basic conditions: a1) exomoon occults after the exoplanet; a2) exomoon occults before the exoplanet; b1) observationally favourable case of large eccentricity increasing the plateau duration; b2) unfavourable case of large eccentricity decreases the plateau duration; c1) favourable case of large inclination (relative to the plane perpendicular to the line of sight); c2) unfavourable case of large inclination. The sizes of the objects are not to scale. |
| In the text | |
 |
Fig. 2 Schematic representation of the light curve (case a1 in Fig. 1) during the occultation of an exoplanet with an exomoon. |
| In the text | |
 |
Fig. 3 The so-called plateau duration for different stellar and planetary distances. The masses of the star and the planet are 1 solar mass and 1MJ, respectively, for all cases. Black and white colours indicate the longest (41 h) and the shortest (6 min) plateau durations, respectively. The dashed grey line separates those cases where the moon’s orbital velocity is high enough to reach 25% of its orbit before the plateau duration ends (in the bottom right corner). The solid horizontal white line at about 1 393 000 km (2 R⋆) indicates that the plateau duration is constant above this planetary distance. Examples from the solar system are plotted for comparison. |
| In the text | |
 |
Fig. 4 Top panel: spectrum of water clouds on Earth. Bottom panel: spectra of Enceladus (both the leading and the trailing hemispheres are indicated with blue and red colours, respectively) and Eris (black) from Verbiscer et al. (2006) and Alvarez-Candal et al. (2011), respectively. The visible spectrum of Enceladus is not shown, but the geometric albedo is known to be 1.375 (Verbiscer et al. 2007). Yellow vertical bands indicate the full widths at half maximum of the V, R, I, J, H and K photometric bands. The green vertical band indicates the F140M filter band where the cloud spectrum is low but the water ice spectrum is relatively high. |
| In the text | |
 |
Fig. 5 Radius of icy moons around different late-type stars with a given MO depth. The moon’s geometric albedo was set to Ag = 1.38 in each case (according to the reflectance of ice in the V photometric band), and the distance from the star is at the snowline, that is calculated from Eq. (16), and indicated in the top axis, too. Brown, blue, green and purple curves indicate the estimated photon noise levels with 5σ confidence of PLATO 2.0, CHEOPS, HST and Kepler, respectively. The dashed curves for PLATO 2.0 and Kepler indicate that these are survey missions in contrast with the HST and CHEOPS observatories. Grey vertical lines indicate the 60, 90 and 120 min MO duration contours for a moon in circular orbit around a Neptune-mass planet. |
| In the text | |
 |
Fig. 6 Radius of icy moons around different late-type stars with a given MO depth. The moon’s geometric albedo was set to Ag = 0.84 in each case (according to the reflectance of ice in the J photometric band), and the distance from the star is at the snowline, that is calculated from Eq. (16), and indicated in the top axis, too. Green and light blue coloured curves indicate the estimated photon noise levels with 5σ confidence of HST and E-ELT, respectively. Orange and red curves depict the same for JWST but with two different filters (F140N and F115W, respectively). Grey vertical lines indicate the 60, 90 and 120 min MO duration contours for a moon in circular orbit around a Neptune-mass planet. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


