| Issue |
A&A
Volume 591, July 2016
|
|
|---|---|---|
| Article Number | A47 | |
| Number of page(s) | 11 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201527590 | |
| Published online | 09 June 2016 | |
Mid-infrared interferometry of 23 AGN tori: On the significance of polar-elongated emission
1 Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
e-mail: nlopez@strw.leidenuniv.nl
2 Max-Planck-Institut für extraterrestrische Physik, Postfach 1312, Gießenbachstr., 85741 Garching, Germany
3 European Southern Observatory, Alonso de Córdova 3107, Vitacura, Santiago, Chile
4 Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
5 Centre for Astrophysics and Supercomputing, Swinburne University of Technology, PO Box 218, Hawthorn, Victoria 3122, Australia
Received: 19 October 2015
Accepted: 11 February 2016
Context. Detailed high-resolution studies of active galactic nuclei (AGN) with mid-infrared (MIR) interferometry have revealed parsec-sized dust emission that is elongated in the polar direction in four sources.
Aims. Using a larger, coherently analyzed sample of AGN observed with MIR interferometry, we aim to identify elongated MIR emission in a statistical sample of sources. More specifically, we wish to determine if there is indeed a preferred direction of the elongation and whether this direction is consistent with a torus-like structure or with a polar emission.
Methods. We investigated the significance of the detection of an elongated shape in the MIR emission by fitting elongated Gaussian models to the interferometric data at 12 μm. We paid special attention to (1) the uncertainties caused by an inhomogeneous (u,v) coverage; (2) the typical errors in the measurements; and (3) the spatial resolution achieved for each object.
Results. From our sample of 23 sources, we are able to find elongated parsec-scale, MIR emission in five sources: three type 2s, one type 1i, and one type 1. Elongated emission in four of these sources has been published before; NGC 5506 is a new detection. The observed axis ratios are typically around 2 and the position angle of the 12 μm emission for all the elongated sources always seems to be closer to the polar axis of the system than to the equatorial axis. Two other objects, NGC 4507 and MCG-5-23-16, with reasonably well-mapped (u,v) coverage and good signal-to-noise ratios, appear to have a less elongated 12 μm emission.
Conclusions. Our finding that sources showing elongated MIR emission are preferentially extended in polar direction sets strong constraints on torus models or implies that both the torus and NLR/outflow region have to be modeled together. In addition, models used for SED fitting will have to be revised to include emission from polar dust.
Key words: techniques: interferometric / galaxies: active / galaxies: nuclei / galaxies: Seyfert / techniques: high angular resolution / infrared: galaxies
© ESO, 2016
1. Introduction.
In active galactic nuclei (AGN), a dusty toroidal structure is thought to be responsible for obscuring our line of sight onto the accreting super massive black hole (SMBH) for some inclination angles. Obscured (“type 2”) AGNs, where only relatively narrow (≲1000 km s-1) forbidden emission lines are seen and unobscured (“type 1”) AGNs, which also show broad (>1000 km s-1) permitted lines are then unified to the same class of objects simply by orientation (Antonucci & Miller 1985; Antonucci 1993; Urry & Padovani 1995). This circum-nuclear dust, usually referred to as the “dusty torus”, absorbs a fraction of the optical and UV light and re-emits the energy in the infrared regime. The infrared bands are therefore a suitable window to analyze the structure of this dusty region.
Infrared observations at the diffraction limit of 10 m class telescopes (~300 mas resolution) allow us to isolate the emission of the circum-nuclear dust spatially from the surrounding starburst emission, but these observations do not usually resolve the structure of the torus (e.g., Siebenmorgen et al. 2008; Raban et al. 2008; Gandhi et al. 2009; Reunanen et al. 2010; Horst et al. 2009; Ramos Almeida et al. 2009, 2011; Asmus et al. 2011; Mason et al. 2012). Asmus et al. (2014) only detected extended emission on arcsecond scales in some 18% of objects. In those cases, Asmus et al. (2014) found that the extended emission usually coincides with the position angle (PA) of the narrow line region (NLR), supporting the view that warm dust exists there (see also Schweitzer et al. 2008).
In recent years, infrared interferometry became an important tool to observe the dusty nuclear regions of AGNs. With a resolution that can easily be more than ten times better than that of a single-aperture telescope, this technique has allowed to resolve the cores of more than two dozen AGNs by now (e.g., Jaffe et al. 2004; Kishimoto et al. 2009a,b; Tristram et al. 2009; Burtscher et al. 2013). The analysis of the entire sample has shown that the mid-infrared (MIR) emission comes from a region about 4−20 times larger than the sublimation radius of dust, but also that the sample is very diverse in the sense that the size and structure is different in each object. To the extent that this allows for statements about the average, no differences between type 1 and type 2 AGNs have been found. For details, we refer to Burtscher et al. (2013, hereafter B13).
Previous interferometric studies of individual objects (e.g., Raban et al. 2009; Hönig et al. 2012, 2013; Tristram et al. 2014; López-Gonzaga et al. 2014), on the other hand, are often able to resolve not only the basic structure, i.e., size and number of components, but also constrain the shape of the resolved emission. In the four objects that have been studied in detail, the dusty emission is always found along the polar direction rather than in an azimuthal configuration as one may naively expect from simple torus pictures (Antonucci & Miller 1985).
The aim of this work is to coherently analyze the interferometric data of the MIDI AGN large programme (LP) sample (B13) to identify intrinsic elongations in the MIR emission of the dusty region of the entire sample. The outline of this paper is the following: Sect. 2 includes a brief explanation of the AGN sample and the interferometric data. In Sect. 3 we explain our geometric model and the procedure followed to fit and identify candidates with elongations. Our results are presented and discussed in Sect. 4. We summarize our results in Sect. 5.
2. The AGN sample, observations, and data processing
Here we use the sample first presented in B13. It consists of the MIDI AGN large programme and all other extragalactic MIR observations publicly available until the time of publishing. These are 23 AGN, all observed with the MID-infrared interferometric Instrument (MIDI; Leinert et al. 2003) at the European Southern Observatory’s (ESO’s) Very Large Telescope Interferometer (VLTI) on Cerro Paranal, Chile. The classical Michelson interferometer MIDI combines the beams of two telescopes at a time in the atmospheric N-band, i.e., the wavelength region 8−13 μm. As a result of the high background in the thermal infrared (exacerbated by ~20 reflections along the VLTI optical train), severe flux limits apply. Our sample is therefore essentially flux-selected among the brightest and most well-known AGNs. It includes 12 type 1, nine type 2 Seyfert galaxies, one radio galaxy, and a quasar, with a median luminosity distance of 53 Mpc. For this work, we additionally collect the published data for the Circinus galaxy (Tristram et al. 2014), NGC 1068 (López-Gonzaga et al. 2014), and NGC 3783 (Hönig et al. 2013), which are three galaxies whose interferometric data showed clear signs of elongated emission. For details about the observation sequence and data reduction, we refer to Burtscher et al. (2012).
All sources were observed with pairs of 8 m Unit Telescopes (UTs) in at least three different baseline configurations. Additionally, for the two brightest and closest AGNs, Circinus and NGC 1068, observations were also carried out using configurations with the 1.8 m Auxiliary Telescopes (ATs) to cover shorter baselines. These two sources are almost completely resolved out in the interferometric data, while in the other galaxies less than 60% of the flux is resolved out. The reason is that the relative resolution, with respect to the dust sublimation radius, is much higher in these two galaxies than for the rest of the sources in the sample. We, therefore, only use the interferometric data obtained from projected baselines < 40 m for the two bright sources to achieve a sample with homogeneous spatial resolution (in multiples of the innermost radius of dust).
The instrument MIDI also provides limited spectral information in the N-band. This information can be used to study several physical properties of the torus, such as temperature profiles or the nature of the silicate feature. As the purpose of our study is to investigate the general geometrical shape of the continuum MIR emission, we restrict ourselves to the 12 μm (rest-frame) fluxes, following B13. At this wavelength, the sources are best resolved and observations are least affected by instrumental and calibration errors, such as correlation losses, the silicate feature, or atmospheric absorption.
The lack of true phase information from the instrument and the sparse (u,v) coverage due to the time-consuming observations, do not allow us to apply image reconstruction techniques. Instead, we can only forward model simple geometrical brightness distributions and compare them with the observed visibilities. These models need to be kept as simple as possible to avoid degeneracies. While the true brightness distribution of the objects might be relatively complex, it has been shown that simple analytical surface brightness distributions, such as Gaussian or uniform disks, can be used to provide a first order approximation of the shape and size and serve as building blocks for more complex geometries (see, e.g., Jaffe et al. 2004; Poncelet et al. 2006; Burtscher et al. 2009, 2013).
2.1. Averaging adjacent (u,v) points
Before modeling the interferometric data, we replaced measurements of adjacent (u,v) points with a weighted average. According to López-Gonzaga et al. (2014), if the size of the emission is smaller or similar to the resolution of the single-aperture telescope, measurements taken with adjacent (u,v) points should not vary too much if the distance Δu between them is Δu ≲ D, where D is the diameter of the telescope. Since all of our objects are essentially unresolved with the single-aperture telescope, we average (u,v) points with Δu ≲ 8 m, except for NGC 1068 and Circinus, where we use a Δu ≲ 1 m as they were observed with the ATs and show significant extension at arcsecond resolutions.
Points within a distance Δu from each other are averaged together using their corresponding uncertainty as a weight. Because the actual changes over the (u,v) plane in terms of correlated flux are small compared to our measurement error, we can assume that the differences in adjacent points is mostly dominated by noise. The averaging process not only serves to obtain more precise visibilities, but it also serves as a way of rebinning the (u,v) plane to reduce the nonuniform sampling.
3. Finding elongations
3.1. Elongated model
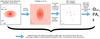 |
Fig. 1 Outline of the test setup to determine the reliability of our model fit for each source. First, we generate a simple model image (left panel) consisting of a point source and an elongated Gaussian of arbitrary axis ratio and position angle. Since the intensity of the point source is largely model independent and well constrained by the observations, its visibility can be set to the actual value of the respective source. Next, this image is Fourier transformed (center left). From these model visibilities we take the values that correspond to the actually observed (u,v) coverage for the specific source (center right panel). After adding appropriate noise, we fit the mock data set with our three-parameter fit (minor axis FWHM θm, position angle PA, and axis ratio ϵ) and compare the result with the known input parameters. This procedure is repeated for different axis ratios and position angles and for the specific (u,v) coverage of each source. |
Previous results from B13 using symmetric distributions, allowed us to determine an average size of the infrared emission for the AGN tori of our sample. However, from the residual plots in Figs. 5−27 of B13 it was already clear that, for some objects, the data contain more information about the shape than just an average size.
The 12 μm emission of the large program sources observed with MIDI can be described with one or two components: 1) an unresolved emission and sometimes 2) an (over-)resolved component. For every object, the level of unresolved emission (the minimum visibility of point source fraction) is well determined even without any model fitting in most of the sources (see B13), this emission is best described by a point source distribution. If there is evidence for a second component, we can describe it by using an elongated Gaussian component as we did for this work (the circular Gaussian component used in B13 is a particular case of the elongated model).
The correlated fluxes are defined by the following equation: 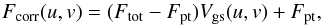 (1)where Fcorr is the correlated flux, Ftot is the total flux measured by the single-aperture telescope, Fpt is the flux of the point source, and Vgs is the visibility of the elongated Gaussian distribution. The elongated Gaussian distribution is defined by three parameters: the full width at half maximum (FWHM) of the minor axis (θm), an axis ratio ε = ΘM/θm defining the ratio between the FWHM of the major axis (ΘM) and the FWHM of the minor axis (θm), and the position angle (PA) of the major axis measured in degrees from east of north. The analytical description of the correlated fluxes is given by the following formula:
(1)where Fcorr is the correlated flux, Ftot is the total flux measured by the single-aperture telescope, Fpt is the flux of the point source, and Vgs is the visibility of the elongated Gaussian distribution. The elongated Gaussian distribution is defined by three parameters: the full width at half maximum (FWHM) of the minor axis (θm), an axis ratio ε = ΘM/θm defining the ratio between the FWHM of the major axis (ΘM) and the FWHM of the minor axis (θm), and the position angle (PA) of the major axis measured in degrees from east of north. The analytical description of the correlated fluxes is given by the following formula: ![\begin{equation} V_{\rm gs}(u,v) = \exp \left[-\frac{\left(\pi\, \theta_{\rm m} \sqrt{u'^2+ \varepsilon^2 v'^2}\,\right)^2}{4 \ln 2}\right] , \end{equation}](/articles/aa/full_html/2016/07/aa27590-15/aa27590-15-eq27.png) (2)where u′ = ucos(PA)−vsin(PA), v′ = usin(PA) + vcos(PA). For most of our objects, the total 12 μm flux has a relatively low uncertainty, so we ignore this error and in the following we consider the total single-aperture flux as a fixed quantity and treat the correlated fluxes as visibilities.
(2)where u′ = ucos(PA)−vsin(PA), v′ = usin(PA) + vcos(PA). For most of our objects, the total 12 μm flux has a relatively low uncertainty, so we ignore this error and in the following we consider the total single-aperture flux as a fixed quantity and treat the correlated fluxes as visibilities.
 |
Fig. 2 Results of our reliability analysis for sources where an elongation should be detectable given the observed (u,v) coverage, signal-to-noise ratio and minimum visibility. First column: (u,v) coverage of the object. The point source fraction (fpt) and typical uncertainty of the interferometric measurements (erravg in percentage) are given for every object. Second column: probability density function of the axis ratio for three different input axis ratios: ϵ = 1 in red, ϵ = 2 in green, and ϵ = 3 in blue. For visualization purposes, we normalized the maximum value of the PDF’s to a value of one. Third column: probability density function of the recovered position angle of the major axis minus the input position angle. The colors are the same as for the second column. Intentionally, we do not plot the resulting PDF for an input axis ratio equal to 1. Fourth column: two-dimensional confidence interval for the axis ratio and FWHM of the minor axis from the fits using data from actual observations. The 1σ, 2σ, and 3σ region are delimited by purple, orange, and red lines, respectively. |
 |
Fig. 3 Similar to Fig. 2, but for sources where the mid-infrared emission is consistent with a nearly circular shape. |
3.2. Reliability of model fits. The role of the (u,v) coverage
Using interferometric measurements to constrain a possibly elongated shape of the emission is not straightforward if the (u,v) coverage is very sparse and inhomogeneous. Beam effects can easily dominate the shape of the reconstructed model image.
Therefore, we need to investigate the influence of the (u,v) coverage in the final determination of the axis ratio and position angle. For this, we set up a series of specific tests to assess the reliability of our fitting routines given the actual (u,v) coverage of every object and the noise levels and known minimum visibility (see Fig. 1 for an outline).
For this experiment, we first create models of elongated Gaussians with a few specified axis ratios and all possible position angles (0−180° in 0.5° steps). We set the major axis FWHM such that this component is marginally resolved (30%) at the shortest observed baselines. We also explored different size scales for the minor axis FWHM (15%, 60%) and the results regarding the reliability of the fit do not change significantly. For this experiment, we include a point source to the model image with the known parameters. This is important since elongated emission is much easier to detect if the source is well-resolved than if the source is largely unresolved.
We then compute the Fourier transform of this model image and “observe” the model ten times by taking the visibilities at the same (u,v) positions as the actual observations and adding Gaussian noise to the modeled data so that they are of the same signal-to-noise ratio (S/N) as the actual data. We apply our fitting routines on these mock observations to derive the best-fit parameters and repeat this experiment for all sources.
As a last step, we compare the best-fit values of axis ratio and position angle with the known model input values and plot the probability of retrieving the correct axis ratio and input position angle for the different realizations of our model image. The (u,v) coverage, the probability density function (PDF) of the axis ratio, and the PDF of the position angle from this experiment are shown for every source in Figs. 2−A.1 along with the χ2 plane of the fit to the actual data.
These figures allow us to judge for each source the significance of the result of our model fit. As a (somewhat arbitrary) distinction between the reliable (Figs. 2 and 3) and less reliable (Fig. A.1) objects we use as a criterion whether the data would allow us to discriminate between a round source (ϵ = 1) and an elongated source with an axis ratio of 2. This can be easily read off from the center-left plot for each source: If the PDFs for the round (ϵ = 1) and the ϵ = 2 model source do not overlap at 1σ (68.3%), we consider this set of observations as a reliable means of detecting elongated emission.
The results from this experiment can be summarize as follows:
-
1)
We cannot recover reliable axis ratios or position angles forobjects with an (u,v) coverage that consists of measurements along essentially two directions (e.g., ESO 323-77, NGC 5995, see Fig. A.1) or if the extended emission is over-resolved (e.g., NGC 5128, see Fig. A.1).
-
2)
It is also not possible to determine the axis ratio or position angle for objects with a point source fraction above 70% and with typical uncertainties of about 10% (e.g., NGC 3218, see Fig. A.1).
-
3)
The position angle can be determined well for the objects shown in Figs. 2 and 3, in these objects the (u,v) coverage has precise measurements along three or more well-spaced directions in the (u,v) plane. We observe from their respective PDFs that for any direction, the position angle can be recovered with an accuracy of about 10°.
We only need to test the reproducibility of the axis ratio test to decide whether we can recover elongated emission since all sets of observations with fully recoverable axis ratios also have well-defined position angles, while the inverse is not true.
Parameters of the best-fit models.
4. Results and discussion
Based on our reliability analysis (Sect. 3.2) and Figs. 2 and 3, we find seven sources where the existing observations would allow us to reliably detect elongated emission. For these sources, we give the best-fitting parameters for the elongated Gaussian model fits together with auxiliary data in Table 1.
Elongated MIR emission on the parsec-scale was found previously in four of the sources in this sample: NGC 424 (Hönig et al. 2012), NGC 3783 (Hönig et al. 2013), NGC 1068 (López-Gonzaga et al. 2014), and the Circinus galaxy (Tristram et al. 2014). These are among the brightest and very well-studied sources (≳30 (u,v) points) where elongation and position angle can be constrained well. Our results (Table 1) are in excellent agreement with those previously published, confirming the reliability of the detected elongations. For NGC 1068 and Circinus, higher spatial resolution data show a distinct disk-like structure, which contributes ~ 20% to the total flux. This disk has a different PA than the large-scale structure that we model here. We ignore the small-scale structure for our large-scale fits since we would not be able to resolve such a structure in any of the other sources because of the lower spatial resolutions achieved here. The FWHM sizes and PAs derived from our large-scale analysis only, are however, very similar to those derived with the more complex disk + large-scale model.
 |
Fig. 4 Best-fit models for elongated objects. For every object, we show the 12 μm image obtained from our best-fit model using a square root scale. We add as a reference for the polar axis of the system, when available, the PA obtained from optical polarimetry (green dashed line) and from the symmetry axis of the ionization cone (red dotted line). |
 |
Fig. 5 Top: comparison between the position angle of the mid-infrared emission from the parsec-scale structure (PAMIR) and the inferred position angle of the system polar axis (PApolar) for the elongated objects. For completeness we also include the marginally elongated object NGC 4507 (blue triangle), no error bars are determined for this object. The dashed line represents a one-to-one relation for the position angles. Bottom: histogram of the difference between the inferred system polar axis and the mid-infrared position angle obtained using interferometry. The histogram including the marginally elongated object NGC 4507 is shown in blue bars, while elongated objects are indicated with black bars. Only objects with elongations obtained from interferometric data have been used here. |
Our reliability analysis has shown that we should also be able to detect elongated emission in MCG-5-23-16, NGC 4507, and NGC 5506. In NGC 5506, our fits indicate that the emission is indeed elongated. The confidence limit of the fit show that the axis ratio is inconsistent with 1 (circular) at 3σ level (Fig. 2). The best-fit elongated model has an axis ratio of 2.5 with a well-defined lower limit, but with its major axis less well determined. The position angle of the major axis of the elongation is 8.3° ± 9.0.
For MCG-5-23-16 and NGC 4507, on the other hand, the 12 μm emission at subparsec scales is consistent with a near circular shape, see Fig. 3. The best-fit axis ratios are 1.3+0.5 and 1.2+0.3 for the two sources, respectively. For the remaining 16 objects, the (u,v) coverage and typical uncertainties do not allow us to recover the shape of the input brightness distribution.
4.1. Polar or equatorial emission?
Determining the axis ratio and position angle of the MIR emission provides valuable information about the geometrical shape of the dusty emission, but we need to locate the position angle of the dust emission with respect to a known axis of the system to learn more about its nature. In principle, [OIII] line emission produced along the ionization cone can be used to determine the direction of the polar axis. Fischer et al. (2013) were able to identify the direction of the ionization cones by using biconical outflow models to describe the kinematic information of the NLR, given by long-slit spectra from the Space Telescope Imaging Spectrograph and [OIII] imaging. We can in principle assume that the symmetry axis of such a cone is a reasonable estimate of the polar axis of the system. The values reported for our sources by Fischer et al. (2013) are shown in Table 1. Since the axis of the ionization cone might be considered as model dependent1, we additionally obtain an estimate of the system axis from optical polarimetry. As discussed by Marin (2014), the degree of polarization observed in Type 1 sources is relatively small, but any position angle detected for the optical polarization should be roughly parallel to the polar axis of the system. For type 2 sources, the degree of polarization should be higher and have a position angle of the polarized light that is roughly perpendicular to the polar axis (e.g., Kishimoto 1999). This explanation could be a simplified version of reality since there might also be a transition region between type 1 and type 2 objects, where the position angle follows a different behavior. Keeping this possible ambiguity in mind, we nevertheless use also the polarization measurements to infer a system axis and list them in Col. 8 of Table 1 and plot them in Fig. 4 as green dashed lines. We find a reasonable agreement between the system axis determined by the NLR modeling and polarimetry with the largest discrepancy of 39° between the two inferred angles in the case of NGC 5506. For our purpose of determining whether the MIR dust emission is rather polar or equatorial elongated, this is sufficient accuracy.
In principle, we could also obtain information about the polar system axis from observing the direction of an existing jet. Synchrotron emission from the jet has been observed intensively at radio bands. We have collected information about the position angle of the jet from the literature and compare them with the values obtained for the polar axis from optical polarimetry and from the NLR (see Table 1). For the objects NGC 4507, NGC 3783, and NGC 424, the emission is unresolved and therefore we cannot obtain any relevant information about the PA. In the case of Circinus, NGC 1068, and NGC 5506, the position angle of the jet agrees very well with the values obtained from optical polarimetry and a bit less well with the values from the NLR.
We observe that in all five objects, where we report an elongation, the position angle of the major axis of the MIR emission is always closer to the inferred polar axis of the system than perpendicular to it; see Fig. 5. If we assume a marginally elongation for the object NGC 4507 to be true, then the mid-infrared PA for this object is also close to the polar system axis. Additionally, we observe that if the estimates of the polar axis system are indeed representative of the true polar axis system, then there is a lack of axial symmetry of the MIR emission around the polar axis (see bottom plot of Fig. 5). In all the objects the emission is always leaned slightly toward one side of the polar axis. In the Circinus galaxy, for example, the difference is 20−30 deg and in this source the positions angles of both the MIR emission and the ionization cone are very reliably determined.
Additionally, the multiple infrared shapes (Elongated: 1 type I, 3 type 2s, and 1 type 1i and nearly circular: 1 type 2 and 1 type 1i) almost regardless of the Seyfert Type may be a surprising result if one has a picture in mind of a donut-like torus (e.g., Fig. 1 of Antonucci 1993).
It has been long realized, however, that such a simple structure cannot represent the actual distribution of dust. Instead, the dust must be in a clumpy configuration (e.g., Schartmann et al. 2008) whose image, as simulated using radiative transfer, is complex and its reduction to an “elongated Gaussian model” is not at all obvious. If we also take hydrodynamical effects into account, even a more or less azimuthal dust configuration can produce images that are polar elongated (e.g., Fig. 8 of Schartmann et al. 2009; and Fig. 5 of Schartmann et al. 2014). In fact, models that produce an infrared emission with a X-shaped morphologies (e.g., Schartmann et al. 2005) also show polar extension to the zeroth order. Slight asymmetries in the density distribution produced by filaments or clouds could then explain the lack of asymmetry around the polar axis system. Additional information, such as kinematics, would be needed to distinguish such a scenario from, for example, a disk wind scenario, which would also produce polar-elongated emission (e.g., Wada 2012; Gallagher et al. 2013; Schartmann et al. 2014).
While with infrared images alone we cannot provide a complete panorama about the structure of the torus, our result of the polar extended emission should serve as a constraint for dusty models that attempt to provide a description of the dusty environment in AGNs. Current SED fitting studies do not take this into account as the SED does not provide any geometrical information. Further investigation needs to be carried out to see if derived torus properties, such as covering factors, torus sizes, and cloud numbers from torus models that reproduce the polar-like extended emission, are consistent with the current models used by the community.
4.2. Future improvements
In our reliability analysis, we studied how the (u,v) coverage and the S/N influence our ability to measure an intrinsic elongation. From this study, we learned that filling the (u,v) coverage is most relevant to determine an elongation. Without improving the accuracy of the measurements but just by obtaining more equally distributed (u,v) points at different position angles, we would be able to confirm or rule out elongations in at least six objects (LEDA17155, NGC 4151, NGC 4593, IC 4239A, NGC 5995, and NGC 7469). These objects have relatively low-to-intermediate point source fractions (<0.6), but their current (u,v) coverage typically has only measurements at resolutions where the emission is resolved, along two distinct position angles. For the objects IZwicky1, H0557-385, and NGC 3281, owing to their relatively high point source fractions ~ 0.8, an improvement of both the (u,v) coverage and S/N would be needed to learn more about the MIR geometry of these objects. It is worth noting that for the objects NGC 4151, NGC 4593, and NGC 3281 there is evidence for a 100 pc scale elongated structure with an orientation that is also close to the polar axis system (Asmus et al. 2014). For these three objects, new infrared interferometric observations would be required to filled the missing (u,v) points and be able to investigate the nature of the elongated emission.
The remaining objects NGC 1365, Mrk 1239, 3C 273, ESO 323-77, NGC 5128 (Cen A), and other objects with point source fractions ≈ 1 require longer baselines to resolve their compact MIR emission. Results from our reliability analysis should be used to plan future observations with the second generation instrument MATISSE (Lopez et al. 2014) to improve our view of the MIR emission in AGNs.
5. Conclusions
We have analyzed the mid-infrared interferometric data of 23 sources observed with the instrument MIDI at the VLTI and investigated in how many objects we should be able to find elongations given the observed (u,v) coverages along with the achieved S/N and the minimum visibilities. We found that we should be able to find elongated emission in seven out of 23 objects and indeed in five of these seven elongated emission is found (four objects are already published, NGC 5506 is a new detection). However, we also find two sources (NGC 4507 and MCG-5-23-16) that are compatible with nonelongated, i.e., circular emission. In the sources where deviations from a circular emission geometry are detected, the elongation is always much closer to the polar than the equatorial direction of the system. The trend of polar elongated emission at parsec scales is compatible with what is observed at 100 pc scales by Asmus et al. (2016; out of 21 Seyferts with extended MIR emission on single-dish images, 18 objects show MIR polar emission including objects such as NGC 4593, NGC 3281, Asmus et al. 2014; NGC 4151, Radomski et al. 2003; Circinus, Packham et al. 2005; Reunanen et al. 2010; NGC 1068, Galliano et al. 2005).
This needs to be followed up with higher S/N and more homogeneous (u,v) coverage before further conclusions can be drawn. Most importantly, a complete sample of AGN tori (e.g., selected by hard X-rays such as Davies et al. 2015) should be observed with the upcoming four-beam MIR interferometer MATISSE at the VLTI (Lopez et al. 2014) to assess the shape and sizes of AGN tori in a representative sample.
In the case of NGC 3783, the model reported by Fischer et al. (2013) differs in inclination from the model provided by Müller-Sánchez et al. (2011), although the position angles are rather similar (–20° and –177°, respectively).
Acknowledgments
The authors thank the anonymous referee for the thoughtful and helpful comments. N. López-Gonzaga was supported by grant 614.000 from the Nederlandse Organisatie voor Wetenschappelijk Onderzoek and acknowledges support from a CONACyT graduate fellowship. L. Burtscher is supported by a DFG grant within the SPP 1573 “Physics of the interstellar medium”.
References
- Antonucci, R. 1993, ARA&A, 31, 473 [Google Scholar]
- Antonucci, R. R. J., & Miller, J. S. 1985, ApJ, 297, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Asmus, D., Gandhi, P., Smette, A., Hönig, S. F., & Duschl, W. J. 2011, A&A, 536, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asmus, D., Hönig, S. F., Gandhi, P., Smette, A., & Duschl, W. J. 2014, MNRAS, 439, 1648 [NASA ADS] [CrossRef] [Google Scholar]
- Asmus, D., Hönig, S. F., & Gandhi, P. 2016, ApJ, 822, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Bransford, M. A., Appleton, P. N., Heisler, C. A., Norris, R. P., & Marston, A. P. 1998, ApJ, 497, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Burtscher, L., Jaffe, W., Raban, D., et al. 2009, ApJ, 705, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Burtscher, L., Tristram, K. R. W., Jaffe, W. J., & Meisenheimer, K. 2012, in SPIE Conf. Ser., 8445, 84451G [Google Scholar]
- Burtscher, L., Meisenheimer, K., Tristram, K. R. W., et al. 2013, A&A, 558, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davies, R. I., Burtscher, L., Rosario, D., et al. 2015, ApJ, 806, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Elmouttie, M., Haynes, R. F., Jones, K. L., Sadler, E. M., & Ehle, M. 1998, MNRAS, 297, 1202 [NASA ADS] [CrossRef] [Google Scholar]
- Fischer, T. C., Crenshaw, D. M., Kraemer, S. B., & Schmitt, H. R. 2013, ApJS, 209, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Gallagher, S. C., Abado, M. M., Everett, J. E., Keating, S., & Deo, R. P. 2013, ArXiv e-prints [arXiv:1303.7142] [Google Scholar]
- Galliano, E., Pantin, E., Alloin, D., & Lagage, P. O. 2005, MNRAS, 363, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Gandhi, P., Horst, H., Smette, A., et al. 2009, A&A, 502, 457 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hönig, S. F., Kishimoto, M., Antonucci, R., et al. 2012, ApJ, 755, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Hönig, S. F., Kishimoto, M., Tristram, K. R. W., et al. 2013, ApJ, 771, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Horst, H., Duschl, W. J., Gandhi, P., & Smette, A. 2009, A&A, 495, 137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jaffe, W., Meisenheimer, K., Röttgering, H. J. A., et al. 2004, Nature, 429, 47 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kinney, A. L., Schmitt, H. R., Clarke, C. J., et al. 2000, ApJ, 537, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Kishimoto, M. 1999, ApJ, 518, 676 [NASA ADS] [CrossRef] [Google Scholar]
- Kishimoto, M., Hönig, S. F., Antonucci, R., et al. 2009a, A&A, 507, L57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kishimoto, M., Hönig, S. F., Tristram, K. R. W., & Weigelt, G. 2009b, A&A, 493, L57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leinert, C., Graser, U., Przygodda, F., et al. 2003, Ap&SS, 286, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Lopez, B., Lagarde, S., Jaffe, W., et al. 2014, The Messenger, 157, 5 [NASA ADS] [Google Scholar]
- López-Gonzaga, N., Jaffe, W., Burtscher, L., Tristram, K. R. W., & Meisenheimer, K. 2014, A&A, 565, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marin, F. 2014, MNRAS, 441, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Mason, R. E., Lopez-Rodriguez, E., Packham, C., et al. 2012, AJ, 144, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Müller-Sánchez, F., Prieto, M. A., Hicks, E. K. S., et al. 2011, ApJ, 739, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Mundell, C. G., Wilson, A. S., Ulvestad, J. S., & Roy, A. L. 2000, ApJ, 529, 816 [NASA ADS] [CrossRef] [Google Scholar]
- Mundell, C. G., Ferruit, P., Nagar, N., & Wilson, A. S. 2009, ApJ, 703, 802 [NASA ADS] [CrossRef] [Google Scholar]
- Orienti, M., & Prieto, M. A. 2010, MNRAS, 401, 2599 [NASA ADS] [CrossRef] [Google Scholar]
- Packham, C., Radomski, J. T., Roche, P. F., et al. 2005, ApJ, 618, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Poncelet, A., Perrin, G., & Sol, H. 2006, A&A, 450, 483 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raban, D., Heijligers, B., Röttgering, H., et al. 2008, A&A, 484, 341 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raban, D., Jaffe, W., Röttgering, H., Meisenheimer, K., & Tristram, K. R. W. 2009, MNRAS, 394, 1325 [NASA ADS] [CrossRef] [Google Scholar]
- Radomski, J. T., Piña, R. K., Packham, C., et al. 2003, ApJ, 587, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Ramos Almeida, C., Levenson, N. A., Rodríguez Espinosa, J. M., et al. 2009, ApJ, 702, 1127 [NASA ADS] [CrossRef] [Google Scholar]
- Ramos Almeida, C., Levenson, N. A., Alonso-Herrero, A., et al. 2011, ApJ, 731, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Reunanen, J., Prieto, M. A., & Siebenmorgen, R. 2010, MNRAS, 402, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Schartmann, M., Meisenheimer, K., Camenzind, M., Wolf, S., & Henning, T. 2005, A&A, 437, 861 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schartmann, M., Meisenheimer, K., Camenzind, M., et al. 2008, A&A, 482, 67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schartmann, M., Meisenheimer, K., Klahr, H., et al. 2009, MNRAS, 393, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Schartmann, M., Wada, K., Prieto, M. A., Burkert, A., & Tristram, K. R. W. 2014, MNRAS, 445, 3878 [NASA ADS] [CrossRef] [Google Scholar]
- Schweitzer, M., Groves, B., Netzer, H., et al. 2008, ApJ, 679, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Siebenmorgen, R., Haas, M., Pantin, E., et al. 2008, A&A, 488, 83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tristram, K. R. W., Raban, D., Meisenheimer, K., et al. 2009, A&A, 502, 67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tristram, K. R. W., Burtscher, L., Jaffe, W., et al. 2014, A&A, 563, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Wada, K. 2012, ApJ, 758, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Xanthopoulos, E., Thean, A. H. C., Pedlar, A., & Richards, A. M. S. 2010, MNRAS, 404, 1966 [NASA ADS] [Google Scholar]
Appendix A
 |
Fig. A.1 Like Fig. 2, but for sources where an elongation is not reliably detectable owing to either bad (u,v) coverage, low signal-to-noise ratio or high minimum visibility (or a combination of these factors). |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
All Tables
All Figures
 |
Fig. 1 Outline of the test setup to determine the reliability of our model fit for each source. First, we generate a simple model image (left panel) consisting of a point source and an elongated Gaussian of arbitrary axis ratio and position angle. Since the intensity of the point source is largely model independent and well constrained by the observations, its visibility can be set to the actual value of the respective source. Next, this image is Fourier transformed (center left). From these model visibilities we take the values that correspond to the actually observed (u,v) coverage for the specific source (center right panel). After adding appropriate noise, we fit the mock data set with our three-parameter fit (minor axis FWHM θm, position angle PA, and axis ratio ϵ) and compare the result with the known input parameters. This procedure is repeated for different axis ratios and position angles and for the specific (u,v) coverage of each source. |
| In the text | |
 |
Fig. 2 Results of our reliability analysis for sources where an elongation should be detectable given the observed (u,v) coverage, signal-to-noise ratio and minimum visibility. First column: (u,v) coverage of the object. The point source fraction (fpt) and typical uncertainty of the interferometric measurements (erravg in percentage) are given for every object. Second column: probability density function of the axis ratio for three different input axis ratios: ϵ = 1 in red, ϵ = 2 in green, and ϵ = 3 in blue. For visualization purposes, we normalized the maximum value of the PDF’s to a value of one. Third column: probability density function of the recovered position angle of the major axis minus the input position angle. The colors are the same as for the second column. Intentionally, we do not plot the resulting PDF for an input axis ratio equal to 1. Fourth column: two-dimensional confidence interval for the axis ratio and FWHM of the minor axis from the fits using data from actual observations. The 1σ, 2σ, and 3σ region are delimited by purple, orange, and red lines, respectively. |
| In the text | |
 |
Fig. 3 Similar to Fig. 2, but for sources where the mid-infrared emission is consistent with a nearly circular shape. |
| In the text | |
 |
Fig. 4 Best-fit models for elongated objects. For every object, we show the 12 μm image obtained from our best-fit model using a square root scale. We add as a reference for the polar axis of the system, when available, the PA obtained from optical polarimetry (green dashed line) and from the symmetry axis of the ionization cone (red dotted line). |
| In the text | |
 |
Fig. 5 Top: comparison between the position angle of the mid-infrared emission from the parsec-scale structure (PAMIR) and the inferred position angle of the system polar axis (PApolar) for the elongated objects. For completeness we also include the marginally elongated object NGC 4507 (blue triangle), no error bars are determined for this object. The dashed line represents a one-to-one relation for the position angles. Bottom: histogram of the difference between the inferred system polar axis and the mid-infrared position angle obtained using interferometry. The histogram including the marginally elongated object NGC 4507 is shown in blue bars, while elongated objects are indicated with black bars. Only objects with elongations obtained from interferometric data have been used here. |
| In the text | |
 |
Fig. A.1 Like Fig. 2, but for sources where an elongation is not reliably detectable owing to either bad (u,v) coverage, low signal-to-noise ratio or high minimum visibility (or a combination of these factors). |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


