| Issue |
A&A
Volume 590, June 2016
|
|
|---|---|---|
| Article Number | A118 | |
| Number of page(s) | 9 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201628570 | |
| Published online | 25 May 2016 | |
How different are the Liège and Hamburg atlases of the solar spectrum? ⋆
1 Max-Planck-Institut für Sonnensystemforschung (MPS), 37077 Göttingen, Germany
e-mail: doerr@mps.mpg.de
2 Instituto de Astrofísica de Canarias (IAC), 38205 La Laguna, Tenerife, Spain
3 Departamento de Astrofísica, Universidad de La Laguna (ULL), 38206 La Laguna, Tenerife, Spain
Received: 21 March 2016
Accepted: 12 April 2016
Context. The high-fidelity solar spectral atlas prepared by Delbouille et al. (Liège atlas, 1973) and the atlas by Neckel (Hamburg atlas, 1999, Sol. Phys., 184, 421) are widely recognised as the most important collection of reference spectra of the Sun at disc centre in the visible wavelength range. The two datasets serve as fundamental resources for many researchers, in particular for chemical abundance analyses. But despite their similar published specifications (spectral resolution and noise level), the shapes of the spectral lines in the two atlases differ significantly and systematically.
Aims. Knowledge of any instrumental degradations is imperative to fully exploit the information content of spectroscopic data. We seek to investigate the magnitude of these differences and explain the possible sources. We provide the wavelength-dependent correction parameters that need to be taken into account when the spectra are to be compared with synthetic data, for instance.
Methods. A parametrically degraded version of the Hamburg spectrum was fitted to the Liège spectrum. The parameters of the model (wavelength shift, broadening, intensity scaling, and intensity offset) represent the different characteristics of the respective instruments, observational strategies, and data processing.
Results. The wavelength scales of the Liège and Hamburg atlases differ on average by 0.5 mÅ with a standard deviation of ± 2 mÅ, except for a peculiar region around 5500 Å. The continuum levels are offset by up to 18% below 5000 Å, but remain stably at a 0.8% difference towards the red. We find no evidence for spectral stray light in the Liège spectrum. Its resolving power is almost independent of wavelength but limited to about 216 000, which is between two to six times lower than specified. When accounting for the degradations determined in this work, the spectra of the two atlases agree to within a few parts in 103.
Key words: atlases / Sun: general / techniques: spectroscopic / line: profiles / Sun: abundances
The fit parameters displayed in Fig. 2 and derived data are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/590/A118
© ESO, 2016
1. Introduction
The solar spectrum is characterised by millions of spectral features that are caused by atomic and molecular energy transitions. The intensities and shapes of these spectral lines show a continuous variation on small spatial and short temporal scales. However, in the time- and space-averaged visible and near-infrared spectrum of the Sun, only the lines formed in the chromosphere show some variation with the solar cycle while photospheric lines remain unchanged, with the exception of the Mn i 5394.7 Å line (Livingston & Wallace 1987; Livingston et al. 1988, 2007).
Because of this lack of variability, it makes sense to record the solar spectrum with high fidelity (spectral resolving power λ/δλ ~ 500 000, signal-to-noise ratio (S/N) ≳1000) for a wide range of wavelengths, tabulating it in the form of an atlas so that it can be used as a standard for various research fields. Atlases of the spectrum of a spatially averaged region at the centre of the solar disc (intensity or photospheric spectrum) are used as a benchmark for simulations (e.g. Pereira et al. 2013; Fabbian & Moreno-Insertis 2015), to derive solar chemical abundances (e.g Caffau et al. 2008; Asplund et al. 2009), and as a reference for spectroscopic data calibration (e.g. Allende Prieto et al. 2004; Beck et al. 2011). Likewise, atlases of the disc-averaged sunlight (flux spectrum) play a key role as a solar standard in stellar astrophysics, for example in the derivation of relative chemical abundances.
The first high-quality atlas of the solar disc-centre spectrum was prepared by Minnaert et al. (1940) in Utrecht (the “Photometric atlas of the solar spectrum from λ 3612 to λ 8771”, commonly referred to as the Utrecht atlas) using observations carried out at the Mt. Wilson observatory. Since then, a variety of other high-fidelity spectral atlases of the Sun have been prepared based on steadily improving instrumentation, mainly at the Jungfraujoch observatory in the Swiss Alps (see the review by Delbouille & Roland 1995) and in the United States at Sacramento Peak observatory (Beckers et al. 1976) and Kitt Peak National Solar Observatory (NSO; see e.g. the review by Hinkle et al. 1995). All these developments culminated with the Fourier-Transform Spectrometer (FTS) of the Kitt Peak McMath-Pierce solar facility in the early 1980s.
Solar observations currently focus on imaging spectro-polarimetry with high spatial resolution, often at the expense of spectral coverage and spectral purity. These observations of narrow spectral ranges can be used to target specific spectral lines, for instance for chemical abundance analysis (e.g. Kiselman 1994; Pereira et al. 2009; Caffau et al. 2015), but many of the applications mentioned above rely instead on a broad-band high-quality reference spectrum.
Three different high-fidelity atlases of the intensity spectrum of the Sun in the visible light are commonly used today. The first is the “Photometric Atlas of The Solar Spectrum from λ 3000 to λ 10000”, which was prepared with data from the Jungfraujoch Observatory and was first published in a printed edition by the University of Liège, Belgium (Delbouille et al. 1973, hereafter DNR73). We refer to this atlas as the Liège visible-light disc-centre atlas, or just Liège atlas for brevity. The second atlas is the “Spectral Atlas of Solar Absolute Disk-Center Intensity from 3290 to 12 510 Å”, which was prepared using data from the FTS of the McMath-Pierce telescope and was published in digital format by Neckel (1999), hereafter N99, at the University of Hamburg, Germany. We refer to this atlas as the Hamburg disc-centre atlas, or just Hamburg atlas. The third atlas is “An atlas of the spectrum of the solar photosphere from 3570 to 7405 Å” (Wallace et al. 1998), which was also compiled from data obtained with the McMath FTS. We focus on the Liège and Hamburg atlases because they are used most often. In addition, the wavelength coverage of the Hamburg atlas is better and its quality is obviously higher than that of the Wallace atlas (e.g. Ayres 2008).
The Liège and Hamburg atlases were made using very different instruments, at different observing sites, and during different epochs of the solar cycle. This naturally raises the question of their respective qualities and of how well they match. Various authors have found inconsistencies in the parameters retrieved from these atlases. Several studies have reported that the continuum level of the Liège atlas needs to be carefully considered (e.g. Ardeberg & Virdefors 1975; Rutten & van der Zalm 1984). Gurtovenko & Kostik (1982) compared equivalent widths derived from their observational data with those from the Liège atlas and found the latter ones to be larger by 5% on average. Asplund et al. (2000) argued that the Hamburg atlas is superior in its wavelength calibration and continuum placement based on the comparative study by Allende Prieto & García López (1998). Caffau et al. (2008, 2009, 2011) found significantly different line shapes in the Hamburg and Liège atlases when comparing specific spectral lines. These authors speculated that the reason might be the different levels of telluric line contamination and considered the necessity for a new high-quality solar atlas. Scott et al. (2015) reported that the equivalent widths derived from these atlases and their own derived synthetic spectra agreed exceptionally well.
To the best of our knowledge, no systematic study is available so far that examines the compatibility of these two important spectral atlases, except for the investigation of the wavelength calibration carried out by Allende Prieto & García López (1998). We intend to provide a general quantitative measure of the differences between the Liège and Hamburg atlases. A direct comparison of basic line parameters such as their wavelength positions and equivalent widths is not adequate for this purpose because they are mostly independent of the spectral resolution. On the other hand, absolute parameters such as the line width and line depth are very sensitive to the spectral resolution. Our approach does not depend on detailed knowledge of the instrument specifications because we model the instrumental degradations to find those that result in the best match of the Hamburg and Liège spectra.
2. Spectral atlases
We restrict the analysis to the Liège and Hamburg atlases. A variety of other nicknames can be found in the literature for these two atlases, for instance Jungfraujoch atlas or Delbouille atlas for the first and Neckel atlas, Kitt-Peak atlas, FTS atlas, and variations thereof for the Hamburg atlas. N99 stated that the Hamburg atlas was prepared by “Brault & Neckel (1987)”, a reference that was adopted by some researchers and adds to the confusion because to our best knowledge there is no corresponding publication. The naming is even more unclear as a variety of further solar spectral atlases with similar nicknames (e.g. FTS atlas) made with McMath FTS data were published by other authors. We even sometimes found references in the literature to one of the atlases while obviously a different atlas was used. In an attempt to clarify some of that confusion, we briefly introduce the various visible-light, disc-centre, and disc-averaged McMath FTS atlases before we proceed with a more detailed description of the Liège and Hamburg atlases.
The “Solar flux atlas from 296 to 1300 nm” is probably the most widely used reference spectrum of the disc-averaged Sun in visible light. It was originally published in a printed edition (Kurucz et al. 1984, hereafter KFBT84) but is also available in digital form1. This atlas is often referred to as the NSO atlas.
Kurucz published2 a re-reduced version that he corrected for telluric lines (Kurucz 2005). Another flux atlas based on different data with a correction for telluric features was published3 by Wallace et al. (2011).
The first official disc-centre atlas made with McMath FTS data is “An atlas of the spectrum of the solar photosphere from 13 500 to 28 000 cm-1 (3570 to 7405 Å)” by Wallace et al. (1998)4, which was later extended to a wider wavelength range (Wallace et al. 2007).
The Hamburg disc-centre atlas was prepared from FTS observations different from either of those prepared by Wallace et al., but there is also a Hamburg flux atlas that is based on the same data as the KFBT84 flux atlas.
Recently, Stenflo (2015) published an atlas of the solar spectrum at the disc centre and at the limb. His disc-centre data are identical with the Hamburg spectrum, except for normalising the continuum to the maximum intensity in each 1000 Å wide interval (Stenflo 2015, priv. comm.). The limb spectrum stems from archival McMath FTS data recorded for a former investigation (Stenflo et al. 1983).
More atlases have been made with the McMath FTS, covering the near-infrared and mid-infrared ranges, sunspot atmospheres, etc. (see e.g. Hinkle et al. 1995), but these are not discussed here.
2.1. Liège disc-centre atlas
The data for this atlas were recorded between 1973 and 1988 with a scanning double-pass grating spectrometer at the Jungfraujoch scientific station in the Swiss Alps. The observatory is located at an altitude of 3580 m and thus enables observations through an extremely dry atmosphere during a few days in the year.
Details about the instrument, observational procedures, and the data processing can be found in the introduction to the atlas (DNR73), in the introduction to the older infrared atlas made at Jungfraujoch (Delbouille & Roland 1963), and in the review by Delbouille & Roland (1995). A coelostat with mirrors of 30 cm diameter fed the fixed telescope, which had a focal length of 1250 cm. The solar image of 11.5 cm diameter was centred on the 2.5 cm long (400′′ projected on the Sun) entrance slit of a prism monochromator that was used for order selection. The main spectrometer was based on a Fastie-Ebert setup with 730 cm focal length, modified for double-pass. Two different gratings were used, one with 600 rules mm-1 below 3586 Å and one with 300 rules mm-1 above. The theoretical spectral resolving power is specified with 1 250 000 and 500 000 at the blue and red ends of the atlas. The instrumental profile measured with a laser is provided for four grating orders. The authors emphasise the excellent stray-light suppression and spectral purity obtained with the double-pass configuration.
The atlas covers the range between 3000 and 10 000 Å and was pieced together from many individual segments. Each segment is only a few Å wide and was prepared from 50 repeated scans that were acquired within approximately 45 min. Detector dark currents were measured before and after each segment was recorded, and the mean was subtracted. The data of each segment were processed with several analogue and digital data reduction steps (binning, outlier-rejection, adaptive low-pass filtering) online before the final spectrum was stored on magnetic tape.
The wavelength scale for each of the segments was derived from the line list of Pierce & Breckinridge (1973), hereafter PB73. The wavelengths are therefore given in the solar frame of reference and are corrected for the radial velocities of the observations, but not for the gravitational redshift. The position of the continuum was placed at 100% of the intensity scale by interactively straightening the individual segments to match the slightly overlapping adjacent segments. The noise level is not explicitly stated, but we measured a very high S/N of ~6000 in the continuum at 6300 Å. The spectra for the digital version of the atlas were resampled to constant wavelength increments of 2 mÅ.
The data were originally distributed on magnetic tapes, and copies seem to be used at various research institutes. Unfortunately, the complete atlas does not seem to be available for download. Individual spectral regions can be selected interactively and downloaded in ASCII format from a database provided by the Observatoire de Paris5.
2.2. Hamburg disc-centre atlas
The data for this atlas were recorded around 1980 (the exact observing dates are not published) with the FTS at the McMath-Pierce solar telescope at the Kitt Peak National Observatory. The telescope is located at an altitude of 2096 m.
The disc-centre atlas and an associated flux atlas are a by-product of a former investigation by Neckel & Labs (1984), hereafter NL84. The Hamburg flux atlas is based on the very same FTS observations as the KFBT84 atlas, for which details of the observational parameters and instrument settings were published. Unfortunately, only a few details about the disc-centre data are published, and we did not succeed in identifying the FTS scans that were used in the data archive provided by NSO. The available information in NL84 and N99 indicates, however, that instrumental settings and observational procedures were similar for flux and disc-centre data.
Both atlases cover the wavelength range between 3290 Å and 12 510 Å and were pieced together from seven individually measured segments in slightly overlapping wavelength intervals. The spectral windows were selected with a low-dispersion monochromator and optical filters. Each segment consists of several co-added FTS scans to increase the S/N. Each scan typically took about five minutes. The number of summed scans for each segment of the disc-centre atlas is not published, but for the flux atlas it varies between 16 and 36, leading to total observing times of around two hours (Table 1 in KFBT84). The exact size of the mask used to define the averaging area on the solar disc is not known. According to the meta-data provided by the FTS archive, the data for the Wallace atlas was recorded with a circular mask of 5′′ diameter, and we may assume that similar settings apply for the observations used for the Hamburg atlas. Other commonly used masks were circular with 10′′ or rectangular with a similar effective area (e.g. Balthasar 1988).
According to N99 and NL84, the wavenumber sampling δσ was set to values between 0.035 cm-1 at the blue end and 0.012 cm-1 at the red end. Assuming a strictly Nyquist-critical sampling, this translates into a spectral resolving power σ/ 2δσ of at least 350 000 for all scans in both atlases. We note that this is not necessarily the case; many FTS observations were acquired with at least three samples per resolution element (e.g. Brault 1985). Because of the equidistant wavenumber sampling of an FTS, the resolving power changes with wavelength and reaches values of up to 520 000 at the blue end of some segments (cf. Fig. 6). The wavelength calibration for the disc-centre atlas was derived from the wavelengths given in the line list of PB73, the same reference as used for the Liège spectrum. N99 stated that the fractional wavelength errors are smaller than 1.5 × 10-7.
The atlas provides the line spectrum and the position of the continuum, both in intensity units (W cm-2 ster-1 Å-1) with an accurate (<0.5%) absolute calibration (NL84) that is based on the earlier measurements of Labs & Neckel (1967). In this work, we exclusively use the Hamburg spectrum with the continuum normalised to unity, that is, by dividing the line spectrum by the continuum intensities. We note that this results in some intensity values >1.0 of which the maximum is ~1.01 and the median ~1.001. These numbers are compatible with the stated accuracy of the continuum intensity level. The S/N is not explicitly specified for the disc-centre atlas. We measured a S/N of ~3000 in the continuum at 6300 Å. The spectra have a variable wavelength sampling, a consequence of the conversion from wavenumber into wavelength units.
The Hamburg atlas is available in ASCII format from the ftp server of the University of Hamburg6.
2.3. Remarks
A summary of the basic specifications of the two atlases is shown in Table 1. Based on these numbers, the Liège spectrum is expected to be of higher quality than the Hamburg spectrum. A direct side-by-side plot in Fig. 1 (cf. also Fig. 7) indicates a very similar noise level, but it also reveals a loss of spectral detail in the Liège spectrum where the hyper-fine splitting of the manganese line at 5420.4 Å can barely be seen, while it is clearly resolved in the Hamburg spectrum and also in the Wallace atlas. The right panel shows details in the red wing of the Hα line, a region that is heavily contaminated with telluric H2O lines. The H2O features are much less pronounced in the Liège spectrum than in the other atlases. The Wallace atlas is also provided with a correction for telluric lines which sometimes fails in the core of very deep lines, however, therefore we used the non-modified spectrum here. The Wallace atlas shows a pronounced high-frequency fringe pattern with varying amplitude. The behaviour mentioned above can be observed at all wavelengths covered by the atlases and is not unique to the spectral windows selected here. Despite these issues, we found that the Liège and Hamburg atlases provide a more consistent quality throughout the whole spectral range. For this reasons, we discarded the Wallace atlas and restrict the analysis to the Hamburg and Liège spectra (see also Ayres 2008).
 |
Fig. 1 Details in the Liège, Hamburg, and the Wallace disc-centre atlases in two spectral regions. Line identifications are from the list of PB73. |
Summary of the basic atlas properties.
3. Method
We assumed that the better resolved Hamburg spectrum (IHa) can be transformed to the Liège spectrum, ![\begin{equation} {I}[\lambda_1,\lambda_2]_{\text{Li}} = S\left(\text{I}[\lambda_1+L,\lambda_2+L]_{\text{Ha}} * \Psi(B) + O\right), \label{eq:transformation} \end{equation}](/articles/aa/full_html/2016/06/aa28570-16/aa28570-16-eq22.png) (1)by modelling the degradations in the wavelength interval λ1 + L to λ2 + L as an additional broadening (B) of the spectral lines that is due to a lower spectral resolution, a wavelength shift (L) due to fluctuations in the wavelength calibrations, a scaling factor (S) due to differently placed continuum levels, and an offset (O) due to undispersed scattered light. The broadening is modelled as the convolution with an instrumental profile Ψ(B) with a full-width at half-maximum (FWHM) of B.
(1)by modelling the degradations in the wavelength interval λ1 + L to λ2 + L as an additional broadening (B) of the spectral lines that is due to a lower spectral resolution, a wavelength shift (L) due to fluctuations in the wavelength calibrations, a scaling factor (S) due to differently placed continuum levels, and an offset (O) due to undispersed scattered light. The broadening is modelled as the convolution with an instrumental profile Ψ(B) with a full-width at half-maximum (FWHM) of B.
The best-fit parameters B,L,S, and O of the transformation are found by minimising the χ2 between the Liège and the modified Hamburg spectrum with a Levenberg-Marquardt algorithm (Markwardt 2009). The method directly yields the parameters of the Liège atlas relative to the Hamburg atlas. Under the assumption that the characteristics of the Hamburg atlas are well known, the true spectral resolution, wavelength stability, and continuum level of the Liège spectrum can be retrieved. Similar procedures are commonly employed to estimate the instrumental profiles of spectrometers where a direct measurement is not feasible (Valenti et al. 1995).
The two spectra were normalised to have their continuum at unity. The error estimates for the spectra were computed by combining the nominal noise of the Liège spectrum and the effective noise of the modified Hamburg spectrum. The S/N of the latter is increased during the optimisation process because of the convolution with a kernel of non-zero width.
To minimise the effect of blending telluric lines, we applied the fitting procedure to narrow wavelength intervals of ± 150 mÅ around individual solar spectral lines. The line list provided by PB73 was used to select the target lines. The overlapping spectral region of the Hamburg and Liège atlases and the line list is 3290–8770.7 Å. Of the total number of 9073 identified solar lines in this range, we only processed those with a line depression of more than 5% relative to the local maximum intensity. To remove the most extreme outliers from the 8035 processed lines, we discarded those with a reduced χ2 (χ2/n, n: number of degrees of freedom of the fit) larger than the 95th percentile of the initial χ2/n distribution. This left a total of 7634 fits that are analysed in the following.
An initial run was carried out with all four free parameters (L, S, B, O) for the fits. This test verified that the straylight parameter O is indeed compatible with zero throughout the whole spectral range (see discussion in the appendix). The final fits were carried out with only three free parameters (L, S, B).
 |
Fig. 2 Investigated spectral region (topmost panel; blue trace: Hamburg, green trace: Liège) and the results from the fitting procedure (parameters L, S, B of Eq. (1), the rms of the residuals of the fit, and the reduced χ2) versus wavelength. The thin red tick marks and the bold blue tick marks above the topmost panel indicate grating order intersections and FTS scan intersections, respectively. Zero wavelength shift and unity scaling factors are indicated by the horizontal blue lines in the L and S panels. The blue line in the trace of the rms residuals indicates the median value. |
4. Results and discussion
Figure 2 summarises the results of all fits (see Fig. 7 for an example of one individual fit). The topmost panel displays a trace of the Hamburg and Liège spectra in the investigated wavelength interval. The L, S, and B parameters are plotted versus wavelength in panels two to four. In the lowest two panels, the root mean square (rms) of the residuals for each fit and the reduced χ2 are plotted. The individual parameters are discussed in the following subsections. The results of the fits and derived correction parameters that can be applied for example to synthesized spectra are available at the CDS.
4.1. Reliability of the fits
The quality of the fits is very variable, but the parameters are within a physically meaningful range. The median of χ2/n is 42.4, the 95th percentile is 386.8; 239 fits have a reduced χ2 better than 5. The very good fits are essentially evenly distributed throughout the whole wavelength range, but the χ2 improves with increasing wavelength in general. This is because the line depths decrease towards the red part of the spectrum, which lowers the S/N of the line profiles.
The χ2/n values are always higher than unity, which indicates that within the given very low noise levels our model does not account for all the differences between the two atlases. This can also be seen from the residuals of the fit in Fig. 7. The residuals show systematic variations on a scale narrower than telluric or solar spectral features. This is a typical pattern and indicates that the differences stem from instrumental artefacts (e.g. spectral fringes) or data processing artefacts. Additional effects that are not covered by our model but are most likely imprinted on the data to some degree are non-linearities of the detectors (e.g. the discussion in KFBT84 of the effect on FTS spectra) and intensity gradients within short wavelength intervals. We note that the χ2 values computed here are crude estimates because we do not have noise estimates at all wavelengths and because adjacent data points of the Liège spectrum are correlated to an unknown degree due to the heavy post-processing of the original raw data (low-pass filtering, re-sampling).
A measure of the similarity of the spectra after applying the best-fitting instrumental degradations is the rms of the fit-residuals. The median of the rms residuals of all fits is 1.18 × 10-3, the 95th percentile is 2.5 × 10-3. The histogram of the rms residuals is shown in Fig. 3 in comparison to the case where only the L parameter was fitted, that is, where only the wavelength shift between both spectra was corrected. In the latter case, the distribution of the rms residuals is much broader and the median is about five times larger at 5.7 × 10-3.
 |
Fig. 3 Histogram of the rms of the fit residuals. The case when only the wavelength shifts are fitted is compared to the case where wavelength shift, scaling, and broadening (panel 5 in Fig. 2) are considered. The width of the bins is 1 × 10-4. |
The apparent scatter of the fit parameters that is visible in Fig. 2 is not at all entirely random, but an effect of the compressed display. When they are zoomed to a range where the individual data points can be distinguished (Fig. 4), the values of the parameters are similar or follow a non-random, systematic pattern within short wavelength intervals. The 1-σ errors of the fit parameters are considerably smaller than the observed variations in narrow wavelength intervals, supporting the interpretation that these variations are indeed caused by nonmodelled systematic effects in the atlases. The intersections between the grating orders and FTS scans (indicated in Fig. 2) leave no clear trace on the fitted parameters.
We also note that our method cannot necessarily distinguish between instrumental effects and real differences of the spectra. Some degree of realisation noise has to be present in both atlases and in any other measurement because of the finite temporal and spatial averaging. While the Hamburg spectrum is pieced together from only seven individual realisations of the average photospheric spectrum, the Liège atlas is made of thousands of these realisations in different stages of the solar cycle. But while the resulting fluctuations could explain some of the scatter we see in the fitted parameters, the statistics of the large sample of realisations makes the mean values of our results more reliable.
 |
Fig. 4 Zoom on a narrow wavelength window in Fig. 2. The gap in the very core of the Ca ii 3934 Å line is caused by the lack of strong enough spectral features. Error bars represent the 1σ parameter uncertainties provided by the minimisation routine. |
4.1.1. Effect of telluric lines
Telluric lines increasingly affect the fits redward of 5800 Å. This is partly because telluric lines (especially H2O lines) are stronger in the Hamburg spectrum in general, but also because the different wavelength shifts of the telluric lines with respect to the solar lines. The impact of telluric lines is demonstrated in Fig. 5 where we applied the fitting method to consecutive intervals of 1 Å width, which are therefore more susceptible to telluric blends. Shown are only the parameter S, the reduced χ2, and a synthetic telluric spectrum that was provided by Kurucz (2015, priv. comm.). The χ2/n is strongly correlated with the telluric spectrum and to some degree also with the S parameter.
4.2. Wavelength calibration
The wavelength calibrations of both atlases agree within the accuracy of the used calibration reference when excluding the region 4900–5800 Å. The mean of L is + 0.5 mÅ, with a standard deviation of 1.8 mÅ in that region. This is expected because both atlases are calibrated to the same reference.
We do not have an explanation for the bump at 5000 Å, but it is clearly due to a miscalibration in the Liège spectrum, not in the Hamburg spectrum. We verified this by comparing measured positions of iron lines in the two atlases to the PB73 line list and to the respective laboratory wavelengths provided by Nave et al. (1994). In both cases the same bump only appears for the Liège spectrum, not for the Hamburg spectrum. Interestingly, Allende Prieto & García López (1998), who used the same approach to compare the Hamburg and the Liège atlases, concluded that the Liège spectrum is affected by a substantial miscalibration with a strong wavelength dependence. A closer inspection revealed that these authors used a particular version of the Liège atlas that has a constant wavelength offset of 14 mÅ with respect to the official version used in this work. When converted into a velocity, this offset fully explains the apparent wavelength dependence observed by these authors.
In short wavelength intervals, the L parameter sometimes follows arc-shaped patterns. In the zoomed region around 3950 Å in Fig. 4, the width of these arcs is about 4−5 Å, which is compatible with the width of the individually observed segments at that wavelength. The pattern could be an artefact from the non-linearity of the spectrograph’s dispersion that may not have been modelled in the wavelength scale of the individual segments. Furthermore, PB73 estimated that their systematic errors can be as large as 2 mÅ. Because of the fundamental differences in how the Hamburg and Liège atlas were pieced together from individual observations, the systematic errors in the line list will to some degree also be detectable in this analysis.
 |
Fig. 5 Scaling parameter derived from fitting consecutive 1 Å intervals. A synthetic telluric spectrum is plotted for comparison with the pattern of the χ2 in the lowest panel. |
4.3. Continuum level
The scaling parameter S represents the ratio of the continuum intensity of the Hamburg and Liège spectra. At wavelengths larger than ~5000 Å, S is close to unity with a mean of 0.992 and a standard deviation of 0.006. Large deviations from unity occur below ~5000 Å, where we find several peaks between 0.94 and 1.175. Some of these peaks coincide with the Balmer lines (4861 Å, 4340 Å, 4101 Å, and 3970 Å) and the Ca ii lines at 3934 Å and 3968 Å (cf. Fig. 4). The departures from unity farther to the blue seem not to be clearly coinciding with strong spectral lines, but are probably caused by the general lack of continuum in this region. NL84 also provided a calibration for the Liège spectrum with respect to their absolute intensities and found a very similar pattern (cf. their Fig. 12).
The S parameter is less susceptible to telluric contamination than the L and B parameters. However, a comparison between Figs. 5 and 2 suggests that some of the spikes in S redward of 5500 Å are caused by telluric contamination.
DNR73 explicitly stated that the continuum level of the Liège spectrum is not entirely reliable. The manufacturing process of the Liège atlas makes it even surprising that the continuum level agrees so well with the Hamburg spectrum in most spectral regions and emphasises the careful work of DNR73.
4.4. Line broadening and spectral resolution
The broadening parameter B increases approximately linearly with wavelength from ~12 mÅ to ~40 mÅ. It shows the strongest scatter of the three fitted parameters. There is no clear and pronounced systematic pattern visible on short wavelength intervals as for the other parameters (cf. Fig. 4). This scatter might be related to the automatic adaptive low-pass filtering that was applied online during data acquisition.
The strong broadening that we observe throughout the whole Liège spectrum is in clear contrast to the stated spectral resolution. From the fitted parameter B(λ) we derive the effective absolute broadening of the Liège spectrum, 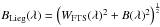 , by taking into account the known finite width WFTS(λ) of the instrumental profile of the FTS. The spectral resolving power computed from R = λ/BLieg is plotted in Fig. 6 in comparison to the theoretical performance of the gratings and the measured resolving power. The laser measurements of DNR73 yield a nearly constant resolving power of ~800 000, which is only in accordance with the theoretical resolution at 5682 Å (order 10). The mean resolving power derived from BLieg is almost constant with wavelength with a mean of 216 000. This is more than three times lower than suggested by the laser measurements and between two to six times lower than the theoretical grating performance.
, by taking into account the known finite width WFTS(λ) of the instrumental profile of the FTS. The spectral resolving power computed from R = λ/BLieg is plotted in Fig. 6 in comparison to the theoretical performance of the gratings and the measured resolving power. The laser measurements of DNR73 yield a nearly constant resolving power of ~800 000, which is only in accordance with the theoretical resolution at 5682 Å (order 10). The mean resolving power derived from BLieg is almost constant with wavelength with a mean of 216 000. This is more than three times lower than suggested by the laser measurements and between two to six times lower than the theoretical grating performance.
 |
Fig. 6 Theoretical and measured resolving power of the Liège atlas. The resolution settings for the individual segments of the Hamburg atlas are plotted for comparison. The plotted trace of the data measured in this work was filtered with a running median for better visibility. The horizontal black line marks the mean of our measured values. |
We used only a simple Gaussian to model the broadening. However, we carried out tests with the instrumental profiles provided by DNR73 that we scaled to the best-fitting width, and the results are virtually identical to a Gaussian of the same FWHM. As the measured instrumental profiles are available only for four grating orders, we decided to only use the Gaussian model here because it is easier to reproduce. We also need to stress that the published instrumental profiles utterly fail to reproduce the observed line shapes. This is demonstrated in Fig. 7 for a Cr i line at 5214.132 Å. The dashed black curve represents the modified Hamburg spectrum when B is fixed to 6.5 mÅ, which is the FWHM of the published instrumental profile for this wavelength, and only S and L are fitted. This leads to a significant mismatch of the line shapes, and the rms of the fit residuals increases to 2.7 × 10-3 with a χ2/n of 140. With three free parameters, however, the fit yields B = 19.8 mÅ with rms residuals of 5.4 × 10-4 and a χ2/n of 5.3.
 |
Fig. 7 Example of a fit to one spectral line. The blue dots show the original Hamburg spectrum, the red line shows the best-fitting modified Hamburg spectrum according to Eq. (1). The dashed line represents the fitted Hamburg spectrum, but with the parameter B forced to 6.7 mÅ. The lower panel shows the residuals of the fit with three free parameters. Only every second data point is plotted for the Liège spectrum for better visibility. |
We can only speculate about the origin of the reduction in spectral resolution, but two effects would at least qualitatively explain the observed behaviour. 1) If the solar image were to be aligned with the equator parallel to the slit, the velocity gradient of 800 m s-1 along the slit would translate into an approximate broadening of 4 mÅ at the blue end and 14 mÅ at the red end of the Liège spectrum. 2) The so-called slit curvature (“spectrum smile”) is an intrinsic distortion of a grating spectrograph that causes the image of the entrance slit to be curved in the focal plane of the spectrograph camera. With a scanning spectrograph, a spectral gradient is imaged onto the exit slit, which broadens the spectrum registered by the detector. Laser measurements are less prone to the slit curvature in the (likely) case that the slit is not fully illuminated by the laser. We did not try to estimate the magnitude of this effect because it intimately depends on the exact optical configuration of the spectrograph and the detector system.
5. Conclusions
Previous studies based on the Liège and Hamburg spectral atlases sometimes came to contradictory conclusions regarding the compatibility of parameters retrieved from the two datasets.
We carried out a detailed comparison that took the different instrumental degradations (spectral broadening, wavelength shift, intensity scaling, intensity offset) of the two atlases into account. Our approach modelled these degradations and tried to find the best-fitting model parameters to match the Hamburg and Liège spectra, thereby measuring the wavelength calibration, continuum level, and resolution of the Liège spectrum relative to the Hamburg spectrum, whose parameters are well known. The results support the claimed quality metrics of the Liège data except for the spectral resolving power, which we found to be between two to six times lower than specified and which probably explains to a large extent the disagreement in the two atlases found by some authors. Studies based on equivalent widths are susceptible to the position of the continuum but not to the spectral resolution, which affects model fitting, however.
When they are known, however, the degradations can be accounted for. In doing so, we found the rms of the differences of the two atlases to be less than 1.2 × 10-3 for 50% of the 7634 investigated spectral lines in the region between 3290 and 8771 Å. This is a remarkably good agreement given the very different instruments and methods used to produce the two atlases.
The Liége and Hamburg atlases will probably continue to be the main solar reference spectra for the coming years. Efforts are under way at the astronomical institute of the university of Göttingen, Germany, to create new high-resolution high-fidelity FTS atlases of the Sun (Reiners et al. 2016), but since the observations are carried out from virtually sea-level altitude, these data are expected to have an enhanced telluric contamination compared to the Hamburg and Liège data. The high-altitude site and the resulting lower contamination with telluric H2O features make the Liège spectrum still a competitive and in this regard also unique option for many investigations that rely on precise line shapes.
Also available online: ftp://vso.nso.edu/pub/atlas/visatl/
Acknowledgments
The authors thank Robert L. Kurucz for providing his synthetic telluric spectrum, Ginette Roland for providing information about the observations at Jungfraujoch, Frank Hill for guiding us through the McMath FTS archive, and Ansgar Reiners for valuable comments on FT-spectrometers. We are grateful for the comments of the anonymous referee that helped to improve the manuscript. This work is partially supported by the Spanish Ministry of Science through projects AYA2014-55078-P, AYA2011-24808 and CSD2007-00050, and by the German Federal Ministry for Education and Research through the “Role Of the MIddle atmosphere in Climate (ROMIC)” project. This work contributes to the deliverables identified in FP7 European Research Council grant agreement 277829, “Magnetic connectivity through the Solar Partially Ionized Atmo- sphere”. This research has made use of NASA’s Astrophysics Data System.
References
- Allende Prieto, C., & García López, R. J. 1998, A&AS, 129, 41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allende Prieto, C., Asplund, M., & Fabiani Bendicho, P. 2004, A&A, 423, 1109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ardeberg, A., & Virdefors, B. 1975, A&A, 45, 19 [NASA ADS] [Google Scholar]
- Asplund, M., Nordlund, Å., Trampedach, R., Allen de Prieto, C., & Stein, R. F. 2000, A&A, 359, 729 [NASA ADS] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Ayres, T. R. 2008, ApJ, 686, 731 [NASA ADS] [CrossRef] [Google Scholar]
- Balthasar, H. 1988, A&AS, 72, 473 [NASA ADS] [Google Scholar]
- Beck, C., Rezaei, R., & Fabbian, D. 2011, A&A, 535, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beckers, J. M., Bridges, C. A., & Gilliam, L. B. 1976, A high resolution spectral atlas of the solar irradiance from 380 to 700 nanometers, Vol. 2: Graphical form (Massachusetts: Air Force Geophysics Lab.) [Google Scholar]
- Brault, J. W. 1985, in High Resolution in Astronomy, Fifteenth Advanced Course of the Swiss Society of Astronomy and Astrophysics, eds. A. O. Benz, M. Huber, & M. Mayer (Sauverny, Switzerland: Geneva Observatory), 3 [Google Scholar]
- Caffau, E., Ludwig, H.-G., Steffen, M., et al. 2008, A&A, 488, 1031 [CrossRef] [EDP Sciences] [Google Scholar]
- Caffau, E., Maiorca, E., Bonifacio, P., et al. 2009, A&A, 498, 877 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caffau, E., Ludwig, H.-G., Steffen, M., Freytag, B., & Bonifacio, P. 2011, Sol. Phys., 268, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Caffau, E., Ludwig, H.-G., Steffen, M., et al. 2015, A&A, 579, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delbouille, L., & Roland, C. 1995, in Laboratory and Astronomical High Resolution Spectra, eds. A. J. Sauval, R. Blomme, & N. Grevesse, ASP Conf. Ser., 81, 32 [Google Scholar]
- Delbouille, L., & Roland, G. 1963, Atlas photométrique du spectre solaire de λ 7498 à λ 12016. Photometric atlas of the solar spectrum from λ 7498 to λ 12016 (Institut d’Astrophysique de l’Université de Liège) [Google Scholar]
- Delbouille, L., Roland, G., & Neven, L. 1973, Atlas photométrique du spectre solaire de λ 3000 à λ 10 000 (Institut d’Astrophysique de l’Université de Liège) [Google Scholar]
- Fabbian, D., & Moreno-Insertis, F. 2015, ApJ, 802, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Gurtovenko, E. A., & Kostik, R. I. 1982, A&AS, 47, 193 [NASA ADS] [Google Scholar]
- Hinkle, K. H., Wallace, L., & Livingston, W. 1995, in Laboratory and Astronomical High Resolution Spectra, eds. A. J. Sauval, R. Blomme, & N. Grevesse, ASP Conf. Ser., 81, 66 [Google Scholar]
- Kiselman, D. 1994, A&AS, 104 [Google Scholar]
- Kurucz, R. L. 2005, Mem. Soc. Astron. It. Suppl., 8, 189 [Google Scholar]
- Kurucz, R. L., Furenlid, I., Brault, J., & Testerman, L. 1984, Solar flux atlas from 296 to 1300 nm [Google Scholar]
- Labs, D., & Neckel, H. 1967, Z. Astrophys., 65, 133 [NASA ADS] [Google Scholar]
- Livingston, W., & Wallace, L. 1987, ApJ, 314, 808 [NASA ADS] [CrossRef] [Google Scholar]
- Livingston, W. C., Wallace, L., & White, O. R. 1988, Science, 240, 1765 [NASA ADS] [CrossRef] [Google Scholar]
- Livingston, W., Wallace, L., White, O. R., & Giampapa, M. S. 2007, ApJ, 657, 1137 [NASA ADS] [CrossRef] [Google Scholar]
- Markwardt, C. B. 2009, in Astronomical Data Analysis Software and Systems XVIII, eds. D. A. Bohlender, D. Durand, & P. Dowler, ASP Conf. Ser., 411, 251 [Google Scholar]
- Minnaert, M., Houtgast, J., & Mulders, G. F. W. 1940, Photometric atlas of the solar spectrum from λ 3612 to λ 8771 with an appendix from λ 3332 to λ 3637 (Utrecht: Sterrewacht Sonnenborgh) [Google Scholar]
- Nave, G., Johansson, S., Learner, R. C. M., Thorne, A. P., & Brault, J. W. 1994, ApJS, 94, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Neckel, H. 1999, Sol. Phys., 184, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Neckel, H., & Labs, D. 1984, Sol. Phys., 90, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Pereira, T. M. D., Kiselman, D., & Asplund, M. 2009, A&A, 507, 417 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pereira, T. M. D., Asplund, M., Collet, R., et al. 2013, A&A, 554, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pierce, A., & Breckinridge, J. 1973, The Kitt-Peak Table of Solar Spectrum Wavelengths, Vol. Contribution No. 559 (Kitt Peak National Observatory) [Google Scholar]
- Reiners, A., Mrotzek, N., Lemke, U., Hinrichs, J., & Reinsch, K. 2016, A&A, 587, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rutten, R. J., & van der Zalm, E. B. J. 1984, A&AS, 55, 143 [NASA ADS] [Google Scholar]
- Scott, P., Asplund, M., Grevesse, N., Bergemann, M., & Sauval, A. J. 2015, A&A, 573, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stenflo, J. O. 2015a, A&A, 573, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stenflo, J. O., Twerenbold, D., Harvey, J. W., & Brault, J. W. 1983, A&AS, 54, 505 [NASA ADS] [Google Scholar]
- Valenti, J. A., Butler, R. P., & Marcy, G. W. 1995, PASP, 107, 966 [NASA ADS] [CrossRef] [Google Scholar]
- Wallace, L., Hinkle, K., & Livingston, W. 1998, An atlas of the spectrum of the solar photosphere from 13 500 to 28 000 cm-1 (3570 to 7405 Å) (National Solar Observatory) [Google Scholar]
- Wallace, L., Hinkle, K., & Livingston, W. 2007, An Atlas of the Spectrum of the Solar Photosphere from 13 500 to 33 980 cm-1 (2942 to 7405 Å) (National Solar Observatory) [Google Scholar]
- Wallace, L., Hinkle, K. H., Livingston, W. C., & Davis, S. P. 2011, ApJS, 195, 6 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Spectral scattered light
The parameter O in Eq. (1) represents a constant offset which can be caused by spectral stray light. Here we show that the amount of scattered light in the above definition is virtually zero and can be neglected in the analysis. The upper panel of Fig. A.1 shows the parameters S and O plotted vs. wavelength for lines with three different regimes of the line depth (5−15%, 45−55%, 85−95%).
While the mean of O is below 0.1% in all cases, the scatter in S and O decreases dramatically with increasing line depth with standard deviations of 3.2%, 0.6%, and 0.26% for the line depths given above. This dependence on the line depth is expected because only strong intensity variations within the fitted spectral range can simultaneously constrain the O and S parameters.
The strong anti-correlation between O and S becomes also apparent in the scatter plot in the lower panel of Fig. A.1. The fit tries to compensate for a higher continuum level with negative offset parameters and vice versa, except for wavelengths below 400 nm, where the spectrum is dominated by deep lines (cf. Fig. 2). B and O are essentially uncorrelated except for a chromatic effect caused by the wavelength dependence of B.
We can therefore confirm the stated excellent stray-light suppression of the Jungfraujoch spectrograph, and it is justified to enforce O to zero for our analysis. Limiting the optimisation to three free parameters stabilises the fits, and the scatter in the S parameter is greatly reduced with only a slight increase of the χ2 values.
 |
Fig. A.1 Correlation between the scale and offset parameters. Upper panel: scale and offset parameters for lines with three different regimes of line depths. Lower panel: scatter plots of the offset parameter vs. the scale and broadening parameters. The colours represent different spectral intervals to distinguish chromatic effects. |
All Tables
All Figures
 |
Fig. 1 Details in the Liège, Hamburg, and the Wallace disc-centre atlases in two spectral regions. Line identifications are from the list of PB73. |
| In the text | |
 |
Fig. 2 Investigated spectral region (topmost panel; blue trace: Hamburg, green trace: Liège) and the results from the fitting procedure (parameters L, S, B of Eq. (1), the rms of the residuals of the fit, and the reduced χ2) versus wavelength. The thin red tick marks and the bold blue tick marks above the topmost panel indicate grating order intersections and FTS scan intersections, respectively. Zero wavelength shift and unity scaling factors are indicated by the horizontal blue lines in the L and S panels. The blue line in the trace of the rms residuals indicates the median value. |
| In the text | |
 |
Fig. 3 Histogram of the rms of the fit residuals. The case when only the wavelength shifts are fitted is compared to the case where wavelength shift, scaling, and broadening (panel 5 in Fig. 2) are considered. The width of the bins is 1 × 10-4. |
| In the text | |
 |
Fig. 4 Zoom on a narrow wavelength window in Fig. 2. The gap in the very core of the Ca ii 3934 Å line is caused by the lack of strong enough spectral features. Error bars represent the 1σ parameter uncertainties provided by the minimisation routine. |
| In the text | |
 |
Fig. 5 Scaling parameter derived from fitting consecutive 1 Å intervals. A synthetic telluric spectrum is plotted for comparison with the pattern of the χ2 in the lowest panel. |
| In the text | |
 |
Fig. 6 Theoretical and measured resolving power of the Liège atlas. The resolution settings for the individual segments of the Hamburg atlas are plotted for comparison. The plotted trace of the data measured in this work was filtered with a running median for better visibility. The horizontal black line marks the mean of our measured values. |
| In the text | |
 |
Fig. 7 Example of a fit to one spectral line. The blue dots show the original Hamburg spectrum, the red line shows the best-fitting modified Hamburg spectrum according to Eq. (1). The dashed line represents the fitted Hamburg spectrum, but with the parameter B forced to 6.7 mÅ. The lower panel shows the residuals of the fit with three free parameters. Only every second data point is plotted for the Liège spectrum for better visibility. |
| In the text | |
 |
Fig. A.1 Correlation between the scale and offset parameters. Upper panel: scale and offset parameters for lines with three different regimes of line depths. Lower panel: scatter plots of the offset parameter vs. the scale and broadening parameters. The colours represent different spectral intervals to distinguish chromatic effects. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


