| Issue |
A&A
Volume 590, June 2016
|
|
|---|---|---|
| Article Number | A95 | |
| Number of page(s) | 6 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201628291 | |
| Published online | 20 May 2016 | |
Rayleigh scattering in the atmospheres of hot stars
1 Masarykova Univerzita, Přírodovědecká fakulta, Kotlářská 2, Brno, Czech Republic
e-mail: fisak@physics.muni.cz
2 Astronomický ústav, Akademie věd České republiky, Fričova 298, 251 65 Ondřejov, Czech Republic
Received: 10 February 2016
Accepted: 30 March 2016
Context. Rayleigh scattering is a result of an interaction of photons with bound electrons. Rayleigh scattering is mostly neglected in calculations of hot star model atmospheres because most of the hydrogen atoms are ionized and the heavier elements have a lower abundance than hydrogen. In atmospheres of some chemically peculiar stars, helium overabundant regions containing singly ionized helium are present and Rayleigh scattering can be a significant opacity source.
Aims. We evaluate the contribution of Rayleigh scattering by neutral hydrogen and singly ionized helium in the atmospheres of hot stars with solar composition and in the atmospheres of helium overabundant stars.
Methods. We computed several series of model atmospheres using the TLUSTY code and emergent fluxes using the SYNSPEC code. These models describe atmospheres of main sequence B-type stars with different helium abundance. We used an existing grid of models for atmospheres with solar chemical composition and we calculated an additional grid for helium-rich stars with N(He)/N(H) = 10.
Results. Rayleigh scattering by neutral hydrogen can be neglected in atmospheres of hot stars, while Rayleigh scattering by singly ionized helium can be a non-negligible opacity source in some hot stars, especially in helium-rich stars.
Key words: atomic processes / scattering / stars: chemically peculiar / stars: atmospheres / stars: early-type
© ESO, 2016
1. Introduction
The interaction of photons with bound electrons is very important in stellar atmospheres. Processes of excitation and ionization are very well known and have been studied in detail. However, photons may interact with bound electrons even when photon energy is not equal to the energy difference between any bound levels. Rayleigh scattering is one of these processes.
Rayleigh scattering is a special kind of scattering process. According to Loudon (1983), the scattering processes by bound electrons are divided into three cases: fluorescence, Raman scattering, and Rayleigh scattering. In the case of Rayleigh scattering an ion is excited by a photon and transits to a virtual state. This state is very unstable and the electron transits to the original state immediately. If the initial state is different from the final state we call this process Raman scattering.
Rayleigh scattering was studied by John William Strutt (Lord Rayleigh, see Rayleigh 1870). This effect causes the blue colour of the sky and the red colour of sunsets. Scattering centres are oxygen and nitrogen molecules because they have the largest abundance in the Earth’s atmosphere. Rayleigh scattering is also an important opacity source in the atmospheres of other planets (Buenzli et al. 2009).
Rayleigh scattering by H2 was detected in exoplanet atmosphere HD 209458b (Lecavelier des Etangs et al. 2008b) and it is suspected that Rayleigh scattering is responsible for the blue colour of exoplanet HD 189733b (Lecavelier des Etangs et al. 2008a). Rayleigh scattering is an important opacity source in cool stars because of large neutral hydrogen atom population (see Hubeny & Mihalas 2015).
Scattering by bound electrons is often neglected in hot star atmospheres because of the low abundance of Rayleigh scattering atoms. First, both hydrogen and helium are ionized leaving only a small fraction in the neutral state and second, abundances of the other elements are low. In addition, the Rayleigh scattering cross section is smaller for atoms with a higher atomic number.
However, the population of singly ionized helium is much larger than the population of neutral hydrogen in hot main sequence stars with solar composition. In addition, there are stars with helium overabundant atmospheres, which means they have even larger population of singly ionized helium.
The aim of this paper is to investigate the possible effect of Rayleigh scattering by ionized helium on radiation emerging from model atmospheres of hot stars.
2. Rayleigh scattering
Rayleigh scattering is a type of interaction of radiation with bound electrons. The energy of an interacting photon is not equal to any energy difference between an excited state of the atom and the ground state. An electron is excited to an unstable virtual state (in contrast to the line transitions), from which it transfers immediately back to its original state. This is shown in Fig. 1.
The process of Rayleigh scattering is nicely described by the time dependent perturbation theory. Using an electric-dipole approximation and the Krammers-Heisenberg formula for the differential cross-section we obtain in SI units (see Loudon 1983) 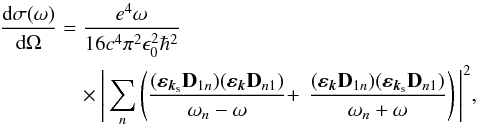 (1)where Dji = ⟨j|r|i⟩ is the matrix element of the sum of the electron position vectors (of the electron position vector for hydrogen-like atoms). Furthermore, εk and εks are the polarization vectors for the incoming photons with wave vector k and for the scattered photons with wave vector ks, respectively, and ωn represents the angular frequency of the transition between the ground state (l) and the nth state
(1)where Dji = ⟨j|r|i⟩ is the matrix element of the sum of the electron position vectors (of the electron position vector for hydrogen-like atoms). Furthermore, εk and εks are the polarization vectors for the incoming photons with wave vector k and for the scattered photons with wave vector ks, respectively, and ωn represents the angular frequency of the transition between the ground state (l) and the nth state 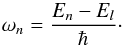 (2)The sum runs over all intermediate states. Here e is the electron charge, ε0 is the vacuum permittivity, c the speed of light, and m the electron mass.
(2)The sum runs over all intermediate states. Here e is the electron charge, ε0 is the vacuum permittivity, c the speed of light, and m the electron mass.
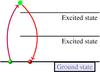 |
Fig. 1 Scheme of the Rayleigh scattering process. The bound electron is excited by an incoming photon to a virtual state which is unstable and the electron transits immediately to the original state. |
After some calculations described in Loudon (1983) and Lee & Kim (2004), and after some mathematical arrangements (Zettili 2009; Bethe & Salpeter 2008; and Landau et al. 1982) we obtain the following equation for Rayleigh scattering cross section in the case of one-electron atoms, 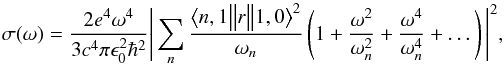 (3)where
(3)where 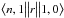 is the reduced matrix element,
is the reduced matrix element, 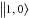 represents the 1s state, and
represents the 1s state, and 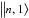 represents the np state, n is the principal quantum number and p is the azimuthal quantum number (both bound states and continuum states are included). The reduced matrix element is given by the Wigner-Eckart theorem valid for any vector operator Âq (see Eq. (7.326) in Zettili 2009):
represents the np state, n is the principal quantum number and p is the azimuthal quantum number (both bound states and continuum states are included). The reduced matrix element is given by the Wigner-Eckart theorem valid for any vector operator Âq (see Eq. (7.326) in Zettili 2009): 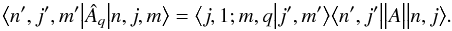 (4)The first matrix element on the right side of Eq. (4)is the Clebsch-Gordan coefficient. It is possible to rewrite Eq. (3) in terms of dimensionless angular frequency
(4)The first matrix element on the right side of Eq. (4)is the Clebsch-Gordan coefficient. It is possible to rewrite Eq. (3) in terms of dimensionless angular frequency 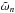 and dimensionless position vector
and dimensionless position vector 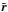 (see Lee & Kim 2004),
(see Lee & Kim 2004), 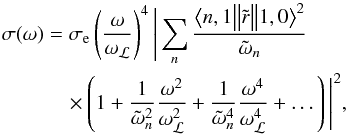 (5)where
(5)where 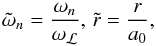 (6)the angular frequency of Lyman limit ωℒ and Bohr radius a0 are
(6)the angular frequency of Lyman limit ωℒ and Bohr radius a0 are 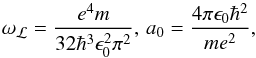 (7)and σe is the Thomson scattering cross section
(7)and σe is the Thomson scattering cross section 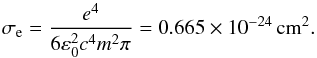 (8)
(8)
2.1. Cross section for Rayleigh scattering on hydrogen
First, we consider only hydrogen atoms. In this case, the reduced matrix elements can be calculated analytically. According to Lee & Kim (2004), the total cross section for Rayleigh scattering by neutral hydrogen is equal to 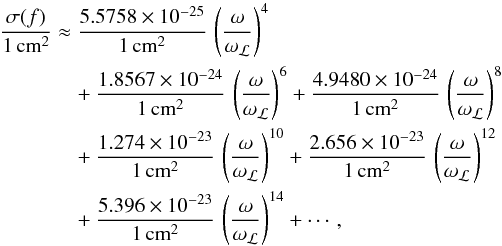 (9)where
(9)where 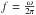 .
.
2.2. Cross section for Rayleigh scattering on hydrogen-like atoms
The radial wavefunction of hydrogen-like atoms is given by (see Landau & Lifshitz 1977) 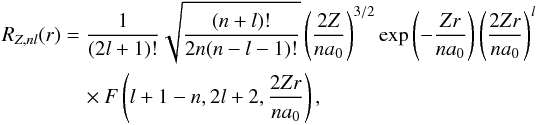 (10)where n is the principal quantum number, l is the orbital quantum number, Z is the atomic number, a0 is the Bohr radius, and
(10)where n is the principal quantum number, l is the orbital quantum number, Z is the atomic number, a0 is the Bohr radius, and 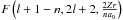 is the hypergeometric function. It can be seen that
is the hypergeometric function. It can be seen that 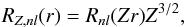 (11)where Rnl(r) are radial wavefunctions of hydrogen. For the matrix element we obtain
(11)where Rnl(r) are radial wavefunctions of hydrogen. For the matrix element we obtain 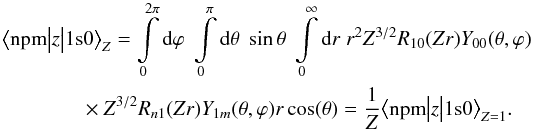 (12)
(12)
Opacity of Rayleigh scattering at τRoss ≈ 1 for a model atmosphere with Teff = 23 000K together with its comparison with the opacities of the Balmer continuum and electron scattering.
Using this result, the Wigner-Eckart theorem, and the fact that the energies of the excited states scale with the factor Z2 we obtain 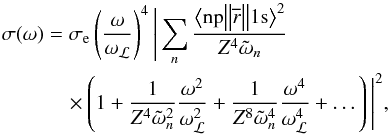 (13)where the meaning of the symbols is the same as in Eq. (5). Using the same approach as in Lee & Kim (2004), we get for the Rayleigh scattering cross section by hydrogen-like atoms
(13)where the meaning of the symbols is the same as in Eq. (5). Using the same approach as in Lee & Kim (2004), we get for the Rayleigh scattering cross section by hydrogen-like atoms 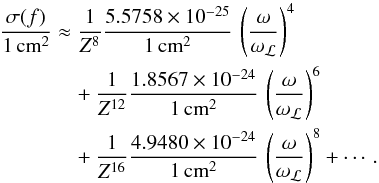 (14)Finally, for singly ionized helium (Z = 2) we obtain
(14)Finally, for singly ionized helium (Z = 2) we obtain 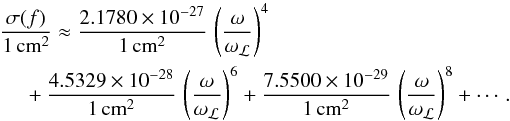 (15)It can be easily seen that the expression on the right-hand side of Eq. (1) adapted to the hydrogen atom and also the corresponding expression on the right-hand side of Eq. (3)converges only for ω/ωℒ ≪ 1. We have checked that for λ> 1500 Å the cross section for the hydrogen atom can be approximated within a precision of about 5% by the sum of the first six terms of the series that are given explicitly in Eq. (9). The cross section for the singly ionized helium can be similarly approximated for λ> 1000 Å by the sum of the first three terms of the corresponding series that are given explicitly in Eq. (15). The results were obtained using the approximations mentioned above.
(15)It can be easily seen that the expression on the right-hand side of Eq. (1) adapted to the hydrogen atom and also the corresponding expression on the right-hand side of Eq. (3)converges only for ω/ωℒ ≪ 1. We have checked that for λ> 1500 Å the cross section for the hydrogen atom can be approximated within a precision of about 5% by the sum of the first six terms of the series that are given explicitly in Eq. (9). The cross section for the singly ionized helium can be similarly approximated for λ> 1000 Å by the sum of the first three terms of the corresponding series that are given explicitly in Eq. (15). The results were obtained using the approximations mentioned above.
2.3. Rayleigh scattering opacity
We can estimate the opacity due to the Rayleigh scattering using the formula 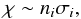 where ni is number density of particles i (which stands for H i or He ii) and σi is the corresponding Rayleigh scattering cross section. In Table 1 we list relative estimates of the opacity caused by Rayleigh scattering for hydrogen and singly ionized helium. The number densities of particles were taken from computed models by the TLUSTY code and cross sections from Hubeny & Mihalas (2015) and Eq. (15). From this table it follows that the opacity of Rayleigh scattering by singly ionized helium is approximately ten times larger than the opacity of Rayleigh scattering by neutral hydrogen in atmospheres with solar chemical composition. It is approximately one thousand times larger in helium-rich atmospheres (N(He) = 10 N(H)). Consequently, Rayleigh scattering by singly ionized helium can be a more significant opacity source than Rayleigh scattering by neutral hydrogen. For stars with enhanced helium abundance, like helium-rich chemically peculiar stars, Rayleigh scattering by singly ionized helium may be an even stronger opacity source. However, the opacity due to Rayleigh scattering by singly ionized helium is significantly smaller than the opacity due to hydrogen bound-free transitions and free electrons, which dominate the continuum opacity in hot star atmospheres.
where ni is number density of particles i (which stands for H i or He ii) and σi is the corresponding Rayleigh scattering cross section. In Table 1 we list relative estimates of the opacity caused by Rayleigh scattering for hydrogen and singly ionized helium. The number densities of particles were taken from computed models by the TLUSTY code and cross sections from Hubeny & Mihalas (2015) and Eq. (15). From this table it follows that the opacity of Rayleigh scattering by singly ionized helium is approximately ten times larger than the opacity of Rayleigh scattering by neutral hydrogen in atmospheres with solar chemical composition. It is approximately one thousand times larger in helium-rich atmospheres (N(He) = 10 N(H)). Consequently, Rayleigh scattering by singly ionized helium can be a more significant opacity source than Rayleigh scattering by neutral hydrogen. For stars with enhanced helium abundance, like helium-rich chemically peculiar stars, Rayleigh scattering by singly ionized helium may be an even stronger opacity source. However, the opacity due to Rayleigh scattering by singly ionized helium is significantly smaller than the opacity due to hydrogen bound-free transitions and free electrons, which dominate the continuum opacity in hot star atmospheres.
3. Computation of model atmospheres
For our analysis we used several series of NLTE models for atmospheres of main sequence B-type stars with solar chemical composition and of helium-rich stars with enhanced helium abundance N(He) /N(H) = 10 (N denotes number density). We used model atmospheres for effective temperatures between 15 and 30 kK and surface gravity log g = 4 (see Table 3).
Solar chemical composition (relative number of particles, adopted from Grevesse & Sauval 1998) and chemical composition of helium-rich stars.
Parameters used for computed models of atmospheres.
For atmospheres with solar chemical composition we used models from the grid (Lanz & Hubeny 2003, 2007) calculated with the TLUSTY1 code. Since there are no model grids available for helium overabundant stars, we calculated them ourselves using the TLUSTY code (Hubeny 1988; Hubeny & Lanz 1995). To be consistent with the precalculated grid of Lanz & Hubeny (2003, 2007), for all other elements except hydrogen and helium we used the solar composition adopted by Grevesse & Sauval (1998).
In the following step we used the SYNSPEC2 code to calculate the emergent flux. In this step we added a new opacity source – Rayleigh scattering by singly ionized helium – to the SYNSPEC source code. This new part of the code is very similar to the part that computes Rayleigh scattering by neutral hydrogen. Using the code we computed synthetic spectra with and without Rayleigh scattering included.
 |
Fig. 2 Adopted values of Rayleigh scattering cross section by neutral hydrogen (full line) and singly ionized helium (dotted line) in comparison with scattering cross section by free electrons (dashed line). |
For easier comparison of the computed synthetic spectra, we convolved the computed emergent fluxes with the Gaussian function g(λ)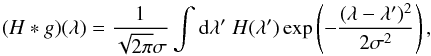 where σ = 10 Å is the width of the Gaussian function, H(λ) is the emergent flux, and λ denotes the wavelength. Convolution makes the emergent flux smoother, and we are mainly interested in continuum changes. We compared convolved emergent fluxes between models with and without Rayleigh scattering. We plotted the difference between emergent spectra in magnitudes given by
where σ = 10 Å is the width of the Gaussian function, H(λ) is the emergent flux, and λ denotes the wavelength. Convolution makes the emergent flux smoother, and we are mainly interested in continuum changes. We compared convolved emergent fluxes between models with and without Rayleigh scattering. We plotted the difference between emergent spectra in magnitudes given by 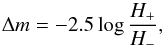 (16)where H+ is the emergent flux with Rayleigh scattering included and H− is the flux without Rayleigh scattering included.
(16)where H+ is the emergent flux with Rayleigh scattering included and H− is the flux without Rayleigh scattering included.
4. Influence of Rayleigh scattering on emergent stellar radiation
The computed difference in emergent fluxes depends on the atmospheric chemical composition and the scattering cross section of the given ion. The difference also depends on the stellar effective temperature because ionization and excitation equilibria depend on temperature.
4.1. Scattering by neutral hydrogen
We expected very small changes when adding Rayleigh scattering by neutral hydrogen. Rayleigh scattering by neutral hydrogen is included in the SYNSPEC code as an optional opacity source. Our calculations confirmed its weaker influence on emergent fluxes for temperatures larger than 21 000 K (in comparison to scattering by He ii; see Fig. 3). The differences decrease rapidly with the increasing effective temperature of the star.
 |
Fig. 3 Dependence of difference of emergent fluxes with and without Rayleigh scattering by H i included for given effective temperatures and solar chemical composition. |
 |
Fig. 4 Dependence of difference of emergent fluxes with and without Rayleigh scattering by He ii included for given effective temperatures and solar chemical composition. |
 |
Fig. 5 Dependence of difference of emergent fluxes with and without Rayleigh scattering by H i and He ii included for given effective temperatures and solar chemical composition. |
 |
Fig. 6 Dependence of difference of emergent fluxes with and without Rayleigh scattering by He ii included for given effective temperatures and helium overabundant chemical composition. |
4.2. Scattering by singly ionized helium
In atmospheres with solar chemical composition the opacity due to the Rayleigh scattering by singly ionized helium is larger than the opacity due to the Rayleigh scattering by hydrogen for the temperatures in the interval (21, 30) kK. This causes greater differences between emergent fluxes, which also depend on the stellar effective temperatures (see Fig. 4, where fluxes for selected models are plotted). For lower effective temperatures the magnitude difference increases with increasing effective temperature, but for effective temperatures higher than about 25 kK the magnitude difference decreases. This behaviour is caused by the population of singly ionized helium, which increases with increasing effective temperature for cooler stars because of neutral helium ionization; instead, in stars with effective temperatures higher than 25 kK, the process of ionization of singly ionized helium becomes more significant and lowers the He ii abundance.
The Rayleigh scattering cross section is larger in the ultraviolet region (see Eq. (15)). Consequently, Rayleigh scattering redistributes the flux from the short-wavelength part of the spectrum to longer wavelengths and the magnitude difference decreases with increasing wavelength.
We show the contribution of Rayleigh scattering by H i and He ii (see Fig. 5). We plotted differences only for temperatures in the interval (18 000, 24 000) K. In this interval the contributions of both processes are of the same order.
The magnitude difference is roughly an order of magnitude larger in the case of helium-rich stars (see Fig. 6). For the case of inhomogeneous surface distribution of helium (like in CP stars) the synthetic spectra or lightcurves with these distributions must be computed. For such stars the changes due to the Rayleigh scattering are larger than a typical precision of space-based photometry.
5. Conclusions
In this paper we study the effect of Rayleigh scattering on the emergent fluxes in hot stars. We derived the Rayleigh scattering cross section for He ii (see Eq. (15)). We included this expression into the SYNSPEC source code. Input models were computed using the TLUSTY code (for helium overabundant stars) or we used a model grid of B stars (for stars with stellar chemical composition). We compared computed emergent fluxes with and without Rayleigh scattering.
The computed differences are relatively small. For stars with solar composition the magnitude difference is of the order of 10-5, while for helium overabundant stars the difference is an order of magnitude higher. The stellar winds are accelerated mostly in the UV region; we can thus expect some influence on the line driving. However, this analysis cannot be done with a static model atmosphere code like TLUSTY (SYNSPEC). Rayleigh scattering is also a potentially important source of opacity in other stars with a large abundance of helium, for example white dwarfs, Wolf-Rayet stars, and subdwarfs.
Acknowledgments
This research was supported by grant GA ČR 14-02385S. Access to computing and storage facilities owned by parties and projects contributing to the National Grid Infrastructure MetaCentrum, provided under the programme “Projects of Large Infrastructure for Research, Development, and Innovations” (LM2010005), is greatly appreciated.
References
- Bethe, H. A., & Salpeter, E. E. 2008, Quantum mechanics of one- and two-electron atoms, Dover edn. (Dover Publications) [Google Scholar]
- Buenzli, E., Schmid, H. M., & Joos, F. 2009, A&A, 105, 153 [Google Scholar]
- Grevesse, N., & Sauval, A. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Hubeny, I. 1988, Comput. Phys. Commun., 52, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Hubeny, I., & Lanz, T. 1995, ApJ, 439, 875 [Google Scholar]
- Hubeny, I., & Mihalas, D. 2015, Theory of stellar atmospheres (Princeton, N.J.: Princeton University Press) [Google Scholar]
- Landau, L. D., & Lifshitz, J. M. 1977, Quantum mechanics, 3rd edn. (Butterworth-Heinemann) [Google Scholar]
- Landau, L. D., Lifshitz, L., Pitaevskii, V., & Berestetskii. 1982, Quantum electrodynamics, 2nd edn. (Pergamon Press) [Google Scholar]
- Lanz, T., & Hubeny, I. 2003, ApJS, 146, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Lanz, T., & Hubeny, I. 2007, ApJS, 169, 83 [CrossRef] [Google Scholar]
- Lecavelier des Etangs, A., Pont, F., Vidal-Madjar, A., & Sing, D. 2008a, A&A, 481, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Lecavelier des Etangs, A., Vidal-Madjar, A., Désert, J.-M., & Sing, D. 2008b, A&A, 485, 865 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, H.-W., & Kim, H. I. 2004, MNRAS, 347, 802 [NASA ADS] [CrossRef] [Google Scholar]
- Loudon, R. 1983, The quantum theory of light, 2nd edn. (Oxford University Press) [Google Scholar]
- Rayleigh, J. 1870, On the Light from the Sky: Its Polarization and Colour (Cambridge University Press) [Google Scholar]
- Zettili, N. 2009, Quantum mechanics, 2nd edn. (Wiley) [Google Scholar]
All Tables
Opacity of Rayleigh scattering at τRoss ≈ 1 for a model atmosphere with Teff = 23 000K together with its comparison with the opacities of the Balmer continuum and electron scattering.
Solar chemical composition (relative number of particles, adopted from Grevesse & Sauval 1998) and chemical composition of helium-rich stars.
All Figures
 |
Fig. 1 Scheme of the Rayleigh scattering process. The bound electron is excited by an incoming photon to a virtual state which is unstable and the electron transits immediately to the original state. |
| In the text | |
 |
Fig. 2 Adopted values of Rayleigh scattering cross section by neutral hydrogen (full line) and singly ionized helium (dotted line) in comparison with scattering cross section by free electrons (dashed line). |
| In the text | |
 |
Fig. 3 Dependence of difference of emergent fluxes with and without Rayleigh scattering by H i included for given effective temperatures and solar chemical composition. |
| In the text | |
 |
Fig. 4 Dependence of difference of emergent fluxes with and without Rayleigh scattering by He ii included for given effective temperatures and solar chemical composition. |
| In the text | |
 |
Fig. 5 Dependence of difference of emergent fluxes with and without Rayleigh scattering by H i and He ii included for given effective temperatures and solar chemical composition. |
| In the text | |
 |
Fig. 6 Dependence of difference of emergent fluxes with and without Rayleigh scattering by He ii included for given effective temperatures and helium overabundant chemical composition. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


