| Issue |
A&A
Volume 590, June 2016
|
|
|---|---|---|
| Article Number | A122 | |
| Number of page(s) | 31 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201628271 | |
| Published online | 26 May 2016 | |
Long-term optical variability of high-mass X-ray binaries
II. Spectroscopy⋆
1
IESL, Foundation for Research and Technology-Hellas,
71110
Heraklion,
Greece
e-mail:
pau@physics.uoc.gr
2
Physics Department, University of Crete,
71003
Heraklion,
Greece
3
Harvard-Smithsonian Center for Astrophysics, 60 Garden
Street, Cambridge,
MA
02138,
USA
4
Observatorio Astronómico, Universidad de Valencia,
46100
Burjassot,
Spain
5
Physics and Astronomy department, University of
Southampton, Southampton
SO17 1BJ,
UK
Received: 8 February 2016
Accepted: 24 March 2016
Context. High-mass X-ray binaries are bright X-ray sources. The high-energy emission is caused by the accretion of matter from the massive companion onto a neutron star. The accreting material comes from either the strong stellar wind in binaries with supergiant companions or the cirscumstellar disk in Be/X-ray binaries. In either case, the Hα line stands out as the main source of information about the state of the accreting material.
Aims. We present the results of our monitoring program to study the long-term variability of the Hα line in high-mass X-ray binaries. Our aim is to characterise the optical variability timescales and study the interaction between the neutron star and the accreting material.
Methods. We fitted the Hα line with Gaussian profiles and obtained the line parameters and equivalent width. The peak separation in split profiles was used to determine the disk velocity law and estimate the disk radius. The relative intensity of the two peaks (V/R ratio) allowed us to investigate the distribution of gas particles in the disk. The equivalent width was used to characterise the degree of variability of the systems. We also studied the variability of the Hα line in correlation with the X-ray activity.
Results. Our results can be summarised as follows: i) we find that Be/X-ray binaries with narrow orbits are more variable than systems with long orbital periods; ii) we show that a Keplerian distribution of gas particles provides a good description of the disks in Be/X-ray binaries, as it does in classical Be stars; iii) a decrease in the Hα equivalent width is generally observed after major X-ray outbursts; iv) we confirm that the Hα equivalent width correlates with disk radius; v) while systems with supergiant companions display multi-structured profiles, most of the Be/X-ray binaries show, at some epoch, double-peak asymmetric profiles, which indicates that density inhomogeneities is a common property in the disk of Be/X-ray binaries; vi) the profile variability (V/R ratio) timescales are shorter and the Hα equivalent widths are smaller in Be/X-ray binaries than in isolated Be stars; and vii) we provide new evidence that the disk in Be/X-ray binaries is, on average, denser than in classical Be stars.
Conclusions. We carried out the most complete optical spectroscopic study of the global properties of high-mass X-ray binaries with the analysis of more than 1100 spectra from 20 sources. Our results provide further evidence for the truncation of the disk in Be/X-ray binaries. We conclude that the interaction between the compact object and the Be-type star works in two directions: the massive companion provides the source of matter for accretion, affecting the surroundings of the compact object, and the continuous revolution of the neutron star around the optical counterpart also produces the truncation of the Be star’s equatorial disk.
Key words: stars: emission-line, Be / stars: massive / X-rays: binaries
The reduced spectra as FITS files are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/590/A122
© ESO, 2016
1. Introduction
High-mass X-ray binaries (HMXB) are accretion-powered binary systems where a neutron star orbits an early-type (O or B) companion. The luminosity class of the optical companion subdivides HMXBs into Be/X-ray binaries (BeXB), when the optical star is a dwarf, subgiant, or giant OBe star (luminosity class III, IV, or V) and supergiant X-ray binaries (SGXBs), when they contain an evolved star of luminosity class I-II. In SGXBs, the donor produces a substantial stellar wind, removing between 10-6−10-8M⊙ yr-1 with terminal velocities up to 2000 km s-1. A neutron star in a relatively close orbit will capture a significant fraction of this wind, sufficient to power a bright X-ray source. In BeXB, the donor is a Be star, i.e. a rapidly rotating star of spectral type early-B or late-O with a gaseous equatorial disk (Ziolkowski 2002; Negueruela 2007; Paul & Naik 2011; Reig 2011).
The disk is the main source of variability in BeXBs because it evolves on much faster timescales than other components of the binary. On one hand, the disk itself emits at optical and infrared wavelengths, contaminating the continuum emission intensity (magnitudes and colours) and the spectral lines of the underlying star, making it difficult to determine astrophysical parameters (Fabregat & Torrejon 1998; Riquelme et al. 2012). On the other hand, the disk is also responsible for the X-ray variability because it constitutes the source of matter available for accretion. Thus the study of the evolution of the disk enables us to characterise the variability timescales at different wavelengths.
We have been monitoring the HMXBs visible from the northern hemisphere in the optical band since 1999. The monitoring consists of BVRI and medium-resolution spectra around the Hα line. JHK photometry has been performed since 2009 and optical polarimetry in the R-band has been regularly obtained since 2013. The results from the photometric study were presented in Reig & Fabregat (2015). In this work, we present the results of the spectroscopic observations. Although we also studied the long-term spectral emission of SGXBs, we primarily focus on BeXBs because of their larger amplitude of variability on long timescales.
In a study of the long-term photometric variability of BeXB, Reig & Fabregat (2015) find that when timescales of years are considered, a good correlation between the X-ray and optical variability is observed. However, photometry gives us information on the optical continuum, which is formed in the innermost part of the disk. The Hα line stands out as a better proxy for the state of the disk (Quirrenbach et al. 1997; Tycner et al. 2005; Grundstrom & Gies 2006) because it is formed further away from the star in a larger part of the disk. Moreover, the outer parts of the disk are expected to be more strongly affected by the gravitational pull of the neutron star companion. Thus, we would, in principle, expect stronger and faster changes in the parameters of the line, which would reflect a major disruption of the disk. Large amplitude changes in the strength and profile shape of the Hα line have been linked to structural changes of the circumstellar decretion disk (Roche et al. 1993b; Haigh et al. 2004; Reig et al. 2007; Moritani et al. 2013; Reig & Zezas 2014).
The main objective of this work is to study the patterns of variability of BeXB as a group with emphasis on two questions. One relates to the long-term variability of the spectral parameters of the Hα line and their relationship with the X-ray activity of the system. Previous works on correlated optical/X-ray variability focused on individual systems, which did no allow general conclusions to be drawn on disk variability timescales and the correlation with X-ray emission in BeXB as a population. The other question relates to the search for further observational evidence of the interaction between the neutron star and the disk. Most of our understanding of the properties of the equatorial disk stems from the study of classical Be stars, i.e. isolated systems without a neutron star companion. However, the conditions in classical Be stars may not be the same as in BeXB. For example, there is growing evidence that the disk in BeXBs is truncated by the neutron star (Reig et al. 1997b; Zamanov et al. 2001; Negueruela et al. 1999; Okazaki & Negueruela 2001; Okazaki et al. 2002; Reig 2011). Being able to understand this interaction could provide new insights into the accretion mechanism in X-ray pulsars.
Targets and relevant information.
2. Observations and data reduction
We have been monitoring the Hα line of HMXBs visible from the northern hemisphere using the 1.3 m telescope of the Skinakas Observatory (SKO) located in the island of Crete (Greece) since 1999. The targets have also been observed regularly using the 1.5 m telescope of the Fred Lawrence Whipple Observatory (FLWO) at Mt. Hopkins (Arizona) since 2007. The instrumental set-up for the 1.3 m telescope of the Skinakas Observatory was a 2000 × 800 ISA SITe CCD and a 1302 l mm-1 grating, giving a nominal dispersion of ~1.04 Å/pixel, while for the 1.5-m telescope at Mt. Hopkins (Arizona), the FAST-II spectrograph (Fabricant et al. 1998) plus FAST3 CCD, a backside-illuminated 2688 × 512 UA STA520A chip with 15 μm pixels and a 1200 l mm-1 grating (0.38 Å/pixel). Occasionally, a 2400 l mm-1 and a 600 l mm-1 grating was used in Skinakas and Mt. Hopkins observations, respectively. Additionally, we also used data obtained in service mode with the 4.2-m William Herschel Telescope (WHT) and the 2.5 m Nordic Optical Telescope (NOT) in El Roque de los Muchachos observatory in La Palma (Canary Islands, Spain). The spectra were reduced with the dedicated packages for spectroscopy of the STARLINK or IRAF projects following the standard procedure. The images were bias-subtracted and flat-field corrected. Spectra of comparison lamps were taken before each exposure to account for small variations of the wavelength calibration during the night. Finally, the spectra were extracted from an aperture that encompassed more than 90% of the flux of the object. Sky subtraction was performed by measuring the sky spectrum from an adjacent object-free region. For the FLWO spectra, this procedure is carried out with the RoadRunner reduction system (Tokarz & Roll 1997).
Some of the observations have been published in papers dedicated to individual sources (Reig et al. 2005, 2007, 2010; Blay et al. 2006; Coe et al. 2006; Reig & Zezas 2014). For ten sources from the target list, we complemented our observations with data taken before 1999. These spectra were obtained in the framework of the Southampton/Valencia collaborative project (Reig et al. 1997a), where a number of telescopes were used: the 2.5 m Isaac Newton Telescope (INT) and the 1.0 m Jacobus Kapteyn Telescope (JKT), both located at the Roque de los Muchachos Observatory in La Palma, the 1.5 m at Palomar Mountain (PAL), the 1.9 m telescope of the South Africa Astronomical Observatory (SAAO), and the 2.2 m telescope at Calar Alto in Almería, Spain (CA), and resulted in numerous publications (Clark et al. 1998, 1999, 2001; Coe et al. 1993, 1996; Gorrod et al. 1993; Haigh et al. 1999, 2004; Negueruela et al. 1997, 1998, 1999, 2001; Norton et al. 1991; Reig et al. 1996, 1997c, 2000; Roche et al. 1993a,b; Unger et al. 1998). For the sake of homogeneity, we re-analysed all the spectra in a consistent way, as explained in the next section. The list of targets is given in Table 1.
3. Data analysis
The spectral analysis was performed with the splot task in IRAF. To ensure homogeneous processing, the spectra were normalized with respect to the local continuum. The definition of the continuum level is crucial because it represents the main source of uncertainty in the determination of the spectral parameters. To normalize the continuum, we divided the spectrum by a smooth curve that was obtained by fitting regions of the continuum devoid of spectral features on both sides of the line. This process sets the continuum to unity, and allows us to measure the lines from spectrum to spectrum in a consistent way. Ten different combinations of spectral regions and fitting functions provided ten measurements of the continuum level and hence ten independent measurements of the spectral parameters. The final value and error were taken to be the average and standard deviation of those ten measurements for each parameter.
The Hα line exhibited a wide range of profiles, both symmetric and asymmetric. Symmetric profiles include single- and double-peaked shapes. In some cases, the central depression between the peaks is sharp and deep, going beyond the continuum. This profile is known as a shell profile and is thought to arise when the observer’s line of sight toward the central star intersects parts of the disk, which is cooler than the stellar photosphere (Hanuschik 1995; Rivinius et al. 2006). Absorption lines were also observed in a number of sources.
To extract the line parameters, we fit these profiles with one, two, or three Gaussian functions, depending on whether the line showed a single, split, or shell profile (in this case the Gaussian that corresponds to the central depression had opposite sign to the other two).
The fits provided the following parameters: line centres, that is, the wavelength at which the intensity of the line is maximum, full-width at half maximum (FWHM), and peak intensity above the normalised continuum. In double-peak lines, the peak at shorter wavelength is referred to as the blue or violet peak, while the peak at longer wavelength is known as the red peak.
Using the best-fit parameters, we obtain the two following quantities:
-
peak separation (ΔV), defined as the difference between the central wavelengths of the red and the blue peak in velocity units ΔV = Δλ/λ0 × c, where c is the speed of light, and λ0 is the wavelength of the Hα line, 6562.8 Å;
-
V/R ratio, defined as the ratio of the relative intensity at the blue and red emission peak maxima (after subtracting the underlying continuum). For plotting purposes, we used the log of this ratio, log (V/R). Thus negative values indicate a red-dominated peak (V<R), positive values a blue-dominated profile (V>R), and values close to zero correspond to equal intensity peaks (V ≈ R).
In addition, the equivalent width (EW(Hα)) of the entire line was also calculated directly from the data, after normalisation. The EW(Hα) of each individual observation is given in Appendix A.
 |
Fig. 1 Evolution of the Hα equivalent width of the BeXBs considered in this work, ordered by increasing value of the orbital period (see Table 1). The orbital period of the four sources at the bottom is not known. |
4. Results
One of the most useful observables that can be used to monitor the spectral variability in HMXBs is the Hα line. Both SGXBs and BeXBs show this line in emission because they present a significant amount of circumstellar material. The Hα line is formed by recombination either in a large part of the equatorial disk, in the case of BeXBs, or in the low-density, high-velocity spherical wind in SGXBs. Other spectral emission lines such as those of helium and iron may also originate in the equatorial disk. However, they either probe only the innermost regions of the disk (He I lines) or are much more difficult to detect because they are narrower and weaker (Fe lines) than hydrogen lines (Hanuschik 1987). In addition, the strength of the Hα line is a good indicator of the size of the equatorial disk. This has become evident thanks to interferometric observations that resolved the disk and allowed the measurement of the angular dimensions of Be star disks. Quirrenbach et al. (1997) and Tycner et al. (2005) showed that there is a clear dependence of the net Hα emission on the physical extent of the emitting region. Grundstrom & Gies (2006) demonstrated that there are monotonic relationships between the emission-line equivalent widths and the ratio of the angular half-width at half-maximum of the projected disk’s major axis to the radius of the star. In addition to the strength of the Hα line, the profile shape is also important to study the conditions in the disk. Asymmetries in the line profile imply a distorted disk due to warping or a perturbed disk owing to density anisotropies (Okazaki 1991; Reig et al. 2000; Negueruela et al. 2001; Okazaki et al. 2013; Martin et al. 2014).
In this section we study the variability of the strength (equivalent width) and shape (line profile) of the Hα line on timescales of months to years, and the impact that the neutron star has on it. We compare the distribution of EW(Hα) in isolated Be stars and BeXB systems and study the variation of the maximum value of EW(Hα) as a function of orbital separation. We also investigate the disk rotational velocity law based on the peak separation of the split profile of the Hα line and find that it is consistent with Keplerian rotation. The peak separation can also be used to estimate the radius of the disk (Andrillat et al. 1990; Jaschek & Jaschek 1992; Dachs et al. 1992). We provide the first observational correlation between the disk radius and EW(Hα) in BeXBs. Finally, we compare the evolution of the EW(Hα) with the X-ray variability and show that the disk is strongly disrupted after major X-ray outbursts.
 |
Fig. 2 Evolution of the Hα equivalent width of wind-fed sources. |
Average, standard deviation, minimum, and maximum values of the Hα equivalent width. Also indicated is the number of spectra analysed. Negative values of the equivalent width mean emission profiles.
4.1. Measuring variability
In this section we perform a variability analysis of the equivalent width of the Hα line. Figures 1 and 2 show the evolution of EW(Hα) for the BeXBs and the SGXBs that were analysed in this work, respectively, and Table 2 gives the mean, standard deviation, largest and smallest values of EW(Hα), and number of observations for each source. To quantify the degree of variability, we used the root-mean-square amplitude defined as 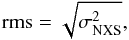 (1)where σNXS is the normalized excess variance (see e.g. Vaughan et al. 2003)
(1)where σNXS is the normalized excess variance (see e.g. Vaughan et al. 2003) 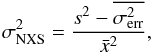 (2)
(2)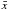 is the mean value and s2 is the observation (or sample) variance, i.e. the square of the standard deviation
is the mean value and s2 is the observation (or sample) variance, i.e. the square of the standard deviation 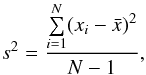 (3)and
(3)and 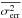 is the variance expected from the errors of the measurements
is the variance expected from the errors of the measurements 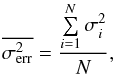 (4)where N is the number of measurements and σi the error of each measurement. Because, in some cases, the excess variance was negative, we also computed the ratio
(4)where N is the number of measurements and σi the error of each measurement. Because, in some cases, the excess variance was negative, we also computed the ratio 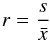 (5)of the standard deviation s over the mean value
(5)of the standard deviation s over the mean value 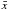 . Here the variable x refers to the equivalent width of the Hα line.
. Here the variable x refers to the equivalent width of the Hα line.
From the definition of excess variance, it is clear that negative values mean that the source is not variable. Negative values of the excess variance imply that the variance based on the entire set of observations s2 (sample variance) is smaller than the variance based on the uncertainty of the individual measurements 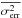 . In other words, the dispersion of the observations is smaller than the mean individual errors.
. In other words, the dispersion of the observations is smaller than the mean individual errors.
Results from the variability analysis.
Finally, we run an F test and computed the probability p-value considering the F-value, 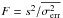 . The null hypothesis is that the two variances are equal. In our case, the rejection of the null hypothesis (low p-value) means that the source is variable. A similar analysis has been used by Jones et al. (2011) for a sample of isolated Be stars1.
. The null hypothesis is that the two variances are equal. In our case, the rejection of the null hypothesis (low p-value) means that the source is variable. A similar analysis has been used by Jones et al. (2011) for a sample of isolated Be stars1.
The optical continuum and line emission probe different parts of the disk. The Hα line is formed in the outer parts of the disk, while continuum emission originates in the inner parts. Thus to have a more complete picture of the disk variability, we also perform the statistical analysis on the flux of the V band given by 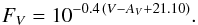 (6)Although the V band has a contribution from both the star and the disk, the long-term changes are expected to have their origin in the disk. For information about the photometric observations and data, see Reig & Fabregat (2015). The constant mz(V) = 21.10 = −2.5log (3.631 × 10-9) is the zero-point magnitude for the V band in erg s-1 cm-2 Å-1 (Bessell et al. 1998). Table 3 summarises the results of our statistical analysis.
(6)Although the V band has a contribution from both the star and the disk, the long-term changes are expected to have their origin in the disk. For information about the photometric observations and data, see Reig & Fabregat (2015). The constant mz(V) = 21.10 = −2.5log (3.631 × 10-9) is the zero-point magnitude for the V band in erg s-1 cm-2 Å-1 (Bessell et al. 1998). Table 3 summarises the results of our statistical analysis.
 |
Fig. 3 Fractional amplitude of variability of the optical continuum (V band) and Hα line. Black filled circles: BeXBs that have gone through a disk-loss phase; blue empty circles: BeXBs with stable disks; red triangles: other BeXBs; green empty squares: wind-fed accreting systems. |
4.2. Variability diagram
Figure 3 shows the relationship between the variability in the continuum and the line. A number of facts are worth noting:
-
Seven binaries exhibited Hα in absorption (EW(Hα) ≳ 0) at some moment during the period covered by our observations (Table 1 and Fig. 1): 4U 0115+63, X Per2, RX J0440.9+44313, 1A 0535+262, IGR J06074+2205, SAX J2103.5+4545, and IGR J21343+4738. This is generally interpreted as the loss of the disk. BeXBs that go through disk-loss episodes (filled black circles in Fig. 3) occupy the upper right part of the diagram, indicating that these systems are the most variable, both spectroscopically and photometrically.
-
On the opposite side of the diagram lie the systems with very stable disks (blue empty circles in Fig. 3). These are systems that do not show significant optical spectral variability in the period covered by the observations. They tend to have very large disks (i.e. large EW(Hα)). IGR J01363+6610, IGR J01583+6713, XTE J1946+274, and KS 1947+300 belong to this category. These systems do not exhibit significant changes in the spectral line parameters. They normally show symmetric single-peaked profiles that remain unchanged for a long period of time. However, they exhibit moderate photometric variability.
-
In between these two extreme cases (red empty triangles in Fig. 3), we find BeXBs displaying structural changes in the disk (V/R variability, long-term weakening) but without losing the disk. Although some systems nearly revert emission into absorption, e.g. RX J0146.9+6121, GRO J2058+42, or SAX J2239.3+6116, EW(Hα) never goes below zero during the time covered by our observations.
-
On average, systems for which X-rays results from accretion from a stellar wind (the SGXBs 2S 0114+65, AX J1845.0-0433, 4U 1907+09, and also 4U 2206+54, green empty squares) display smaller amplitude of variability in EW(Hα) (and brightness) than BeXB systems, although spectroscopically they can be more variable than BeXBs with stable disks4 (Fig. 2). This result implies that, in a stable configuration where the Be star feeds the disk constantly, the optical emission from this type of rotationally supported mass distribution is more stable than from the inhomogeneous fast varying spherical stellar wind.
-
EW(Hα) varies over a larger fractional range than the V magnitude. This can be understood taking into account the different formation loci of continuum and line emission. Non-LTE Monte Carlo radiative transfer simulations (Carciofi & Bjorkman 2006) show that the emission in the V band is formed in the innermost parts of the disk, very close to the star, whereas Hα emission forms further away from the star. For example, in the case of a rapidly rotating B1Ve star, typical of BeXBs, the simulation showed that approximately 95% of the continuum excess comes from within 2 R∗ whereas, for the Hα line, the disk emission only fills the photospheric profile when the disk is about 5R∗ (Carciofi 2011). Figure 3 confirms the idea that the external parts of the disk are more prone to changes that the inner parts.
4.3. Variability versus orbital period
Next we investigated whether the neutron star affects the variability patterns. The idea is simple: one would expect that the closer the two components of the binary are, the stronger the tidal torque exerted on the disk by the neutron star.
In Fig. 1, we have ordered the systems in increasing value of the orbital period (see Table 1). Four systems (IGR J01363+6610, IGR J01583+6713, IGR J06074+2205, and IGR J21343+4738) do not have a known orbital period. Visual inspection of Fig. 1 reveals that systems with short orbital periods (Porb< 50 d) exhibit fast variability, i.e. choppy curves, while systems with longer orbital period show slow changes, i.e. smooth curves. Systems with short orbital periods do not show long-term increasing or decreasing trends. Instead, EW(Hα) “oscillates” around a certain mean value.
We quantified this result in the following way: we divided the long-term EW(Hα) curve into 500-d intervals. For each interval, we computed the ratio of the standard deviation over the mean, 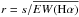 . Finally, we obtain the average
. Finally, we obtain the average 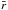 for each source. In this calculation we used intervals with at least four measurements of EW(Hα). Figure 4 shows
for each source. In this calculation we used intervals with at least four measurements of EW(Hα). Figure 4 shows 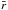 as a function of the orbital period for all the BeXB whose orbital period is known (see Table 1). One can observe a distinct trend with the narrower orbit systems showing more variability. A simple explanation is that wider orbit systems are able to develop stable disks during long periods of time. In contrast, the systems with short orbital periods feel the tidal truncation exerted by the neutron star more strongly and more frequently, so that the disk does not easily achieve a stable configuration.
as a function of the orbital period for all the BeXB whose orbital period is known (see Table 1). One can observe a distinct trend with the narrower orbit systems showing more variability. A simple explanation is that wider orbit systems are able to develop stable disks during long periods of time. In contrast, the systems with short orbital periods feel the tidal truncation exerted by the neutron star more strongly and more frequently, so that the disk does not easily achieve a stable configuration.
 |
Fig. 4 Hα equivalent width variability as a function of the orbital period in BeXBs with orbital solutions. The Y-axis is the average ratio of the standard deviation over the mean calculated in intervals of 500 days (or 1000 days for XTE J1946+274, cross). Empty circles correspond to peculiar systems (see text). |
The choice of the 500-d duration interval is somewhat arbitrary but it is justified by the need to sample the fast variations of the shorter period systems. We note that for large intervals (≳1000 d) the amplitude of variations of long-period systems begins to be comparable to the shorter period systems. We also note that although the value of 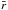 for the individual systems may vary, the decreasing trend of Fig. 4 remains for any choice of the duration of the interval in the range 300–1000 days. The cross symbol in Fig. 4 corresponds to XTE J1946+274 and simply denotes the fact that owing to large observational gaps, the duration of the interval in this source was taken to be 1000 d instead of 500 d, since the shorter duration did not provide enough number of intervals with more than 4 points.
for the individual systems may vary, the decreasing trend of Fig. 4 remains for any choice of the duration of the interval in the range 300–1000 days. The cross symbol in Fig. 4 corresponds to XTE J1946+274 and simply denotes the fact that owing to large observational gaps, the duration of the interval in this source was taken to be 1000 d instead of 500 d, since the shorter duration did not provide enough number of intervals with more than 4 points.
There are three systems that deviate from the general trend: RX J0240.4+6112 and KS 1947+300 (empty circles in Fig. 4) and to a lesser extent V 0332+53. RX J0240.4+6112 is not a typical BeXB. The nature of the compact object (neutron star or black hole) is not known and no X-ray pulsations have been detected so far. It belongs to the class of γ-ray binaries (Dubus 2013) and is the only system of our list that exhibits radio emission, which is associated either with a jet or with the interaction between the relativistic wind of a young non-accreting pulsar and the wind of the donor star. Although the optical counterpart is a B0Ve, the physical conditions that prevail in the disk are unknown.
KS 1947+300 is the only BeXB of our sample with a near circular orbit (Galloway et al. 2004). According to the viscous disk truncation model, these systems are truncated at the 3:1 resonance radius and the gap size between the truncation radius and the radius where the gravity by the neutron star begins to dominate (critical lobe radius) is considerably wider than in systems with larger eccentricities. Wide gaps result in disk truncation that is very effective and the disk can accumulate mass over a long period of time (Okazaki & Negueruela 2001). Assuming typical masses for a B0Ve for the optical and compact components of the binary, the orbital parameters (Porb = 40.4 d and e = 0.03, Galloway et al. 2004), the viscous decretion disk model predicts a gap size of Δr/a ~ 0.24, where a is the binary orbital separation, which is significantly larger than the values found for systems with highly-eccentric orbits (see Table 2 in Okazaki & Negueruela 2001) for which Δr/a ≲ 0.1, typically. Therefore, we conclude that although the neutron star effectively acts as a barrier that prevents the free expansion of the disk, the Be star in KS 1947+300 can reach a stable configuration owing to the large gap between the disk and the neutron star.
The case of V 0332+53 is harder to explain. Of the BeXBs with reliable orbital solutions, it is the only system with a periastron distance of the order of, or smaller than, 10 stellar radii that shows little variability. One possible explanation could be the low inclination angle (≲10°) of the orbit (Negueruela et al. 1999), i.e. the disk is seen pole-on, hence the entire disk is exposed to the observer all the time.
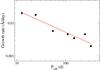 |
Fig. 5 Disk growth rates as a function of orbital period. The solid line represents the best-fit to a power-law function. |
4.4. Disk growth rates
We computed the disk growth rates after the disk-loss episodes in SAX J2103.5+4545 (0.0205 Å/d), 4U 0115+63 (0.0180 Å/d), 1A 0535+262 (0.0058 Å/d), RX J0440.9+4431 (0.0035 Å/d), and X Per (0.0046 Å/d) and after the low states of GRO J2058+42 (0.0058 Å/d) and RX J0146.9+6121 (0.0020 Å/d). The growth rates were calculated as the slope of a linear fit of the EW(Hα) as a function of time between the minima and maxima after the disk-loss event, representing states with no or very weak disk and a full developed disk, respectively. We find that the disk in systems with short orbital periods grows faster than in systems where the neutron star orbits further away. The data fit a power law, y = (0.12 ± 0.01) × x(− 0.67 ± 0.10), well, as shown in Fig. 5.
This result does not necessarily mean that the mechanism that expels matter from the photosphere of the Be star to create the disk, or even the mass-loss rate from the star is different in different systems. The most likely explanation is that, owing to truncation, the disk becomes denser more rapidly in shorter orbital period systems, hence EW(Hα) changes faster. As the disk grows, the effect of the resonant torque from the neutron star becomes stronger and the radial density distribution begins to break at the truncation radius. Since the resonant torque prevents disk material from drifting outwards, the disk density increases faster in systems where the distance between the two components of the binary is shorter. This is the same argument used by Okazaki et al. (2002), which predicts that the disks in BeXBs should be more dense than in classical, isolated Be stars.
This correlation provides further evidence for the truncation of the disk in BeXB systems. However, we advise caution given the uncertainty in some of the orbital periods of the systems in Fig. 5 and the approximate nature of the growth-rate calculation. The results of this section should be confirmed by future observations.
 |
Fig. 6 Correlation between the periastron distance and the largest value of EW(Hα). |
4.5. The equivalent width of the Hα line versus the orbital separation
Figure 6 shows the correlation between the distance to periastron and the maximum value of EW(Hα). Periastron distances were computed assuming the mass, radius, and orbital parameters given in Table 1. Figure 6 should be compared to the analogous relationship between the orbital period and EW(Hα) (Reig et al. 1997b; Reig 2007; Antoniou et al. 2009). The smaller the periastron distance, the smaller the EW(Hα). The disk can grow until the torque exerted by the neutron star begins to be strong, that is, until the disk radius reaches the critical radius of the Roche lobe at periastron. The neutron star removes angular momentum from the disk at each periastron passage, which prevents the disk from expanding further. The closer the neutron star passage, the stronger the tidal torque on the disk, hence the smaller the disk and the lower the EW(Hα).
Quantifying these statements depends on what one considers a large or small disk. Assuming that EW(Hα) ≳−30 Å denotes a large disk, then from Fig. 6 we conclude that for a large disk to form requires that the neutron star does not get closer than ~20 stellar radii during periastron.
 |
Fig. 7 Comparison of the EW(Hα) in classical Be stars (black line) and BeXB (blue dashed hatched histograms). The data for the classical Be stars come from the IPHAS sample and comprises 219 stars with spectral types between O9 and B3. The data for BeXBs are from this work. |
4.6. The equivalent width of the Hα line in Be/X-ray binaries and classical Be stars
Further evidence of the interaction between the neutron star and the disk can be obtained by comparing the strength of the Hα emission in classical Be stars and BeXB. Figure 7 shows a histogram of the equivalent width in isolated Be stars and BeXBs. The data for BeXB systems comes from the present work, and the values of EW(Hα) used to make Fig. 7 were the largest measured so far, while the EW(Hα) of isolated Be stars was taken from the INT Photometric Hα Survey (IPHAS) selected sample and correspond to a single epoch (Gkouvelis et al. 2016, and in prep.). We used only Be stars whose spectral type lies in the range O9–B3 to match those observed in BeXB. The histogram shows the frequency, i.e. the number of sources in the bin divided by the total number of sources. Figure 7 was made using 219 Be stars and 16 BeXBs. Below EW(Hα) = −30 Å, there is only one BeXB in each bin. This figure indicates that, on average, isolated Be stars show distinctly larger EW(Hα), hence larger disks.
A Kolmogorov-Smirnov test of the two data sets gives a probability of 3.4% that they are drawn from the same distribution. We note however that, while in BeXBs we have considered the largest value of EW(Hα) measured so far, for classical Be stars we only have one measurement for each source. Although we cannot be sure that a larger EW(Hα) will not be measured in the BeXB systems, the fact that the observations of BeXBs span many years makes it unlikely, especially in cases where our observations cover several disk dissipation-formation cycles, that future observations will give significantly larger EW(Hα). However, it is likely that many of the classical Be stars will show larger EW(Hα) in the future because only one single epoch measurement was used. Thus, the difference between the strength of the Hα line in classical Be stars and BeXBs is, in fact, more significant than is suggested by Fig. 7.
Statistics of the shape of the Hα line.
4.7. Profile types. V/R peak height variability
While the strength of the Hα line provides information about the size of the emitting region, its morphology indicates whether the distribution of gas particles in the disk is homogeneous. Symmetric lines are believed to be generated in axisymmetric disks. Asymmetric lines are due to a global density perturbation that revolves inside the disk (see e.g. Hummel & Vrancken 1995, and references therein). Transitions from one type of line to the other are common among classical Be stars.
Table 4 summarises the number of times that the different profiles have been observed: absorption (AB), fill-in (FI), single-peak (SP), double-peak (DP), multi-peak (MP), and P Cygni (PC). Fill-in profiles are those cases in which the line has been filled with emission by an amount that approximately covers the photospheric absorption, resulting in a flat spectrum at the position of the line, hence EW(Hα) ≈ 0. The DP type also includes the so-called shell profiles. These are double-peak profiles in which the central absorption that separates the two peaks reaches or goes below the continuum. By multi-peak, we mean a profile that shows a complex structure, typically a main peak whose flanks are affected by smaller peaks or weak absorption features. Finally, P Cygni profiles are emission lines with a blue-shifted absorption component, which is produced by material moving away from the star (i.e. stellar wind) towards the observer’s line of sight. Representative Hα line profiles for SGXBs and BeXBs are given in Figs. 8 and 9, respectively.
Although the shape of the line greatly depends on the spectral resolution, a statistical analysis of the various types of profiles may still be useful to study the connection of the line profile with other properties of the system and gain some insight into the mass transfer process. Taking into account the resolution of our spectra (typically R ≲ 2500), an inspection of Table 4 reveals the following general results: i) which systems went through disk-loss episodes (those showing absorption profiles); ii) that MP and PC types are only seen in SGXBs5; iii) that a double-peak profile is the dominant shape in most BeXBs, especially at low and intermediate EW(Hα); and iv) together with Table 2, that large EW(Hα) in BeXBs tends to be associated with single peak profiles. Items iii) and iv) are a natural consequence of emission lines whose widths essentially have a kinematic origin (Hanuschik 1989).
The most prominent spectroscopic evidence of disk activity is the long-term V/R variability, which refers to the variation in the relative intensity of the blue (V) and red (R) peaks in the split profile of the line. In long-lasting disks, it is possible to observe more than one cycle V>R − → V ≈ R − → V<R. However, owing to the very nature of the source of variability, namely, the precession of a density perturbation in the disk, we do not expect the process to be precisely periodic with a high degree of coherence. The duration of the V/R cycle presumably depends on disk parameters such as viscosity, density, and size, which are not only poorly known but also change as the disk grows. In addition, observational gaps in the data introduce extra complications. Therefore software packages designed to search for periodicities in data do not generally produce a significant result. Nevertheless, by isolating periods where the V/R cycle appears to be coherent and using algorithms that can handle gaps (e.g. Lomb-Scargle), it is possible to obtain the V/R quasiperiods. Otherwise, we just estimated the quasiperiod of the data by eye.
 |
Fig. 8 Representative Hα profiles in SGXBs: left: multipeak profile observed in AX J1845.0-0433; right: P Cygni profile observed in 2S 0114+65. |
 |
Fig. 9 Representative double-peak Hα profiles in BeXB (from RX J0440.9+4431). |
 |
Fig. 10 Variability of the Hα line profile quantified as the log (V/R), where V and R are the intensity of the left and right peaks. Arrows indicate the occurrence of large X-ray outbursts. |
All but three sources of our BeXB sample6 (IGR J01363+6610, XTE J1946+274, and KS 1947+300) showed double-peaked profiles at some point, whereas SGXBs show broad (FWHM ~ 300–900 km s-1) multi-peak lines. 4U 2206+54 consistently shows a slightly red dominated profile with an almost constant ratio of V/R = 0.8 ± 0.1. In RX J0240.4+6112, only four spectra have V>R, while the remaining 40 have V<R, also with an average ratio of V/R = 0.8 ± 0.1. Figure 10 shows the evolution of log (V/R) for the most variable systems. Of particular interest are systems 1A 0535+262, RX J0440.9+4431, 4U 0115+63, and RX J0146.9+6121.
RX J0146.9+6121 was in a bright optical state between March 1993 and October 2001 (MJD 49 000–52 500). EW(Hα) remained below –8 Å reaching a historical maximum of –20 Å in September 1993 (Fig. 1). Then EW(Hα) began to decrease until July-August 2005, when the lowest value of −3.7 Å was recorded. During the faint state (MJD 53 000–54 800), the line showed a symmetric double-peaked profile with V = R (Fig. 10). When the EW(Hα) began to increase again, the asymmetries returned, starting with V<R. Before the disk minimum, we computed a V/R quasi-period of ~1300 d (MJD 49 000–52 500) while, after the minimum, the quasi-period was half ~650 d (MJD 54 700–56 600). The shorter period after the faint state can be attributed to a smaller disk: initially the disk was large, as indicated by the larger values of EW(Hα). Slowly and progressively the disk decreased in size to a minimum. At this time, the disk is so small that it cannot support the perturbation, which vanishes. Without a perturbed disk, the V/R ratio becomes close to 1 (V ≈ R), i.e. a symmetric profile. As soon as the disk recovers a certain size, the perturbation appears again, but because the disk is smaller than previously, the perturbation revolves faster, resulting in a smaller period.
The case of RX J0440.9+4431, 1A 0535+262, and 4U 0115+63 is similar. After a disk-loss episode (see Fig. 1), the disk reformed slowly, with the EW(Hα) increasing progressively. Once the disk attained a large size, V/R variability set in. We measured a quasiperiod of ~525 d in RX J0440.9+4431 and ~1100 d in 1A 0535+262. In 4U 0115+63 the disk forms and dissipates on timescales of 3–5 years (Fig. 1, see also Reig et al. 2007) and the V/R quasiperiod (1000–1500 d) is bound by these fast changes. Eventually, the growth of the disk in these three systems led to a major (type II) outburst. An interesting result is the fact that the asymmetric profiles are observed before the onset of the X-ray outburst, supporting the models that invoke highly distorted disks to explain Type II accretion events (Okazaki et al. 2013; Martin et al. 2014).
Although the disk in IGR J06074+2205 and SAX J2103.5+ 4545 does not reach a stable configuration for a long enough time to measure a periodicity, the two systems display fast V/R variability with the V/R ratio reverting from V/R> 1 to V/R< 1 on timescales of ≲1 yr.
 |
Fig. 11 Correlation between the peak separation and the Hα equivalent width for six BeXBs. The line represents the best fit to a linear regression (see Table 5). The scale of the axes was the same in all plots to facilitate comparison. |
4.8. Disk velocity law
A long standing issue since the discovery of the first Be stars has been the nature of the velocity law that is followed by the particles in the disk. The correlations between the various spectral parameters of the Hα line (FWHM, EW, peak separation in double-peaked profiles) and with the stellar rotational velocity that have been observed in many Be stars are interpreted as evidence for rotationally dominated circumstellar disks (Dachs et al. 1986; Hanuschik 1989; Dachs et al. 1992). The velocity profile in a circumstellar disk can be expressed as 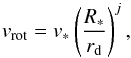 (7)where v∗ and R∗ are the star rotational velocity and radius and j is the disk rotational velocity law parameter, which may adopt three values (see e.g. Dachs et al. 1992): i) j = 1 represents the case of conservation of angular momentum, where the circumstellar gas has the same angular momentum per unit mass as that at the stellar surface; ii) j = −1 corresponds to rigid rotation, which might occur in the innermost regions of the disk; and iii) j = 0.5 for a Keplerian disk.
(7)where v∗ and R∗ are the star rotational velocity and radius and j is the disk rotational velocity law parameter, which may adopt three values (see e.g. Dachs et al. 1992): i) j = 1 represents the case of conservation of angular momentum, where the circumstellar gas has the same angular momentum per unit mass as that at the stellar surface; ii) j = −1 corresponds to rigid rotation, which might occur in the innermost regions of the disk; and iii) j = 0.5 for a Keplerian disk.
Nowadays, there is general consensus, based on the evidence gathered over many years, that the circumstellar disks in classical Be stars are governed by viscosity and follow a Keplerian law (Meilland et al. 2007; Rivinius et al. 2013). A way to estimate the index j, and hence determine the type of dependence of the rotational velocity with radius, is through the relationship between the peak separation, ΔV, and the equivalent width, EW(Hα). Hanuschik et al. (1988) derived the law 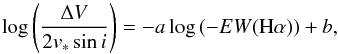 (8)where i is the inclination angle. The equivalent width is expected to be proportional to the visible disk area, i.e. to the disk radius squared (Tycner et al. 2005; Grundstrom & Gies 2006). In this case, a = j/ 2 and b is related to the electron density in the disk (Hanuschik et al. 1988). From a sample of 93 isolated Be stars of all spectral types Hanuschik (1989) found a = 0.32 and b = −0.20. We repeated this calculation using the IPHAS list of isolated Be stars (Gkouvelis et al., in prep.). Of the 230 Be stars with spectral types in the range O9–B3, only 30 displayed double peaked profiles. A fit to this data gave a = 0.24 ± 0.11 and b = −0.15 ± 0.12. For the IPHAS sample of classical Be stars, j ≈ 0.5, as expected for a Keplerian disk.
(8)where i is the inclination angle. The equivalent width is expected to be proportional to the visible disk area, i.e. to the disk radius squared (Tycner et al. 2005; Grundstrom & Gies 2006). In this case, a = j/ 2 and b is related to the electron density in the disk (Hanuschik et al. 1988). From a sample of 93 isolated Be stars of all spectral types Hanuschik (1989) found a = 0.32 and b = −0.20. We repeated this calculation using the IPHAS list of isolated Be stars (Gkouvelis et al., in prep.). Of the 230 Be stars with spectral types in the range O9–B3, only 30 displayed double peaked profiles. A fit to this data gave a = 0.24 ± 0.11 and b = −0.15 ± 0.12. For the IPHAS sample of classical Be stars, j ≈ 0.5, as expected for a Keplerian disk.
The question that we wish to address here is whether the disks of Be stars in X-ray binaries also follow a Keplerian law or, instead, the presence of a neutron star somehow alters the expected behaviour. Figure 11 shows the correlation between the peak separation and the equivalent width of the Hα line for six BeXBs. The result of the fit and the value of the j index are given in Table 5. The correlation is expected to hold for well developed disks, hence data points with log (EW(Hα)) < 0 were ignored in the fit. None of the sources deviate by more than 2σ from the value of j = 0.5. Hence we conclude that the circumstellar disks in BeXBs are also Keplerian. The only exception is IGR J06074+2205, which might be explained by the fast timescales for disk formation and dissipation. Although the data span almost eight years, this source never reaches a stable state with a well developed disk for more than a year (see Fig. 1). Thus most of the data may correspond to phases where the disk is forming or dissipating, where a Keplerian supported disk may not be at work.
Linear regression between the peak separation and the equivalent width of the Hα line.
Although the slope of the correlation, i.e., the j index, is similar in classical Be stars and BeXBs, the intercept is clearly different. Figure 12 again shows the relationship between the EW(Hα) and the peak separation of our BeXB, but this time all the data are plotted together. The solid line represents the average behaviour of the 30 IPHAS classical Be stars with spectral types in the range O9–B3 and the dotted line corresponds to 93 classical Be stars of all spectral types (Hanuschik 1989). The best-fit to the BeXB data points is given by the dashed red line.
As can be seen, BeXBs lie above the mean behaviour of classical Be stars, i.e. they appear shifted vertically with respect the Be star line fit. According to Hanuschik et al. (1988), the intercept b is related to disk density. Thus this shift implies that the circumstellar disks in BeXBs are denser than disks in isolated Be stars. We find a difference of log (ΔV/ 2vsini)BeXB − log (ΔV/ 2vsini)Be ≈ 0.15−0.2, implying that the disks of BeXB systems are about 1.5 times denser than those of classical Be stars. This result agrees with Zamanov et al. (2001) who found that on average the disks of BeXBs are about twice as dense as those of classical Be stars, a result that was attributed to disk truncation.
4.9. Circumstellar disk radius
 |
Fig. 12 Relationship between the peak separation and the Hα equivalent width. The solid and dashed line represents the average behaviour of 30 classical Be stars with spectral type in the range O9–B3 (Gkouvelis et al., in prep.) and 93 Be stars of all spectral types (Hanuschik 1989), respectively. BeXBs lie systematically above the Be stars’ lines. |
According to Huang (1972), the separation of the emission line peaks can be interpreted as the outer radius of the emission line forming region7. We can estimate the outer radius from Eq. (7) and the relationship between the peak separation and the velocity at which gas rotates in the disk ΔV = 2vrotsini, where i is the inclination angle. Isolating r from Eq. (7), the radius of the Hα emitting disk is given by 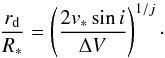 (9)We used Eq. (9) and j = 1 / 2 to estimate the radius of the line-emitting region for those systems with known values of the star projected rotational velocity and studied the relationship with EW(Hα). A positive correlation between EW(Hα) and the disk radius is found (see Fig. 13). This relationship confirms the well-known result that EW(Hα) gives a measure of the size of the disk (Quirrenbach et al. 1997; Grundstrom & Gies 2006).
(9)We used Eq. (9) and j = 1 / 2 to estimate the radius of the line-emitting region for those systems with known values of the star projected rotational velocity and studied the relationship with EW(Hα). A positive correlation between EW(Hα) and the disk radius is found (see Fig. 13). This relationship confirms the well-known result that EW(Hα) gives a measure of the size of the disk (Quirrenbach et al. 1997; Grundstrom & Gies 2006).
We note that the anticorrelation between ΔV and EW(Hα), see Figs. 11 and 12, rules out a velocity law with j< 0. Moreover, this anticorrelation means that, as the disk radius or, equivalently, EW(Hα), increases, the peak separation decreases until the two peaks merge and a single peak is observed. Indeed, systems that display large amplitude changes in EW(Hα) show single-peak profiles when EW(Hα) is large and double-peak profiles when EW(Hα) is small. The transition from double- to single-peak profiles occurs when EW(Hα) increases above ~−15 Å, although this value is expected to depend on the spectral resolution.
From Fig. 13, we see that disk radii in BeXBs are typically Rdisk ≲ 6R∗. This result can be compared with the average radii of the Hα-emitting regions in classical Be stars: ⟨ Rdisk ⟩ = 14 R∗ (Hummel & Vrancken 1995), ⟨ Rdisk ⟩ = 22 R∗ (Dachs et al. 1992), ⟨ Rdisk ⟩ = 17 R∗ (Hanuschik 1986), and ⟨ Rdisk ⟩ = 20 R∗ (Hanuschik et al. 1988). BeXBs have smaller disks than classical Be stars, in agreement with the results presented in Sect. 4.6.
 |
Fig. 13 Relationship between Hα equivalent width and disk radius. |
4.10. Circumstellar disk and X-ray variability
Because the disk constitutes the main reservoir of matter available for accretion, a correlation between X-rays and optical emission should be expected. X-ray outbursts in BeXB are commonly classified into a simple scheme of normal (Type I) and giant (Type II) outbursts:
-
Type I outbursts are regular and (quasi-)periodic outbursts, normally peaking at or close to periastron passage of the neutron star. They are short-lived, i.e. tend to cover a relatively small fraction of the orbital period (typically 0.2–0.3 Porb). The X-ray flux increases by up to two orders of magnitude with respect to the pre-outburst state, reaching peak luminosities LX ≲ 1037 erg s-1. The number of detected Type I outbursts varies from source to source but typically the source remains active for 3–8 periastron passages. A remarkable case is EXO 2030+375, which shows type I outbursts almost permanently (Wilson et al. 2002).
-
Type II outbursts represent major increases of the X-ray flux, 103−104 times that at quiescence. They may reach the Eddington luminosity for a neutron star (LX ~ 1038 erg s-1) and become the brightest objects of the X-ray sky. They do not show any preferred orbital phase and last for a large fraction of an orbital period or even for several orbital periods.
The standard picture is that Type I X-ray outbursts are triggered by the mass transfer from a tidally truncated Be star’s disk (Negueruela & Okazaki 2001; Okazaki & Negueruela 2001; Okazaki 2001) at or near periastron, while Type II outbursts are associated with unstable disk configurations such as warped disks. A recent work by Okazaki et al. (2013) shows that the standard disk model cannot explain the large and rapid X-ray flux variations and the short duration of normal Type I outbursts because the accretion timescales are expected to extend beyond a few orbital periods. Okazaki et al. (2013) propose that normal outbursts can be explained by radiatively inefficient accretion flows, while giant outbursts are due to Bondi-Hoyle-Lyttleton accretion of material transferred from the outermost part of a Be disk that is misaligned with the binary orbital plane. Martin et al. (2014) find that, in addition to being warped and highly misaligned, the disk has to be eccentric to explain giant outbursts.
In this section, we concentrate on the changes experienced by the disk after a major X-ray outburst. Because of the good correlation between disk radius and EW(Hα) and because EW(Hα) is more easily measured, we used the equivalent width rather than the disk radius to investigate the correlation between the optical and X-ray variability. Moreover, the radius can be computed only when a double peak is observed, hence the use of EW(Hα) provide more data points and more sources where the relationship can be studied.
 |
Fig. 14 Hα equivalent width and X-ray variability. The light curves of the RXTE/ASM (2–10 keV) in black and the Swift/BAT (15–50 keV) in red were rebinned to 5-day bins. |
Figure 14 shows the relationship between EW(Hα) and the X-ray intensity for all the sources in our list that display significant X-ray variability during the time span covered by our optical observations. The lower panels shows the long-term X-ray light curve from the all-sky monitors on board RXTE (ASM) and Swift (BAT)8.
Because the X-rays are powered by matter transferred from the disk into the neutron star, we would expect to observe a smaller disk, i.e. a decrease of the EW(Hα) after X-ray outbursts. This expected behaviour is indeed seen in half of the systems (Fig. 14). In RX J0440.9+4431, 1A 0535+262, SAX J2103.5+4545, and 4U 0115+63, we observe that X-ray outbursts occur when the disk radius is large, i.e. when EW(Hα) is close to a local maximum. We also see a significant decline after the outburst. We note that in some cases (4U 0115+63 and SAX J2103.5+4545), the X-ray outburst is such a dramatic event that disrupts the disk completely and leads to its loss, as implied by the fact that EW(Hα) becomes positive.
However, some other systems do not show such a clear correlation. The X-ray activity in V 0332+53, XTE J1946+274, and KS 1947+300 does not seem to have any significant effect on the EW(Hα), if one considers the data from this work (filled circles). In particular, the X-ray outburst observed in V 0332+53 in December 2004 is one of the brightest events detected in a BeXB. The peak luminosity reached 3.5 × 1038 erg s-1 (Tsygankov et al. 2010) twice the value of the Eddington limit for a typical 1.4M⊙ neutron star (Reig & Nespoli 2013). Surprisingly, EW(Hα) did not vary substantially. Similar behaviour is seen in XTE J1946+274 and KS 1947+300, although in these two sources the X-ray event was not so bright (LX< 1038 erg s-1).
One possible reason that we do not observe a significant decrease of EW(Hα) after the X-ray outburst could be attributed to observational gaps, i.e. we cannot be sure that our data before and after the X-ray outburst represent the real maximum and minimum value of the EW(Hα). The peak of the outburst in V 0332+53 occurred on MJD 53 365, but our largest value of EW(Hα) before the outburst is −8.3 Å at MJD 53 304, while after the outburst our first value is at MJD 53 582 and the minimum is found at MJD 53 670 with −5.4 Å. However, we do not know whether EW(Hα) was larger before MJD 53 304 and smaller after MJD 53 670. To investigate this issue, we searched the literature for other measurements of EW(Hα) in the interval MJD 52 920–54 033 and found two values at MJD 53 378 (Masetti et al. 2005) and MJD 54 005 (Caballero-Garcia et al. 2016) with Hα equivalent widths of −10 Å and −6.2 Å, respectively. These two points have been depicted in Fig. 14 with empty red squares. Although the data point from Caballero-Garcia et al. (2016) narrows the gap of a possible minimum after the outburst, it does not help solve the issue of whether our data after the outburst represent the actual minimum value achieved by the source. The measurement by Masetti et al. (2005) shows that the disk was larger, hence the decrease in EW(Hα) after the X-ray outburst was more significant than what our data alone suggested. The low inclination of the system may also explain the smaller amplitude change in EW(Hα) after the outburst with respect to other systems, as pointed out in Sect. 4.3.
Observational gaps may also affect our results on XTE J1946+274. There are no optical observations prior to the 1998 outburst because it was this event that led to the discovery of the source as a BeXB. If we look at our data (filled circles in Fig. 14), we do not see any significant change during or after the second X-ray active phase in 2010. The last X-ray peak occurred in April 2011 (MJD ~ 55 660). Between our observations, taken in August 2011 (MJD 55 795) and September 2012 (MJD 56 176), there is a gap of more than a year. We found ten observations (empty red squares) from Özbey Arabacı et al. (2015) during the gap period, in which the equivalent width of two of them was significantly smaller. Therefore, the disk in XTE J1946+274 did indeed weaken after the X-ray activity, although the minimum EW(Hα) measured after the outburst is still large (~−20 Å).
Although KS 1947+300 does show a small decrease of about 10–15% immediately after the peak of the outburst both in the 2000 and 2013 events and displays a long-term gradual decrease of EW(Hα) between the outbursts, which is in excellent agreement with the fading of the photometric magnitudes (Reig & Fabregat 2015), the pre-outburst level is quickly recovered. We did not find any more data after the X-ray activity phase in the literature. The gaps are, however, shorter, hence it is unlikely that we have missed an extended decrease of EW(Hα). The lack of any major observational change in the disk of KS 1947+300 after a giant X-ray outburst might be attributed to its circular orbit, as explained in Sect. 4.3. We note that, owing to its circular orbit, the radius of the disk must reach the orbital separation (a) to produce an X-ray outburst. For Porb = 40 d, M∗ = 17.5 M⊙, and R∗ = 7.7 R⊙ this implies a ≈ 9 × 1012 cm ~ 17 R∗.
The same arguments can be used for X Per. This system also has a low-eccentric orbit (e = 0.1) and shows no correlation between optical and X-ray emission. The difference with KS 1947+300 is the much longer orbital period of 250 days (hence the gap between the disk’s outer radius and the periastron distance is even wider than in KS 1947+300) and the fact that X Per is a persistent X-ray source. X Per does not show the typical Type I or II X-ray outbursts, but shows extended periods of low and high X-ray activity. The lack of a correlation between optical and X-ray flux in X Per has been reported before (Lutovinov et al. 2012; Li et al. 2014).
Another explanation for the lack of a large amplitude change in EW(Hα) after major X-ray outbursts is the fact that the amount of mass accreted to produce the increased X-ray flux represents a small part of the total mass of the disk. KS 1947+300, XTE J1946+274, and X Per share in common a relatively large separation between the two components of the binary, which is either due to the long orbital period or the low eccentricity of the orbit. As explained before, this implies the possibility of developing very large disks. Following Reig & Fabregat (2015)9, and assuming a disk radius Rdisk = 8R∗, we estimate that less than 20% of the material in the disk needs be accreted to produce the kind of outburst (LX ~ 1 × 1037 for about 100 days) observed in KS 1947+300 or XTE J1946+274.
5. Discussion
Be stars may exist as isolated systems (classical Be stars) or be part of X-ray binaries (BeXBs), where the companion is a neutron star. In both cases, the circumstellar disk is responsible for their long-term spectral variability. Given the large mass ratio between the two components in a BeXB, the neutron star exerts a negligible effect on the underlying massive companion. Hence it is normally assumed that the physical properties (mass, radius, and luminosity) of the B star in an isolated Be star and in a BeXB are the same for the same spectral type. However, the circumstellar disk may extend over several stellar radii and occasionally reach periastron distance. It is sensible to think that the presence of a second body (the neutron star) must have some effect on the observational properties of the disk. As the equatorial disk is more exposed to the action of the neutron star, we would expect to see different properties in the disks of isolated Be stars compared to those of BeXBs. The most important difference is the truncation of the disk (Reig et al. 1997b; Negueruela & Okazaki 2001; Okazaki & Negueruela 2001; Okazaki 2001; Okazaki et al. 2002; Reig 2011).
If there is no physical difference between the B star in an isolated Be star and the B star in a BeXB, and the optical spectral variability is driven by changes in the disk, then any difference in the observational properties between classical Be stars and BeXBs must come from the effect of the neutron star on the disk. In this work, we searched for these types of differences in the variability patterns of various physical parameters and found important differences in disk density and size, and the characteristic variability timescales associated with the evolution of the disk (V/R changes, disk dissipation and reformation). Further evidence for the interaction between the disk and the neutron star comes from the correlation of disk parameters and the orbital period because one would expect that the closer the two components, the larger the strength of the interaction.
In what follows, we summarise the observational evidence for the truncation of the disk, gathered in two groups: correlations with the orbital period and comparison between BeXB systems and classical Be stars. Some of the results presented here are new, others confirm previous studies. However, it is worth mentioning that our work constitutes the first attempt to explain the long-term optical variability of BeXB as a group using the largest data set so far analysed.
5.1. Correlation with the orbital period
-
The Porb-variability correlation. In Sect. 4.2, we showed that systems with small orbital periods are more variable both in the continuum and line optical emission (Figs. 3 and 4). A similar result was found by analysing the variability in the X-ray band (Reig 2007). These results strongly suggest that the circumstellar disk in BeXBs is truncated. Because the disk of systems with short orbital periods are more exposed to the action of the neutron star, they cannot reach a stable configuration over long timescales.
-
Disk recovery after dissipation. In Sect. 4.4, we showed a correlation between disk growth rate (change of EW(Hα) with time) and orbital period after a low state. Systems with shorter orbital periods display larger growth rates. Owing to truncation, the disk density increases faster in closer binaries, leading to a faster increase in EW(Hα). Not only the disk formation, but also the entire formation and dissipation cycle appears to be faster in systems with short orbital periods, while longer timescales are associated with longer orbital periods. This can be deduced from Fig. 1, where the systems are ordered in increasing orbital period. Disk-loss phases can be easily identified as intervals in which EW(Hα) > 0.
-
Orbital separation and disk size. In Sect. 4.5, we showed a correlation between the periastron distance and the maximum measured value of EW(Hα). This relationship is similar to the one between the orbital period and EW(Hα) (Reig et al. 1997b; Reig 2007; Antoniou et al. 2009) or between the orbital separation and the size of the circumstellar disk (Coe & Kirk 2015). In all these diagrams, the larger the orbital size (i.e. orbital period, periastron or distance between the components), the larger the EW(Hα). Since the equivalent width is directly related to the size of the disk (see Sect. 4.9), these correlations imply that large disks can only develop in systems in which the two components are well apart. In systems with small orbital separation, the tidal torque exerted by the neutron star prevents the disk from expanding.
5.2. BeXB versus classical Be stars
-
On average, BeXBs have denser disks. In Sect. 4.8 (see also Reig et al. 2000; Zamanov et al. 2001), we showed that the disks in BeXB are at least 1.5 times denser than disks in isolated Be stars. These results find theoretical confirmation in the work by Okazaki et al. (2002). Using a 3D, smoothed particle hydrodynamics code Okazaki et al. (2002) studied the viscous effect on the interaction between the Be star’s disk and the neutron star and find that, owing to truncation, the material decreted from the Be star accumulates and the disk becomes denser more rapidly than in isolated Be stars.
-
On average, BeXBs have smaller disks. In Sects. 4.6 and 4.9 (see also Reig et al. 1997b), we showed that, on average, classical Be stars have larger Hα equivalent widths, hence larger disks. A Kolmogorov-Smirnov test of the two populations gives a probability of 3.4% that they are drawn from the same population. A similar result was found between the isolated Be stars and BeXBs in the Small Magellanic Cloud, with a probability of 0.9% that they are drawn from the same population (Coe & Kirk 2015).
-
BeXBs have shorter V/R quasiperiods. The period of long-term V/R variations is typically in the range 5–10 yr for isolated Be stars, with a statistical average of ~7 years (Okazaki 1991, 1997). In contrast, the V/R quasiperiods of BeXB are significantly shorter (<5 yr). Oktariani & Okazaki (2009) find that the one-armed oscillations are well confined in systems with disks larger than a few tens of stellar radii. In such systems, the oscillation period scarcely depends on the binary parameters. On the other hand, in systems with smaller disks, where mode confinement is incomplete, the oscillation period increases with increasing orbital separation and/or decreasing binary mass ratio. The trend of shorter periods in smaller systems is mainly due to the fact that the tidal field is stronger in smaller systems. The difference in V/R quasiperiods between classical Be stars and BeXBs can be explained by the smaller size of the Be star’s disks in BeXB systems (see Sect. 4.9).
6. Conclusion
We have investigated the long-term optical spectroscopic variability of the counterparts to high-mass X-ray binaries visible from the northern hemisphere. Our work represents the most complete optical spectroscopic study on the global properties of HMXBs, not only because of the number of systems included, but also because of the long monitoring baseline, cadence, and large amount of data analysed (1164 spectra of 20 sources).
We have focused on the variability of the Hα line since this feature is closely related to the conditions in the equatorial disk. We have shown that, as in classical Be stars, the disk in BeXB follows a Keplerian velocity distribution. The radius of the disk correlates with the Hα line equivalent width. Double peak profiles are found when the equivalent width is small, indicating a small disk. We have provided evidence for the truncation of the disk by the neutron star. This evidence is based on the correlation between variability timescales and the orbital period and on the different properties of disks in isolated Be stars and BeXBs.
We conclude that the interaction between the compact object and the Be-type star works in two directions: the massive companion provides the source of matter for accretion; the amount of matter captured and the way it is captured (transfer mechanism) change the physical conditions of the neutron star (e.g. by spinning it up or down and shrinking or expanding the magnetosphere). But also, the continuous revolution of the neutron star around the optical counterpart produces observable effects, the most important of which is the truncation of the Be star’s equatorial disk.
Progress in understanding the interaction between the neutron star and the circumstellar disk requires long-term monitoring campaigns to probe the disk variability timescales (months to years). Small and medium size telescopes are ideal for this type of study.
Note that we use the average of the square of the errors while Jones et al. (2011) calculated the square of the average error as the internal variance.
Although a full absorption profile was not observed in the Hα line of RX J0440.9+4431, a disk-loss episode is likely to have occurred in early 2001, when there is a gap of about ten months in the observations (see discussion in Reig et al. 2005). In Fig. 3, this source is the filled black circle that lies closer to the triangle symbols.
Although some BeXBs may show multi-peaked structures, these peaks normally appear on the top of the line and are observed at very high resolution (Moritani et al. 2013). The multi-peaked profiles that we observe in the SGXBs of our list show peaks or absorption features not only on the top but also on the flanks of the line.
Count rates were converted into flux by taking into account the count rate to flux conversion factors of the two instruments (1 mCrab corresponds to 0.075 ASM count s-1 and to 0.00022 BAT count cm-2 s-1) and assuming that 1 Crab equals ~2.4 × 10-8 erg s-1 cm-2 in the 2–10 keV and ~1.3 × 10-8 erg s-1 cm-2 in the 15–50 keV band. The conversion factors were taken from http://www.dsf.unica.it/~riggio/calcs.html, based on Kirsch et al. (2005).
Note that in Reig & Fabregat (2015) there is an erratum, Ṁ should read 5.4 × 1016 g s-1 instead of 2.7 × 1017 g s-1. This does not affect the conclusion stated therein because the subsequent calculations are correct.
Acknowledgments
Skinakas Observatory is a collaborative project of the University of Crete and the Foundation for Research and Technology-Hellas. This paper uses observations made at the South African Astronomical Observatory (SAAO) and data products produced by the OIR Telescope Data Center, supported by the Smithsonian Astrophysical Observatory. We thank observers P. Berlind and M. Calkins for performing the FLWO observations. This work was supported in part by the European Union Marie Curie grant MTKD-CT-2006-039965 and EU FP7 Capacities GA No206469. A.Z. acknowledges funding from the European Research Council under the European Union’s Seventh Framework Programme (FP/2007–2013)/ERC Grant Agreement No. 617001. During the period of this work AZ has also been supported by the Chandra grant GO3-14051X, NASA ADAP grant NNX12AN05G, NASA LTSA grant NAG5-13056, and the EU IRG grant 224878. This work used NASA’s Astrophysics Data System Bibliographic Services and of the SIMBAD database, operated at the CDS, Strasbourg, France. The WHT and its service programme (service proposal references SW2012b14 and SW2013a19) are operated on the island of La Palma by the Isaac Newton Group in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias. Swift/BAT transient monitor results provided by the Swift/BAT team. Quick-look results provided by the ASM/RXTE team.
References
- Andrillat, A., Jaschek, M., & Jaschek, C. 1990, A&AS, 84, 11 [NASA ADS] [Google Scholar]
- Antoniou, V., Hatzidimitriou, D., Zezas, A., & Reig, P. 2009, ApJ, 707, 1080 [NASA ADS] [CrossRef] [Google Scholar]
- Aragona, C., McSwain, M. V., Grundstrom, E. D., et al. 2009, ApJ, 698, 514 [NASA ADS] [CrossRef] [Google Scholar]
- Baykal, A., Inam, S. Ç., Stark, M. J., et al. 2007, MNRAS, 374, 1108 [NASA ADS] [CrossRef] [Google Scholar]
- Bessell, M. S., Castelli, F., & Plez, B. 1998, A&A, 333, 231 [NASA ADS] [Google Scholar]
- Blay, P., Negueruela, I., Reig, P., et al. 2006, A&A, 446, 1095 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caballero-Garcia, M. D., Camero-Arranz, A., Ozbey Arabaci, M., et al. 2016, A&A, 589, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carciofi, A. C. 2011, in IAU Symp. 272, eds. C. Neiner, G. Wade, G. Meynet, & G. Peters, 325 [Google Scholar]
- Carciofi, A. C., & Bjorkman, J. E. 2006, ApJ, 639, 1081 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, J. S., Tarasov, A. E., Steele, I. A., et al. 1998, MNRAS, 294, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, J. S., Lyuty, V. M., Zaitseva, G. V., et al. 1999, MNRAS, 302, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, J. S., Tarasov, A. E., Okazaki, A. T., Roche, P., & Lyuty, V. M. 2001, A&A, 380, 615 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coe, M. J., & Kirk, J. 2015, MNRAS, 452, 969 [NASA ADS] [CrossRef] [Google Scholar]
- Coe, M. J., Everall, C., Norton, A. J., et al. 1993, MNRAS, 261, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Coe, M. J., Fabregat, J., Negueruela, I., Roche, P., & Steele, I. A. 1996, MNRAS, 281, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Coe, M. J., Reig, P., McBride, V. A., Galache, J. L., & Fabregat, J. 2006, MNRAS, 368, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Dachs, J., Hanuschik, R., Kaiser, D., & Rohe, D. 1986, A&A, 159, 276 [NASA ADS] [Google Scholar]
- Dachs, J., Hummel, W., & Hanuschik, R. W. 1992, A&AS, 95, 437 [NASA ADS] [Google Scholar]
- Delgado-Martí, H., Levine, A. M., Pfahl, E., & Rappaport, S. A. 2001, ApJ, 546, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Dubus, G. 2013, A&ARv, 21, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Fabregat, J., & Torrejon, J. M. 1998, A&A, 332, 643 [NASA ADS] [Google Scholar]
- Fabricant, D., Cheimets, P., Caldwell, N., & Geary, J. 1998, PASP, 110, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrigno, C., Farinelli, R., Bozzo, E., et al. 2013, A&A, 553, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galloway, D. K., Morgan, E. H., & Levine, A. M. 2004, ApJ, 613, 1164 [NASA ADS] [CrossRef] [Google Scholar]
- Gkouvelis, L., Fabregat, J., Zorec, J., et al. 2016, A&A, in press, DOI: 10.1051/0004-6361/201527090 [Google Scholar]
- González-Galán, A. 2015, Ph.D. Thesis, ArXiv e-prints [arXiv:1503.01087] [Google Scholar]
- Gorrod, M. J., Coe, M. J., Fabregat, J., Kastner, J. H., & Spinoglio, L. 1993, Ap&SS, 208, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Grundstrom, E. D., & Gies, D. R. 2006, ApJ, 651, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Grundstrom, E. D., Blair, J. L., Gies, D. R., et al. 2007, ApJ, 656, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Haigh, N. J., Coe, M. J., Steele, I. A., & Fabregat, J. 1999, MNRAS, 310, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Haigh, N. J., Coe, M. J., & Fabregat, J. 2004, MNRAS, 350, 1457 [NASA ADS] [CrossRef] [Google Scholar]
- Hanuschik, R. W. 1986, A&A, 166, 185 [NASA ADS] [Google Scholar]
- Hanuschik, R. W. 1987, A&A, 173, 299 [NASA ADS] [Google Scholar]
- Hanuschik, R. W. 1989, Ap&SS, 161, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Hanuschik, R. W. 1995, A&A, 295, 423 [NASA ADS] [Google Scholar]
- Hanuschik, R. W., Kozok, J. R., & Kaiser, D. 1988, A&A, 189, 147 [NASA ADS] [Google Scholar]
- Huang, S.-S. 1972, ApJ, 171, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Hummel, W., & Vrancken, M. 1995, A&A, 302, 751 [NASA ADS] [Google Scholar]
- in ’t Zand, J. J. M., Baykal, A., & Strohmayer, T. E. 1998, ApJ, 496, 386 [NASA ADS] [CrossRef] [Google Scholar]
- in’t Zand, J. J. M., Swank, J., Corbet, R. H. D., & Markwardt, C. B. 2001, A&A, 380, L26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Janot-Pacheco, E., Motch, C., & Mouchet, M. 1987, A&A, 177, 91 [NASA ADS] [Google Scholar]
- Jaschek, C., & Jaschek, M. 1992, A&AS, 95, 535 [NASA ADS] [Google Scholar]
- Jones, C. E., Tycner, C., & Smith, A. D. 2011, AJ, 141, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Kirsch, M. G., Briel, U. G., Burrows, D., et al. 2005, in UV, X-Ray, and Gamma-Ray Space Instrumentation for Astronomy XIV, ed. O. H. W. Siegmund, SPIE Conf. Ser., 5898, 22 [Google Scholar]
- Li, H., Yan, J., Zhou, J., & Liu, Q. 2014, AJ, 148, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Lutovinov, A., Tsygankov, S., & Chernyakova, M. 2012, MNRAS, 423, 1978 [NASA ADS] [CrossRef] [Google Scholar]
- Marcu-Cheatham, D. M., Pottschmidt, K., Kühnel, M., et al. 2015, ApJ, 815, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Martins, F., Schaerer, D., & Hillier, D. J. 2005, A&A, 436, 1049 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martin, R. G., Nixon, C., Armitage, P. J., Lubow, S. H., & Price, D. J. 2014, ApJ, 790, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Masetti, N., Orlandini, M., Marinoni, S., & Santangelo, A. 2005, ATel, 388, 1 [NASA ADS] [Google Scholar]
- Meilland, A., Stee, P., Vannier, M., et al. 2007, A&A, 464, 59 [Google Scholar]
- Moritani, Y., Nogami, D., Okazaki, A. T., et al. 2013, PASJ, 65, 83 [NASA ADS] [Google Scholar]
- Negueruela, I. 2007, in Massive Stars in Interactive Binaries, eds. N. St.-Louis, & A. F. J. Moffat, ASP Conf. Ser., 367, 477 [Google Scholar]
- Negueruela, I., & Okazaki, A. T. 2001, A&A, 369, 108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Negueruela, I., Grove, J. E., Coe, M. J., et al. 1997, MNRAS, 284, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Negueruela, I., Reig, P., Coe, M. J., & Fabregat, J. 1998, A&A, 336, 251 [NASA ADS] [Google Scholar]
- Negueruela, I., Roche, P., Fabregat, J., & Coe, M. J. 1999, MNRAS, 307, 695 [NASA ADS] [CrossRef] [Google Scholar]
- Negueruela, I., Okazaki, A. T., Fabregat, J., et al. 2001, A&A, 369, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Norton, A. J., Coe, M. J., Estela, A., et al. 1991, MNRAS, 253, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Okazaki, A. T. 1991, PASJ, 43, 75 [NASA ADS] [Google Scholar]
- Okazaki, A. T. 1997, A&A, 318, 548 [NASA ADS] [Google Scholar]
- Okazaki, A. T. 2001, PASJ, 53, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Okazaki, A. T., & Negueruela, I. 2001, A&A, 377, 161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Okazaki, A. T., Bate, M. R., Ogilvie, G. I., & Pringle, J. E. 2002, MNRAS, 337, 967 [NASA ADS] [CrossRef] [Google Scholar]
- Okazaki, A. T., Hayasaki, K., & Moritani, Y. 2013, PASJ, 65, 41 [NASA ADS] [Google Scholar]
- Oktariani, F., & Okazaki, A. T. 2009, PASJ, 61, 57 [NASA ADS] [Google Scholar]
- Özbey Arabacı, M., Camero-Arranz, A., Zurita, C., et al. 2015, A&A, 582, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paul, B., & Naik, S. 2011, Bull. Astron. Soc. India, 39, 429 [NASA ADS] [Google Scholar]
- Porter, J. M. 1996, MNRAS, 280, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Quirrenbach, A., Bjorkman, K. S., Bjorkman, J. E., et al. 1997, ApJ, 479, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Raichur, H., & Paul, B. 2010, MNRAS, 406, 2663 [NASA ADS] [CrossRef] [Google Scholar]
- Reig, P. 2007, MNRAS, 377, 867 [NASA ADS] [CrossRef] [Google Scholar]
- Reig, P. 2011, Ap&SS, 332, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Reig, P., & Fabregat, J. 2015, A&A, 574, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reig, P., & Nespoli, E. 2013, A&A, 551, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reig, P., & Zezas, A. 2014, A&A, 561, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reig, P., Chakrabarty, D., Coe, M. J., et al. 1996, A&A, 311, 879 [NASA ADS] [Google Scholar]
- Reig, P., Coe, M. J., Stevens, J. B., et al. 1997a, in The Transparent Universe, eds. C. Winkler, T. J.-L. Courvoisier, & P. Durouchoux, ESA SP, 382, 175 [Google Scholar]
- Reig, P., Fabregat, J., & Coe, M. J. 1997b, A&A, 322, 193 [NASA ADS] [Google Scholar]
- Reig, P., Fabregat, J., Coe, M. J., et al. 1997c, A&A, 322, 183 [NASA ADS] [Google Scholar]
- Reig, P., Negueruela, I., Coe, M. J., et al. 2000, MNRAS, 317, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Reig, P., Negueruela, I., Fabregat, J., Chato, R., & Coe, M. J. 2005, A&A, 440, 1079 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reig, P., Larionov, V., Negueruela, I., Arkharov, A. A., & Kudryavtseva, N. A. 2007, A&A, 462, 1081 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reig, P., Zezas, A., & Gkouvelis, L. 2010, A&A, 522, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Riquelme, M. S., Torrejón, J. M., & Negueruela, I. 2012, A&A, 539, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rivinius, T., Štefl, S., & Baade, D. 2006, A&A, 459, 137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rivinius, T., Carciofi, A. C., & Martayan, C. 2013, A&ARv, 21, 69 [Google Scholar]
- Roche, P., Coe, M. J., Everall, C., et al. 1993a, A&AS, 97, 277 [NASA ADS] [Google Scholar]
- Roche, P., Coe, M. J., Fabregat, J., et al. 1993b, A&A, 270, 122 [NASA ADS] [Google Scholar]
- Roche, P., Larionov, V., Tarasov, A. E., et al. 1997, A&A, 322, 139 [NASA ADS] [Google Scholar]
- Sarty, G. E., Kiss, L. L., Huziak, R., et al. 2009, MNRAS, 392, 1242 [NASA ADS] [CrossRef] [Google Scholar]
- Stoyanov, K. A., Zamanov, R. K., Latev, G. Y., Abedin, A. Y., & Tomov, N. A. 2014, Astron. Nachr., 335, 1060 [NASA ADS] [CrossRef] [Google Scholar]
- Tokarz, S. P., & Roll, J. 1997, in Astronomical Data Analysis Software and Systems VI, eds. G. Hunt, & H. Payne, ASP Conf. Ser., 125, 140 [Google Scholar]
- Tsygankov, S. S., Lutovinov, A. A., & Serber, A. V. 2010, MNRAS, 401, 1628 [NASA ADS] [CrossRef] [Google Scholar]
- Tycner, C., Lester, J. B., Hajian, A. R., et al. 2005, ApJ, 624, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Unger, S. J., Roche, P., Negueruela, I., et al. 1998, A&A, 336, 960 [NASA ADS] [Google Scholar]
- Vaughan, S., Edelson, R., Warwick, R. S., & Uttley, P. 2003, MNRAS, 345, 1271 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, C. A., Finger, M. H., Coe, M. J., Laycock, S., & Fabregat, J. 2002, ApJ, 570, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, C. A., Weisskopf, M. C., Finger, M. H., et al. 2005, ApJ, 622, 1024 [NASA ADS] [CrossRef] [Google Scholar]
- Zamanov, R. K., Reig, P., Martí, J., et al. 2001, A&A, 367, 884 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ziolkowski, J. 2002, Mem. Soc. Astron. It., 73, 1038 [NASA ADS] [Google Scholar]
Appendix A: Data
The following tables provide the equivalent width of the Hα line, the type of the Hα profile, and the telescope used for the sources analysed in this work. Our optical spectroscopic monitoring programme of BeXB systems started in 1999 using the 1.3 m telescope of the Skinakas Observatory. During the period 2007–2014, the targets were also regularly observed from the 1.5 m of the Fred Lawrence Whipple Observatory. The star symbol in some of the observations taken from SKO and FLWO indicates that the grating with 2400 l mm-1 and 600 l mm-1 was used instead of the default set-up of 1302 l mm-1 and 1200 l mm-1 gratings, respectively (see Sect. 2). The identification of the line profile is as follows (see Sect. 4.7): absorption (AB), single-peak (SP), fill-in (FI), double-peak (DP), multi-peak (MP), shell (SH), and P Cygni (PC).
Although the observations from Skinakas and Fred Lawrence Whipple observatories represent the main bulk of data used in this work, we complemented these data with older observations made in the framework of the Southampton/Valencia collaboration. Those observations were made with a variety of telescopes as indicated in the tables.
The identification of the telescopes is as follows: 1.3 m Skinakas Observatory (SKO), 1.5 m Fred Lawrence Wripple Observatory (FLWO), 4.2 m William Herschel Telescope (WHT), 2.5 m Isaac Newton Telescope (INT), 1.0 m Jacobus Kapteyn Telescope (JKT), 2.5 m Nordic Optical Telescope (NOT), 1.9 m South Africa Astronomical Observatory (SAAO), 1.5 m at Palomar Mountain (PAL), and 2.2 m telescope at Calar Alto (CAL), 2.1 m telescope of Kitt Peak National Observatory (KPNO).
Results for 2S 0114+65.
Results for 4U 0115+63.
Results for IGR J01363+6610.
Results for RX J0146.9+6121.
Results for IGR J01583+6713.
Results for RX J0240.4+6112.
Results for V 0332+53.
Results for X Per.
Results for RX J0440.9+4431.
Results for 1A 0535+262.
Results for IGR J06074+2205.
Results for AX J1845.0-0433.
Results for 4U 1907+09.
Results for XTE J1946+274.
Results for KS 1947+300.
Results for GRO J2058+42.
Results for SAX J2103.5+4545.
Results for IGR J21343+4738.
Results for 4U 2206+54.
Results for SAX J2239.3+6116.
All Tables
Average, standard deviation, minimum, and maximum values of the Hα equivalent width. Also indicated is the number of spectra analysed. Negative values of the equivalent width mean emission profiles.
Linear regression between the peak separation and the equivalent width of the Hα line.
All Figures
 |
Fig. 1 Evolution of the Hα equivalent width of the BeXBs considered in this work, ordered by increasing value of the orbital period (see Table 1). The orbital period of the four sources at the bottom is not known. |
| In the text | |
 |
Fig. 2 Evolution of the Hα equivalent width of wind-fed sources. |
| In the text | |
 |
Fig. 3 Fractional amplitude of variability of the optical continuum (V band) and Hα line. Black filled circles: BeXBs that have gone through a disk-loss phase; blue empty circles: BeXBs with stable disks; red triangles: other BeXBs; green empty squares: wind-fed accreting systems. |
| In the text | |
 |
Fig. 4 Hα equivalent width variability as a function of the orbital period in BeXBs with orbital solutions. The Y-axis is the average ratio of the standard deviation over the mean calculated in intervals of 500 days (or 1000 days for XTE J1946+274, cross). Empty circles correspond to peculiar systems (see text). |
| In the text | |
 |
Fig. 5 Disk growth rates as a function of orbital period. The solid line represents the best-fit to a power-law function. |
| In the text | |
 |
Fig. 6 Correlation between the periastron distance and the largest value of EW(Hα). |
| In the text | |
 |
Fig. 7 Comparison of the EW(Hα) in classical Be stars (black line) and BeXB (blue dashed hatched histograms). The data for the classical Be stars come from the IPHAS sample and comprises 219 stars with spectral types between O9 and B3. The data for BeXBs are from this work. |
| In the text | |
 |
Fig. 8 Representative Hα profiles in SGXBs: left: multipeak profile observed in AX J1845.0-0433; right: P Cygni profile observed in 2S 0114+65. |
| In the text | |
 |
Fig. 9 Representative double-peak Hα profiles in BeXB (from RX J0440.9+4431). |
| In the text | |
 |
Fig. 10 Variability of the Hα line profile quantified as the log (V/R), where V and R are the intensity of the left and right peaks. Arrows indicate the occurrence of large X-ray outbursts. |
| In the text | |
 |
Fig. 11 Correlation between the peak separation and the Hα equivalent width for six BeXBs. The line represents the best fit to a linear regression (see Table 5). The scale of the axes was the same in all plots to facilitate comparison. |
| In the text | |
 |
Fig. 12 Relationship between the peak separation and the Hα equivalent width. The solid and dashed line represents the average behaviour of 30 classical Be stars with spectral type in the range O9–B3 (Gkouvelis et al., in prep.) and 93 Be stars of all spectral types (Hanuschik 1989), respectively. BeXBs lie systematically above the Be stars’ lines. |
| In the text | |
 |
Fig. 13 Relationship between Hα equivalent width and disk radius. |
| In the text | |
 |
Fig. 14 Hα equivalent width and X-ray variability. The light curves of the RXTE/ASM (2–10 keV) in black and the Swift/BAT (15–50 keV) in red were rebinned to 5-day bins. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


