| Issue |
A&A
Volume 590, June 2016
|
|
|---|---|---|
| Article Number | A22 | |
| Number of page(s) | 12 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201527877 | |
| Published online | 29 April 2016 | |
Spiral-driven accretion in protoplanetary discs
II. Self-similar solutions
1
Laboratoire AIM, Paris-Saclay, CEA/IRFU/SAp – CNRS – Université Paris
Diderot, 91191
Gif-sur-Yvette Cedex,
France
e-mail: patrick.hennebelle@cea.fr
2
LERMA (UMR CNRS 8112), École Normale Supérieure, 75231
Paris Cedex,
France
3
Univ. Grenoble Alpes, IPAG, 38000
Grenoble,
France
4
CNRS, IPAG, 38000
Grenoble,
France
Received:
2
December
2015
Accepted:
4
February
2016
Context. Accretion discs are ubiquitous in the Universe, and it is crucial to understand how angular momentum and mass are radially transported in these objects.
Aims. Here, we study the role played by non-linear spiral patterns within hydrodynamical and non-self-gravitating accretion discs assuming that external disturbances such as infall onto the disc may trigger them.
Methods. To do so, we computed self-similar solutions that describe discs in which a spiral wave propagates. These solutions present shocks and critical sonic points that were analyzed.
Results. We calculated the wave structure for all allowed temperatures and for several spiral shocks. In particular, we inferred the angle of the spiral pattern, the stress it exerts on the disc, and the associated flux of mass and angular momentum as a function of temperature. We quantified the rate of angular momentum transport by means of the dimensionless α parameter. For the thickest disc we considered (corresponding to h/r values of about one-third), we found values of α as high as 0.1 that scaled with the temperature T such that α ∝ T3 / 2 ∝ (h/r)3. The spiral angle scales with the temperature as arctan(r/h).
Conclusions. These solutions suggests that perturbations occurring at disc outer boundaries, such as perturbations due to infall motions, can propagate deep inside the disc and therefore should not be ignored, even when considering small radii.
Key words: protoplanetary disks / instabilities / hydrodynamics / accretion, accretion disks
© ESO, 2016
1. Introduction
Accretion discs play a major role in astrophysics because they are ubiquitously observed around stars and black holes. A central question regarding disc evolution obviously is how angular momentum and mass are transported radially in reasonably short times (e.g. Pringle 1981). It is widely admitted that local instabilities such as the magneto-rotational instability (MRI, e.g. Balbus 2003) or the gravitational instability (e.g. Lodato & Rice 2004) are responsible for triggering the transport of momentum and mass. Alternatively, winds emitted by magnetic processes into the disc may carry away angular momentum (Turner et al. 2014). While it is now widely accepted that such instabilities and wind launching lead to efficient transport, the conditions under which they operate are still the focus of active research. For example, it is still a matter of debate whether protoplanetary (PP) discs are always sufficiently ionised (e.g. Lesur et al. 2014).
The main effect of these instabilities is to trigger either non-axisymmetric motions or magnetic field configurations within the discs, which in turn exert a torque on the gas and lead to an outward flux of angular momentum. For simplicity reasons, accretion discs have been studied in isolation most of the time, generally starting with discs at equilibrium. A notable exception are the studies that have addressed the question of disc formation in the context of molecular core collapse. In that case, the discs are usually massive and self-gravitating, and it is generally admitted that angular momentum can then be transported by gravitational torques or by magnetic braking (e.g. Vorobyov & Basu 2008; Machida et al. 2010; Joos et al. 2012; Li et al. 2013; Vorobyov et al. 2015). The importance of pressure exerted at the accretion shock on the fragmentation of self-gravitating discs within dense cores was also stressed by Hennebelle et al. (2004) in this context (see also Harsono et al. 2011).
The possible specific role that external accretion may have on more evolved accretion discs has received much less attention, and only a few studies have investigated its effect in detail. This includes in particular the analytical study of Spruit (1987), who computed non-axisymmetric and stationary solutions with shocks (see also Larson 1990; Vishniac & Diamond 1989), and the numerical simulations performed by Sawada et al. (1987), Spruit et al. (1987), Rozyczka & Spruit (1993) and Yukawa et al. (1997), who studied the effect of external accretion on mass and angular momentum transport within the disc of a mass-transferring binary system. In this last case, since accretion is due to the companion of the accreting object, it constitutes an obvious cause for the disc to be maintained in a non-axisymmetric state on long timescales, possibly resulting in a significant torque within the system. Indeed, all these studies show that accretion is a possible powerful source of symmetry breaking and results in an efficient mass transfer.
In the context of PP discs, the possible effect of accretion has been described by Padoan et al. (2005), Throop & Bally (2008), Klessen & Hennebelle (2010), Padoan et al. (2014), who noted either from measuring the accretion rate Ṁd onto the disc itself from simulations or from using analytical arguments that 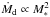 , where M∗ is the mass of the star. This relation is very similar to what can be inferred for the accretion rate Ṁ onto the young stars themselves (e.g. Muzerolle et al. 2005) and suggests that accretion onto PP discs and accretion onto the star are related in some way. We note that recent results indicate a weaker relation with
, where M∗ is the mass of the star. This relation is very similar to what can be inferred for the accretion rate Ṁ onto the young stars themselves (e.g. Muzerolle et al. 2005) and suggests that accretion onto PP discs and accretion onto the star are related in some way. We note that recent results indicate a weaker relation with 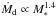 (Venuti et al. 2014), which may therefore weaken this argument. However (Venuti et al. 2014) also find an anti-correlation between the accretion rate and the age of the source that is broadly compatible with the idea that infall onto the disc may trigger accretion since infall is likely to decrease with time as well. Recently, Vorobyov et al. (2015; see also Harsono et al. 2011; Bae et al. 2015) performed a series of 2D simulations of self-gravitating and viscous discs embedded in their parent cores and showed that the infall of material, and particularly its specific angular momentum content, has a dramatic effect on their evolution.
(Venuti et al. 2014), which may therefore weaken this argument. However (Venuti et al. 2014) also find an anti-correlation between the accretion rate and the age of the source that is broadly compatible with the idea that infall onto the disc may trigger accretion since infall is likely to decrease with time as well. Recently, Vorobyov et al. (2015; see also Harsono et al. 2011; Bae et al. 2015) performed a series of 2D simulations of self-gravitating and viscous discs embedded in their parent cores and showed that the infall of material, and particularly its specific angular momentum content, has a dramatic effect on their evolution.
In most of these studies, the exact role played by accretion is not straightforward to identify since other processes (such as self-gravity and/or explicit viscosity) are generally considered (e.g. Vorobyov et al. 2015). In addition, the accretion fluxes that are considered usually correspond to rapidly accreting system such as class 0 or class I embedded protostars. However, investigating the exact role of accretion alone is important because i) it is mandatory to distinguish between the various mechanisms to separate their respective contributions; and ii) there are objects for which the role of other mechanisms remains debated, such as low-mass protoplanetary discs. It is therefore important to quantify the possible effect that external accretion onto the disc could have, and in particular, whether it could trigger a flux of mass down to the star.
As a first step toward solving this question, we recently performed a series of 2D numerical simulations (Lesur et al. 2015, see also Bae et al.2015) to investigate the transport that is triggered by infalling material within a disc that is both unmagnetized and non-self-gravitating. We have found that the infalling flow generates very significant disturbances at the outer edge of the disc: when quantified in terms of the classical α parameter (Eq. (39)) and for typical accretion rate of 10-7M⊙ yr-1, they lead to α ~ 10-2. Moreover, at small radii, the effective α does not go to zero, but instead seems to reach a plateau with values of about a few times 10-4. These important results therefore open up the possibility that external disturbances propagate through the disc and generate angular momentum transport even at small radii.
As the physical understanding leading to such a behaviour remains to be clarified, it is useful to study analytical solutions. This is the aim of the present paper, where we re-visit and extend the self-similar solutions of non-axisymmetric stationary flows studied by Spruit (1987). In these solutions, there is no explicit viscosity, and the necessary dissipation is provided by shocks. Such solutions provide a simple framework and give a strong indication of the physics at play in large-scale accretion-driven discs. Section 2 presents the formalism and the method we used to solve the equations. Particular emphasis is given to the nature and the role played by the critical or transonic points present in the flow, which plays an important role in understanding their mathematical nature. In Sect. 3 we study the physical properties of these solutions as a function of the disc temperature and discuss the implications. Section 4 concludes the paper.
2. Self-similar solutions of externally driven accretion
Following Spruit (1987), we searched for self-similar solutions that could describe the mass and angular momentum flux within a disc that would result from a non-axisymmetry induced by an external influence such as non-axisymmetric accretion onto the disc. The existence of these solutions is important to establish since it suggests that spiral modes indeed exist and can propagate from large radii down to small ones. Our solutions, although close to the case investigated by Spruit (1987), are nevertheless different. First of all, Spruit (1987) included radiation at the surface of the disc (assuming an appropriate spatial dependence for the opacity), while we restrict the discussion to locally isothermal discs. This is indeed a more realistic approximation for PP discs and has been used by many authors in numerical simulations. This particular point is important since Spruit (1987) found a significant dependence on γ, the adiabatic index, and it is thus important to clarify the effect that the effective equation of state has on the behaviour of the solution. In particular, within the limit where γ → 1, the spiral angle seems to converge towards a value close to 90 deg (see Fig. 2 of Spruit 1987). Since PP discs are typically locally isothermal, the question arises whether such a mode could develop and whether it could lead to significant transport. Second, we explicitly give the dependence of various quantities as a function of the gas temperature, while Spruit (1987) focused on the dependence on γ. Third, we find that there are two (instead of one as found by Spruit 1987) possible choices for the disc surface density radial profiles. While similar in nature, the two families of solutions differ in an important manner, since they correspond to the two limiting cases of vanishing angular momentum flux and vanishing mass flux. Fourth, we clarify the mathematical nature of the solutions and in particular the topology of the critical points, which play a key role for these solutions. It is important to solve the equations numerically. Finally, we describe a simple method to obtain these solutions that may serve as reference to compare them with simulations and observational results.
2.1. Ordinary equations for self-similar solutions
The equations we solve are the usual fluid equations. Written in cylindrical geometry, averaged along the z-direction over the disc scale height, h, and assuming stationarity, they write 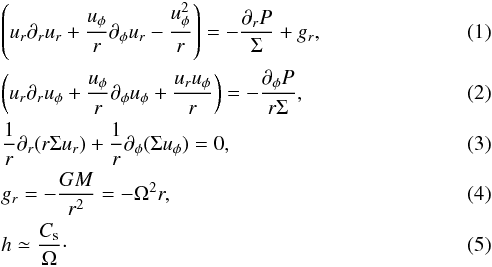 The disc is assumed to be locally isothermal, meaning that P = Cs(r)2Σ, that is to say, the sound speed, Cs, and the temperature, T, depend only on the radius, r. We note that P is the vertically averaged pressure, Σ ≃ 2hρ is the column density, and ρ is the midplane density. All the other quantities have their usual meaning. Since no explicit dissipation is considered here, the solutions must necessarily entail shocks, which will then lead to finite energy dissipation. Angular momentum and mass transport imply such energy dissipation.
The disc is assumed to be locally isothermal, meaning that P = Cs(r)2Σ, that is to say, the sound speed, Cs, and the temperature, T, depend only on the radius, r. We note that P is the vertically averaged pressure, Σ ≃ 2hρ is the column density, and ρ is the midplane density. All the other quantities have their usual meaning. Since no explicit dissipation is considered here, the solutions must necessarily entail shocks, which will then lead to finite energy dissipation. Angular momentum and mass transport imply such energy dissipation.
To normalise the system, we use similar conventions as Spruit (1987), namely 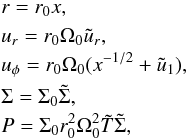 (6)where r0 and Σ0 are arbitrary radius and surface density,
(6)where r0 and Σ0 are arbitrary radius and surface density, 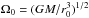 . In particular, r0Ω0x− 1 / 2 is simply the Keplerian velocity.
. In particular, r0Ω0x− 1 / 2 is simply the Keplerian velocity.
To obtain self-similar solutions, we introduce a new angular variable, ψ = φ + β(x), that is to say, the new angular variable shifts with respect to φ when r varies, and we look for solutions that can be written as f(x′,ψ) instead of f(x,φ). Using the definitions stated by Eqs. (6), Eqs. (1)−(3) become 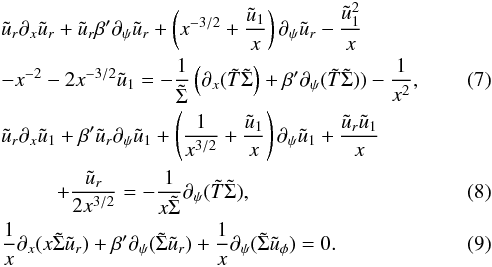 Finally, we seek for self-similar solutions in the radius, x and we set
Finally, we seek for self-similar solutions in the radius, x and we set 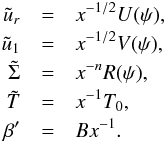 (10)The parameter B, which is equal to r∂rψ represents the tangent of θ, the angle between the spiral pattern and the radial direction. Inserting these expressions into Eqs. (7)−(9), we get
(10)The parameter B, which is equal to r∂rψ represents the tangent of θ, the angle between the spiral pattern and the radial direction. Inserting these expressions into Eqs. (7)−(9), we get 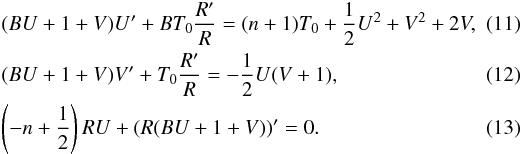 It is convenient to introduce the variables
It is convenient to introduce the variables 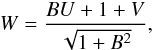 (14)which represents the velocity component normal to the spiral pattern and to the shock wave, and
(14)which represents the velocity component normal to the spiral pattern and to the shock wave, and 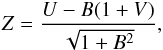 (15)which represents the velocity component parallel to the shock wave.
(15)which represents the velocity component parallel to the shock wave.
With these definitions, Eq. (13) can be rewritten as 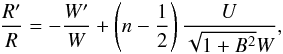 (16)and easily combines with Eqs. (11), (12), leading to
(16)and easily combines with Eqs. (11), (12), leading to 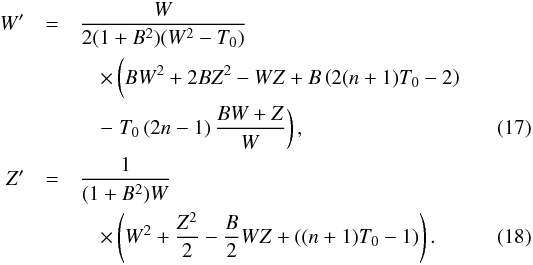 Equations (17), (18) are ordinary equations of W and Z. They present a critical point at
Equations (17), (18) are ordinary equations of W and Z. They present a critical point at 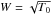 , that is to say, when the velocity perpendicular to the spiral pattern is equal to the sound speed. As discussed in the next session, the critical point, which must be crossed smoothly, plays an important role in obtaining these solutions.
, that is to say, when the velocity perpendicular to the spiral pattern is equal to the sound speed. As discussed in the next session, the critical point, which must be crossed smoothly, plays an important role in obtaining these solutions.
2.2. Boundary conditions
The boundary conditions are 2π periodic. However, we allow the disc to have several identical spiral arms, so we require that our solutions be 2π/m-periodic, where m is the number of spiral arms of the solution.
2.3. Conserved quantities
Conservation of mass and momentum in the disc leads to several constraints that have to be satisfied by the solutions. These constraints are of two types: jump conditions and integral conditions. These two types of conditions express the continuity of mass and momentum fluxes.
2.3.1. Jump conditions
As discussed above, since the solutions ought to describe transport of angular momentum and mass, there is unavoidably energy dissipation in the process. Because the equations do not entail any viscous terms, it implies that shocks must be present. Therefore the present solutions must satisfy Rankine-Hugoniot conditions through the shock, that is to say, the flux of mass and momentum must be continuous. This leads to 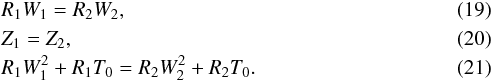 The last expression can be replaced by the relation
The last expression can be replaced by the relation 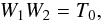 (22)where the subscripts 1 and 2 represent the pre- and post-shock material. To obtain this last relation, we can simply combine Eqs. (19) and (21).
(22)where the subscripts 1 and 2 represent the pre- and post-shock material. To obtain this last relation, we can simply combine Eqs. (19) and (21).
2.3.2. Integral conditions
Our disc model exhibits two important conservation equations, the conservation of mass (Eq. (13)) and the conservation of angular momentum 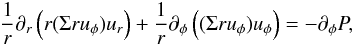 (23)which can easily be obtained by combining Eqs. (2), (3) and where, as before, stationarity is assumed and integration through the disc is performed. Using the self-similar variables, we obtain
(23)which can easily be obtained by combining Eqs. (2), (3) and where, as before, stationarity is assumed and integration through the disc is performed. Using the self-similar variables, we obtain 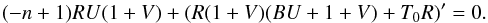 (24)Integrating Eqs. (13) and (24) between 0 and 2π/m, and making use of the periodic boundary conditions, we obtain the constraints
(24)Integrating Eqs. (13) and (24) between 0 and 2π/m, and making use of the periodic boundary conditions, we obtain the constraints 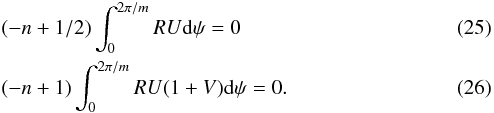 This implies that either the azimuthally averaged mass flux
This implies that either the azimuthally averaged mass flux 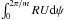 or the angular momentum flux
or the angular momentum flux 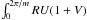 has to be zero. Although solutions with zero mass and angular momentum flux are a priori possible for arbitrary n (but probably do not satisfy Eq. (19)), we focus on more physical solutions: constant mass flux solutions with n = 1 / 2 (which corresponds to the choice made in Spruit 1987) or constant angular momentum flux solutions with n = 1. We note that since the temperature is proportional to 1 /r, this implies that the disc thickness, h ≃ Cs/ Ω ∝ r. Thus the density profile is ρ ∝ r− (n + 1) = r− 3 / 2 for n = 1 / 2 and ρ ∝ r-2 for n = 1.
has to be zero. Although solutions with zero mass and angular momentum flux are a priori possible for arbitrary n (but probably do not satisfy Eq. (19)), we focus on more physical solutions: constant mass flux solutions with n = 1 / 2 (which corresponds to the choice made in Spruit 1987) or constant angular momentum flux solutions with n = 1. We note that since the temperature is proportional to 1 /r, this implies that the disc thickness, h ≃ Cs/ Ω ∝ r. Thus the density profile is ρ ∝ r− (n + 1) = r− 3 / 2 for n = 1 / 2 and ρ ∝ r-2 for n = 1.
In the constant mass flux case (n = 1 / 2), we see from Eq. (13) that 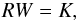 (27)where K is an arbitrary constant. In other words, the density variable R is inversely proportional to the velocity component perpendicular to the shock. This automatically ensures that Eq. (19) is satisfied. We note that since the present solutions are stationary, a mass flux through the disc implies that the central mass increases with time (as we show below, the flux is inwards, as expected).
(27)where K is an arbitrary constant. In other words, the density variable R is inversely proportional to the velocity component perpendicular to the shock. This automatically ensures that Eq. (19) is satisfied. We note that since the present solutions are stationary, a mass flux through the disc implies that the central mass increases with time (as we show below, the flux is inwards, as expected).
On the other hand, solutions with n = 1 present a flux of angular momentum through the disc, but no flux of mass. This implies that while the particle fluids move on closed orbits, angular momentum is transported radially during one cycle. Therefore this implies that a source of angular momentum must be present in the centre. What this source exactly represents physically can be debated. One possibility is that these solutions could represent regimes, limited in time, during which the inner part of the disc provides the corresponding amount of angular momentum. This is typically what happens in the context of the so-called dead disk as emphasized by Siuniaev & Shakura (1977) and D’Angelo & Spruit (2012), which can arise when a central object is magnetically coupled to the disc and exchanges angular momentum with it. While generally the solutions are time-dependent, in some circumstance a stationary regime has been inferred. The solutions, however, assume an axisymetric disc and use the α modelling. The present solutions may therefore offer a complementary description in which the mechanisms responsible for the angular momentum transport through the disc are explicitly described. It is also interesting to note that Siuniaev & Shakura (1977) predicted the column density of the dead disc to have n = 11 / 10, while it has n = 1 in our case. Similarly, the steady α disc has n = 3 / 4 while it is n = 1 / 2 for the self-similar non-axisymetric disc. For different values of n, the disc is probably not stationary1. The solutions corresponding to n = 1 would be limited in time since the amount of angular momentum that a star possesses is fairly limited. In this respect, another possible interesting application could be the circumbinary discs (Dubus et al. 2002).
Using Eq. (24) and n = 1, we obtain 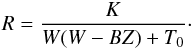 (28)With this expression, it is easy to show that Eq. (19) is automatically satisfied when conditions (20) and (21) are valid. Therefore these solutions are physically meaningful, at least in this respect.
(28)With this expression, it is easy to show that Eq. (19) is automatically satisfied when conditions (20) and (21) are valid. Therefore these solutions are physically meaningful, at least in this respect.
2.4. Critical point
The other constraint comes from the critical point that must be crossed smoothly. Since the existence of shocks connecting supersonic and subsonic regions is necessary, and since the solutions are 2π/m periodic, there must be a smooth transition between the subsonic and the supersonic regions, implying that crossing the critical point is unavoidable. Mathematically, this implies that both the numerator and the denominator of Eq. (17) must vanish at that location, leading to the two conditions 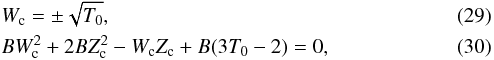 which gives
which gives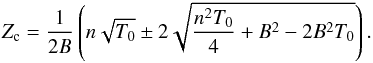 (31)This last equation reveals in particular that the condition
(31)This last equation reveals in particular that the condition 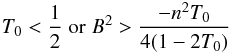 (32)must be satisfied for Zc to be real. Since discs are flat objects,
(32)must be satisfied for Zc to be real. Since discs are flat objects, 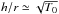 is expected to be small. Therefore, in practice, this condition does not restrict the values of B and T0.
is expected to be small. Therefore, in practice, this condition does not restrict the values of B and T0.
The consequence of the critical point is that throughout most of the possible parameter ranges, the critical point constitutes a constraint that must be fulfilled, thereby reducing by one the number of degrees of freedom of the system. We note that strictly speaking, a careful study of its topology is required to exactly understand the constraints it brings to the system (see Appendix A).
2.5. Numerical method
The problem we face consists of solving the two ordinary equations given by Eqs. (17), (18) between 0 and 2π/m. Mathematically, there are thus five independent parameters, the values W(0) and Z(0), and B, T0 and m. On the other hand, there are two constraints coming from the shock conditions and one from the critical point. This implies that there are two free parameters that should be varied. In the following we adopt the temperature, T0, and the mode number m as the free parameters and determine the values of B, W(0) and Z(0) that satisfy the three constraints. We note that some solutions may entail several non-identical shocks and could constitute a broader class of solutions than the periodic solutions considered here.
One difficulty in solving Eqs. (17), (18) is to treat the critical point, which, as described in Appendix A, is a saddle. To solve this system, we first introduce a new variable s as described in Appendix A. The new equations Eqs. (A.1)−(A.3) do not present any singularity, and we used these to perform the numerical integration with a standard Runge-Kutta integration. For this purpose we first specified a grid of the s variable in decreasing order. To initialise the solution, it is necessary to perform an expansion around the critical point as specified by Eqs. (A.4)−(A.6), in particular specifying the sign of dψ. The two other quantities δW and δZ are along the eigenvector of the negative eigenvalue. We performed two integrations, one toward the left (dψ< 0) and one toward the right (dψ> 0). We then integrated toward the right (left) until either ψ reaches the value 2π/m (−2π/m) or a stagnation point; in other words, until ψ starts to decrease (increase).
We then searched for pairs of points that i) were located at two different sides of the critical point and ii) satisfied the Rankine-Hugoniot conditions. To do so, we defined a norm, 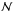 , given by
, given by 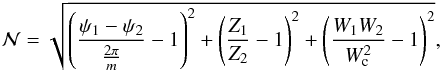 (33)and we then selected the pair of points that corresponds to the lowest value. Finally, we iterated on B, the spiral angle, using a simple bisection method, to minimise the norm. We used about 250 000 grid points for each of the two trajectories and required the iterations to stop when B varied by less than 10-5 with respect to the last iteration. We typically obtained a clear minimum of
(33)and we then selected the pair of points that corresponds to the lowest value. Finally, we iterated on B, the spiral angle, using a simple bisection method, to minimise the norm. We used about 250 000 grid points for each of the two trajectories and required the iterations to stop when B varied by less than 10-5 with respect to the last iteration. We typically obtained a clear minimum of 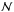 with values of about 10-5. To demonstrate that convergence has been reached, we also used 50 000 grid points instead. The corresponding norm is, as expected, larger, with values of about 10-4. The solutions obtained with these two numbers of grid points are nearly indistinguishable.
with values of about 10-5. To demonstrate that convergence has been reached, we also used 50 000 grid points instead. The corresponding norm is, as expected, larger, with values of about 10-4. The solutions obtained with these two numbers of grid points are nearly indistinguishable.
 |
Fig. 1 Mode m = 2 for n = 1 / 2 (left) and for n = 1 (right). Various fields for a series of temperatures equally spaced between T0 = 0.18 (corresponding to the curves with more pronounced variations) and T0 = 0.012 (corresponding to flatter curves). The red parts of the curve correspond to the subsonic and the blue parts to the supersonic regions. |
Finally, to show a fully analytical expression of the solutions, we present in Appendix C an approximated resolution that is valid at low temperature and high m.
3. Results
3.1. Sample of solutions
Figure 1 shows the m = 2 solutions for 15 temperature values equally spaced between 0.18 and 0.012 (the lowest temperatures correspond to the more uniform profiles). The left column corresponds to n = 1 / 2 and the right column to n = 1. The red part of the curves corresponds to the subsonic regions, while the blue part represents the supersonic part of the flow. The critical point is at the junction of the two. For high temperatures, all fields vary substantially, with ψ implying rather dynamical regimes. For example, the velocity perpendicular to the spiral pattern, W, becomes up to two times higher than the sound speed, while the azimuthal velocity, v, is as small as −0.7, implying that the gas then rotates at a velocity of about ≃ 0.3 times the Keplerian velocity (equal to 1 with these units). At the highest temperature, the density varies by a factor of about 4, while at lower temperatures (T0 ≃ a few 0.01), the variations present a much smaller amplitude. Typically, the radial velocity, W, varies by about 20% at these low temperatures, while the azimuthal velocity presents even smaller variations. These solutions therefore describe a flow that is close to rotational equilibrium. Interestingly, the radial velocity, U, changes sign typically around ψ ≃ 1. It is always negative in the subsonic region and positive at the end of the supersonic region. This structure is necessary to ensure an inward (outward) flow of matter (momentum) and a vanishing flow of angular momentum (mass). We discuss and quantify this point in Sect. 3.3. The shape of the two families of solutions (n = 1 / 2 and n = 1) remains altogether very similar. As discussed previously and confirmed below, the solutions are quite different in terms of global mass and angular momentum fluxes, however.
We also show the m = 5 modes in Appendix B.
3.2. Dependence of spiral angles on T0
Figure 2 displays the logarithm of the angle of the spiral pattern, B = tanθ, as a function of log (T0) for the m = 2−5 modes. At low temperatures, T0< 0.1, we find that 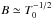 , meaning that the spiral pattern angle is inversely proportional to the local sound speed.
, meaning that the spiral pattern angle is inversely proportional to the local sound speed.
This can be easily understood in the weak shock regime, which is relevant in the limit T0 ≪ 1 (thin disc limit). In this limit, the shock front speed is equal to the sound speed Cs and the Keplerian rotation profile is barely perturbed by the presence of a shock. For the spiral shock to be stationary, the Keplerian velocity projected onto the normal to the shock has to be equal to the sound speed Cs(R) ≃ ΩRcos(θ), which can be transformed into 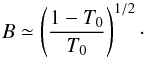 (34)Stiffer variations are found for higher temperatures where B increases more rapidly with T0, as expected from this simple linear analysis. Finally, the angle also slightly increases with the mode number, m.
(34)Stiffer variations are found for higher temperatures where B increases more rapidly with T0, as expected from this simple linear analysis. Finally, the angle also slightly increases with the mode number, m.
 |
Fig. 2 B = tanθ, the angle of the spiral pattern as a function of T0 for the four modes m = 2,3,4,and5. The top panel shows n = 1 / 2, the bottom panel n = 1. |
3.3. Mass flux and stress
3.3.1. Definitions
We now describe and quantify the global mass and momentum fluxes associated with these solutions. More precisely, we are interested in the flux of mass 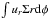 that we write as
that we write as 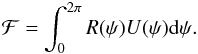 (35)It is known (e.g. Balbus & Papaloizou 1999) that the fluxes of mass and the stress are related to each other through the relation
(35)It is known (e.g. Balbus & Papaloizou 1999) that the fluxes of mass and the stress are related to each other through the relation 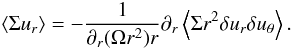 (36)In this expression, δur = ur − ⟨ur⟩, δuθ = uθ − ⟨uθ⟩ and Ω is the mean rotation value, Ω = ⟨uθ⟩ /r. While this relation is a good approximation in the general case (because it neglects a time-dependent term), we stress here that it is an exact relation in the present, stationary case. It must therefore be satisfied and constitutes a test for the accuracy of the numerical solutions.
(36)In this expression, δur = ur − ⟨ur⟩, δuθ = uθ − ⟨uθ⟩ and Ω is the mean rotation value, Ω = ⟨uθ⟩ /r. While this relation is a good approximation in the general case (because it neglects a time-dependent term), we stress here that it is an exact relation in the present, stationary case. It must therefore be satisfied and constitutes a test for the accuracy of the numerical solutions.
With the self-similar variables, Eq. (36) becomes 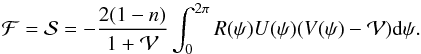 (37)where
(37)where 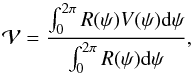 (38)is the mean value of V. While for n = 1 / 2 the coefficient 2(1 − n) is equal to 1, it is equal to 0 for n = 1, which indicates that in this latter case the mass flux should be zero, as discussed above.
(38)is the mean value of V. While for n = 1 / 2 the coefficient 2(1 − n) is equal to 1, it is equal to 0 for n = 1, which indicates that in this latter case the mass flux should be zero, as discussed above.
The quantity α is commonly described as given by 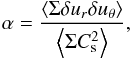 (39)which leads to
(39)which leads to 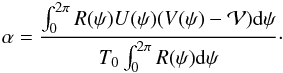 (40)In this last expression U is used instead of U − ⟨U⟩ since
(40)In this last expression U is used instead of U − ⟨U⟩ since 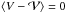 .
.
Finally, we also compute the flux of angular momentum through the disc, which as discussed before is expected to vanish for n = 1 / 2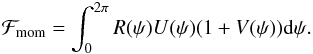 (41)We note that when n = 1, since the mass flux vanishes, ∫R(ψ)U(ψ)dψ = 0, we have the identity
(41)We note that when n = 1, since the mass flux vanishes, ∫R(ψ)U(ψ)dψ = 0, we have the identity 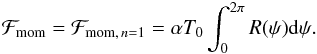 (42)This expression is valid only if the flux of mass vanishes.
(42)This expression is valid only if the flux of mass vanishes.
In the following section, we restrict our attention to α because all quantities depend on it.
 |
Fig. 3 α value for n = 1 / 2 (top panel) and n = 1 (bottom panel) as a function of T0 for the four modes m = 2,3,4,and5. |
3.3.2. Resulting fluxes: the α value
The top panel of Fig. 3 displays the values of α as a function of T0 for the modes m = 2,3,4,and5. First of all, we see that significant stresses leading to significant mass fluxes are inferred. In terms of the canonical α, values as high as ≃ 0.1 are obtained at high temperature. We also find that α scales with temperature roughly as 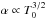 and decreases as m increases. This is expected since α is proportional to the product of the velocity fluctuations. Indeed, the velocity fields vary over a smaller domain, and the typical value of the gradient is obtained at the critical point and does not vary significantly with m (since it depends only on B, which does not vary strongly with m). Physically, higher m modes tend to be closer to an axisymmetric configuration.
and decreases as m increases. This is expected since α is proportional to the product of the velocity fluctuations. Indeed, the velocity fields vary over a smaller domain, and the typical value of the gradient is obtained at the critical point and does not vary significantly with m (since it depends only on B, which does not vary strongly with m). Physically, higher m modes tend to be closer to an axisymmetric configuration.
We verified that the fluxes of mass obtained from expression ℱ and 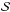 are very close to each other. They are not identical, however, because of the numerical integration. In particular, the flux of mass calculated using expression ℱ appears to be more noisy. This is because U changes sign and the integral values of the regions where it is either positive or negative are very close. On the other hand, when α is evaluated,
are very close to each other. They are not identical, however, because of the numerical integration. In particular, the flux of mass calculated using expression ℱ appears to be more noisy. This is because U changes sign and the integral values of the regions where it is either positive or negative are very close. On the other hand, when α is evaluated, 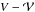 also changes sign at the same locations as U (reflecting the fact that the radial and azimuthal velocity components are highly correlated), and therefore the sign of the integrand is generally positive, making it less sensitive to the fluctuations.
also changes sign at the same locations as U (reflecting the fact that the radial and azimuthal velocity components are highly correlated), and therefore the sign of the integrand is generally positive, making it less sensitive to the fluctuations.
We also verified that as expected, the flux of angular momentum is extremely low and indeed equal to zero within the accuracy of the calculation (not displayed here for conciseness).
 |
Fig. 4 Case n = 1 / 2. Bidimensional representation of the self-similar spiral pattern for a temperature of T0 = 0.17 leading to values of B = tanθ equal to 1 and to a value of θ equal to about 45 deg. The yellow line corresponds to the trajectory of a fluid particle, the red circle shows a circular orbit that the same fluid particle would have in a symmetrical disc. Fluid particles are found to spiral inward because of dissipation. |
 |
Fig. 5 Radial, azimuthal velocities and angular momentum of the fluid particles along the trajectories displayed in Fig. 4 corresponding to a radius of r ≃ 60 for n = 1 / 2. |
Figure 3 also shows (bottom panel) α for n = 1 as a function of T0. The value of α remains quite similar to the case n = 1 / 2 although a little lower (by typically about 20%). This confirms that the influence of the density profile on the various fields is not too dramatic. The fluxes are quite different, however, as discussed above. The mass flux is equal to zero within numerical precision (not displayed here for conciseness), while the momentum flux is a simple power law of the temperature, 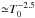 similar to the dependence of the mass flux when n = 1 / 2.
similar to the dependence of the mass flux when n = 1 / 2.
3.4. Lagrangian analysis
To gain physical insight, it is interesting to follow the trajectory of a fluid particle, that is to say, a particle that follows the stream lines. Figure 4 displays a bidimensional view of the density field for a temperature T0 = 0.17 corresponding to an angle θ = 45 deg. The yellow curves show the trajectory of a fluid particle. It was obtained by simply solving the two equations  A circle representing the trajectory that would be followed by a fluid particle in a symmetrical unperturbed disc is also plotted for comparison. Because of the self-similar nature of the solutions, we stress that all trajectories are identical to the one displayed there once rescaled and rotated.
A circle representing the trajectory that would be followed by a fluid particle in a symmetrical unperturbed disc is also plotted for comparison. Because of the self-similar nature of the solutions, we stress that all trajectories are identical to the one displayed there once rescaled and rotated.
 |
Fig. 6 Case n = 1. Bidimensional representation of the self-similar spiral pattern for T0 = 0.17, leading to values of B = tanθ equal to ≃1.0 and θ equal to about 45 deg. The yellow line corresponds to the trajectory of a fluid particle, the red circle shows a circular orbit that the same fluid particle would have in a symmetrical disc. The trajectory of the fluid particle shows that while the fluid particle has a non-circular orbit, it is nevertheless closed. This is because the mass flux vanishes. There is an outwards flux of angular momentum, however. |
As can be seen in Fig. 4, when the fluid particle encounters the shock, it is deflected inwards (since the velocity, v⊥ decreases while v∥ is unchanged). Consequently, it tends to fall toward the disc centre. However, as is clear from Fig. 4, there is a density and therefore a pressure gradient, due to the spiral structure, that pushes the fluid particle outwards. Therefore the fluid particle is decelerated in the radial direction and accelerated in the azimuthal direction. This is even clearer in Fig. 5, in which the radial and azimuthal velocity along with the angular momentum are displayed along the fluid particle trajectory as a function of the curvilinear abscissa s: ur increases continuously after the shock until the next shock (with a short phase during which it further decreases). Similarly, uφ increases continuously between s ≃ 130 and s ≃ 250 and then decreases. This last phase arises because since the fluid particle moves outwards, its Keplerian velocity decreases. The evolution of the specific angular momentum is also enlightening. After a steep decrease through the shock, it increases continuously and tends toward a constant value. The physical picture is thus that the fluid particle at the shock is suddenly slowed down, which results in an exchange of angular momentum through the pressure forces with the post-shock gas. After this point, the particle momentum increases because of the pressure gradient. Thus the fluid particle is being given angular momentum from the gas that is located at smaller radii. This momentum is then carried along until the next shock, when it will be delivered to material at higher radii.
Although the radii of the fluid particle vary non-monotonically during one cycle (i.e. during two shocks), they globally decrease with time and the particles spiral inwards, as expected (the mass flux being negative in that case).
By comparison, Fig. 6 shows the density profile and fluid particle trajectory for n = 1 and B ≃ 1 (similar to the first panel of Fig. 4). As expected, the orbit (yellow curve) is closed, although it is not circular.
4. Conclusion
We have investigated self-similar solutions of a spiral pattern within a disc. They are similar to the solution studied by Spruit (1987), but a different assumption was made regarding the temperature distribution. In addition, different density profiles were considered. These solutions, which are self-similar in radius, depend on the azimuthal angle and describe a non-linear spiral wave propagating in a centrifugally supported and locally isothermal disc. They feature shocks at whose location dissipation takes place. Because the flow is supersonic when the gas enters the shock and subsonic as it emerges, the solutions present a critical sonic point, which describes the transition from subsonic to supersonic motions. Since the equations have eventually to be solved numerically, we studied the nature of this critical point and showed that it is a saddle rather than a node almost everywhere.
By numerically solving the ordinary equations under the constraint that the flow must satisfy the Rankine-Hugoniot conditions through the shock, we obtained a series of profiles for various temperatures and mode number m. We inferred the values of α and showed that it can be as high as ~0.1 for the thickest discs for which solutions exist (h/r ≃ 1 / 3). For lower temperatures, it then drops as T1.5 or equivalently as (h/r)3. We found that the spiral angle, θ, increases when T diminishes roughly as θ = arctan(r/h). Two density profiles were explored. For the first one (n = 1 / 2), we found a non-vanishing mass flux and a zero angular momentum flux. For the second one (n = 1), the first vanishes, but not the latter. The parameter α is very similar for these two cases, however, with the steeper profile presenting slightly lower values.
From a Lagrangian analysis of the solutions, we concluded that for n = 1 / 2 the fluid particles spiral inwards and undergo a series of shocks, followed by a pressure acceleration due to the global spiral pattern. During these two phases the fluid particles respectively lose and gain angular momentum due to momentum exchange with the surrounding gas. This leads to an inward flux of mass through the disc. For n = 1, the fluid particles follow a non-circular closed orbit. There is an outward flux of angular momentum, however. While these two types of solutions present different behaviours in terms of fluxes, they are rather similar and typically differ by only a few tens of percent. Their Lagrangian behaviours are also very similar.
Although restricted to particular temperature and density profiles, the existence of these solutions suggests that external perturbations exerted on accretion discs can propagate deep into the discs and therefore should not be ignored. In many systems, the most natural source of external perturbations is the accretion of external gas that produce shocks at the disc surface.
An interesting unsolved question is whether different values of n would correspond to unstationary discs whose average momentum and mass fluxes could be reasonably described by the expression we obtain here. As we show below, the effective α we derive does not change much between n = 1 / 2 and n = 1, and it is therefore tempting to assume that this might also be the case when n is not too different from these two values.
Acknowledgments
We thank the anonymous referee for a constructive and helpful report. This research has received funding from the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007-2013 Grant Agreement No. 306483).
References
- Bae, J., Hartmann, L., & Zhu, Z. 2015, ApJ, 805, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Balbus, S. A. 2003, ARA&A, 41, 555 [NASA ADS] [CrossRef] [Google Scholar]
- Balbus, S. A., & Papaloizou, J. C. B. 1999, ApJ, 521, 650 [NASA ADS] [CrossRef] [Google Scholar]
- D’Angelo, C. R., & Spruit, H. C. 2012, MNRAS, 420, 416 [NASA ADS] [CrossRef] [Google Scholar]
- Dubus, G., Taam, R. E., & Spruit, H. C. 2002, ApJ, 569, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Harsono, D., Alexander, R. D., & Levin, Y. 2011, MNRAS, 413, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Hennebelle, P., Whitworth, A. P., Cha, S.-H., & Goodwin, S. P. 2004, MNRAS, 348, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Joos, M., Hennebelle, P., & Ciardi, A. 2012, A&A, 543, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klessen, R. S., & Hennebelle, P. 2010, A&A, 520, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Larson, R. B. 1990, MNRAS, 243, 588 [NASA ADS] [Google Scholar]
- Lesur, G., Kunz, M. W., & Fromang, S. 2014, A&A, 566, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lesur, G., Hennebelle, P., & Fromang, S. 2015, A&A, 582, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, Z.-Y., Krasnopolsky, R., & Shang, H. 2013, ApJ, 774, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Lodato, G., & Rice, W. K. M. 2004, MNRAS, 351, 630 [Google Scholar]
- Machida, M. N., Inutsuka, S.-I., & Matsumoto, T. 2010, ApJ, 724, 1006 [NASA ADS] [CrossRef] [Google Scholar]
- Muzerolle, J., Luhman, K. L., Briceño, C., Hartmann, L., & Calvet, N. 2005, ApJ, 625, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Padoan, P., Kritsuk, A., Norman, M. L., & Nordlund, Å. 2005, ApJ, 622, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Padoan, P., Haugbølle, T., & Nordlund, Å. 2014, ApJ, 797, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Pringle, J. E. 1981, ARA&A, 19, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Rozyczka, M., & Spruit, H. C. 1993, ApJ, 417, 677 [NASA ADS] [CrossRef] [Google Scholar]
- Sawada, K., Matsuda, T., Inoue, M., & Hachisu, I. 1987, MNRAS, 224, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Siuniaev, R. A., & Shakura, N. I. 1977, Pisma v Astronomicheskii Zhurnal, 3, 262 [NASA ADS] [Google Scholar]
- Spruit, H. C. 1987, A&A, 184, 173 [NASA ADS] [Google Scholar]
- Spruit, H. C., Matsuda, T., Inoue, M., & Sawada, K. 1987, MNRAS, 229, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Throop, H. B., & Bally, J. 2008, AJ, 135, 2380 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, N. J., Fromang, S., Gammie, C., et al. 2014, Protostars and Planets VI, 411 [Google Scholar]
- Venuti, L., Bouvier, J., Flaccomio, E., et al. 2014, A&A, 570, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vishniac, E. T., & Diamond, P. 1989, ApJ, 347, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Vorobyov, E. I., & Basu, S. 2008, ApJ, 676, L139 [NASA ADS] [CrossRef] [Google Scholar]
- Vorobyov, E. I., Lin, D. N. C., & Guedel, M. 2015, A&A, 573, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yukawa, H., Boffin, H. M. J., & Matsuda, T. 1997, MNRAS, 292, 321 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Topology of the critical points
The topological nature of the critical point is worth studying as it also constrains the values of T0 and B. In particular, it is important to know whether it is a node or a saddle. In the first case, a one-dimensional ensemble of trajectories will be able to cross it, while in the second case, only a discrete set of trajectories will have to be considered. To achieve this, we introduce a new variable, s, such that 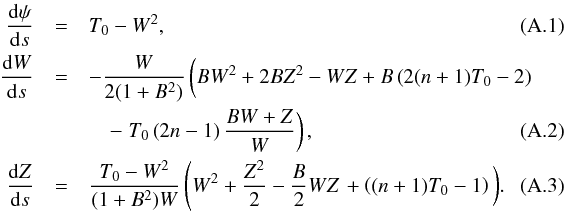 We note that it is also possible to consider −s instead of s, but this leads to unphysical solutions that entail a rarefaction shock, meaning that the gas enters the shock subsonically and leaves it supersonically.
We note that it is also possible to consider −s instead of s, but this leads to unphysical solutions that entail a rarefaction shock, meaning that the gas enters the shock subsonically and leaves it supersonically.
To study the topology of the critical point, we make an expansion in its neighbourhood and obtain a linear system 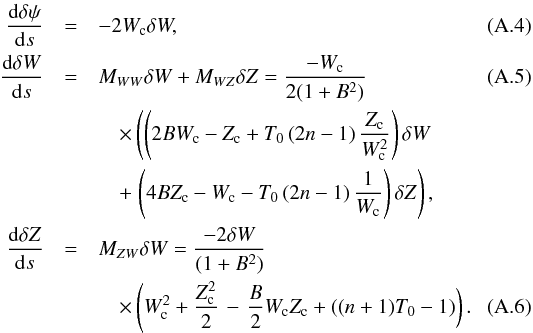 The matrix of this linear system admits three eigenvalues, 0, and
The matrix of this linear system admits three eigenvalues, 0, and 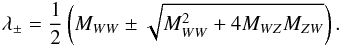 (A.7)Let
(A.7)Let 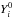 be the three eigenvectors associated with the three eigenvalues. In the neighbourhood of the critical point, the solutions of the linear system Eqs. (A.4)−(A.6) are a linear combination of
be the three eigenvectors associated with the three eigenvalues. In the neighbourhood of the critical point, the solutions of the linear system Eqs. (A.4)−(A.6) are a linear combination of 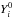 and can be written as
and can be written as 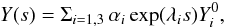 (A.8)\newpagewhere αi are real coefficients. Obviously, if λi> 0, Y(s) → ∞, implying that αi must be 0 for the corresponding solution to cross the critical point. It is therefore important to know the sign of λ+ and λ−. Another possibility is that λ+ and λ− are complex conjugate. In this case, the solutions approach the critical point with an oscillating behaviour. Such solutions are not physical either since they imply multi-valuate physical variables at the same location ψ. It is therefore important to study the signs of MWW, MWZ, MZW, and
(A.8)\newpagewhere αi are real coefficients. Obviously, if λi> 0, Y(s) → ∞, implying that αi must be 0 for the corresponding solution to cross the critical point. It is therefore important to know the sign of λ+ and λ−. Another possibility is that λ+ and λ− are complex conjugate. In this case, the solutions approach the critical point with an oscillating behaviour. Such solutions are not physical either since they imply multi-valuate physical variables at the same location ψ. It is therefore important to study the signs of MWW, MWZ, MZW, and 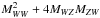 . Inserting the expression of Wc and Zc (selecting the “-” sign in Eq. (31)), we obtain their values. It is easy to verify that MWW< 0, while MWZ> 0.
. Inserting the expression of Wc and Zc (selecting the “-” sign in Eq. (31)), we obtain their values. It is easy to verify that MWW< 0, while MWZ> 0.
 |
Fig. A.1 Topology of the critical points for n = 1 / 2. Blue: points satisfying MZW = 0. This represents the transition from saddle to node critical points (one negative and one positive eigenvalue). Red: points satisfying |
The signs of MZW and 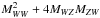 are less straightforward, and we studied their values numerically (the sign of MZW can be obtained through a second-order polynomial). Figure A.1 shows the curves in the B − T0 plane, which correspond to MZW = 0 (blue curve) and
are less straightforward, and we studied their values numerically (the sign of MZW can be obtained through a second-order polynomial). Figure A.1 shows the curves in the B − T0 plane, which correspond to MZW = 0 (blue curve) and 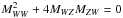 (red curve). The possible solutions are located in the dashed region that has one negative eigenvalue. In this region the critical points are a saddle. Strictly speaking, it is also possible to have solutions with critical points located in between the blue and red curves, where the eigenvalues are both negative and the critical points are nodes. These solution would present a weak discontinuity, however, that is to say, the derivatives of the fluid variables (density and velocity) are discontinuous.
(red curve). The possible solutions are located in the dashed region that has one negative eigenvalue. In this region the critical points are a saddle. Strictly speaking, it is also possible to have solutions with critical points located in between the blue and red curves, where the eigenvalues are both negative and the critical points are nodes. These solution would present a weak discontinuity, however, that is to say, the derivatives of the fluid variables (density and velocity) are discontinuous.
Appendix B: m=5 mode
For completeness, Fig. B.1 shows the m = 5 solutions for the same temperatures as in Fig. 1. The solutions all have similar shapes as the m = 2 mode, but present less variations, therefore, as we showed in Sect. 3.3, they lead to lower mass fluxes than the m = 2 mode.
Appendix C: Analytical expansion in the low-temperature limit
Here we present an analytic expansion of Eqs. ((17), (18)) that is valid in the low-temperature limit. Since we solved these equations numerically, the aim is more to make the various dependences more explicit and not to obtain accurate expressions. The approximated expressions are typically good at low temperature and at large m.
Let us expand the perpendicular and parallel velocity, W and Z as ![\appendix \setcounter{section}{3} \begin{eqnarray} \nonumber W(\psi) &=& \sqrt{T_0} ( 1 + w(\psi) ), \\[2mm] Z(\psi) &=& Z_{\rm c} + z(\psi), \label{expand} \end{eqnarray}](/articles/aa/full_html/2016/06/aa27877-15/aa27877-15-eq184.png) (C.1)where
we assume that w ≪
1 and z ≪
Zc. Since at the critical point
w = 0 and
z = 0, this
assumption is clearly verified in the vicinity of the critical point and therefore
particularly in the limit of large m. Moreover, as discussed previously, the spiral
parameter, B =
tan(θ), is on the order of
(C.1)where
we assume that w ≪
1 and z ≪
Zc. Since at the critical point
w = 0 and
z = 0, this
assumption is clearly verified in the vicinity of the critical point and therefore
particularly in the limit of large m. Moreover, as discussed previously, the spiral
parameter, B =
tan(θ), is on the order of
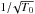 .
Thus we write
.
Thus we write 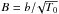 .
Finally, we restrict the calculation to the case n = 1 / 2.
.
Finally, we restrict the calculation to the case n = 1 / 2.
Inserting these expressions into Eqs. (17), (18), we obtain 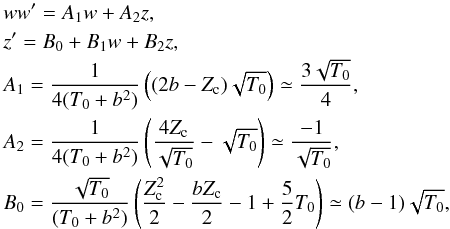 (C.2)
(C.2)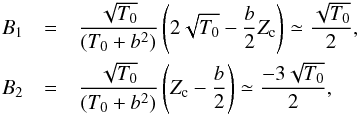 where
to derive the simplified expressions, we used that in the limit of low T0
where
to derive the simplified expressions, we used that in the limit of low T0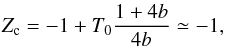 (C.3)while
(C.3)while
 (C.4)To
obtain an approximation of Eq. (C.2),
we expand w
and z to the
second order in ψ −
ψc,
(C.4)To
obtain an approximation of Eq. (C.2),
we expand w
and z to the
second order in ψ −
ψc, 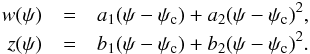 The
coefficents a1,2 and
b1,2 are solutions of
the following equations
The
coefficents a1,2 and
b1,2 are solutions of
the following equations ![\appendix \setcounter{section}{3} \begin{eqnarray} \nonumber &&a_1^2 = A_1 a_1 + A_2 b_1, \\[1mm] \nonumber &&3 a_1 a_2 = A_1 a_2 + A_2 b_2, \\[1mm] \nonumber &&b_1 = B_0, \\ &&2 b_2 = B_1 a_1 + B_2 b_1, \end{eqnarray}](/articles/aa/full_html/2016/06/aa27877-15/aa27877-15-eq201.png) (C.5)which
leads to
(C.5)which
leads to 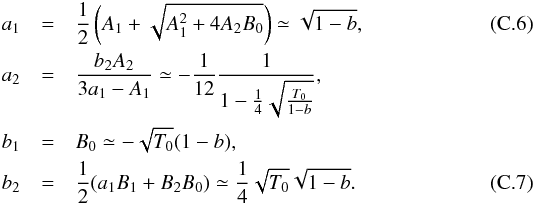
At this stage we have two free parameters, ψc and b. They are determined by the two boundary conditions as given by Eqs. (20)−(22), which
 |
Fig. C.1 Comparison between the numerical solutions (red and blue curves) obtained numerically and the approximated solutions presented in this appendix (magenta curves) for m = 5 and T0 = 0.048, 0.036, 0.024, and 0.012. They are quite close, demonstrating the validity of the approximation. |
in the limit w ≪
1 leads to 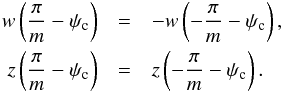 (C.8)Combining
them with Eqs. (C.7), we obtain
(C.8)Combining
them with Eqs. (C.7), we obtain
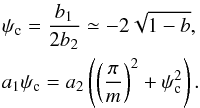 (C.9)Combining
these two last equations, we obtain a non-linear equation of b, which can be easily
solved using a standard root finder. Knowing b, all quantities are known. A comparison between
the numerical and approximated solutions is displayed in Fig. C.1.
(C.9)Combining
these two last equations, we obtain a non-linear equation of b, which can be easily
solved using a standard root finder. Knowing b, all quantities are known. A comparison between
the numerical and approximated solutions is displayed in Fig. C.1.
All Figures
 |
Fig. 1 Mode m = 2 for n = 1 / 2 (left) and for n = 1 (right). Various fields for a series of temperatures equally spaced between T0 = 0.18 (corresponding to the curves with more pronounced variations) and T0 = 0.012 (corresponding to flatter curves). The red parts of the curve correspond to the subsonic and the blue parts to the supersonic regions. |
| In the text | |
 |
Fig. 2 B = tanθ, the angle of the spiral pattern as a function of T0 for the four modes m = 2,3,4,and5. The top panel shows n = 1 / 2, the bottom panel n = 1. |
| In the text | |
 |
Fig. 3 α value for n = 1 / 2 (top panel) and n = 1 (bottom panel) as a function of T0 for the four modes m = 2,3,4,and5. |
| In the text | |
 |
Fig. 4 Case n = 1 / 2. Bidimensional representation of the self-similar spiral pattern for a temperature of T0 = 0.17 leading to values of B = tanθ equal to 1 and to a value of θ equal to about 45 deg. The yellow line corresponds to the trajectory of a fluid particle, the red circle shows a circular orbit that the same fluid particle would have in a symmetrical disc. Fluid particles are found to spiral inward because of dissipation. |
| In the text | |
 |
Fig. 5 Radial, azimuthal velocities and angular momentum of the fluid particles along the trajectories displayed in Fig. 4 corresponding to a radius of r ≃ 60 for n = 1 / 2. |
| In the text | |
 |
Fig. 6 Case n = 1. Bidimensional representation of the self-similar spiral pattern for T0 = 0.17, leading to values of B = tanθ equal to ≃1.0 and θ equal to about 45 deg. The yellow line corresponds to the trajectory of a fluid particle, the red circle shows a circular orbit that the same fluid particle would have in a symmetrical disc. The trajectory of the fluid particle shows that while the fluid particle has a non-circular orbit, it is nevertheless closed. This is because the mass flux vanishes. There is an outwards flux of angular momentum, however. |
| In the text | |
 |
Fig. A.1 Topology of the critical points for n = 1 / 2. Blue: points satisfying MZW = 0. This represents the transition from saddle to node critical points (one negative and one positive eigenvalue). Red: points satisfying |
| In the text | |
 |
Fig. B.1 Same as Fig. 1 for the modes m = 5. |
| In the text | |
 |
Fig. C.1 Comparison between the numerical solutions (red and blue curves) obtained numerically and the approximated solutions presented in this appendix (magenta curves) for m = 5 and T0 = 0.048, 0.036, 0.024, and 0.012. They are quite close, demonstrating the validity of the approximation. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


