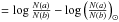| Issue |
A&A
Volume 590, June 2016
|
|
|---|---|---|
| Article Number | A74 | |
| Number of page(s) | 6 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201527827 | |
| Published online | 13 May 2016 | |
Cosmic variance in [O/Fe] in the Galactic disk
1
Instituto de Astrofísica de Canarias, vía Láctea, 38205 La Laguna, Tenerife, Spain
e-mail:
sarabertrandelis@gmail.com
2
Universidad de La Laguna, Departamento de
Astrofísica, 38206, La
Laguna, Tenerife,
Spain
3
Department of Astronomy, University of Virginia,
Charlottesville, VA
22904-4325,
USA
4
Astrophysics Research Institute, Liverpool John Moores
University, Liverpool, L3
5RF, UK
5
New Mexico State University, Las Cruces, NM
88003,
USA
6
University of Texas at Austin, McDonald Observatory,
Fort Davis, TX
79734,
USA
7
ELTE Gothard Astrophysical Observatory,
Szent Imre herceg st. 112,
9704
Szombathely,
Hungary
8
Texas Christian University, Fort Worth, TX
76129,
USA
9
405 Davey Laboratory, Pennsylvania State University,
University Park
PA,
USA
10
Large Synoptic Survey Telescope, 950 North Cherry
Ave, Tucson,
AZ
85719,
USA
11
Steward Observatory, 933 North Cherry Ave, Tucson, AZ
85719,
USA
12
Johns Hopkins University, Baltimore, MD
21218,
USA
13
Department of Astronomy, University of Florida,
Bryant Space Science Center,
Gainesville, FL
32611-2055,
USA
Received: 24 November 2015
Accepted: 8 March 2016
We examine the distribution of the [O/Fe] abundance ratio in stars across the Galactic disk using H-band spectra from the Apache Point Galactic Evolution Experiment (APOGEE). We minimize systematic errors by considering groups of stars with similar atmospheric parameters. The APOGEE measurements in the Sloan Digital Sky Survey data release 12 reveal that the square root of the star-to-star cosmic variance in the oxygen-to-iron ratio at a given metallicity is about 0.03–0.04 dex in both the thin and thick disk. This is about twice as high as the spread found for solar twins in the immediate solar neighborhood and the difference is probably associated to the wider range of galactocentric distances spanned by APOGEE stars. We quantify the uncertainties by examining the spread among stars with the same parameters in clusters; these errors are a function of effective temperature and metallicity, ranging between 0.005 dex at 4000 K and solar metallicity, to about 0.03 dex at 4500 K and [Fe/H] ≃ −0.6. We argue that measuring the spread in [O/Fe] and other abundance ratios provides strong constraints for models of Galactic chemical evolution.
Key words: stars: abundances / stars: fundamental parameters / Galaxy: stellar content / Galaxy: disk
© ESO, 2016
1. Introduction
Cosmic variance in the chemical composition of stars in a galaxy is a natural outcome of the discrete character of the production and return of nucleosynthetic yields from preceding generations of stars to the interstellar medium (ISM). At a given location within a galaxy, slower supernova (or star formation) rates and higher variance in the yields from different stars will contribute to higher cosmic variance in chemical abundances.
If two metals are produced in the same proportions in supernovae, their abundance ratio in the ISM will remain constant. If they are produced at different sites or with different proportions, they can be used to constrain the chemical enrichment history of a galaxy, even without any explicit reference to time or, equivalently, to the ages of the stars being analyzed. This is the case, for example, for oxygen and iron, with the former being mainly produced in massive stars that die as Type II supernovae, and the latter coming chiefly from Type Ia supernovae, the result of the evolution of lower mass stars. If determined observationally, the scatter in the abundance ratios of O/Fe at any given Fe can provide valuable information on the star formation rate and nucleosynthetic yields, complementing present-day abundance distributions in stars.
For years, efforts to determine the spread in oxygen abundances, or [O/Fe]1, at any given [Fe/H] have been unsuccessful. Reddy et al. (2006) found a spread of about 0.07 dex for both thin- and thick-disk members based on abundances from the O I triplet at 777 nm that were calibrated to other lines to minimize departures from local thermodynamical equilibrium (LTE). Ramírez et al. (2013), using again the O I triplet and including detailed non-LTE calculations for their sample, found a spread of about 0.05 dex among kinematically high-confidence members of the thin or thick disks. Most likely, in these and other studies, the observational and analysis uncertainties were at the same level as the observed spread in each population.
Recent progress in differential studies of solar analogs has shown that a precision better than 0.01 dex is possible (Meléndez et al. 2009; Ramírez et al. 2009; Beck et al. 2016). Nissen (2015) examined the abundances of 14 elements in about twenty nearby stars with atmospheric parameters very close to solar (within 100 K in Teff, about 0.1 dex in log g or [Fe/H]) and found a scatter in [Ca/Fe] or [Cr/Fe] of about 0.01 dex for the thin-disk members in his sample. In contrast, the scatter for other elements is several times larger and in all cases clearly higher than the measurement uncertainties. For the α-elements Mg, Si, S, and Ti, Nissen found a tight correlation between their abundance ratio to iron and stellar age, inferred from the comparison with models of stellar structure and evolution, and thanks to the extreme accuracy of the atmospheric parameters provided by the differential analysis relative to the Sun.
These results have revealed the cosmic scatter in the abundance ratios of thin-disk stars and provide new strong constraints for chemical evolution models of the solar vicinity. Obviously, it is desirable to extend these measurements beyond the solar neighborhood, and in particular to carry out similar analyses for thick-disk stars. As we describe in this paper, the Apache Point Galactic Evolution Experiment (APOGEE) provides such data.
We present oxygen abundances from OH lines in the H-band (1.5–1.7 μm) for disk stars over a wide range of distances observed by APOGEE, which is part of the Sloan Digital Sky Survey (SDSS). We overcome systematic effects by considering subsamples with similar atmospheric parameters. Within these subsamples, we show that oxygen abundances are extremely precise, as quantified by the spread observed in open clusters, about 0.005 dex at 4000 K and solar metallicity. Based on these measurements, for a sample that is roughly 100 times larger than in any previous study and extends to the inner parts of the Galaxy, we discuss the cosmic scatter in the oxygen-to-iron abundances for the thin- and thick-disk stellar populations.
2. Analysis
Using the SDSS 2.5 m telescope (Gunn et al. 2006), APOGEE started in 2011 to map the chemical abundances of Milky Way stars, with an emphasis on the dust-obscured populations in the central parts of the Galaxy and the disk (Majewski et al. 2015). The latest data release (SDSS-III DR12; Alam et al. 2015; Holtzman et al. 2015) includes spectra, atmospheric parameters, and chemical abundances for some 150 000 stars. We refer to Zasowski et al. (2013), Nidever et al. (2015), García Pérez et al. (2016), Shetrone et al. (2015), and Zamora et al. (2015) for the details of the APOGEE targeting, data processing, and analysis pipeline. The observations continue and will be complemented with a second, basically identical, instrument from the southern hemisphere, starting later in 2016 (Wilson et al. 2012).
2.1. Sample selection
We based our analysis on the stars in DR12, adopting atmospheric parameters and abundances included in that data release2. Nidever et al. (2014) examined the spread in [α/Fe] for stars in the thin disk as a function of the median signal-to-noise ratio per pixel (S/N) in the DR10 APOGEE spectra3 (Ahn et al. 2014), finding that the value flattened at about 0.025 dex for S/N> 300 (most APOGEE targets have been observed to 100 <S/N< 200). The APOGEE Atmospheric Parameters and Chemical Abundance Pipeline (ASPCAP; García Pérez et al. 2016) determines an “average” α-element to iron ratio simultaneously with the effective temperature, surface gravity, metallicity, and the abundances of carbon and nitrogen. This α-abundance is derived by varying in block the abundances of O, Mg, Si, S, Ca, and Ti. At low effective temperature Teff< 4500 K, the inferred [α/Fe] follows mainly [O/Fe] due to the many OH lines in the H-band, but with contributions from atomic transitions of the other α-elements.
Instead of [α/Fe], we examined the [O/Fe] values derived from OH lines exclusively (the “calibrated” values provided as part of the ELEM array of abundances in DR12 – see Holtzman et al. 2015 for details). Our [Fe/H] values are from the corresponding calibrated values in the PARAM array. In an attempt to retain the maximum precision avoiding systematic errors, we separated stars into different Teff intervals and analyzed each bin independently.
We selected stars in the APOGEE sample observed with the SDSS 2.5 m telescope that comply with the following requirements: 4000 <Teff< 4600 K, −0.65 < [Fe/H] < + 0.25 dex, S/N> 80, 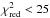 , and since we rely on the calibrated ASPCAP parameters, only low-gravity stars were selected (log g< 3.8). The lowest effective temperature was set at 4000 K to avoid problems with the oxygen abundances from APOGEE for cooler stars (Mészáros et al. 2013; Holtzman et al. 2015). In addition, we avoided bulge stars by restricting the range of projected galactocentric radii to Rg> 3 kpc and with | zg | < 2.5 kpc (distances from Hayden et al. 2015). After applying these filters, our sample contains 16 870 stars.
, and since we rely on the calibrated ASPCAP parameters, only low-gravity stars were selected (log g< 3.8). The lowest effective temperature was set at 4000 K to avoid problems with the oxygen abundances from APOGEE for cooler stars (Mészáros et al. 2013; Holtzman et al. 2015). In addition, we avoided bulge stars by restricting the range of projected galactocentric radii to Rg> 3 kpc and with | zg | < 2.5 kpc (distances from Hayden et al. 2015). After applying these filters, our sample contains 16 870 stars.
2.2. Chemical split between the thin and thick disk
 |
Fig. 1 Example of the procedure used to chemically separate thin and thick disks by fitting a double Gaussian to the [O/Fe] distribution. Data correspond to the bin 4200 <Teff< 4400 K. In the right panel the [O/Fe] distribution for the bin −0.35 < [M/H] < −0.25 dex is shown. The separation between disks is marked with dots on the left panel and with a straight line between the Gaussians for the corresponding [M/H] bin on the right side. |
Stars in the thin and thick disks can be statistically distinguished based on their distance to the plane, age, kinematics, or chemical compositions. The kinematic properties of both disks overlap, and the available distances are not very accurate. On the other hand, the intrinsic uncertainties in the determination of abundances by the ASPCAP pipeline are very small, and therefore we prefer to use chemistry to distinguish the membership of stars in one of the two disk populations. From all the α-element abundances provided by ASPCAP, we selected oxygen because of the large number of OH lines detected in the APOGEE spectra.
We split our sample into three bins in temperature and nine bins in metallicity, with widths of 200 K and 0.1 dex, respectively. The number of stars in each bin ranges from 210 to 1100.
Stars in the thin and thick disk split quite nicely using [α/Fe] from the APOGEE measurements (Anders et al. 2014; Hayden et al. 2014; Nidever et al. 2014). To separate the two components, we used a least-squares fit with a double Gaussian to the [O/Fe] distribution from each bin, as illustrated in Fig. 1. The standard deviation of each Gaussian is taken as the measured scatter (cosmic plus measurement uncertainties). This method provides reliable estimates of the scatter, even when the separation between disks is not clear and they overlap, as is usually the case. In addition, we can define a chemical division between the disks in the intersection between the two Gaussians, except at high [Fe/H] when the two populations completely overlap (see Fig. 1).
The uncertainty for each bin in the [O/Fe] histogram (see the right-hand panel in Fig. 1) was taken as the square root of the number of stars in the bin. These were considered when fitting double Gaussians. The square root of the diagonal of the inverse of the curvature matrix provides the errors in the mean and σ for both Gaussians.
2.3. Estimating the [O/Fe] uncertainties
To measure the cosmic dispersion of a certain element, we need to not only measure the spread, but also properly estimate the actual uncertainties in our abundance measurements. The expected errors in abundance measurements are often underestimated because it is difficult to account for all relevant contributions. For this reason, we did not attempt to calculate the uncertainties in the oxygen abundances, but instead derived them empirically. Thanks to the wide sky coverage of the APOGEE survey, multiple clusters are included in our sample (Frinchaboy et al. 2013; Mészáros et al. 2015).
We assumed that the cosmic variance in a cluster is negligible, and therefore the measured scatter mainly reflects our analysis uncertainties. Bovy (2016) has recently argued that the APOGEE data can be used to set tight limits to the intrinsic spread in the abundances of carbon and iron in open clusters at ≲0.01, and at ≲0.015 for oxygen, which supports this argument. Globular clusters show multiple populations and abundance anomalies, and therefore the measured spread in these systems provides only upper limits to the intrinsic uncertainties, but even these are useful for our purposes.
 |
Fig. 2 Spread in the ratio of oxygen to iron abundances measured in different clusters as a function of the mean Teff and [Fe/H]. The background color indicates the variations predicted by the polynomial fit to the data (capped to have minimum value of 0.005 dex), and follows the same color code as used for the individual data points. The error bars shown for the data points reflect the standard deviation. The stars from our sample lie in the region marked with dashed lines. |
We selected clusters from the list of APOGEE calibration clusters with metallicity above −1.3 dex: M 5, M 67, M 71, M 107, NGC 2158, NGC 6791, and NGC 6819. Stars observed in the field of each cluster were first selected as potential members according to their coordinates (stars within the cluster tidal radius), radial velocity (RV) in the range of ±30 km s-1 around the mean cluster value, and avoiding dwarf stars. The mean cluster RVs were taken from the SIMBAD astronomical database (Wenger et al. 2000), and the cluster radii are the same as those used in Mészáros et al. (2013). The final sample retains stars within a 2σ interval around the mean [Fe/H] and RV of the potential members.
 |
Fig. 3 1σ standard deviation in the ratio of oxygen to iron abundances as a function of the S/N for stars with 4200 <Teff< 4600 K and 0.05 < [Fe/H] < −0.45 dex. An exponential is fitted to the data points, weighted with the corresponding uncertainties. The point at very high S/N corresponds to the M 67 bin that contains a star whose [O/Fe] is remarkably different from the cluster average (see Sect. 2.3). |
We explored a broader range in [Fe/H] and Teff than in our sample (Sect. 2.1) to better map the sensitivity of the uncertainties to these parameters. For each cluster we divided the stars into Teff bins and measured the [O/Fe] rms scatter in those with more than one star. Since the stars in some clusters span multiple bins, we have more data points than clusters. The results are shown in Fig. 2. We find that the scatter is a smooth function of effective temperature and metallicity and that the polynomial ![\begin{eqnarray} \sigma[{\rm O/Fe}]_{\rm err} & \! \!=\! \!& 1.915 - 9.143\times 10^{-4} T_{\rm eff} \nonumber \\ &&+ 2.837\times 10^{-1} {\rm [Fe/H]} - 6.108\times10^{-5} T_{\rm eff} {\rm [Fe/H]} \nonumber \\ && + 1.091\times 10^{-7} T_{\rm eff}^2 + 4.119\times 10^{-2} {\rm [Fe/H]}^2 \nonumber \end{eqnarray}](/articles/aa/full_html/2016/06/aa27827-15/aa27827-15-eq28.png) closely follows the data with an rms scatter of 0.01 dex, but we capped the polynomial predictions (σ[O/Fe]err) to avoid values lower than 0.005 dex, the average of the three lowest data points in our measurements. The M 67 data point at Teff ~ 4300 K is the only one that clearly deviates from the fitted polynomial. This is due to a star, 2MASS J08493465+1151256, whose RV and [Fe/H] values agree with the cluster mean, but which shows a remarkable difference of 0.09 dex in [O/Fe] with respect to the mean value of the cluster. Nevertheless, we decided to keep this star and avoid exceptions to our cluster selection criteria, since it has a negligible effect on our derived polynomial. In addition, we did not discard the possibility that M 67 might be chemically inhomogeneous at the level of ~0.02 dex, as has previously been found in other open clusters (Liu et al. 2016).
closely follows the data with an rms scatter of 0.01 dex, but we capped the polynomial predictions (σ[O/Fe]err) to avoid values lower than 0.005 dex, the average of the three lowest data points in our measurements. The M 67 data point at Teff ~ 4300 K is the only one that clearly deviates from the fitted polynomial. This is due to a star, 2MASS J08493465+1151256, whose RV and [Fe/H] values agree with the cluster mean, but which shows a remarkable difference of 0.09 dex in [O/Fe] with respect to the mean value of the cluster. Nevertheless, we decided to keep this star and avoid exceptions to our cluster selection criteria, since it has a negligible effect on our derived polynomial. In addition, we did not discard the possibility that M 67 might be chemically inhomogeneous at the level of ~0.02 dex, as has previously been found in other open clusters (Liu et al. 2016).
To ensure that the cluster sample is representative of the whole sample, we also examined the S/N4 of the data. While the mean S/N of our sample is 295, clusters have on average lower S/N values, except for M 67 (S/N ~ 545), NGC 6819 (S/N ~ 324), and NGC 2420 (S/N ~ 316). The remaining clusters have a S/N between 150 and 200. We study this matter in more detail below.
2.4. [O/Fe] dispersion against signal-to-noise ratio
Nidever et al. (2014) have shown that the empirical scatter in [α/Fe] for the low-α stars in APOGEE decreases exponentially as a function of S/N, reaching a plateau of ~0.023 dex at S/N ≳ 200.
After we separated between thin- and thick-disk stars in our sample, we calculated the dependence of the standard deviation in [O/Fe] on S/N. We selected stars with 4200 <Teff< 4600 K and 0.05 < [Fe/H] < −0.45. Lower temperatures or higher metallicities were avoided to guarantee a minimum number of 25 stars per bin for both the thin and thick disks. Following the same method used to calculate the scatter and split the disks, we divided our sample into bins of Teff and S/N. For each bin we fit a third-order polynomial to the [O/Fe] vs. [Fe/H] trend to subtract it, and then fit a Gaussian profile to the [O/Fe] histogram. The scatter in [O/Fe] was taken as the standard deviation of this Gaussian. Finally, we averaged the scatter found for different temperatures at the same S/N. As can be seen in Fig. 3, the dispersion in [O/Fe] does indeed depend on S/N. Although we do not reach a dispersion as small as Nidever et al. (2014) for the thin disk, the trends are very similar.
We also show data for the clusters, avoiding those with parameters that are very different from those in our sample. The scatter in this case is calculated as the standard deviation of [O/Fe] for each bin since we do not have enough stars per bin to perform a Gaussian fit. Our cluster sample spans a wide range in S/N, but their dispersions are still remarkably lower than those for field stars. We therefore conclude that our estimates of the measurement uncertainties from clusters are not underestimated because of the differences between clusters and sample S/N. We note, nonetheless, that the uncertainties in the cluster data are larger than in the sample data as a result of the limited number of stars per cluster for each bin.
3. Results and conclusions
Figure 4 shows the 1σ scatter measured for the thin- (red) and thick-disk (blue) populations in each temperature and metallicity bin. The black line shows the estimated uncertainties in the APOGEE [O/Fe] ratios from the dispersion empirically measured in open clusters, while the gray area indicates the variation between extreme temperature values in each temperature bin. The estimated uncertainties reach a minimum value of 0.005 dex for solar-metallicity stars with Teff ≃ 4000 K and increase for warmer or more metal-poor stars.
The APOGEE measurements unambiguously detect the cosmic scatter in [O/Fe] at any given metallicity. The [O/Fe] scatter is not very different in the thin and thick disks, and the disks show an approximately flat value between 0.03–0.04 dex over the entire range of metallicity considered.
Our APOGEE sample includes disk stars at distances of up to 30 kpc from the Sun (75% of the sample are within 6 <Rg< 12 kpc), and therefore it is interesting to compare our derived scatter in [O/Fe] with the value for the thin disk from Nissen (2015), which was based on solar twins within ~40 pc. Nissen’s oxygen abundances are based on a single feature, the weak forbidden line at 630 nm, which is blended with a Ni I transition, and this is likely to cause part of the scatter in [O/Fe] he reported. We therefore chose to compare our results with the scatter he reported for other α elements that show a similar correlation between abundance and age, namely Mg, Si, S, or Ti. In these, the scatter in [X/Fe] is 0.022, 0.016, 0.021, and 0.017 dex, respectively. Taking σ [α/ Fe] local = 0.02 dex as a representative value, marked in Fig. 4 with a green solid line, the APOGEE [O/Fe] ratios show nearly twice as much scatter as the value found in the immediate vicinity of the Sun.
Nissen (2015) found that a significant fraction of the scatter in [Mg/Fe], [Si/Fe], [S/Fe], or [Ti/Fe] among thin-disk stars in the solar neighborhood can be attributed to chemical evolution. These abundance ratios correlate tightly with stellar age, and when the age trend is removed, the scatter reduces to ~0.01 dex, or about half of that before removing the trend. Obviously, this contribution must be present in the APOGEE sample, but since the volume probed by APOGEE observations is much larger, additional effects are likely to contribute to the scatter.
The abundance of [Fe/H] or the alpha elements [α/H] decreases significantly with galactocentric distance for the thin disk at about 0.05 dex/kpc, while variations are much smaller for the thick disk (Hayden et al. 2014). On the other hand, at any given [Fe/H], the changes in [O/Fe] as a function of galactocentric distance are very small for both populations. If we use the APOGEE data to evaluate how much the mean radial and vertical gradients contribute to the scatter, we find that its contribution is negligible.
As a result of radial migration, stars currently in the solar neighborhood were formed at a wide range of galactocentric distances, between 2 and 13 kpc, with about 75% of them formed at galactocentric distances between 3 and 9 kpc (e.g., Minchev et al. 2013). This range, however, is not much larger than that spanned by the stars in the APOGEE sample, but the latter have also been subjected to radial mixing and therefore sample a larger volume of the disk. Spatial variations in the star formation rate or in the gas outflow rate could be responsible for an increased scatter. Indeed, limiting our APOGEE sample to stars at less than 1 kpc from the Sun, we measure a scatter of ~0.03 dex in the solar neighborhood. On the other hand, stars at more than 4 kpc from the Galactic plane show a scatter that rises to ~0.1 dex, suggesting that the dispersion in [O/Fe] is larger in the Milky Way halo than in the disk.
 |
Fig. 4 1σ scatter measured in the thin (red solid curve) and thick (blue dashed line) disks. The black line shows the estimated uncertainties in the APOGEE [O/Fe] ratios from the dispersion empirically measured in clusters, while the gray area indicates the size of the variation in these uncertainties between the extreme temperature values in each temperature bin. |
The potential use of information on the spread in abundance ratios at any given metallicity can be illustrated with a back-of-the-envelope calculation. With an average expansion speed of 103 km s-1 and a time for the ejecta to merge into the ISM of about 104 yr, a supernova remnant can pollute a region ~10 pc in radius5. Assuming a typical mass of metals in the ejecta of ~1 M⊙, a single supernova increases the density of metals in the surrounding ISM by ~5 × 1026 kg pc-3. A maximum density for the ISM where stars form is given by the typical density for a molecular cloud, about 5 × 1032 kg pc-3, and therefore the first Galactic supernova would bring the metallicity of the surrounding ISM to [Fe/H] ~ −3.
The variance in metallicity across individual zones, ~10 pc in size, will be large in the early Galaxy, but as more and more supernova explode, this variance will be progressively reduced. Considering the metallicity distribution at the present time involves measuring the variance both spatially (across zones) and over time. Considering the spread in abundance ratios at any given metallicity would be more similar to evaluating the variance across zones at a particular moment in time, but we note that this is a rough approximation because the age metallicity relationship in the Milky Way disk is only loosely defined (e.g., Edvardsson et al. 1993; Haywood et al. 2013).
Based on these order-of-magnitude arguments and assuming that low-mass stars form at a constant rate, we can show numerically that a constant supernova rate of about 0.01 to 0.1 per 10-pc zone per million years would lead, after 1010 yr, to a metallicity distribution with a 1σ dispersion across zones and over all ages of about 0.2 dex. This supernovae rate would at the same time produce a dispersion about ten times smaller over zones at any given moment in time in the last ~5 × 109 yr. These figures are consistent with the spread in the metallicity distribution in the thin or thick disks (about 0.2 dex) and with the spread in oxygen abundances that we find at any given metallicity (0.02−0.04 dex).
We can further support this claim by assuming that the Galactic disk is a flat cylinder 30 kpc in diameter and 1 kpc in height. The cylinder would contain some 108 zones of 10 pc each6. A supernova rate of 0.01 per zone per million years implies n = 1010 supernovae in the entire Galactic disk in 1010 yr. The events would be distributed following a binomial distribution with a mean of 1010 × 10-8 = 102 supernovae per zone and a standard deviation of 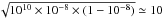 , which leads to a spread in metals of 10/100/ln(10.) = 0.04 dex.
, which leads to a spread in metals of 10/100/ln(10.) = 0.04 dex.
These simple arguments show that the star formation rate must have been much higher in the past than it is now – one supernova per century, the current rate, is roughly equivalent to 10-4 supernova per 10-pc zone per million years. A quantitative discussion requires more sophisticated models, but we conclude that as the precision of our abundance analyses reaches and surpasses 0.01 dex, new diagnostics will become available to constrain models of the formation and evolution of the Milky Way.
Acknowledgments
We thank the anonymous referee for his/her thorough review and suggestions, which significantly contributed to improving the quality of the publication. We are also grateful to I. Minchev and J. Bovy for useful comments. S.B. and C.A.P. acknowledge financial support from the Spanish Government through the project AYA2014-56359-P. P.M.F. is supported by NSF grant AST-1311835. S.M. has been supported by the János Bolyai Research Scholarship of the Hungarian Academy of Sciences. Funding for SDSS-III has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, and the US Department of Energy Office of Science. The SDSS-III web site is http://www.sdss3.org/. SDSS-III is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS-III Collaboration including the University of Arizona, the Brazilian Participation Group, Brookhaven National Laboratory, Carnegie Mellon University, University of Florida, the French Participation Group, the German Participation Group, Harvard University, the Instituto de Astrofisica de Canarias, the Michigan State/Notre Dame/JINA Participation Group, Johns Hopkins University, Lawrence Berkeley National Laboratory, Max Planck Institute for Astrophysics, Max Planck Institute for Extraterrestrial Physics, New Mexico State University, New York University, Ohio State University, Pennsylvania State University, University of Portsmouth, Princeton University, the Spanish Participation Group, University of Tokyo, University of Utah, Vanderbilt University, University of Virginia, University of Washington, and Yale University.
References
- Ahn, C. P., Alexandroff, R., Allen de Prieto, C., et al. 2014, ApJS, 211, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Alam, S., Albareti, F. D., Allen de Prieto, C., et al. 2015, ApJS, 219, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Anders, F., Chiappini, C., Santiago, B. X., et al. 2014, A&A, 564, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, P. G., Allen de Prieto, C., Van Reeth, T., et al. 2016, A&A, 589, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bovy, J. 2016, ApJ, 817, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Edvardsson, B., Andersen, J., Gustafsson, B., et al. 1993, A&A, 275, 101 [NASA ADS] [Google Scholar]
- Frinchaboy, P. M., Thompson, B., Jackson, K. M., et al. 2013, ApJ, 777, L1 [NASA ADS] [CrossRef] [Google Scholar]
- García Pérez, A. E., Allende Prieto, C., Holtzman, J. A., et al. 2016, AJ, submitted [arXiv:1510.07635] [Google Scholar]
- Gunn, J. E., Siegmund, W. A., Mannery, E. J., et al. 2006, AJ, 131, 2332 [NASA ADS] [CrossRef] [Google Scholar]
- Hayden, M. R., Holtzman, J. A., Bovy, J., et al. 2014, AJ, 147, 116 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Hayden, M. R., Bovy, J., Holtzman, J. A., et al. 2015, ApJ, 808, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Haywood, M., Di Matteo, P., Lehnert, M. D., Katz, D., & Gómez, A. 2013, A&A, 560, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holtzman, J. A., Shetrone, M., Johnson, J. A., et al. 2015, AJ, 150, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, F., Yong, D., Asplund, M., Ramírez, I., & Meléndez, J. 2016, MNRAS, 457, 3934 [NASA ADS] [CrossRef] [Google Scholar]
- Majewski, S. R., Schiavon, R. P., Frinchaboy, P. M., et al. 2015, AJ, submitted [arXiv:1509.05420] [Google Scholar]
- Meléndez, J., Asplund, M., Gustafsson, B., & Yong, D. 2009, ApJ, 704, L66 [NASA ADS] [CrossRef] [Google Scholar]
- Mészáros, S., Holtzman, J., García Pérez, A. E., et al. 2013, AJ, 146, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Mészáros, S., Martell, S. L., Shetrone, M., et al. 2015, AJ, 149, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Minchev, I., Chiappini, C., & Martig, M. 2013, A&A, 558, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nidever, D. L., Bovy, J., Bird, J. C., et al. 2014, ApJ, 796, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Nidever, D. L., Holtzman, J. A., Allen de Prieto, C., et al. 2015, AJ, 150, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Nissen, P. E. 2015, A&A, 579, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramírez, I., Meléndez, J., & Asplund, M. 2009, A&A, 508, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramírez, I., Allen de Prieto, C., & Lambert, D. L. 2013, ApJ, 764, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, B. E., Lambert, D. L., & Allen de Prieto, C. 2006, MNRAS, 367, 1329 [NASA ADS] [CrossRef] [Google Scholar]
- Shetrone, M., Bizyaev, D., Lawler, J. E., et al. 2015, ApJS, 221, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Wenger, M., Ochsenbein, F., Egret, D., et al. 2000, A&AS, 143, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilson, J. C., Hearty, F., Skrutskie, M. F., et al. 2012, in Ground-based and Airborne Instrumentation for Astronomy IV, Proc. SPIE, 8446, 84460 [Google Scholar]
- Zamora, O., García-Hernández, D. A., Allen de Prieto, C., et al. 2015, AJ, 149, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Zasowski, G., Johnson, J. A., Frinchaboy, P. M., et al. 2013, AJ, 146, 81 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Example of the procedure used to chemically separate thin and thick disks by fitting a double Gaussian to the [O/Fe] distribution. Data correspond to the bin 4200 <Teff< 4400 K. In the right panel the [O/Fe] distribution for the bin −0.35 < [M/H] < −0.25 dex is shown. The separation between disks is marked with dots on the left panel and with a straight line between the Gaussians for the corresponding [M/H] bin on the right side. |
| In the text | |
 |
Fig. 2 Spread in the ratio of oxygen to iron abundances measured in different clusters as a function of the mean Teff and [Fe/H]. The background color indicates the variations predicted by the polynomial fit to the data (capped to have minimum value of 0.005 dex), and follows the same color code as used for the individual data points. The error bars shown for the data points reflect the standard deviation. The stars from our sample lie in the region marked with dashed lines. |
| In the text | |
 |
Fig. 3 1σ standard deviation in the ratio of oxygen to iron abundances as a function of the S/N for stars with 4200 <Teff< 4600 K and 0.05 < [Fe/H] < −0.45 dex. An exponential is fitted to the data points, weighted with the corresponding uncertainties. The point at very high S/N corresponds to the M 67 bin that contains a star whose [O/Fe] is remarkably different from the cluster average (see Sect. 2.3). |
| In the text | |
 |
Fig. 4 1σ scatter measured in the thin (red solid curve) and thick (blue dashed line) disks. The black line shows the estimated uncertainties in the APOGEE [O/Fe] ratios from the dispersion empirically measured in clusters, while the gray area indicates the size of the variation in these uncertainties between the extreme temperature values in each temperature bin. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.