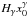| Issue |
A&A
Volume 590, June 2016
|
|
|---|---|---|
| Article Number | A23 | |
| Number of page(s) | 9 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201527814 | |
| Published online | 02 May 2016 | |
Comparison of spatial and angular clustering of X-ray AGN
1
IAASARS, National Observatory of Athens,
I. Metaxa & V. Pavlou 1,
15236
Penteli,
Greece
e-mail:
mplionis@physics.auth.gr
2
Astronomical Laboratory, Department of Physics, University of
Patras, 26500
Rio-Patras,
Greece
3
Physics Department, University of Thessaloniki,
54124
Thessaloniki,
Greece
4
Instituto Nacional de Astrofísica, Óptica y Electronica, Luis Enrique Erro l,
Tonantzilla, Puebla, Mexico
5
Max-Planck-Institut
frü Extraterrestrische Physik (MPE), Postfach 1312, 85741
Garching,
Germany
6
Academy of Athens, Research Center for Astronomy and Applied Mathematics, Soranou
Efesiou 4, 11527
Athens,
Greece
Received: 24 November 2015
Accepted: 27 February 2016
The angular correlation function is a powerful tool for deriving the clustering properties of active galactic nuclei (AGN) and hence the mass of the corresponding dark matter halos in which they reside. However, recent studies based on the application of the angular correlation function on X-ray samples, yield results that are apparently inconsistent with those based on the direct estimation of the spatial correlation function. The goal of the present paper is to attempt to investigate this issue by analysing a well-defined sample. To this end we use the hard-band (2–10 keV) X-ray selected sources of the Chandra AEGIS fields, chosen because of the availability of accurately derived flux sensitivity maps. In particular we use the 186 hard-band sources with spectroscopic redshifts in the range z = 0.3–1.3, a range selected in order to contain the bulk of the AGN while minimizing the contribution of unknown clustering and luminosity evolution from very high redshifts. Using the projected spatial auto-correlation function, we derive a comoving clustering length of x0 = 5.4 ± 1.0h-1 Mpc (for γ = 1.8), which is consistent with results in the literature. We further derive the angular correlation function and corresponding spatial clustering length using the Limber’s inversion equation and a novel parametrization of the clustering evolution model that also takes the bias evolution of the host dark matter halo into account. The Limber’s inverted spatial comoving clustering length of x0 = 5.5 ± 1.2h-1 Mpc at a median redshift of z ≃ 0.75 matches the clustering length that is directly measured from the spatial correlation function analysis, but after introducing a significant non-linear contribution to the growing mode of perturbations; this contribution is estimated independently from literature results of x0 at different redshifts. Therefore, using this sample of hard X-ray AGN and our clustering evolution parametrization, we find an excellent consistency between the angular and spatial clustering analysis.
Key words: galaxies: active / large-scale structure of Universe / galaxies: statistics
© ESO, 2016
1. Introduction
The triggering mechanism for active galactic nucleus (AGN) activity is still an open issue (Alexander & Hickox 2012). Several semi-analytical models that include major galaxy mergers can explain the triggering mechanism for the most luminous AGN (Di Matteo et al. 2005; Hopkins et al. 2006), while it is possible that, in the lowest luminosity AGN regime, secular evolution (disk instabilities or minor interactions) may play the key role (Hopkins & Hernquist 2006; Bournaud et al. 2011).
Measuring the clustering of AGN can place valuable constraints on the AGN fueling modes and also provide us important information for AGN activity and their dark matter halo hosts. Merger models appear to reproduce the clustering of quasi stellar objects (QSOs) and the mass of dark matter halo in which they reside. However in the X-ray regime, clustering of X-ray AGN shows evidence that they live in more massive dark matter halos that are one order of magnitude larger (Koutoulidis et al. 2013) than the optical QSOs. This result suggests that the main accretion mode is the so-called hot halo mode (Fanidakis et al. 2012, 2013).
The clustering of AGN has been studied with excellent number statistics in the optical bands, particularly in large area surveys such as the 2QZ (Croom et al. 2005; Porciani & Norberg 2006) and the Sloan Digital Sky Survey (Li et al. 2006; Shen et al. 2009; Ross et al. 2009). However, optical QSO may represent only the tip of the iceberg of the AGN population. X-ray surveys find a surface density of about 20 000 deg-2 (Xue et al. 2011), which is about two orders of magnitude higher than that found in optical QSO surveys (Wolf et al. 2003). X-ray selected AGN form a superset of the optical selected AGN population since a large fraction of hard X-ray selected AGNs do not show strong optical activity (Barger 2005). Therefore, to study the clustering of the total AGN population, we need X-ray samples. Recently, several studies have attempted to measure the spatial correlation function of X-ray selected AGN, using spectroscopic redshifts to estimate their distances at moderate redshifts (Mullis et al. 2004; Gilli et al. 2005, 2009; Yang et al. 2006; Hickox et al. 2009; Coil et al. 2009; Krumpe et al. 2010; Starikova et al. 2011; Allevato et al. 2011; Koutoulidis et al. 2013) and at low redshifts (Cappelluti et al. 2010). Better statistics can be achieved using a cross-correlation analysis with galaxies, either using spectroscopic AGN and galaxy samples (Coil et al. 2009; Krumpe et al. 2010; Mountrichas & Georgakakis 2012) or using spectroscopy for the AGNs and photometric redshifts (their pdfs) for the galaxies alone (Mountrichas et al. 2013). An extensive spectroscopic campaign or high quality of photometric redshift measurements is required to derive the spatial clustering length for a large sample of X-ray AGN directly. However, even better statistics can be provided via the angular correlation function (ACF) for which all the detected sources are used independent of the availability of spectroscopy.
Several studies have explored the angular clustering of AGN in X-ray wavelengths using data from ROSAT (Vikhlinin & Forman 1995; Akylas et al. 2000), from XMM-Newton (Basilakos et al. 2004, 2005; Puccetti et al. 2006; Ebrero et al. 2009; Miyaji et al. 2007; Elyiv et al. 2012) or deep pencil CDFs fields (Gilli et al. 2005; Plionis et al. 2008). These studies measure the projected angular clustering and then via Limber’s equation (Peebles 1980) derive the corresponding spatial clustering length. Their results however appear to contradict the direct measurements of spatial clustering with all the angular correlation analyses finding systematically larger correlation amplitudes. Possible reasons for this discrepancy include uncertainties in the X-ray AGN luminosity function and thus in the corresponding redshift distribution and the clustering evolution model, both of which are necessary for the Limber’s inversion.
A way to break this impasse is to derive both the angular and spatial clustering for the same set of objects and compare their results directly. In this paper, we derive the spatial correlation function in the AEGIS field in the hard band, using 186 sources with spectroscopic redshift information. Then we derive the angular correlation function (ACF) for exactly the same sources, to infer the spatial correlation length, in one case, using the redshift distribution providing from luminosity function and, in the other case, using the redshift distribution as it is observed from the sources with spectroscopic redshifts.
The paper is organized as follows. In Sect. 2 we present the AEGIS data, in Sect. 3 we present our methodology and our modelling of the clustering evolution, while the results from our spatial and angular correlation function analysis, the Limber’s inversion of this analysis, and the comparison of the two clustering lengths are presented in Sect. 4. Discussion and conclusions are presented in Sect. 5. Throughout this work, we adopt a flat Λ cold dark matter (ΛCDM) cosmological model with H0 = 100 km s-1 Mpc-1.
2. AEGIS catalog
The ultra-deep field survey comprises of pointings at eight separate positions, each with a nominal exposure 200 ks, covering a total area of approximately 0.67 deg2 and centred at a = 14h17m, δ = + 52°30′ in a strip of 2 degrees in length with a flux limit of 3.8 × 10-16 erg s-1 cm-2 in the hard band. We use the X-ray source catalogue of Laird et al. (2009). In the hard band, we have a total of 741 X-ray sources. Spectroscopic redshifts are available from the DEEP2 survey (Davis et al. 2001, 2003; Coil et al. 2009) for 312 sources spanning the 0 <z< 4.3 range. However, in the current work we restrict our analysis to within the redshift interval z = 0.3–1.3, comprising 186 sources to minimize strong evolutionary effects of the spatial correlation function and of the hard-band X-ray luminosity function, while having enough sources to obtain a relatively robust clustering signal. The median redshift of this spectroscopic subsample is 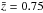 .
.
The advantage of using the AEGIS field for the purpose of this study is that source detection and sensitivity maps are constructed self-consistently following the method described in detail in Laird et al. (2009) and Georgakakis et al. (2008), which is an analytical method that accurately estimates the probability of detecting a source with a given X-ray flux at a given position on the detector accounting for vignetting and flux biases. Such sensitivity maps are essential for the production of accurate random catalogues and therefore for the reliable determination of the angular correlation function. It is likely that inconsistencies between the spatial and angular correlation function could, at least partially, originate from using sensitivity maps that are not consistent with the provided X-ray source lists.
3. Methodology
In order to quantify the low-order clustering of a distribution of sources, one uses the two-point correlation function that describes the excess probability over random of finding pairs of sources within a range of separations.
Depending on the availability of redshifts or not, one can use the spatial or angular correlation function. The former, ξ(r) involves sources within elemental volumes dVi separated by a distance r (e.g. Peebles 1980) and is given by dP = ⟨ n ⟩ 2 [ 1 + ξ(r) ] dV1dV2, where ⟨ n ⟩ is the mean space source density.
If redshifts are not available, one can measure the angular correlation function, w(θ), on the plane of sky, which involves finding pairs of sources within infinitesimal solid angles, dωi, separated by an angle θ. The equivalent mathematical description is given by dP = ⟨ n ⟩ 2 [ 1 + w(θ) ] dω1dω2. On small scales w(θ) has also been found to follow a power-law behaviour: w(θ) = (θ/θ0)β with β ≃ 1 − γ.
The actual correlation function estimator used, which is either spatial or angular (generically indicated with 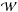 ), is given by the expression (Hamilton 1993)
), is given by the expression (Hamilton 1993) 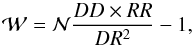 (1)with DD, RR, and DR the data-data, random-random, data-random pairs, respectively, at some separation r or θ, while
(1)with DD, RR, and DR the data-data, random-random, data-random pairs, respectively, at some separation r or θ, while 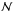 is a small correction equal to the ratio (NDNR)2/ND(ND − 1)NR(NR − 1), where ND and NR are the numbers of real and random data, respectively.
is a small correction equal to the ratio (NDNR)2/ND(ND − 1)NR(NR − 1), where ND and NR are the numbers of real and random data, respectively.
The variance of the correlation function at each separation is estimated according to 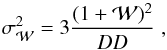 (2)which corresponds to that expected by the bootstrap resampling technique (Mo et al. 1992). To estimate the values of the correlation length (r0 or θ0) and slope γ from the derived correlation function, we use a χ2 minimization procedure between the derived
(2)which corresponds to that expected by the bootstrap resampling technique (Mo et al. 1992). To estimate the values of the correlation length (r0 or θ0) and slope γ from the derived correlation function, we use a χ2 minimization procedure between the derived 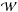 and a power-law model for the correlation function:
and a power-law model for the correlation function: 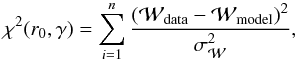 (3)where n is the number of separation bins. The minimization is over scales where the power law appears to be a reasonable fit to the data (thus, very large and very small scales are excluded from the fit, which in our case translate to: rp ≲ 1 and rp ≳ 20h-1 Mpc).
(3)where n is the number of separation bins. The minimization is over scales where the power law appears to be a reasonable fit to the data (thus, very large and very small scales are excluded from the fit, which in our case translate to: rp ≲ 1 and rp ≳ 20h-1 Mpc).
3.1. Modelling the two-point correlation function
The spatial correlation function of all different mass tracers of the large-scale structure of the Universe, i.e. galaxies, AGN or clusters of galaxies, is described well by a power law with two free parameters, r0 and γ; the former is related to the amplitude of clustering and the latter to the slope of the power law. Locally, at z ≃ 0, it takes the form 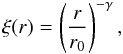 (4)where r is the proper separation between any two tracers. It has been found that γ ≃ 1.8 for a wide range of mass tracers. In an evolving Universe the spatial correlation function is a function of redshift, as expected from the fact that the density perturbations evolve with redshift.
(4)where r is the proper separation between any two tracers. It has been found that γ ≃ 1.8 for a wide range of mass tracers. In an evolving Universe the spatial correlation function is a function of redshift, as expected from the fact that the density perturbations evolve with redshift.
Traditionally the evolution of clustering has been parametrized with the use of the ϵ parameter, proposed originally within the framework of the EdS model (Groth & Peebles 1977; Peebles 1980; de Zotti et al. 1990), which characterizes the different clustering evolution models according to 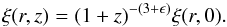 (5)Evidently, the value ϵ = −3 for which ξ(r,z) = ξ(r,0) corresponds to constant clustering in proper coordinates and the value ϵ = 0 corresponds to the stable clustering scenario in which clusters remain bound and stable; however the background density drops by (1 + z)3 as a result of the expansion, the value ϵ = −1 corresponds to the linear evolution (within the EdS model and neglecting the evolution of bias), while for ϵ = γ − 3 the clustering is constant in comoving coordinates. This can be appreciated from the evolution of the correlation length given, for the case of a power law (Eq. (4)), by
(5)Evidently, the value ϵ = −3 for which ξ(r,z) = ξ(r,0) corresponds to constant clustering in proper coordinates and the value ϵ = 0 corresponds to the stable clustering scenario in which clusters remain bound and stable; however the background density drops by (1 + z)3 as a result of the expansion, the value ϵ = −1 corresponds to the linear evolution (within the EdS model and neglecting the evolution of bias), while for ϵ = γ − 3 the clustering is constant in comoving coordinates. This can be appreciated from the evolution of the correlation length given, for the case of a power law (Eq. (4)), by 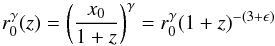 (6)and thus
(6)and thus 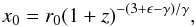 (7)where x0 is the comoving correlation length at redshift z (and r0 = x0(0)). We can now see that indeed if ϵ = γ − 3 we have a constant correlation length in comoving coordinates.
(7)where x0 is the comoving correlation length at redshift z (and r0 = x0(0)). We can now see that indeed if ϵ = γ − 3 we have a constant correlation length in comoving coordinates.
We prefer to use a more physical modelling that takes both the cosmological evolution of perturbations and of the linear bias of the mass tracers into account. We start from the definition of the correlation function, given by 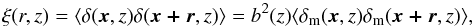 (8)where δ and δm are the linear density contrasts for the tracers (in our case X-ray AGNs) and for the underlying dark matter (DM), respectively, and b(z) is the evolution of the linear bias factor. Therefore, since δm evolves in the linear regime according to
(8)where δ and δm are the linear density contrasts for the tracers (in our case X-ray AGNs) and for the underlying dark matter (DM), respectively, and b(z) is the evolution of the linear bias factor. Therefore, since δm evolves in the linear regime according to 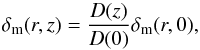 (9)with D(z) the linear growing mode of the density perturbations, we have that
(9)with D(z) the linear growing mode of the density perturbations, we have that 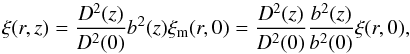 (10)with ξ(r,0) the present epoch spatial correlation function of the X-ray AGN. Introducing the normalized to the present linear growing mode and bias as
(10)with ξ(r,0) the present epoch spatial correlation function of the X-ray AGN. Introducing the normalized to the present linear growing mode and bias as 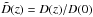 and
and 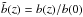 , respectively, we write Eq. (10) as
, respectively, we write Eq. (10) as 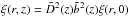 . However scales of a few Mpc, i.e. around the clustering length of the spatial correlation function, should be affected by non-linear effects and therefore modelling its evolution by the linear factor
. However scales of a few Mpc, i.e. around the clustering length of the spatial correlation function, should be affected by non-linear effects and therefore modelling its evolution by the linear factor 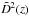 alone is inadequate. We therefore introduce a further factor
alone is inadequate. We therefore introduce a further factor 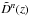 where the exponent n absorbs the non-linear effects. Therefore, Eq. (10) becomes
where the exponent n absorbs the non-linear effects. Therefore, Eq. (10) becomes  (11)and for a power-law correlation function we obtain the evolution of the correlation length in proper coordinates, r0(z), as
(11)and for a power-law correlation function we obtain the evolution of the correlation length in proper coordinates, r0(z), as 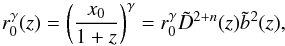 (12)which translates in comoving coordinates to
(12)which translates in comoving coordinates to 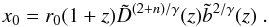 (13)It is important to appreciate the correspondence of the two different parametrizations of the clustering evolution. Comparing the generic formulation of Eq. (11) with that of the ϵ paremetrization (Eq. (5)), we see that what is implied is the equivalence of
(13)It is important to appreciate the correspondence of the two different parametrizations of the clustering evolution. Comparing the generic formulation of Eq. (11) with that of the ϵ paremetrization (Eq. (5)), we see that what is implied is the equivalence of 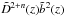 with (1 + z)− (3 + ϵ). This however is only valid for as long as both
with (1 + z)− (3 + ϵ). This however is only valid for as long as both 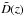 (as for example in the EdS model) and
(as for example in the EdS model) and 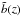 (as for example in the usual galaxy conserving bias model Fry 1996), are power-law functions of 1 + z. However, in the general case other than the EdS cosmological models and a more general bias evolution model, which is also valid at large redshifts, (e.g. Sheth & Tormen 1999; Tinker et al. 2010; Basilakos et al. 2008), the above inferred equivalence and thus the ϵ parametrization are not valid. For example, for the ΛCDM model the growing mode for the evolution of linear perturbations is given by (e.g. Peebles 1993)
(as for example in the usual galaxy conserving bias model Fry 1996), are power-law functions of 1 + z. However, in the general case other than the EdS cosmological models and a more general bias evolution model, which is also valid at large redshifts, (e.g. Sheth & Tormen 1999; Tinker et al. 2010; Basilakos et al. 2008), the above inferred equivalence and thus the ϵ parametrization are not valid. For example, for the ΛCDM model the growing mode for the evolution of linear perturbations is given by (e.g. Peebles 1993) 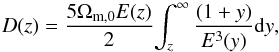 (14)where E(z) = [ Ωm,0(1 + z)3 + ΩΛ ] 1 / 2 (for a flat Λ ≠ 0 model), while Ωm,0 and ΩΛ are the parametrized present epoch matter and cosmological constant density parameters, respectively. An EdS look-alike (normalized) fitting function of Eq. (14) is
(14)where E(z) = [ Ωm,0(1 + z)3 + ΩΛ ] 1 / 2 (for a flat Λ ≠ 0 model), while Ωm,0 and ΩΛ are the parametrized present epoch matter and cosmological constant density parameters, respectively. An EdS look-alike (normalized) fitting function of Eq. (14) is 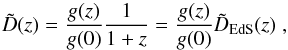 (15)where g(z) is a function of redshift, Ωm,0 and ΩΛ (Carroll et al. 1992; Lahav & Suto 2004).
(15)where g(z) is a function of redshift, Ωm,0 and ΩΛ (Carroll et al. 1992; Lahav & Suto 2004).
It will be instructive to graphically compare the two parametrizations and appreciate their differences. To this end we use the bias evolution scheme of Basilakos & Plionis (2001, 2003), which is based on linear perturbation theory and given by (Basilakos et al. 2011) 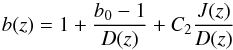 (16)with
(16)with 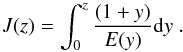 (17)The constants b0 (the present day bias factor) and C2 depend on the host dark matter halo mass and for the ΛCDM model are given by
(17)The constants b0 (the present day bias factor) and C2 depend on the host dark matter halo mass and for the ΛCDM model are given by ![\begin{equation} b_0(M_{\rm h})=0.857\left[1+\left(C_{\rm m} \frac{M_{\rm h}}{10^{14} ~h^{-1}~M_{\odot}}\right)^{0.55}\right] \end{equation}](/articles/aa/full_html/2016/06/aa27814-15/aa27814-15-eq96.png) (18)
(18)![\begin{equation} C_2(M_{\rm h})=1.105\left[1+\left(C_{\rm m} \frac{M_{\rm h}}{10^{14}~ h^{-1}~M_{\odot}}\right)^{0.255}\right] , \end{equation}](/articles/aa/full_html/2016/06/aa27814-15/aa27814-15-eq97.png) (19)where Cm = Ωm,0/ 0.27 (Basilakos et al. 2012). This bias evolution model has been thoroughly tested and found to rate very well in reproducing N-body simulation data (Basilakos et al. 2008) as well as fitting observational data (Papageorgiou et al. 2012).
(19)where Cm = Ωm,0/ 0.27 (Basilakos et al. 2012). This bias evolution model has been thoroughly tested and found to rate very well in reproducing N-body simulation data (Basilakos et al. 2008) as well as fitting observational data (Papageorgiou et al. 2012).
 |
Fig. 1 Redshift evolution of the comoving clustering length for the two different parametrizations of clustering evolution. For the case of our model (Eq. (13)), shown as black and blue curves, the different evolution behaviours shown correspond to the indicated parameters (n,Mh). The specific values of these parameters have been chosen such as to resemble the ϵ = −1.2 and ϵ = 0 models of the traditional parametrization of Eq. (7), shown in red, which correspond to the constant in comoving coordinates clustering (for γ = 1.8) and to the stable clustering models (for details see the text). |
We therefore see that through the dependence of the bias factor on the dark matter halo mass, one expects a different clustering evolution for dark matter halos of different mass for the same values of n and γ. In order to appreciate our parametrization of the clustering evolution we present in Fig. 1 the evolution of the comoving clustering length x0 for models that have been purposely selected to resemble some ϵ based models. As can be seen the model with (n,Mh) = (3.5,1013M⊙) is equivalent with the constant in comoving coordinates clustering model (ϵ = γ − 3 = −1.2) up to very large redshifts (z ~ 6). No other (n,Mh) combination can provide such an equivalence up to such high redshifts. However, as we can again see in Fig. 1, one can find (n,Mh) combinations that correspond to the comoving clustering model, but up to z ≃ 1.2, as the example shown with (n,Mh) = (2.5,1012M⊙). In fact one can derive the degeneracy between the n and Mh parameters such that the clustering evolution is constant in comoving coordinates (ϵ = −1.2), but up to z ~ 1.2, since beyond this redshift the equivalence is unattainable. In Fig. 2 we present the corresponding 1, 2, and 3σ contours in the (n,Mh) parameter space of the solution that provides the above equivalence with the ϵ = −1.2 model. The range is dictated by the uncertainty that we have imposed on x0, which is taken to be 10% of x0, typical of current accurate measurements. The degeneracy is clear and it can only be broken if we either impose a value of n, for example from the expected slope of the power spectrum on these scales, or from an independent estimate of the mass of the dark matter halos in which the tracers (in our case X-ray selected AGN) reside.
 |
Fig. 2 Contour ranges of 1, 2 and 3σ in the n,Mh parameter plane for the case where our clustering evolution scheme corresponds to the constant in comoving coordinates model (imposed up to z = 1 in this example). The strong degeneracy of the parameters is evident. |
Similarly, larger values of n provide clustering evolution behaviours that start resembling the ϵ = 0 stable clustering model. For example, in Fig. 1 we show (n,Mh) = (5,1013M⊙) and (4.3,1012M⊙), which closely follow the ϵ = 0 model, indicating again the degeneracy problem discussed previously.
In the following, we use a value for the dark matter halo mass derived from our previous spatial clustering analysis of Chandra X-ray selected AGN (Koutoulidis et al. 2013), ie., Mh ≃ 1.3 × 1013h-1M⊙. As we already saw, for this value of the halo mass and for n ≃ 5.5, one obtains the constant in comoving coordinates model for the evolution of clustering.
3.2. Estimating the spatial correlation function
Although the recessional velocities of extragalactic sources are used as distance indicators, they are contaminated by local peculiar velocities and thus the corresponding distances are distorted by the so-called redshift-space distortion effect. An estimator that avoids such effects, while using redshifts to infer distances, is the projected correlation function wp(rp) (Davis & Peebles 1983), which is based on deconvolving the redshift-based comoving distance, s, in a component parallel and perpendicular to the line of sight, π and rp, respectively, i.e. 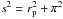 . The redshift-space correlation function can therefore be written as
. The redshift-space correlation function can therefore be written as 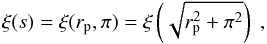 (20)and the so-called projected correlation function can be found by integrating ξ(rp,π) along the π direction
(20)and the so-called projected correlation function can be found by integrating ξ(rp,π) along the π direction 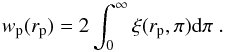 (21)Then the real space correlation function can be recovered according to (Davis & Peebles 1983)
(21)Then the real space correlation function can be recovered according to (Davis & Peebles 1983) 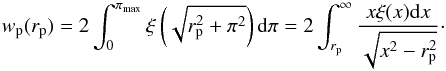 (22)Modelling ξ(x) as a power law one obtains
(22)Modelling ξ(x) as a power law one obtains 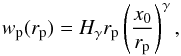 (23)with x0 the comoving clustering length at the effective (median) redshift of the sample and
(23)with x0 the comoving clustering length at the effective (median) redshift of the sample and 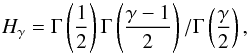 (24)with Γ the usual gamma function. Equation (22) holds strictly for πmax = ∞, while the integral is performed up to a finite value of πmax to avoid redshift-space distortions, which in turn produces an underestimation of the underlying correlation function. For a power-law correlation function, this underestimation is easily inferred from Eq. (22) and is given by (e.g. Starikova et al. 2011)
(24)with Γ the usual gamma function. Equation (22) holds strictly for πmax = ∞, while the integral is performed up to a finite value of πmax to avoid redshift-space distortions, which in turn produces an underestimation of the underlying correlation function. For a power-law correlation function, this underestimation is easily inferred from Eq. (22) and is given by (e.g. Starikova et al. 2011) 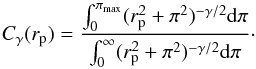 (25)The free of redshift-space distortions correlation function, taking into account the above statistical correction and under the power-law assumption, is then provided by
(25)The free of redshift-space distortions correlation function, taking into account the above statistical correction and under the power-law assumption, is then provided by 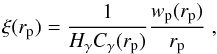 (26)which can then be fitted to the power-law model (using Eq. (3)) to estimate the final and corrected values of the clustering amplitude and slope. Alternatively, one can crudely derive the corrected correlation amplitude (for the slope γ and amplitude x0 estimated by fitting Eq. (23)) by
(26)which can then be fitted to the power-law model (using Eq. (3)) to estimate the final and corrected values of the clustering amplitude and slope. Alternatively, one can crudely derive the corrected correlation amplitude (for the slope γ and amplitude x0 estimated by fitting Eq. (23)) by 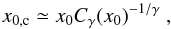 (27)(e.g. Starikova et al. 2011; Koutoulidis et al. 2013). The correction factor values range between Cγ ≃ 0.85, at rp = 3 h-1 Mpc and Cγ ≃ 0.45 at rp = 10 h-1 Mpc (for the πmax = 10 h-1 Mpc case).
(27)(e.g. Starikova et al. 2011; Koutoulidis et al. 2013). The correction factor values range between Cγ ≃ 0.85, at rp = 3 h-1 Mpc and Cγ ≃ 0.45 at rp = 10 h-1 Mpc (for the πmax = 10 h-1 Mpc case).
3.3. Estimating the angular correlation function and Limber’s Inversion
Another approach that completely avoids redshift-space distortion effects is to measure the angular correlation function, and then under some assumptions to infer the spatial correlation function through the Limber’s inversion equation (Limber 1953).
To this end we estimate the angular correlation function in angular logarithmic bins, covering the range 10′′<θ< 3800′′ for both the complete source sample and the spectroscopic subsample. Furthermore, we numerically estimated the amplitude of the integral constraint correction (Roche & Eales 1999), which however was found to be negligible and thus we neglect it in what follows.
It has been demonstrated (Limber 1953) that the angular correlation function, w(θ), can be deprojected to yield the spatial correlation function, ξ(r), via an integral equation. Under the power-law representation of ξ(r) (Eq. (4)) the angular correlation length, θ0, is related to the corresponding spatial correlation length, x0, at z = 0. According to (Peebles 1980) 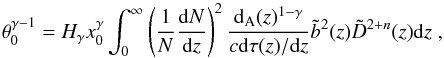 (28)where dA is the angular diameter distance, τ(z) is the look-back time, and dN/ dz is the number of sources per unit redshift interval within a solid angle ωs given by
(28)where dA is the angular diameter distance, τ(z) is the look-back time, and dN/ dz is the number of sources per unit redshift interval within a solid angle ωs given by 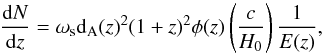 (29)where
(29)where 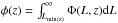 is the redshift selection function of the sources, i.e. the probability that a source at a comoving distance x is detected, and Φ(L,z) is the luminosity function of the sources1.
is the redshift selection function of the sources, i.e. the probability that a source at a comoving distance x is detected, and Φ(L,z) is the luminosity function of the sources1.
3.4. Construction of the random catalogues
We follow the standard approach for creating the comparison random sample, mimicking the source catalogue systematic effects and biases, according to which each simulated source is placed at a random position on the part of the sky covered by the survey in hand with a flux randomly extracted from the observed source log N − log S (Georgakakis et al. 2008). If the flux is above the value allowed by the sensitivity map at that position, the simulated source is kept in the random sample. In the current work, we use the AEGIS field sensitivity maps of (Laird et al. 2009).
For the spatial correlation function, a random redshift is also assigned to each source from the observed source redshift distribution N(z) (optimally taking into account its variation as a function of flux). As a test of possible disadvantages of this method, caused by the fact that it does not take any unknown inhomogeneities and systematics of the follow-up spectroscopic observations into account, we follow the alternative random catalogue construction approach of Gilli et al. (2005) (hereafter G05). This is based on keeping the angular coordinates of the sources unaltered while reshuffling their redshifts and smoothing the corresponding redshift distribution. For the smoothing we use a Gaussian kernel with a standard deviation of σz = 0.2. This offers a compromise between scales that are either too small, and thus may reproduce the z-space clustering, or too large and thus over-smooth the observed redshift distribution. We verified that our results do not change significantly when using the range σz = 0.1–0.3.
 |
Fig. 3 Projected wp(rp) correlation function for the AEGIS field. The black line corresponds to the fit with free γ, while the red line corresponds to that for γ = 1.8. The inset panel show the 1, 2, and 3σ likelihood contours in the two-parameter plane of power-law solutions. The y-axis of the inset plot is the combined parameter |
4. Results
4.1. Direct spatial correlation function
We use the estimator provided by Eq. (1) and 12 logarithmic separation bins covering the range 0.5 <rp< 40 h-1 Mpc to estimate the projected correlation function, wp(rp). As for the choice of πmax, it should be a compromise between having an optimal correlation signal-to-noise ratio and reducing the excess noise from high π separations, which are affected by redshift-space distortions. We investigated the sensitivity of wp(rp) on πmax, which we varied in the range [ 5,25 ] h-1 Mpc (see also Koutoulidis et al. 2013), and we found that it is very stable. We present the results based on πmax = 10 h-1 Mpc. In Fig. 3 we present the derived hard-band projected correlation function. The results of the corresponding power-law fits to the correlation function data are listed in Table 1.
Using the G05 method to construct the random catalogue, we find the best-fit correlation length of wp(rp) to be x0 = 4.4 ± 0.7 h-1 Mpc (with γ = 1.7 ± 0.1), which is in excellent agreement with the total (0.5–8 keV) band result (x0 = 4.3 ± 0.6 h-1 Mpc, γ = 1.6 ± 0.1, reported in Table 2 of Koutoulidis et al. 2013). Once we correct for the factor Cγ(rp) (Eq. (25)), the above result translates to a ξ(rp) with x0,c = 5.4 ± 1.0h-1 Mpc (for γ = 1.8), which implies that had we not corrected for the instrinsic underestimation of ξ(r) when using the wp(rp) estimator and a finite value of πmax (in our case 10h-1 Mpc), we would have underestimated the true correlation length by ~20%.
We also tested and found that these results remain robust when changing the random construction method to that based on the sensitivity map. Our results also agree with other previously derived clustering results of the same field. Coil et al. (2009) derived the AGN/galaxy cross-correlation using 113 Chandra AGN in the full 0.5–7 keV and found x0 = 5.9 ± 0.9 h-1 Mpc at a median 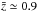 .
.
4.2. Angular correlation function
In Table 2 we present the best-fit values of the ACF parameters γ and θ0 for the whole and for the spectroscopic subsample, while in Fig. 4 we plot the corresponding w(θ) for both samples. It is evident that the angular clustering amplitude for the spectroscopic sample (Spec) appears significantly larger than that of the whole sample (All). We should also point out that the w(θ) of the All sample has negative values at some separations (as can be inferred from Fig. 4), while the power-law fit was only performed on the positive values, a fact that implies that the derived amplitude is an upper limit to the true clustering of this sample. The apparent difference between the ACF of the Spec and All samples could be attributed to the dependence of clustering on the limiting flux (e.g. Plionis et al. 2008; Ebrero et al. 2009; Elyiv et al. 2012). Indeed, as we show in Fig. 5, the flux distributions for the spectroscopic sample (red shaded region) is shifted to higher fluxes with respect to the complete sample of sources (All, black thick line), where corresponding mean fluxes are fx ≃ 7.8 × 10-15 and 5.4 × 10-15 erg s-1 cm-2, respectively. The observed difference is indeed statistically significant as shown by the Kolmogorov-Smirnov two-sample test, which provides a probability of consistency between the two distributions of only ~2 × 10-8.
 |
Fig. 4 Angular correlation function of the AEGIS field for the subsample with spectroscopic information within 0.3 <z< 1.3 (i.e. 186 sources, black filled circles) and for the complete X-ray source sample (i.e. 741 sources, red filled triangles) in the hard band. The solid line corresponds to the fixed γ = 1.8 fit, while the dashed line represents the best power-law fit. The error bars correspond to 1σ uncertainties. The inset plot presents the 1 and 3σ contours in the fitted (θ0,γ) parameter space. |
Spatial clustering results for the spectroscopic subsample of the AEGIS field (186 sources within 0.3 <z< 1.3).
AEGIS hard-band angular correlation function results for the complete sample (All) and for those sources with spectroscopic redshifts (Spec, 0.3 <z< 1.3).
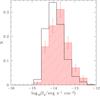 |
Fig. 5 Comparison of the normalized flux distributions of the complete sample (thick black line) and of the spectroscopic subsample (red shaded region). |
4.3. Correlation length by inverting w(θ)
We use Eq. (28) to derive the spatial clustering length from the angular correlation function and, as the source N(z) distribution, we use either the integral of the hard-band luminosity and density evolution (LADE) luminosity function (Aird et al. 2010) or the redshift distribution of the sources with available spectroscopic redshifts directly. Both approaches lead to exactly the same results and thus we present results based on the later approach.
The next step to derive the spatial clustering length is to somehow estimate the exponent of the growth factor, 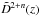 . One could therefore use literature clustering estimates of hard-band AGN samples, dominating different redshits, and fit Eq. (13) to such data. Since however, the available hard-band results are very few, i.e. that of (Mountrichas & Georgakakis 2012) with r0 = 4.8 ± 1 h-1 Mpc at
. One could therefore use literature clustering estimates of hard-band AGN samples, dominating different redshits, and fit Eq. (13) to such data. Since however, the available hard-band results are very few, i.e. that of (Mountrichas & Georgakakis 2012) with r0 = 4.8 ± 1 h-1 Mpc at  and of CDF-N with r0 = 5 ± 1 h-1 Mpc at
and of CDF-N with r0 = 5 ± 1 h-1 Mpc at  (Gilli et al. 2005)2, we also use total band (0.5–8 keV) clustering results (e.g. Coil et al. 2009; Starikova et al. 2011; Allevato et al. 2011; Koutoulidis et al. 2013) and exclude the results of
(Gilli et al. 2005)2, we also use total band (0.5–8 keV) clustering results (e.g. Coil et al. 2009; Starikova et al. 2011; Allevato et al. 2011; Koutoulidis et al. 2013) and exclude the results of 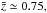 which appear to present an erratic behaviour in all available studies (see Fig. 8 and relevant discussion in Koutoulidis et al. 2013). It appears that there is a weak but consistent increase of the value of x0 with redshift. The use of total band results is also supported by the fact that the corresponding AEGIS correlation function results are in excellent agreement with those of the hard-band, as discussed previously.
which appear to present an erratic behaviour in all available studies (see Fig. 8 and relevant discussion in Koutoulidis et al. 2013). It appears that there is a weak but consistent increase of the value of x0 with redshift. The use of total band results is also supported by the fact that the corresponding AEGIS correlation function results are in excellent agreement with those of the hard-band, as discussed previously.
Subsequently, we perform a χ2 minimization fitting of the above data to Eq. (13), leaving as a free parameter the exponent n and fixing the halo mass to Mh = 1.3 × 1013M⊙, which we derived in Koutoulidis et al. (2013). The resulting best-fit value for the exponent is 2 + n = 5.03 ± 0.2. The corresponding 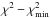 and clustering evolution curves can be seen in the left and right panels of Fig. 6, respectively (in black). Alternatively, we can leave both the exponent n and the halo mass Mh as free parameters. In this case the minimization procedure provides a degenerate solution, which is similar to that of Fig. 2. As an example, we present in the right panel of Fig. 6 another clustering evolution model (red curve), that with (n,Mn) ≃ (2.0,2 × 1012M⊙), consistent with the data and selected from within the 1σ range of the degenerate solution.
and clustering evolution curves can be seen in the left and right panels of Fig. 6, respectively (in black). Alternatively, we can leave both the exponent n and the halo mass Mh as free parameters. In this case the minimization procedure provides a degenerate solution, which is similar to that of Fig. 2. As an example, we present in the right panel of Fig. 6 another clustering evolution model (red curve), that with (n,Mn) ≃ (2.0,2 × 1012M⊙), consistent with the data and selected from within the 1σ range of the degenerate solution.
Taking the above parameters into account and using Eq. (28), we deproject the ACF and derive the spatial clustering length. Because the Limber’s inversion provides the spatial clustering length at z = 0, to predict its value at another redshift it is necessary to normalize Eq. (13) to that redshift. As seen in Table 3, normalizing to z = 0.75, which corresponds to the median redshift of the spectroscopic AEGIS hard-band sample, we find an excellent agreement between the direct measure of x0 and the corresponding Limber’s inverted measure. Similarly, normalizing to z = 0.1, which is the median redshift of the sample studied in (Mountrichas & Georgakakis 2012), we again find an excellent agreement with the direct x0 measure (see Table 3).
 |
Fig. 6 Left panel: result of the χ2 minimization procedure of fitting the parameter 2 + n. Right panel: the clustering evolution model (black curve), corresponding to the best fit value (n = 3.03) for Mh = 1.3 × 1013M⊙, overplotting the literature x0 data in the hard and total band. Our direct estimate (not used in the χ2 minimization procedure) is shown as the filled circle. As a manifestation of the degeneracy discussed in Sect. 2, we show the expected clustering evolution for another (n,Mn) pair ≃ (2.0,2 × 1012M⊙) which is consistent with the data (red curve). |
Comparison of the inverted ACF AEGIS hard-band correlation length, x0 (in h-1 Mpc) and that directly measured by at  (Mountrichas & Georgakakis 2012) and
(Mountrichas & Georgakakis 2012) and 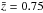 (our current measure).
(our current measure).
Since the parameterization of X-ray AGN clustering evolution (Eq. (10)) reproduces the direct spatial correlation length for a particular value of n, we also apply it to the clustering results of the whole AEGIS X-ray source sample (θ0 = 1.2 ± 0.6 arcsec with γ = 1.8 – Table 2). We use the expected N(z), based on the LADE luminosity function of Aird et al. (2010), but for the whole interval z = 0–4, since we cannot a priori assess whether the sources without redshifts correspond to nearby low-luminosity or distant high-luminosity sources. The predicted median redshift of this sample is 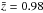 . Using Limber’s inversion, we obtain r0 = 4.8 ± 0.9h-1 Mpc at z = 0.1 and r0 = 5.5 ± 1.0h-1 Mpc at z = 0.1 and z = 0.75, respectively, which are in excellent agreement with the scaled 0.3 <z< 1.3 and the direct ξ(rp) results (see Table 3). Given these results, we can infer that the sources without redshift information seem to follow roughly the same clustering evolution as the observed. Moreover the above procedure indicates the potential for an accurate derivation of the spatial correlation length using only the angular clustering of all the available sources, independent of the availability of complete spectral information or not, for as long as the luminosity function in hand relates to the whole sample of sources.
. Using Limber’s inversion, we obtain r0 = 4.8 ± 0.9h-1 Mpc at z = 0.1 and r0 = 5.5 ± 1.0h-1 Mpc at z = 0.1 and z = 0.75, respectively, which are in excellent agreement with the scaled 0.3 <z< 1.3 and the direct ξ(rp) results (see Table 3). Given these results, we can infer that the sources without redshift information seem to follow roughly the same clustering evolution as the observed. Moreover the above procedure indicates the potential for an accurate derivation of the spatial correlation length using only the angular clustering of all the available sources, independent of the availability of complete spectral information or not, for as long as the luminosity function in hand relates to the whole sample of sources.
5. Discussion and conclusions
A variety of studies have measured the projected angular clustering of X-ray AGN, and then via Limber’s equation derived the corresponding spatial clustering length. Although there are obvious merits in this approach, for example the fact that one uses all the available sources while being unaffected by redshift-space distortions, there are disadvantages and inherent assumptions in the deprojection; the most important of these is the unknown clustering evolution model of the sources. There have been interesting parametrizations of such an evolution, the most common of which is the 1 + z power-law model (the so-called ϵ models; see Eq. (5)), which has been used extensively to model the evolution of clustering. However, it is rather phenomenological in nature and thus it does not provide a good physical insight into the evolution governed by the clustering of dark matter halos (McCracken et al. 2001). We presented a more generic parametrization that allows for different cosmological models and different host dark matter halo masses via their different bias evolution, and we showed the regimes where the two parametrizations coincide.
One can identify two interesting extremes of the clustering evolution: The stable clustering scenario (ϵ = 0 or n ≳ 4.2 depending also on the halo mass, for the two different parametrizations, respectively) in which clusters remain bound and stable, while owing to the expansion the background density drops by (1 + z)3; and the constant in comoving coordinates scenario (ϵ = γ−3 or n ≲ 3.5; see Sect. 2) in which pairs of sources follow the Hubble flow, meaning that their separation remains constant in comoving coordinates. Interestingly, the correlation function analyses of optically selected QSO samples (Croom et al. 2005; Ross et al. 2009) seem to suggest a roughly comoving evolution model of their clustering, while simulations also seem to disfavour the stable clustering evolution model (Jain 1997).
We used the comoving clustering lengths of X-ray AGN at a variety of different redshifts provided in the literature (Gilli et al. 2005; Coil et al. 2009; Starikova et al. 2011; Allevato et al. 2011; Mountrichas & Georgakakis 2012; Koutoulidis et al. 2013) to fit the unknown slope of the non-linear contribution to the growing mode of perturbations to model the evolution of clustering of X-ray AGN. We then applied this to the Limber’s inversion of the angular correlation function of the subsample of AEGIS X-ray AGN with spectroscopic data within 0.3 <z< 1.3 to find an excellent agreement with the directly measured spatial clustering of the same sources.
The reason for the discrepancies between angular and spatial clustering results of various previous studies is still not clearly identified, although the clustering evolution parametrization used in this work does hint at the possibility that the different host halo masses for the different sources, and thus their different bias evolution, induce a different clustering evolution than one assumes when using the phenomenological ϵ parametrization.
The present work appears to pave the way for the application of the angular correlation function analysis on large X-ray selected AGN samples, such as the eROSITA survey which is expected to detect over 3 × 106 AGN. These large numbers of sources render the use of spectroscopic redshifts to derive their spatial clustering rather impossible, as this would demand unrealistically large follow-up optical telescope time.
In our case the sources are X-ray selected AGN and the luminosity function that we use is that of the hard-band from (Aird et al. 2010).
The correlation length of CDF-S (r0 = 9.8 ± 1 h-1Mpc at 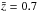 ) is not considered due to the presence of superclusters which affect the clustering amplitude (Gilli et al. 2003).
) is not considered due to the presence of superclusters which affect the clustering amplitude (Gilli et al. 2003).
References
- Aird, J., Nandra, K., Laird, E. S., et al. 2010, MNRAS, 401, 2531 [NASA ADS] [CrossRef] [Google Scholar]
- Akylas, A., Georgantopoulos, I., & Plionis, M. 2000, MNRAS, 318, 1036 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, D. M., & Hickox, R. C. 2012, New Astron. Rev., 56, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Allevato, V., Finoguenov, A., Cappelluti, N., et al. 2011, ApJ, 736, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Barger, A. J. 2005, Roy. Soc. Lond. Phil. Trans. Ser. A, 363, 685 [NASA ADS] [CrossRef] [Google Scholar]
- Basilakos, S., & Plionis, M. 2001, ApJ, 550, 522 [NASA ADS] [CrossRef] [Google Scholar]
- Basilakos, S., & Plionis, M. 2003, ApJ, 593, L61 [Google Scholar]
- Basilakos, S., Georgakakis, A., Plionis, M., & Georgantopoulos, I. 2004, ApJ, 607, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Basilakos, S., Plionis, M., Georgakakis, A., & Georgantopoulos, I. 2005, MNRAS, 356, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Basilakos, S., Plionis, M., & Ragone-Figueroa, C. 2008, ApJ, 678, 627 [NASA ADS] [CrossRef] [Google Scholar]
- Basilakos, S., Plionis, M., & Pouri, A. 2011, Phys. Rev. D, 83, 123525 [NASA ADS] [CrossRef] [Google Scholar]
- Basilakos, S., Dent, J. B., Dutta, S., Perivolaropoulos, L., & Plionis, M. 2012, Phys. Rev. D, 85, 123501 [NASA ADS] [CrossRef] [Google Scholar]
- Bournaud, F., Dekel, A., Teyssier, R., et al. 2011, ApJ, 741, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Cappelluti, N., Ajello, M., Burlon, D., et al. 2010, ApJ, 716, L209 [NASA ADS] [CrossRef] [Google Scholar]
- Carroll, S. M., Press, W. H., Turner, E. L., et al. 1992, ARA&A, 30, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Coil, A. L., Georgakakis, A., Newman, J. A., et al. 2009, ApJ, 701, 1484 [NASA ADS] [CrossRef] [Google Scholar]
- Croom, S. M., Boyle, B. J., Shanks, T., et al. 2005, MNRAS, 356, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, M., & Peebles, P. J. E. 1983, ApJ, 267, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, M., Newman, J. A., Faber, S. M., & Phillips, A. C. 2001, in Deep Fields, eds. S. Cristiani, A. Renzini, & R. E. Williams, Proc. ESO Workshop, 241 [Google Scholar]
- Davis, M., Faber, S. M., Newman, J., et al. 2003, in SPIE Conf. Ser. 4834, ed. P. Guhathakurta, 161 [Google Scholar]
- de Zotti, G., Persic, M., Franceschini, A., et al. 1990, ApJ, 351, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Di Matteo, T., Springel, V., & Hernquist, L. 2005, in Growing Black Holes: Accretion in a Cosmological Context, eds. A. Merloni, S. Nayakshin, & R. A. Sunyaev, 340 [Google Scholar]
- Ebrero, J., Mateos, S., Stewart, G. C., Carrera, F. J., & Watson, M. G. 2009, A&A, 500, 749 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elyiv, A., Clerc, N., Plionis, M., et al. 2012, A&A, 537, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fanidakis, N., Baugh, C. M., Benson, A. J., et al. 2012, MNRAS, 419, 2797 [NASA ADS] [CrossRef] [Google Scholar]
- Fanidakis, N., Georgakakis, A., Mountrichas, G., et al. 2013, MNRAS, 435, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Fry, J. N. 1996, ApJ, 461, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Georgakakis, A., Nandra, K., Laird, E. S., Aird, J., & Trichas, M. 2008, MNRAS, 388, 1205 [NASA ADS] [CrossRef] [Google Scholar]
- Gilli, R., Cimatti, A., Daddi, E., et al. 2003, ApJ, 592, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Gilli, R., Daddi, E., Zamorani, G., et al. 2005, A&A, 430, 811 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gilli, R., Zamorani, G., Miyaji, T., et al. 2009, A&A, 494, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Groth, E. J., & Peebles, P. J. E. 1977, ApJ, 217, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Hamilton, A. J. S. 1993, ApJ, 417, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Hickox, R. C., Jones, C., Forman, W. R., et al. 2009, ApJ, 696, 891 [Google Scholar]
- Hopkins, P. F., & Hernquist, L. 2006, ApJS, 166, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Hernquist, L., Cox, T. J., et al. 2006, ApJ, 163, 1 [NASA ADS] [Google Scholar]
- Jain, B. 1997, MNRAS, 287, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Koutoulidis, L., Plionis, M., Georgantopoulos, I., & Fanidakis, N. 2013, MNRAS, 428, 1382 [NASA ADS] [CrossRef] [Google Scholar]
- Krumpe, M., Miyaji, T., & Coil, A. L. 2010, ApJ, 713, 558 [NASA ADS] [CrossRef] [Google Scholar]
- Lahav, O., & Suto, Y. 2004, Liv. Rev. Rel., 7, 8 [Google Scholar]
- Laird, E. S., Nandra, K., Georgakakis, A., et al. 2009, ApJ, 180, 102 [Google Scholar]
- Li, C., Kauffmann, G., Wang, L., et al. 2006, MNRAS, 373, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Limber, D. N. 1953, ApJ, 117, 134 [NASA ADS] [CrossRef] [Google Scholar]
- McCracken, H. J., Le Fèvre, O., Brodwin, M., et al. 2001, A&A, 376, 756 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miyaji, T., Zamorani, G., Cappelluti, N., et al. 2007, ApJ, 172, 396 [Google Scholar]
- Mo, H. J., Jing, Y. P., & Boerner, G. 1992, ApJ, 392, 452 [NASA ADS] [CrossRef] [Google Scholar]
- Mountrichas, G., & Georgakakis, A. 2012, MNRAS, 420, 514 [NASA ADS] [CrossRef] [Google Scholar]
- Mountrichas, G., Georgakakis, A., Finoguenov, A., et al. 2013, MNRAS, 430, 661 [NASA ADS] [CrossRef] [Google Scholar]
- Mullis, C. R., Henry, J. P., Gioia, I. M., et al. 2004, ApJ, 617, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Papageorgiou, A., Plionis, M., Basilakos, S., & Ragone-Figueroa, C. 2012, MNRAS, 422, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Peebles, P. J. E. 1980, The large-scale structure of the universe (Princeton University Press) [Google Scholar]
- Peebles, P. J. E. 1993, Principles of Physical Cosmology (Princeton University Press) [Google Scholar]
- Plionis, M., Rovilos, M., Basilakos, S., Georgantopoulos, I., & Bauer, F. 2008, ApJ, 674, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Porciani, C., & Norberg, P. 2006, MNRAS, 371, 1824 [NASA ADS] [CrossRef] [Google Scholar]
- Puccetti, S., Fiore, F., D’Elia, V., et al. 2006, A&A, 457, 501 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roche, N., & Eales, S. A. 1999, MNRAS, 307, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Ross, N. P., Shen, Y., Strauss, M. A., et al. 2009, ApJ, 697, 1634 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., Strauss, M. A., Ross, N. P., et al. 2009, ApJ, 697, 1656 [NASA ADS] [CrossRef] [Google Scholar]
- Sheth, R. K., & Tormen, G. 1999, MNRAS, 308, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Starikova, S., Cool, R., Eisenstein, D., et al. 2011, ApJ, 741, 15 [Google Scholar]
- Tinker, J. L., Robertson, B. E., Kravtsov, A. V., et al. 2010, ApJ, 724, 878 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., & Forman, W. 1995, ApJ, 455, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, C., Wisotzki, L., Borch, A., et al. 2003, A&A, 408, 499 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xue, Y. Q., Luo, B., Brandt, W. N., et al. 2011, ApJS, 195, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, Y., Mushotzky, R. F., Barger, A. J., & Cowie, L. L. 2006, ApJ, 645, 68 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Spatial clustering results for the spectroscopic subsample of the AEGIS field (186 sources within 0.3 <z< 1.3).
AEGIS hard-band angular correlation function results for the complete sample (All) and for those sources with spectroscopic redshifts (Spec, 0.3 <z< 1.3).
Comparison of the inverted ACF AEGIS hard-band correlation length, x0 (in h-1 Mpc) and that directly measured by at  (Mountrichas & Georgakakis 2012) and
(Mountrichas & Georgakakis 2012) and 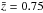 (our current measure).
(our current measure).
All Figures
 |
Fig. 1 Redshift evolution of the comoving clustering length for the two different parametrizations of clustering evolution. For the case of our model (Eq. (13)), shown as black and blue curves, the different evolution behaviours shown correspond to the indicated parameters (n,Mh). The specific values of these parameters have been chosen such as to resemble the ϵ = −1.2 and ϵ = 0 models of the traditional parametrization of Eq. (7), shown in red, which correspond to the constant in comoving coordinates clustering (for γ = 1.8) and to the stable clustering models (for details see the text). |
| In the text | |
 |
Fig. 2 Contour ranges of 1, 2 and 3σ in the n,Mh parameter plane for the case where our clustering evolution scheme corresponds to the constant in comoving coordinates model (imposed up to z = 1 in this example). The strong degeneracy of the parameters is evident. |
| In the text | |
 |
Fig. 3 Projected wp(rp) correlation function for the AEGIS field. The black line corresponds to the fit with free γ, while the red line corresponds to that for γ = 1.8. The inset panel show the 1, 2, and 3σ likelihood contours in the two-parameter plane of power-law solutions. The y-axis of the inset plot is the combined parameter |
| In the text | |
 |
Fig. 4 Angular correlation function of the AEGIS field for the subsample with spectroscopic information within 0.3 <z< 1.3 (i.e. 186 sources, black filled circles) and for the complete X-ray source sample (i.e. 741 sources, red filled triangles) in the hard band. The solid line corresponds to the fixed γ = 1.8 fit, while the dashed line represents the best power-law fit. The error bars correspond to 1σ uncertainties. The inset plot presents the 1 and 3σ contours in the fitted (θ0,γ) parameter space. |
| In the text | |
 |
Fig. 5 Comparison of the normalized flux distributions of the complete sample (thick black line) and of the spectroscopic subsample (red shaded region). |
| In the text | |
 |
Fig. 6 Left panel: result of the χ2 minimization procedure of fitting the parameter 2 + n. Right panel: the clustering evolution model (black curve), corresponding to the best fit value (n = 3.03) for Mh = 1.3 × 1013M⊙, overplotting the literature x0 data in the hard and total band. Our direct estimate (not used in the χ2 minimization procedure) is shown as the filled circle. As a manifestation of the degeneracy discussed in Sect. 2, we show the expected clustering evolution for another (n,Mn) pair ≃ (2.0,2 × 1012M⊙) which is consistent with the data (red curve). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.