| Issue |
A&A
Volume 590, June 2016
|
|
|---|---|---|
| Article Number | A81 | |
| Number of page(s) | 6 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201527723 | |
| Published online | 16 May 2016 | |
Symmetry and structure of reflection matrices of celestial bodies with particulate surfaces
1
Astronomical Institute “Anton Pannekoek”, University of
Amsterdam,
Science Park 904,
1098 XH
Amsterdam,
The Netherlands
e-mail:
J.W.Hovenier@uva.nl
2
Instituto de Astrofísica de Andalucía,
CSIC, Glorieta de la Astronomía,
sn, 18008
Granada,
Spain
e-mail:
olga@iaa.es
Received: 10 November 2015
Accepted: 26 February 2016
The polarization of electromagnetic radiation reflected by a particulate surface is determined by a four by four reflection matrix. Symmetry relations are quite common for such reflection matrices. The reciprocity and mirror symmetry relations are combined to derive a third symmetry relation. These three relations are used to simplify reflection matrices for a variety of special directions of incident and reflected radiation. We show that some elements of the reflection matrix can vanish or equal other elements that have the same or opposite sign. Several applications of the results for studies of particulate surfaces and atmospheres above them are pointed out.
Key words: planets and satellites: surfaces / planets and satellites: atmospheres / polarization / scattering
© ESO, 2016
1. Introduction
The surfaces of planets, moons, and asteroids are often covered with solid particles that have various sizes, compositions, and shapes. We call this kind of surface a particulate surface. The brightness and polarization of light reflected by these surfaces has been the subject of many observational and experimental studies (Mishchenko et al. 2010; Muinonen et al. 2015; Shkuratov et al. 2004; Morozhenko & Vid’machenko 2004; Litvinov et al. 2010). A rigorous analytical theory for reflection by densely packed media is still at an early stage of development (e.g. Tishkovets et al. 2011), while direct computer solutions of the Maxwell equations for these media are still limited (e.g. Mishchenko 2014).
The polarization of the reflected light, for incident unpolarized light coming from the Sun, has been observed for many solar system bodies. For incident electromagnetic radiation, the intensity and polarization of the diffusely reflected radiation can be computed when the so-called (bidirectional) reflection matrix is known. This is a 4 × 4 matrix that transforms the Stokes parameters of an incident beam of radiation into the Stokes parameters of a reflected beam of radiation. This matrix is not only important for studies of light, but also for lidar and radar investigations of the Earth and other astronomical bodies. In some cases, the reflected radiation comes directly from a particulate surface (e.g. the Moon), but in other cases the observed radiation comes from an atmosphere above a surface (e.g. Earth, Mars). In the latter cases, the reflection matrix of the surface must be known for an accurate interpretation of the observed radiation, unless the surface is black or the optical thickness of the atmosphere above the surface is very large. Quite often, however, one simply assumes that the light reflected by the surface into the atmosphere is unpolarized and isotropic or that the surface can be modelled as a collection of facets that obey Fresnel’s laws. Such unrealistic surfaces are often used in remote sensing studies of the Earth and other planets. Evidently, more knowledge about the reflection matrix of particulate surfaces is necessary for polarization studies of celestial bodies.
Usually the average surface of an astronomical body is assumed to be locally plane-parallel, so that this average surface can be used for regional studies, such as inhomogeneities on a disk (Hovenier 1970). More generally, one needs to perform an integration of the intensity vector of the locally reflected radiation over the illuminated and detectable part of the object (Stam et al. 2006).
In this paper we consider diffuse reflection by flat layers of infinite horizontal extent that have rotational symmetry about a vertical axis owing to the random nature of particulate material on the surface. We also assume that the reciprocity principle and mirror principle hold. These are three well known symmetry principles for sparsely packed media like atmospheres containing spheres and randomly oriented particles with a plane of symmetry (Hovenier 1969; Hovenier et al. 2004). In this paper we postulate that the same three symmetry principles also hold for densely packed layers containing the same kind of particles. Natural layers may not exactly obey these symmetry principles, but we shall suppose that the effects of deviations are so small that they can be neglected for all practical purposes (Minnaert 1941; Van de Hulst 1980; Chandrasekhar 1950). We also presume that there is no birefringence or dichroism of any kind. The material in the layer may be loosely or densely packed or anything between the two. Consequently, the packing density and the type of physical processes inside the layer play no role in this paper. The layer may be inhomogeneous in the vertical direction. There may be single or multiple scattering inside the layer, including coherent backscattering. The incident radiation may be unpolarized or polarized. It will be shown that several properties of the reflection matrix regarding its structure can be derived from symmetry principles.
In Sect. 2, some elementary concepts are provided. Three basic symmetry relations are presented in Sect. 3. These relations are employed in Sect. 4 to obtain the structure of the reflection matrix for various directions of the incident and reflected radiation. Conclusions and applications are presented in Sect. 5.
2. Basic concepts
Let us consider a particulate layer of infinite horizontal extent filled with randomly distributed particles in random orientation. The particles may be sparsely or densely packed and the layer may have an arbitrary thickness. In this section, we assume there is nothing above and below the layer. We use a right-handed cartesian coordinate system with coordinates x and y parallel to the surface and its z-axis in the direction of the upward normal to the surface (see Fig. 1). The properties of the layer are independent of the coordinates x and y, but may vary with depth. In other words, the layer may be homogeneous or inhomogeneous in the vertical direction. The layer does not emit radiation on its own and is illuminated at the top by a parallel beam of quasi-monochromatic electromagnetic radiation, which is called radiation hereon. The incoming radiation is reflected by the layer in all upward directions. We use concepts of radiative transfer theory to describe the incident and reflected radiation.
The direction of propagation of a radiation beam is generally specified by means of an azimuthal angle, ϕ, and a direction cosine, u, which is the cosine of the angle the direction of propagation makes with the downward normal. At the top layer, we make use of μ which is the absolute value of u, with an indication as to whether the radiation is incident or reflected. For the direction of the incident radiation we use μ0, and ϕ0 and for the direction of the reflected radiation, μ and ϕ. Both μ and μ0 vary between 0 and 1. The sense in which azimuthal angles are measured is clockwise when looking upwards (see Fig. 1). Owing to the rotational symmetry about the z-axis the zero value of the azimuthal angles is arbitrary, so that only differences of azimuthal angles need to be considered, i.e. ϕ − ϕ0. Clearly, rotation of the layer about the z-axis would increase or decrease both ϕ and ϕ0 by the same amount, so that their difference would not change. Thus ϕ − ϕ0 varies from zero to 2π, plus or minus 2π.
To describe the intensity, flux and state of polarization of a beam of radiation, we use the same definitions of Stokes parameters as given by, for example, Chandrasekhar (1950), Van de Hulst (1957), and Hovenier et al. (2004). These are always defined with respect to a plane of reference, which is a plane through the direction of propagation. Each radiation beam is characterized by a Stokes vector, which is a column vector with four elements called Stokes parameters. If we rotate the reference plane through an angle α, which is larger than zero in the anti-clockwise direction when looking in the direction of propagation of the beam, the Stokes vector must be pre-multiplied by the rotation matrix 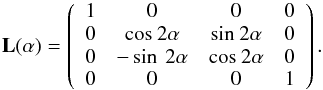 (1)The meridian plane of each non-perpendicular direction is determined by its azimuthal angle and acts as the plane of reference for its Stokes parameters. Perpendicular directions do not have a unique meridian plane and require a special treatment, as explained in Sect. 4.2. We can now write for the Stokes vector of the reflected far-field radiation
(1)The meridian plane of each non-perpendicular direction is determined by its azimuthal angle and acts as the plane of reference for its Stokes parameters. Perpendicular directions do not have a unique meridian plane and require a special treatment, as explained in Sect. 4.2. We can now write for the Stokes vector of the reflected far-field radiation 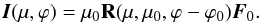 (2)Here, I(μ,ϕ) is the so called specific intensity column vector of the reflected radiation, with elements I, Q, U, and V. Furthermore, R(μ,μ0,ϕ − ϕ0) is the four by four reflection matrix. The first element of the column vector π times F0 is the incident net flux per unit area perpendicular to the direction of the monodirectional incident radiation. The reflection matrix used in this paper is the same as that used earlier by Van de Hulst (1980), Hovenier (1969), and Hovenier et al. (2004). When the incident radiation at the top comes from several directions and its specific intensity vector is It(μ′,ϕ′) we have
(2)Here, I(μ,ϕ) is the so called specific intensity column vector of the reflected radiation, with elements I, Q, U, and V. Furthermore, R(μ,μ0,ϕ − ϕ0) is the four by four reflection matrix. The first element of the column vector π times F0 is the incident net flux per unit area perpendicular to the direction of the monodirectional incident radiation. The reflection matrix used in this paper is the same as that used earlier by Van de Hulst (1980), Hovenier (1969), and Hovenier et al. (2004). When the incident radiation at the top comes from several directions and its specific intensity vector is It(μ′,ϕ′) we have 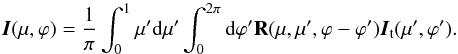 (3)The degree of polarization of the reflected radiation
(3)The degree of polarization of the reflected radiation 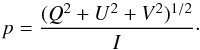 (4)
(4)
3. Symmetries
In this section, we present a mathematical description of the symmetry principles presented in Sect. 1. The first one is rotational symmetry about the vertical axis. As mentioned before, a result of this symmetry is that we only need to consider azimuth differences like ϕ − ϕ0, instead of ϕ and ϕ0 separately.
 |
Fig. 1 Directions of the incident radiation (μ0, φ0) and reflected radiation (μ, φ) at an arbitrary point of the top of the layer. |
The second fundamental symmetry principle is the reciprocity principle. This may be regarded as a symmetry principle since it is basically due to time-reversal invariance. As a result the reflection matrix in the situation that is mentioned in Sect. 2 obeys the reciprocity relation 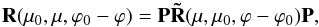 (5)where the matrix
(5)where the matrix 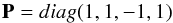 (6)and the tilde above a matrix stands for the transposed matrix. So the inversion of the directions of the incident and reflected beam of radiation causes each element Ri,j to be changed to Rj,i, while the non-diagonal elements of the third row and column change sign. Here and hereafter, we make use of the fact that two matrices are equal if, and only if, they are identical.
(6)and the tilde above a matrix stands for the transposed matrix. So the inversion of the directions of the incident and reflected beam of radiation causes each element Ri,j to be changed to Rj,i, while the non-diagonal elements of the third row and column change sign. Here and hereafter, we make use of the fact that two matrices are equal if, and only if, they are identical.
The third fundamental symmetry principle is mirror symmetry. This means that mirror symmetry exists for any beam of reflected radiation with respect to the plane through the vertical and the direction of propagation of the incident light, as shown in Fig. 2. For a more detailed description, we refer to the literature Hovenier (1969, 1970) and Hovenier et al. (2004). The mirror principle gives the mirror symmetry relation 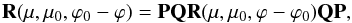 (7)where
(7)where 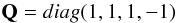 (8)and
(8)and 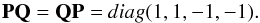 (9)So, taking the mirror images of the incident and reflected beams of radiation causes an inversion of the signs of the eight elements R31,R32,R41,R42,R13,R14,R23, and R24 of R(μ,μ0,ϕ − ϕ0). Consequently, these elements are odd functions of ϕ − ϕ0 and the other eight elements are even functions of ϕ − ϕ0. In a Fourier series, expansion the first eight elements will therefore contain only sine terms, while the remaining eight elements will only contain a constant and cosine terms. It should be noted that the diagonal matrices P, Q, PQ, and QP are equal to their inverses and transposed matrices.
(9)So, taking the mirror images of the incident and reflected beams of radiation causes an inversion of the signs of the eight elements R31,R32,R41,R42,R13,R14,R23, and R24 of R(μ,μ0,ϕ − ϕ0). Consequently, these elements are odd functions of ϕ − ϕ0 and the other eight elements are even functions of ϕ − ϕ0. In a Fourier series, expansion the first eight elements will therefore contain only sine terms, while the remaining eight elements will only contain a constant and cosine terms. It should be noted that the diagonal matrices P, Q, PQ, and QP are equal to their inverses and transposed matrices.
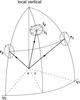 |
Fig. 2 Illustration of the mirror symmetry principle for the reflection matrix. If the incident beam of radiation, i1, produces (among others), a beam of reflected radiation, r1, then the incident beam of radiation, i2, creates (among others) a beam of reflected radiation r2. We note that i2 and r2 are mirror images of i1 and r1, respectively, with respect to the plane of incidence. (After Hovenier 1970.) |
In the reciprocity relation (5), μ and μ0, as well as ϕ and ϕ0, are interchanged, while in the mirror-symmetry relation (7), only ϕ and ϕ0 are interchanged. So by combining these two relations, we should find a relation in which only μ and μ0 are interchanged. This can be done as follows. Using Eq. (5) and then Eq. (7) we find ![\begin{equation} {\bf R}(\mu_{0}, \mu, \varphi-\varphi_{0})={\bf PQ}[{\bf P\tilde{R}}(\mu, \mu_{0}, \varphi-\varphi_{0}{\bf P}]{\bf QP} \end{equation}](/articles/aa/full_html/2016/06/aa27723-15/aa27723-15-eq42.png) (10)so that
(10)so that 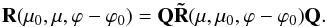 (11)We call this symmetry relation the combination relation.
(11)We call this symmetry relation the combination relation.
In summary, we started with three fundamental symmetry principles and we have now obtained three basic symmetry relations, namely, Eqs. (5), (7), and (11), for arbitrary directions of the incident and reflected beams. The rotational symmetry principle has been used by employing the azimuth difference ϕ − ϕ0, instead of ϕ and ϕ0 separately. In practice, the preferred order of Eqs. (5), (7), and (11) may be (11), (7), and (5), since only μ and μ0 are interchanged in Eq. (11) and only ϕ and ϕ0 in Eq. (7), whereas μ and μ0 as well as ϕ and ϕ0 are interchanged in Eq. (5).
4. Structure
In general the reflection matrix may have 16 different elements. In this section, we show that this number is smaller for several special directions of the incident and reflected radiation. Indeed, by using symmetry relations, some elements of a reflection matrix can be shown to be equal, opposite, or identically zero. In this way the structure of the matrix can be simplified. This is shown in the following two subsections.
4.1. Non-perpendicular directions
We first consider five cases for non-perpendicular directions of incidence and reflection.
Case (i). Suppose μ = μ0 and both are smaller than 1, but ϕ − ϕ0 is arbitrary. The combination relation Eq. (11) shows that in this case 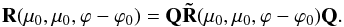 (12)This is an equation for R(μ0,μ0,ϕ − ϕ0) with many matrix solutions. For example, all diagonal 4 × 4 matrices obey this equation.
(12)This is an equation for R(μ0,μ0,ϕ − ϕ0) with many matrix solutions. For example, all diagonal 4 × 4 matrices obey this equation.
Yet, Eq. (12) is useful since it gives information about the structure of R(μ0,μ0,ϕ − ϕ0). To show this we start with writing the elements of a general 4 × 4 reflection matrix as follows 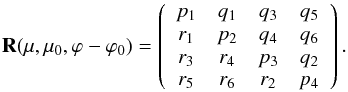 (13)Here and hereafter, the variables of the functions pi, qi, and ri with i = 1 − 6 are not shown, but they are the same as those of the matrix on the left-hand side of the equation. Therefore, the pi are not necessarily the same functions for the matrices with different variables that occur further in this paper and the same holds for the functions qi and ri. Now Eq. (12) shows that we can write
(13)Here and hereafter, the variables of the functions pi, qi, and ri with i = 1 − 6 are not shown, but they are the same as those of the matrix on the left-hand side of the equation. Therefore, the pi are not necessarily the same functions for the matrices with different variables that occur further in this paper and the same holds for the functions qi and ri. Now Eq. (12) shows that we can write 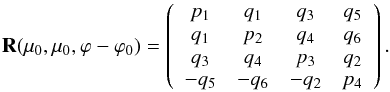 (14)Consequently, we have eliminated six functions, namely r1 − r6, which makes the structure of R(μ0,μ0,ϕ − ϕ0) much simpler. We note that the matrix of Eq. (14) is symmetrical, apart from three minus signs, and does not have more than thirteen different elements, while the elements of the fourth row and column are opposite, except for element 44.
(14)Consequently, we have eliminated six functions, namely r1 − r6, which makes the structure of R(μ0,μ0,ϕ − ϕ0) much simpler. We note that the matrix of Eq. (14) is symmetrical, apart from three minus signs, and does not have more than thirteen different elements, while the elements of the fourth row and column are opposite, except for element 44.
Case (ii). Suppose ϕ − ϕ0 = 0 and μ and μ0 are both arbitrary, but smaller than one (see OP2 in Fig. 3). The mirror symmetry relation (7) provides 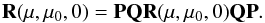 (15)Writing out this equation shows that the elements of the two non-diagonal 2 × 2 submatrices of R(μ,μ0,0) must be identically zero since these elements differ in sign on the left-hand and right-hand side, but have the same absolute value.
(15)Writing out this equation shows that the elements of the two non-diagonal 2 × 2 submatrices of R(μ,μ0,0) must be identically zero since these elements differ in sign on the left-hand and right-hand side, but have the same absolute value.
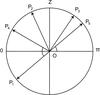 |
Fig. 3 Reflection at a point, O, of the top of the layer in the meridian plane with the local vertical OZ. Here ϕ − ϕ0 = 0 in the left half and φ − φ0 = π in the right half plane. OP1 is the direction of the incident radiation. OP2,OP3,OP4, and OP5 are directions of reflected radiation. |
Therefore we have (cf. Eq. (13)) 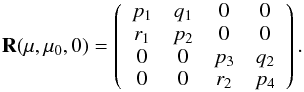 (16)Here and hereafter, the elements indicated by zero are identically equal to zero. A matrix of the type of Eq. (16) is called a block-diagonal matrix. It does not have more than eight different non-zero elements.
(16)Here and hereafter, the elements indicated by zero are identically equal to zero. A matrix of the type of Eq. (16) is called a block-diagonal matrix. It does not have more than eight different non-zero elements.
Case (iii). Suppose ϕ − ϕ0 = π and μ and μ0 are both arbitrary, but smaller than one (see OP3 in Fig. 3). Because of the periodicity in azimuth 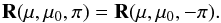 (17)Therefore relation (7) gives
(17)Therefore relation (7) gives 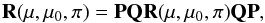 (18)so that
(18)so that 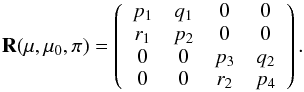 (19)Which has the same structure as the matrix in Eq. (16). The plane given by ϕ − ϕ0 = 0 and ϕ − ϕ0 = π is often called the principal plane. The reflection matrix is always block-diagonal in this plane (see also Eqs. (25), (28), (34), and (36)).
(19)Which has the same structure as the matrix in Eq. (16). The plane given by ϕ − ϕ0 = 0 and ϕ − ϕ0 = π is often called the principal plane. The reflection matrix is always block-diagonal in this plane (see also Eqs. (25), (28), (34), and (36)).
Case (iv). Suppose μ and μ0 are both smaller than one and μ = μ0. Also ϕ − ϕ0 = 0 (see OP4 in Fig. 3).
Combining Eq. (12) with Eq. (16) yields 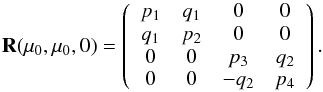 (20)A matrix of this type is called special block-diagonal. It does not have more than seven different non-zero elements, while elements 34 and 43 are opposite.
(20)A matrix of this type is called special block-diagonal. It does not have more than seven different non-zero elements, while elements 34 and 43 are opposite.
Case (v). Suppose ϕ − ϕ0 = π and μ = μ0 is smaller than one. This is a very interesting case since it means reflection in the exact backscattering direction (see OP5 in Fig. 3).
Equations (14) and (19) provide 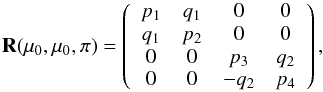 (21)which has the same structure as the matrix in Eq. (20). A simple check for Eqs. (20) and (21) can be obtained from the reciprocity relation (5). The matrices in Eqs. (16), (19)−(21) are all block-diagonal for the same reason, namely mirror symmetry. Block-diagonal matrices frequently occur in polarization studies.
(21)which has the same structure as the matrix in Eq. (20). A simple check for Eqs. (20) and (21) can be obtained from the reciprocity relation (5). The matrices in Eqs. (16), (19)−(21) are all block-diagonal for the same reason, namely mirror symmetry. Block-diagonal matrices frequently occur in polarization studies.
4.2. Perpendicular directions
For perpendicular directions of incident and/or reflected radiation, we make use of some earlier results for the reflection matrix of an atmosphere or a sparsely packed slab of randomly oriented particles that have a plane of symmetry (Hovenier & de Haan 1985). The reason is that those results were solely based on rotational, reciprocity and mirror symmetry and are, therefore, also valid for densely packed slabs when the same symmetry principles are valid. First of all, we note that Stokes parameters only make sense when a plane of reference has been chosen. The reference plane of the Stokes parameters of radiation propagating in a perpendicular direction up or down contains the local vertical and is therefore a meridian plane. We now consider several cases for the structure of the reflection matrix for perpendicular directions of incidence and/or reflection of radiation.
Case (vi). Suppose μ0 = 1 and μ is smaller than 1.
Here the direction of the incident radiation is perpendicular and the plane of reference for its Stokes parameters has an azimuthal angle ϕ0. The reflected radiation is non-perpendicular and its plane of reference has an azimuthal angle ϕ. We have in this case 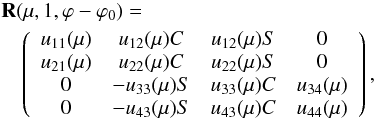 (22)where
(22)where ![\begin{equation} C=\cos [2(\varphi-\varphi_{0})] \end{equation}](/articles/aa/full_html/2016/06/aa27723-15/aa27723-15-eq76.png) (23)and
(23)and ![\begin{equation} S=\sin [2(\varphi-\varphi_{0})]. \end{equation}](/articles/aa/full_html/2016/06/aa27723-15/aa27723-15-eq77.png) (24)Equation (22) gives the following two cases.
(24)Equation (22) gives the following two cases.
Case (vii). ![\begin{eqnarray} \label{reflection8} &&{\bf R}(\mu, 1, 0)={\bf R}(\mu, 1, \pi)= \nonumber\\[2mm] && \quad \left( \begin{array}{c c c c} u_{11}(\mu) & u_{12}(\mu) & 0 & 0 \\ u_{21}(\mu) & u_{22}(\mu) & 0 & 0 \\ 0 & 0 & u_{33}(\mu) & u_{34}(\mu) \\ 0 & 0 & u_{43}(\mu) & u_{44}(\mu) \end{array}\right). \end{eqnarray}](/articles/aa/full_html/2016/06/aa27723-15/aa27723-15-eq78.png) (25)Case (viii).
(25)Case (viii). ![\begin{eqnarray} \label{reflection9} &&{\bf R}(\mu, 1, -\pi/2) = {\bf R}(\mu, 1, \pi/2)=\nonumber \\[2mm] &&\quad \left( \begin{array}{c c c c} u_{11}(\mu) & -u_{12}(\mu) & 0 & 0 \\ u_{21}(\mu) & -u_{22}(\mu) & 0 & 0 \\ 0 & 0 & -u_{33}(\mu) & u_{34}(\mu) \\ 0 & 0 & -u_{43}(\mu) & u_{44}(\mu) \end{array}\right). \end{eqnarray}](/articles/aa/full_html/2016/06/aa27723-15/aa27723-15-eq79.png) (26)Case (ix). Suppose μ = 1 and μ0 is smaller than 1.
(26)Case (ix). Suppose μ = 1 and μ0 is smaller than 1.
Here the direction of the reflected radiation is perpendicular and its plane of reference for its Stokes parameters has an azimuthal angle ϕ but the direction of the incident radiation is not perpendicular. In this case ![\begin{eqnarray} \label{reflection10} &&{\bf R}(1, \mu_{0}, \varphi-\varphi_{0}) =\nonumber\\[2mm] & &\quad \left( \begin{array}{c c c c} v_{11}(\mu_{0}) & v_{12}(\mu_{0}) & 0 & 0 \\ v_{21}(\mu_{0})C & v_{22}(\mu_{0})C & -v_{33}(\mu_{0})S & -v_{34}(\mu_{0})S \\ v_{21}(\mu_{0})S & v_{22}(\mu_{0})S & v_{33}(\mu_{0})C & v_{34}(\mu_{0})C \\ 0 & 0 & v_{43}(\mu_{0}) & v_{44}(\mu_{0}) \end{array}\right). \end{eqnarray}](/articles/aa/full_html/2016/06/aa27723-15/aa27723-15-eq81.png) (27)Equation (27) gives the following two cases.
(27)Equation (27) gives the following two cases.
Case (x). ![\begin{eqnarray} \label{reflection11} &&{\bf R}(1, \mu_{0}, 0)={\bf R}(1, \mu_{0}, \pi) = \nonumber\\[2mm] && \quad \left( \begin{array}{c c c c} v_{11}(\mu_{0}) & v_{12}(\mu_{0}) & 0 & 0 \\ v_{21}(\mu_{0}) & v_{22}(\mu_{0}) & 0 & 0 \\ 0 & 0 & v_{33}(\mu_{0}) & v_{34}(\mu_{0}) \\ 0 & 0 & v_{43}(\mu_{0}) & v_{44}(\mu_{0}) \end{array}\right). \end{eqnarray}](/articles/aa/full_html/2016/06/aa27723-15/aa27723-15-eq82.png) (28)Case (xi).
(28)Case (xi). ![\begin{eqnarray} \label{reflection12} &&{\bf R}(1, \mu_{0}, -\pi/2)={\bf R}(1, \mu_{0}, \pi/2) = \nonumber \\[2mm] && \quad \left( \begin{array}{c c c c} v_{11}(\mu_{0}) & v_{12}(\mu_{0}) & 0 & 0 \\ -v_{21}(\mu_{0}) & -v_{22}(\mu_{0}) & 0 & 0 \\ 0 & 0 & -v_{33}(\mu_{0}) & -v_{34}(\mu_{0}) \\ 0 & 0 & v_{43}(\mu_{0}) & v_{44}(\mu_{0}) \end{array}\right). \end{eqnarray}](/articles/aa/full_html/2016/06/aa27723-15/aa27723-15-eq83.png) (29)The Fourier series expansions of the azimuth dependence are apparently very short in Eqs. (22) and (27).
(29)The Fourier series expansions of the azimuth dependence are apparently very short in Eqs. (22) and (27).
Case (xii.)
Suppose μ0 = 1 and μ = 1. This can be regarded as a subcase of case (vi) or (ix). The directions of the incident and reflected radiation are both perpendicular. From Eqs. (22) and (25), we find 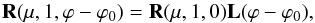 (30)where the rotation matrix L(α) has been defined by Eq. (1) in Sect. 2.
(30)where the rotation matrix L(α) has been defined by Eq. (1) in Sect. 2.
Similarly, Eqs. (27) and (28) give 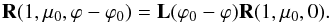 (31)Since μ = μ0 =1 we find from Eqs. (30) and (31) by subtraction
(31)Since μ = μ0 =1 we find from Eqs. (30) and (31) by subtraction 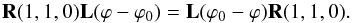 (32)Postmultiplying both sides of this equation by L(ϕ0 − ϕ) gives
(32)Postmultiplying both sides of this equation by L(ϕ0 − ϕ) gives 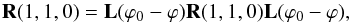 (33)since the product L(ϕ − ϕ0) L(ϕ0 − ϕ) gives the identity matrix.
(33)since the product L(ϕ − ϕ0) L(ϕ0 − ϕ) gives the identity matrix.
Using the fact that the left-hand side of Eq. (33) is independent of azimuth we find the diagonal matrix ![\begin{equation} \label{perpendicular7} {\bf R}(1, 1, 0)=diag[u_{11}(1), u_{22}(1), -u_{22}(1), u_{44}(1)]. \end{equation}](/articles/aa/full_html/2016/06/aa27723-15/aa27723-15-eq92.png) (34)On substituting this in Eqs. (30) or (31) we obtain
(34)On substituting this in Eqs. (30) or (31) we obtain 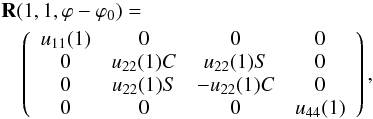 (35)which shows that
(35)which shows that 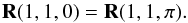 (36)Consequently, Eqs. (34) and (36) show that no more than three different numbers are needed for the reflection matrix for backscattering in the perpendicular direction, when the same reference plane is chosen for the Stokes parameters of the incident and reflected radiation beams.
(36)Consequently, Eqs. (34) and (36) show that no more than three different numbers are needed for the reflection matrix for backscattering in the perpendicular direction, when the same reference plane is chosen for the Stokes parameters of the incident and reflected radiation beams.
Using the combination relation Eq. (11) and also Eq. (22), as well as Eq. (27) gives for i = 1, 2, 3, 4 
5. Conclusions and applications
We have shown that rotational symmetry and only two quite general symmetry principles, namely reciprocity and mirror symmetry, are sufficient to obtain three basic symmetry relations. These symmetry relations make it possible to reduce the number of non-zero elements of the reflection matrix of a particulate surface for several directions of the incident and reflected radiation. In practice, all three basic symmetry relations have their own advantages and disadvantages.
Clearly, the results of this paper not only hold for particulate surfaces, but also for random rough surfaces and plane-parallel atmospheres if they obey the same symmetry relations. Moreover, the incident radiation is often not directly reflected by a bare surface, but first passes an overlying atmosphere on its way to the surface and then again on its way to the distant observer. In this situation the results of this paper are also valid for the reflection matrix of the combined slab, i.e. atmosphere plus surface, provided the reciprocity and mirror symmetry relations hold for the reflection matrix of the combined slab.
We expect the results of this paper to be useful for a variety of polarization studies of diffuse reflection by plane-parallel media and in particular for the structure of their reflection matrices. We mention the following examples.
-
Providing constraints and testing results of theoretical models and computations for more realistic models than, for example, a Lambert surface below an atmosphere,
-
preparing and testing experiments and observations for particulate surfaces,
-
expansion of data obtained for a confined number of directions to a larger domain of directions of incident and reflected radiation,
-
remote sensing by lidar and radar of the Earth, e.g. to determine properties of aerosols,
-
studies of atmospheres and surfaces of bodies in the solar system and objects in the surroundings of exoplanets,
-
studies of the reflection by densely packed flat media.
Concerning applications of this paper for astrophysical purposes, it is important to realize that accurate computations of the reflection matrix of densely packed layers, which are based on Maxwell’s equations, are very difficult. But much progress in this field is expected in the near future owing to rapid improvements in modern computers (Mishchenko et al. 2011).
The results of this paper for the structure of reflections matrices of densely packed layers and atmospheres will be helpful to facilitate computations and to test results. We now consider three different cases for the reflection matrices of celestial bodies.
-
(a)
Solid bodies with a particulate surface and virtually noatmosphere above this surface. Suppose that, approximately, theparticles are spherical or have a plane of symmetry while inrandom orientation, and the reflection matrix can be computed atvarious wavelengths. We can then use all equations of this paper toderive characteristics (size, shape, composition) of the particleson the surface by means of model computations. This is relevantfor celestial bodies like Mercury, as well as many moons andasteroids in the solar system and beyond.
-
(b)
Our second case concerns bodies with an atmosphere, having a large optical thickness, above a particulate surface. Suppose virtually no radiation incident at the top of the atmosphere reaches the particulate surface. As in the preceding case we can derive characteristics of the particles in the atmosphere from the reflection matrix. An example is provided by the work of Hansen & Hovenier (1974) who derived characteristics of the cloud particles of Venus from polarization measurements. They used the adding method for the reflection and transmission matrices of sub-layers of the atmosphere. Similar investigations are possible for other planets.
-
(c)
Our third case deals with solid bodies having an atmosphere with a small or intermediate optical thickness above a particulate surface. Here we need the reflection matrix of the surface, as well as the reflection and transmission matrices of the atmosphere alone for incident light from above and below to compute the reflection matrix of the combined layer by means of the adding method. On Earth, characterization of aerosols by remote sensing is at present seriously hampered by insufficient knowledge of the reflection matrix of the surface (Litvinov et al. 2010).
Acknowledgments
It is a great pleasure to thank Dr. M.I. Mishchenko and Dr. K. Muinonen for their thoughtful comments. The work of Olga Muñoz has been supported by the Plan Nacional de Astronomía y Astrofísica contract AYA2015-67152-R.
References
- Chandrasekhar, S. 1950, Radiative Transfer (London: Oxford University Press; reprinted by Dover, New York 1960) [Google Scholar]
- Hansen, J. E., Hovenier, J. W. 1974, JQSRT, 11, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Hovenier, J. W. 1969, J. Atm. Sci., 26, 488 [Google Scholar]
- Hovenier, J. W. 1970, A&A, 7, 86 [NASA ADS] [Google Scholar]
- Hovenier, J. W., & de Haan, J. F. 1985, A&A, 146, 185 [NASA ADS] [Google Scholar]
- Hovenier, J. W., van der Mee, C. V. M., & Domke, H. 2004, Transfer of polarized light in planetary atmospheres: Basic concepts and practical methods (Dordrecht: Kluwer/ Springer) [Google Scholar]
- Litvinov, P., Hasekamp, O., Cairns, B., et al. 2010, in Polarimetric Detection, Characterization and Remote Sensing, eds. M. Mishchenko et al. (Dordrecht: Springer), 313 [Google Scholar]
- Minnaert, M. 1941, ApJ., 93, 403 [NASA ADS] [CrossRef] [Google Scholar]
- Mishchenko, M. I. 2014. Electromagnetic Scattering by Particles and Particle Groups: An Introduction (Cambridge: Cambridge University Press) [Google Scholar]
- Mishchenko, M. I., Rosenbush, V. K., Kiselev, N. N., et al. 2010. Polarimetric Remote Sensing of Solar System Objects (Kyiv: Akademperiodyka) [arXiv:1010.1171] [Google Scholar]
- Mishchenko, M. I., Tishkovets, V. P., Travis, L. D., et al. 2011, J. Quant. Spectr. Rad. Transf., 112, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Morozhenko, A., & Vid’machenko, A. 2004, in Photopolarimetry in Remote Sensing, eds. G. Videen, Y. Yatskiv, & M. Mishchenko (Dordrecht: Kluwer), 369 [Google Scholar]
- Muinonen, K., Penttilä, A., & Videen, G. 2015, in Polarimetry of Stars and Planetary systems, eds. L. Kolokolova, J. Hough, & A. C. Levasseur-Regourd (Cambridge: Cambridge University Press), 114 [Google Scholar]
- Shkuratov, Y., Videen, G., Kreslavsky, M., et al. 2004, in Photopolarimetry in Remote Sensing, eds. G. Videen, Y. Yatskiv, & M. Mishchenko (Dordrecht: Kluwer), 191 [Google Scholar]
- Stam, D. M., de Rooij, W. A., Cornet, G., & Hovenier, J. W. 2006, A&A, 452, 669 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Tishkovets, V. P., Petrova, E. V., & Mishchenko, M. I. 2011, J. Quant. Spectr. Rad. Transf., 112, 2095 [NASA ADS] [CrossRef] [Google Scholar]
- Van de Hulst, H. C. 1957, Light scattering by small particles (John Wiley & and Sons Inc., N. Y. Also Dover Publications Inc. N.Y., 1981) [Google Scholar]
- Van de Hulst, H. C. 1980 Multiple light scattering, (New york: Academic Press) [Google Scholar]
All Figures
 |
Fig. 1 Directions of the incident radiation (μ0, φ0) and reflected radiation (μ, φ) at an arbitrary point of the top of the layer. |
| In the text | |
 |
Fig. 2 Illustration of the mirror symmetry principle for the reflection matrix. If the incident beam of radiation, i1, produces (among others), a beam of reflected radiation, r1, then the incident beam of radiation, i2, creates (among others) a beam of reflected radiation r2. We note that i2 and r2 are mirror images of i1 and r1, respectively, with respect to the plane of incidence. (After Hovenier 1970.) |
| In the text | |
 |
Fig. 3 Reflection at a point, O, of the top of the layer in the meridian plane with the local vertical OZ. Here ϕ − ϕ0 = 0 in the left half and φ − φ0 = π in the right half plane. OP1 is the direction of the incident radiation. OP2,OP3,OP4, and OP5 are directions of reflected radiation. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


