| Issue |
A&A
Volume 590, June 2016
|
|
|---|---|---|
| Article Number | A4 | |
| Number of page(s) | 9 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201527306 | |
| Published online | 28 April 2016 | |
Quasi-periodic processes in the flare loop generated by sudden temperature enhancements at loop footpoints
1
Astronomical Institute of the Czech Academy of Sciences,
Fričova 258,
251 65
Ondřejov,
Czech Republic
e-mail:
karlicky@asu.cas.cz
2
University of South Bohemia, Faculty of Science, Institute of
Physics and Biophysics, Branišovská
10, 370 05
České Budějovice, Czech
Republic
Received: 4 September 2015
Accepted: 8 March 2016
Aims. During the impulsive flare phase, the plasma at the flare loop footpoints is rapidly heated by particle beams. In the present paper, we study processes that occur after this sudden heating in a two-dimensional magnetic loop.
Methods. We adopt a 2D magnetohydrodynamic (MHD) model, in which we solve a full set of the ideal time-dependent MHD equations by means of the FLASH code, using the adaptive mesh refinement (AMR) method. Periods in the processes are estimated by the wavelet analysis technique.
Results. We consider a model of the solar atmosphere with a symmetric magnetic loop. The length of this loop in the corona is approximately 21.5 Mm. At both loop footpoints, at the transition region, we initiate the Gaussian temperature (pressure) perturbation with the maximum temperature 14, 7, or 3.5 times higher than the unperturbed temperature. In the corona, the perturbations produce supersonic blast shocks with the Mach number of about 1.1, but well below Alfvén velocities. We consider cases with the same perturbations at both footpoints (symmetric case) and one with different perturbations (asymmetric case). In the symmetric case, the shocks move along both loop legs upwards to the top of the loop, where they interact and form a transient compressed region. Then they continue in their motion to the transition region at the opposite side of the loop, where they are reflected upwards, and so on. At the top of the loop, the shock appears periodically with the period of about 170 s. In the loop legs during this period, a double peak of the plasma parameters, which is connected with two arrivals of shocks, is detected: firstly, when the shock moves up and then when the shock, propagating from the opposite loop leg, moves down. Increasing the distance of the detection point in the loop leg from the top of the loop, the time interval between these shock arrivals increases. Thus, at these detection points, the processes with shorter periods can be detected. After ~500 s the process with the periodically interacting shocks slowly changes to slow mode magnetosonic free oscillation. Furthermore, we detected quasi-periodic processes, even in the chromosphere under the location of the pressure perturbation. These processes can be observed in intensities and Doppler shifts of optical chromospheric lines. In the case with the asymmetric perturbations, we found that the processes are even more complex.
Key words: Sun: flares / Sun: oscillations / magnetohydrodynamics (MHD) / methods: numerical
© ESO, 2016
1. Introduction
In solar flares, oscillations are commonly observed in radio, soft X-ray, hard X-ray, ultraviolet, and even in gamma-ray emissions (Roberts et al. 1984; Fárník et al. 2003; Wang et al. 2005; Nakariakov et al. 2006, 2010).
The period of these oscillations ranges from sub-seconds to tens of minutes (Mészárosová et al. 2006; Tan 2008; Karlický et al. 2010; Kupriyanova et al. 2010; Huang et al. 2014; Nisticò et al. 2014). Several theoretical models have been proposed to explain a generation of these oscillations (Nakariakov & Melnikov 2009).
Many oscillations and various modes of waves, especially in coronal loops, were already numerically studied, see, e.g., Ofman & Wang (2002), De Moortel & Hood (2003), Nakariakov et al. (2004, 2005), Selwa et al. (2005), Jelínek & Karlický (2009, 2010), Konkol et al. (2010), Ofman et al. (2012), Pascoe & De Moortel (2014), Mészárosová et al. (2014). Recent numerical results are summarized by Pascoe (2014).
During the impulsive phase in the “standard” CSHKP solar flare model (Carmichael 1964; Sturrock 1966; Hirayama 1974; Kopp & Pneuman 1976), particle beams, which are accelerated by magnetic reconnection processes in the low corona, propagate downwards along the legs of flare loop and bombard dense chromospheric layers at both its footpoints. Owing to this bombardment, the chromosphere at loop footpoints is rapidly heated and the hard X-ray emission is generated (MacNeice et al. 1984; Mariska & Poland 1985; Fisher et al. 1985a,b,c; Mariska et al. 1989; Karlický 1990; Karlický & Henoux 1992; Hawley & Fisher 1994; Abbett & Hawley 1999; Allred et al. 2005; Brown 1971; Varady et al. 2014).
The chromosphere is also heated by the thermal conduction from a very hot flare plasma (Švestka 1973). However, in the impulsive flare phase, the heating of the chromosphere by the strong particle beams is faster than that by the thermal conduction. Namely, at this flare phase there is not enough hot coronal flare plasma. Thus, the thermal conduction heating of the chromosphere is more important in later flare phases.
Now a question arises: what happens in the flare loop after impulsive heating by particle beams at its footpoints. It is known that the fast and localized heating produces shocks. When these shocks are generated at both loop footpoints then the shocks interact inside the loop. Moreover, the flare loop is a closed system, where shocks can be reflected at boundaries and thus some periodic processes can be expected.
We study just these processes in the present paper. We note that these processes differ from the free oscillations of flare loops that have been studied in previous papers. Similar papers about shocks above and in the post-flare loop have been presented recently by Takasao et al. (2015). But in contrast to the present paper, the authors consider the magnetic reconnection, which is localized above the loop, as a source of the shocks.
In this paper, we consider a symmetric loop described by a two-dimensional (2D) magnetohydrodynamic (MHD) model. Shocks are generated by sudden temperature enhancements at loop footpoints. We study two cases: a) with the same initial perturbation in both loop footpoints (symmetric case) and b) with different perturbations (asymmetric case). We selected perturbations generating the plasma velocities, which are well below Alfvén velocities.
The paper is structured as follows: in Sect. 2, we present our numerical model, including the initial equilibrium and perturbations. The results of numerical simulations and their interpretation are summarized in Sect. 3. Finally, we complete the paper with conclusions in Sect. 4.
2. Model
2.1. Governing equations
Our numerical model describes the gravitationally stratified solar atmosphere, in which the plasma dynamics are described by the 2D, time-dependent ideal MHD equations. We use the FLASH code (Lee & Deane 2009; Lee 2013), where MHD equations are formulated in the conservative form as ![\begin{eqnarray} \label{eq1} &&\frac{\partial \varrho}{\partial t} + \nabla \cdot(\varrho \vec{v}) = 0, \\ \label{eq2} &&\frac{\partial \varrho \vec{v}}{\partial t} + \nabla \cdot \left(\varrho \vec{v} \vec{v} -\vec{B}\vec{B}\right) + \nabla p_{*}=\varrho \vec{g}, \\ \label{eq3} &&\frac{\partial \varrho E}{\partial t} + \nabla \cdot \left[\left(\varrho E+p_{*}\right)\vec{v} - \vec{B}(\vec{v} \cdot \vec{B})\right] = \varrho \vec{g} \cdot \vec{v}, \\ \label{eq4} &&\frac{\partial \vec{B}}{\partial t} + \nabla \cdot (\vec{v}\vec{B}-\vec{B}\vec{v})=0, \\ \label{eq5} &&\nabla\cdot\vec{B}=0. \end{eqnarray}](/articles/aa/full_html/2016/06/aa27306-15/aa27306-15-eq3.png) Here ϱ is a mass density, v is flow velocity, B is the magnetic field, g = [ 0, −g⊙,0 ] is the gravitational acceleration with g⊙ = 274 ms-2. The total pressure p∗ is given by
Here ϱ is a mass density, v is flow velocity, B is the magnetic field, g = [ 0, −g⊙,0 ] is the gravitational acceleration with g⊙ = 274 ms-2. The total pressure p∗ is given by 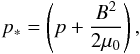 (6)where p is the fluid thermal pressure and B is the magnitude of magnetic field. Specific total energy E in Eq. (3) is expressed as
(6)where p is the fluid thermal pressure and B is the magnitude of magnetic field. Specific total energy E in Eq. (3) is expressed as 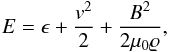 (7)where ϵ is the specific internal energy
(7)where ϵ is the specific internal energy 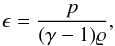 (8)with the adiabatic coefficient γ = 5/3, v is the magnitude of the flow velocity, and μ0 = 1.26 × 10-6 Hm-1 is the magnetic permeability of free space.
(8)with the adiabatic coefficient γ = 5/3, v is the magnitude of the flow velocity, and μ0 = 1.26 × 10-6 Hm-1 is the magnetic permeability of free space.
Generally, the terms expressing the radiative losses Rloss, thermal conduction Tcond, and heating H should be added to the set of MHD equations. In its initial state, it is assumed that the radiative losses and thermal conduction are fully compensated for by the heating H, i.e., Rloss + Tcond + H = 0, otherwise the unperturbed atmosphere is not in equilibrium, e.g., owing to the steep temperature gradient in the transition region. Problems appear when the atmosphere is perturbed. Namely, there is no simple expression for the heating term H which, in the unperturbed atmosphere, fully compensates Rloss and Tcond and, in the perturbed atmosphere, correctly describes the heating. Therefore, for the purpose of our study, we assume that Rloss + Tcond + H = 0 is valid during the whole studied processes.
2.2. Initial state
For a still (v = 0) equilibrium, the Lorentz and gravity forces have to be balanced by the pressure gradient in the entire physical domain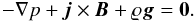 (9)Assuming a force-free magnetic field, j × B = 0, the solution of the remaining hydrostatic equation yields
(9)Assuming a force-free magnetic field, j × B = 0, the solution of the remaining hydrostatic equation yields
Here 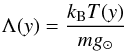 (12)is the pressure scale-height which, in the case of isothermal atmosphere, represents the vertical distance over which the gas pressure falls off by a factor of e, kB = 1.38 × 10-23 JK-1 is the Boltzmann constant and
(12)is the pressure scale-height which, in the case of isothermal atmosphere, represents the vertical distance over which the gas pressure falls off by a factor of e, kB = 1.38 × 10-23 JK-1 is the Boltzmann constant and 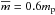 is the mean particle mass (mp = 1.672 × 10-27 kg is the proton mass), p0 in Eq. (10) denotes the gas pressure at the reference level yref. In our calculations we set and hold fixed yref = 10 Mm. For the solar atmosphere, we use the temperature profile T(y) as derived by Avrett & Loeser (2008).
is the mean particle mass (mp = 1.672 × 10-27 kg is the proton mass), p0 in Eq. (10) denotes the gas pressure at the reference level yref. In our calculations we set and hold fixed yref = 10 Mm. For the solar atmosphere, we use the temperature profile T(y) as derived by Avrett & Loeser (2008).
Coordinates of selected detection points, and Alfvén vA and sound cs speeds in the initial state at these points.
The solenoidal condition, ∇·B = 0, is identically satisfied with the implementation of the magnetic flux function, A, such as  (13)For the calculation of a 2D magnetic field with symmetric loops, we use A = [ 0,0,A ] as Konkol et al. (2012) or Jelínek & Murawski (2013):
(13)For the calculation of a 2D magnetic field with symmetric loops, we use A = [ 0,0,A ] as Konkol et al. (2012) or Jelínek & Murawski (2013): 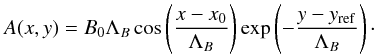 (14)The magnetic field components (Bx,By) are then given by
(14)The magnetic field components (Bx,By) are then given by ![\begin{eqnarray} \label{eq14} (B_x,B_y) =&B_0&\left[-\cos\left(\frac{x-x_0}{\Lambda_B}\right),\sin\left(\frac{x-x_0}{\Lambda_B}\right)\right] \nonumber \\ &\times&\exp\left(\frac{y-y_\mathrm{ref}}{\Lambda_B}\right)\cdot \end{eqnarray}](/articles/aa/full_html/2016/06/aa27306-15/aa27306-15-eq50.png) (15)Here B0 is the magnetic field in the reference level yref and ΛB = 2L/π is the magnetic scale height. We choose the ratio between Alfvén cA and sound cs, speeds as
(15)Here B0 is the magnetic field in the reference level yref and ΛB = 2L/π is the magnetic scale height. We choose the ratio between Alfvén cA and sound cs, speeds as 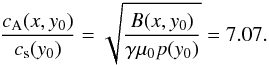 (16)The plasma β is defined as
(16)The plasma β is defined as 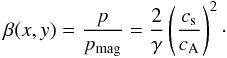 (17)
(17)
2.3. Perturbations
To generate an evaporation process, at the start of the numerical simulation (t = 0 s), the equilibrium in the chromosphere is perturbed by the Gaussian pulse in the temperature (pressure) and has the following form: ![\begin{equation} \label{eq17} T = T_0 \left[1 + \mathcal{A}\cdot \exp{\left\{-\frac{(x-x_{\mathrm{P}})^2}{\lambda_x^2}\right]}\cdot \exp{\left[-\frac{(y-y_{\mathrm{P}})^2}{\lambda_y^2}\right]}\right\}, \end{equation}](/articles/aa/full_html/2016/06/aa27306-15/aa27306-15-eq58.png) (18)where T0 is the initial temperature,
(18)where T0 is the initial temperature, 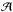 is the initial amplitude of the pulse, and λx, and λy are the widths of the temperature pulse in x and y directions, respectively.
is the initial amplitude of the pulse, and λx, and λy are the widths of the temperature pulse in x and y directions, respectively.
2.4. Wavelet method
For the wavelet analysis we used the Morlet wavelet, which consists of a plane wave modulated by a Gaussian: 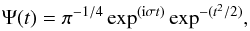 (19)where the parameter σ allows a trade between time and frequency resolutions. Here we assumed the value of parameter σ = 6, as recommended by Farge (1992). More details about the wavelet method and its implementation can be found on the web page of R. Sych (http:// [0]pwf. [0]iszf. [0]irk. [0]ru/) and in the paper by Torrence & Compo (1998).
(19)where the parameter σ allows a trade between time and frequency resolutions. Here we assumed the value of parameter σ = 6, as recommended by Farge (1992). More details about the wavelet method and its implementation can be found on the web page of R. Sych (http:// [0]pwf. [0]iszf. [0]irk. [0]ru/) and in the paper by Torrence & Compo (1998).
2.5. Numerical code
To solve the MHD Eqs. (1)–(4), we use the FLASH code, which is well tested, fully modular, parallel, multiphysical, open science, simulation code that implements second- and third-order unsplit Godunov solvers with various slope limiters and Riemann solvers, as well as adaptive mesh refinement (AMR; Chung 2002). The Godunov solver combines the corner transport upwind method for multi-dimensional integration and the constrained transport algorithm for preserving the divergence-free constraint on the magnetic field (Lee & Deane 2009). We used the minmod slope limiter and the Riemann solver (Toro 2006). The main advantage of using the AMR technique is to refine a numerical grid at steep spatial profiles while keeping a coarse grid at the places where fine spatial resolution is not essential. In this case, the AMR strategy is based on controlling the numerical errors in a gradient of mass density that leads to the reduction of the numerical diffusion within the entire simulation region.
For our numerical simulations, we use a 2D Eulerian box of its height H = 10 Mm and width W = 20 Mm. The spatial resolution of the numerical grid is determined with the AMR method. We use the AMR grid with the minimum (maximum) level of the refinement blocks set to 3 (7). The whole simulation region is covered by 2626 blocks. Since every block consists of 8 × 8 numerical cells, this number of blocks corresponds to 168 064 numerical cells and the smallest spatial resolution is Δx = Δy = 3.9 km.
At all boundaries, we fix all plasma quantities to their equilibrium values using fixed-in-time boundary conditions, which lead to only negligibly small numerical reflections of incident wave signals.
 |
Fig. 1 Spatial distribution of plasma mass density at t = 71 s. At this time we observe maximal compression of the plasma at the top of the loop (see the zoomed part) owing to the collision of shocks generated by the temperature (pressure) enhancements at loop footpoints. The solid curved lines show representative magnetic field lines. The red one determines the magnetic field line along the loop axis. |
Parameters of perturbations in computational runs.
3. Numerical results
To present our results, we selected the detection points shown in Table 1, where their locations and Alfvén and sound velocities in the initial state at these points are shown. These detection points are distributed along the axis of the loop, which is expressed by the red magnetic field line in Fig. 1.
The detection points 1−9 are in the coronal part and in the left side of the loop. Detection point 9 is at the top of the loop. Namely, in the symmetric case, plasma processes in the loop are symmetric. The detection point 10 is chosen for the asymmetric case, and is located at the right side of the loop, symmetrically to detection point 4. To study associated processes in the chromosphere, under the perturbation point, we also selected detection points A, B, and C.
We consider two perturbation points P1 and P2 at the transition region. They are located at 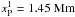 ,
, 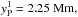 and at
and at 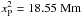 ,
, 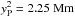 , i.e., at both the loop footpoints.
, i.e., at both the loop footpoints.
In the symmetric case, the temperature perturbation amplitude is chosen as 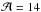 or 7 at both footpoints P1 and P2 and, in the asymmetric case, as
or 7 at both footpoints P1 and P2 and, in the asymmetric case, as 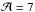 at P1 and
at P1 and 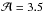 at P2.
at P2.
As shown in Table 2, where the parameters of perturbations are summarized, we made several numerical runs. Owing to the similarity of their results, we present here mainly the results of Run I.
 |
Fig. 2 Profiles of the mass density, velocity, temperature, and magnetic field along the loop axis from the detection point A to the top of the loop at 71 s (i.e., at the same time as in Fig. 1 – full line) and at the initial state with the pressure (temperature) perturbation (dashed line). |
 |
Fig. 3 Time-distance diagram of the mass density along the loop axis in the coronal part of the loop for Run I. The vertical dashed line expresses the loop top position. |
 |
Fig. 4 Time profiles of the plasma velocity, temperature, and mass density at the detection points: 9 (top of the loop; full line), 7 (dotted line), and 5 (dashed line) in the time interval 0−1000 s. |
 |
Fig. 5 Comparison of time profiles of the pressure p (full line) and magnetic field B (dashed line) at the top of the loop (detection point 9). |
 |
Fig. 6 Time profile of the relative X-ray emission intensity at the top of the loop (detection point 9) for the energy ϵx = 1.549 keV (8 Å). |
In Fig. 1, we show an example of the spatial distribution of the plasma density for Run I with the same perturbations at both loop footpoints (symmetric case), at t = 71 s, i.e., at the time of maximal plasma compression at the loop top region. The spatial profiles of the density, velocity, temperature, and magnetic field along the loop axis at the same time are presented in Fig. 2. Comparing these profiles with those in the initial state (dashed lines in Fig. 2) show how dense and hot plasma moves from the transition region to the low corona.
3.1. Quasi-periodic processes in the coronal part of the loop
Now, let us look in more detail at processes in the coronal part of the loop, i.e., at the region with the coordinates y ≥ 2 Mm.
Analyzing Figs. 1 and 2, we can see that, at the time t = 71 s at the top of the loop, a region with plasma that is denser and hotter than the surrounding plasma is formed. This happens owing to the plasma compression during the collision of the shocks moving upwards from both loop footpoints. This region is transient, but it appears periodically with the repeated collisions of the shocks at the top of the flare loop (see the processes described in the following).
The global time evolution of the processes in the corona after the perturbation initiation is shown in Fig. 3, where the time-distance diagram of the mass density along the loop axis is shown. As can be seen in Figs. 2 and 3, after the initiation of temperature perturbations at both footpoints, the heated plasma from the transition region is evaporated to coronal parts of the loop and counter-streaming evaporation shocks are formed. These shocks collide at the top of the loop at t = 71 s. In the following times, the shocks continue in their motion to the transition region at the opposite side of the loop, where they are reflected back to the corona (at t ≈ 150 s), and so on (Fig. 3).
At first, the shocks propagate with a velocity slightly greater than the local sound velocity, see Table 1. Considering their velocity and corresponding plasma flow velocities (Fig. 4), we found that the shocks are of the blast type. Using the relation (Priest 1982) 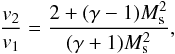 (20)where v1 and v2 are the inflow and outflow plasma velocities in the shock frame, we determined the Mach number, Ms, of these shocks along the loop and in the time interval 40−70 s as about 1.1. Afterwards, their Mach number decreases and shocks slowly change to waves (see the quasi-periodic variations of the plasma velocity, temperature and plasma density at three detection points 5, 7, and 9 in Fig. 4).
(20)where v1 and v2 are the inflow and outflow plasma velocities in the shock frame, we determined the Mach number, Ms, of these shocks along the loop and in the time interval 40−70 s as about 1.1. Afterwards, their Mach number decreases and shocks slowly change to waves (see the quasi-periodic variations of the plasma velocity, temperature and plasma density at three detection points 5, 7, and 9 in Fig. 4).
During these processes, which are with the low plasma beta parameter, the magnetic field changes only very weakly, see the time profile of the magnetic field at the top of the loop in Fig. 5. Here, the most distinct change in the magnetic field was detected at the first arrival of the shock at t = 71 s (~0.5 G). Later the amplitude of the magnetic field variation decreases. The amplitude of the magnetic field variation is in the anti-phase to the pressure variation. It shows that these shocks and waves (after ~500 s) are of slow magnetosonic mode.
As already mentioned, at the top of the loop, a region with enhanced temperature and density is periodically formed owing to shock collisions. We propose that this region could be observed in the soft X-rays or EUV lines as a periodic and transient loop-top source. For example, the X-ray bremsstrahlung thermal emission I(ϵx) is proportional to (Tandberg-Hanssen & Emslie 1988) 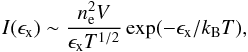 (21)where, ϵx is the X-ray photon energy, ne is the plasma density, T is the plasma temperature, V is the region volume, and kB is the Boltzmann constant. In our case, considering the emission from the constant volume element, we computed the relative X-ray emission intensity (the X-ray emission intensity in ratio to its initial value) at the top of the loop for ϵx = 1.549 keV (8 Å), see Fig. 6. As shown here, at t = 71 s (the time of the maximum plasma compression at the loop-top region), the increase in the relative intensity of the X-ray emission is about 1000. This relatively high value is due to the fact that the plasma temperature at the top of the loop is relatively low and the X-ray photon energy ϵx = 1.549 keV corresponds to a very steep part of the X-ray spectrum.
(21)where, ϵx is the X-ray photon energy, ne is the plasma density, T is the plasma temperature, V is the region volume, and kB is the Boltzmann constant. In our case, considering the emission from the constant volume element, we computed the relative X-ray emission intensity (the X-ray emission intensity in ratio to its initial value) at the top of the loop for ϵx = 1.549 keV (8 Å), see Fig. 6. As shown here, at t = 71 s (the time of the maximum plasma compression at the loop-top region), the increase in the relative intensity of the X-ray emission is about 1000. This relatively high value is due to the fact that the plasma temperature at the top of the loop is relatively low and the X-ray photon energy ϵx = 1.549 keV corresponds to a very steep part of the X-ray spectrum.
Analyzing these quasi-periodic processes further, we recognize a further aspect of these processes that could be observed. Figure 7 presents the pressure variations in nine detection points along the left side of the loop (Table 1). While at the top of the loop (the uppermost profile – detection point 9) there is a simple variation, at detection points in the loop leg variations are more complex; the double peak with the shorter period appears. By increasing the distance of the detection point in the loop leg from the top of the loop, the time interval between peaks in the double peak increases. To explain this effect, we note that each peak in Fig. 7 indicates a passage of the shock through some detection point. One shock arrival to the loop-top detection point is always connected with two shock passages (shock propagating up and shock propagating down) at the loop-leg detection points. Clearly, increasing the distance of the detection point in the loop leg from the top of the loop, the time interval between shock passages increases. From a diagnostic point of view, this means that, in the signal from the loop leg, a shorter period in these processes also appears.
 |
Fig. 7 Series of pressure evolution profiles at nine detection points: From the bottom, the profile at point 1 up to the profile at point 9 (top of the loop) in the time interval 0−1000 s. The arrows show trajectories of shocks. |
To show this, we analyzed the pressure variations at the top of the loop (detection point 9) and at the loop leg (detection point 4) by the wavelet technique. The first and the strongest peak in these variations is close to the beginning of the time series, see Fig. 5. To eliminate the edge effects in computed wavelet spectra, we added data with unperturbed pressures (lasting 300 s) before the computed time series. As a result, the analyzed time series now lasts 1300 s.
The results of the wavelet analysis are presented in Fig. 8. As shown in Fig. 8 (upper part) the dominant period of the pressure variation at the top of the loop (detection point 9) is of about 170 s. On the other hand, in Fig. 8 (bottom part) the dominant period of pressure variation at the loop leg (detection point 4) is shorter (~80 s). However, this shorter period is accompanied by the same period as that in the loop-top detection point, but with a lower power.
 |
Fig. 8 Wavelet spectrum of the pressure variation at detection point 9 (top of the loop; upper part), and at detection point 4 (bottom part), symmetric case (Run I). For the periods, see the pink areas. The period and time are in seconds. The hatched regions belong to the cone of influence by edge effects owing to finite-length time series. |
3.2. Quasi-periodic processes in the chromosphere
Pressure perturbations at loop footpoints generate not only shocks in the coronal part of the loop, but the perturbation also propagates downwards in chromospheric layers, as presented in Fig. 9. An analysis shows that the perturbation is the sound wave propagating with a sound speed of about 13.5 km s-1. During its downward propagation, the chromospheric plasma is heated from ~6500 K up to ~9000 K. Simultaneously, the plasma moves downwards with a velocity of up to ~5 km s-1. After this process, there is the phase with temperature decreases and upward plasma velocities. All these processes repeat in correspondence with the quasi-periodic processes in the coronal part of the loop.
 |
Fig. 9 Time profiles of the plasma velocity, temperature, and mass density at the detection points: A (full line); B (dotted line); and C (dashed line) in the time interval 0−1000 s. |
3.3. Comparison of results obtained in different numerical runs
In this paper, we mainly present the results obtained from Run I. Other runs give similar results. For example, the change in the form of the perturbation in Run IV provides only a small decrease in the shock amplitudes, otherwise the results are very similar to Run I.
The most distinct change can be found when comparing Run II (symmetric case) and Run III (asymmetric case). While in the symmetric case, at the symmetrically taken detection points (4 and 10, see Table 1), the time profiles of the pressure, temperature, and plasma density are the same, in the asymmetric case they differ, see Fig. 10. Here the time profiles of the pressure for Run III (asymmetric case) at the detection points 4 and 10 are shown. As can be seen, the shock generated in the left-side loop leg (detected at detection point 4 at the time 42 s) is stronger and appears earlier than that in the right-side loop leg (detected at detection point 10) owing to to the higher amplitude of the temperature perturbation at the left-side loop footpoint than that in the right-side loop footpoint. In the following time (at about 120 s) it is the reverse. This is due to that after the interaction of the shocks near the top of the loop, the shocks continue in their motion to the opposite side of the loop, where they are then reflected at the transition region, and so on.
 |
Fig. 10 Time profiles of the pressure for Run III (asymmetric case) at detection points 4 (full line) and 10 (dashed line) in the time interval 0−1000 s. |
To show these processes in more detail, we computed the time-distance diagram of the mass density along the loop axis in the coronal part of the loop (Fig. 11). Compared to the symmetric case (Fig. 3), the location of the shock interaction is shifted outside of the loop top position. We note that the position of the first shock interaction is on the right side, outside of the loop top position, and the position of the second shock interaction is on the left side, outside the loop top position.
Similar to the symmetric case, we present the wavelet spectra of the pressure variation (Fig. 12). They are computed for the detection point 4 and 10, i.e., symmetrically to the top of the loop. They differ not only in dominant periods in the interval 50−100 s, but the period of about 200 s is only in the wavelet spectrum from detection point 4. These spectra also differ from the wavelet spectrum at detection point 4 for the symmetric case (Fig. 8). We note that, in different detection points, the wavelet spectra can be different.
 |
Fig. 11 Time-distance diagram of the mass density along the loop axis for Run III (asymmetric case). The vertical dashed line shows the loop top position. |
 |
Fig. 12 Wavelet spectrum of the pressure variation at detection point 4 (upper part) and 10 (bottom part; located symmetrically in the left- and right-side of the loop, see Table 1), asymmetric case (Run III). The period and time are in seconds. The hatched regions belong to the cone of influence by edge effects, owing to finite-length time series. |
4. Conclusions
We studied processes in the flare loop after sudden temperature enhancements at loop footpoints. After the initiation of temperature (pressure) perturbations at loop footpoints, blast shocks that propagate upwards along the loop are generated. In our case, at the beginning of these processes, at t = 40−70 s, the Mach number of these shocks is Ms ~ 1.1. At the top of the loop, these shocks collide and compress the plasma, forming the region with enhanced plasma density and temperature, see also Falewicz et al. (2015). In the symmetric case, this compressed region appears at the top of the loop, and in the asymmetric case this region is slightly shifted outside of the top of the loop. Although, this compressed region is only transient, it could explain some observed soft X-ray or EUV loop-top sources. Owing to the periodic arrival of shocks to the top of the loop, these loop-top sources should appears periodically. Moreover if, in the loop, some superthermal electrons are trapped, then this transient loop-top region can be observed even in hard X-rays, as was shown by Karlický & Henoux (1994).
After the interaction of these shocks at the top of the loop, the shocks continue in their motion downwards to the transition region on the opposite side of the loop, where they are reflected back to the coronal part of the loop, and so on. These processes generate variations (forced oscillations) of plasma parameters in the flare loop. In a later phase of these processes (after about 500 s), the shocks slowly change to waves. In our case, however, the magnetic field varies very weakly in the anti-phase to the pressure variations. This shows that the presented shocks and waves are of slow magnetosonic mode. It would appear that this type of plasma variations was recently recognized in the EUV observations of the 20 July 2013 flare by Kumar et al. (2015).
In the symmetric loop, which has a length of approximately 21.5 Mm, using the wavelet spectral technique, we found variations in the range of 40−170 s. This shows that the period of these variations depends on the detection point location. While the simplest variations are found at the top of the loop with the dominant period of about ~170 s, at the detection point in the loop leg (detection point 4) the dominant period is shorter (~80 s). Considering the loop length (L ~ 21.5 Mm) and the sound speed in the corona (cs ~ 130 km s-1), the period found at the top (170 s) can be described by ~L/cs = 165 s. Similarly, the period found in the leg (80 s) can be explained by ~L/ 2cs = 82.5 s. The factor 2 is due to the contribution of both of the slow shocks.
Increasing the distance in the detection point in the loop leg from the loop top, the time interval between peaks in the double peak increases (Fig. 7). This is due to two passages of shocks through the loop-leg detection point (the shock propagation upward and downward).
In the asymmetric case, the plasma variations and corresponding wavelet spectra are even more complex. The displacement of the interaction point near the loop top is small in spite of the large difference in the amplitude of the initial disturbance between the two foot points. This is because the Mach number of the two shocks is close to unity and they propagate with a similar speed.
We also found that the quasi-periodic processes in the coronal part of the loop are closely associated with processes in the chromospheric layers, located below the perturbation locations. Here, we found variations in the temperature, plasma velocities, and plasma densities that propagated with the sound velocity (~13.5 km s-1). These quasi-periodic variations certainly change intensities and produce Doppler shifts of the optical chromospheric lines, which means that these processes should be observable.
Acknowledgments
The authors thank the referee for constructive comments that improved the paper. M.K. and P.J. acknowledge support from Grants P209/12/0103 and 16-13277S of the Grant Agency of the Czech Republic and European grant FP7-SPACE-2013-1 F-CHROMA (No. 606862) and the Marie Curie FP7-PIRSES-GA-2011-295272 RadioSun project. The authors also express their thanks to Prof. Kris Murawski for valuable discussions and Dr. Robert Sych for his wavelet package http:// [0]pwf. [0]iszf. [0]irk. [0]ru/. The FLASH code used in this work was developed by the DOE-supported ASC/Alliances Center for Astrophysical Thermonuclear Flashes at the University of Chicago.
References
- Abbett, W. P., & Hawley, S. L. 1999, ApJ, 521, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Allred, J. C., Hawley, S. L., Abbett, W. P., & Carlsson, M. 2005, ApJ, 630, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Avrett, E. H., & Loeser, R. 2008, ApJS, 175, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. C. 1971, Sol. Phys., 18, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Carmichael, H. 1964, NASA SP, 50, 451 [Google Scholar]
- Chung, T. J. 2002, Computational Fluid Dynamics (Cambridge, UK: Cambridge University Press) [Google Scholar]
- De Moortel, I., & Hood, A. W. 2003, A&A, 408, 755 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Falewicz, R., Rudawy, P., Murawski, K., & Srivastava, A. K. 2015, ApJ, 813, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Farge, M. 1992, Ann. Rev. Fluid Mech., 24, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Fárník, F., Karlický, M., & Švestka, Z. 2003, Sol. Phys., 218, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Fisher, G. H., Canfield, R. C., & McClymont, A. N. 1985a, ApJ, 289, 434 [NASA ADS] [CrossRef] [Google Scholar]
- Fisher, G. H., Canfield, R. C., & McClymont, A. N. 1985b, ApJ, 289, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Fisher, G. H., Canfield, R. C., & McClymont, A. N. 1985c, ApJ, 289, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley, S. L., & Fisher, G. H. 1994, ApJ, 426, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Hirayama, T. 1974, Sol. Phys., 34, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, J., Tan, B., Zhang, Y., Karlický, M., & Mészárosová, H. 2014, ApJ, 791, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Jelínek, P., & Karlický, M. 2009, Eur. Phys. J. D, 54, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jelínek, P., & Karlický, M. 2010, IEEE Transactions on Plasma Science, 38, 2243 [NASA ADS] [CrossRef] [Google Scholar]
- Jelínek, P., & Murawski, K. 2013, MNRAS, 434, 2347 [NASA ADS] [CrossRef] [Google Scholar]
- Karlický, M. 1990, Sol. Phys., 130, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Karlický, M., & Henoux, J.-C. 1992, A&A, 264, 679 [NASA ADS] [Google Scholar]
- Karlický, M., & Henoux, J.-C. 1994, A&A, 283, 202 [NASA ADS] [Google Scholar]
- Karlický, M., Zlobec, P., & Mészárosová, H. 2010, Sol. Phys., 261, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Konkol, P., Murawski, K., Lee, D., & Weide, K. 2010, A&A, 521, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Konkol, P., Murawski, K., & Zaqarashvili, T. V. 2012, A&A, 537, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kopp, R. A., & Pneuman, G. W. 1976, Sol. Phys., 50, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Kumar, P., Nakariakov, V. M., & Cho, K.-S. 2015, ApJ, 804, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Kupriyanova, E. G., Melnikov, V. F., Nakariakov, V. M., & Shibasaki, K. 2010, Sol. Phys., 267, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, D. 2013, J. Comput. Phys., 243, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, D., & Deane, A. E. 2009, J. Comput. Phys., 228, 952 [NASA ADS] [CrossRef] [Google Scholar]
- MacNeice, P., Burgess, A., McWhirter, R. W. P., & Spicer, D. S. 1984, Sol. Phys., 90, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Mariska, J. T., & Poland, A. I. 1985, Sol. Phys., 96, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Mariska, J. T., Emslie, A. G., & Li, P. 1989, ApJ, 341, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Mészárosová, H., Karlický, M., Rybák, J., Fárník, F., & Jiřička, K. 2006, A&A, 460, 865 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mészárosová, H., Karlický, M., Jelínek, P., & Rybák, J. 2014, ApJ, 788, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Nakariakov, V. M., & Melnikov, V. F. 2009, Space Sci. Rev., 149, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Nakariakov, V. M., Tsiklauri, D., Kelly, A., Arber, T. D., & Aschwanden, M. J. 2004, A&A, 414, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakariakov, V. M., Pascoe, D. J., & Arber, T. D. 2005, Space Sci. Rev., 121, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Nakariakov, V. M., Foullon, C., Verwichte, E., & Young, N. P. 2006, A&A, 452, 343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakariakov, V. M., Inglis, A. R., Zimovets, I. V., et al. 2010, Plasma Physics and Controlled Fusion, 52, 124009 [Google Scholar]
- Nisticò, G., Pascoe, D. J., & Nakariakov, V. M. 2014, A&A, 569, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ofman, L., & Wang, T. 2002, ApJ, 580, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Ofman, L., Wang, T. J., & Davila, J. M. 2012, ApJ, 754, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Pascoe, D. J. 2014, RA&A, 14, 805 [Google Scholar]
- Pascoe, D. J., & De Moortel, I. 2014, ApJ, 784, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Priest, E. R. 1982, Solar magneto-hydrodynamics (Dordrecht, Holland: D. Reidel Pub.), 195 [Google Scholar]
- Roberts, B., Edwin, P. M., & Benz, A. O. 1984, ApJ, 279, 857 [NASA ADS] [CrossRef] [Google Scholar]
- Selwa, M., Murawski, K., & Solanki, S. K. 2005, A&A, 436, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sturrock, P. A. 1966, Nature, 211, 695 [NASA ADS] [CrossRef] [Google Scholar]
- Takasao, S., Matsumoto, T., Nakamura, N., & Shibata, K. 2015, ApJ, 805, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Tan, B. 2008, Sol. Phys., 253, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Tandberg-Hanssen, E., & Emslie, A. G. 1988, The physics of solar flares (Cambridge, New York, USA: Cambridge Uni. Press), 114 [Google Scholar]
- Toro, E. F. 2006, Int. J. Numerical Methods in Fluids, 52, 433 [Google Scholar]
- Torrence, C., & Compo, G. P. 1998, Bull. Am. Met. Soc., 79, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Švestka, Z. 1973, Sol. Phys., 31, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Varady, M., Karlický, M., Moravec, Z., & Kašparová, J. 2014, A&A, 563, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, T. J., Solanki, S. K., Innes, D. E., & Curdt, W. 2005, A&A, 435, 753 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Coordinates of selected detection points, and Alfvén vA and sound cs speeds in the initial state at these points.
All Figures
 |
Fig. 1 Spatial distribution of plasma mass density at t = 71 s. At this time we observe maximal compression of the plasma at the top of the loop (see the zoomed part) owing to the collision of shocks generated by the temperature (pressure) enhancements at loop footpoints. The solid curved lines show representative magnetic field lines. The red one determines the magnetic field line along the loop axis. |
| In the text | |
 |
Fig. 2 Profiles of the mass density, velocity, temperature, and magnetic field along the loop axis from the detection point A to the top of the loop at 71 s (i.e., at the same time as in Fig. 1 – full line) and at the initial state with the pressure (temperature) perturbation (dashed line). |
| In the text | |
 |
Fig. 3 Time-distance diagram of the mass density along the loop axis in the coronal part of the loop for Run I. The vertical dashed line expresses the loop top position. |
| In the text | |
 |
Fig. 4 Time profiles of the plasma velocity, temperature, and mass density at the detection points: 9 (top of the loop; full line), 7 (dotted line), and 5 (dashed line) in the time interval 0−1000 s. |
| In the text | |
 |
Fig. 5 Comparison of time profiles of the pressure p (full line) and magnetic field B (dashed line) at the top of the loop (detection point 9). |
| In the text | |
 |
Fig. 6 Time profile of the relative X-ray emission intensity at the top of the loop (detection point 9) for the energy ϵx = 1.549 keV (8 Å). |
| In the text | |
 |
Fig. 7 Series of pressure evolution profiles at nine detection points: From the bottom, the profile at point 1 up to the profile at point 9 (top of the loop) in the time interval 0−1000 s. The arrows show trajectories of shocks. |
| In the text | |
 |
Fig. 8 Wavelet spectrum of the pressure variation at detection point 9 (top of the loop; upper part), and at detection point 4 (bottom part), symmetric case (Run I). For the periods, see the pink areas. The period and time are in seconds. The hatched regions belong to the cone of influence by edge effects owing to finite-length time series. |
| In the text | |
 |
Fig. 9 Time profiles of the plasma velocity, temperature, and mass density at the detection points: A (full line); B (dotted line); and C (dashed line) in the time interval 0−1000 s. |
| In the text | |
 |
Fig. 10 Time profiles of the pressure for Run III (asymmetric case) at detection points 4 (full line) and 10 (dashed line) in the time interval 0−1000 s. |
| In the text | |
 |
Fig. 11 Time-distance diagram of the mass density along the loop axis for Run III (asymmetric case). The vertical dashed line shows the loop top position. |
| In the text | |
 |
Fig. 12 Wavelet spectrum of the pressure variation at detection point 4 (upper part) and 10 (bottom part; located symmetrically in the left- and right-side of the loop, see Table 1), asymmetric case (Run III). The period and time are in seconds. The hatched regions belong to the cone of influence by edge effects, owing to finite-length time series. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{eqnarray} \label{eq9} &&p(y) = p_0 \exp\left[-\int\limits_{y_0}^{y} \frac{1}{\Lambda(\tilde{y})}\mathrm{d}\tilde{y}\right], \\ \label{eq10} &&\varrho(y) = \frac{p(y)}{g_{\sun}\Lambda(y)}\cdot \end{eqnarray}](/articles/aa/full_html/2016/06/aa27306-15/aa27306-15-eq28.png)