| Issue |
A&A
Volume 589, May 2016
|
|
|---|---|---|
| Article Number | A105 | |
| Number of page(s) | 11 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201628092 | |
| Published online | 20 April 2016 | |
Reactions of N+ (3P) ions with H2 and HD molecules at low temperatures
1
Institute of Physics, University of Belgrade,
Pregrevica118,
11080
Belgrade,
Serbia
e-mail:
tasko@ipb.ac.rs
2
Sorbonne Universités, Université Pierre et Marie Curie, UMR 7614
du CNRS, Laboratoire de Chimie Physique-Matière et Rayonnement,
75231
Paris Cedex 05,
France
e-mail:
ronald.mac_carroll@upmc.fr
3
LERMA, Observatoire de Paris, PSL Research University, CNRS,
Sorbonne Universités, UPMC Univ.
Paris 06, 92195
Meudon Cedex,
France
e-mail:
evelyne.roueff@obspm.fr
Received: 8 January 2016
Accepted: 25 February 2016
Context. This work is motivated by the necessity to take account of both the nuclear spin symmetries of H2 and the spin-orbit interaction of N+ ions in order to investigate gas phase reactions in interstellar chemistry, leading to the formation of nitrogenous and deuterated compounds.
Aims. The main objective in this work is to determine the rate coefficients for each possible initial quantum state of the reactants N+ (3Pj) + H2 (J) (and their isotopic variants). Only in this way does it become possible both to analyse experimental data and to develop realistic applications to interstellar chemical models to constrain the gas phase chemistry of ammonia and its isotopologues.
Methods. A statistical treatment is presented of state selective reactive collisions involving N+ ions in fine structure state j with H2 or HD molecules in a rotation level J of the ground vibration state, leading either to the production of NH+ ions and H in the case of the H2 reactant, and to the production of either NH+ ions or ND+ in the case of the HD reactant. The energies of fine structure states (j = 0,1,2) of the N+ ions are treated on an equal footing with the other energies of internal motions. All fine structure states are considered to be reactive.
Results. Cross sections for state-to-state collisions are calculated for collision energies ranging from 0.1–30 meV. These cross sections are then averaged over the kinetic energies of the reactants for each (J,j) to obtain the rate coefficients for a range of kinetic temperatures 10–200 K. The exo/endothermicity of the reactions involving N+ (3Pj) + H2 (J) (and isotopic variants) is derived from the difference ΔEe between the dissociation energies of the electronic molecular potentials of NH+ and H2. The value ΔEe = 101 meV is found to satisfactorily reproduce the experiments performed with ortho-H2 and to a lesser extent with para-H2. This value is used to determine the rate coefficient of the N+ + HD reaction leading to the formation of ND+. The calculated value is consistent with the available experimental data.
Conclusions. The present results allow for the determination of reaction rate coefficients for any given distribution of specific fine structure and rotational state populations of the reactants. In interstellar conditions, where N+ is in its 3P0 state and para- and ortho-H2 respectively in J = 0 and J = 1. Our results enable a study of the influence of the ortho/para evolution of molecular hydrogen on the formation of nitrogen compounds.
Key words: astrochemistry / molecular processes / molecular data / ISM: molecules
© ESO, 2016
1. Introduction
Reactive collisions of N+ (3P) ions with H2, D2, and HD molecules have been the object of extensive experimental and theoretical investigations in past years (Adams & Smith 1985; Ervin & Armentrout 1987; Marquette et al. 1988; Gerlich 1989; Nyman 1992; Tosi et al. 1994; Sunderlin & Armentrout 1994) and also in recent years (Zymak et al. 2013; Grozdanov & McCarroll 2015). This is due in part to their fundamental importance for the understanding of ion molecule reaction dynamics and in part to their importance in initiating the reaction chain for the formation of nitrogenous molecules in astrochemistry. There is a general consensus that reactions involving ground-state reactants leading to the production of NH+ and ND+ ions are weakly endothermic, requiring a minimal energy input ΔE of the order of a few meV for the reaction to occur. However, since the energies of the excited fine structure states of N+ and also of the excited rotation states of H2 or HD, are of the same order as ΔE, a strong dependence of the rate coefficients on the initial state of the reactants can be expected. Unfortunately, while the kinetic energy of the reactants is usually well-determined, in most experiments the initial state distribution of the reactants is rarely known with much precision and it is often assumed that the rotation temperature of the reactant molecule is identical to the kinetic temperature. However, the validity of this assumption depends on the experimental conditions and a meaningful comparison between theory and experiment is not always possible. For this reason, the direct use of experimentally measured rate coefficients in astrochemical models may be a major source of error in situations where the rotation state distribution of reactants is likely to be non-thermal when conditions of local thermodynamic equilibrium are not satisfied.
Recent work by Grozdanov & McCarroll (2015) has clarified some aspects of the problem. Using a statistical model, they took full account of all the accessible fine structure states of the N+ (3Pj) ion and all the accessible rotation states of the reactant molecule. Cross sections were calculated for the N+ (3Pj) ion in a given fine structure j state (j = 0,1,2) with molecules in a given rotation state J (in general for J = 0 − 5). These collision cross sections were then averaged over the distribution of j,J states of interest. In the experiments of Sunderlin & Armentrout (1994) the fine structure states had a thermal distribution of 300 K, whereas two different temperatures were considered (300 K and 105 K) for the reactant molecules. With these initial distributions, the cross sections for the production of NH+ and ND+ were compared with experiment as a function of ion collision energy from 10 meV up to a few eV. The most interesting part of the work concerned the reaction of N+ with HD in the low energy range from 10 to 100 meV. Both NH+ and ND+ are produced in the reaction and the ratio of their rate coefficients depends critically on the relative values ΔE, corresponding to the NH+ and ND+ products. In this way, it was possible to improve previous estimates of the absolute values of ΔE to within a few meV of the true value. Another important result concerns the importance of fine structure states of N+ in the reaction. The energies of the fine structure states (j = 0, 1, 2) of the N+ ions are treated on equal footing with other energies of internal rotation motions. All fine structure states are considered to be reactive.
In this work, our main objective is to apply statistical methods to treat reactions at even lower energies, corresponding to temperatures in the range of 10–200 K. In this temperature range, reliable results can be obtained only if the value of ΔE for the reaction is known precisely. The recent experimental results of Zymak et al. (2013) on reactions of N+ (3P) with controlled mixtures of para-H2 and ortho-H2 and, together with the older measurements of Marquette et al. (1988) of pure para-H2 and normal-H2, offer a direct way of putting new limits on ΔE.
A direct comparison of theory with experiment requires a knowledge of the initial state distribution of the reactants. Zymak et al. (2013) give convincing reasons why the three fine structure states of N+ (3P), initially populated according to their statistical weights, do indeed relax rapidly at low temperatures, although no claim is made of a complete thermalization. On the other hand, Marquette et al. (1988) make the claim that in their experiments, the fine structure states of N+ (3P) are completely thermalized. Concerning the distribution of the rotation states of the reactant molecule, Zymak et al. (2013) assert that in their experiments a complete relaxation of the rotation states is guaranteed. However, Marquette et al. (1988) evoke the possibility of an incomplete rotational relaxation of para-H2, which might account for an anomalously large rate constant at 27 K.
The reaction of N+ (3Pj) with HD has only been studied in the low temperature range by Marquette et al. (1988), but unfortunately their results are only presented for a single temperature, namely 20 K. However, their measured value of 1.4 × 10-10 cm3 s-1 is surprisingly large compared with a rate of 4 × 10-11 cm3 s-1 for the less endothermic reaction of N+ with n-H2 at the same temperature. A possible explanation might be an incomplete relaxation of the rotation states of HD, but such a possibility was discounted by Marquette et al. (1988).
The objective in this paper is to apply our theoretical model to calculate the rate coefficients for the production of NH+ and ND+ molecular ions in reactive collision of N+ (3P) in a given initial fine structure state with H2 and HD molecules in a specific rotation state. In this way, the total reaction rate can then easily be obtained by averaging over the distribution of the initial states. It should be emphasized that the theoretical model used in this work takes account of all possible reactive and non-reactive processes in the collision. In other words, all reactive collisions leading to the formation of NH+ or ND+ are taken into account, as are non-reactive processes involving excitation and de-excitation of the fine structure and rotation states of the reactants.
2. Statistical model and results for N++ H2 collisions
2.1. Statistical model
The statistical model assumes collisions between N+ ions and H2 molecules at low energies to react via the formation of the (NH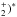 intermediate complex, the decay of which can result in the products
intermediate complex, the decay of which can result in the products 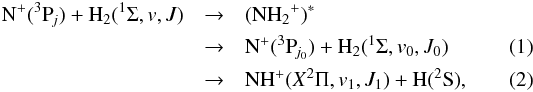 where j = 0,1,2 are the fine structure quantum numbers of the initial state of the N+ (3Pj) ion; (v,J) are the initial vibrational and rotational quantum numbers of H2; and j0 and (vk,Jk), k = 0,1, are the corresponding quantum numbers in non-reactive (k = 0) and reactive (k = 1) channels. For collision energies Ec = (0.1 − 30) meV, and assuming an initial v = 0, in the present work we have in all cases considered v0 = v1 = 0, i.e. no vibrational excitation. The molecules are assumed to be in their ground electronic states, H2(1Σ) and NH+(X2Π), with no fine-structure effects taken into account. The neglect of fine structure effects in the NH+(X2Π) product molecule is certainly a simplification, but it should be satisfactory since we are only interested in the sum over all final fine structure states of the products. If information is required on the distribution of the fine structure states of the reaction products, a more complete treatment, such as the approach of Maergoiz et al. (2014), can be used.
where j = 0,1,2 are the fine structure quantum numbers of the initial state of the N+ (3Pj) ion; (v,J) are the initial vibrational and rotational quantum numbers of H2; and j0 and (vk,Jk), k = 0,1, are the corresponding quantum numbers in non-reactive (k = 0) and reactive (k = 1) channels. For collision energies Ec = (0.1 − 30) meV, and assuming an initial v = 0, in the present work we have in all cases considered v0 = v1 = 0, i.e. no vibrational excitation. The molecules are assumed to be in their ground electronic states, H2(1Σ) and NH+(X2Π), with no fine-structure effects taken into account. The neglect of fine structure effects in the NH+(X2Π) product molecule is certainly a simplification, but it should be satisfactory since we are only interested in the sum over all final fine structure states of the products. If information is required on the distribution of the fine structure states of the reaction products, a more complete treatment, such as the approach of Maergoiz et al. (2014), can be used.
The total energy is defined as ![\begin{eqnarray} E&=&E_{\rm c}+E^{\rm H_2}_{vJ}+E_{{\it j}}=E_{\rm c}^0+E^{\rm H_2}_{v_0J_0}+E_{{\it j}_0}\label{e0} \\[3mm] &=&E_{\rm c}^1+E^{\rm N H^+}_{v_1J_1}+\Delta E_{\rm e}\label{e1} , \end{eqnarray}](/articles/aa/full_html/2016/05/aa28092-16/aa28092-16-eq55.png) where (Ej0) are the fine structure electronic energies of the N+ ion (E0 = 0, E1 = 6.04 meV, and E2 = 16.22 meV), Ec(
where (Ej0) are the fine structure electronic energies of the N+ ion (E0 = 0, E1 = 6.04 meV, and E2 = 16.22 meV), Ec(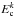 ) and
) and 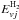 (
(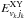 ) are respectively centre-of-mass translational collision energies and internal rovibrational energies in the reactant (product, k = 0 for non-reactive and k = 1 for reactive) arrangements. The term ΔEe is the equilibrium ergicity (or vibrationless energy change) of reaction Eq. (2),
) are respectively centre-of-mass translational collision energies and internal rovibrational energies in the reactant (product, k = 0 for non-reactive and k = 1 for reactive) arrangements. The term ΔEe is the equilibrium ergicity (or vibrationless energy change) of reaction Eq. (2), 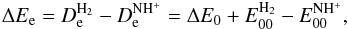 (5)with
(5)with 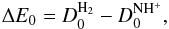 (6)where
(6)where 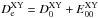 designates the equilibrium dissociation energy of the XY diatomic and
designates the equilibrium dissociation energy of the XY diatomic and 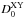 is the potentially experimentally measurable (from the zero-point energy) dissociation energy.
is the potentially experimentally measurable (from the zero-point energy) dissociation energy.
Unfortunately, 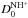 is not known either experimentally or theoretically with sufficient precision, so that the ergicity ΔE0 has been used as a fitting parameter in previous works (see Ervin & Armentrout 1987; Gerlich 1989; Sunderlin & Armentrout 1994, and references therein). Since in the Born-Oppenheimer approximation (without isotope-mass-dependent adiabatic corrections) we have
is not known either experimentally or theoretically with sufficient precision, so that the ergicity ΔE0 has been used as a fitting parameter in previous works (see Ervin & Armentrout 1987; Gerlich 1989; Sunderlin & Armentrout 1994, and references therein). Since in the Born-Oppenheimer approximation (without isotope-mass-dependent adiabatic corrections) we have 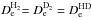 and
and 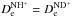 , it follows from the first part of Eq. (5) and analogous relations for the HD targets that ΔEe is the same in both cases of reactants: H2 and HD. Once the ΔEe is fixed, the ergicities ΔE0 (which are different in each of the cases) follow from the second part of Eq. (5) and analogous relations for the HD targets. In the previous study of Grozdanov & McCarroll (2015), the ΔEe value is constrained in the range between 101 and 106 meV. Table A.1 lists the different endoergicities for the different fine structure and rotational levels involved in the reactions for the value ΔEe = 101 meV, which corresponds to our best choice. The zero-point energies are computed from the spectroscopic constants of H2 reported in Huber & Herzberg (1979), whereas the ZPE values of NH+ and its isotopologues are obtained from the values reported in Colin (1989).
, it follows from the first part of Eq. (5) and analogous relations for the HD targets that ΔEe is the same in both cases of reactants: H2 and HD. Once the ΔEe is fixed, the ergicities ΔE0 (which are different in each of the cases) follow from the second part of Eq. (5) and analogous relations for the HD targets. In the previous study of Grozdanov & McCarroll (2015), the ΔEe value is constrained in the range between 101 and 106 meV. Table A.1 lists the different endoergicities for the different fine structure and rotational levels involved in the reactions for the value ΔEe = 101 meV, which corresponds to our best choice. The zero-point energies are computed from the spectroscopic constants of H2 reported in Huber & Herzberg (1979), whereas the ZPE values of NH+ and its isotopologues are obtained from the values reported in Colin (1989).
The initial-state specific cross sections for processes 1 and 2 are calculated using the standard expressions of the statistical theory of reactive collisions (Light 1964; Miller 1970; Truhlar 1975; Park & Light 2007; Grozdanov & McCarroll 2012), 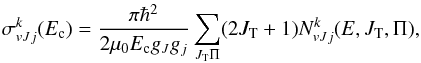 (7)where the partial cumulative reaction probabilities
(7)where the partial cumulative reaction probabilities 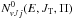 and
and 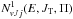 are given respectively by
are given respectively by 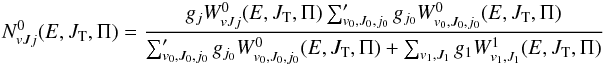 (8)and
(8)and 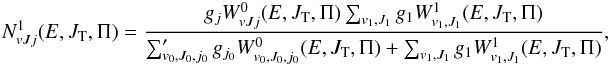 (9)and μ0 is the reduced mass in the reactant arrangement, JT is the total motional angular momentum and Π = ± 1 is the total parity. The reactant and product arrangements are specified by the index k; k = 0 corresponds to the reactant channel, k = 1 corresponds to the product arrangements. The summations in the numerator and denominator are performed over all energetically accessible states and “primes” indicate that the sums over J0 are restricted to the values of the same parity as J. The electronic degeneracy factors (spin and orbital) are taken to be gj0 = 2j0 + 1,g1 = 8, as the NH+ ground state is 2Π. In the past, some account was taken by Gerlich (1989) and Zymak et al. (2013) of the factors in the reactant arrangement gj0< 2j0 + 1 in order to simulate the non-reactivity of some of the asymptotically degenerate electronic surfaces. We have found, however, that only by assuming all surfaces to be reactive can reasonable agreement with experimental absolute cross sections be achieved. The cumulative complex-formation probabilities are given by
(9)and μ0 is the reduced mass in the reactant arrangement, JT is the total motional angular momentum and Π = ± 1 is the total parity. The reactant and product arrangements are specified by the index k; k = 0 corresponds to the reactant channel, k = 1 corresponds to the product arrangements. The summations in the numerator and denominator are performed over all energetically accessible states and “primes” indicate that the sums over J0 are restricted to the values of the same parity as J. The electronic degeneracy factors (spin and orbital) are taken to be gj0 = 2j0 + 1,g1 = 8, as the NH+ ground state is 2Π. In the past, some account was taken by Gerlich (1989) and Zymak et al. (2013) of the factors in the reactant arrangement gj0< 2j0 + 1 in order to simulate the non-reactivity of some of the asymptotically degenerate electronic surfaces. We have found, however, that only by assuming all surfaces to be reactive can reasonable agreement with experimental absolute cross sections be achieved. The cumulative complex-formation probabilities are given by 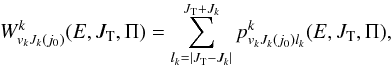 (10)where lk is the relative orbital angular momentum quantum number of the reactants (k = 0) or products (k = 1). The index j0 should be included only in the k = 0 case. The complex formation (or capture) probabilities
(10)where lk is the relative orbital angular momentum quantum number of the reactants (k = 0) or products (k = 1). The index j0 should be included only in the k = 0 case. The complex formation (or capture) probabilities 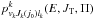 can be calculated using various methods of different degrees of sophistication (for example, by solving the single-arrangement-channel scattering calculations of Rackham et al. (2001)) or running bunches of classical trajectories on the limited parts of the full potential energy surface (Aoiz et al. 2007). Here we use the simplest Langevin-type model, assuming that the complex formation, in both reactant and product arrangements, is determined by the asymptotic, spherically symmetric, ion-neutral polarization interaction. In that case
can be calculated using various methods of different degrees of sophistication (for example, by solving the single-arrangement-channel scattering calculations of Rackham et al. (2001)) or running bunches of classical trajectories on the limited parts of the full potential energy surface (Aoiz et al. 2007). Here we use the simplest Langevin-type model, assuming that the complex formation, in both reactant and product arrangements, is determined by the asymptotic, spherically symmetric, ion-neutral polarization interaction. In that case ![\begin{equation} p^k_{v_kJ_k(j_0)l_k}(E,J_{\rm T},\Pi)=\left\{\begin{array}{ll} \delta_{\Pi,(-1)^{J_k+l_k}} & l_k\le l_{k{\rm m}}(E^k_{\rm c}) \\[3mm] 0 & l_k>l_{k{\rm m}}(E^k_{\rm c}),\end{array} \right. \label{pl} \end{equation}](/articles/aa/full_html/2016/05/aa28092-16/aa28092-16-eq91.png) (11)where
(11)where 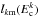 is defined as the maximum integer lk that satisfies (CGS units)
is defined as the maximum integer lk that satisfies (CGS units) 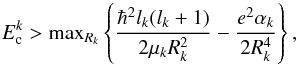 (12)where Rk is the distance between the atom and the centre of mass of the diatom in arrangement k. The polarizabilities are α0 = 8.02 × 10-25 cm3 (5.414 atomic units, a.u.) for the H2 diatom and α1 = 6.67 × 10-25 cm3 (4.5 a.u.) for the H atom.
(12)where Rk is the distance between the atom and the centre of mass of the diatom in arrangement k. The polarizabilities are α0 = 8.02 × 10-25 cm3 (5.414 atomic units, a.u.) for the H2 diatom and α1 = 6.67 × 10-25 cm3 (4.5 a.u.) for the H atom.
When the centre-of-mass energy Ec has a thermal distribution characterized by a kinetic temperature T, the rate constant may be obtained simply by integrating the collision rate over a Maxwellian distribution. The comparison with experiment is made separately for para-H2 and ortho-H2 assuming a Boltzmann distribution of the fine structure states. Only the J = 0 state of p-H2 and the J = 1 state of o-H2 are significantly populated. The para/ortho ratio is 1/3. However, in an astrochemical context, neither the fine structure states of N+(3P) nor the rotation states of the reactant H2 molecule are likely to be in local thermodynamic equilibrium, which means that the rate constants for a specific initial state of the reactants are required.
2.2. Results
2.2.1. 14N+ + H2
In our calculations, the only parameter subject to some uncertainty is the dissociation energy of NH+, to which the values of ΔE for all the reactive processes of N+ with H2 or HD are related. The estimation of the value of ΔE given to within a few meV by Sunderlin & Armentrout (1994) is indeed adequate to explain the experimental rate coefficients at temperatures in excess of ΔE/k; however, at lower temperatures an accuracy of 0.1 meV is required to give a satisfactory result. Unfortunately, comparison with experiment is difficult since the initial distribution of the fine structure states of N+ under the experimental conditions may not be thermal. However, the measured experimental results of the rate constants for the reaction of N+ with n-H2 can give an indication of whether the fine structure states are thermalized or not. For temperatures lower than 100 K this reaction is dominated by the ortho-H2 fraction of H2. We list in Table A.2 the state-to-state reaction rate constants for the individual fine structure states of N+ in reaction with H2, J = 1 computed for the value of ΔEe = 101 meV, and the corresponding thermalized average together with the experimental results of Marquette et al. (1988) and Zymak et al. (2013) for which the authors claim that thermalization has occurred1. The present theoretical values given represent a compromise amongst different choices of ΔEe, between 101 and 106 meV. We chose to fit the results of Marquette et al. (1988) where the significant density of the buffer gas allows thermalization of the fine structure levels of the nitrogen ion (see Dupeyrat et al. 1985). We also focused our efforts on the low temperature regime, which is the most relevant for interstellar conditions.
 |
Fig. 1 Comparison between present theoretical calculations of the thermal rate coefficient of the N+ + o-H2 reaction. The filled circles and squares refer respectively to the Marquette et al. (1988) and Zymak et al. (2013) experimental results. |
The theoretical thermal average results are also displayed in Fig. 1 as a function of 100 K/T, together with the experimental results of Marquette et al. (1988) and Zymak et al. (2013). While the experiments of Marquette et al. (1988) are in reasonable agreement with the more recent results of experiments of Zymak et al. (2013) for temperatures greater than 50 K, there is a significant divergence between the experiments for temperatures less than 20 K. In this range of temperatures, only the j = 0 state is appreciably populated under thermal conditions (91.9% at 20 K). We should point out that the values corresponding to Zymak et al. (2013) experiment, are obtained from the fit given in Eq. (3) of that paper computed with an ortho fraction f = 1 for ortho-H2. As these experiments have been conducted down to 20 K only, the value recorded at 8 K (corresponding to 100 K/T = 12.5), in order to perform the comparison with Marquette et al. (1988) experiment, is obtained from the extrapolation as shown in their Fig. 4 and thus, quoted in italics in our Table A.2. Our calculations seem to indicate that the divergence between the different experiments is more likely to arise from an incomplete thermalization of the fine structure states of N+ in the experiments of Zymak et al. (2013) at low temperature, where the 3P0 level of N+ is the most populated. The present results are indeed compatible with the results of Zymak et al. (2013) in the case of a small population of N+ in the excited fine structure states j = 1,2.
All the results presented subsequently are performed with the value ΔEe = 101 meV. Individual state-to-state and thermalized rate coefficients of the reaction involving para-H2, J = 0 are displayed in Table A.3 together with the experimental results of Marquette et al. (1988) and Zymak et al. (2013). The listed values of Zymak et al. (2013) are derived from their formula (3) with the fraction of ortho-H2, f = 0. The comparison between computed and measured thermal rate coefficients is moderately satisfactory at low temperatures. It should be stressed out that a pure sample of para-H2, J = 0, is very difficult to achieve.
2.2.2. 15N+ + H2
Rate coefficients for the 15N+(3Pj) + H2-ortho (J = 1) reaction for specific j fine structure states and thermalized populations as a function of temperature T.
The substituted 15NH3 is detected in several sources. For that reason, it is of some interest to also compute the corresponding reaction rate coefficients within the same approximations. In that case, no experimental data is available. The results for the reaction with H2-ortho (J = 1) molecules are shown in Table 1. We compare the results of the j = 0 fine structure level of 15N+ with those relevant for 14N+ in Fig. 2. The reaction rate coefficients with 15N+ are slightly larger than those for the main isotope, which is due to the reduced values of ΔE, as shown in Table A.1.
 |
Fig. 2 Comparison between present rate coefficients for the reactions of 14N+ and 15N+ with o-H2. The j = 0 rate coefficient is displayed as a full line whereas dotted lines correspond to thermalized value. |
We also report on Table A.4 the reaction rate coefficients when para H2 react with 15N+. As the second rotational state of H2 is only at 510 K above J = 0, we consider the possible effect of J = 2 of H2 as shown in the 6th column of Table A.4. A factor of about 2 is obtained for T = 160 K.
3. Statistical model and results for N++ HD collisions
3.1. Statistical model
The reaction with the HD isotope: ![\begin{eqnarray} { {\rm N^+ (^3P_{{\it j}})} + {{ \rm HD}~(^1\Sigma,v,J)}} & \to & {({\rm NHD}^+)^* } \nonumber \\[2mm] & \to & {\rm N ^+(^3P_{{\it j}_0}) }+ {{ \rm HD}~ (^1\Sigma, v_0,J_0)} \label{rHD0} \\[2mm] & \to & {\rm D~(^2S)} + {{ \rm NH}^+(X^2\Pi, v_1,J_1)}\label{rHD1} \\[2mm] & \to & {\rm H~(^2S)} + {{ \rm ND}^+(X^2\Pi, v_2,J_2)} \label{rHD2} \end{eqnarray}](/articles/aa/full_html/2016/05/aa28092-16/aa28092-16-eq158.png) is different from the previous case in that there are three possible arrangements labeled with k = 0,1 and 2 and there are no indistinguishable nuclei.
is different from the previous case in that there are three possible arrangements labeled with k = 0,1 and 2 and there are no indistinguishable nuclei.
The total energy is defined as: ![\begin{eqnarray} E=E_{\rm c}+E^{\rm HD}_{vJ}+E_{j}&=&E_{\rm c}^0+E^{\rm HD}_{v_0J_0}+E_{j_{0}}\label{e0hd} \\[2mm] &=&E_{\rm c}^1+E^{\rm N H^+}_{v_1J_1}+\Delta E_{\rm e}\label{e1hd} \\[2mm] &=&E_{\rm c}^2+E^{\rm ND^+}_{v_2J_2}+\Delta E_{\rm e}.\label{e2hd} \end{eqnarray}](/articles/aa/full_html/2016/05/aa28092-16/aa28092-16-eq160.png) The relations analogous to Eq. (5) hold:
The relations analogous to Eq. (5) hold: ![\begin{eqnarray} \Delta E_{\rm e}=D_{\rm e}^{\rm HD}-D_{\rm e}^{\rm NH^+}=\Delta E_0^1+E_{00}^{\rm HD}-E_{00}^{\rm NH^+}, \label{delE1hd} \\[2mm] \Delta E_{\rm e}=D_{\rm e}^{\rm HD}-D_{\rm e}^{\rm ND^+}=\Delta E_0^2+E_{00}^{\rm HD}-E_{00}^{\rm ND^+}. \label{delE2hd} \end{eqnarray}](/articles/aa/full_html/2016/05/aa28092-16/aa28092-16-eq161.png) The expressions for cumulative reaction probabilities
The expressions for cumulative reaction probabilities 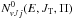 and
and 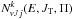 to be used in Eq. (7) are given respectively by:
to be used in Eq. (7) are given respectively by: 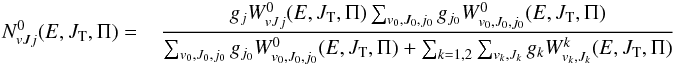 (21)and
(21)and 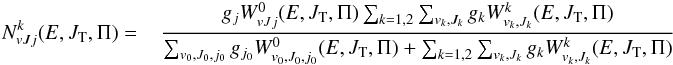 (22)for k = 1,2, with no restrictions on parity in summations over J0 and g1 = g2 = 8. All other formulas Eqs. (10)–12 are applicable and we used polarizabilities: α0 = 8.02 × 10-25 cm3 (5.414 a.u.) corresponding to HD and α1 = α2 = 6.67 × 10-25 cm3 (4.5 a.u.) corresponding to H and D.
(22)for k = 1,2, with no restrictions on parity in summations over J0 and g1 = g2 = 8. All other formulas Eqs. (10)–12 are applicable and we used polarizabilities: α0 = 8.02 × 10-25 cm3 (5.414 a.u.) corresponding to HD and α1 = α2 = 6.67 × 10-25 cm3 (4.5 a.u.) corresponding to H and D.
3.2. Results
The value of ΔE (54.12 meV) of the reaction for the formation of NH+ is so large that the rate coefficient is negligible over the range of temperature considered here. So only the reaction rate for the formation of ND+ needs to be calculated and we give the corresponding values in Table A.5 together with the sole experimental measurement of Marquette et al. (1988) at 20 K and the measured rate coefficient with o-H2 at this same temperature. This makes a meaningful comparison with the theoretical calculations a little difficult. The measured value of the rate coefficient at 20 K is greater by a factor of about 3 than the rate coefficient of the N+ reaction with ortho-H2. However, given that the reaction for ND+ formation is more endothermic by a fraction of meV than the N+ – ortho-H2 reaction for the formation of NH+ (see Table A.1), it is expected that the rate constant for the N++ HD reaction should be smaller than the N+ – ortho-H2 rate constant, or at least about the same value2. Our calculated rate constant at 20 K fulfils this requirement. Our values are also compatible with the measurements of Adams & Smith (1985) at higher temperatures. The origin of the discrepancy between calculated and measured values at 20 K is not obvious. It could be due to non-thermalization of the HD gas sample. A re-evaluation of that measurement at low temperatures is highly desirable. Figure 3 shows the present results obtained for the two isotopologues together with the fit advocated by Marquette et al. (1988). We note the significant decrease of the present results compared to the previous assumption. The 15N+ + HD reaction is slightly favoured compared to 14N+ as the value of ΔE is smaller for the heavier isotope.
 |
Fig. 3 Temperature dependence of the rate coefficients for the reactions of 14N+ (j = 0) and 15N+ (j = 0) with HD. |
We also give the results for the 15N+ + HD reaction in Table A.6.
4. Astrophysical relevance
In the low density regions present in the interstellar medium, nitrogen ions are almost exclusively present in their fine structure ground state, whereas the population of molecular hydrogen is distributed amongst the lowest J = 0 and J = 1 levels of para and ortho forms. The actual repartition depends on various parameters such as the temperature, the formation mechanism, and the history of the cloud, as discussed by Pagani et al. (2011, 2012).
4.1. N+ + H2
The ortho/para ratio of hydrogen has a significant impact not only on deuterium chemistry, as was recognized early on by Pagani et al. (1992), but also on the gas phase nitrogen chemistry, as was first pointed out by Le Bourlot (1991) who recognized that the formation of nitrogenous molecules initiated by the formation of NH+ in the reaction of N+with H2 was dependent on the ortho/para ratio of H2. More recently Dislaire et al. (2012), using the experimental results of Marquette et al. (1988), made a more detailed investigation of the dependence of the rate coefficient as a function of the ortho/para ratio of H2. However, they concluded that the extraction of the detailed reaction rates required for the astrophysical models from the experimental measurement is difficult. It is clear from our results that the reaction rate is highly dependent both on the initial fine structure state of N+ and on the rotation state of the hydrogen molecule. So an incomplete relaxation of the reactants in the experiments can lead to a false conclusion. In Fig. 4 we show the reaction rate coefficients of N+ with o- and p-H2, as suggested by Dislaire et al. (2012) and our computed values obtained for the ground fine structure level of N+, j = 0. For completeness, we also show the experimental results of Marquette et al. (1988) and Zymak et al. (2013) because they are quoted in our Tables 2 and 3.
 |
Fig. 4 Comparison between computed rate coefficients for the reactions of 14N+ (j = 0) with para- and ortho-H2 (blue and red solid lines, respectively) with the analytic forms suggested by Dislaire et al. (2012) (dotted lines). The experimental values of Marquette et al. (1988) are indicated as full circles, whereas the results of Zymak et al. (2013) are full squares. |
We see that the analytic expression of Dislaire et al. (2012) is a very good representation of our computed points for j = 0, J = 1 for ortho-H2. However, our results are significantly different for para-hydrogen. Such a discrepancy is not critical for the low temperature conditions present in cold interstellar clouds as both values are negligible compared to other chemical reactions. We then suggest that the 15N+ + H2 reaction rate coefficient, which initiates the 15NH3 chemistry, is also well described by our computations. The analytic expression 5.35 × 10-10 × exp( − 37.0 /T) cm3 s-1 is found to be an excellent representation of the rate coefficient of the 15N+ + H2 (J = 1) reaction. The corresponding values are also very close to those derived in Roueff et al. (2015) from the analysis of the values of ΔE involved in various reactions. Such a representation, based on statistical calculations of state-to-state reactions, explains the nitrogen fractionation observed in ammonia (Roueff et al. 2015; Daniel et al. 2014).
4.2. N+ + HD
We now discuss the N+ + HD reaction for which our results significantly differ from those of Marquette et al. (1988) which are included in all astrochemical models. The expression fitting the present results obtained for ground-state N+ reacting with HD (J = 0) is 4.77 × 10-10 × exp( − 50.1 /T) cm3 s-1. This expression should be compared to that suggested by Marquette et al. (1988), 3.17 × 10-10 × exp( − 16.3 /T) cm3 s-1, which involves a slightly smaller exponential decrease. Figure 3 shows the corresponding temperature dependences. We note that our computations lead to a reaction rate coefficient which is smaller than the currently used value by more than one order of magnitude at 10 K. The differences decrease with increasing temperature (or decreasing 100/T). We investigated the importance of this difference in the dark cloud models, defined in Table 4 of Roueff et al. (2015) for TMC1 and L183. We list in Table A.7 the steady-state results for several nitrogen compounds corresponding to these models where a fixed ortho/para molecular hydrogen ratio of 10-3 is assumed.
We note in Table A.7 that the deuterium fractionation ratio of NH2 and NH3, as well as their 15N substituted counterparts, are significantly affected by the new estimate of the N+ + HD reaction rate coefficient by a factor of 2–3. The other nitrogen deuterated species, DCN and DNC, are slightly decreased with the new reaction rate coefficient as they mainly result from the dissociative recombination of HCND+, DCNH+, and HDNC+, which are formed principally via the C+ + NH2D reaction. Both N2H+ and N2D+, which are formed via the N2 + H (H2D+ respectively) reactions, remain identical, as do NH and ND, which result from the dissociative recombination of N2H+ and N2D+ (Le Gal et al. 2014; Roueff et al. 2015).
(H2D+ respectively) reactions, remain identical, as do NH and ND, which result from the dissociative recombination of N2H+ and N2D+ (Le Gal et al. 2014; Roueff et al. 2015).
5. Conclusions
The main conclusion of this work concerns the strong dependence of the rate coefficients for reactions of N+(3Pj) ions with H2(J) and HD(J) both on the initial fine structure state j of the N+ ion and on the initial rotation state J of the reactant molecule. A detailed comparison with experiment is not possible unless either the initial distributions of both the fine structure and rotation states J are thermal or are known with precision. Fortunately, for reactions of N+ with n-H2 only the o-H2 fraction is strongly reactive for temperatures lower than 100 K, and it is only for temperatures exceeding 150 K that the contribution from p-H2 becomes significant. So if the fine structure states of N+ can be assumed to be thermally populated, a comparison with experiment becomes possible. This is the case in the experiments of Marquette et al. (1988) and our calculations are indeed in good agreement with the measured values of the rate coefficients for n-H2 when the value ΔEe = 101 meV is used for the statistical calculations.
On the other hand, when there is an incomplete relaxation of excited rotation states, as would appear to be the case both for para-H2 and for HD, a meaningful comparison of theory with existing experiments yields little information. The large values of the reaction rates reported for the reaction with o-H2 at low temperatures by Zymak et al. (2013) together with the significant discrepancy with the Marquette et al. (1988) results could be explained if some slightly non-thermal population of excited fine structure level of N+ is present in these experiments, as suggested by the authors.
The choice of ΔEe unequivocally establishes that the reactions involving isotopic compounds are endothermic. Then we find that the reaction with HD is more endothermic than suggested in Marquette et al. (1988). The corresponding reaction rate coefficient is somewhat smaller at low temperatures than previously admitted. However, it should be emphasized that the previous value contradicted the results obtained with o-H2 because the reaction with HD (J = 0) is more endothermic than the reaction with ortho-H2 (see Table A.1). Another possibility could be the presence of a small barrier on the entrance or exit channel potential energy surface.
The theoretical treatment adopted in this work is limited by the validity of statistical theory and by the assumption that the resonances can be defined by the long-range interactions. So it would be interesting indeed to have available more accurate potential surfaces of the initial reactant channel and the final reaction product channels which would allow for a more precise characterization of the resonances which lead to reactions. However, taking a detailed account of all possible reactive and non-reactive pathways, involving all accessible fine structure and rotation states, would be a formidable task.
As far as astrophysical applications are concerned, the relevant reaction rate coefficients are those computed for ground-state N+ interacting with ground-state para- (J = 0) and ortho- (J = 1) H2 or ground-state (J = 0) HD. The results are very close to the values derived by Dislaire et al. (2012) for the reactions with molecular ortho-hydrogen, which reflects our requirement to harmonize our computations with the Marquette et al. (1988) results. The increased value of ΔE derived for the N+ + HD → ND+ + H reaction leads to a smaller deuteration enhancement of NH2 and NH3 by a factor of 2–3 at 10 K. Neither ND nor N2D+ is affected because the corresponding formation channels are different. We summarize in Table A.8 our recommendations for the fitting expressions to be used in astrochemical models, which correspond to our calculations involving the ground state of N+ interacting with the ground rotational state of H2 and HD when the value ΔEe = 101 meV is chosen for the difference between the electronic dissociation energies of NH+ and H2.
Additional experiments with HD are highly desirable as the interpretation of the single-point result of Marquette et al. (1988) is subject to some uncertainty.
The experimental values reported for Marquette et al. (1988) experiments have been derived by assuming that k(ortho-H2) = 4/3 [k(n-H2) − 1 / 4k(p-H2)].
Acknowledgments
We thank J.B. Marquette, B.R. Rowe, and D. Gerlich for discussions and information about their experimental results. T.P.G. acknowledges support by the Ministry of Education, Science and Technological Development of the Republic of Serbia through project No. 171020. ER acknowledges support from the French national program PCMI.
References
- Adams, N. G., & Smith, D. 1985, Chem. Phys. Lett., 117, 67 [Google Scholar]
- Aoiz, F. J., Sáez Rábanos, V., González-Lezana, T., & Manolopoulos, D. E. 2007, J. Chem. Phys., 126, 161101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Colin, R. 1989, J. Mol. Spectr., 136, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Daniel, F., Faure, A., Wiesenfeld, L., et al. 2014, MNRAS, 444, 2544 [NASA ADS] [CrossRef] [Google Scholar]
- Dislaire, V., Hily-Blant, P., Faure, A., et al. 2012, A&A, 537, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dupeyrat, G., Marquette, J. B., & Rowe, B. R. 1985, Phys. Fluids, 28, 1273 [NASA ADS] [CrossRef] [Google Scholar]
- Ervin, K. M., & Armentrout, P. B. 1987, J. Chem. Phys., 86, 2659 [NASA ADS] [CrossRef] [Google Scholar]
- Gerlich, D. 1989, J. Chem. Phys., 90, 3574 [NASA ADS] [CrossRef] [Google Scholar]
- Grozdanov, T. P., & McCarroll, R. 2012, J. Phys. Chem. A, 388, 4569 [CrossRef] [Google Scholar]
- Grozdanov, T. P., & McCarroll, R. 2015, J. Phys. Chem. A, 119 [Google Scholar]
- Huber, K. P., & Herzberg, G. 1979, Molecular spectra and Molecular Structure: IV. Constants of Diatomic Molecules (New York: van Nostrand Reinhold) [Google Scholar]
- Le Bourlot, J. 1991, A&A, 242, 235 [NASA ADS] [Google Scholar]
- Le Gal, R., Hily-Blant, P., Faure, A., et al. 2014, A&A, 562, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Light, J. C. 1964, Discuss. Faraday Soc., 44, 14 [CrossRef] [Google Scholar]
- Maergoiz, A. I., Nikitin, E. E., & Troe, J. 2014, J. Chem. Phys., 141, 044302 [NASA ADS] [CrossRef] [Google Scholar]
- Marquette, J. B., Rebrion, C., & Rowe, B. R. 1988, J. Chem. Phys., 89, 2041 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, W. H. 1970, J. Chem. Phys., 52, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Nyman, G. 1992, J. Chem. Phys., 96, 3603 [NASA ADS] [CrossRef] [Google Scholar]
- Pagani, L., Salez, M., & Wannier, P. G. 1992, A&A, 258, 479 [NASA ADS] [Google Scholar]
- Pagani, L., Roueff, E., & Lesaffre, P. 2011, ApJ, 739, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Pagani, L., Lesaffre, P., Roueff, E., et al. 2012, Phil. Trans. Roy. Soc. Lond. Ser. A, 370, 5200 [NASA ADS] [CrossRef] [Google Scholar]
- Park, K., & Light, J. C. 2007, J. Chem. Phys., 127, 224101 [NASA ADS] [CrossRef] [Google Scholar]
- Rackham, E. J., Huarte-Larranaga, F., & Manolopoulos, D. E. 2001, Chem. Phys. Lett., 343, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Roueff, E., Loison, J. C., & Hickson, K. M. 2015, A&A, 576, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sunderlin, L. S., & Armentrout, P. B. 1994, J. Chem. Phys., 100, 5639 [NASA ADS] [CrossRef] [Google Scholar]
- Tosi, P., Dmitriev, O., Bassi, D., Wick, O., & Gerlich, D. 1994, J. Chem. Phys., 100, 4300 [NASA ADS] [CrossRef] [Google Scholar]
- Truhlar, D. G. 1975, J. Am. Chem. Soc., 97, 6310 [CrossRef] [Google Scholar]
- Zymak, I., Hejduk, M., Mulin, D., et al. 2013, ApJ, 768, 86 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Additional tables
Values of ΔE for the different reactions computed with the assumption that ΔEe = 101 meV.
Rate coefficients for the N+ (3Pj) + H2-ortho (J = 1) reaction for specific j fine structure states and thermalized populations as a function of temperature T.
Rate coefficients for the N+ (3Pj) + para -H2 reaction for specific j fine structure states and thermalized populations as a function of temperature T.
Rate coefficients for the 15N+(3Pj) + para-H2 reaction for specific j fine structure states and thermalized populations as a function of temperature T.
Rate coefficients (in cm3 s-1) for the N+(3Pj) + HD(J) reaction for specific j fine structure and J = 0 rotational states, as well as thermalized populations as a function of temperature T.
Rate coefficients (in cm3 s-1) for the 15N+(3Pj) + HD(J) reaction for specific j fine structure and J = 0 rotational states, as well as thermalized populations as a function of temperature T.
Steady-state model results for nitrogen compounds and their deuterated counterparts.
Recommended fits of the reaction rate coefficients of N+ (3P0) + H2 and isotopic variants from the present study.
All Tables
Rate coefficients for the 15N+(3Pj) + H2-ortho (J = 1) reaction for specific j fine structure states and thermalized populations as a function of temperature T.
Values of ΔE for the different reactions computed with the assumption that ΔEe = 101 meV.
Rate coefficients for the N+ (3Pj) + H2-ortho (J = 1) reaction for specific j fine structure states and thermalized populations as a function of temperature T.
Rate coefficients for the N+ (3Pj) + para -H2 reaction for specific j fine structure states and thermalized populations as a function of temperature T.
Rate coefficients for the 15N+(3Pj) + para-H2 reaction for specific j fine structure states and thermalized populations as a function of temperature T.
Rate coefficients (in cm3 s-1) for the N+(3Pj) + HD(J) reaction for specific j fine structure and J = 0 rotational states, as well as thermalized populations as a function of temperature T.
Rate coefficients (in cm3 s-1) for the 15N+(3Pj) + HD(J) reaction for specific j fine structure and J = 0 rotational states, as well as thermalized populations as a function of temperature T.
Steady-state model results for nitrogen compounds and their deuterated counterparts.
Recommended fits of the reaction rate coefficients of N+ (3P0) + H2 and isotopic variants from the present study.
All Figures
 |
Fig. 1 Comparison between present theoretical calculations of the thermal rate coefficient of the N+ + o-H2 reaction. The filled circles and squares refer respectively to the Marquette et al. (1988) and Zymak et al. (2013) experimental results. |
| In the text | |
 |
Fig. 2 Comparison between present rate coefficients for the reactions of 14N+ and 15N+ with o-H2. The j = 0 rate coefficient is displayed as a full line whereas dotted lines correspond to thermalized value. |
| In the text | |
 |
Fig. 3 Temperature dependence of the rate coefficients for the reactions of 14N+ (j = 0) and 15N+ (j = 0) with HD. |
| In the text | |
 |
Fig. 4 Comparison between computed rate coefficients for the reactions of 14N+ (j = 0) with para- and ortho-H2 (blue and red solid lines, respectively) with the analytic forms suggested by Dislaire et al. (2012) (dotted lines). The experimental values of Marquette et al. (1988) are indicated as full circles, whereas the results of Zymak et al. (2013) are full squares. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


