| Issue |
A&A
Volume 589, May 2016
|
|
|---|---|---|
| Article Number | A85 | |
| Number of page(s) | 5 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201628082 | |
| Published online | 18 April 2016 | |
Debye screening under non-equilibrium plasma conditions
1 Argelander Institut für Astronomie, Universität Bonn Auf dem Hügel 71, 53121 Bonn, Germany
e-mail: hfahr@astro.uni-bonn.de
2 Deutsches Zentrum für Luft und Raumfahrt (DLR), Königswinterer Str. 522–524, 53227 Bonn, Germany
e-mail: michael.heyl@DLR.de
Received: 6 January 2016
Accepted: 16 March 2016
As has been revealed in a number of more recent astrophysical papers, in most of the tenuous space plasmas Maxwellian distribution functions cannot be expected for ions or electrons because of the lack of efficient relaxation processes. Many of the classical characteristics of plasmas, such as plasma frequency or Debye length, are calculated on the basis of the assumption, however, that Maxwellians prevail, which under most of the relevant astrophysical plasma conditions is not the case. We here therefore consider this specific problem of Debye shieldings of single charges in a plasma for the case of prevailing non-equilibrium distribution functions for ions and electrons. As typical non-equilibrium functions, so-called Kappa functions were considered with clear preference, and we therefore study here the Debye shielding in a plasma with Kappa-distributed electrons and ions. We show that the so-called Debye shielding increases with increasing extent of the high-velocity tail of the electron distribution function, or in other words, with lower Kappa index of the underlying Kappa function. In our calculations we demonstrate that the Debye lengths become enlarged by about a factor of 10 with respect to its classically expexted value if highly suprathermal electron distributions prevail with Kappa indices close to 1.5.
Key words: plasmas
© ESO, 2016
1. Introduction
In many of the more recent papers of plasma physics it has repeatedly been recognized that under the most probable astrophysical plasma scenarios, that is, in collision-free magnetized space plasmas, the upcoming distribution functions of electrons or protons cannot be expected to be of Maxwellian type (e.g., see Shlesinger et al. 1987, 1993; Zanette & Alemany 1995; Collier 1995; Ma & Summers 1998; Yoon 2011). While the latter, however, should be expected to be the case under quasi-equilibrium conditions, the actual non-Maxwellian distribution functions obviously appear to reflect thermodynamic states far from equilibrium, when relaxation processes operate that are not effective enough. Under such nonstandard conditions, many plasmaphysical properties are very different from those presented in textbook literature, as has been pointed out by Treumann (2001) and Treumann et al. (2004), for instance.
We here wish to study specifically the Debye screening property in a plasma, which screens single-point charges out of electric action over characteristic dimensions that are called the Debye length. In this context, it may be interesting, however, to recognize that although it is commonly agreed that Kappa functions are the adequate means to replace Maxwellians under non-equilibrium conditions (see Scudder & Olbert 1979; Meyer-Vernet & Perche 1989; Ma & Summers 1998; and Issautier et al. 1999), there is nevertheless no good consensus about how to then adequately describe the non-equilibrium Debye screening under such non-local thermal equilibrium (non-LTE) kinetic conditions. This fairly astonishing because the correct answer here should in principle be straightforward, but in fact it is not. This point is the focus of our interest here.
Results presented for the Debye screening under non-equilibrium plasma conditions are highly disjunct, controversial, and substantially in conflict with each other (Hansen & Fajans 2015; Meyer-Vernet & Perche 1989; Bryant 1996; Treumann et al. 2004; Livadiotis & McComas 2014; Fahr et al. 2015). This is the case even though directly connected with highly nonthermal Kappa-type distribution functions 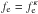 , Debye lengths should in principle be directly calculable. The associated degenerated Debye lengths following standard procedures (see Chen 1977; Spatschek 1990; Baumjohann & Treumann 1996) can be applied in a straightforward manner, but nevertheless have led to very controversial results. Plasma electrons that generate a largely extended velocity power-law tail with an effective temperature Te,κ screen single-point charges not as effectively as Maxwellian thermal electrons with a much lower temperature Te ≤ Te,κ. This can easily be ascribed to the fact that when more high-velocity electrons are available, fewer electrons are available that can be influenced at small distance from an electric point charge to create enough compensating space charge.
, Debye lengths should in principle be directly calculable. The associated degenerated Debye lengths following standard procedures (see Chen 1977; Spatschek 1990; Baumjohann & Treumann 1996) can be applied in a straightforward manner, but nevertheless have led to very controversial results. Plasma electrons that generate a largely extended velocity power-law tail with an effective temperature Te,κ screen single-point charges not as effectively as Maxwellian thermal electrons with a much lower temperature Te ≤ Te,κ. This can easily be ascribed to the fact that when more high-velocity electrons are available, fewer electrons are available that can be influenced at small distance from an electric point charge to create enough compensating space charge.
As a first impression of what to expect in terms of Kappa index variabilities in close-by astrophysical plasmas, we briefly mention the situation in the lower solar corona and then follow the solar wind plasma, which originates in the upper corona because of its dynamical expansion to increasingly large solar distances (see Parker 1965). In the lower corona the plasma is Coulomb-collision dominated and particle distribution functions are naturally isotropic Mono-Maxwellians (i.e., κ ≫ 10). However, when the coronal plasma expands, ions and electrons are rapidly no longer collision-controlled and their distribution functions degenerate from Maxwellians to non-equilibrium functions in many respects (see, e.g., Griffel & Davis 1969; Scudder & Olbert 1979; Fahr & Shizgal 1983; Meyer-Vernet & Issautier 1998; Meyer-Vernet 1999; Chashei & Fahr 2000). They become anisotropic, solar-antisolar asymmetric, and, if they are at all Maxwellian-like, then they are different for a core- and a halo-population (see Feldman et al. 1975; Scime et al. 2000). The fully developed complication of upcoming electron distribution functions at distances beyond 0.3 AU can be seen in direct in-situ plasma observations made with HELIOS-A/B (Pilipp et al. 1989).
For solar wind ion distributions and their behavior with solar distance r, Fahr et al. (2014a) have recently published a detailed study in which they describe the radially varying solar proton distribution with a local r-dependent Kappa distribution. They took pick-up ion injection into the supersonic solar wind into account together with adiabatic cooling and velocity-space diffusion. They obtained (see their Fig. 1) κ -functions with a locally best-fitting Kappa index κ = κ(r) that develops from high κ-values higher than 10 at 1 AU (i.e., quasi-Maxwellian limit) and decrease in different forms dependent on the effectiveness of the velocity-space diffusion, to systematically lower κ-values (asymptotically approaching κ = 1,5, i.e., v-5 power-law distributions). This may express how far the range of Kappa values covered at the evolution of the solar wind ion distribution function extends outward from the corona to the termination shock and what it means in terms of κ = κ(r) (for a basic interpretation of what this means in terms of a non-equilibrium state see, e.g., Lazar et al. 2015).
This latter fact is known to explain the well-known classical Debye screening length of 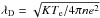 (with K the Boltzmann constant, Te the electron temperature, n the electron density, and e the electric charge), showing that the screening length increases with the percentage of high-velocity electrons, that is, with the temperature Te. The question then is which quantity will influence the associated non-LTE Debye screening if instead of Maxwellians Kappa distributions are considered. This point of degenerating Debye lengths has been carefully investigated by Treumann et al. (2004), who showed that especially for low electron Kappa indices κe ≃ 1.5 (i.e., suprathermal electrons) the resulting Debye length
(with K the Boltzmann constant, Te the electron temperature, n the electron density, and e the electric charge), showing that the screening length increases with the percentage of high-velocity electrons, that is, with the temperature Te. The question then is which quantity will influence the associated non-LTE Debye screening if instead of Maxwellians Kappa distributions are considered. This point of degenerating Debye lengths has been carefully investigated by Treumann et al. (2004), who showed that especially for low electron Kappa indices κe ≃ 1.5 (i.e., suprathermal electrons) the resulting Debye length 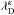 may easily increase by factors of
may easily increase by factors of 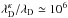 with respect to the associated classical value λD . With a simpler approach, but completely along their lines, Fahr et al. (2015) reached a very similar conclusion. They assumed that the effective screening by Kappa electrons can be calculated by replacing the Maxwellian temperature
with respect to the associated classical value λD . With a simpler approach, but completely along their lines, Fahr et al. (2015) reached a very similar conclusion. They assumed that the effective screening by Kappa electrons can be calculated by replacing the Maxwellian temperature 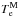 by the corresponding Kappa temperature of the electrons,
by the corresponding Kappa temperature of the electrons, 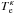 , which is given by (e.g., Heerikhuisen et al. 2008)
, which is given by (e.g., Heerikhuisen et al. 2008) 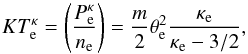 (1)where κe denotes the electron Kappa index and θe is the mean velocity spread of the central Maxwellian core population. Consequently, and taking for the asymptotically Maxwellian case
(1)where κe denotes the electron Kappa index and θe is the mean velocity spread of the central Maxwellian core population. Consequently, and taking for the asymptotically Maxwellian case 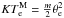 , we then find
, we then find 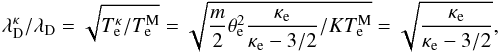 (2)which, like in the case presented by Treumann et al. (2004), also indicates that the degenerated Debye length should grow to high multiples of the classical Debye length λD if the index of the Kappa function approaches values close to κe = 3/2.
(2)which, like in the case presented by Treumann et al. (2004), also indicates that the degenerated Debye length should grow to high multiples of the classical Debye length λD if the index of the Kappa function approaches values close to κe = 3/2.
It is then even more astonishing that Livadiotis & McComas (2014) arrived at a completely different result when considering the same context and instead of the above relation obtained 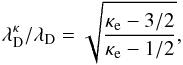 (3)which is opposite to the result before, namely that the κ - associated Debye length
(3)which is opposite to the result before, namely that the κ - associated Debye length 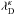 decreases even down to vanishing values for highly suprathermal populations with κe ≃ 3/2. This more or less means that completely suprathermal electrons with a power-law velocity distribution according to ~ v5 should ideally screen out any electric charge immediately, that is, over vanishingly small distances
decreases even down to vanishing values for highly suprathermal populations with κe ≃ 3/2. This more or less means that completely suprathermal electrons with a power-law velocity distribution according to ~ v5 should ideally screen out any electric charge immediately, that is, over vanishingly small distances  . An analysis, perhaps of the background of this surprising result, is offered in recent considerations by Lazar et al. (2015) of the plasma dynamic scenario. This clarifies how, why, and in which form at all Kappa distributions originate. It becomes evident that according to the understanding of Livadiotis & McComas (2014), the electron temperature of the Kappa distribution function is not κ - dependent, but constant, while in the understanding of the other authors the change from thermal to suprathermal electron populations (i.e., lowering κe-indices from higher to lower values) also is followed with a corresponding change, that is, an increase, of the electron temperatures. We examine this problem again from a slightly different aspect below.
. An analysis, perhaps of the background of this surprising result, is offered in recent considerations by Lazar et al. (2015) of the plasma dynamic scenario. This clarifies how, why, and in which form at all Kappa distributions originate. It becomes evident that according to the understanding of Livadiotis & McComas (2014), the electron temperature of the Kappa distribution function is not κ - dependent, but constant, while in the understanding of the other authors the change from thermal to suprathermal electron populations (i.e., lowering κe-indices from higher to lower values) also is followed with a corresponding change, that is, an increase, of the electron temperatures. We examine this problem again from a slightly different aspect below.
2. Debye screening solved as integration boundary problem
We start by representing electrons in velocity space by a Kappa distribution in the most general thermodynamic form, including a modulation by an electric potential (e.g., in the form given by Treumann 2001; and Treumann et al. 2004). We considered an isotropic Kappa-distribution function given by ![\begin{eqnarray} f^{\kappa}(v,r)&=&\frac{n_{0}}{\pi }\frac{\Gamma (\kappa +1)}{\Gamma (\kappa -3/2)}\frac{1}{\kappa ^{3/2}\theta ^{3}}\left(1+\frac{v^{2}-\mu }{\kappa \theta ^{2}}\right)^{-(\kappa +1)} \\[3mm] &=&A\cdot \left(1+\frac{v^{2}-\mu }{\kappa \theta ^{2}} \right)^{-(\kappa +1)} , \end{eqnarray}](/articles/aa/full_html/2016/05/aa28082-16/aa28082-16-eq41.png) where n0 is the electron density at the place where the electric potential vanishes, that is, where μ = 0 is valid, and v is the velocity magnitude. The potential μ is given by
where n0 is the electron density at the place where the electric potential vanishes, that is, where μ = 0 is valid, and v is the velocity magnitude. The potential μ is given by 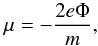 (6)with Φ being the electric potential.
(6)with Φ being the electric potential.
Taking for normalization purposes 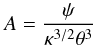 (7)with
(7)with 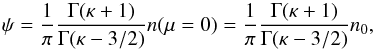 (8)where A by its value and dimension guarantees that
(8)where A by its value and dimension guarantees that 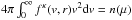 , that is, is the density at a local place where the local value of the potential is μ.
, that is, is the density at a local place where the local value of the potential is μ.
Let us emphasize at this point that the form of the distribution function given in Eq. (5), at this level of an undetermined theoretical background, is nothing else but an appropriate algorithm of describing both equilibrium distributions (i.e. Maxwellians at limκ → ∞fκ(v,r)) and non-equilibrium distributions (i.e. pure power laws with v-5 = limκ → 3/2fκ(v,r)).
Hence, for appropriately normalized velocities, that is, for 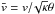 and normalized potentials
and normalized potentials 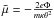 , a well-defined relation for the ratio of densities n(μ) at the place with the potential μ and those n(μ = 0) = n0 at the place with potential μ = 0 is required. As a result of the normalizations we made, the integral in the nominator of this ratio yields n0, and thus we find
, a well-defined relation for the ratio of densities n(μ) at the place with the potential μ and those n(μ = 0) = n0 at the place with potential μ = 0 is required. As a result of the normalizations we made, the integral in the nominator of this ratio yields n0, and thus we find ![\begin{eqnarray} \frac{n(\mu )}{n_{0}} &=& \frac{\frac{n_{0}}{\pi }4\pi \frac{\Gamma (\kappa +1)}{\Gamma (\kappa -3/2)}\int \frac{1}{\kappa ^{3/2}\theta ^{3}}\left(1+\frac{ v^{2}-\mu }{\kappa \theta ^{2}}\right)^{-(\kappa +1)}v^{2}{\rm d}v}{\frac{n_{0}}{\pi } 4\pi \frac{\Gamma (\kappa +1)}{\Gamma (\kappa -3/2)}\int \frac{1}{\kappa ^{3/2}\theta ^{3}}\left(1+\frac{v^{2}}{\kappa \theta ^{2}}\right)^{-(\kappa +1)}v^{2}{\rm d}v} \\[3mm] &= &4\frac{\Gamma (\kappa +1)}{\Gamma (\kappa -3/2)}\int \frac{1}{\kappa ^{3/2}\theta ^{3}}\left(1+\frac{v^{2}-\mu }{\kappa \theta ^{2}}\right)^{-(\kappa +1)}v^{2}{\rm d}v . \end{eqnarray}](/articles/aa/full_html/2016/05/aa28082-16/aa28082-16-eq61.png) Now, after normalizing velocities by
Now, after normalizing velocities by  , the remaining integral can be evaluated along the following line:
, the remaining integral can be evaluated along the following line: 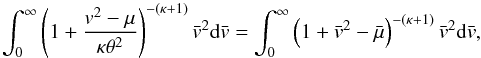 (11)and hence, after introducing the new velocity coordinate
(11)and hence, after introducing the new velocity coordinate 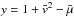 and setting
and setting 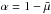 , the above ratio becomes
, the above ratio becomes ![\begin{eqnarray} \frac{n(\mu )}{n_{0}}&=&4\frac{\Gamma (\kappa +1)}{\Gamma (\kappa -3/2)}\frac{1 }{2}\int_{1-\bar{\mu}}^{\infty }\frac{\sqrt{y+\bar{\mu}-1}}{y^{\kappa +1}}{\rm d}y \\[3mm] &=& \frac{2\Gamma (\kappa +1)}{\Gamma (\kappa -3/2)}\int_{\alpha }^{\infty } \frac{\sqrt{y-\alpha }}{y^{\kappa +1}}{\rm d}y . \end{eqnarray}](/articles/aa/full_html/2016/05/aa28082-16/aa28082-16-eq66.png) We now assume that the potential Φ is due to an unscreened Coulomb potential of a point charge e, that is, by Φ = e/r, where r is the radial coordinate taken as centered on the point charge.
We now assume that the potential Φ is due to an unscreened Coulomb potential of a point charge e, that is, by Φ = e/r, where r is the radial coordinate taken as centered on the point charge.
For κ → ∞ (Maxwellian limit!) we expect a typical density reduction 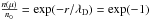 at the classical Debye length
at the classical Debye length 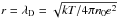 with kT = (1/2)mθ2, that is, at a distance
with kT = (1/2)mθ2, that is, at a distance 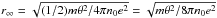 . This implies the following request
. This implies the following request ![\begin{equation} \frac{n(\mu )}{n_{0}}=\lim_{\kappa\, \rightarrow \,\infty }\text{ }\left[\int_{\alpha (\kappa )}^{\infty }\frac{\sqrt{y-\alpha (\kappa )}}{y^{\kappa +1}}{\rm d}y\right]=\frac{ \Gamma (\kappa -3/2)}{2\Gamma (\kappa +1)}\exp (-1) . \end{equation}](/articles/aa/full_html/2016/05/aa28082-16/aa28082-16-eq74.png) (14)The lower integration boundary is given by
(14)The lower integration boundary is given by 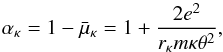 (15)and for high values of κ∞ → ∞ , we therefore correspondingly expect
(15)and for high values of κ∞ → ∞ , we therefore correspondingly expect 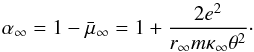 (16)This can be expressed by the following requirement:
(16)This can be expressed by the following requirement: 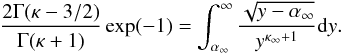 (17)If, on the other hand, we require that under nonthermal conditions (κ ≤ κ∞ ) we find the exp(−1)-reduction at an appropriately associated Debye length rκ, then instead of r∞, this correspondingly means
(17)If, on the other hand, we require that under nonthermal conditions (κ ≤ κ∞ ) we find the exp(−1)-reduction at an appropriately associated Debye length rκ, then instead of r∞, this correspondingly means  (18)when an appropriately selected screening radius r = rκ is selected for this nonthermal case. To solve the problem simply by requiring a value rκ in relation to r∞ such that ακ = α∞, which would guarantee the identity of the two integrals, this then simply leads to the following request:
(18)when an appropriately selected screening radius r = rκ is selected for this nonthermal case. To solve the problem simply by requiring a value rκ in relation to r∞ such that ακ = α∞, which would guarantee the identity of the two integrals, this then simply leads to the following request: 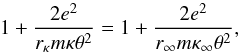 (19)leading to the requirement
(19)leading to the requirement 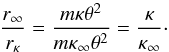 (20)This then means that the corresponding Debye length rκ is expected to vary according to
(20)This then means that the corresponding Debye length rκ is expected to vary according to 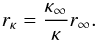 (21)The question here is only which value to choose for κ∞. This can be answered in the following way: for high values of κ we expect
(21)The question here is only which value to choose for κ∞. This can be answered in the following way: for high values of κ we expect 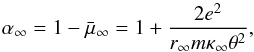 (22)and for a sufficiently high value of κ∞ we therefore request that
(22)and for a sufficiently high value of κ∞ we therefore request that 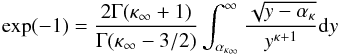 (23)is valid. Assuming that for the thermal case the classical Debye length
(23)is valid. Assuming that for the thermal case the classical Debye length
 |
Fig. 1 Debye depletion vs. Kappa index κ. |
λD(θ2) = r∞ is valid and assuming that the mean thermal energies and the electric potential energies at the Debye length are identical, that is, 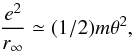 (24)then leads to the result shown in Fig. 1: the appropriate asymptotic value is κ∞ = 15. Hence the above relation between the nonthermal Debye length and the prevailing κ -index finally writes in the following form:
(24)then leads to the result shown in Fig. 1: the appropriate asymptotic value is κ∞ = 15. Hence the above relation between the nonthermal Debye length and the prevailing κ -index finally writes in the following form: 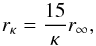 (25)indicating that Debye lengths for highly nonthermal electron distributions (i.e., κ → 1.5) may exceed thermal Debye lengths by about a factor
(25)indicating that Debye lengths for highly nonthermal electron distributions (i.e., κ → 1.5) may exceed thermal Debye lengths by about a factor 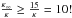
 |
Fig. 2 Kappa index vs. solar distance given in AU. |
3. Conclusions
We here showed that under non-equilibrium conditions with suprathermal electron distributions the Debye length of a plasma will degenerate. This degeneration, however, is found to be much less pronounced than predicted in earlier publications. For highly nonthermal electron distributions (i.e., κ → 3/2), the Debye length neither degenerates toward zero (Liviadotis 2014) nor degenerates toward very high values of millions of its classical value (Treumann et al. 2004; Fahr et al. 2015). Approaching the case of κ = 3/2, according to our study presented here, the Debye length definitely increases, but by no more than a factor of about 10.
We here consider some more concrete applications of the above derived result. First we give some examples for theoretically calculated Kappa values under well-determined locally valid plasma conditions. There is unfortunately no straightforward way to give one selected Kappa value for a typical astrophysical plasma scenario. Everything depends very much on the mutual strength of different plasma processes that concertedly operate on the ions or electrons. For example, Fahr et al. (2015) studied the ion injection into the supersonic solar wind, convective changes, adiabatic cooling, and velocity space diffusion, to obtain their range of Kappa values between 1.5 ≤ κ ≤ 10.
In Fig. 2 we display this evolution of the κ − index with solar distance r for a velocity diffusion index α = 2.5 (see Fahr et al. 2015) together with the associated local ion temperatures Tκ(r) = (m/ 2k)θ2 [κ(r)/(κ(r)−3/2)] , where θ2 is the core width of this ion κ − distribution given by the width of the PUI injection shell in the comoving solar wind frame, that is, by θ2 ≃ U2. There is no analogous calculation available for electron κ -indices as yet, but the calculations carried out by Fahr et al. (2014b) for the temperature moment of the electron transport equation obtained from an energy transport equation confirm that electron temperatures and associated κ − indices may have a radial development that is very similar to that of the corresponding ion values (see Fig. 4).
 |
Fig. 3 Lambda (normalized by its Maxwellian value) vs. solar distance given in AU. |
 |
Fig. 4 Temperature vs. solar distance given in AU. |
Under these conditions, we can then also display in Fig. 3 the local Debye lengths 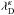 as elaborated in Eq. (25). When normalizing these non-equilibrium Debye lengths in units of Maxwellian Debye lengths
as elaborated in Eq. (25). When normalizing these non-equilibrium Debye lengths in units of Maxwellian Debye lengths 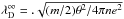 , we obtain the result also presented in Fig. 3.
, we obtain the result also presented in Fig. 3.
Furthermore, considering the passage of ions and pick-up ions over the solar wind termination shock, Fahr & Siewert (2013) obtained for the joint ion distribution downstream of the shock a value of ki,2 = 1.65. In a similar study, but carried out for electrons, Fahr et al. (2015) considered electron injection into the downstream plasma frame and Whistler wave relaxation and obtained electron Kappa values of κe,2 = 1.522. These endeavors all prove how much both the ion and electron distribution functions under these plasma scenarios are characterized by clearly pronounced non-equilibrium signatures, and as we showed here, these lead to non-equilibrium Debye shieldings as shown in Fig. 3.
References
- Chashei, I. V., & Fahr, H. J. 2000,A&A, 363, 295 [Google Scholar]
- Chen, F. F. 1977, Introduction to plasma physics (New York: Plenum Press) [Google Scholar]
- Collier, M. R. 1995, Geophys. Res. Lett., 22, 2673 [NASA ADS] [CrossRef] [Google Scholar]
- Baumjohann, W., & Treumann, R. A. 1996, Basic space plasma physics (London: Imperial College Press) [Google Scholar]
- Bryant, D. A. 1996, Plasma Phys., 56, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Fahr, H. J., & Shizgal, B. 1983, Rev. Geophys. Space Phys., 21, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Fahr, H. J., & Siewert, M. 2013, A&A, 558, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fahr, H. J., Fichtner, H., & Scherer, K. 2014a, J. Geophys. Res. (Space), 119, 7998 [NASA ADS] [CrossRef] [Google Scholar]
- Fahr, H. J., Chashei, I. V., & Verscharen, D. 2014b, A&A, 571, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fahr, H. J., Richardson, J. D., & Verscharen, D. 2015, A&A, 579, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feldman, W. C., Asbridge, J. R., Bame, S. J., & Montgomery, M. D. 1975, J. Geophys. Res. (Space), 80, 4181 [NASA ADS] [CrossRef] [Google Scholar]
- Griffel, D. H., & Davis, L. 1969, Planet. Space Sci., 17, 1009 [Google Scholar]
- Hansen, C., & Fajans, J. 1995, Phys. Rev. Lett. 74, 4209 [Google Scholar]
- Heerikhuisen, J., Pogorelov, N. V., Florinski, V., Zank, G. P., & Le Roux, J. A. 2008, ApJ, 682, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Issautier, K., Meyer-Vernet, N., Montcuquet, M., & Hoang, S. 1999, J. Geophys. Res., 104, 6704 [Google Scholar]
- Lazar, M., Poedts, S., & Fichtner, H. 2015, A&A, 582, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Livadiotis, G., & McComas, D. J. 2014, J. Plasma Phys., 80, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Ma, C., & Summers, D. 1998, Geophys. Res. Lett., 25, 4099 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer-Vernet, N. 1999, Eur. J. Phys., 20, 167 [CrossRef] [Google Scholar]
- Meyer-Vernet, N., & Issautier, K. 1998, J. Geophys. Res., 103, 29705 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer-Vernet, N., & Perche, C. 1989, J. Geophys. Res., 94, 2405 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1965, Space Sci. Rev., 4, 666 [NASA ADS] [CrossRef] [Google Scholar]
- Pilipp, W. G., Miggenrieder, H., Mühlhäuser, K. H., Rosenbauer, H., & Schlickeiser, R. 1989, ApJ, 336, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Scime, E. E., Bame, W. C., Feldman, S. P., et al. 2000, J. Geophys. Res., 105, 15887 [NASA ADS] [CrossRef] [Google Scholar]
- Scudder, J. D., & Olbert, S. 1979, J. Geophys. Res., 84, 6603 [NASA ADS] [CrossRef] [Google Scholar]
- Shlesinger, M. F., West, B. J., & Klafter, J. 1987, Phys. Rev. Lett., 58, 1100 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Shlesinger, M. F., Zaslasky, G. M., & Klafter, J. 1993, Nature, 363, 31 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Spatschek, K. H. 1990, Theoretische Plasmaphysik (Stuttgart: Teubner) [Google Scholar]
- Treumann, R. A. 2001, Astrophys. Space Sci., 277, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Treumann, R. A., Jaroschek, C. H., & Scholer, M. 2004, Phys. Plasmas, 11, 1317 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, P. H. 2001, Phys. Plasmas, 18, 122303 [NASA ADS] [CrossRef] [Google Scholar]
- Zanette, D. H., & Alemany, P. A. 1995, Phys. Rev. Lett., 75, 366 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
All Figures
 |
Fig. 1 Debye depletion vs. Kappa index κ. |
| In the text | |
 |
Fig. 2 Kappa index vs. solar distance given in AU. |
| In the text | |
 |
Fig. 3 Lambda (normalized by its Maxwellian value) vs. solar distance given in AU. |
| In the text | |
 |
Fig. 4 Temperature vs. solar distance given in AU. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


