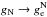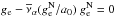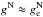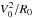| Issue |
A&A
Volume 589, May 2016
|
|
|---|---|---|
| Article Number | A63 | |
| Number of page(s) | 19 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201527713 | |
| Published online | 14 April 2016 | |
Sedna and the cloud of comets surrounding the solar system in Milgromian dynamics
Faculty of Mathematics, Physics and Informatics, Comenius University in Bratislava, Mlynská dolina, 842 48 Bratislava, Slovakia
e-mail: pauco@fmph.uniba.sk
Received: 7 November 2015
Accepted: 8 February 2016
We reconsider the hypothesis of a vast cometary reservoir surrounding the solar system – the Oort cloud of comets – within the framework of Milgromian dynamics (MD or MOND). For this purpose we built a numerical model of the cloud, assuming the theory of modified gravity, QUMOND. In modified gravity versions of MD, the internal dynamics of a system is influenced by the external gravitational field in which the system is embedded, even when this external field is constant and uniform, a phenomenon dubbed the external field effect (EFE). Adopting the popular pair ν(x) = [1−exp(−x1 / 2)] -1 for the MD interpolating function and a0 = 1.2 × 10-10 m s-2 for the MD acceleration scale, we found that the observationally inferred Milgromian cloud of comets is much more radially compact than its Newtonian counterpart. The comets of the Milgromian cloud stay away from the zone where the Galactic tide can torque their orbits significantly. However, this does not need to be an obstacle for the injection of the comets into the inner solar system as the EFE can induce significant change in perihelion distance during one revolution of a comet around the Sun. Adopting constraints on different interpolating function families and a revised value of a0 (provided recently by the Cassini spacecraft), the aforementioned qualitative results no longer hold, and, in conclusion, the Milgromian cloud is very similar to the Newtonian in its overall size, binding energies of comets and hence the operation of the Jupiter-Saturn barrier. However, EFE torquing of perihelia still play a significant role in the inner parts of the cloud. Consequently Sedna-like orbits and orbits of large semi-major axis Centaurs are easily comprehensible in MD. In MD, they both belong to the same population, just in different modes of their evolution.
Key words: comets: general / Galaxy: general / solar neighborhood / gravitation / Oort Cloud
© ESO, 2016
1. Introduction
Our present day theoretical framework of the Universe is the general theory of relativity (GTR; with a final piece in Einstein 1915), celebrating 100 years of its existence. GTR can, at an appropriate limit, be well substituted with Newtonian gravity since it was constructed for this, thus at some point GTR was adjusted to observations made in Newton’s era. To explain the modern large-scale observations of the Universe with GTR, we have to insist on a nearly flat non-monotonously accelerating Universe filled with never directly observed ingredients, the so-called dark energy (well represented by the cosmological constant Λ) and non-baryonic dark matter (DM, or CDM for cold dark matter), both having very finely-tuned properties (e.g. Copeland et al. 2006; Famaey & McGaugh 2013).
Unfortunately the ΛCDM model of the Universe is mute in addressing observed dynamical regularities of galaxies, the building blocks of the Universe: the baryonic Tully-Fisher relation (Tully & Fisher 1977; McGaugh et al. 2000; McGaugh 2005b), the Faber-Jackson relation (Faber & Jackson 1976; Sanders 2010), or the mass discrepancy-acceleration correlation (McGaugh 2004, 2005a). These observations reveal a strong coupling between the baryonic matter and the hypothetical DM. Moreover, they self-consistently point to the existence of a special acceleration scale (Famaey & McGaugh 2012).
Observations of our closest cosmic neighbourhood, the Local Group, highly disfavour the standard cosmology based on the particle dark matter (e.g. Kroupa et al. 2010; Kroupa 2012). One of the observations that is hard to accommodate within ΛCDM, even after baryonic physics is incorporated into the model, is the highly anisotropic distribution of the Local Group members – existence of thin co-orbiting planes of satellites around the Milky Way and M 31 (Pawlowski et al. 2012b, 2013, 2014, 2015; Ibata et al. 2013). It has recently been discovered that similarly anisotropic distributions of satellites are possibly common in a low redshift Universe (z< 0.05; Ibata et al. 2014, 2015). All these issues signal that, after 100 years, we have probably reached the boundaries of GTR and it happened very naturally with empirical progress. Thus we should try to find and test a new theory that provides a better explanation for present-day observations.
The aforementioned galactic phenomenology can be well explained within the framework of Milgromian dynamics (MD or MOND; Milgrom 1983b; Famaey & McGaugh 2012 for a review of 30 years of its evolution). For instance, the thin co-orbiting planes of Local Group satellites can be a by-product of a past close fly-by that the Milky Way and M 31 have undergone about 7–11 Gyr ago (Zhao et al. 2013; Pawlowski et al. 2012a). Thus, we can make the claim that the new theoretical framework of the Universe that we are looking for will explain why everything happens as if galaxies are Milgromian, and not Newtonian objects.
The current status of MD is quite analogous to Newton’s gravitational law, explaining the Kepler laws of planetary motion, in Newton’s era: MD has strong predictive power although its parent (generally-covariant) theory is still absent (Famaey & McGaugh 2012). MD proposes a modification of dynamics that is most apparent in low-acceleration regions of astrophysical systems. In MD, a test particle in a point mass gravitational field accelerates towards the point mass with magnitude (gNa0)1 / 2 if gN ≪ a0, where gN is expected Newtonian gravitational acceleration and a0 is a constant with units of acceleration. The constant a0 ~ 10-10 m s-2 plays the role of a moderator and vice-versa when gN ≫ a0 the classical limit is recovered. However, MD also states (at least when considered as modified gravity) that the internal gravitational dynamics of a system is influenced by the existence of a constant external gravitational field1 in which the system is embedded (Milgrom 1983b). In MD, external gravity does not decouple from internal dynamics as it does in Newtonian dynamics; the strong equivalence principle is apparently broken. This so-called external field effect (EFE) can attenuate or erase MD effects in the presence of an external field of magnitude that is larger than a0, even when internal accelerations are well below a0, see Sect. 2.3.
Many of new comets entering the inner solar system can be good probes of modified dynamics as we expect them to originate at large heliocentric distances where the Sun-comet acceleration is very small2. When astronomers observing motion of new comets entering the inner solar system interpret these observations in the framework of Newtonian dynamics (Newtonian astronomers) they end up with the idea of a vast reservoir (radius ~100 kau) of bodies, the Oort cloud (OC; Öpik 1932; Oort 1950), from which the comets are steadily replenished. In the language of the Newtonian orbital elements this happens because they find: (1) a sharp peak in the distribution of the original (i.e. before entering the planetary zone) reciprocal semi-major axes 0 < 1 /aorig ≲ 10-4 (i.e. orbital energies); and (2) isotropically distributed perihelia directions. We reserve the terms “near-parabolic comet” and “Oort-spike comet” for a comet with semi-major axis greater than 10 kau and perihelion distance between 0 and ~8 au (i.e. to be observable), as derived by a Newtonian astronomer.
In this paper, we investigate the change of the view about the solar system cometary reservoir when Newtonian dynamics is substituted with Milgromian. We consider the exclusively quasi-linear formulation of MD (QUMOND; Milgrom 2010), the classical modified gravity theory that was constructed in the spirit of MOND (Milgrom 1983b). We emphasize that the comet is observable only in the deep Newtonian regime where gravity is much larger than the MD threshold value a0. The basic structure of the hypothetical cloud in MD can be thus probed by tracing the motion of Oort-spike comets back in time, with the actual observations (positions and velocities) serving as the initial conditions. Extending our mainly qualitative analysis into quantitative type presents a profound test of MD.
In the rest of Sect. 1 we briefly review the classical picture of the cometary reservoir. In Sect. 2 we introduce a quasi-linear formulation of MD (QUMOND) and the numerical procedure of “how to move things” in QUMOND. Section 3 presents various models of the solar system that is nested in the local Galactic environment, as considered in this paper. The crude picture of the Milgromian OC (MOC) is presented in Sect. 4. In Sect. 5 we examine past QUMOND trajectories of 31 observed near-parabolic comets. In Sect. 6 we investigate torquing of perihelia induced by the MD’s EFE. Constraints on the MD interpolating function families, as recently found by Hees et al. (2016), are taken into account in Sect. 7. We conclude and discuss our results in Sect. 8.
1.1. The classical Oort cloud
We refer to the OC, whose existence, size and structure are inferred by a Newtonian astronomer as “the classical OC”.
The standard picture is that the OC with a radius of several tens of kau is a natural product of an interplay between the scattering of planetesimals by the giant planets – inflating bodies’ semi-major axes – and tidal torquing by the Galaxy, and random passing stars – lifting bodies’ perihelia out of the planetary zone (Duncan et al. 1987; Dones et al. 2004). Vice-versa reinjection of these bodies into the inner solar system is moderated by the same dynamical agents (Heisler & Tremaine 1986; Kaib & Quinn 2009). The pivotal role of the Galactic tide, in both enriching and eroding the OC, was fully recognized after the paper of Heisler & Tremaine (1986). Their simplified analytical theory of the Galactic disk tide, taking only its vertical component into consideration (if we assume that the Galactic equatorial plane is “horizontal”), as the radial components are nearly an order of magnitude weaker, reveals that the effect of the tides is analogous to the effect of the planets on comets of shorter periods – causing the Lydov-Kozai cycles. The vertical component of the comet’s orbital angular momentum is conserved and comets follow closed trajectories in the q−ω plane (q is the perihelion distance and ω is the argument of perihelion). Thus, q can be traded for a Galactic inclination back and forth, while ω librates around some fixed value. Since the component of the tidal force that brings comets into visibility is ~sin(2bG), where bG is the galactic latitude of the line of apsides3, a comet experiences the most rapid changes of q per orbit when bG = ± π/ 4, while when bG = 0, or bG = ± π/ 2, the changes in the perihelion distance are nil (Torbett 1986). Using a sample of long periodic comets (LPCs), with periods longer than 10 000 yrs and accurately known original orbits, Delsemme (1987) also noted these features observationally in the distribution of bG among the sample comets, confirming the significance of the Galactic tide.
The comets with q< 15 au are usually considered lost from the OC, either to the interstellar region or a more tightly bound orbit, owing to planetary perturbations (phenomenon also called Jupiter-Saturn barrier). The planetary kick they receive is typically much larger than the width of the Oort spike. Thus, to be observable, a comet has to decrease its perihelia by at least ~10 au during the revolution that precedes its possible discovery from the zone where planets have a minor effect down to the observability zone (typically less than 5 au from the Sun). Only comets with a> 20−30 kau (defining outer OC; a is the semi-major axis) experience large enough tidal torque to cause this kind of large decrease in q in one revolution (e.g. Dones et al. 2004; Rickman 2014). But, there are many observed Oort spike comets with much smaller semi-major axes (Dybczyński & Królikowska 2011, hereafter DK11). The concept of the Jupiter-Saturn barrier should actually be revised as about 15% of the near-parabolic comets can migrate through it without any significant orbital change (DK11; Dybczyński & Królikowska 2015).
Kaib & Quinn (2009) demonstrate the importance of a special dynamical pathway capable of delivering inner OC bodies (initial a< 20 kau, often even <10 kau) into the observable orbits – but at first into the outer OC region a> 20 kau – by a cooperation between the planetary perturbations and the Galactic tide. According to Kaib & Quinn (2009), the new comets entering the inner solar system could originate in both the inner, and the outer, OC, with nearly equal probability.
Passing Galactic-field stars, although their implied injection rate is 1.5–2 times less than that of the Galactic tide4 (Heisler & Tremaine 1986), have their own important role – they keep the OC isotropic. The trajectories with “course inner solar system” would quickly be depleted if there were no passing stars. Synergy between the Galactic tide and the passing stars ensures almost steady flow of new comets into the inner solar system (Rickman et al. 2008). Thus all above-mentioned dynamical agents are important in the delivery process.
1.2. Puzzles
Here we briefly review some of the persistent puzzles that challenge the classical OC theory.
Simulations of OC formation indicate that only 1–3% of all bodies that are scattered by the giant planets are trapped to the present day outer OC orbits (or ~5% into the whole cloud; Dones et al. 2004; Kaib et al. 2011). This low trapping efficiency leads to some inconsistencies in the standard theory, if we presume that the outer OC is the source of the observed LPCs. Specifically, the primordial protoplanetary disk of planetesimals of the total mass 70–300 M⊕ is required to explain the observed LPC flux near Earth. Such a massive disk is at odds with giant planets formation theory, leading to their excessive migration and/or formation of additional giant planets (Dones et al. 2004, and references therein).
The existence of the mentioned special dynamical pathway described in Kaib & Quinn (2009) could serve as a possible solution to this problem, because the trapping efficiency of the inner OC can be an order of magnitude larger than that in the outer OC if the OC formation began in an open cluster (Kaib & Quinn 2008). In any case, the Sun was more probably born in an embedded cluster (Lada & Lada 2003), encased in interstellar gas and dust. The sketched simple solution could be problematic in the presence of a vast amount of gas as in the embedded cluster environment. Aerodynamic gas drag on planetesimals prevents kilometre-sized bodies from entering the cloud and, in the most extreme case, this first stage of the solar system evolution does not make any contribution to the cloud (Brasser et al. 2007).
Another outstanding puzzle concerns the observed population ratio between the OC and the scattered disk5 (SD). Observations suggest that this ratio lies between 100 and 1000 but simulations that produce these two reservoirs simultaneously, yield the value of the order of 10 (Duncan & Levison 1997; Levison et al. 2008; Kaib & Quinn 2009). The populations are inferred from the observed fluxes of new LPCs and Jupiter-family comets (JFCs), which are brighter than some reference total magnitude. However, the population ratio estimated in the simulations of the OC and SD formation refers to objects larger than a given size. Accounting for the fact that “an LPC is smaller than a JFC with the same total absolute magnitude”, Brasser & Morbidelli (2013) arrive at the discrepancy of a factor of “only” 4.
As early as the first numerical simulations of the OC formation were performed, it was recognized that only bodies with semi-major axes a beyond ~2000 au could have their perihelia torqued out of the planetary zone into the OC (Duncan et al. 1987). Bodies with smaller a would still have their perihelia settled near planets. The observed orbital distribution of trans-Neptunian objects (TNOs) have largely agreed with this result. In any case, two striking exceptions have been found – the orbit of Sedna (Brown et al. 2004) and 2012 VP113 (Trujillo & Sheppard 2014). With perihelia (q) of 76 and 80 au respectively, these objects no longer interact with planets, yet their large semi-major axes of ~500 and ~250 respectively, point to strong planetary perturbations in the past. Although their semi-major axes are larger than most TNOs, they are still too small to be significantly perturbed by the current local Galactic tide. Thus, these orbits remain unexplained by any known dynamical process in the solar system (Morbidelli & Levison 2004). An interesting solution to this problem was offered by Kaib et al. (2011), namely, radial migration of the Sun (Sellwood & Binney 2002), which has not been accounted properly in any past study. The simulation of Kaib et al. (2011) began with the formation of the Galaxy in a large N-body + smooth-particle-hydrodynamics simulation where solar analogues were identified. Then the OC formation around these stars (often substantial radial migrants) were followed under the influence of the four giant planets, the Galaxy and randomly passing stars, leading to the conclusion that Sedna can be a classical OC body. Unfortunately, the enhanced tidal field that is due to the Sun’s radial migration (inward with respect to its current position, if we are looking back in time) also enhances erosion of the outer OC, and thus deepens the primordial disk-mass problem (Kaib et al. 2011).
1.3. Basics of MOND
According to the MOND6 algorithm (Milgrom 1983b), the true gravitational acceleration in spherically symetric systems has to be calculated as 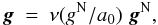 (1)where a0 ≈ 10-10 m s-2 ~ cH0 ~ c Λ1 / 2 is the transition acceleration, c is the speed of light, H0 is the Hubble constant, Λ is the cosmological constant, gN is the expected Newtonian acceleration, | gN | ≡ gN, and ν(β) is an interpolating function that reflects the underlying general theory with properties ν(β) → 1 for β ≫ 1 and ν(β) → β− 1 / 2 for β ≪ 1. Equation (1) implies that
(1)where a0 ≈ 10-10 m s-2 ~ cH0 ~ c Λ1 / 2 is the transition acceleration, c is the speed of light, H0 is the Hubble constant, Λ is the cosmological constant, gN is the expected Newtonian acceleration, | gN | ≡ gN, and ν(β) is an interpolating function that reflects the underlying general theory with properties ν(β) → 1 for β ≫ 1 and ν(β) → β− 1 / 2 for β ≪ 1. Equation (1) implies that 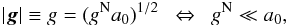 (2)and thus it yields exactly the well-known scaling relations (McGaugh et al. 2000; Faber & Jackson 1976; Milgrom 1983a). The basics of MOND in Eq. (1) can be written equivalently in the form
(2)and thus it yields exactly the well-known scaling relations (McGaugh et al. 2000; Faber & Jackson 1976; Milgrom 1983a). The basics of MOND in Eq. (1) can be written equivalently in the form 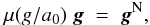 (3)where μ(α) = 1 /ν(β), β = αμ(α), satisfies μ(α) → 1 for α ≫ 1 and μ(α) → α for α ≪ 1. Equation (2), the backbone of MOND/MD, is the equivalent of stating that: (i) equations of motion are invariant under transformation (t,r) → (λt,λr), λ ∈R (Milgrom 2009c); or (ii) the gravitational field is enhanced by anti-screening of ordinary masses in some gravitationally polarizable medium that is characterized by “gravitational permittivity” equal to g/a0 (Blanchet & Le Tiec 2008, 2009; Blanchet & Bernard 2014). Eventually, MOND can be related to quantum-mechanical processes in the vacuum (Milgrom 1999). Another interesting theory taking the best of both worlds of MD and ΛCDM, is the recent DM superfluid model (Berezhiani & Khoury 2016, 2015).
(3)where μ(α) = 1 /ν(β), β = αμ(α), satisfies μ(α) → 1 for α ≫ 1 and μ(α) → α for α ≪ 1. Equation (2), the backbone of MOND/MD, is the equivalent of stating that: (i) equations of motion are invariant under transformation (t,r) → (λt,λr), λ ∈R (Milgrom 2009c); or (ii) the gravitational field is enhanced by anti-screening of ordinary masses in some gravitationally polarizable medium that is characterized by “gravitational permittivity” equal to g/a0 (Blanchet & Le Tiec 2008, 2009; Blanchet & Bernard 2014). Eventually, MOND can be related to quantum-mechanical processes in the vacuum (Milgrom 1999). Another interesting theory taking the best of both worlds of MD and ΛCDM, is the recent DM superfluid model (Berezhiani & Khoury 2016, 2015).
As MD has higher predictive power in galaxies than the ΛCDM model, although its parent (generally-covariant) theory is still missing, and as most of the classical OC lies in the MD acceleration regime, which is modulated by the external field of the Galaxy ~2a0, it is asking for the motion of the Oort spike comets to be investigated as it is prescribed by MD. Science is mainly about formulating and testing hypotheses. The possible inevitable tension between the theory and observations could be a disproof of some formulations of MD, incorporating Eq. (2).
Maybe application of the non-standard physics does not yield inconsistencies between the OC formation/OC body-injection models, which are calibrated by the observed LPC flux, and those of giant planets formation, which are calibrated by the appearance of the outer planets region.
2. Milgromian dynamics
The simple formula of Eq. (1), when considered as modified gravity7, cannot be regarded as a universal theory that is applicable to any self-gravitating system of interest, e.g. for not obeying conservation laws out of highly symmetric problems (Famaey & McGaugh 2012). In any case, it was recognised, as early on by Bekenstein & Milgrom (1984) at the classical level and by Bekenstein (2004) at the Lorentz-covariant level, that construction of a universal theory, reproducing Eq. (1) in the special case of the static weak field limit and spherical symmetry, is possible.
2.1. Quasi-linear formulation of MD
Several Lorentz covariant theories of MD have been devised in recent years (e.g. Bekenstein 2004; Sanders 2005; Zlosnik et al. 2007; Milgrom 2009a) which reproduce Eq. (1) in the static weak field limit and spherical symmetry, but differing from each other outside of it (Zhao & Famaey 2010). At a classical level these theories generally transform to one of the two types of modified Poisson equation (Bekenstein & Milgrom 1984; Milgrom 2010). Both classical theories are derived from action, thus benefiting from the standard conservation laws. The theory from Milgrom (2010), dubbed QUMOND for quasi-linear formulation of MD, can be considered as especially attractive for its computational friendliness.
In QUMOND the field equation that determines MD potential, Φ, reads ![\begin{eqnarray} \label{QFE} \nabla\cdot\left(\nabla\Phi\right)=\nabla\cdot\left[\nu\left(\vert\nabla\phi^{\rm N}\vert/a_{0}\right)\nabla\phi^{\rm N}\right], \end{eqnarray}](/articles/aa/full_html/2016/05/aa27713-15/aa27713-15-eq59.png) (4)where φN is the Newtonian potential fulfilling ∇·(∇φN) = 4πGϱb, ϱb is baryonic mass density. QUMOND comes from modifying only the gravitational part of the classical action hence the equation of motion stays the same
(4)where φN is the Newtonian potential fulfilling ∇·(∇φN) = 4πGϱb, ϱb is baryonic mass density. QUMOND comes from modifying only the gravitational part of the classical action hence the equation of motion stays the same 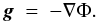 (5)Let us define the so-called phantom matter density (PMD)
(5)Let us define the so-called phantom matter density (PMD) ![\begin{eqnarray} \label{roph} \varrho_{\rm ph}~=~\frac{\nabla\cdot[\widetilde{\nu}(|\nabla\phi^{\rm N}|/a_{0})\nabla\phi^{\rm N}]}{4\pi G}, \end{eqnarray}](/articles/aa/full_html/2016/05/aa27713-15/aa27713-15-eq64.png) (6)
(6)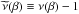 . Equation (6) does not represent any real physical quantity, particle, or field. PMD is only a mathematical object that allows us to take advantage of the already mentioned QUMOND formulation of MD and write the equations in our intuitive Newtonian sense with “dark matter”. With aid of Eq. (6), the MD potential Φ can be written as a sum
. Equation (6) does not represent any real physical quantity, particle, or field. PMD is only a mathematical object that allows us to take advantage of the already mentioned QUMOND formulation of MD and write the equations in our intuitive Newtonian sense with “dark matter”. With aid of Eq. (6), the MD potential Φ can be written as a sum 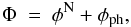 (7)where the phantom potential φph fulfils normal Poisson equation
(7)where the phantom potential φph fulfils normal Poisson equation 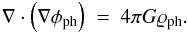 (8)Once the Newtonian potential is specified, PMD can be found and hence the motion in MD can be traced.
(8)Once the Newtonian potential is specified, PMD can be found and hence the motion in MD can be traced.
The widely used family of 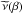 functions, corresponding to the special behaviour of ν(β) in Eq. (1), is
functions, corresponding to the special behaviour of ν(β) in Eq. (1), is ![\begin{eqnarray} \label{A3} \widetilde{\nu}_{n}(\beta)~=~\left[\frac{1+\left(1+4\beta^{-n}\right)^{1/2}}{2}\right]^{1/n}-1, \end{eqnarray}](/articles/aa/full_html/2016/05/aa27713-15/aa27713-15-eq70.png) (9)see, e.g. Famaey & McGaugh (2012). It is well known that the simple n = 1 function (Famaey & Binney 2005) reproduces the rotation curves of the most spiral galaxies well, e.g. Gentile et al. (2011). However, this function is because of its rather gradual transition to the Newtonian regime excluded by solar system tests, e.g. Sereno & Jetzer (2006), Blanchet & Novak (2011). It is possible to construct an interpolating function with more rapid transition to the Newtonian regime (less impact on the solar system) and, at the same time, very similar to the simple interpolating function on the galactic scales where accelerations are ~a0 (see Fig. 19 in Famaey & McGaugh 2012). An example of this is McGaugh (2008):
(9)see, e.g. Famaey & McGaugh (2012). It is well known that the simple n = 1 function (Famaey & Binney 2005) reproduces the rotation curves of the most spiral galaxies well, e.g. Gentile et al. (2011). However, this function is because of its rather gradual transition to the Newtonian regime excluded by solar system tests, e.g. Sereno & Jetzer (2006), Blanchet & Novak (2011). It is possible to construct an interpolating function with more rapid transition to the Newtonian regime (less impact on the solar system) and, at the same time, very similar to the simple interpolating function on the galactic scales where accelerations are ~a0 (see Fig. 19 in Famaey & McGaugh 2012). An example of this is McGaugh (2008): 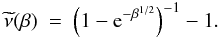 (10)Unless stated otherwise, we use this function throughout the paper, together with the standard value a0 = 1.2 × 10-10 m s-2 = 3700 km2 s-2 kpc-1 (Begeman et al. 1991; Gentile et al. 2011; Famaey & McGaugh 2012).
(10)Unless stated otherwise, we use this function throughout the paper, together with the standard value a0 = 1.2 × 10-10 m s-2 = 3700 km2 s-2 kpc-1 (Begeman et al. 1991; Gentile et al. 2011; Famaey & McGaugh 2012).
MD greatly reduces the missing mass in galaxy clusters but leaves consistent mass discrepancy of a factor of about 2 (e.g. Sanders 2003; see also Famaey & McGaugh 2012). This fact is frequently used as a reason to completely refute any consideration of MD8. There is a suggestion to avoid the remaining discrepancies with a variation of a0, and that a0 is larger in clusters than it is in galaxies (e.g., Zhao & Famaey 2012; Khoury 2015). We do not develop this idea in this paper. In MD, the remaining missing mass does not need to be non-baryonic. Instructed by the history and motivated by the missing baryons problem9 it is completely possible that we still do not know the whole baryonic budget of galaxy clusters. The recent discovery of more than a thousand ultra-diffuse galaxy-like objects in the Coma cluster (Koda et al. 2015) further promotes this suggestion (Milgrom 2015).
2.2. Solving for the Milgromian potential of the Galaxy on a grid
One can convert known baryonic matter distribution to QUMOND potential and hence the real acceleration. But in general this has to be done numerically. According to the scheme sketched in Eqs. (5)–(8) first we have to know the Newtonian potential φN(r), thus we have to solve the Poisson equation ΔφN(r) = 4πGϱb(r), where the baryonic mass density ϱb(r) is specified by the adopted model of the Galaxy, see Sect. 3.1. For this purpose, we employ a fast Poisson solver on a Cartesian grid with the boundary condition that corresponds to a point mass, φN(r) = −GMb/r, on the last grid point, where r is the centre of mass distance of the baryonic mass density grid and Mb is the total baryonic mass.
For a given Newtonian potential φN discretised on a Cartesian grid (x,y,z) of step h, the discretised version of Eq. (6) is given on a grid point (i,j,k) by: ![\begin{eqnarray} \label{A4} \varrho_{\rm ph}^{i,j,k}&=&\frac{1}{4\pi G h^{2}}\Big{[} \left(\phi^{\rm N}_{~i+1,j,k}-\phi^{\rm N}_{~i,j,k}\right)\widetilde{\nu}_{B_{x}} \nonumber \\ &&-\left(\phi^{\rm N}_{~i,j,k}-\phi^{\rm N}_{~i-1,j,k}\right)\widetilde{\nu}_{A_{x}}\nonumber \\ &&+\left(\phi^{\rm N}_{~i,j+1,k}-\phi^{\rm N}_{~i,j,k}\right)\widetilde{\nu}_{B_{y}}\nonumber \\ &&-\left(\phi^{\rm N}_{~i,j,k}-\phi^{\rm N}_{~i,j-1,k}\right)\widetilde{\nu}_{A_{y}}\nonumber \\ &&+\left(\phi^{\rm N}_{~i,j,k+1}-\phi^{\rm N}_{~i,j,k}\right)\widetilde{\nu}_{B_{z}}\nonumber \\ &&-\left(\phi^{\rm N}_{~i,j,k}-\phi^{\rm N}_{~i,j,k-1}\right)\widetilde{\nu}_{A_{z}}~\Big{]}, \end{eqnarray}](/articles/aa/full_html/2016/05/aa27713-15/aa27713-15-eq85.png) (11)where
(11)where 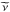 function is evaluated in a particular midpoint, e.g.
function is evaluated in a particular midpoint, e.g. 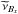 is evaluated in (i + 1 / 2,j,k),
is evaluated in (i + 1 / 2,j,k), 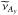 in (i,j−1 / 2,k), and so on, half a cell from (i,j,k) in each of the three orthogonal directions, see, e.g. Famaey & McGaugh (2012), Lüghausen et al. (2013, 2014, 2015) for illustration. The gradient of φN in
in (i,j−1 / 2,k), and so on, half a cell from (i,j,k) in each of the three orthogonal directions, see, e.g. Famaey & McGaugh (2012), Lüghausen et al. (2013, 2014, 2015) for illustration. The gradient of φN in 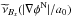 is approximated by
is approximated by 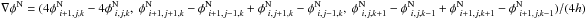 , and so forth.
, and so forth.
Finally, knowing the PMD we can solve for the effective Milgromian potential Φ(r) in ΔΦ(r) = 4πG [ϱb(r) + ϱph(r)] on the same grid. As the boundary condition 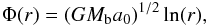 (12)where r is the centre of mass distance of the “mass density” grid and Mb is the total baryonic mass, is assumed on the last grid point, in accordance with Eq. (1). In the whole procedure of obtaining Φ, we assume that the Galaxy is isolated from external gravitational fields10, see Sect. 2.3 for a discussion on EFE. This is a good approximation until the internal gravity becomes comparable with the external field generated by the large scale structure, which is of the order of a0/ 100 (Famaey et al. 2007). At the position of the Sun the internal gravity is ~a0.
(12)where r is the centre of mass distance of the “mass density” grid and Mb is the total baryonic mass, is assumed on the last grid point, in accordance with Eq. (1). In the whole procedure of obtaining Φ, we assume that the Galaxy is isolated from external gravitational fields10, see Sect. 2.3 for a discussion on EFE. This is a good approximation until the internal gravity becomes comparable with the external field generated by the large scale structure, which is of the order of a0/ 100 (Famaey et al. 2007). At the position of the Sun the internal gravity is ~a0.
2.3. External field effect
A special feature of MD as modified gravity is that its formulation breaks the strong equivalence principle (Milgrom 1986b).
If we have a system s that rests in the gravitational field of a larger system S. Say that S generates gravitational acceleration ge = −∇Φe within s. We assume that the gravitational field that is acting on a body within s, g = −∇Φ, can be separated into internal gi = −∇Φi (| gi | ≡ gi) and external ge = −∇Φe (| ge | ≡ ge) part. We can then substitute 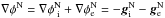 into Eq. (4), where
into Eq. (4), where 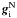 (
(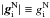 ) and
) and 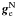 (
(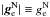 ) are internal and external Newtonian gravitational accelerations. After removing divergences, dropping the curl-field and considering only directions in the plane perpendicular to the external field this gives (Angus et al. 2014)
) are internal and external Newtonian gravitational accelerations. After removing divergences, dropping the curl-field and considering only directions in the plane perpendicular to the external field this gives (Angus et al. 2014) 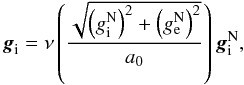 (13)where we have further assumed
(13)where we have further assumed 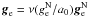 . The internal gravity in s depends not only on internal gravitational sources (in our case – the Sun) but also on the strength of the external field at the position of s (in our case – the local strength of the Galactic gravitational field), even when the external field is considered as being constant within s.
. The internal gravity in s depends not only on internal gravitational sources (in our case – the Sun) but also on the strength of the external field at the position of s (in our case – the local strength of the Galactic gravitational field), even when the external field is considered as being constant within s.
This effect should not be confused with tidal forces that arise from the non-uniformity of the external gravitational field across the system s. A person in the (arbitrarily small) falling elevator in s can find out about the existence and properties of the external gravitational field through its influence on the internal dynamics. Say  is constant, if
is constant, if  in Eq. (13) the system s behaves purely as Newton said, with no sign of the modified dynamics as ν(gN/a0) tends to 1 then, similarly as in the case
in Eq. (13) the system s behaves purely as Newton said, with no sign of the modified dynamics as ν(gN/a0) tends to 1 then, similarly as in the case 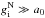 . The opposite deep-MD regime applies when
. The opposite deep-MD regime applies when 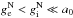 . The standard MD effects are observed only when both internal and external gravity are sufficiently small (≲a0) and, moreover, the external field does not dominate over the internal one. Eventually, if the hierarchy goes as
. The standard MD effects are observed only when both internal and external gravity are sufficiently small (≲a0) and, moreover, the external field does not dominate over the internal one. Eventually, if the hierarchy goes as 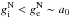 , the dynamics is Newtonian with rescaled gravitational constant
, the dynamics is Newtonian with rescaled gravitational constant 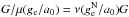 , where G is the Newtonian gravitational constant. Moreover, the dynamics is anisotropic with dilatation along the direction of the external field11.
, where G is the Newtonian gravitational constant. Moreover, the dynamics is anisotropic with dilatation along the direction of the external field11.
The external field of the Galaxy, ge, thus has to be considered carefully beyond its tidal effects when modelling MOC. We use the constant value 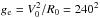 km2 s-2/(8.3 kpc) ≐ 1.87 a0, where V0 is the circular speed of the Sun at R0, and R0 is the distance between the Sun and the Galactic centre (GC), throughout the paper. Compare the values of V0 and R0 with for example those given by Schönrich (2012). We take the Newtonian value
km2 s-2/(8.3 kpc) ≐ 1.87 a0, where V0 is the circular speed of the Sun at R0, and R0 is the distance between the Sun and the Galactic centre (GC), throughout the paper. Compare the values of V0 and R0 with for example those given by Schönrich (2012). We take the Newtonian value 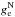 as a solution of
as a solution of 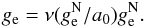 (14)Equation (14) is known to be a good approximation at the position of the Sun (Brada & Milgrom 1995) (the Galaxy can be well modelled as being made up of bulge plus exponential disks).
(14)Equation (14) is known to be a good approximation at the position of the Sun (Brada & Milgrom 1995) (the Galaxy can be well modelled as being made up of bulge plus exponential disks).
We note that the Galactic tide is modelled as a separate effect, see Sect. 3.1.3 for details.
To better visualise the gravity-boosting effect of MD and also the importance of EFE on the solar system scales, we plot ν interpolating function as a function of heliocentric distance Ξ in Fig. 1. The simple ν(β) = [1 + (1 + 4β-1)1 / 2] / 2 and the exponential ν(β) = [1−exp(−β1 / 2)] -1 interpolating functions are depicted. β ≡ gN/a0 is approximated with ![\hbox{$[(g^{\rm N}_{\rm e})^{2} + (GM_{\odot}/\Xi^{2})^{2}]^{1/2}/a_{0}$}](/articles/aa/full_html/2016/05/aa27713-15/aa27713-15-eq132.png) , i.e. vectors of external and internal Newtonian gravitational acceleration are assumed to be perpendicular to each other for simplicity. The characteristic distance scale (MD transition scale) is
, i.e. vectors of external and internal Newtonian gravitational acceleration are assumed to be perpendicular to each other for simplicity. The characteristic distance scale (MD transition scale) is 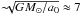 kau. Because of the action of EFE, ν(β) does not diverge with Ξ → ∞, but asymptotes to the constant value
kau. Because of the action of EFE, ν(β) does not diverge with Ξ → ∞, but asymptotes to the constant value 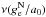 .
.
EFE is important, even in the high-acceleration regime, where the gravity-boosting effect of MD is very weak. It has been shown that, at 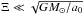 , which is well fulfilled in the planetary region, EFE manifests primarily through an anomalous quadrupolar correction to the Newtonian potential, which increases with the heliocentric distance Ξ (Milgrom 2009b; Blanchet & Novak 2011). This dynamical effect is thus analogous to that of a massive body hidden at a large heliocentric distance, lying in the direction to GC, ge/ge, (Hogg et al. 1991; Iorio 2010b). As the external field ge rotates with period ~210 Myr, this corresponds to an unfeasible configuration in Newtonian dynamics (too massive body in a very distant circular orbit around the Sun). Hence the effect of MD should be distinguishable from that of the distant planet in simulations that are carried out on large timescales.
, which is well fulfilled in the planetary region, EFE manifests primarily through an anomalous quadrupolar correction to the Newtonian potential, which increases with the heliocentric distance Ξ (Milgrom 2009b; Blanchet & Novak 2011). This dynamical effect is thus analogous to that of a massive body hidden at a large heliocentric distance, lying in the direction to GC, ge/ge, (Hogg et al. 1991; Iorio 2010b). As the external field ge rotates with period ~210 Myr, this corresponds to an unfeasible configuration in Newtonian dynamics (too massive body in a very distant circular orbit around the Sun). Hence the effect of MD should be distinguishable from that of the distant planet in simulations that are carried out on large timescales.
 |
Fig. 1 Interpolating functions ν(β) = [1 + (1 + 4β-1)1 / 2] / 2 (dot-dashed line) and ν(β) = [1−exp(−β1 / 2)] -1 (solid line) as functions of heliocentric distance Ξ. β ≡ gN/a0 is approximated with |
3. Models
In Sect. 3.1 the adopted model of the Milky Way matter distribution is presented and in Sect. 3.1.1 the appropriate PMD for this model is calculated. This “complicated” model is considered solely to estimate matter density in the solar neighborhood and hence estimate the effect of the Galactic tide, see Sects. 3.1.3, 5 and 6. In Sect. 3.2 the simplified model of the MOC that is embedded in a constant external field is introduced. The majority of the qualitative analysis performed in the paper is carried out assuming this simple model. Moreover, it will be shown that the Galactic tide is of much less importance for MOC comets than for classical OC comets.
Firstly, we erect a rectangular Galilean coordinate system O⊙(ξ′,η′,ζ′) that is centred on the Sun. At time t = 0 (present time), the inertial reference frame O⊙(ξ′,η′,ζ′) coincides with the rotating Galactic rectangular coordinate system, i.e. ξ′ axis is directed from the Sun to the GC at t = 0. We also use an inertial frame that is centred on the GC, denoted OGC(x,y,z), with x−y plane being the Galactic plane and x axis directed from the GC to the Sun at t = 0.
3.1. Milky Way
We adopt the Milky Way mass model of McGaugh (2008), similar to that used in Lüghausen et al. (2014). McGaugh (2008) concluded that MOND prefers short disk scale lengths in the range 2.0 <rd< 2.5 kpc. The modelled Milky Way consists of a stellar double-exponential disk with the scale length Rd = 2.3 kpc and the scale height zd = 0.3 kpc with the disk mass 4.2 × 1010M⊙. Moreover, it has a thin gas disk of the total mass 1.2 × 1010M⊙ with the same scale length and half scale height as the stellar one and a bulge modelled as a Plummer’s sphere, with the mass 0.7 × 1010M⊙ and the half-mass radius 1 kpc.
3.1.1. Phantom matter density
MD predicts the complex structure of a “Newtonist’s dark halo” with a pure disk component and rounder component with radius-dependent flattening that becomes spherical at great distances (Milgrom 2001), see also Fig. 5 in Lüghausen et al. (2015).
We calculated the PMD of the Milky Way model according to the numerical scheme of Sect. 2.2. A Cartesian (x,y,z) grid with 512 × 512 × 256 cells and resolution of 0.1 × 0.1 × 0.02 kpc was used. This resolution was tested as being sufficiently fine enough so that the calculated PMD changes only negligibly if the resolution is further increased. Figure 2 shows the vertical PMD ϱph(z) at R = R0 = 8.3 kpc within | z | < 1 kpc. The Kz force perpendicular to the Galactic plane will be obviously enhanced in this case, compared to the Galaxy that resides in a spherical DM halo, as predicted by Milgrom already in his pioneer paper (Milgrom 1983b).
Owing to small stellar samples (Hipparcos data), one cannot precisely recover the shape of Kz(z) or of the dynamical density, only the surface density below some 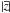 , where
, where 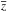 is the mean distance of the samples from the Galactic plane (Bienaymé et al. 2009). We should compare the calculated surface density of the baryonic matter plus the phantom matter with observations. Holmberg & Flynn (2004) find the dynamical surface density Σ0 = 74 ± 6M⊙ pc-2 within | z | < 1.1 kpc. By fitting the calculated local PMD with a superposition of three exponential disks, we find Σ0 = 80M⊙ pc-2 within | z | < 1.1 kpc, which is consistent with the value of Holmberg & Flynn (2004). The portion 43 M⊙ pc-2 resides in the normal matter and 37 M⊙ pc-2 in the phantom.
is the mean distance of the samples from the Galactic plane (Bienaymé et al. 2009). We should compare the calculated surface density of the baryonic matter plus the phantom matter with observations. Holmberg & Flynn (2004) find the dynamical surface density Σ0 = 74 ± 6M⊙ pc-2 within | z | < 1.1 kpc. By fitting the calculated local PMD with a superposition of three exponential disks, we find Σ0 = 80M⊙ pc-2 within | z | < 1.1 kpc, which is consistent with the value of Holmberg & Flynn (2004). The portion 43 M⊙ pc-2 resides in the normal matter and 37 M⊙ pc-2 in the phantom.
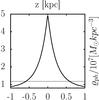 |
Fig. 2 PMD of the Milky Way (solid), modelled as in Sect. 3.1 at R = R0 = 8.3 kpc within | z | < 1 kpc. NFW dark matter density (dashed line) is also depicted. |
3.1.2. The dark matter halo of Newtonian Galaxy
The Navarro-Frenk-White (NFW) halo model (Navarro et al. 1997) 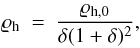 (15)where δ ≡ r/rh, rh is the scale radius (spherically symmetric halo, r is radial coordinate), ϱh,0 is a constant, represents the culmination of the present day theoretical knowledge in the standard CDM-based cosmology.
(15)where δ ≡ r/rh, rh is the scale radius (spherically symmetric halo, r is radial coordinate), ϱh,0 is a constant, represents the culmination of the present day theoretical knowledge in the standard CDM-based cosmology.
In Sect. 6 we aim to compare the effect of the Galaxy on the MOC and the classical OC. We use the NFW model as the model of the Milky Way dark matter halo in the Newtonian framework in order to find local mass density in the solar neighbourhood and quantify the Galactic tide.
CDM haloes are routinely described in terms of their virial mass, Mvir, which is the mass that is contained within the virial radius rvir, and the concentration parameter c = r-2/rvir, where r-2 is the radius at which the logarithmic slope of the density profile dlog ϱh/dlog r = −2 (for the NFW profile, r-2 = rh). The virial radius rvir is defined as the radius of a sphere that is centred on the halo centre, which has an average density that is Δ times the critical density 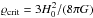 , where H0 is the Hubble constant. Δ varies with redshift, with Δ ≈ 100 today. For the NFW model
, where H0 is the Hubble constant. Δ varies with redshift, with Δ ≈ 100 today. For the NFW model 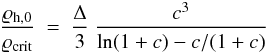 (16)holds. Thus knowing the concentration parameter c we can find ϱh,0 of Eq. (15). Boylan-Kolchin et al. (2010) examined (NFW) haloes taken from the Millennium-II simulations at redshift zero, in the mass range 1011.5 ≤ Mvir [h-1M⊙]≤1012.5, a mass range that the Milky Way’s halo is likely to lie in, and determined that the probability distribution of the concentration parameter was well-fitted by a Gaussian distribution in lnc, with ⟨ lnc ⟩ = 2.56 and σlnc = 0.272. We adopt c = exp(2.56) as the concentration parameter of the Galaxy. The remaining degree of freedom in Eq. (15), represented by the scale radius rh, can be eliminated by fitting the circular speed V0 at radial distance R0:
(16)holds. Thus knowing the concentration parameter c we can find ϱh,0 of Eq. (15). Boylan-Kolchin et al. (2010) examined (NFW) haloes taken from the Millennium-II simulations at redshift zero, in the mass range 1011.5 ≤ Mvir [h-1M⊙]≤1012.5, a mass range that the Milky Way’s halo is likely to lie in, and determined that the probability distribution of the concentration parameter was well-fitted by a Gaussian distribution in lnc, with ⟨ lnc ⟩ = 2.56 and σlnc = 0.272. We adopt c = exp(2.56) as the concentration parameter of the Galaxy. The remaining degree of freedom in Eq. (15), represented by the scale radius rh, can be eliminated by fitting the circular speed V0 at radial distance R0: 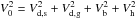 , where the added squared speeds represent particular Galactic components (stellar disk, gas disk, bulge, dark halo) determined by the particular masses that are enclosed within R0. Doing so for V0 = 240 km s-1, R0 = 8.3 kpc we find: ϱh,0 = 5.750 × 106M⊙ kpc-3, rh = 28.4 kpc. Surface density of the NFW halo within | z | < 1.1 kpc is 26 M⊙ pc-2, consistent with the lower bound on Σ0 (Holmberg & Flynn 2004).
, where the added squared speeds represent particular Galactic components (stellar disk, gas disk, bulge, dark halo) determined by the particular masses that are enclosed within R0. Doing so for V0 = 240 km s-1, R0 = 8.3 kpc we find: ϱh,0 = 5.750 × 106M⊙ kpc-3, rh = 28.4 kpc. Surface density of the NFW halo within | z | < 1.1 kpc is 26 M⊙ pc-2, consistent with the lower bound on Σ0 (Holmberg & Flynn 2004).
3.1.3. Galactic tide
We use a 1D model of the Sun’s motion through the Galaxy with the Sun moving in a circular orbit upon which are superimposed small vertical oscillations. For the vertical (perpendicular to the Galactic midplane) acceleration of the Sun at z = z⊙ we assume 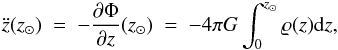 (17)where in MD, ϱ(z) = ϱb(z) + ϱph(z), is the local vertical “matter density” which is sum of the baryonic and the phantom density at R = R0 and Φ is the QUMOND potential of the Galaxy, see Sects. 2.2 and 3.1. In Newtonian dynamics, ϱ(z) = ϱb(z) + ϱh(z), where ϱh(z) is the vertical density of the DM halo at R = R0. Equation (17) hangs on the fact that the rotation curve of the Galaxy is approximately flat at the position of the Sun – for an axisimmetric model of the Galaxy: (1 /R)∂(R∂Φ /∂R) /∂R + ∂2Φ /∂z2 = 4πGϱ(R,z) with ∂(R∂Φ /∂R) /∂R ≈ 0 holds. Figure 3 shows the oscillations of the Sun through the Galactic disk governed by Eq. (17). The oscillations have a period of 76.7 Myr. The model of the Galaxy of Sect. 3.1 is employed.
(17)where in MD, ϱ(z) = ϱb(z) + ϱph(z), is the local vertical “matter density” which is sum of the baryonic and the phantom density at R = R0 and Φ is the QUMOND potential of the Galaxy, see Sects. 2.2 and 3.1. In Newtonian dynamics, ϱ(z) = ϱb(z) + ϱh(z), where ϱh(z) is the vertical density of the DM halo at R = R0. Equation (17) hangs on the fact that the rotation curve of the Galaxy is approximately flat at the position of the Sun – for an axisimmetric model of the Galaxy: (1 /R)∂(R∂Φ /∂R) /∂R + ∂2Φ /∂z2 = 4πGϱ(R,z) with ∂(R∂Φ /∂R) /∂R ≈ 0 holds. Figure 3 shows the oscillations of the Sun through the Galactic disk governed by Eq. (17). The oscillations have a period of 76.7 Myr. The model of the Galaxy of Sect. 3.1 is employed.
 |
Fig. 3 Left: oscillation of the Sun governed by Eq. (17) in MD. We used z⊙(0) = 30 pc and vz⊙(0) = 7.25 km s-1 as the initial conditions of the Sun’s motion. Middle: local “total matter density” ϱ = ϱb + ϱph, as experienced by the oscillating Sun. Right: local PMD, as experienced by the oscillating Sun. |
We approximate the tidal acceleration of a comet12 in the inertial frame of reference O⊙(ξ′,η′,ζ′) centred on the Sun as 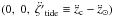 with
with 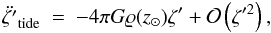 (18)where zc and z⊙ are vertical components (perpendicular to the Galactic midplane) of the position vector of the comet and the Sun with respect to the GC and zc = z⊙ + ζ′ holds. We omit the ξ′ and η′ components of the tide since these are approximately an order of magnitude smaller than the ζ′ component (Heisler & Tremaine 1986). We note that this is true not only in Newtonian dynamics, but also in MD as the distribution of the phantom matter resembles that of a disk close to the galactic midplane.
(18)where zc and z⊙ are vertical components (perpendicular to the Galactic midplane) of the position vector of the comet and the Sun with respect to the GC and zc = z⊙ + ζ′ holds. We omit the ξ′ and η′ components of the tide since these are approximately an order of magnitude smaller than the ζ′ component (Heisler & Tremaine 1986). We note that this is true not only in Newtonian dynamics, but also in MD as the distribution of the phantom matter resembles that of a disk close to the galactic midplane.
3.2. Simple model of the Milgromian Oort cloud
Here we introduce a simple model of the MOC embedded in an external field of constant magnitude (no tides). Accounting for the external field is a necessary step as in MD the external field does not decouple from the internal dynamics.
We assume that the Sun travels with angular frequency ω0 = V0/R0 in a circular orbit of radius R0 which lies in the Galactic midplane (z = 0).
Let the Newtonian external field of the Galaxy at the position of the Sun be approximated by the time-dependent vector: ![\begin{eqnarray} \label{gesimple} \vec{g}^{\rm N}_{\rm e}=\left[g^{\rm N}_{\rm e}~\cos(\omega_{0}t),~g^{\rm N}_{\rm e}~\sin(\omega_{0}t),~0\right] \end{eqnarray}](/articles/aa/full_html/2016/05/aa27713-15/aa27713-15-eq219.png) (19)in O⊙(ξ′,η′,ζ′). So that at t = 0,
(19)in O⊙(ξ′,η′,ζ′). So that at t = 0, 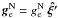 , where
, where 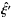 is the unit vector. In Eq. (19) we assume that the Sun orbits counterclockwise in the plane ξ′−η′ of O⊙(ξ′,η′,ζ′).
is the unit vector. In Eq. (19) we assume that the Sun orbits counterclockwise in the plane ξ′−η′ of O⊙(ξ′,η′,ζ′).
In Eq. (6) we now have 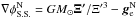 , where Ξ′ = [ξ′,η′,ζ′], Ξ′ ≡ (ξ′2 + η′2 + ζ′2)1 / 2 and the lower index “S.S.” stresses that we are dealing with the solar system embedded in the external field of the Galaxy. For the PMD we thus obtain
, where Ξ′ = [ξ′,η′,ζ′], Ξ′ ≡ (ξ′2 + η′2 + ζ′2)1 / 2 and the lower index “S.S.” stresses that we are dealing with the solar system embedded in the external field of the Galaxy. For the PMD we thus obtain 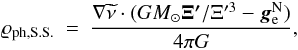 (20)where
(20)where 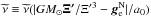 . The phantom potential φph,S.S. can be found by solving the ordinary Poisson equation
. The phantom potential φph,S.S. can be found by solving the ordinary Poisson equation 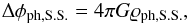 (21)with the boundary condition: φph,S.S. = −ge·Ξ′. The equation of motion in O⊙(ξ′,η′,ζ′) then reads
(21)with the boundary condition: φph,S.S. = −ge·Ξ′. The equation of motion in O⊙(ξ′,η′,ζ′) then reads 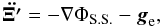 (22)where ΦS.S. = −GM⊙/ Ξ′ + φph,S.S..
(22)where ΦS.S. = −GM⊙/ Ξ′ + φph,S.S..
As QUMOND equations are linear when formulated with the aid of phantom matter, we can also look for a solution of Eq. (21) with the vacuum boundary condition (φph,S.S. = 0 at the boundary) and then evolve a body with 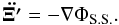 (23)
(23)
3.2.1. Simple model of the Oort cloud – numerical solution at t = 0
For integration of cometary orbits throughout the paper we employ the well-tested RA15 routine (Everhart 1985) as part of the MERCURY 6 gravitational dynamics software package (Chambers 1999), which we have modified appropriately to be compatible with the MD framework. Equation (19) has to be transformed from O⊙(ξ′,η′,ζ′) to a coordinate system used by MERCURY 6. This transformation and subsequent modification of Eqs. (20) and (22) are straightforward. O⊙(ξ,η,ζ) denotes from now on the rectangular coordinate system we use in MERCURY 6, i.e. Galilean coordinates coinciding at t = 0 with the heliocentric ecliptical coordinate system13.
During short time periods, compared to the period of the Sun’s revolution around the GC, ~210 Myr, one can approximate Eq. (19) with the constant vector ![\hbox{$\vec{g}^{\rm N}_{\rm e}=[g^{\rm N}_{\rm e},~0,~0]$}](/articles/aa/full_html/2016/05/aa27713-15/aa27713-15-eq236.png) ,
, 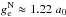 , in O⊙(ξ′,η′,ζ′). We used this approximation to find the phantom potential φph,S.S. experienced by a body in the MOC model that is represented by Eqs. (19)–(22). The numerical procedure is analogous to the one described in Sect. 2.2. The boundary conditions are described under Eq. (21). We employed a regular Cartesian grid with 5123 cells and resolution of 390 au that is centred on the Sun. This resolution was tested to be sufficiently fine enough so that the trajectories of comets do not change significantly if the resolution is further increased. In the case of inner OC orbits in Sects. 6.2 and 7.1 we used a resolution of 78 au with the same result. The calculated phantom acceleration, −∇φph,S.S., is linearly interpolated to an instaneous position of the body within each integration cycle. We refer to this simplified dynamical model of the MOC as “simple model of the MOC”.
, in O⊙(ξ′,η′,ζ′). We used this approximation to find the phantom potential φph,S.S. experienced by a body in the MOC model that is represented by Eqs. (19)–(22). The numerical procedure is analogous to the one described in Sect. 2.2. The boundary conditions are described under Eq. (21). We employed a regular Cartesian grid with 5123 cells and resolution of 390 au that is centred on the Sun. This resolution was tested to be sufficiently fine enough so that the trajectories of comets do not change significantly if the resolution is further increased. In the case of inner OC orbits in Sects. 6.2 and 7.1 we used a resolution of 78 au with the same result. The calculated phantom acceleration, −∇φph,S.S., is linearly interpolated to an instaneous position of the body within each integration cycle. We refer to this simplified dynamical model of the MOC as “simple model of the MOC”.
3.3. Escape speed
An isolated point mass M at distance r ≫ (GM/a0)1 / 2 is in MD source of the potential of the form 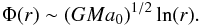 (24)Equation (24) yields asymptotically flat rotation curves but also means that there is no escape from the central field produced by the isolated point mass in MD, since
(24)Equation (24) yields asymptotically flat rotation curves but also means that there is no escape from the central field produced by the isolated point mass in MD, since  . But, an external field (which is always intrinsically present) actually regularizes the former divergent potential, so that it is possible to escape from non-isolated point masses in MD (Famaey et al. 2007), as we have already seen in Sect. 2.3.
. But, an external field (which is always intrinsically present) actually regularizes the former divergent potential, so that it is possible to escape from non-isolated point masses in MD (Famaey et al. 2007), as we have already seen in Sect. 2.3.
The escape speed of a comet can be well defined as (Wu et al. 2007, 2008) 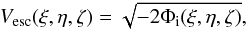 (25)with
(25)with 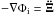 . The estimate of the escape in the direction perpendicular to the external field can be found by approximating the Galactic EFE that is acting on the OC with the simple curl-free formula of Eq. (13), where now gi = −GM⊙Ξ/ Ξ3. For the escape speed at Ξ = rC, we then have
. The estimate of the escape in the direction perpendicular to the external field can be found by approximating the Galactic EFE that is acting on the OC with the simple curl-free formula of Eq. (13), where now gi = −GM⊙Ξ/ Ξ3. For the escape speed at Ξ = rC, we then have ![\begin{eqnarray} \label{vesc} V_{\rm esc}(r_{\rm c})=\left[2\int^{\infty}_{r_{\rm c}}g_{\rm i}(\Xi){\rm d}\Xi\right]^{1/2}, \end{eqnarray}](/articles/aa/full_html/2016/05/aa27713-15/aa27713-15-eq248.png) (26)where
(26)where 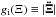 . We use Eq. (26) in Sects. 4.1 and 4.2 to estimate binding energy of a comet.
. We use Eq. (26) in Sects. 4.1 and 4.2 to estimate binding energy of a comet.
4. The Oort cloud as seen by a Milgromian astronomer
Do the observations lead us to hypothesize the existence of a vast cloud of bodies as a reservoir of new comets also if we interpret the data with the laws of MD? If so, how vast and shaped, in a rough sense, would be the cloud, compared to the classical one?
DK11 studied the dynamical evolution of 64 Oort spike comets with orbits what were determined with the highest precision, discovered after 1970, with their original semi-major axes larger than 10 kau and osculating perihelion distances q> 3 au (to minimise non-gravitational effects). They identified 31 comets as dynamically new (having their first approach to the zone of significant planetary perturbations; for the detailed definition see the paper), and one of these comets as possibly hyperbolic14. Median value of the original reciprocal semi-major axis for the 30 comets on the certainly bound orbits is 22.385 × 10-6 au-1, which corresponds to 44.7 kau, maximum and minimum values in the sample read 250.6 and 21.9 kau, respectively. All the orbits have osculating q< 9 au. The orbits of dynamically new comets are free from planetary perturbations and can be used to study the source region of these comets. We emphasize that for a comet being dynamically new under Newtonian dynamics does not necessary mean to be dynamically new under MD. A reconsideration of the dynamical status in MD would require a similar approach as in DK11 with an extensive use of orbital clones to cover the large errors that are in the original orbital energy.
 |
Fig. 4 Past Milgromian trajectories of 3 × 100 Monte Carlo particles projected to 3 mutually orthogonal planes of O⊙(ξ,η,ζ). The particles were initialised with original Newtonian orbital elements: a = 10 (top row), 50 (middle row), 100 (bottom row) kau, q distributed uniformly on the interval (0,8) au, cos(i) distributed uniformly on the interval (− 1,1), ω and Ω distributed uniformly on the interval (0,2π), among the particles, and mean anomaly M = 0. Then the particles were evolved back in time in the simple model of the MOC, Sect. 3.2, for one Keplerian period (≈1 Myr) in the case of a = 10 kau, and for 10 Myr in the case of a = 50 and 100 kau. The concentric circles at the top right corner of figures A, B, and C represent relative radii of the Milgromian (always the smaller circle) and Newtonian OC (radius = 2a; always the larger circle) as determined by the simulation and assuming that the cloud is the smallest sphere encompassing all orbits of given initial a. The Sun resides at [0, 0], as indicated by the symbol. |
To acquire vital motivation we have used a more straightforward approach as a first step. Employing the aforementioned simple model of the MOC, we traced the past trajectories of 300 Monte Carlo test particles that represent a sample of Oort spike comets. We consider this a fairly small sample since, in reality, observed samples are of similar or even smaller numbers. We considered three values of the particle’s initial semi-major axis a = 10, 50 and 100 kau. For each of the three values of a we initialised 100 test particles at their perihelia – all the perihelia lie in the deep Newtonian regime – with the following randomly generated original Newtonian orbital elements: q distributed uniformly on the interval (0,8) au, cos(i) distributed uniformly on the interval (− 1,1), ω and Ω distributed uniformly on the interval (0,2π), among the test particles, here q is perihelion distance, i is inclination with respect to the ecliptics, ω is argument of periapsis, and Ω is the longitude of the ascending node. The initial Newtonian orbital elements are immediately transformed into the initial Cartesian positions and velocities, the notions being independent of the dynamical framework; also these are the observables on the basis of which the orbital elements are calculated15. We followed the particles with a = 10 kau back in time for one Keplerian period (which is by no means the real period assuming MD), 2π (a[au])3/2/k days, where k is Gaussian gravitational constant, and the particles with a = 50 and 100 kau for 10 Myr. We do not use the integration time of one Keplerian period in the latter case because, during this time, the change in the external field direction cannot be neglected (a = 100 kau orbit has the Keplerian period TKep ≈ 32 Myr). In any case, as will be shown, all the particles with initial a = 50 and 100 kau revolve many times during 10 Myr.
By the term “original orbit” we want to emphasise the fact that, in reality, the outer planets and non-gravitational effects are important dynamical agents, primarily changing the value of the semi-major axis. We can imagine the ensemble of the initial orbital elements as the result of backward integration of observed osculating (instantaneous) orbits to the time when the comets/particles enter the planetary zone.
The past QUMOND trajectories of the particles are shown in Fig. 4. Trajectories can be typically described as ellipses with a quickly precessed line of apsides. Moreover, the external field often changes perihelion distances of the particles rapidly and almost irrespective of their initial semi-major axis. This important fact is discussed in Sect. 6. In this case, the orbits change their shape dramatically, as was previously illustrated in Iorio (2010a), but only for the deep-MD orbits.
A small departure from the isotropy of the cloud can be seen in Fig. 4. The cloud is prolonged in the direction of the η axis. Also an indistinct pac-man shape of ξ−η and η−ζ plane cuts emerges. This is because of the external field of the Galaxy, which points in the direction of 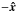 of OGC(x,y,z) (the direction Sun-GC at t = 0), which also corresponds to the direction of
of OGC(x,y,z) (the direction Sun-GC at t = 0), which also corresponds to the direction of 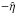 of O⊙(ξ,η,ζ). The gravity is stronger at negative η than at positive. This can be most easily noticed on the ν(β) dependence on the vector sum in the grossly approximative formula
of O⊙(ξ,η,ζ). The gravity is stronger at negative η than at positive. This can be most easily noticed on the ν(β) dependence on the vector sum in the grossly approximative formula 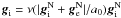 (note that larger β means smaller ν(β)). We also note the smaller precession rate of the projected orbits in ξ−ζ plane. Again, this is because the ξ and ζ components of the Galactic external field are much smaller than the η component.
(note that larger β means smaller ν(β)). We also note the smaller precession rate of the projected orbits in ξ−ζ plane. Again, this is because the ξ and ζ components of the Galactic external field are much smaller than the η component.
In any case, the most important result is that even the orbits with initial a = 100 kau are confined in a cube of side ~28 kau. in this case, the Newtonian cube would be of side ~400 kau. This implies that the OC as revealed by comets with original 0 <a< 100 kau and interpreted by MD could be much more compact than the Newtonian one.
These findings looks problematic for MD at first sight. The classical picture of the Galactic tide, as the most effective comet injector, is that the sufficient decrease in a comet’s perihelion distance during one revolution – to be able to penetrate the Jupiter-Saturn barrier – can be made only for comets with a> 20−30 kau (e.g. Levison et al. 2001; Rickman 2014), hence the comets with aphelion distances that are larger than 40–60 kau, if eccentricity is close to 1. These are much larger heliocentric distances than those comets encountered in MOC. Also, comets of the classical inner OC, which take advantage of the Jupiter-Saturn barrier by inflating their semi-major axes, come through this outer region (a> 20−30 kau; i.e. the comets appear to be from the outer OC) where the final decrease in perihelion distance is effectively made (Kaib & Quinn 2009). All these findings are of course Newtonian. The tidal field of the Newtonian Galaxy that is embedded in the DM halo is a little different from the QUMOND one, especially its vertical (perpendicular to the Galactic midplane) part. Moreover, completely beyond the tides, the MD’s EFE can have a decisive influence on the dynamics. We address this issue more rigorously in Sect. 6, where injection of the bodies from the inner OC (in the classical jargon) is studied. Since MD enhances binding energy of a comet, the classical effect of the Jupiter-Saturn barrier, in fact, has to be revised, see Sect. 4.2. Last but not least we have to emphasise that the steady-state distribution of the bodies in the cloud could look different in MD, see discussion in Sect. 8.
 |
Fig. 5 Past trajectories of two slightly hyperbolic comets in the simple model of the MOC. Both were initialised at their perihelia, one with q = 8 au, e = 1.00150, ω = π/ 4 (solid line), the other with q = 3 au, e = 1.00055, ω = π/ 4 (dot-dashed line). All the other orbital elements were set to 0. The integration time was 20 Myr. As can be seen these comets are bound (returning) in MD. The Sun resides at [0, 0], as indicated by the symbol. |
4.1. Escaping comets?
We use the term “hyperbolic comet” for a comet whose Newtonian two-body orbital energy is positive and which is, according to a Newtonian astronomer, not bound (not returning) to the solar system. In this section, we investigate the idea that slightly hyperbolic comets can be bound to the Milgromian solar system, as first pointed out by Milgrom (1986b).
The statistics of the original reciprocal semi-major axes, 1 /aorig, also reveals, besides the famous Oort spike, a small but non-negligible number of slightly hyperbolic comets (e slightly larger than 1; e.g. Fig. 1b in Dones et al. 2004). These are usually considered to follow very eccentric elliptic orbits in reality, rather than to be interstellar intrudes, but owing to observational errors or the inappropriate modelling of non-gravitational forces, they seem to occupy hyperbolic orbits (Dones et al. 2004). Thanks to the boosted gravity in MD, the slightly hyperbolic comet could be still bound to the solar system16.
Comparing the escape speed at perihelion, Vesc(q), see Eqs. (13) and (26), with the tangential speed at the perihelion, Vperi(e,q), we can decide whether a comet is bound or not. Vperi(e,q) can be computed in the usual way. We are at the perihelion – in the deep Newtonian regime, and it depends only on the local gravitational field. The opposite case is the escape speed, which has to be calculated from the MD gravity, no matter where we start from, see Eq. (26). Assuming motion in the ecliptic plane, i = 0, we have 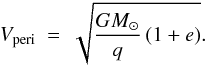 (27)Radial speed at the perihelion is 0. Thus for a given q, we can find the limiting eccentricity elim, so e>elim implies Vperi(e,q) >Vesc(q). For example q = 3 au implies elim = 1.00075 and q = 8 au leads to elim = 1.00199. Slightly hyperbolic comets with e<elim are bound in MD. Figure 5 shows the trajectories of two comets that were initialised with the orbital elements q = 3 au, e = 1.00055, ω = π/ 4 (all the other elements are set to 0) and q = 8 au, e = 1.00150, ω = π/ 4 (all the other elements are set to 0), and then integrated backwards for 20 Myr, assuming the simple model of the MOC. This is quite a long time interval to assume the stationarity of the external field, thus the real trajectories would be a little different, as the external field changes its direction. In any case, we only intend to illustrate as slightly hyperbolic comets can be bound in MD, and this qualitative result remains the same.
(27)Radial speed at the perihelion is 0. Thus for a given q, we can find the limiting eccentricity elim, so e>elim implies Vperi(e,q) >Vesc(q). For example q = 3 au implies elim = 1.00075 and q = 8 au leads to elim = 1.00199. Slightly hyperbolic comets with e<elim are bound in MD. Figure 5 shows the trajectories of two comets that were initialised with the orbital elements q = 3 au, e = 1.00055, ω = π/ 4 (all the other elements are set to 0) and q = 8 au, e = 1.00150, ω = π/ 4 (all the other elements are set to 0), and then integrated backwards for 20 Myr, assuming the simple model of the MOC. This is quite a long time interval to assume the stationarity of the external field, thus the real trajectories would be a little different, as the external field changes its direction. In any case, we only intend to illustrate as slightly hyperbolic comets can be bound in MD, and this qualitative result remains the same.
Observations of comets with similar original orbital elements could inflate the former conservative estimate of the MOC size to sizes comparable with the classical OC. In Sect. 5 we take real cometary data and look at what they say about the size and shape of the MOC.
4.2. Do Jupiter and Saturn act as a barrier in MD?
The enhanced binding energy of MOC comets raises a question: how does the mechanism of the planetary barrier that is operating in the classical OC change in the MD case?
QUMOND conserves energy. We use Eqs. (13) and (26) to approximate QUMOND and assume energy conservation. We take a comet at perihelion, lying deeply in the Newtonian regime, with kinematics characterised by the Newtonian orbital elements, a and q. We can find its specific binding energy in MD, simply as ![\begin{eqnarray} \label{orb} E_{\rm BM}~=~-\frac{1}{2}\left[V_{\rm peri}^{2}(a,q)-V^{2}_{\rm esc}(q)\right], \end{eqnarray}](/articles/aa/full_html/2016/05/aa27713-15/aa27713-15-eq300.png) (28)where we can use Eq. (27) under the assumption i = 0. We note that we have put a minus sign in front of the factor 1/2 on the RHS of Eq. (28) because the binding energy is defined as a positive number. For comets with a = 10, 50, and 100 kau, the ratio EBM/EBN, where EBN = [GM⊙/ (2a)] is the Newtonian binding energy per unit mass, is approximately equal to 3, 13, and 26 respectively. Using the 1D QUMOND approximation, Eq. (60) in Famaey & McGaugh (2012), instead of Eq. (13), these ratios are 2, 7, and 13 respectively. For near-parabolic orbits the value of EBM depends only weakly on q.
(28)where we can use Eq. (27) under the assumption i = 0. We note that we have put a minus sign in front of the factor 1/2 on the RHS of Eq. (28) because the binding energy is defined as a positive number. For comets with a = 10, 50, and 100 kau, the ratio EBM/EBN, where EBN = [GM⊙/ (2a)] is the Newtonian binding energy per unit mass, is approximately equal to 3, 13, and 26 respectively. Using the 1D QUMOND approximation, Eq. (60) in Famaey & McGaugh (2012), instead of Eq. (13), these ratios are 2, 7, and 13 respectively. For near-parabolic orbits the value of EBM depends only weakly on q.
A comet of the classical OC in a typical orbit of, for example, a = 50 kau, experiences an energy change per perihelion passage proportional to its own binding energy17 at q ~ 15 au, see Fig. 1 in Fernández & Brunini (2000). Making the binding energy of this comet in MD ~10 times larger this criterion is met at q ~ 7 au. Roughly speaking this means that MOC comets with q< 7 au, instead of the classical value ~15 au, are removed from the cloud due to planetary perturbations. The planetary barrier similarly to the whole cloud shifts inward in MD. Anyway it can still act in a way of inflating semi-major axes for those comets having q> 7 au, but these are not a priori prevented from being injected inside the inner solar system as in the case of the removed comets of the classical OC.
5. Observed near-parabolic comets in Milgromian dynamics
Motivated by the crude picture of the OC outlined in Sect. 4, we have used real cometary data to investigate origin of the near-parabolic comets in the framework of MD.
We have approximated action of QUMOND by the simple model of the MOC, with the constant external field of the Galaxy ge coupled to the QUMOND equations, see Sect. 3.2. The rotation of ge has period of ~210 Myr, therefore we use integration times to be Keplerian periods for those comets having these lesser than 10 Myr. For those that have Keplerian periods larger than 10 Myr we use integration time of 10 Myr as all these have much shorter real (QUMOND) “periods”, i.e. times between two successive perihelia. Moreover, the tidal effect, which comes from the Galactic gravity gradient across the OC, is also accounted. The Galactic tide model is described in Sect. 3.1.3. This model reflects the local density of the baryonic + phantom matter as determined by QUMOND for the adopted baryonic model of the Galaxy, see Sects. 2.2 and 3.1. We have simply added the tidal acceleration (0, 0,  ), Eq. (18), to RHS of Eq. (22). This is only an approximation in non-linear MD. But, it proves to be good idea to model EFE (assuming a spatially invariant field) and tides as two separate effects of the Galaxy, see Sects. 5.2 and 6.1.
), Eq. (18), to RHS of Eq. (22). This is only an approximation in non-linear MD. But, it proves to be good idea to model EFE (assuming a spatially invariant field) and tides as two separate effects of the Galaxy, see Sects. 5.2 and 6.1.
We have taken the original orbits from the sample of near-parabolic comets that were identified as dynamically new in DK11, converted them to initial positions and velocities of test particles, and integrated these back in time, looking for their past Milgromian trajectories.
5.1. Data
Our sample consists of the 31 comets identified as dynamically new in DK11. We omitted errors in the lengths of original semi-major axes aorig, the only orbital element with significant error and, instead, only took their expected values as these are fairly typical for Oort spike comets. A more exact approach would proceed in a similar manner as DK11 did, covering the error in the orbital energy determination with a large number of virtual orbits, but this is much more processor-time consuming in MD than in Newtonian dynamics.
The sample also contains one slightly hyperbolic comet, C/1978 G2, with perihelion q = 6.28 au and eccentricity e = 1.00014083. We also note the orbit of the comet C/2005 B1, with a very large semi-major axis of 250.6 kau.
Original orbital elements of sample comets were retrieved from Królikowska (2014) and are displayed in Table 1. These were calculated at a heliocentric distance 250 au, which is still well within the Newtonian regime.
5.2. Results
The past QUMOND trajectories of the sample comets are shown in Fig. 6. The resulting size and overall shape of the MOC is in large agreement with the one obtained in Sect. 4. The trajectory of the single comet with e> 1 in our sample, C/1978 G2, is redrawn in Fig. 7. In Milgromian framework the comet is bound, visiting similar heliocentric distances to the other comets in our sample.
In MD, we expect the Galactic tide to be stronger than in the Newtonian dynamics, see Fig. 2 and Sect. 3.1.3. However, the changes in orbits – perihelia positions and precession rates – induced by the Galactic tide are negligible, compared to those induced by the EFE, see also Sect. 6. Figures 6 and 7 would not look different if the Galactic tide model as presented in Sect. 3.1.3 was not incorporated. This is a natural consequence of the compactness of the cloud. The comets cruise up to Ξ ~ 13 kau, where the tidal torquing is still minute, but EFE plays a dominant role. As mentioned above, we model the EFE and the Galactic tide as the separate effects.
In Fig. 8 we show the specific angular momentum as a function of time, L(t), for the comet C/1974 V1 in the simple model of the MOC. Tides are omitted this time. Periodic changes in angular momentum are induced purely by EFE. Similar behaviour can also be found by checking the other comets in the sample. Taking into account the Galactic tide only has a minor effect and L(t) is very much the same.
 |
Fig. 6 Past Milgromian trajectories of 31 near-parabolic comets, those identified as dynamically new in DK11, projected to 3 mutually orthogonal planes of O⊙(ξ,η,ζ). Dynamical model of the OC consists of the stationary Galactic field coupled to the QUMOND equations, see Sect. 3.2, and the Galactic tide model, see Sect. 3.1.3. The comets with Keplerian periods TKep lesser than 10 Myr were followed for the time of TKep, those with TKep> 10 Myr were followed for 10 Myr. Inferred MOC is much smaller than the classical OC, see Table 1 for comparison with Newtonian orbits. At [0, 0] resides the Sun as indicated by the symbol. |
 |
Fig. 7 Past Milgromian trajectory of the comet C/1978 G2, the slightly hyperbolic comet. Initial q = 6.28 au and e = 1.00014083. At [0, 0] resides the Sun as indicated by the symbol. |
6. Galactic torque
We have shown that MOC is much smaller than the classical OC. The MOC boundary, as found by tracing Oort spike comets with an initial eccentricity e< 1 (which is the vast majority of observed comets) back in time, lies at heliocentric distances that correspond to the classical inner OC. Also the single comet with e> 1 in the Sect. 5 sample, C/1978 G2, orbits in bound orbit at similarly small heliocentric distances in MD. It is presumed that the tidal force at these heliocentric distances is not large enough to sufficiently quickly decrease perihelion distance so that a comet bypasses the Jupiter-Saturn barrier, e.g. Dones et al. (2004). In MD, the compactness of the OC does not need to be an obstacle for the injection of a comet into the inner solar system because of the action of EFE.
6.1. Angular momentum change
In this section, we preserve the classical idea of the Jupiter-Saturn barrier at ~15 au, although in Sect. 4.2 we have shown that the barrier actually shifts inwards in MD. This shift naturally increases the inflow of comets.
To illustrate the capability of the EFE to deliver OC bodies into the inner solar system, we have run similar simulation to those in Sect. 4. In this case, we intended to mimic the sample of comets that are about to enter/leave the planetary zone. Consequently, we chose the initial perihelion distance of each particle, q, to be a random number that is uniformly distributed on the interval (15,100) au. All the other initial orbital elements of the test particles were randomly generated in the same way as in Sect. 4. The orbital elements were at t = 0, transformed to initial Cartesian positions and velocities, the real observables.
 |
Fig. 8 Specific angular momentum L as a function of time for the comet C/1974 V1. We have assumed the simple model of the MOC (tides are omitted). The periodic changes are induced solely by EFE. The negative time means that we are dealing with the past trajectory of the comet. |
 |
Fig. 9 Heliocentric distance, Ξ(t), and change in magnitude of the specific angular momentum, δL(t) ≡ L(t)−L(0), as a function of time, t, for 100 Monte Carlo test particles initialised with a = 10 kau, and q uniformly distributed on the interval (15,100) au. The top row represents an output of the Milgromian simulation, the bottom row, the Newtonian simulation. In MD simulation, the follow up time, Trev, is set to 0.26 Myr (see top left quarter of the figure for motivation), in Newtonian simulation Trev is set to be the Keplerian period TKep(a = 10 kau) ≈1 Myr. |
We employed two distinct dynamical models of the OC, one of which is Milgromian and the other, Newtonian: (i) the simple model of the MOC; and (ii) Sun + Galactic tide in the Newtonian framework. We tested the fact that incorporation of the Galactic tide model, as described in Sect. 3.1.3, into the simple model of the MOC has negligible effects for the times that correspond to one revolution of a comet. This is obviously because the comets of the MOC orbit in Ξ ≲ 15 kau, at these heliocentric distances, the tidal force is too weak. Two distinct ϱ(z⊙) were used: ϱ(z⊙) = ϱb(z⊙) + ϱph(z⊙) in MD and ϱ(z⊙) = ϱb(z⊙) + ϱh(z⊙) in Newtonian dynamics, where ϱb(z⊙) is the local vertical density of baryons and ϱh(z⊙) is the local vertical density of the NFW DM halo.
Figures 9 (a = 10 kau), 11 (a = 50 kau), and 13 (a = 100 kau) show the heliocentric distance, Ξ(t), and change in magnitude of the specific angular momentum, δL(t) ≡ L(t)−L(0), of the particles, as a function of time. The followed time window, Trev, corresponds approximately to one revolution that succeeds the perihelion initialisation. In Figs. 10 (a = 10 kau), 12 (a = 50 kau), and 14 (a = 100 kau) we show the value of ΔL ≡ Lmax−Lmin of the individual particles, where Lmax ≡ [L(t)] max and Lmin ≡ [L(t)] min are the maximal and the minimal value of L(t) during Trev.
 |
Fig. 10 Histogram of ΔL ≡ Lmax−Lmin for 100 Monte Carlo test particles initialised with a = 10 kau and q uniformly distributed on the interval (15,100) au. Here Lmax (Lmin) is maximal (minimal) magnitude of the specific angular momentum, as found during one revolution, Trev, succeeding the initialisation of a comet at perihelion. In the MD simulation Trev = 0.26 Myr, in the Newtonian simulation Trev = TKep(a = 10 kau) ≈1 Myr. A single bin corresponds to a single test particle in the simulation. Solid bins are ΔL in the simple model of the MOC, shaded bins (here barely visible), stacked on the solid bins, are ΔL in Newtonian dynamics, with the gravity of the Sun and the Galactic tide accounted for. |
When interpreting these figures, we have to bear in mind the timescales of the angular momentum changes, these are ~4 (a = 10 kau) to ~80 (a = 100 kau) times smaller in the MOC than in the classical OC. We also note that the particles that are initialised with a as large as 100 kau are travelling in Ξ ≲ 15 kau in the MOC. It is evident that the injection could be very efficient in the MOC, nevertheless the MOC is much more radially compact than the classical OC. In MD, the rapid changes in the angular momentum are induced by EFE. Moreover the bodies that are hidden in the classical OC – i.e. not able to reach the observability region, because of either their immunity from the action of the external perturbers, the hypothesized inner core, or, the inability to overshoot the Jupiter-Saturn barrier, the inner OC bodies with a ~ 10 kau, can, because of EFE, also be delivered from the MOC into the inner solar system, see also Sect. 6.2.
Figures 12 and 14 show that Newtonian tides (OC) overcome EFE (MOC) in Δq per revolution only for comets with a as large as ~50–100 kau. This is 9 out of 30 comets with e< 1 in the Sect. 5 sample.
 |
Fig. 11 Same as for Fig. 9, but now the particles are initialised with a = 50 kau. The top row represents an output of the Milgromian simulation, the bottom row, the Newtonian simulation. In MD simulation, the follow-up time, Trev, is set to 0.4 Myr (see top left quarter of this figure for motivation), in the Newtonian simulation Trev is set to be the Keplerian period TKep(a = 50 kau) ≈11 Myr. |
 |
Fig. 12 Same as for Fig. 10 but now the particles are initialized with a = 50 kau. In the MD simulation Trev = 0.4 Myr, in the Newtonian simulation Trev = TKep(a = 50 kau) ≈11 Myr. A single bin corresponds to a single test particle in the simulation. Solid bins are ΔL in the simple model of the MOC, shaded bins, stacked on the solid bins, are ΔL in Newtonian dynamics, with the gravity of the Sun and the Galactic tide accounted for. |
6.2. Sedna
We have shown that cometary perihelia can be very effectively torqued in and out by EFE, even for those comets that are travelling in fairly small heliocentric distances, ~10 kau. Is torquing due to EFE important at even smaller heliocentric distances? Is EFE responsible for the shape of the current puzzling orbit of the trans-Neptunian planetoid Sedna? To address these questions we ran the following simulation: 100 Monte Carlo test particles (Sedna progenitors – Sednitos) with initial a = 524 au (Sedna’s heliocentric a at epoch 2 457 000.5 JD, according to JPL’s service HORIZONS) and, among the particles, uniformly distributed q in bounds (5,30) au, i in bounds (− 10,10) deg, ω and Ω in bounds (0,2π), were initialised at their perihelia and then followed for 5.9 Myr in the simple model of the MOC. These initial orbital elements have been chosen to mimic the protoplanetary disk origin of Sedna. We assumed that Sednito’s semi-major axis was already pumped to the current Sedna’s value at the beginning of the simulation, owing to past planetary encounters. The planets were omitted in the simulation.
In Fig. 15 we show Δq ≡ qmax−qmin for 100 simulated Sednitos, where qmax and qmin are Sednito’s maximal and minimal value of q, per 5.9 Myr. As can be seen in some cases, Δq is as large as 100 au. At the end of the simulation, 7 Sednitos had q ~ 75 au, hence very close to the Sedna’s perihelion distance. Sedna-like orbits (here simplified as specific a and q values) can be produced by EFE in a few Myr. The catch is that, as q oscillates in and out on timescales of millions of years, the trans-Neptunian bodies with similar orbits as Sedna could possibly wander into the inner solar system. It is also possible that substantial migrants have already been removed from these orbits and the current population is relatively stable against migration.
Figure 16 depicts perihelion distance as a function of time for all known bodies with q> 30 au and a> 150 au in the simple model of the MOC during the next 10 Myr. Initial orbital elements of the bodies were retrieved from Trujillo & Sheppard (2014), see their Table 1 and extended data Table 2. Only one of the followed objects, 2010 GB174, migrates under 30 au in the next 10 Myr. To investigate the migration of these objects thoroughly, we would have to improve our dynamical model of the MOC to account for the change in the external field direction, since long integration times would be necessary, and also to account for the planetary perturbations. We leave this task to our future studies.
 |
Fig. 13 Same as for Fig. 9, but now the particles are initialised with a = 100 kau. The top row represents an output of the Milgromian simulation, the bottom row, the Newtonian simulation. In the MD simulation, the follow-up time, Trev, is set to 0.4 Myr (see top left quarter of this figure for motivation), in the Newtonian simulation, Trev is set to be the Keplerian period TKep(a = 100 kau) ≈32 Myr. |
7. Varying interpolating function and a0
Hees et al. (2016, hereafter H+16) recently constrained the most frequently used families of the MD interpolating (transition) function (e.g. Sect. 6.2 in Famaey & McGaugh 2012) with the Cassini spacecraft radio tracking data (Hees et al. 2014). These constraints come from EFE, which produces small quadrupole correction to the Newtonian potential in the planetary region. They concluded the following constraints (on n): ![% subequation 5167 0 \begin{align} \nu_{n}(\beta) &~=~\left[\frac{1+\left(1+4\beta^{-n}\right)^{1/2}}{2}\right]^{1/n},~~~n\geq7,\label{if1}\\ \widehat{\nu}_{n}(\beta) &~=~\left[1-\exp(-\beta^{~n/2})\right]^{-1/n},~~~n\geq6,\label{if2}\\ \overline{\nu}_{n}(\beta) &~=~\left[\widehat{\nu}_{2n}(\beta)\right] +\left(1-\frac{1}{2n}\right)\exp(-\beta^{n}),~~~n\geq2,\label{if3} \end{align}](/articles/aa/full_html/2016/05/aa27713-15/aa27713-15-eq362.png) where Eqs. (29)–(29b) are three different families of the interpolating function ν. We note that
where Eqs. (29)–(29b) are three different families of the interpolating function ν. We note that 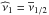 . So far we have only used
. So far we have only used 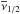 in our calculations. But according to the findings of H+16 this interpolating function, although very popular, is ruled out. H+16 also revised the value of a0, based on rotation curve fits (taking care whether EFE plays a role) and found optimum (best-fit) value for a given interpolating function. For example
in our calculations. But according to the findings of H+16 this interpolating function, although very popular, is ruled out. H+16 also revised the value of a0, based on rotation curve fits (taking care whether EFE plays a role) and found optimum (best-fit) value for a given interpolating function. For example 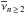 yields a0 ≲ 8.1 × 10-11 m s-2, where the boundary value is a bit smaller than the standard value a0 = 1.2 × 10-10 m s-2, but still well compatible with the baryonic Tully-Fisher or Faber-Jackson relation. In what follows, we consider only the
yields a0 ≲ 8.1 × 10-11 m s-2, where the boundary value is a bit smaller than the standard value a0 = 1.2 × 10-10 m s-2, but still well compatible with the baryonic Tully-Fisher or Faber-Jackson relation. In what follows, we consider only the 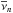 family.
family.
Figure 17 shows 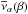 for 1 ≤ β ≤ 3 and three different alphas, α = 0.5, 1.5, and 2.0. The rightmost dashed vertical line indicates the smallest possible β for the solar system in the field of the Galaxy assuming
for 1 ≤ β ≤ 3 and three different alphas, α = 0.5, 1.5, and 2.0. The rightmost dashed vertical line indicates the smallest possible β for the solar system in the field of the Galaxy assuming 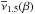 and a0 = 8.1 × 10-11 m s-2. This was found by assuming the external field dominance and solving for
and a0 = 8.1 × 10-11 m s-2. This was found by assuming the external field dominance and solving for  in
in 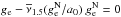 , which yields β = 2.75. If the internal field is non-negligible then β is always larger. We note that
, which yields β = 2.75. If the internal field is non-negligible then β is always larger. We note that 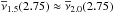 ; as for this and the numerical convenience of using
; as for this and the numerical convenience of using 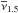 , we consider combination
, we consider combination 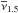 and a0 = 8.1 × 10-11 m s-2 in our calculations.
and a0 = 8.1 × 10-11 m s-2 in our calculations.
 |
Fig. 14 Same as for Fig. 10, but now the particles are initialized with a = 100 kau. In the MD simulation Trev = 0.4 Myr, in the Newtonian simulation, Trev = TKep(a = 100 kau) ≈32 Myr. A single bin corresponds to a single test particle in the simulation. Solid bins are ΔL in the simple model of the MOC, shaded bins, stacked on the solid bins, are ΔL in Newtonian dynamics, with the gravity of the Sun and the Galactic tide accounted for. |
PMD, Eq. (20), as a function of heliocentric distance, Ξ, is depicted in Fig. 18 along ξ, η, and ζ axes of O⊙(ξ,η,ζ). The simple model of the MOC, 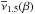 interpolating function and a0 = 8.1 × 10-11 m s-2, were assumed. The peaks in the positive values of ϱph are ~800 (left) and ~400 (right) times smaller than in the case of
interpolating function and a0 = 8.1 × 10-11 m s-2, were assumed. The peaks in the positive values of ϱph are ~800 (left) and ~400 (right) times smaller than in the case of  and a0 = 1.2 × 10-10 m s-2. We note that MD predicts the existence of regions with negative PMD in the solar system which is imposed to the gravitational field of the Galaxy (Milgrom 1986a). In theory, this speciality of PMD makes MD observationally distinguishable from the DM hypothesis.
and a0 = 1.2 × 10-10 m s-2. We note that MD predicts the existence of regions with negative PMD in the solar system which is imposed to the gravitational field of the Galaxy (Milgrom 1986a). In theory, this speciality of PMD makes MD observationally distinguishable from the DM hypothesis.
We can conclude that, by adopting 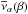 with α = 1.5 or 2.0 and a0 = 8.1 × 10-11 m s-2 – or even larger α and smaller a0 (H+16), we can expect the MOC to be very much Newtonian, since EFE, in this case, essentially suppresses the Milgromian regime at any distance from the Sun. The MOC is then of comparable overall size, comets have similar binding energies, and the Jupiter-Saturn barrier operates in a similar way to that found in Newtonian dynamics. Aphelia directions of observed, dynamically new comets were shown to avoid Galactic latitudes, bG, close to the polar caps and the Galactic equator (Delsemme 1987). This is conventionally considered to be a signature of the Galactic-tide-induced injection of the comets (Torbett 1986; Delsemme 1987). We note that in the case
with α = 1.5 or 2.0 and a0 = 8.1 × 10-11 m s-2 – or even larger α and smaller a0 (H+16), we can expect the MOC to be very much Newtonian, since EFE, in this case, essentially suppresses the Milgromian regime at any distance from the Sun. The MOC is then of comparable overall size, comets have similar binding energies, and the Jupiter-Saturn barrier operates in a similar way to that found in Newtonian dynamics. Aphelia directions of observed, dynamically new comets were shown to avoid Galactic latitudes, bG, close to the polar caps and the Galactic equator (Delsemme 1987). This is conventionally considered to be a signature of the Galactic-tide-induced injection of the comets (Torbett 1986; Delsemme 1987). We note that in the case  and a0 = 1.2 × 10-10 m s-2 the MOC was shown to be compact and weakly influenced by the Galactic tide, which therefore also suggests that an interpolating function that is steeper in the transition regime should be favoured18.
and a0 = 1.2 × 10-10 m s-2 the MOC was shown to be compact and weakly influenced by the Galactic tide, which therefore also suggests that an interpolating function that is steeper in the transition regime should be favoured18.
 |
Fig. 15 Δq ≡ qmax−qmin per 5.9 Myr for 100 Sedna progenitors (Sednitos) moving under the action of EFE. Sednitos were initialised at perihelia with a = 524 au, uniformly distributed q ∈ (5,30) au, i ∈ (−10,10)deg, ω and Ω ∈ (0,2π). |
 |
Fig. 16 Perihelion distance as a function of time under the action of EFE for the known population of trans-Neptunian bodies with a> 150 au and q> 30 au. Thick solid lines are 2012 VP113 and Sedna. |
 |
Fig. 17 Transition to the Newtonian regime for different alphas in |
 |
Fig. 18 PMD in the simple model of the MOC in the direction of ξ (solid line), η (dotted line), and ζ (dashed line) axis of O⊙(ξ,η,ζ). |
In any event, even when interpolating functions and a0 that are in line with the Cassini data are applied, some effects of MD can be still present. Torquing of cometary perihelia owing to EFE at heliocentric distances where the Galactic tide is weak, can be important. To illustrate and quantify this effect, we plotted ΔL for the same a = 10 kau Monte Carlo comets as in Sect. 6.1 but now assuming QUMOND with 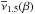 and a0 = 8.1 × 10-11 m s-2 instead of
and a0 = 8.1 × 10-11 m s-2 instead of  and a0 = 1.2 × 10-10 m s-2. One revolution of a comet now corresponds well to a Keplerian period since we are effectively in the Newtonian regime. We have used α = 1.5, although H+16 found that α is constrained as α ≥ 2.0, both for its numerical convenience as well as to speed up our numerical calculations. Our aim is to see how effective the torquing is owing to the EFE when the whole MOC is essentially in the Newtonian regime, see Fig. 17. In this sense α = 1.5 with a0 = 8.1 × 10-11 m s-2 serve us well.
and a0 = 1.2 × 10-10 m s-2. One revolution of a comet now corresponds well to a Keplerian period since we are effectively in the Newtonian regime. We have used α = 1.5, although H+16 found that α is constrained as α ≥ 2.0, both for its numerical convenience as well as to speed up our numerical calculations. Our aim is to see how effective the torquing is owing to the EFE when the whole MOC is essentially in the Newtonian regime, see Fig. 17. In this sense α = 1.5 with a0 = 8.1 × 10-11 m s-2 serve us well.
 |
Fig. 19 Histogram of ΔL ≡ Lmax−Lmin for 100 Monte Carlo test particles initialised at perihelia with a = 10 kau and q uniformly distributed on the interval (15,100) au and then evolved in the simple model of the MOC for Trev ≈ TKep ≈ 1 Myr. |
Figure 19 shows the value of ΔL ≡ Lmax−Lmin of the individual comets, where, again Lmax ≡ [L(t)] max and Lmin ≡ [L(t)] min are the maximal and the minimal value of L(t) during Trev, assumed to be the Keplerian period TKep, since now Trev ≈ TKep. We can directly compare Figs. 10 and 19. On average, ΔL is naturally smaller in the case of a steeper interpolation function and smaller a0, but extremal values in both cases are similar. This could explain why we observe comets with relatively small semi-major axes, which should be prevented from being delivered into the inner solar system due to the Jupiter-Saturn barrier (DK11), and at the same time, an imprint of the Galactic tide as inferred from the majority of observed comets.
 |
Fig. 20 Δq ≡ qmax−qmin per 10.0 Myr for 100 Sedna progenitors (Sednitos) moving under the action of EFE. |
7.1. Sedna
We are interested in how important the torquing of perihelion is owing to EFE in the trans-Neptunian region when one substitutes α = 0.5 of 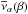 interpolating function and the standard value a0 = 1.2 × 10-10 m s-2 with larger values of α and a0 ≤ 8.1 × 10-11 m s-2 (H+16).
interpolating function and the standard value a0 = 1.2 × 10-10 m s-2 with larger values of α and a0 ≤ 8.1 × 10-11 m s-2 (H+16).
We ran similar QUMOND simulation as in Sect. 6.2, assuming 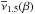 and a0 = 8.1 × 10-11 m s-2. We used the same initial orbit assignment for Sednitos as in Sect. 6.2, except for the value of q which is now a random number uniformly distributed on the interval (25, 30) au, to maximise Δq. In Fig. 20, we show Δq per 10.0 Myr for 100 simulated Sednitos. The extremal Δq is about 50 au per 10.0 Myr. At the end of the simulation, two Sednitos had q ~ 75 au, hence very close to the Sedna’s perihelion distance. Sedna-like orbits (here simplified as specific a and q values) can be produced by EFE from those having a protoplanetary-disk origin in ~10 Myr.
and a0 = 8.1 × 10-11 m s-2. We used the same initial orbit assignment for Sednitos as in Sect. 6.2, except for the value of q which is now a random number uniformly distributed on the interval (25, 30) au, to maximise Δq. In Fig. 20, we show Δq per 10.0 Myr for 100 simulated Sednitos. The extremal Δq is about 50 au per 10.0 Myr. At the end of the simulation, two Sednitos had q ~ 75 au, hence very close to the Sedna’s perihelion distance. Sedna-like orbits (here simplified as specific a and q values) can be produced by EFE from those having a protoplanetary-disk origin in ~10 Myr.
If interpolating function 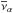 with α ≥ 2.0 would be used instead, then we can expect larger times would be necessary to produce the given Δq. We have tested this in an approximation of the EFE-induced quadrupole anomaly19 (Milgrom 2009b; Blanchet & Novak 2011) and the quadrupole strengths that are listed in Hees et al. (2016). For
with α ≥ 2.0 would be used instead, then we can expect larger times would be necessary to produce the given Δq. We have tested this in an approximation of the EFE-induced quadrupole anomaly19 (Milgrom 2009b; Blanchet & Novak 2011) and the quadrupole strengths that are listed in Hees et al. (2016). For 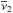 and a0 = 8.1 × 10-11 m s-2 the timescale of producing given Δq is in average, by a factor of few times greater.
and a0 = 8.1 × 10-11 m s-2 the timescale of producing given Δq is in average, by a factor of few times greater.
In Fig. 21, we depict the perihelion distance as a function of time, q(t), for the known TNOs with q> 30 au and a> 150 au, in the next 10 Myr, assuming 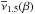 and a0 = 8.1 × 10-11 m s-2. None of the followed objects migrates under 30 au in the next 10 Myr.
and a0 = 8.1 × 10-11 m s-2. None of the followed objects migrates under 30 au in the next 10 Myr.
 |
Fig. 21 Perihelion distance as a function of time under action of EFE for the known population of trans-Neptunian bodies, with a> 150 au and q> 30 au. |
8. Discussion and conclusion
We have investigated how the (Newtonian) paradigm of a vast cometary reservoir, the Oort cloud (OC), changes in Milgromian dynamics (MD), specifically in the modified gravity QUMOND. The results are dependent on the choice of the MD interpolating function and value of the constant a0.
For the popular pair, 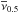 (Eq. (29b) with α = 0.5) and a0 = 1.2 × 10-10 m s-2, we have found the following qualitative properties of the Milgromian OC (MOC):
(Eq. (29b) with α = 0.5) and a0 = 1.2 × 10-10 m s-2, we have found the following qualitative properties of the Milgromian OC (MOC):
-
The observationally inferred MOC is compact with a radius~15 kau.
-
Binding energies of comets are significantly increased compared to those of the classical OC. The planetary barrier shifts significantly inward.
-
An injection of comets into the inner solar system is mainly driven by the external field effect (EFE) from the Galaxy, the specific feature of non-linear MD, see Sect. 2.3. The Galactic tide can be, owing to small heliocentric distances of MOC bodies, neglected.
-
EFE-induced injection of comets is very efficient and the cometary influx can be significantly larger than in the Newtonian case, if we assume the zeroth approximation of the same, Newtonian, source population and its distribution in both frameworks.
-
The orbit of a body with a proto-planetary disk origin can, under the action of EFE, be transformed into a Sedna-like orbit on a timescale of several Myr.
Trans-Neptunian bodies in Sedna-like orbits are not “fossil” objects with frozen perihelia (like in the Sun-in-a-cluster model) but rather they could repeatedly migrate through the inner solar system as EFE raises and lowers their perihelia repeatedly.
During the preparation of this paper, H+16 published constraints on various commonly-used MD interpolating function families. The constraints are based on the Cassini spacecraft radio tracking data (Hees et al. 2014). Many popular MD interpolating functions have been proven incompatible with the data, including 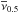 . Adopting
. Adopting 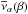 with α ≳ 1.5 and a0 ≤ 8.11 × 10-11 m s-2 in line with H+16, the MD-regime is essentially suppressed at any distance from the Sun owing to EFE, see Fig. 17. The cloud is, in this case, very much Newtonian in its overall size, binding energies of comets and operation of the Jupiter-Saturn barrier. However, even in this case, EFE substantially torques orbits in the inner parts of the cloud where the tidal force is weak, with the potential to transform primordial orbits to Sedna-like orbits, as was shown in the case α = 1.5 and a0 = 8.11 × 10-11 m s-2 on the timescale of ~10 Myr. Steeper interpolating functions imply larger timescales for these transformations.
with α ≳ 1.5 and a0 ≤ 8.11 × 10-11 m s-2 in line with H+16, the MD-regime is essentially suppressed at any distance from the Sun owing to EFE, see Fig. 17. The cloud is, in this case, very much Newtonian in its overall size, binding energies of comets and operation of the Jupiter-Saturn barrier. However, even in this case, EFE substantially torques orbits in the inner parts of the cloud where the tidal force is weak, with the potential to transform primordial orbits to Sedna-like orbits, as was shown in the case α = 1.5 and a0 = 8.11 × 10-11 m s-2 on the timescale of ~10 Myr. Steeper interpolating functions imply larger timescales for these transformations.
To sum up, if the results presented in Hees et al. (2014) are correct, and there is no other hidden dynamical effect acting on the spacecraft, then the results presented in Sects. 4–6 are only of academic character. Still, it is instructive to see how the MOC changes with a varying description of the transition regime.
We further discuss the MOC in line of the new constraints on the MD interpolating function. We emphasise that the influence of EFE on inner OC bodies and Centaurs, Kuiper belt objects, and scattered disk objects in high-a orbits is even under these circumstances substantial. Consequently Sedna-like orbits and orbits of large semi-major axis Centaurs are easily comprehensible in MD. In MD, they both belong to the same population, just in different modes of their evolution.
MD could eventually shed light on many open problems in the cis and trans-Neptunian region. Besides the already mentioned puzzling orbits of Sedna and 2012 VP113, the clustering in argument of perihelion, ω, near ω ≈ 0deg, for bodies in orbits with q> 30 au and a> 150 au (Trujillo & Sheppard 2014), and the origin of high-a-Centaurs (Gomes et al. 2015), could be elucidated in MD. With regards to ω-clustering, EFE would manifest in this region through an anomalous force that increases with heliocentric distance and is aligned with the direction to the Galactic centre (Milgrom 2009b; Blanchet & Novak 2011). Hence bodies, that are protected from encountering the planets frequently, should bear an imprint of EFE, similarly, as if there was a distant massive body hidden deep in the OC. In MD, one could expect nodal (Ω) or apsidal (ω + Ω) confinement, or eventually both (Paučo, in prep.). The fact that a subsample of the stable objects (with a> 250 au) is actually clustered in the physical space was recently shown in Batygin & Brown (2016).
EFE is an important dynamical agent, raising and lowering perihelia in the inner parts of the outer solar system very effectively, with no such counterpart in Newtonian dynamics. Thus, we could intuitively expect MOC, and especially its inner part, to be more populous at the formation phase than the classical OC, as planetesimals with mildly pumped semi-major axes (a ~ 0.1–1 kau) could have their perihelia lifted sufficiently rapidly to be protected from being ejected or captured by planets. Also, we could expect this primordial outward migration to be followed by a period of high influx of interplanetary material, after which (or after several such cycles) this inner region was radically depleted. Here timing is important because this phenomenon could coincide with the late heavy bombardment, hinted at by the Moon’s petrology record (Hartmann et al. 2000), at ~700 Myr after planets formed. Although this kind of event is rather abrupt and of relatively short duration, it was well accounted for in the Newtonian framework with the model of rapid migration of the outer planets (Gomes et al. 2005). We plan to investigate this topic in a subsequent work.
It is questionable whether the primordial disk mass and OC-to-scattered-disk population ratio problems arise in the context of MD since nobody has ever simulated solar system formation and evolution (with its outermost parts) in MD. EFE torquing is important in the context of the (re)distribution of material within the cloud, which could be then expected to be different in MD to that in Newtonian dynamics. The preference for high semi-major axis orbits (where tides are sufficiently strong) in the classical OC does not need to be so eminent in MOC. In the perihelion distance, q, vs. semi-major axis, a, diagram, where in the classical OC theory there is more or less empty space at q ≳ 100 au, a ~ 1000 au, we expect some residual population in MD. In the future, this could be tested against observations. Also, a simulation similar to that in Sects. 6.2 and 7.1, but including the outer planets and more Sednitos, would yield steady populations of bodies with q> 30 au and q< 30 au (high-a Centaurs), after some time, which could be tested against observations on a similar basis to Gomes et al. (2015). There is obviously some tension between the theory and observations in the Newtonian framework (Gomes et al. 2015).
At this stage, we cannot claim MD to be self-consistent solution of the puzzles that bother classical OC theory, but it has been shown that it can well form a new, testable, paradigm with a specific signature in the outer parts of the solar system.
But note that EFE always attenuates classical MD effects, see Sect. 2.3 for discussion.
If we do not consider very close encounters (which can occur because the process is stochastic) occurring on very large time scales, probably leading to comet showers (Hills 1981).
It is believed that the scattered disk is the source region of the Jupiter-family comets (Duncan & Levison 1997).
From now on, when we write “MOND” we mean the 1983 Milgrom’s formulation (Milgrom 1983b), the simple formula in Eq. (1). When we write “Milgromian dynamics (MD)” we mean general theory, like in Bekenstein & Milgrom (1984) on the classical level or in Bekenstein (2004) on the Lorentz-covariant level.
Equations (1) and (3) can be equivalently considered as modified inertia and the whole theory can be built around modifying the kinetic part of the classical action (Milgrom 1994, 2011). We do not consider modified inertia theories in this paper. Note that these are generically non-local theories (Milgrom 1994).
≳50 per cent of the baryons constrained by the observations of the cosmic microwave background are hidden in some undetected form. Only a small fraction of these hidden baryons would be necessary to account for the mass discrepancy in galaxy clusters (Famaey & McGaugh 2012).
DK11 found the original reciprocal semi-major axis of the comet C/1978 G2 to be −22.4 ± 37.8 × 10-6 au-1.
To be thorough, in Newtonian dynamics it is vice-versa possible for a comet to appear to be bound but to originate in the interstellar space as a result of Galactic tidal influence (Neslušan & Jakubík 2013). In any case, this special configuration is highly improbable (Neslušan & Jakubík 2013).
This certainly depends on the orbital inclination, as can be seen in Fig. 1 in Fernández & Brunini (2000). The footnoted sentence is true for highly inclined orbits with i ∈ (120, 150) deg. For orbits close to ecliptics, the planetary kick at 15 au is about 6 times larger.
In Newtonian dynamics, anisotropy in bG distribution (see Sect. 1.1) is introduced owing to the existence of a preferred direction, perpendicular to the Galactic midplane. By considering the MOC with  and a0 = 1.2 × 10-10 m s-2 – where injection of a comet due to tides is secondary – there is also a preferred direction in the cloud, which is, although varying with time, the direction of the external field of the Galaxy. Maybe the longterm effect of the external field is to produce this kind of anisotropy in bG distribution for MOC comets.
and a0 = 1.2 × 10-10 m s-2 – where injection of a comet due to tides is secondary – there is also a preferred direction in the cloud, which is, although varying with time, the direction of the external field of the Galaxy. Maybe the longterm effect of the external field is to produce this kind of anisotropy in bG distribution for MOC comets.
The inner OC can be crudely investigated with the aid of the multipole expansion approach (Milgrom 2009b; Blanchet & Novak 2011), taking into account only the dominant quadrupole term and assuming the constancy of the parameter Q2 (Blanchet & Novak 2011; Hees et al. 2016). Rotation of the external field can, in this case, be easily incorporated.
Acknowledgments
We are thankful to Leonard Kornoš and Luboš Neslušan for valuable discussions on orbital integrators and the classical Oort cloud. We also thank the referee, Rodney Gomes, for an open-minded review and comments, which helped to improve the clarity of the paper and also inspired us to realize additional motivation for Milgromian dynamics in the solar system. J.K. is supported by the Slovak National Grant Agency VEGA, grant No. 1/067/13.
References
- Angus, G. W., Gentile, G., Diaferio, A., Famaey, B., & van der Heyden, K. J. 2014, MNRAS, 440, 746 [NASA ADS] [CrossRef] [Google Scholar]
- Batygin, K., & Brown, M. E. 2016, AJ, 151, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Begeman, K. G., Broeils, A. H., & Sanders, R. H. 1991, MNRAS, 249, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Bekenstein, J. D. 2004, Phys. Rev. D, 70, 083509 [NASA ADS] [CrossRef] [Google Scholar]
- Bekenstein, J., & Milgrom, M. 1984, ApJ, 286, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Berezhiani, L., & Khoury, J. 2015, Phys. Rev. D, 92, 103510 [NASA ADS] [CrossRef] [Google Scholar]
- Berezhiani, L., & Khoury, J., 2016, Phys. Lett. B, 753, 639 [NASA ADS] [CrossRef] [Google Scholar]
- Bienaymé, O., Famaey, B., Wu, X., Zhao, H. S., & Aubert, D. 2009, A&A, 500, 801 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blanchet, L., & Bernard, L. 2014, Int. J. Mod. Phys. Conf. Ser., 30, 60271 [CrossRef] [Google Scholar]
- Blanchet, L., & Le Tiec, A. 2008, Phys. Rev. D, 78, 024031 [NASA ADS] [CrossRef] [Google Scholar]
- Blanchet, L., & Le Tiec, A. 2009, Phys. Rev. D, 80, 023524 [NASA ADS] [CrossRef] [Google Scholar]
- Blanchet, L., & Novak, J. 2011, MNRAS, 412, 2530 [NASA ADS] [CrossRef] [Google Scholar]
- Boylan-Kolchin, M., Springel, V., White, S. D. M., & Jenkins, A. 2010, MNRAS, 406, 896 [Google Scholar]
- Brada, R., & Milgrom, M. 1995, MNRAS, 276, 453 [Google Scholar]
- Brasser, R., & Morbidelli, A. 2013, Icarus, 225, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Brasser, R., Duncan, M. J., & Levison, H. F. 2007, Icarus, 191, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, M. E., Trujillo, C., & Rabinowitz, D. 2004, ApJ, 617, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Chambers, J. E. 1999, MNRAS, 304, 793 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Copeland, E. J., Sami, M., & Tsujikawa, S. 2006, Int. J. Mod. Phys. D, 15, 1753 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Delsemme, A. H. 1987, A&A, 187, 913 [NASA ADS] [Google Scholar]
- Dones, L., Weissman, P. R., Levison, H. F., & Duncan, M. J. 2004, Oort cloud formation and dynamics, in Comets II, eds. M. C. Festou, H. U. Keller, & H. A. Weaver (University of Arizona Press), 153 [Google Scholar]
- Duncan, M. J., & Levison, H. F. 1997, Science, 276, 1670 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Duncan, M., Quinn, T., & Tremaine, S. 1987, AJ, 94, 1330 [NASA ADS] [CrossRef] [Google Scholar]
- Dybczyński, P. A., & Królikowska, M. 2011, MNRAS, 416, 51 [NASA ADS] [Google Scholar]
- Dybczyński, P. A., & Królikowska, M. 2015, MNRAS, 448, 588 [NASA ADS] [CrossRef] [Google Scholar]
- Einstein, A. 1915, in Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften (Berlin), 844 [Google Scholar]
- Everhart, E. 1985, in Dynamics of Comets: Their Origin and Evolution, Proc. IAU Colloq. 83, eds. A. Carusi, & G. B. Valsecchi (Dordrecht: Reidel), Astrophysics and Space Science Library, 115, 185 [Google Scholar]
- Faber, S. M., & Jackson, R. E. 1976, ApJ, 204, 668 [NASA ADS] [CrossRef] [Google Scholar]
- Famaey, B., & Binney, J. 2005, MNRAS, 363, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Famaey, B., & McGaugh, S. S. 2012, Liv. Rev. Relat., 15, 10 [Google Scholar]
- Famaey, B., & McGaugh, S. 2013, J. Phys. Conf. Ser., 437, 012001 [NASA ADS] [CrossRef] [Google Scholar]
- Famaey, B., Bruneton, J.-P., & Zhao, H. 2007, MNRAS, 377, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Fernández, J. A., & Brunini, A. 2000, Icarus, 145, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Gentile, G., Famaey, B., & de Blok, W. J. G. 2011, A&A, 527, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gomes, R., Levison, H. F., Tsiganis, K., & Morbidelli, A. 2005, Nature, 435, 466 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gomes, R. S., Soares, J. S., & Brasser, R. 2015, Icarus, 258, 37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartmann, W. K., Ryder, G., Dones, L., & Grinspoon, D. 2000, The Time-Dependent Intense Bombardment of the Primordial Earth/Moon System, eds. R. M. Canup, K. Righter, et al. (University of Arizona Press), 493 [Google Scholar]
- Hees, A., Famaey, B., Angus, G. W., & Gentile, G. 2016, MNRAS, 455, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Hees, A., Folkner, W. M., Jacobson, R. A., & Park, R. S. 2014, Phys. Rev. D, 89, 102002 [NASA ADS] [CrossRef] [Google Scholar]
- Heisler, J., & Tremaine, S. 1986, Icarus, 65, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Hills, J. G. 1981, AJ, 86, 1730 [NASA ADS] [CrossRef] [Google Scholar]
- Hogg, D. W., Quinlan, G. D., & Tremaine, S. 1991, AJ, 101, 2274 [NASA ADS] [CrossRef] [Google Scholar]
- Holmberg, J., & Flynn, C. 2004, MNRAS, 352, 440 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R. A., Lewis, G. F., Conn, A. R., et al. 2013, Nature, 493, 62 [CrossRef] [Google Scholar]
- Ibata, N. G., Ibata, R. A., Famaey, B., & Lewis, G. F. 2014, Nature, 511, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R. A., Famaey, B., Lewis, G. F., Ibata, N. G., & Martin, N. 2015, ApJ, 805, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Iorio, L. 2010a, The Open Astron. J., 3, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Iorio, L. 2010b, The Open Astron. J., 3, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Kaib, N. A., & Quinn, T. 2008, Icarus, 197, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Kaib, N. A., & Quinn, T. 2009, Science, 325, 1234 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kaib, N. A., Roškar, R., & Quinn, T. 2011, Icarus, 215, 491 [NASA ADS] [CrossRef] [Google Scholar]
- Khoury, J. 2015, Phys. Rev. D, 91, 024022 [NASA ADS] [CrossRef] [Google Scholar]
- Koda, J., Yagi, M., Yamanoi, H., & Komiyama, Y. 2015, ApJ, 807, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Królikowska, M. 2014, A&A, 567, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kroupa, P. 2012, PASA, 29, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., Famaey, B., de Boer, K. S., et al. 2010, A&A, 523, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lada, C. J., & Lada, E. A. 2003, ARA&A, 41, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Levison, H. F., Dones, L., & Duncan, M. J. 2001, AJ, 121, 2253 [NASA ADS] [CrossRef] [Google Scholar]
- Levison, H. F., Morbidelli, A., Vokrouhlický, D., & Bottke, W. F. 2008, AJ, 136, 1079 [NASA ADS] [CrossRef] [Google Scholar]
- Lüghausen, F., Famaey, B., Kroupa, P., et al. 2013, MNRAS, 432, 2846 [NASA ADS] [CrossRef] [Google Scholar]
- Lüghausen, F., Famaey, B., & Kroupa, P. 2014, MNRAS, 441, 2497 [NASA ADS] [CrossRef] [Google Scholar]
- Lüghausen, F., Famaey, B., & Kroupa, P. 2015, Can. J. Phys., 93, 232 [NASA ADS] [CrossRef] [Google Scholar]
- McGaugh, S. S. 2004, ApJ, 609, 652 [NASA ADS] [CrossRef] [Google Scholar]
- McGaugh, S. S. 2005a, Phys. Rev. Lett., 95, 171302 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- McGaugh, S. S. 2005b, ApJ, 632, 859 [NASA ADS] [CrossRef] [Google Scholar]
- McGaugh, S. S. 2008, ApJ, 683, 137 [NASA ADS] [CrossRef] [Google Scholar]
- McGaugh, S. S., Schombert, J. M., Bothun, G. D., & de Blok, W. J. G. 2000, ApJ, 533, L99 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Milgrom, M. 1983a, ApJ, 270, 371 [Google Scholar]
- Milgrom, M. 1983b, ApJ, 270, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M. 1986a, ApJ, 306, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M. 1986b, ApJ, 302, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M. 1994, Annals of Physics, 229, 384 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M. 1999, Phys. Lett. A, 253, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M. 2001, MNRAS, 326, 1261 [Google Scholar]
- Milgrom, M. 2009a, Phys. Rev. D, 80, 123536 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M. 2009b, MNRAS, 399, 474 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M. 2009c, ApJ, 698, 1630 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M. 2010, MNRAS, 403, 886 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M. 2011, Acta Phys. Polonica B, 42, 2175 [Google Scholar]
- Milgrom, M. 2015, MNRAS, 454, 3810 [NASA ADS] [CrossRef] [Google Scholar]
- Morbidelli, A., & Levison, H. F. 2004, AJ, 128, 2564 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Neslušan, L., & Jakubík, M. 2013, Contributions of the Astronomical Observatory Skalnate Pleso, Proc. of Workshop, 43, 109 [Google Scholar]
- Oort, J. H. 1950, Bull. Astron. Inst. Netherlands, 11, 91 [Google Scholar]
- Öpik, J. H. 1932, Proc. Amer. Acad. Art Sc., 67, 169 [CrossRef] [Google Scholar]
- Pawlowski, M. S., Kroupa, P., Angus, G., et al. 2012a, MNRAS, 424, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Pawlowski, M. S., Pflamm-Altenburg, J., & Kroupa, P. 2012b, MNRAS, 423, 1109 [NASA ADS] [CrossRef] [Google Scholar]
- Pawlowski, M. S., Kroupa, P., & Jerjen, H. 2013, MNRAS, 435, 1928 [NASA ADS] [CrossRef] [Google Scholar]
- Pawlowski, M. S., Famaey, B., Jerjen, H., et al. 2014, MNRAS, 442, 2362 [NASA ADS] [CrossRef] [Google Scholar]
- Pawlowski, M. S., Famaey, B., Merritt, D., & Kroupa, P. 2015, ApJ, 815, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Rickman, H. 2014, Meteorit. Planet. Sci., 49, 8 [Google Scholar]
- Rickman, H., Fouchard, M., Froeschlé, C., & Valsecchi, G. B. 2008, Celest. Mech. Dyn. Astron., 102, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, R. H. 2003, MNRAS, 342, 901 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, R. H. 2005, MNRAS, 363, 459 [NASA ADS] [Google Scholar]
- Sanders, R. H. 2010, MNRAS, 407, 1128 [NASA ADS] [CrossRef] [Google Scholar]
- Schönrich, R. 2012, MNRAS, 427, 274 [NASA ADS] [CrossRef] [Google Scholar]
- Sellwood, J. A., & Binney, J. J. 2002, MNRAS, 336, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Sereno, M., & Jetzer, P. 2006, MNRAS, 371, 626 [NASA ADS] [CrossRef] [Google Scholar]
- Torbett, M. V. 1986, MNRAS, 223, 885 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo, C. A., & Sheppard, S. S. 2014, Nature, 507, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Tully, R. B., & Fisher, J. R. 1977, A&A, 54, 661 [NASA ADS] [Google Scholar]
- Wu, X., Zhao, H., Famaey, B., et al. 2007, ApJ, 665, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, X., Famaey, B., Gentile, G., Perets, H., & Zhao, H. 2008, MNRAS, 386, 2199 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, H., & Famaey, B. 2010, Phys. Rev. D, 81, 087304 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, H., & Famaey, B. 2012, Phys. Rev. D, 86, 067301 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhao, H., Famaey, B., Lüghausen, F., & Kroupa, P. 2013, A&A, 557, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zlosnik, T. G., Ferreira, P. G., & Starkman, G. D. 2007, Phys. Rev. D, 75, 044017 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Interpolating functions ν(β) = [1 + (1 + 4β-1)1 / 2] / 2 (dot-dashed line) and ν(β) = [1−exp(−β1 / 2)] -1 (solid line) as functions of heliocentric distance Ξ. β ≡ gN/a0 is approximated with |
| In the text | |
 |
Fig. 2 PMD of the Milky Way (solid), modelled as in Sect. 3.1 at R = R0 = 8.3 kpc within | z | < 1 kpc. NFW dark matter density (dashed line) is also depicted. |
| In the text | |
 |
Fig. 3 Left: oscillation of the Sun governed by Eq. (17) in MD. We used z⊙(0) = 30 pc and vz⊙(0) = 7.25 km s-1 as the initial conditions of the Sun’s motion. Middle: local “total matter density” ϱ = ϱb + ϱph, as experienced by the oscillating Sun. Right: local PMD, as experienced by the oscillating Sun. |
| In the text | |
 |
Fig. 4 Past Milgromian trajectories of 3 × 100 Monte Carlo particles projected to 3 mutually orthogonal planes of O⊙(ξ,η,ζ). The particles were initialised with original Newtonian orbital elements: a = 10 (top row), 50 (middle row), 100 (bottom row) kau, q distributed uniformly on the interval (0,8) au, cos(i) distributed uniformly on the interval (− 1,1), ω and Ω distributed uniformly on the interval (0,2π), among the particles, and mean anomaly M = 0. Then the particles were evolved back in time in the simple model of the MOC, Sect. 3.2, for one Keplerian period (≈1 Myr) in the case of a = 10 kau, and for 10 Myr in the case of a = 50 and 100 kau. The concentric circles at the top right corner of figures A, B, and C represent relative radii of the Milgromian (always the smaller circle) and Newtonian OC (radius = 2a; always the larger circle) as determined by the simulation and assuming that the cloud is the smallest sphere encompassing all orbits of given initial a. The Sun resides at [0, 0], as indicated by the symbol. |
| In the text | |
 |
Fig. 5 Past trajectories of two slightly hyperbolic comets in the simple model of the MOC. Both were initialised at their perihelia, one with q = 8 au, e = 1.00150, ω = π/ 4 (solid line), the other with q = 3 au, e = 1.00055, ω = π/ 4 (dot-dashed line). All the other orbital elements were set to 0. The integration time was 20 Myr. As can be seen these comets are bound (returning) in MD. The Sun resides at [0, 0], as indicated by the symbol. |
| In the text | |
 |
Fig. 6 Past Milgromian trajectories of 31 near-parabolic comets, those identified as dynamically new in DK11, projected to 3 mutually orthogonal planes of O⊙(ξ,η,ζ). Dynamical model of the OC consists of the stationary Galactic field coupled to the QUMOND equations, see Sect. 3.2, and the Galactic tide model, see Sect. 3.1.3. The comets with Keplerian periods TKep lesser than 10 Myr were followed for the time of TKep, those with TKep> 10 Myr were followed for 10 Myr. Inferred MOC is much smaller than the classical OC, see Table 1 for comparison with Newtonian orbits. At [0, 0] resides the Sun as indicated by the symbol. |
| In the text | |
 |
Fig. 7 Past Milgromian trajectory of the comet C/1978 G2, the slightly hyperbolic comet. Initial q = 6.28 au and e = 1.00014083. At [0, 0] resides the Sun as indicated by the symbol. |
| In the text | |
 |
Fig. 8 Specific angular momentum L as a function of time for the comet C/1974 V1. We have assumed the simple model of the MOC (tides are omitted). The periodic changes are induced solely by EFE. The negative time means that we are dealing with the past trajectory of the comet. |
| In the text | |
 |
Fig. 9 Heliocentric distance, Ξ(t), and change in magnitude of the specific angular momentum, δL(t) ≡ L(t)−L(0), as a function of time, t, for 100 Monte Carlo test particles initialised with a = 10 kau, and q uniformly distributed on the interval (15,100) au. The top row represents an output of the Milgromian simulation, the bottom row, the Newtonian simulation. In MD simulation, the follow up time, Trev, is set to 0.26 Myr (see top left quarter of the figure for motivation), in Newtonian simulation Trev is set to be the Keplerian period TKep(a = 10 kau) ≈1 Myr. |
| In the text | |
 |
Fig. 10 Histogram of ΔL ≡ Lmax−Lmin for 100 Monte Carlo test particles initialised with a = 10 kau and q uniformly distributed on the interval (15,100) au. Here Lmax (Lmin) is maximal (minimal) magnitude of the specific angular momentum, as found during one revolution, Trev, succeeding the initialisation of a comet at perihelion. In the MD simulation Trev = 0.26 Myr, in the Newtonian simulation Trev = TKep(a = 10 kau) ≈1 Myr. A single bin corresponds to a single test particle in the simulation. Solid bins are ΔL in the simple model of the MOC, shaded bins (here barely visible), stacked on the solid bins, are ΔL in Newtonian dynamics, with the gravity of the Sun and the Galactic tide accounted for. |
| In the text | |
 |
Fig. 11 Same as for Fig. 9, but now the particles are initialised with a = 50 kau. The top row represents an output of the Milgromian simulation, the bottom row, the Newtonian simulation. In MD simulation, the follow-up time, Trev, is set to 0.4 Myr (see top left quarter of this figure for motivation), in the Newtonian simulation Trev is set to be the Keplerian period TKep(a = 50 kau) ≈11 Myr. |
| In the text | |
 |
Fig. 12 Same as for Fig. 10 but now the particles are initialized with a = 50 kau. In the MD simulation Trev = 0.4 Myr, in the Newtonian simulation Trev = TKep(a = 50 kau) ≈11 Myr. A single bin corresponds to a single test particle in the simulation. Solid bins are ΔL in the simple model of the MOC, shaded bins, stacked on the solid bins, are ΔL in Newtonian dynamics, with the gravity of the Sun and the Galactic tide accounted for. |
| In the text | |
 |
Fig. 13 Same as for Fig. 9, but now the particles are initialised with a = 100 kau. The top row represents an output of the Milgromian simulation, the bottom row, the Newtonian simulation. In the MD simulation, the follow-up time, Trev, is set to 0.4 Myr (see top left quarter of this figure for motivation), in the Newtonian simulation, Trev is set to be the Keplerian period TKep(a = 100 kau) ≈32 Myr. |
| In the text | |
 |
Fig. 14 Same as for Fig. 10, but now the particles are initialized with a = 100 kau. In the MD simulation Trev = 0.4 Myr, in the Newtonian simulation, Trev = TKep(a = 100 kau) ≈32 Myr. A single bin corresponds to a single test particle in the simulation. Solid bins are ΔL in the simple model of the MOC, shaded bins, stacked on the solid bins, are ΔL in Newtonian dynamics, with the gravity of the Sun and the Galactic tide accounted for. |
| In the text | |
 |
Fig. 15 Δq ≡ qmax−qmin per 5.9 Myr for 100 Sedna progenitors (Sednitos) moving under the action of EFE. Sednitos were initialised at perihelia with a = 524 au, uniformly distributed q ∈ (5,30) au, i ∈ (−10,10)deg, ω and Ω ∈ (0,2π). |
| In the text | |
 |
Fig. 16 Perihelion distance as a function of time under the action of EFE for the known population of trans-Neptunian bodies with a> 150 au and q> 30 au. Thick solid lines are 2012 VP113 and Sedna. |
| In the text | |
 |
Fig. 17 Transition to the Newtonian regime for different alphas in |
| In the text | |
 |
Fig. 18 PMD in the simple model of the MOC in the direction of ξ (solid line), η (dotted line), and ζ (dashed line) axis of O⊙(ξ,η,ζ). |
| In the text | |
 |
Fig. 19 Histogram of ΔL ≡ Lmax−Lmin for 100 Monte Carlo test particles initialised at perihelia with a = 10 kau and q uniformly distributed on the interval (15,100) au and then evolved in the simple model of the MOC for Trev ≈ TKep ≈ 1 Myr. |
| In the text | |
 |
Fig. 20 Δq ≡ qmax−qmin per 10.0 Myr for 100 Sedna progenitors (Sednitos) moving under the action of EFE. |
| In the text | |
 |
Fig. 21 Perihelion distance as a function of time under action of EFE for the known population of trans-Neptunian bodies, with a> 150 au and q> 30 au. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.