| Issue |
A&A
Volume 589, May 2016
|
|
|---|---|---|
| Article Number | A54 | |
| Number of page(s) | 9 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201527387 | |
| Published online | 13 April 2016 | |
Low-rank plus sparse decomposition for exoplanet detection in direct-imaging ADI sequences
The LLSG algorithm
1
Institut d’Astrophysique et de Géophysique, Université de
Liège,
Allée du Six Août 19c,
4000
Liège,
Belgium
e-mail:
cgomez@ulg.ac.be
2
Department of Mathematical Engineering, Université Catholique de
Louvain, 1348
Louvain-la-Neuve,
Belgium
3
Montefiore Institute, Université de Liège,
4000
Liège,
Belgium
4
Department of Astronomy, California Institute of
Technology, Pasadena,
CA
91125,
USA
Received: 17 September 2015
Accepted: 20 January 2016
Context. Data processing constitutes a critical component of high-contrast exoplanet imaging. Its role is almost as important as the choice of a coronagraph or a wavefront control system, and it is intertwined with the chosen observing strategy. Among the data processing techniques for angular differential imaging (ADI), the most recent is the family of principal component analysis (PCA) based algorithms. It is a widely used statistical tool developed during the first half of the past century. PCA serves, in this case, as a subspace projection technique for constructing a reference point spread function (PSF) that can be subtracted from the science data for boosting the detectability of potential companions present in the data. Unfortunately, when building this reference PSF from the science data itself, PCA comes with certain limitations such as the sensitivity of the lower dimensional orthogonal subspace to non-Gaussian noise.
Aims. Inspired by recent advances in machine learning algorithms such as robust PCA, we aim to propose a localized subspace projection technique that surpasses current PCA-based post-processing algorithms in terms of the detectability of companions at near real-time speed, a quality that will be useful for future direct imaging surveys.
Methods. We used randomized low-rank approximation methods recently proposed in the machine learning literature, coupled with entry-wise thresholding to decompose an ADI image sequence locally into low-rank, sparse, and Gaussian noise components (LLSG). This local three-term decomposition separates the starlight and the associated speckle noise from the planetary signal, which mostly remains in the sparse term. We tested the performance of our new algorithm on a long ADI sequence obtained on β Pictoris with VLT/NACO.
Results. Compared to a standard PCA approach, LLSG decomposition reaches a higher signal-to-noise ratio and has an overall better performance in the receiver operating characteristic space. This three-term decomposition brings a detectability boost compared to the full-frame standard PCA approach, especially in the small inner working angle region where complex speckle noise prevents PCA from discerning true companions from noise.
Key words: methods: data analysis / techniques: high angular resolution / techniques: image processing / planetary systems / planets and satellites: detection
© ESO, 2016
1. Introduction
Only a small fraction (less than 2%) of the confirmed exoplanet candidates known to date have been discovered through direct imaging1. Indeed the task of finding exoplanets around their host stars with direct observations is very challenging. The main difficulties in direct imaging from the ground are the image degradation caused by the Earth’s turbulent atmosphere, the huge difference in contrast between the host star and its potential companions (typically ranging from 10-3 to 10-10), and the small angular separation between them. Detecting close-in planets with high-contrast imaging nowadays relies on four main pillars (Mawet et al. 2012):
-
1.
optimized wavefront control;
-
2.
state-of-the-art coronagraphs;
-
3.
appropriate observing strategies;
-
4.
dedicated post-processing algorithms.
The role of the coronagraphs is to suppress starlight and reduce the contrast between the star and its potential companions, while wavefront control helps reduce the amount and variability of diffracted starlight by correcting the distorted wavefront in real time. Unfortunately, even when combining these two technologies, the images suffer from quasi-static speckle noise originating in the telescope and instruments (Marois et al. 2003). These speckles, produced by slow variations in the instrument aberrations, vary on timescales of several minutes to several hours and follow modified Rician statistics (Soummer & Aime 2004; Fitzgerald & Graham 2006) instead of having a Gaussian nature. Moreover, these quasi-static speckles mimic the presence of point-like sources (since they are comparable in angular size and brightness) and dominate the close vicinity of the star. Therefore, the need for optimal observing strategies and fine-tuned post-processing procedures becomes evident.
Observing strategies such as angular differential imaging (Marois et al. 2006) and spectral differential imaging using multiple spectral channels (SDI, Sparks & Ford 2002) allow decoupling, on the image plane, the planetary signal from the speckle noise field, a situation that can be exploited by algorithms of different complexities. In ADI the images are acquired with an altitude/azimuth telescope in pupil-tracking mode, which means that the instrument field derotator remains off, thereby keeping the instrument and telescope optics aligned while the image rotates with time. For each image, a reference point-spread function (PSF) can be constructed from appropriately selected images contained in the same ADI sequence in such a way that, when it is subtracted from the image, it reduces the stellar contribution and the associated quasi-static speckle noise. Another consequence is that owing to the field-of-view rotation, the residual noise averages incoherently after rotating the images to a common north. From the central limit theorem, the noise in the final combined image mostly becomes Gaussian (Marois et al. 2008; Mawet et al. 2014).
Different approaches exist for generating this reference PSF from ADI sequences, taking the basic idea into account that the planet moves in circular trajectories with respect to the speckle field. This is where post-processing algorithms come into play as a critical step for boosting the detectability of faint true companions in noisy background. In ADI, as originally conceived, the reference PSF is constructed by taking the median of the reference images. Some improvement can be achieved by processing the frames in an annulus-wise fashion and applying a rotation criterion for selecting the references. LOCI (locally optimized combination of images, Lafrenière et al. 2007) and its various modifications (Marois et al. 2014; Wahhaj et al. 2015) aim to create a reference PSF as a linear combination of the reference images independently inside multiple subregions, in which the residual noise is minimized. This approach provides a significant gain in sensitivity compared to the classical median reference PSF. ANDROMEDA (ANgular Differential OptiMal Exoplanet Detection Algorithm, Mugnier et al. 2009; Cantalloube et al. 2015) treats the ADI sequence in a pair-wise way and ensures that the images are chosen close enough in time to guarantee the stability of the speckle noise and thereby allow its suppression. In this approach the second image from every pair is used as a reference PSF for the first.
More recently, principal component analysis (PCA) based algorithms (Soummer et al. 2012; Amara & Quanz 2012) have been proposed for reference PSF subtraction. The reference PSF is constructed for each image as the projection of the image onto a lower-dimensional orthogonal basis extracted from the references via PCA. The main advantages of this approach are that it can be applied to the full images very efficiently using singular value decomposition (SVD), the reduced number of free parameters (basically the size of the basis) and that PCA enables forward modeling of astrophysical sources by fitting an astrophysical model directly to the reduced images without introducing degeneracies (Soummer et al. 2012).
Plain PCA extracts a lower-dimensional basis that is optimal in the least-square sense. More recently, alternatives to the least-square criterion have been proposed in the field of computer vision to consider other objectives, such as sparsity of the noise or robustness to outliers. In this paper, we propose one implementation of these algorithms applied to ADI image sequences. In our approach we decompose the images locally into low-rank, sparse, and Gaussian noise components to enhance residual speckle noise suppression and improve the detectability of point-like sources in the final combined image.
Throughout the paper we use upper-case letters to denote matrices, rank(X) to denote the rank of a matrix X, and card(X) to denote the cardinality (l0-pseudo norm or number of non-zero elements) of X.
2. Subspace projection models and low-rank plus sparse decompositions
The problem of matrix low-rank approximation has been studied extensively in recent years in many different fields, such as natural language processing, bioinformatics, and computer vision. In particular for image analysis, there are multiple tasks that can be achieved using low-rank modeling, such as image compression, denoising, restoration, alignment, face recognition, and background subtraction (or foreground detection in video sequences; Zhou et al. 2014). The applicability of low-rank approximations is guided by the fact that the latent structure of high-dimensional data usually lies in a low-dimensional subspace. If we consider a sequence of n images and a matrix M ∈ Rm × n whose columns are vectorized versions of those images, the above statement can be expressed as M = L + E, where L has low rank and E is a small perturbation matrix. An estimate of L is given by a best low-rank approximation of M in the least-square sense: 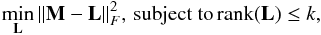 where
where 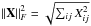 denotes the Frobenius norm of a matrix X, and k is the rank of the low-rank approximation L. This can be solved analytically through SVD (Eckart & Young 1936; Candès et al. 2009):
denotes the Frobenius norm of a matrix X, and k is the rank of the low-rank approximation L. This can be solved analytically through SVD (Eckart & Young 1936; Candès et al. 2009): 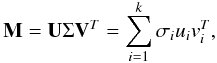 where the vectors ui and vi are the left and right singular vectors, and σi the singular values of M. Choosing the first k left singular vectors forms an orthonormal basis for the low-dimensional subspace that captures most of the variance of M. This procedure corresponds to PCA (Hotelling 1933), as it is usually called in statistics.
where the vectors ui and vi are the left and right singular vectors, and σi the singular values of M. Choosing the first k left singular vectors forms an orthonormal basis for the low-dimensional subspace that captures most of the variance of M. This procedure corresponds to PCA (Hotelling 1933), as it is usually called in statistics.
In computer vision, for the task of segmentation of an image sequence into background and foreground pixels, PCA was proposed by Oliver et al. (2000), who modeled the background pixels using an eigenspace model. Each image is approximated by its projection onto the first k principal components. They noted that, because they do not appear at the same location in the n sample images and are typically small, moving objects do not make a significant contribution to the PCA model. The foreground pixels are found by subtracting from each image its low-rank PCA approximation and thresholding the pixel values in the residual images.
In astronomy PCA has proven to be effective for modeling time- and position-dependent PSF variations of the Sloan Digital Sky Survey and later for the Advanced Camera for Surveys on the Hubble Space Telescope (see Jee et al. 2007). In the context of reference PSF subtraction for high-contrast imaging, a PCA-based approach has been proposed independently by Soummer et al. (2012) and Amara & Quanz (2012). The problem of modeling and subtracting a reference PSF with the purpose of detecting a moving planet in an ADI image sequence has a lot in common with the segmentation of video sequences into background and foreground pixels (e.g., for video surveillance and detection of moving objects), since the reference PSF and quasi-static speckles can be modeled using a low-rank PCA approximation. The orthogonal basis formed by the first principal components (PCs) is learnt from the ADI sequence itself, which adds complications to the low-rank approximation task because some part of the foreground signal is absorbed in the background model. This relates to the fact that PCA gives a suitable low-rank approximation only when the term E (foreground signal) is small and independent and identically distributed Gaussian (see Sect. 1.1 in Candès et al. 2009). This is unfortunately not the case for moving planets in ADI images.
2.1. Robust PCA
In recent computer vision literature, several subspace projection algorithms exploiting the low-rank structure of video sequences have been proposed to solve the weaknesses of the basic PCA model and provide more versatile and robust background models (Bouwmans & Zahzah 2014). The most notable is the family of robust PCA (RPCA) algorithms, which model the data as the superposition of low-rank and sparse components, containing the background and the foreground pixels, respectively. One of the first approaches for solving this decomposition was proposed by Candès et al. (2009), with an algorithm called principal component pursuit (PCP). PCP aims at decomposing M into low-rank plus sparse (L + S) matrices by solving the following problem: 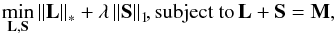 where L is low-rank, S contains sparse signal of arbitrarily large magnitude, ∥S∥1 = ∑ ij|Sij| is the l1-norm of S, and ∥L∥∗ denotes the nuclear norm of L or sum of its singular values. The nuclear norm and the l1-norm are the convex relaxations of rank(L) and card(S) and provide the best computationally tractable approximation to this problem. Under rather weak assumptions, this convex optimization recovers the low-rank and sparse components that separate the varying background and the foreground outliers. Important limitations of this algorithm are its high computational cost and the assumption that the low-rank component is exactly low-rank, and the sparse component is exactly sparse, contrary to what we find in real data, which is often corrupted by noise affecting a large part of the entries of M (Bouwmans & Zahzah 2014). In the ideal case, when applying such decomposition to an ADI image sequence, the reference PSF would be captured by the low-rank component and the small moving planets (realizations of the instrumental PSF) by the sparse component. In real ADI coronagraphic images, the reference PSF, composed of the stellar PSF and speckles, is never exactly low-rank owing to the quasi-static component of the speckle noise. Therefore the exact decomposition into low-rank and sparse components does not exist, and the S component recovered by PCP becomes polluted by residual noise from the quasi-static speckles that will produce a final image resembling the results of standard PCA.
where L is low-rank, S contains sparse signal of arbitrarily large magnitude, ∥S∥1 = ∑ ij|Sij| is the l1-norm of S, and ∥L∥∗ denotes the nuclear norm of L or sum of its singular values. The nuclear norm and the l1-norm are the convex relaxations of rank(L) and card(S) and provide the best computationally tractable approximation to this problem. Under rather weak assumptions, this convex optimization recovers the low-rank and sparse components that separate the varying background and the foreground outliers. Important limitations of this algorithm are its high computational cost and the assumption that the low-rank component is exactly low-rank, and the sparse component is exactly sparse, contrary to what we find in real data, which is often corrupted by noise affecting a large part of the entries of M (Bouwmans & Zahzah 2014). In the ideal case, when applying such decomposition to an ADI image sequence, the reference PSF would be captured by the low-rank component and the small moving planets (realizations of the instrumental PSF) by the sparse component. In real ADI coronagraphic images, the reference PSF, composed of the stellar PSF and speckles, is never exactly low-rank owing to the quasi-static component of the speckle noise. Therefore the exact decomposition into low-rank and sparse components does not exist, and the S component recovered by PCP becomes polluted by residual noise from the quasi-static speckles that will produce a final image resembling the results of standard PCA.
2.2. GoDec
Several modifications of PCP have been proposed to address its limitations with real data for the problem of foreground detection (see Bouwmans & Zahzah 2014, for a complete review). Beyond PCP, there are different approaches to RPCA via low-rank plus sparse matrix decomposition.
Among them, GoDec (Go Decomposition, Zhou & Tao 2011b) is a convenient approach, in terms of computational cost, to the decomposition of M. It proposes a three-term decomposition (instead of the typical low-rank plus sparse one): 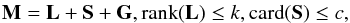 where G is a dense noise component, and k and c the constraints on the rank of L and the cardinality of S. GoDec produces an approximated decomposition of M, whose exact low-rank plus sparse decomposition does not exist because of additive noise G, restricting rank(L) and card(S) in order to control model complexity. This three-term decomposition can be expressed as the minimization of the decomposition error:
where G is a dense noise component, and k and c the constraints on the rank of L and the cardinality of S. GoDec produces an approximated decomposition of M, whose exact low-rank plus sparse decomposition does not exist because of additive noise G, restricting rank(L) and card(S) in order to control model complexity. This three-term decomposition can be expressed as the minimization of the decomposition error: 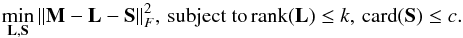 (1)The optimization problem of Eq. (1)is tackled by alternatively solving the following two subproblems until convergence, when the decomposition error reaches a small error bound (=10-3):
(1)The optimization problem of Eq. (1)is tackled by alternatively solving the following two subproblems until convergence, when the decomposition error reaches a small error bound (=10-3): ![\begin{equation} \label{godec2} \left\{\begin{array} {l}\displaystyle {\bf L}_{t} = {\rm argmin}_{\substack{{\rm rank}({\bf L})\le k }}{ \left\| {\bf M}-{\bf L}-{\bf S}_{t-1} \right\|_{F}^{2}} ;\\[3mm] \displaystyle {\bf S}_{t} = {\rm argmin}_{{\rm card}({\bf S})\le c }{ \left\| {\bf M}-{\bf L}_{t}-{\bf S} \right\|_{F}^{2}} . \end{array}\right. \end{equation}](/articles/aa/full_html/2016/05/aa27387-15/aa27387-15-eq36.png) (2)In Eq. (2), Lt can be updated via singular value hard thresholding of M − St − 1 (via SVD in each iteration), and St via entry-wise hard thresholding of M − Lt. It must be noted that singular value hard thresholding is equivalent to the truncation of the number of PCs in the PCA low-rank approximation.
(2)In Eq. (2), Lt can be updated via singular value hard thresholding of M − St − 1 (via SVD in each iteration), and St via entry-wise hard thresholding of M − Lt. It must be noted that singular value hard thresholding is equivalent to the truncation of the number of PCs in the PCA low-rank approximation.
A randomized and improved version of GoDec was proposed by the same authors with SSGoDec. In this approximated RPCA algorithm, the cardinality constraint is modified by introducing an l1 regularization, which induces soft-thresholding when updating S (Zhou & Tao 2013). The soft-thresholding operator 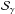 with threshold γ applied to the elements of a matrix X can be expressed as
with threshold γ applied to the elements of a matrix X can be expressed as 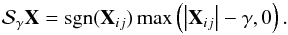 The reduced computational cost of SSGoDec mostly comes from using, on each iteration, the bilateral random projections (Zhou & Tao 2011a) of M instead of singular value thresholding for its low-rank approximation. BRP is a fast randomized low-rank approximation technique making use of M’s left and right random projections, Y1 = MA1 and Y2 = MTA2, where A1 ∈ Rn × k and A2 ∈ Rm × k are random matrices. The rank-k approximation of M is computed as
The reduced computational cost of SSGoDec mostly comes from using, on each iteration, the bilateral random projections (Zhou & Tao 2011a) of M instead of singular value thresholding for its low-rank approximation. BRP is a fast randomized low-rank approximation technique making use of M’s left and right random projections, Y1 = MA1 and Y2 = MTA2, where A1 ∈ Rn × k and A2 ∈ Rm × k are random matrices. The rank-k approximation of M is computed as 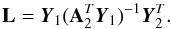 The computation of this approximated L requires less floating-point operations than the SVD-based approximation. The bounds of the approximation error in BRP are close to the error of the SVD approximation under mild conditions (Zhou & Tao 2011a).
The computation of this approximated L requires less floating-point operations than the SVD-based approximation. The bounds of the approximation error in BRP are close to the error of the SVD approximation under mild conditions (Zhou & Tao 2011a).
3. Local randomized low-rank plus sparse decomposition of ADI datasets
 |
Fig. 1 LLSG decomposition of ADI data (left) into low-rank (middle left) plus sparse (middle right) plus Gaussian noise (right) terms. In the ideal case, this decomposition separates the reference PSF and quasi-static speckle field from the signal of the moving planets, which stays in the sparse component. |
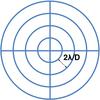 |
Fig. 2 Quadrants of annuli used for partitioning the images. |
Restricting the cardinality of M − Lt while operating on whole images is problematic in the presence of multiple companions, as the dimmest one could get severely subtracted from the data (especially for close-in companions), or bright speckles could turn into false positives. We find that applying a local three-term decomposition, which exploits the geometrical structure of ADI image sequences, can alleviate the problem of a global thresholding and in addition provide a better low-rank approximation for the given patch.
These ideas were put together to build an ADI post-processing algorithm for boosting point-like source detection, the Local Low-rank plus Sparse plus Gaussian-noise decomposition (LLSG). A schematic illustration of this decomposition is shown in Fig. 1. The algorithm follows four main steps:
-
1.
the images of the cube are broken into patches, specifically in quadrants of annuli of width 2λ/D (see Fig. 2);
-
2.
each of these quadrants is decomposed separately as in Eq. (2), alternatively updating its L and S components for a fixed number of iterations;
-
3.
for each patch, the S component of the decomposition is kept;
-
4.
all frames are rotated to a common north and are median combined in a final image.
The soft-thresholding will enforce the sparsity of the S component throughout the iterations. Instead of using a common threshold parameter γ, we use a different one for each patch. Values of γ that are too high will remove the signal of companions too much along with the residual speckle noise, while values that are too low will not lead to much improvement over PCA processing, therefore hindering the detection of potential very faint companions. Instead of leaving this as a free parameter, our algorithm defines γ for each patch as the square root of the median absolute deviation of the entries in St. This thresholding can be scaled up or down safely by the user with a tunable parameter in case it is needed. Partitioning the frames using quadrants of annuli does not increase the computational cost and alleviates the problem of applying entry-wise soft thresholding globally (on the whole frames), thereby giving better results in the case of several companions with different brightnesses or when very bright speckles are present.
Among the free parameters of LLSG, the rank (low integer value) is certainly the most important one. This parameter is equivalent to the number of PCs in the PCA algorithm and defines the size of the low-rank approximation of our dataset (L term). Values of the rank that are too high cause too much planetary signal to be absorbed by the low-rank term, whereas a low value produces a noisier sparse term. The sweet spot depends on data. The sparsity level (for scaling the soft-thresholding, by default is equal to one) is the second parameter of LLSG, which controls how sparse the S term is and how much noise goes into the G term. It usually does not require user intervention since it is internally defined for each image patch. The third parameter of LLSG is the number of iterations. A small number of iterations is enough (the default is ten) to achieve good decomposition according to our tests on several datasets, but it can be fine-tuned by the user. The number of iterations affects the running time of LLSG and generally by doubling the number of iterations we double the computation time.
As explained before, the sparse component is the main product of this algorithm, where potential companions will have a higher signal-to-noise ratio (S/N). The two other components in this decomposition, the low-rank and the noise, can serve as estimates of the total noise of our data. The L component will contain the starlight and most of the static and quasi-static structures, while G will capture the small and dense residual noise that was not captured by the low-rank approximation. An implementation of LLSG for ADI data is provided in the Vortex Image Processing (VIP) pipeline2. VIP is written in Python 2.7 programming language (Gomez Gonzalez et al., in prep.).
This idea of a three-term decomposition with some modifications, e.g. a different partitioning of the images, could be used as well for spectrally dispersed data obtained with an integral field spectrograph (IFS). After rescaling IFS data, the companions will appear to move radially through the speckle noise field. Therefore, LLSG can be a good choice for decomposing the image sequence and capturing potential planets in the sparse term.
4. Application to real data
4.1. Data used
The application of the LLSG decomposition to real data gives a first taste of its capabilities. In this paper, we use the data set of β Pic and its planetary companion β Pic b (Lagrange et al. 2010) obtained on January 2013 with VLT/NACO in its AGPM coronagraphic mode (Absil et al. 2013). The observations made at L′-band were performed under poor conditions, nevertheless β Pic b could be seen on the real-time display thanks to the excellent peak starlight extinction provided by the AGPM. The total on-source integration time was 114 min with a parallactic angle ranging from −15° to 68°. A clean cube was obtained after basic preprocessing steps, such as flat fielding, bad pixel removal, bad frames removal, recentering of frames, and sky subtraction. After temporal subsampling, by averaging 40 successive frames, a new cube of 612 individual frames with 8 s of effective integration time was created (for details see Absil et al. 2013). As a final step the central 161 × 161 pixels were cropped on each frame.
4.2. Results
Figure 3 shows the final post-processed frames using full-frame PCA and the three terms of the LLSG decomposition. We see clearly how LLSG can separate the starlight and quasi-static speckles from the planetary signal. The sparse term is where most of the signal of β Pic b is present. In the following discussion, we use the S/N between the planet signal and the background pixels to compare the performance of the two algorithms for the task of detection of point-like sources.
For calculating the S/N, we depart from the previously used definition in high-contrast imaging where the pixels are assumed to be statistically independent and the S/N is basically considered as the ratio of the flux in an aperture centered on the planet to the standard deviation of the pixels in an annulus at the same radius. We instead adopt the definition proposed by Mawet et al. (2014) that considers the problem of small sample statistics applied to small-angle high-contrast imaging. The number of resolution elements (λ/D) decreases rapidly toward small angles, thereby dramatically affecting confidence levels and false alarm probabilities. In this small sample regime, a two-sample t-test is used to see whether the intensity of a given resolution element is statistically different from the flux of similar λ/D circular apertures at the same radius r from the star. When one of the samples contains the single test resolution element, the two-sample t-test brings a better definition of S/N and is given by 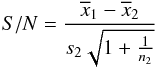 where
where 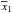 is the intensity of the single test resolution element, n2 the number of background resolution elements at the same radius (n2 = round(2πr) − 1, where r is given in λ/D units), and
is the intensity of the single test resolution element, n2 the number of background resolution elements at the same radius (n2 = round(2πr) − 1, where r is given in λ/D units), and 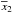 and s2 are the mean intensity and the empirical standard deviation computed over the n2 resolution elements.
and s2 are the mean intensity and the empirical standard deviation computed over the n2 resolution elements.
 |
Fig. 3 Final result of post-processing with PCA (left) and the three terms of the LLSG decomposition (middle and right) for β Pic NACO data. 38 PCs were used to maximize the S/N for β Pic b in the full-frame PCA approach. For the LLSG decomposition a rank of 10 gave a significant improvement on b’s S/N (see Fig. 4). All the frames were normalized to the maximum value of the LLSG sparse frame (middle panel). |
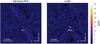 |
Fig. 4 S/N maps for PCA (left) and LLSG (right) computed from the final frames shown in Fig. 3 (left and middle panels). Planet β Pic b has roughly three times higher S/N when processed with our LLSG decomposition. |
 |
Fig. 5 Final result of post-processing with PCA (left), annular PCA (middle), and our LLSG decomposition (right). The images were normalized to their own maximum value. Four synthetic companions a(285°), b(185°), c(5°), and d(85°) were injected at 2, 5, 8, and 13 λ/D from the center, respectively. The injected PSFs were scaled at 0.5, 5, 5, and 7 times the noise of the respective annulus. We used 13 PCs when applying full-frame PCA and 25 PCs for the annular PCA (applying the same number of PCs in every annulus) in order to maximize the S/N of the innermost fake companion in each case. |
The use of the S/N as a metric for comparing algorithms can become problematic when, in some cases, the noise can be almost totally suppressed, making the S/N infinite. In this scenario, if a companion is present, a clear detection through visual vetting can be claimed. We have encountered this situation when processing other datasets of better quality (conditions of observation and/or better wavefront sensing). We also note that, the S/N of a point-like source depends on the choice of the aperture sizes and the position of the apertures themselves, especially at small angular separations where the small sample statistics effect becomes dominant (Quanz et al. 2015). Throughout this paper we use an aperture size of 4.6 pixels, which is the Gaussian full width at half maximum (FWHM) measured on the off-axis PSF of β Pic.
Also, the positioning of the apertures is done in an automatic way and is the same for each realization, when measuring S/Ns on the final frames of the compared algorithms. As an example, we only have 24 background apertures (n2) for the case of β Pic b (using the FWHM as an approximation for the value of the λ/D parameter). In spite of these limitations, we stick to the use of the S/N for its practicality for the task of detecting point-like sources.
Figure 4 shows the S/N maps corresponding to full-frame PCA and the sparse term of the LLSG algorithm. With LLSG the S/N of β Pic b is roughly three times higher than with full-frame PCA thanks to the small amount of residual noise in S. To maximize the S/N with full-frame PCA, we varied the number of PCs in the interval from 1 to 100, measuring at every step the S/N at the location of β Pic b. The highest S/N (=16.7) was achieved with 38 PCs. In the case of LLSG, the best compromise between residual noise subtraction and companion signal recovery was obtained with a rank equal to 10. The default number of iterations worked well for this ADI sequence.
As we can see in Fig. 3, roughly 25% of the planetary signal leaks into the LLSG noise term. However, this is less than the amount of companion signal absorbed in the PCA low-rank approximation, when using the 38 PCs that maximized the S/N of β Pic b. In this case, the leaking into the G term does not hinder the goal of LLSG for improving the detectability of a point-like source. In the following section, we test whether this holds true for more complicated scenarios with fainter companions. Nevertheless, the ultimate goal is to avoid any signal loss. This will be the subject of future work.
5. Simulations with synthetic companions
 |
Fig. 6 S/N maps for full-frame PCA (left), annular PCA (middle), and our LLSG decomposition (right) showing the values of each fake companion S/N. With our algorithm the four injected companions are clearly revealed. The S/N of the fake companion at 2λ/D is clearly at the level of the noise (false negative) in the case of full-frame PCA and its annular version. With LLSG we reach a peak S/N that is three times higher. For the rest of synthetic companions, the S/N obtained with LLSG is up to three times higher than the one obtained with full-frame PCA. |
5.1. Single test case
The use of on-sky data with simulated companions allows us to probe the performance of the detection algorithms with planets at different locations on the image plane and with varying brightness. This enables us to test how LLSG deals with a fainter and closer-in companion than β Pic b, which presented a rather easy scenario. To obtain a data cube without any companion, β Pic b was subtracted using the negative fake companion technique (Lagrange et al. 2010; Absil et al. 2013), which uses the off-axis PSF as a template to remove the planet from each frame by optimizing the position and flux (of the injected negative candidate). This optimization is performed by minimizing the sum of the absolute values of the pixels in a 4 × FWHM aperture on the PCA processed final frame. We used a downhill simplex minimization algorithm (Nelder & Mead 1965) for this purpose, which is enough to obtain a planet-free cube.
In the empty cube, we injected the normalized off-axis PSF to create four synthetic companions and compared the results of full-frame PCA and our approach (see Figs. 5 and 6). The companions a(285°), b(185°), c(5°), and d(85°) were injected at 2, 5, 8, and 13 λ/D from the center, respectively. The brightness of the fake companions was scaled as a function of the local noise before injection. The noise was measured as the standard deviation of the fluxes of the resolution elements inside the corresponding annulus in the classical ADI processed frame (which means it has been median-subtracted, derotated, and median-combined). The injected PSFs were scaled at 0.5, 5, 5, and 7 times the noise of the respective annulus.
In this particular example of processing a cube with several injected synthetic companions, we encounter a first problem with full-frame PCA: it is not possible to optimize the S/N for each individual companion at the same time by adjusting the number of PCs used. For the innermost injected planet, we need to use 13 PCs for full-frame PCA in order to reduce the residual speckle noise and achieve the best possible S/N. As done previously, the number of PCs was varied from 1 to 40, each time measuring the S/N at the location where the innermost planet was injected. This number of PCs may not be optimal for farther companions, which could achieve higher S/Ns with a smaller number of PCs. The optimal number of PCs in general decreases when the planet is farther away from the star in the photon-noise limited regime, since the planets have more rotation and the speckle noise is not dominant.
A better strategy in this case is to use the PCA low-rank approximation annulus-wise (see middle panel in Fig. 5). In this case, it is even possible to apply a frame-rejection criterion based on a parallactic angle threshold (Absil et al. 2013). The motivation behind this is that an annular PCA low-rank approximation will capture the background and speckle noise in a better way for a given patch. Furthermore, keeping only the frames where the planet has rotated by at least 1λ/D in our PCA reference library, we prevent the planetary signal from being captured by the low-rank approximation and subsequently subtracted from the science images, thereby increasing the S/N in the final frame. We provide a parallelized implementation of this algorithm in the VIP repository. For the innermost planet, located at 2λ/D, we can obtain a maximum S/N of 3.2 after optimizing the number of PCs (by testing from 15 to 35 PCs) and using 2λ/D wide annuli. For LLSG we kept the same rank as we used before and slightly reduced the sparsity level to achieve the highest S/N for the innermost fake companion.
As seen in the S/N maps shown in Fig. 6, our LLSG algorithm provides a gain of a factor three in S/N at 2λ/D with respect to full-frame PCA, resulting in a clear detection instead of the false negative in the case of full-frame PCA (even after careful optimization of the PCA truncation and knowledge of the coordinates of the planet). For the three other synthetic companions, located farther from the star, the S/N becomes between two and three times higher compared to full-frame PCA. The annular version of PCA does not provide much improvement over full-frame PCA in the small inner working angle region, even for an ADI sequence that has a large parallactic angle rotation range (~80°) and after adjusting the number of PCs. In this single simulation, we show some practical disadvantages of a full-frame PCA and the gain in S/N we obtain by using local versions of PCA and the proposed three-term decomposition.
5.2. Performance
 |
Fig. 7 ROC curves for our LLSG decomposition and full-frame PCA. The S/N thresholds τ are shown for integer values. Our algorithm ROC curve is close to the oracle (perfect classifier) in the upper left corner. |
Of course, based on a single realization, we cannot characterize the detection performance of the algorithms. More exhaustive approaches are needed, such as the use of receiver operating characteristic (ROC) curves. The performance of a detection algorithm is quantified using ROC analysis, and several meaningful figures of merit can be derived from it (Barrett et al. 2006). ROC and localization ROC curves are widely used tools in statistics and machine learning for visualizing the performance of a binary classifier system in a true positive rate (TPR) – false positive rate (FPR) plot as a decision threshold τ varies. The ultimate goal of high-contrast imaging, as for any signal detection application, is to maximize the TPR while minimizing the FPR, which can be achieved by maximizing the area under the curve (AUC) in the ROC space (Mawet et al. 2014). In general the goal of a classifier in the ROC space is to be as close as possible to the upper lefthand corner (perfect classifier, referred to as “oracle” with FPR=0 and TPR=1) and away from the random classifier line (TPR=FPR).
Building this plot for any exoplanet detection algorithm requires a large number of fake companion simulations, especially if a single planet is injected for each realization as in our case. One hundred realizations were made per annulus, centered at 2, 4, 6, 8, 10, and 14 λ/D, in a random way, meaning that there is a 50% chance that the datacube contains a synthetic planet. In the case of an injection, the fake companion has a random azimuthal position in the given annulus and a random brightness, scaling the PSF (ranging from 0.5 times to 5 times the noise in the considered annulus) as described previously. We consider localization ROC curves for which the decision of whether there is a planet or not is tied to a given position in the image plane.
The detection decision is based on comparing the value of the peak S/N of a given resolution element with a threshold τ. We call the peak S/N here the maximum S/N value obtained from shifting the center of the test resolution element inside a λ/D circular aperture centered on the considered coordinates. This is equivalent to taking the maximum S/N value in a λ/D circular aperture, centered on the considered coordinates, from an S/N map. We find this is in practice better than using the S/N of a resolution element centered on some given injection coordinates, because the maximum S/N for a point-like source (blob) will usually be shifted by a small amount because of post-processing. A true positive (TP) means that, in the case of an injection, the tested resolution element has a peak S/N ≥ τ. A false positive (FP) arises in case of a non-injection, when a random resolution element inside the considered annulus has a peak S/N ≥ τ. It is important to notice that we inspect only one resolution element each time instead of the total number of resolution elements in the image (even for the FP count) to preserve the 50–50 prior we described previously. We vary τ from 0 to 8 in steps of 0.1 in order to have enough points in our empirical ROC curve.
The TPR and FPR for these ROC curves are the averaged TPR and FPR over all brightnesses and the tested annuli. The ROC curves are shown in Fig. 7. It is important to emphasize that every point, for every τ, of the LLSG decomposition ROC curve is higher than the one for PCA, which means that the LLSG detection algorithm is closer to the perfect classifier. The full range of values of FPR (up to one) in our ROC curves is not fully covered even when testing unrealistically low values of τ. In this case calculating the AUC becomes problematic, and using other metrics derived from a ROC curve becomes more suitable for comparing algorithms (classifiers). An example of such a metric is the Euclidean distance to the upper lefthand corner or “oracle” (Braham et al. 2014). In the case of PCA, the minimum distance to the upper lefthand corner is 0.3, while for our algorithm it is 0.2, which again confirms its superiority.
For generating these ROC curves, we used fifteen PCs, which corresponds to 90% of the explained variance of M, a common approach for choosing the number of PCs for PCA in machine learning and statistics. The rank of the three-term decomposition was set to fifteen, and the number of iterations was set to ten. Tuning parameters instead of having them fixed for all the realizations could lead to minor improvements in the ROC curves. Tuning the parameters would also increase the complexity in the procedure of generating the ROC curves and would in general be a less fair approach.
The TPR (completeness) is generally a more relevant measure than the FPR, especially for surveys and for obtaining planet population constraints (Mawet et al. 2014). Therefore it is important to evaluate the TPR as a function of the distance from the star for a S/N threshold of 5, which is equivalent to 5σ under the assumption of nearly Gaussian residuals in the final images. The TPR for both algorithms for the tested annuli and τ = 5 are shown in Fig. 8. The TPR for the LLSG decomposition is higher for each one of the tested annuli compared to PCA. It is especially interesting how at 2λ/D, where the speckle noise is dominant, the TPR for our algorithm reaches 83% instead of the 55% achieved by PCA.
 |
Fig. 8 TPR as a function of the distance from the star for an S/N threshold τ = 5. |
Another great advantage of the LLSG decomposition over more expensive algorithms is that its computational cost is comparable to that of full-frame PCA. For instance, it can process the 612 × 161 × 161 (~15.8 × 106) pixel datacube used in our simulations in about ten seconds (when using only one process), whereas full-frame PCA (equivalent to KLIP or pynpoint implementations) using the LAPACK optimized multithreading library can do it in four seconds. This timing depends, as explained before, on the number of iterations for the three-term decomposition.
It is important to clarify that LLSG is an algorithm for improving detection of faint exoplanets, which decomposes the images, separating the static and quasi-static structures from the moving planets. This process penalizes the signal of the potential companions, and in consequence the final LLSG frames cannot be used for estimating in a robust way the position or flux of those companions. We still need to rely on the injection of negative companion candidates, as we described in a previous section, to calibrate the photometry and astrometry of potential detections, as well as their uncertainties.
In the case of ADI data, the range of rotation (parallactic angles) affects the efficiency of post-processing algorithms when searching for potential companions. With small rotation, the signal of a planet remains more static through the sequence of frames (this effect gets worse in the innermost part of the frames), and a low-rank approximation based algorithm will fail to retrieve it. This effect combines with other factors, such as the number of frames and the PSF decorrelation rate during the sequence, and will limit different post-processing algorithms in different ways. Better understanding of the correlation between these various factors will be useful for choosing algorithms and for designing optimal observing runs.
6. Conclusions
In this paper we have shown, for the first time, how recent subspace projection techniques and robust subspace models proposed in the computer vision literature can be applied to ADI high-contrast image sequences. In particular our implementation of a randomized low rank-approximation recently proposed in the machine learning literature coupled with entry-wise thresholding allowed us to decompose an ADI image sequence locally into low-rank, sparse, and noise components. LLSG brings a detectability boost compared to full-frame PCA approach at all positions of the field of view as can be seen in the ROC curves with averaged TPR and FPR, and in the plot of the TPR as a function of distance. This is especially important because it allows us to access the small inner working angle region (~2λ/D for this dataset), where complex speckle noise prevents PCA from finding faint companions.
One important advantage of this algorithm is that it can process a typical 612 × 161 × 161 pixel cube without sacrificing too much of the computational cost compared to the fast full-frame PCA approach. That the patches can be processed separately leads to real-time processing if coupled with parallelism to exploit modern multicore architectures, making this algorithm suitable for coming survey pipelines.
We have shown the enormous potential of low-rank plus sparse decompositions and, in particular, the LLSG decomposition for high-contrast imaging. More expensive formulations of these decompositions coupled with a fine-tuned model of the noise could lead to even better reference PSF subtraction for exoplanet detection than the one we proposed in the present paper and will be the focus of future work.
Acknowledgments
We would like to thank the anonymous referee for the very useful comments that helped us improve the quality of this paper. The research leading to these results has received funding from the European Research Council Under the European Union’s Seventh Framework Program (ERC Grant Agreement No. 337569) and from the French Community of Belgium through an ARC grant for Concerted Research Action.
References
- Absil, O., Milli, J., Mawet, D., et al. 2013, A&A, 559, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Amara, A., & Quanz, S. P. 2012, MNRAS, 427, 948 [NASA ADS] [CrossRef] [Google Scholar]
- Barrett, H. H., Myers, K. J., Devaney, N., Dainty, J. C., & Caucci, L. 2006, in Advances in Adaptive Optics II, eds. B. L. Ellerbroek, & D. Bonaccini Calia, SPIE Conf. Ser., 6272, 1 [Google Scholar]
- Bouwmans, T., & Zahzah, E.-H. 2014, Computer Vision and Image Understanding, 122, 22 [CrossRef] [Google Scholar]
- Braham, M., Lejeune, A., & Van Droogenbroeck, M. 2014, in Int. Conf. on 3D Imaging (IC3D), Liège, Belgium, 1 [Google Scholar]
- Candès, E. J., Li, X., Ma, Y., & Wright, J. 2009, Arxiv e-prints [arXiv:0912.3599] [Google Scholar]
- Cantalloube, F., Mouillet, D., Mugnier, L. M., et al. 2015, A&A, 582, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eckart, C., & Young, G. 1936, Psychometrika, 1, 211 [CrossRef] [Google Scholar]
- Fitzgerald, M. P., & Graham, J. R. 2006, ApJ, 637, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Hotelling, H. 1933, J. Educational Psychology, 24, 417 [Google Scholar]
- Jee, M. J., Blakeslee, J. P., Sirianni, M., et al. 2007, PASP, 119, 1403 [NASA ADS] [CrossRef] [Google Scholar]
- Lafrenière, D., Marois, C., Doyon, R., Nadeau, D., & Artigau, É. 2007, ApJ, 660, 770 [NASA ADS] [CrossRef] [Google Scholar]
- Lagrange, A.-M., Bonnefoy, M., Chauvin, G., et al. 2010, Science, 329, 57 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Marois, C., Doyon, R., Nadeau, D., Racine, R., & Walker, G. A. H. 2003, in EAS Pub. Ser. 8, eds. C. Aime, & R. Soummer, 233 [Google Scholar]
- Marois, C., Lafrenière, D., Doyon, R., Macintosh, B., & Nadeau, D. 2006, ApJ, 641, 556 [Google Scholar]
- Marois, C., Lafrenière, D., Macintosh, B., & Doyon, R. 2008, ApJ, 673, 647 [NASA ADS] [CrossRef] [Google Scholar]
- Marois, C., Correia, C., Galicher, R., et al. 2014, in SPIE Conf. Ser., 9148 [Google Scholar]
- Mawet, D., Pueyo, L., Lawson, P., et al. 2012, in Space Telescopes and Instrumentation 2012: Optical, Infrared, and Millimeter Wave, eds. M. C. Clampin, G. G. Fazio, H. A. MacEwen, & J. M. Oschmann, SPIE Conf. Ser., 8442, 04 [Google Scholar]
- Mawet, D., Milli, J., Wahhaj, Z., et al. 2014, ApJ, 792, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Mugnier, L. M., Cornia, A., Sauvage, J.-F., et al. 2009, J. Opt. Soc. Am. A, 26, 1326 [NASA ADS] [CrossRef] [Google Scholar]
- Nelder, J. A., & Mead, R. 1965, Comput. J., 7, 308 [CrossRef] [Google Scholar]
- Oliver, N., Rosario, B., & Pentland, A. 2000, IEEE Trans. Pattern Anal. Mach. Intell., 22, 831 [CrossRef] [Google Scholar]
- Quanz, S. P., Amara, A., Meyer, M. R., et al. 2015, ApJ, 807, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Soummer, R., & Aime, C. 2004, in Advancements in Adaptive Optics, eds. D. Bonaccini Calia, B. L. Ellerbroek, & R. Ragazzoni, SPIE Conf. Ser., 5490, 495 [Google Scholar]
- Soummer, R., Pueyo, L., & Larkin, J. 2012, ApJ, 755, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Sparks, W. B., & Ford, H. C. 2002, ApJ, 578, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Wahhaj, Z., Cieza, L. A., Mawet, D., et al. 2015, A&A, 581, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhou, T., & Tao, D. 2011a, ArXiv e-prints [arXiv:1112.5215] [Google Scholar]
- Zhou, T., & Tao, D. 2011b, in Proc. 28th International Conference on Machine Learning (ICML-11), eds. L. Getoor, & T. Scheffer, ICML ’11 (New York: ACM), 33 [Google Scholar]
- Zhou, T., & Tao, D. 2013, ArXiv e-prints [arXiv:1309.0302] [Google Scholar]
- Zhou, X., Yang, C., Zhao, H., & Yu, W. 2014, ACM Comput. Surv., 47, 36 [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 LLSG decomposition of ADI data (left) into low-rank (middle left) plus sparse (middle right) plus Gaussian noise (right) terms. In the ideal case, this decomposition separates the reference PSF and quasi-static speckle field from the signal of the moving planets, which stays in the sparse component. |
| In the text | |
 |
Fig. 2 Quadrants of annuli used for partitioning the images. |
| In the text | |
 |
Fig. 3 Final result of post-processing with PCA (left) and the three terms of the LLSG decomposition (middle and right) for β Pic NACO data. 38 PCs were used to maximize the S/N for β Pic b in the full-frame PCA approach. For the LLSG decomposition a rank of 10 gave a significant improvement on b’s S/N (see Fig. 4). All the frames were normalized to the maximum value of the LLSG sparse frame (middle panel). |
| In the text | |
 |
Fig. 4 S/N maps for PCA (left) and LLSG (right) computed from the final frames shown in Fig. 3 (left and middle panels). Planet β Pic b has roughly three times higher S/N when processed with our LLSG decomposition. |
| In the text | |
 |
Fig. 5 Final result of post-processing with PCA (left), annular PCA (middle), and our LLSG decomposition (right). The images were normalized to their own maximum value. Four synthetic companions a(285°), b(185°), c(5°), and d(85°) were injected at 2, 5, 8, and 13 λ/D from the center, respectively. The injected PSFs were scaled at 0.5, 5, 5, and 7 times the noise of the respective annulus. We used 13 PCs when applying full-frame PCA and 25 PCs for the annular PCA (applying the same number of PCs in every annulus) in order to maximize the S/N of the innermost fake companion in each case. |
| In the text | |
 |
Fig. 6 S/N maps for full-frame PCA (left), annular PCA (middle), and our LLSG decomposition (right) showing the values of each fake companion S/N. With our algorithm the four injected companions are clearly revealed. The S/N of the fake companion at 2λ/D is clearly at the level of the noise (false negative) in the case of full-frame PCA and its annular version. With LLSG we reach a peak S/N that is three times higher. For the rest of synthetic companions, the S/N obtained with LLSG is up to three times higher than the one obtained with full-frame PCA. |
| In the text | |
 |
Fig. 7 ROC curves for our LLSG decomposition and full-frame PCA. The S/N thresholds τ are shown for integer values. Our algorithm ROC curve is close to the oracle (perfect classifier) in the upper left corner. |
| In the text | |
 |
Fig. 8 TPR as a function of the distance from the star for an S/N threshold τ = 5. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


