| Issue |
A&A
Volume 589, May 2016
|
|
|---|---|---|
| Article Number | A103 | |
| Number of page(s) | 7 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201425408 | |
| Published online | 20 April 2016 | |
Magnetic activity cycles in solar-like stars: The cross-correlation technique of p-mode frequency shifts
1 Instituto de Astrofísica de Canarias, 38205 La Laguna, Tenerife, Spain
e-mail: crr@iac.es
2 Universidad de La Laguna, Dpto de Astrofísica, 38206 La Laguna, Tenerife, Spain
3 Laboratoire AIM Paris-Saclay, CEA/DRF-CNRS-Université Paris Diderot, IRFU/SAp, Centre de Saclay, 91191 Gif-sur-Yvette Cedex, France
4 CNRS, Institut de Recherche en Astrophysique et Planétologie, 14 avenue Édouard Belin, 31400 Toulouse, France
5 Université de Toulouse, UPS-OMP, IRAP, 31400 Toulouse, France
Received: 26 November 2014
Accepted: 15 March 2016
Aims. We set out to study the use of cross-correlation techniques to infer the frequency shifts that are induced by changing magnetic fields in p-mode frequencies and to provide a precise estimation of error bars.
Methods. This technique and the calculation of the associated errors is first tested and validated on the Sun where p-mode magnetic behaviour is very well known. These validation tests are performed on 6000-day time series of Sun-as-a-star observations delivered by the SoHO spacecraft. Errors of the frequency shifts are quantified through Monte Carlo simulations. The same methodology is then applied to three solar-like oscillating stars: HD 49933, observed by CoRoT, as well as KIC 3733735 and KIC 7940546, observed by Kepler.
Results. We first demonstrate the reliability of the error bars computed with the Monte Carlo simulations using the Sun. From the three stars analyzed, we confirm the presence of a magnetic activity cycle in HD 49933 with this methodology and we unveil the seismic signature of ongoing magnetic variations in KIC 3733735. Finally, the third star, KIC 7940546, seems to be in a quiet regime.
Key words: asteroseismology / stars: activity / stars: solar-type / stars: oscillations
© ESO, 2016
1. Introduction
The ultra-high precision photometric time series obtained with satellites such as CoRoT (Convection Rotation and planetary Transits, Baglin et al. 2006) and Kepler (Borucki et al. 2010) has opened a new window on the study of magnetic activity cycles in solar-like pulsating stars (e.g. Mathur et al. 2013b, 2014a,b). The active regions crossing the visible surface of a star produce a modulation in the observed light curve that provides information about the rotation rate and stellar magnetic activity (e.g. García et al. 2014). Moreover, it is even possible to detect magnetic frequency shifts of the acoustic modes along the activity cycle (García et al. 2010) as is commonly done for the Sun (e.g. Woodard & Noyes 1985; Anguera Gubau et al. 1992; Chaplin et al. 2001).
To study the temporal evolution of p-mode frequency shifts, it is necessary to extract reliable p-mode frequencies of individual modes during short periods of time, typically 30 to 60 days. This can be a big challenge in asteroseismology, especially when changes of about a few μHz are expected and the signal-to-noise ratio (S/N) can be small. An alternative method consists of computing average frequency shifts by using cross-correlation techniques. This method was first successfully used in the Sun with single site observations (e.g. Pallé et al. 1989). With the arrival of long time series of hundreds of solar-like stars from space missions, the cross-correlation method may help us again in the study of magnetic activity cycles. Thanks to this technique, obtaining frequencies of individual p-modes in short time series, which requires high S/N, is not needed. Instead, the cross-correlation of the full (or part) p-mode power excess (the frequency range in which the power of the modes is found) of each subseries and a reference spectrum can be computed, which provides the average shift of the acoustic modes during the analyzed time span.
A problem in the use of the cross-correlation methods could be the way in which the individual uncertainties are computed. In previous works in which this technique has been used, these uncertainties were obtained as the statistical error of the fit of a Gaussian function to the cross-correlation profile (e.g. Pallé et al. 1989; García et al. 2010; Mathur et al. 2013b). This fit is the way to determine the average frequency shift between two different periods of time. These errors underestimate total errors since systematic and model errors are neglected. To better quantify the errors, in the present work we propose using a Monte Carlo simulation. We analyze the limit of the methodology using 6000 days of solar data obtained with the blue channel of the solar photometer of VIRGO instrument (Fröhlich et al. 1995) onboard the SoHO spacecraft (Domingo et al. 1995).
This method is applied to three solar-like stars: one from CoRoT, HD 49933, and two from Kepler, KIC 3733735 and KIC 7940546. It is well known that the first two stars have ongoing magnetic cycles (García et al. 2010; Mathur et al. 2014a), while the third star, KIC 7940546, does not show any significant variation in the light curve, which could be a consequence of a low inclination angle or because the star is in a quiet magnetic state.
The structure of the paper is as follows. In Sect. 2 we explain the methodology used. In Sect. 3, the method is validated using 6000-day timed series of Sun-as-a-star observation. In Sect. 4, three solar-like stars, one from CoRoT and two from the Kepler satellite are analyzed. The last section is devoted to a discussion and conclusions.
2. Method
We use the cross-correlation technique to measure p-mode frequency shifts. For this method, we first divide the whole light curve of the analyzed stars into shorter subseries that can overlap, or not. The size of each chunk depends on the overall length of the observations, the quality of the data, and the length of the activity cycle we want to investigate. According to these restrictions, we used series between 30 and 180 days for the three analyzed solar-like stars. For the Sun, we use longer subseries – up to a year – because we have more than 16 yr of observations and because the solar magnetic cycle is long (eleven years on average from maximum to maximum). The power spectrum of each subseries is computed.
Next, each power spectrum is cross-correlated with a reference spectrum defined as the average of all the individual spectra. The profile of the cross-correlation function almost has a Gaussian shape. Therefore, a Gaussian function is fitted to each cross-correlation function. The position of the maximum is considered as the average shift of the p-mode frequencies that are present in the range of the spectrum used in the analysis.
To obtain the error bars of the cross-correlation analysis we follow the following steps:
-
1 –
At high frequencies, well above the p-mode region, where the spectrum is dominated by the photon noise, the standard deviation of this noise is obtained for both spectra, one being the reference one and the other the target.
-
2 –
The absolute difference between the standard deviations of the target spectrum and the reference one is added to the latter to have both spectrum with the same noise level.
-
3 –
The reference spectrum with the new level of white noise is shifted by the computed shift (if any).
-
4 –
We produce 100 simulated power spectra by multiplying the reference shifted spectrum by a random noise distribution following a χ2 with 2 degrees of freedom.
-
5 –
Each of these simulated spectra is cross-correlated with its original reference to obtain a new frequency shift.
-
6 –
The standard deviation of all the obtained displacements of the simulated spectra, with respect to the real one, is considered the error of the measure.
We verified that the results are unbiased by comparing the mean extracted values to the expected one. We have also verified that using an averaged spectrum as a reference spectrum does not introduce significant biases. Moreover, we checked that a higher number of simulated realizations (e.g. 500 or 1000) does not change the final result. Therefore, we decided to use 100 realizations to reduce the computation time.
3. Validation: application to the Sun
To study the behaviour and the limits of the cross-correlation analysis as well as the error estimation, we use the Sun as a reference. Time series of 6000 days cadenced at 60 s – from April 11 1996 to September 14 2012 – are used in this analysis, which almost covers one and half solar magnetic cycles. Solar observations were obtained by the blue channel of the Sun photometers of the VIRGO instrument, onboard the SoHO spacecraft. With these observations we study the behaviour of the method attending the range of p-mode frequencies used, the length of the subseries, the influence of a pre-smooth of the spectra, the S/N, and the width of the modes. To do so, we divided the time series into independent subseries (without any overlap) of 30, 60, 90, 120, 180, 240, 300, and 365 days. An example of the resultant frequency shifts, using 60 and 365 days subseries, is shown in Fig. 1.
 |
Fig. 1 Frequency shifts along the solar cycle, using subseries of 60 (open triangles) and 365 days (full circles). The error bars were obtained using Monte Carlo simulations following the methodology described in this work. Starting on April 11 1996. |
As a first step, we checked that the computation of the errors is unbiased by calculating a histogram of the difference between the expected shift (νexp) and the measured shifts (νmed) in the Monte Carlo simulations. This was done for series of 365 days and the results are shown in Fig. 2 for 100, 500, and 1000 realizations. As expected from an unbiased computation, the histograms are well fitted by a Gaussian profile that is centred in zero. In our case, the small deviation from zero that the Gaussian profiles show is 0.003 μHz, inside the dispersion of 0.005 μHz that was obtained from the errors associated with the frequency shifts, which were calculated from the series of 365 days.
To verify that using an averaged spectrum as a reference spectrum is not introducing significant biases, we create a synthetic limit spectrum that mimes the solar spectra observed by VIRGO within the range 2000–4000 μHz. This includes a background and modes of degree l = 0 to 3. We consider two spectral resolutions that correspond to 60-day- and 365-day-long observations. For each resolution, we generate 100 synthetic observations by multiplying the limit spectrum by a random noise distribution following a χ2 with 2 degrees of freedom. Then, we consider sequences of 100, 50, 20, 10, 5, or even 2 independent observations. Each sequence is analyzed with the previously described technique (measurement of the shift – expected to be zero – and of the error bar). We compare the results obtained by directly using the limit spectrum as a reference instead of an average spectrum. We did not see any significant difference. Only when the number of spectra in the sequence is small (2 or 5) do we see two marginal effects: a slight bias of the determined shift towards zero and a slight increase of the estimated error bars. However, these effects are weak compared to the errors themselves.
 |
Fig. 2 Histogram with fitted Gaussian profiles of the differences between the expected and the measured shifts in the Monte Carlo simulation for 100, 500 and 1000 realizations. Series of 365 days are used. |
After that, we start to analyze the behaviour of the computed errors that depend on the length of the subseries, following the method explained in the previous section. In Fig. 3, we show the average errors and their dispersions (σerror) as a function of the length of the subseries. The frequency shifts were computed using a range of ±600 μHz centered at 3000 μHz and without smoothing the spectra. The errors decrease with the increase of the length of subseries T. It varies as T− 0.65 ± 0.14, which is almost compatible with a squared-root decay.
 |
Fig. 3 Mean errors and associated dispersions (σerror) of the frequency shifts as a function of the length of the subseries. |
We use this range of ±600 μHz because it is a good compromise between the size and dispersion of the obtained errors, as can be seen in Fig. 4. Indeed, different ranges of p-modes centred at 3000 μHz: ±200, 400, 600, 800, 1000, and 1200 μHz were compared. Two sets of results were plotted. Triangles correspond to the results obtained when white noise is added to the time series to reproduce noisy data with a S/N that is three times lower than the original (S/N = 1.1). The S/N is estimated as the mean value of the ratio between the mode amplitude in the power spectra and the fitted background in the analyzed range. Circles correspond to the original signal (S/N = 3.3). Although the results are quite similar, smaller errors were obtained when a range of ±600 μHz around the central frequency of 3000 μHz is used.
 |
Fig. 4 Average errors and associated dispersions of the frequency shifts using series of 365 days and different ranges of p-modes. Triangles correspond to time series with an S/N = 1.1, while circles correspond to the nominal VIRGO/SPM observations (S/N = 3.3). In this later case the average errors were multiplied by 7 to adjust the scale. |
The next step is to analyze the behaviour of the errors when the spectra are smoothed before computing the cross correlation. In Fig. 5, we plot the mean errors and their dispersions for series of 365 and 180 days using ±600 μHz centred in 3000 μHz, but with different levels of smoothness. The number of points used for the smoothing are: 65, 125, 191, 251, and 315, corresponding approximately with a length of: 2, 4, 6, 8, and 10 μHz. Smaller errors and dispersions are obtained when smoothing factors of 65 or 125 points are applied, corresponding to smoothing windows of 2 or 4 μHz, which depends on the amount of noise of the time series. Once again, triangles correspond to noisy data (S/N = 1.1) and circles to the original time series (S/N = 3.3). The series of 365 days are plotted in black and the series of 180 days in pink. We emphasize that increased smoothing degrades the results, probably because it smears out the spectra too much, thus attenuating the effect of searched shifts.
 |
Fig. 5 Average errors and dispersions of the frequency shifts as a function of the smooth factor of the power spectrum for series of 365 days (black) and 180 days (pink) using a range of ±600 μHz centred at 3000 μHz. Same symbol code as in Fig. 4 for circles and triangles. The results from the original series (without noise added) have been connected by dashed lines. |
To study the behaviour of the cross-correlation technique with different levels of noise and different p-mode widths, the mean spectrum of 365 days has been fitted to obtain the width of the individual p-modes and the S/N of the spectrum. The fit was done in a global way using a maximum likelihood estimator (e.g. Appourchaux et al. 2008), where the same width is used for each group of one l = 0, 1, and 2 modes. The so-called noise background (e.g. Mathur et al. 2011) was modelled with three components: a flat white noise component dominating the high-frequency part of the spectrum, a power law at low frequency, and one Harvey component (Harvey 1985) to take into account the granulation contribution. This noisy background is fitted first and then fixed when the p-modes are fitted as is usually done in asteroseismology (e.g. Appourchaux et al. 2012; Mathur et al. 2013a). The errors in the fitted parameters were obtained from the Hessian matrix.
The resulting mode widths as a function of frequency are shown in Fig. 6. The spectrum has p-modes with widths less than 1 μHz below 3000 μHz and wider than 2 μHz above 3300 μHz.
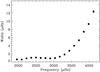 |
Fig. 6 Solar p-mode widths as a function of frequency. |
Obtained frequency shifts for two different computed regions and smoothing factors (no smooth, s0, and a smooth window of 65 points, s65).
We computed the cross-correlation for the spectra of 365 days in two different ranges, from 2100 to 2900 μHz and from 3300 to 4100 μHz without smoothing and with a smoothing of 2 μHz (65 points). In these two ranges the mean S/N is 2.0 for the first range and 2.9 for the second.
As is well known (e.g. Salabert et al. 2004), the frequency shift is higher for the Sun at high frequencies. At the same time, the S/N is better at high frequencies. However, when the mean values of the errors are obtained for both ranges, see Table 1, the errors are ~60% higher at high frequencies. This can only be attributed to the higher width of the modes at high frequencies because the height of the modes are similar in both regions. In the range where the width of the p-modes increase, we analyzed the errors obtained in the computation of the frequency shifts for series of 365 days with no smoothing and centred at 3200, 3500 and 3800 μHz in a range of ±300 μHz. The result is shown in Fig. 7. The errors increase with the mode width Γ as Γ0.7 ± 0.1. We expect that the variation goes as Γ0.5, following a similar argument to Libbrecht (1992). Nevertheless, we need to be cautious for two reasons. First, we must keep in mind that we only get three points, which is a small number to derive a fine quantitative law. Second, the squared-root dependency is only a lower limit of the errors.
 |
Fig. 7 Errors in the frequency shifts and associated dispersions as a function of the p-mode widths for series of 365 days with no smoothing. and centred at 3200, 3500, and 3800 μHz in a range of ±300 μHz. |
To study the influence of S/N on the cross-correlation analysis, we have added different levels of normal white noise to the origianl VIRGO/SPM time series of 6000 days. The cross-correlation was computed as being between 2400 and 3600 μHz and no smoothing was applied. Results are shown in Fig. 8. The errors drop drastically with the increase of S/N until reaching S/N = 2. For higher S/N, the reduction is very small.
 |
Fig. 8 Average frequency shift errors against the S/N. The range used for the calculation is from 2400 to 3600 μHz and no smoothing has been applied. Circles correspond to series of 365 days and triangles to series of 180 days. |
4. Application to solar-like stars
4.1. The CoRoT target HD 49933
HD 49933 is an F5 main-sequence star observed twice by CoRoT, with a first run of 60 days in 2007 and a second of 137 days in 2008. The light curves were obtained with a cadence of 32 s. This star is hotter than the Sun, with an effective temperature of around 6700 K, an estimated mass of 1.3 solar mass, and an estimated radius of 1.34 solar radius. This star has been widely analyzed (e.g. Appourchaux et al. 2008; Benomar et al. 2009; Kallinger et al. 2010), and it was also the first star, apart from the Sun, where asteroseismic measurements of global changes in the frequencies of their acoustic modes were reported (García et al. 2010; Salabert et al. 2011), confirming the development of an ongoing stellar magnetic activity cycle.
In this work, we use the series of 137 days long to analyze the behaviour of the errors of the cross-correlation signal using Monte Carlo simulations. In particular, we have used series of 30 and 60 days shifted every 15 days. The reference spectrum is the average spectrum obtained from independent series, i.e. four spectra are used in the case of 30-day long subseries, while only two subseries are averaged when the length of the subseries is 60 days. The power spectrum of each subseries is centred at νmax = 1850 μHz (the frequency of maximum power), and we study different frequency ranges, as well as smoothing factors. The number of points used to smooth the spectrum are 11, 21, and 41, corresponding to smoothing windows of 2, 4, and 8 μHz in the case of the subseries of 60 days. We note that the smaller errors are obtained with the 11-point smoothing factor.
A summary of the results obtained for the different ranges using subseries of 60 days’ length with an 11-point smoothing factor is shown in Table 2. Using the range of ±400 μHz around νmax, we obtain the smallest errors in the computed frequency shifts.
 |
Fig. 9 Frequency shifts obtained for HD 49933 computed with subseries of 30 days (triangles) and 60 days (circles) shifted every 15 days. The region used is centred at νmax = 1850 μHz with a range of ±400 μHz and a smoothing factor of 11 points. |
Average errors obtained in the analysis of the 60-day subseries covering different frequency ranges for HD 49933.
The temporal evolution of the frequency shifts of HD 49933 is shown in Fig. 9 for series of 30 and 60 days centred in νmax = 1850 μHz with a range of ±400 μHz and a smoothing factor of 11 points. These results are well in agreement with those obtained by García et al. (2010).
For this star, the width of the p-modes is between 3 and 11 μHz (Benomar et al. 2009). In the range of ±400 μHz around νmax, the average p-mode width is 6.3 μHz, and the S/N for the 60-day average spectrum is 2.1, see Table 3.
As we expected from the width of the acoustic modes and the level of noise, the computed errors are quite big. The use of 60-day subseries produces smaller errors. However, when longer subseries are used, the resultant maximum frequency shift is reduced owing to the short period of magnetic activity cycle of the star and the short amount of data available (137 days). Indeed the maximum frequency shifts are 1.12 ± 0.32 μHz and 0.43 ± 0.21 μHz, respectively, for the calculation using 30- and 60-day subseries.
S/N and mean width in the analyzed range, for all the analyzed stars.
4.2. The Kepler targets KIC 3733735 and KIC 7940546
KIC 3733735 is also an F5 main-sequence star, observed by Kepler in short cadence (58.85 s, Gilliland et al. 2010; García et al. 2011) along 1114 days. A seismic study was performed by Appourchaux et al. (2012), and its magnetic activity was analyzed by Mathur et al. (2014a), where a cycle-like behaviour was detected from the study of the temporal evolution of the light curve. KIC 3733735 has a Teff around 6700 K, a radius of 1.66 solar radius, and a mass of 1.95 solar masses (Mathur et al. 2012). The acoustic modes of this star are wider than the modes of the previous analyzed CoRoT star, from 4 to 14 μHz (Appourchaux et al. 2014). Thus, the mean linewidth is 8.9 μHz in the range 1650−2250 μHz.
In Fig. 10, we show the computed frequency shifts using subseries of 180 days shifted every 60 days. Each spectrum is centred in νmax = 1950 μHz, with a range of ±300 μHz and smoothed by 31 points, corresponding to a smoothing window of 2 μHz (black curve). The reference spectrum is the mean of the independent spectra. This combination of parameters produces the smallest errors. The S/N of the mean 180-day spectrum in the selected range of p-modes is 1.7.
As the level of noise and the width of the modes is something that we cannot change in the observations, we can only check the effects of changing the length of the subseries, the p-mode range, and the smoothing factor. Similar to the solar case, the length of the series is the dominant factor, producing a bigger change in the computed errors.
For this star, and using the optimal configuration of a range of ±300 μHz and a smoothing of 31 points, series of 30, 60, 90, and 180 days have been computed and the obtained mean errors from the cross-correlation with their associated dispersions are shown in Table 4. The errors decrease with the length of the subseries, which is similar to the solar case.
In Fig. 10, superimposed on the computed frequency shift, is the time evolution of the photospheric activity proxy (Sph, Mathur et al. 2014b) obtained from the long cadence Kepler data shown in the bottom panel of Fig. 1 by Mathur et al. (2014a). We have integrated these values to the same 180 days as in the frequency shifts (pink triangles) for the independent series, that are shown as black full circles in the frequency shift plot. The error bars of these points correspond to the dispersion of Sph in each 180-d segment. Comparing both proxies of the activity, we see that they are compatible inside the error bars, but we observe a lag of about 120 days between the two. Several authors (e.g. Jain et al. 2009; Salabert et al. 2009, 2015) have already discussed the possibility that there could be a time lag between the manifestation of the magnetism in the photosphere and the perturbation in the frequency of the acoustic modes.
 |
Fig. 10 Frequency shifts of KIC 3733735 calculated using 180-day subseries shifted every 60 days.The points obtained from independent spectra are shown as full black circles. The power spectrum is centred at a νmax = 1950 μHz with a range of ±300 μHz and a smoothing of 31 points. The mean spectra used as the reference for the cross-correlation are generated with independent spectra. The pink curve is the Sph computed by Mathur et al. (2014a). The pink triangles are the integration of the Sph to the same 180-d ranges as the frequency shifts. |
Mean errors of the frequency shifts of KIC 3733735 and associated errors for series of 30, 60, 90, and 180 days.
KIC 7940546 is the second Kepler star that we have analyzed. It is also an F main-sequence star with a Teff around 6350 K, a radius of 1.95 solar radius, and a mass of 1.41 solar mass. Its surface magnetic activity was also studied by Mathur et al. (2014a), and it was one of the less active stars in their sample.
KIC 7940546 was observed in short cadence along 928 days. Spectra from series of 30, 60, 90, and 180 days were produced to obtain the frequency shifts in a range of ±400 μHz around νmax = 1080 μHz. In Table 5, the average errors in the frequency shifts and their dispersions obtained from the different subseries’ lengths are shown. We note that the mean errors are very small compared with those obtained for KIC 3733735 (see Table 4) and they are comparable with the solar ones, (see Fig. 3).
 |
Fig. 11 Frequency shifts of KIC 7940546 calculated using independent 60-day subseries centred in νmax = 1080 μHz and with a range of ±400 μHz (triangles), and using 180-day subseries shifted 60 days (circles). The reference spectra is the average of the independent subseries. In both cases the spectra have not been smoothed. |
Mean errors for KIC7940546 frequency-shift with their dispersion (σ) for series of 30, 60, 90, and 180 days.
The seismic study of this star has not yet been performed. Therefore, we did a similar global analysis to the one described for the Sun. We found a mean width of the p-modes of 3.5 μHz and a very good S/N of 3.0. From these values, we thus expect small errors.
In Fig. 11, we plot the obtained frequency shifts for the independent subseries of 60 days and for the subseries of 180 days shifted every 60 days. As for the previous stars, the reference spectrum for the calculation of the cross-correlation is the mean spectrum obtained from independent subseries of data. As we expect from the magnetic analysis performed by Mathur et al. (2014a), this star does not show any frequency shifts during the whole observation time.
5. Discussion and conclusion
The cross-correlation technique is a simple, fast, and non-demanding method to implement to unveil the possible existence of ongoing stellar magnetic activity cycles. This is particularly interesting when studying hundreds to thousands stars with the present and future space instruments, because we can avoid the process of fitting the individual p-modes of a huge number of stars, and this for every subseries.
As the significance of the solution depends on calculated errors, in the present paper we derive a method to properly compute the errors of the frequency shifts using Monte Carlo simulations. We have first tested the methodology using the Sun and then with three well-known solar-like stars that were observed with CoRoT and Kepler.
We have found that the errors fall following a power law with the length of the series and with the S/N, while they increase with the width of the p-modes.
Related to the length of the subseries used, these are limited by two factors: the length of the data and the length of the activity cycle. In several cases, a small level of smoothing in the power spectrum seems to help reduce the final errors of the frequency shifts.
In the case of the Sun, where we can use subseries that are as long as one year with high S/N, we have managed to obtain errors as small as 0.02 μHz in a signal with a global change of 0.45 μHz. That is an error of ~4% of the signal.
In the case of HD 49933, the maximum length we managed to use was 60 days because the length of the observations was 137 days. For this star, we obtain errors of 48% of the global shift. These high errors are principally related with the short lengths of the used series.
In the case of KIC 3733735, the maximum length of the used series was 180 days because the change in activity was no longer than 250 days from maximum to minimum. The obtained errors for this star were around 45% of the signal. These large errors are due to the low S/N and the large widths of the p-modes.
For comparison, we have also analyzed a star, KIC 7940546, which does not show any surface magnetic activity cycle during the observing time. Moreover, this star does not have very broad p-modes and has a very good S/N around νmax. Thus, the obtained errors were small. The computed frequency shifts are zero inside 1σ of the errors, which are as small as we expected from the characteristics of the spectra.
Even with the error levels obtained, the difference in the results between the active and the quiet star are clear enough to justify the use of the cross-correlation technique as a fast way to analyze the mean frequency shifts of the huge number of solar-like stars that we have today and in the near future.
Acknowledgments
The authors wish to thank the entire Kepler team, without whom these results would not be possible. Funding for this Discovery mission is provided by NASA’s Science Mission Directorate. SoHO is a mission of international cooperation between ESA and NASA.This research was supported in part by the Spanish National Research Plan under projects AYA2010-17803 and AYA2012-39346-C02-02 of the Spanish Secretary of State for R&D&i (MINECO). R.A.G. received funding from the CNES GOLF and CoRoT grants at CEA and the ANR (Agence Nationale de la Recherche, France) program IDEE (No. ANR-12-BS05-0008) Interaction Des Étoiles et des Exoplanètes. J.B. acknowledges support from CNES. This research has also received funding from the European Community’s Seventh Framework Programme [FP7/2007−2013] under grant agreement No. 312844 (SPACEINN).
References
- Anguera Gubau, M., Palle, P. L., Perez Hernandez, F., Regulo, C., & Roca Cortes, T. 1992, A&A, 255, 363 [NASA ADS] [Google Scholar]
- Appourchaux, T., Michel, E., Auvergne, M., et al. 2008, A&A, 488, 705 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Appourchaux, T., Chaplin, W. J., García, R. A., et al. 2012, A&A, 543, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Appourchaux, T., Antia, H. M., Benomar, O., et al. 2014, A&A, 566, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baglin, A., Auvergne, M., Boisnard, L., et al. 2006, in COSPAR, Plenary Meeting, 36th COSPAR Scientific Assembly, 36, 3749 [Google Scholar]
- Benomar, O., Baudin, F., Campante, T. L., et al. 2009, A&A, 507, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Chaplin, W. J., Elsworth, Y., Isaak, G. R., et al. 2001, MNRAS, 322, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Domingo, V., Fleck, B., & Poland, A. I. 1995, Sol. Phys., 162, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Fröhlich, C., Romero, J., Roth, H., et al. 1995, Sol. Phys., 162, 101 [NASA ADS] [CrossRef] [Google Scholar]
- García, R. A., Mathur, S., Salabert, D., et al. 2010, Science, 329, 1032 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- García, R. A., Hekker, S., Stello, D., et al. 2011, MNRAS, 414, L6 [NASA ADS] [CrossRef] [Google Scholar]
- García, R. A., Ceillier, T., Salabert, D., et al. 2014, A&A, 572, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gilliland, R. L., Jenkins, J. M., Borucki, W. J., et al. 2010, ApJ, 713, L160 [NASA ADS] [CrossRef] [Google Scholar]
- Harvey, J. W. 1985, in Probing the depths of a star: the study of solar oscillations, eds. R. W. Noyes, & E. J. Rhodes, JPL, 400, 327 [Google Scholar]
- Jain, K., Tripathy, S. C., & Hill, F. 2009, ApJ, 695, 1567 [NASA ADS] [CrossRef] [Google Scholar]
- Kallinger, T., Gruberbauer, M., Guenther, D. B., Fossati, L., & Weiss, W. W. 2010, A&A, 510, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Libbrecht, K. G. 1992, ApJ, 387, 712 [NASA ADS] [CrossRef] [Google Scholar]
- Mathur, S., Hekker, S., Trampedach, R., et al. 2011, ApJ, 741, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Mathur, S., Metcalfe, T. S., Woitaszek, M., et al. 2012, ApJ, 749, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Mathur, S., Bruntt, H., Catala, C., et al. 2013a, A&A, 549, A12 [CrossRef] [EDP Sciences] [Google Scholar]
- Mathur, S., García, R. A., Morgenthaler, A., et al. 2013b, A&A, 550, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathur, S., García, R. A., Ballot, J., et al. 2014a, A&A, 562, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathur, S., Salabert, D., García, R. A., & Ceillier, T. 2014b, J. Space Weather Space Clim., 4, A15 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Pallé, P. L., Régulo, C., & Roca Cortés, T. 1989, A&A, 224, 253 [NASA ADS] [Google Scholar]
- Salabert, D., Fossat, E., Gelly, B., et al. 2004, A&A, 413, 1135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salabert, D., García, R. A., Pallé, P. L., & Jiménez-Reyes, S. J. 2009, A&A, 504, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salabert, D., Régulo, C., Ballot, J., García, R. A., & Mathur, S. 2011, A&A, 530, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salabert, D., García, R. A., & Turck-Chièze, S. 2015, A&A, 578, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woodard, M. F., & Noyes, R. W. 1985, Nature, 318, 449 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Obtained frequency shifts for two different computed regions and smoothing factors (no smooth, s0, and a smooth window of 65 points, s65).
Average errors obtained in the analysis of the 60-day subseries covering different frequency ranges for HD 49933.
Mean errors of the frequency shifts of KIC 3733735 and associated errors for series of 30, 60, 90, and 180 days.
Mean errors for KIC7940546 frequency-shift with their dispersion (σ) for series of 30, 60, 90, and 180 days.
All Figures
 |
Fig. 1 Frequency shifts along the solar cycle, using subseries of 60 (open triangles) and 365 days (full circles). The error bars were obtained using Monte Carlo simulations following the methodology described in this work. Starting on April 11 1996. |
| In the text | |
 |
Fig. 2 Histogram with fitted Gaussian profiles of the differences between the expected and the measured shifts in the Monte Carlo simulation for 100, 500 and 1000 realizations. Series of 365 days are used. |
| In the text | |
 |
Fig. 3 Mean errors and associated dispersions (σerror) of the frequency shifts as a function of the length of the subseries. |
| In the text | |
 |
Fig. 4 Average errors and associated dispersions of the frequency shifts using series of 365 days and different ranges of p-modes. Triangles correspond to time series with an S/N = 1.1, while circles correspond to the nominal VIRGO/SPM observations (S/N = 3.3). In this later case the average errors were multiplied by 7 to adjust the scale. |
| In the text | |
 |
Fig. 5 Average errors and dispersions of the frequency shifts as a function of the smooth factor of the power spectrum for series of 365 days (black) and 180 days (pink) using a range of ±600 μHz centred at 3000 μHz. Same symbol code as in Fig. 4 for circles and triangles. The results from the original series (without noise added) have been connected by dashed lines. |
| In the text | |
 |
Fig. 6 Solar p-mode widths as a function of frequency. |
| In the text | |
 |
Fig. 7 Errors in the frequency shifts and associated dispersions as a function of the p-mode widths for series of 365 days with no smoothing. and centred at 3200, 3500, and 3800 μHz in a range of ±300 μHz. |
| In the text | |
 |
Fig. 8 Average frequency shift errors against the S/N. The range used for the calculation is from 2400 to 3600 μHz and no smoothing has been applied. Circles correspond to series of 365 days and triangles to series of 180 days. |
| In the text | |
 |
Fig. 9 Frequency shifts obtained for HD 49933 computed with subseries of 30 days (triangles) and 60 days (circles) shifted every 15 days. The region used is centred at νmax = 1850 μHz with a range of ±400 μHz and a smoothing factor of 11 points. |
| In the text | |
 |
Fig. 10 Frequency shifts of KIC 3733735 calculated using 180-day subseries shifted every 60 days.The points obtained from independent spectra are shown as full black circles. The power spectrum is centred at a νmax = 1950 μHz with a range of ±300 μHz and a smoothing of 31 points. The mean spectra used as the reference for the cross-correlation are generated with independent spectra. The pink curve is the Sph computed by Mathur et al. (2014a). The pink triangles are the integration of the Sph to the same 180-d ranges as the frequency shifts. |
| In the text | |
 |
Fig. 11 Frequency shifts of KIC 7940546 calculated using independent 60-day subseries centred in νmax = 1080 μHz and with a range of ±400 μHz (triangles), and using 180-day subseries shifted 60 days (circles). The reference spectra is the average of the independent subseries. In both cases the spectra have not been smoothed. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


