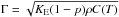| Issue |
A&A
Volume 588, April 2016
|
|
|---|---|---|
| Article Number | A133 | |
| Number of page(s) | 14 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201527625 | |
| Published online | 30 March 2016 | |
Low thermal inertias of icy planetary surfaces
Evidence for amorphous ice?
Laboratoire AIM Paris-Saclay, UMR 7158, Université Paris-Diderot CEA/Irfu CNRS/INSU, 91191 Gif-sur-Yvette, France
e-mail: cferrari@cea.fr
Received: 23 October 2015
Accepted: 1 February 2016
Context. Thermal inertias of atmosphereless icy planetary bodies happen to be very low.
Aims. We relate the thermal inertia to the regolith properties such as porosity, grain size, ice form and heat transfer processes to understand why it is low. We interpret the dichotomy in thermal inertia of the surface of Mimas in terms of changes in regolith properties. We predict how the thermal inertia of these bodies may vary with heliocentric distance depending on these properties.
Methods. We combine available models of conductivity by contact or radiation to understand what heat transfer process is predominant.
Results. The magnitude of the thermal inertia of a porous icy regolith is mainly governed by the crystalline or amorphous ice forms, and the quality of contacts between grains. Beyond the orbit of Jupiter, thermal inertias as low as a few tens J/m2/ K/s1/2 are difficult to reproduce with plausible porosity and grains sizes made of crystalline ice unless contacts are loose. This is, on the contrary, straightforward for regoliths of sub-cm-sized grains made of amorphous water ice. This study points out the importance of including the temperature dependence of thermophysical properties of water ice forms and the radiative conduction in thermal models of these bodies. The relatively high thermal inertia of the leading face of Mimas can be explained by a regolith of crystalline ice grains in tight contacts, which are eventually sintered by the bombardment of high energy electrons. The low thermal inertia of its trailing face is easily reproduced by a regolith of moderate porosity with sub-mm-sized grains of amorphous ice. The characteristic decrease of thermal inertia with heliocentric distance of icy atmosphereless surfaces and the very low thermal inertia of relevant trans-Neptunian objects are easily explained if amorphous ice is present at cm depths below a thin layer of crystalline ice.
Key words: radiative transfer / planets and satellites: surfaces / infrared: planetary systems / planets and satellites: individual: Mimas
© ESO, 2016
1. Introduction
For the past 30 years, infrared astronomy has been developing intensively and dedicated spectrometers systematically bolted on space observatories around the Earth and on board spacecraft to explore the solar system. Many surfaces of atmosphereless bodies have thence been observed from Mercury to Neptune, icy satellites of Jupiter and Saturn, asteroids like Steins or Vesta, comets as well as trans-Neptunian objects (hereafter noted TNOs). The data analyses have provided either preliminary or more accurate estimates of their thermal inertia, which fall generally below a few hundred, but often below 100J/m2/ K/s1/2, and as low as 2.5 ± 0.5J/m2/ K/s1/2 for TNOs (Delbo et al. 2007; Howett et al. 2010; Lellouch et al. 2013; Capria et al. 2014; Groussin et al. 2013 among others). Some are lower than the thermal inertia of the semitransparent rings of Saturn (30−35J/m2/ K/s1/2), or even of their embedded particles (160−200J/m2/ K/s1/2; Reffet et al. 2015). These values, which are very small compared to the bulk thermal inertia of rock and water ice materials (few thousands J/m2/ K/s1/2), provide evidence that the porous and granular structure of these surfaces, grounded by meteoroid bombardment and exposed to space weathering over billions of years, sets the magnitude of thermal inertia. The thermal inertia is governed by the arrangement, porosity, size and bulk conductivity of grains in the upper layers of the regolith; typically these regoliths are sounded in the infrared in depths of the first mm or cm over the thermal cycles considered, which are either diurnal or eclipse. It may also depend on temperature since the mechanical and thermophysical properties of the bulk material depend on temperature.
Understanding how thermal inertia relates to the regolith and grain properties requires that we figure out how heat transfers through these layers, either by conduction through the solid phase and contacts between grains or by radiation between pores or some intermediate case. Heat transfer by radiation has often been neglected in the thermal modeling of cold icy surfaces because of low temperatures and despite a radiative conductivity scaling with T3. The importance of this process relative to solid conduction through contacts is re-examined here in detail, as a function of grain size, porosity and temperature. Research on this topic largely exceeds the area of planetary sciences. Yet lot of work has been dedicated to this question in the field since the 60 s, starting with the study of rocky regoliths such as the lunar regolith (Winter & Saari 1969; Ulrichs & Campbell 1969). These studies have all recommended taking heat transfer by radiation into account, and referred to experiments on lunar regolith analogs which suggested that a very low thermal conductivity of contacts is summed up with a radiative component at temperatures between 150 and 250 K (Watson 1964). Presley and Christensen completed a major experimental work on the conductivity of granular media in the late 90s under Martian atmospheric pressure (Presley & Christensen 1997). Gundlach & Blum (2012) proceeded later on experiments under vacuum and proposed a way to link thermal inertia with porosity and grain size for small rocky bodies (Gundlach & Blum 2013). Their expressions for thermal conductivity and the influence of porosity include a priori information relative to rocky material together with some empirical formulae developed and calibrated from experiments on rocky dust samples. These investigations remain then specific to rocky small bodies. Kiuchi & Nakamura (2014) also proposed an empirical formula to relate porosity to grain size in this same context, from experiments with silica or alumina particles. Similar experimental works do not exist for icy regolith samples at temperatures below 130 K. But estimations of the bulk thermal conductivity of ice, either in its crystalline or amorphous forms have been provided by Klinger (1980). The case of amorphous ice is still under debate as estimates can vary by order of magnitudes (Kouchi et al. 1992; Andersson & Suga 1994; Baragiola 2003). There are few thermal models of spatially resolved icy atmosphereless porous surfaces and these usually do not develop the case of the dependency of thermal inertia on regolith properties (Spencer et al. 1989).
In this paper, we consider several models of thermal conductivity of contacts, radiative conductivity, and effective conductivity of packed beds as derived from rocky regoliths or other studies, which relate them to regolith grain size, porosity, temperature and bulk properties. We study how the effective thermal inertia of the regolith varies with these parameters and what heat transfer process prevails in what conditions. In light of this study, we address the question of the thermal dichotomy observed on Mimas icy satellite (Howett et al. 2011) and provide constraints on grain size, porosity and ice form, depending on the model used. Having discussed the relative sensitivity of heat transfer in icy regoliths to temperature, we wonder in what conditions a decrease of thermal inertia with heliocentric distance can be expected, which might reveal the efficiency of radiative conduction and possibly the ice form at depths probed by thermal waves.
2. Effective thermal conductivity of porous atmosphereless surfaces
Solar energy is absorbed in the very first mm of the icy surface and heat propagates within the subsurface layers at various depths and rate, depending on the structure and ability of the regolith to conduct or to store it. Heat transfer happens in atmosphereless regoliths via conduction in the solid phase of grains and through contacts, or by radiation through pores. Along the solid phase path, heat transfer is highly limited by the cross section of contacts between grains. Bulk solid conduction KS is indeed much larger than conduction through grain contacts KC. As it is considered that heat transfer through solid phase and contacts happens in series, the effective conduction through the solid porous medium is then about KC. Grains may exchange heat by radiating through pores or radiation may transfer heat in depth through pores and, thereby, heat up grains. The relative contributions of both conductivities, radiative KR and solid KC, to the effective conductivity of the layer KE, depend on the porosity p, the size R of grains and their arrangement, their emissivity, the temperature T of the medium, and the bulk solid conductivity of grains. Heat transfers by radiation and solid conduction are usually considered to follow parallel paths through the medium so that thermal conductivities add up and yield an effective thermal conductivity of the layer KE = KR + KC (in units of W/m/K). The effective thermal inertia Γ of the layer is then related to these structural parameters along with 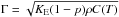 , in units of J/m2/K/s−1/2, where ρ is the volume density of the grains (kg/m3) and C(T) the specific heat capacity (J/kg/K).
, in units of J/m2/K/s−1/2, where ρ is the volume density of the grains (kg/m3) and C(T) the specific heat capacity (J/kg/K).
Heat transfer in porous packed beds has been focusing huge efforts in many research fields in order to relate the effective thermal conductivity of the medium to porosity or grain size, either by the derivation of semiempirical relations from experiments or by analytical modeling via conductance networks, accounting for gas, contact or radiative conductivities (for nonexhaustive list see Rubiolo & Gatt 2002; Slavin et al. 2002; Gusarov et al. 2003; or Gundlach & Blum 2012). This yields numerous models, from most simple original to more complex ones, developed around numerical experiments and usually more parameter dependent.
2.1. Bulk properties of water ice
Below 130 K, water ice may be found in both crystalline and amorphous phases. The ice form is thought to be a probe of the history of the surface. Thermally induced phase change obtained in the lab irreversibly transforms high-density amorphous ice Ia,h to low-density amorphous ice Ia,l when temperature raises above 38 K, and phase Ia,l further crystallizes into cubic Ic ice when the temperature reaches 135–140 K (Mastrapa et al. 2013 for a review). At 100 K, amorphous ice converts into Ic in 104 years and below 70 K, it is stable over the age of the solar system. Inversely, radiation by high energy protons or ions may disrupt the crystalline Ic structure of water ice and yield amorphization. Electrons irradiation may induce phase change of Ia,l into Ia,h below 60 K, but no amorphization by electron irradiation has been observed above 70 K (Mastrapa et al. 2013; Baragiola 2003). However this does not appear as simple among the icy bodies of the solar system. Crystalline water ice is most of the time detected at the very surface of icy bodies, regardless of the temperature (Mastrapa et al. 2013). However amorphous ice has also been detected on Jovian and Saturnian satellites (Hansen & Mc Cord 2004; Newmann et al. 2008) at temperatures much higher than 70K or on the TNO dwarf planet Haumea (Pinilla-Alonso et al. 2009), among others. Amorphous ice may then be present on the near surface or in depth and be probed by the thermal wave at cm depths.
The bulk thermal conductivity KS,C(T) of crystalline hexagonal ice is relatively well known (Klinger 1980; Andersson et al. 1994). It is usually assumed that the conductivity of the crystalline cubic form is not very different from that of hexagonal ice and KS,C(T) = 567 /T, which is about 7.1 W/m/K at T = 80 K (Klinger 1980). There is more confusion about the amorphous form as it can be produced in two ways in the lab: first, in small quantities by vapor deposition and, second, by compression of crystalline ice about 0.9 GPa. In both cases, high- and low- density amorphous ices are observed and it has been found that the low-density forms of both methods are most probably identical (Andersson and Suga 1994). The thermal conductivity of the form obtained by compression ranges about 0.6 W/m/K between 70 and 125 K, close to the theoretical expectation KS,A(T) = C(T)νλρ/ 4, where C(T) is the specific heat capacity, ν = 2500 m/s and λ = 5 × 10-10 m, which yields values about 0.2 W/m/K (Andersson & Suga 1994; Klinger 1980). The volume density of this low-density phase is ρA = 940 kg/m3 (Baragiola 2003), whereas that of the crystalline form is ρC = 918kg/m3. On the other hand, measurements made on the amorphous phase obtained with a vapour deposit yield a much lower estimate of about 10-5 W/m/K (Kouchi et al. 1992), which has been of course contested by previously cited authors (Andersson & Suga 1994; Baragiola 2003).
The specific heat capacity of water ice is not expected to be very different between crystalline and amorphous forms (Shulman 2004). When the approximation by Klinger, C(T) = 7.49T + 90, was systematically used in previous works on cometary amorphous ice, Shulman (2004) pointed out the discrepancy between this model and experimental data on the heat capacity of water ice for temperatures T below 100 K. As most of the icy surfaces considered here are below this limit, the Shulman’s polynomial approximation to experimental data has been used instead, i.e. ![\begin{eqnarray} \label{Eq.1} C(T) &=&7.73 T \left(1-{\rm e}^{-1.263 \times 10^{-3}T^2}\right) \times \left(1+8.47\: T^6 {\rm e}^{-3\sqrt{T}} \right.\nonumber\\[2mm] & &+ \, 2.0825\times 10^{-4}T^4 {\rm e}^{-4.97\times 10^{-2}T}\bigg) \end{eqnarray}](/articles/aa/full_html/2016/04/aa27625-15/aa27625-15-eq36.png) (1)in units of J/kg/K for temperatures expressed in K. In this case C(T) effectively tends to zero at few K, which is expected by the Debye-Sommerfeld equation. Consequently, the thermal inertia of bulk crystalline ice
(1)in units of J/kg/K for temperatures expressed in K. In this case C(T) effectively tends to zero at few K, which is expected by the Debye-Sommerfeld equation. Consequently, the thermal inertia of bulk crystalline ice  is on the order of 2000 J/m2/ K/s1/2 and about constant with temperature, whereas the thermal inertia of the amorphous phase
is on the order of 2000 J/m2/ K/s1/2 and about constant with temperature, whereas the thermal inertia of the amorphous phase 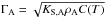 increases significantly with temperature following its heat capacity, from about 30 J/m2/ K/s1/2 at T = 20 K to 500 J/m2/ K/s1/2 at 120 K (Fig. 5). Both ice forms have significantly different temperature dependence and bulk thermal inertias.
increases significantly with temperature following its heat capacity, from about 30 J/m2/ K/s1/2 at T = 20 K to 500 J/m2/ K/s1/2 at 120 K (Fig. 5). Both ice forms have significantly different temperature dependence and bulk thermal inertias.
2.2. Regolith porosity and grain sizes.
If the thermal inertia of the bulk phase of icy grains varies by more than an order of magnitude owing to ice forms, it can also be significantly affected by the porosity and size of grains as they control either the space by which heat transfers by radiation or the area of contact by which solid conduction happens. In this study, the grain sizes range from 10μm to 10 cm at the largest, which includes the usual range of size constrained by NIR spectroscopic observations. As far as arrangements of spherical grains are concerned, the lower limit for the porosity is set by the Kepler conjecture for a pileup of spheres, i.e. p = 0.26. The filling factor of the regolith D = 1−p can be calculated for face-centered-cubic to diamond classical pileups, from D = 0.74 (p = 0.26) to D = 0.34 (p = 0.66), with coordination number nC varying between 12 and 4 respectively (Gusarov et al. 2003, for example). The upper limit of the porosity is limited to p = 0.84 for which the coordination number nC = 2, i.e., there is a minimum contact between spheres within the layer, at least two neighbors. Larger porosities mean that the conduction by contacts is very limited, which is a case we study with a specific theory as well. For a given value of p, the coordination number is linearly interpolated from the nc(p) relationship for known pileups.
 |
Fig. 1 Left panel: radiative conductivity KR as a function of porosity p and grain size R, at mean temperature T = 80 K, emissivity ϵ = 1, solid thermal conductivity KS,C(T) = 567 /T for the crystalline ice form. Curves correspond to Breitbach and Barthels (BB, full line) and Gundbach and Blum (GB, dotted line) models. Right panel: temperature dependence of the radiative conductivity for p = 0.5 and R = 1 cm. Model curves are also plotted for emissivity ϵ = 0.5 in red (BB: dashed line; GB: dot-dashed line). |
2.3. Radiative conductivity
We have reviewed current modeling of the radiative conductivity in packed beds in a previous paper dedicated to the thermal modeling of dense planetary rings (Ferrari & Reffet 2013). The radiative transfer equation governing infrared intensity through the regolith can be expressed as a diffusion equation with a radiative conductivity dependent on temperature. Most recent studies on heat transfer in packed beds of spherical particles tend to express the radiative conductivity in the form of KR = 8RFEσT3 where FE is a dimensionless radiation exchange factor, R the effective size in the medium and T the average bed temperature (for a review see VanAntwerpen et al. 2010; Piqueux & Christensen 2009). The dependency of the radiative exchange factor FE on the structure of the medium is complex and then subject to diverse formulations among authors. We had chosen works taking the dependence of KR on KS into account, i.e., the approach of Breitbach & Barthels (1980). Also this model, hereafter BB, can be used for any range of porosity, solid conductivity and emissivity and is equivalent to the other models at some discrete porosity values. After experimenting on high-temperature nuclear packed beds where solid and radiative conductions dominate, these authors proposed a modified expression for the effective conductivity originally modeled by Zehner & Schlunder (1970), based on the calculation of an equivalent network of thermal conductances of a packed bed of particles of various shapes. The expression used for the radiative exchange factor FE is given by: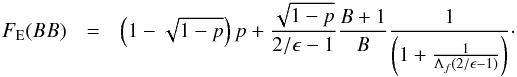 (2)The dimensionless conductivity Λf is the ratio of solid-to-radiative conductivities Λf = KS/ 8RσT3, which remains very large no matter what the size R for crystalline grains is even if it is decreasing with increasing temperature in the range 20–120 K. The parameter B = 1.25((1−p) /p)10/9. In this case FE is mainly dependent on porosity and emissivity. This is also true for grains of amorphous ice of R ≤ 1 cm in size, but for larger sizes, Λf is then as low as a few at T = 120 K and the correction for KS, i.e.
(2)The dimensionless conductivity Λf is the ratio of solid-to-radiative conductivities Λf = KS/ 8RσT3, which remains very large no matter what the size R for crystalline grains is even if it is decreasing with increasing temperature in the range 20–120 K. The parameter B = 1.25((1−p) /p)10/9. In this case FE is mainly dependent on porosity and emissivity. This is also true for grains of amorphous ice of R ≤ 1 cm in size, but for larger sizes, Λf is then as low as a few at T = 120 K and the correction for KS, i.e. 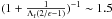 has to be taken into account in the calculation of FE(BB). Gundlach & Blum (2012), hereafter GB, in their recent modeling of heat transport in porous dust layers, make use of a different formulation based on the mean free path in random porous medium as proposed by Dullien (1991), who expressed the radiative conductivity as KR = 8ϵσΛ(R)T3, where
has to be taken into account in the calculation of FE(BB). Gundlach & Blum (2012), hereafter GB, in their recent modeling of heat transport in porous dust layers, make use of a different formulation based on the mean free path in random porous medium as proposed by Dullien (1991), who expressed the radiative conductivity as KR = 8ϵσΛ(R)T3, where 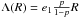 , or equivalently FE(GB) = ϵe1p/ (1−p) with e1 = 1.34, independent of the thermal conductivity of the solid phase. This is the approach commonly used when dealing with gas transport in porous media-like comets.
, or equivalently FE(GB) = ϵe1p/ (1−p) with e1 = 1.34, independent of the thermal conductivity of the solid phase. This is the approach commonly used when dealing with gas transport in porous media-like comets.
Model expressions for Hertz factor h, porosity influence φ(p) on solid phase conductivity KC and exchange factor FE for radiative conductivity KR.
Figure 1 shows the radiative conductivity KR for both formalisms, BB and GB. The radiative conductivity obviously scales linearly with grain size from about 10-5 W/m/K at T = 80 K and 100 μm-sized particles to 10-2 W/m/K for 10 cm-sized grains. The radiative conductivity also increases with porosity as a higher fraction of voids favors heat transfer by radiation to a lesser extent, i.e. by a factor of 2-to-20 when porosity p increases from 0.26 to 0.84 depending on the model. The GB radiative conductivity appears much more sensitive to porosity compared to the BB model. Models yield similar predictions for p = 0.5 and differ by a factor of 0.5-to-2 in the range of porosity 0.26–0.84. The radiative conductivity follows a strict dependence on T3 (Fig. 1, right panel), i.e. it is insensitive in that range to the temperature dependence of the solid phase KS,C(T). Both models mainly differ in their dependence on porosity which relies on the description of the porous medium, either assuming a packed bed of spherical particles (BB) or a random porous structure (GB).
2.4. Conductivity of contacts
The effective conductivity KE of a packed bed also depends on the bulk conductivity of grains and on their arrangement, i.e. on the number of mutual contacts through which heat may transfer. Immeasurable work has been dedicated to this complex question. The models elaborated to estimate the conductivity of contact KC usually combine the Hertz theory and its improvements, describing the morphology of a single contact between two elastic spheres, with calculations of equivalent thermal resistance of the packed bed structure, either organized or random. The reduced radius of contact aH relative to the grain size R limits the resulting thermal conduction within the solid phase. The expression of KC is classically integrating the Hertz factor h = aH/R and the effect of porosity p, which overall reduces the bulk conductivity by a factor φ(p), so that: 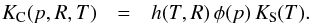 (3)If it is commonly admitted that KC decreases with the increasing size of R, the proposed laws yield values for KC that vary by orders of magnitude among authors. The expression of φ(p) also varies, depending on the structure of the medium (Table 1).
(3)If it is commonly admitted that KC decreases with the increasing size of R, the proposed laws yield values for KC that vary by orders of magnitude among authors. The expression of φ(p) also varies, depending on the structure of the medium (Table 1).
 |
Fig. 2 Contact conductivity KC of a packed bed of grains of size R (from yellow to dark red) as a function of its porosity p at temperature T = 80 K and emissivity ϵ = 1. Left panel: crystalline ice form. Right panel: amorphous ice form. Curves correspond to Watson theory (W, full line; loose contacts), Gusarov model for porosity coupled with JKR contact theory (G+JKR, dashed line; tight contacts) and Gundbach and Blum (GB, dotted line; tight contacts) models. |
The Hertz theory considers the radius of contact aH,H of two elastic spheres under external load F and does not take into account adhesion like Van der Waals forces. In the frame of the Hertz theory, the radius of contact is written as: 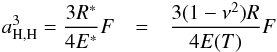 (4)where R∗ = R/ 2 is the radius of curvature and E∗ = E(T)/2(1−ν2) the equivalent Young modulus for the system of two grains. The parameter E(T) is the Young modulus (N/m2) of the bulk material, ν the Poisson ratio and γ the surface tension (J/m2). For solid water ice E = 9 GPa (109 J/m3) at T = 273 K, ν = 0.33, and γ = 0.076 J/m2 (Sirono & Yamamoto 1997). Lindgren (1970) has shown that the Young modulus for type I ice decreases with increasing temperature, along E(T) = 6.6 × 109(4.276−0.012T), i.e. 24.3 GPa ≥ E ≥ 18.8 GPa for 50 K ≤ T ≤ 120 K. Studies on the dependence of the mechanical properties of ice at solar system temperatures are apparently scarce and seem to be difficult to evaluate experimentally. Studies of terrestrial permafrost show high variability of the thermal behavior of the Poisson ratio ν around an average value of 0.37 ± 0.10 in the temperature range 250–273 K, which is compatible with the Sirono and Yamamoto value (Kaplar 1963). Also the measurements of surface tension γ exhibit variability among authors, from 0.07 to 0.37 J/m2 (Gundlach & Blum 2015). Gundlach & Blum (2012) measured γ = 0.19 J/m2 at 210 K and Aumatell & Wurm (2014) γ = 0.37 J/m2 at 200 K. Given the uncertainty on their temperature dependency at this stage, values are fixed at ν = 0.33 and γ = 0.076 J/m2 and are assumed to be independent of temperature. The conductivity of contact may be nearly twice as large as shown if γ = 0.37 J/m2, which does impact the overall results significantly.
(4)where R∗ = R/ 2 is the radius of curvature and E∗ = E(T)/2(1−ν2) the equivalent Young modulus for the system of two grains. The parameter E(T) is the Young modulus (N/m2) of the bulk material, ν the Poisson ratio and γ the surface tension (J/m2). For solid water ice E = 9 GPa (109 J/m3) at T = 273 K, ν = 0.33, and γ = 0.076 J/m2 (Sirono & Yamamoto 1997). Lindgren (1970) has shown that the Young modulus for type I ice decreases with increasing temperature, along E(T) = 6.6 × 109(4.276−0.012T), i.e. 24.3 GPa ≥ E ≥ 18.8 GPa for 50 K ≤ T ≤ 120 K. Studies on the dependence of the mechanical properties of ice at solar system temperatures are apparently scarce and seem to be difficult to evaluate experimentally. Studies of terrestrial permafrost show high variability of the thermal behavior of the Poisson ratio ν around an average value of 0.37 ± 0.10 in the temperature range 250–273 K, which is compatible with the Sirono and Yamamoto value (Kaplar 1963). Also the measurements of surface tension γ exhibit variability among authors, from 0.07 to 0.37 J/m2 (Gundlach & Blum 2015). Gundlach & Blum (2012) measured γ = 0.19 J/m2 at 210 K and Aumatell & Wurm (2014) γ = 0.37 J/m2 at 200 K. Given the uncertainty on their temperature dependency at this stage, values are fixed at ν = 0.33 and γ = 0.076 J/m2 and are assumed to be independent of temperature. The conductivity of contact may be nearly twice as large as shown if γ = 0.37 J/m2, which does impact the overall results significantly.
Given the failure of the Hertz theory at describing residual contact in the absence of external load, the JKR (Johnson et al. 1971; Johnson 1985) and DMT (Derjaguin et al. 1975) theories have provided first-order developments by including adhesion forces in the area of contact and outside of it. According to Johnson et al. (1971), the radius of contact is written as 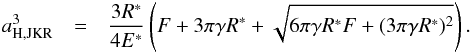 (5)The radius of contact provided by the DMT model may be 1-to-1.5 times as low as JKR estimate depending on γR∗/F. With a reduced load (F = 0), which prevails in a low gravity environment such as the surface of Mimas for sub-cm-sized grains, the Hertz factor resumes to
(5)The radius of contact provided by the DMT model may be 1-to-1.5 times as low as JKR estimate depending on γR∗/F. With a reduced load (F = 0), which prevails in a low gravity environment such as the surface of Mimas for sub-cm-sized grains, the Hertz factor resumes to 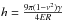 as mentioned in Table 1. For the calculation of the Hertz factor with the JKR theory, however, the full expression as given by Eq. (5) is kept.
as mentioned in Table 1. For the calculation of the Hertz factor with the JKR theory, however, the full expression as given by Eq. (5) is kept.
Gundlach & Blum (2013) proposed an expression for KC (Table 1), which considers ice-free porous dust samples of silica that is based on theoretical modeling (Chan & Tien 1973) and experiments driven at relatively high temperatures (300–600 K) for porosities p within the range 0.25–0.5. The GB expression assumes that the force acting on the contacts are Van der Walls forces and not weight, given the low gravitational compression at the surface of comets they aim to study. The GB model is used here self-consistently, coupling its expressions of h and φ(p).
 |
Fig. 3 Effective thermal conductivity KE as a function of grain size R at T = 80 K, emissivity ϵ = 1 for both crystalline (full line) and amorphous (dotted line) ice forms. Top left panel: high (G+JKR); Top right panel: intermediate (GB); Bottom panels: low (W) contact conductivities are shown, coupled with either Breitbach and Barthels (+BB) or Gundlach and Blum (+GB) models for radiative conductivity (−...− line). Colors correspond to increasing porosity: from p = 0.26 (black), p = 0.5 (red) to p = 0.84 (orange). |
In order to analyze experiments of laser sintering of powder beds, Gusarov et al. (2003) modeled the effective thermal conductivity of powder beds, which are either ordered or randomly dispersed. Grains are tens-to-hundred μm in size. The expression these authors derive for φ(p) depends on the coordination nC of the medium, which is representative of the number of contacts per unit cell in the bed and ranges from 4 to 12 depending on porosity (Table 1). In our model the value for nC for porosity p is linearly interpolated from the values they provide at some porosities only. Their expression is similar to those reported by Argento & Bouvard (1996) from Carlslaw & Jaeger (1959) and Jagota & Hui (1990) works for random packing of spheres.
Finally some authors argue that the thermal conductivity by contacts is much below 10-3 W/m/K (Watson 1964, and references within Piqueux & Christensen 2009). Watson (1964) proposed KC = 1.5 × 10-8KS(T) /R from experiments on silicate powders between 150 and 350 K, which yields a much steeper slope of the contact conductivity relative to grain size and lower conductivities compared to the other models described above. He found no significant dependence of the thermal conductivity of samples to the porosity of the medium. He concluded for highly resistive contacts between grains with a cross section much smaller than that defined by the circle of contact, most probably caused by microscopic roughness there. Watson’s empirical law is chosen here to quantify the contact conductivity KC in case with loose contacts between grains.
The conductivity of contacts is then calculated along Eq. (3) in three cases: the high conductivity case couples tight contacts from the JKR theory with porosity effects given by Gusarov et al. model, alias (G+JKR) model; the intermediate case provided by the GB model; and, finally, the low conductivity case provided by the Watson model, which does not depend on porosity, alias W model. Consequently, the conductivity through the solid phase of the porous medium KC varies by orders of magnitudes as a function of size and porosity (Fig. 2). Models are shown for both forms of water ice, crystalline and amorphous as KC directly scales with KS. The conductivity of contacts estimated by the GB model is, at low porosity, on the order of 0.005 to 0.05 W/m/K, depending on the size R. At larger porosities, its scales down to about 0.001 W/m/K. Watson’s theory provides a contact conductivity independent of porosity p, decreasing with size, from 3 × 10-4 to 10-6 W/m/K for large grains (10 cm). The GB and G+JKR models differ by less than one order of magnitude. The ice form introduces another scaling factor in the conductivity of contacts. The expected ratio is about 35 (see Sect. 2.1). For amorphous ice, the contact conductivity is well below 0.01 W/m/K, at a few 10-4 W/m/K for common size and porosity ranges, even in the most favorable case of tight contacts between grains.
2.5. Effective conductivity
The effective conductivity KE = KC + KR is calculated as a function of porosity p, grain size R and ice forms at temperature T = 80 K with the theories exposed above. The (G+JKR) model is combined with the BB radiative conductivity model. A combination with the GB radiative conductivity model yields very comparable results. The GB model is self-consistent in the combination of contact and radiative conductivities and the W model is combined with both models for radiative conductivities, BB and GB (Table 1). The four combinations are plotted in Fig. 3. As expected, the relative contributions of solid and radiative conductivities are complementary. The first, decreasing with grain size R, dominates at small sizes, while the second, directly scaling with it, dominates at larger sizes. The size for which the transition happens depends on the contact theory, porosity and form of ice at a given temperature. For high/intermediate contact conductivities (G+JKR or GB) and crystalline ice, conduction through the solid phase dominates below mm- to cm-sized grains, the smaller the porosity the larger the threshold (Fig. 3, top plots). At a given size and porosity, the G+JKR model gives larger values of KE and the radiative contribution is only dominant for cm-sized particles and large porosities. The effective conductivity is on the order of 0.01–0.1 W/m/K and only slightly dependent on size. For the amorphous form, this transition happens at lower sizes, on the order of 200 μm to 2 mm and the thermal conductivity is much smaller, on the order of 10-4 to 10-2 W/m/K. As expected, the effective thermal conductivity is more sensitive to porosity at large sizes when the GB radiative conductivity model is used.
With loose contacts (W model), the effective conductivity is rather small for grains that are sub-mm in size and dominated by the radiative conductivity for R ≥ 1 mm. The transition happens at grain sizes of about 100 μm for amorphous ice. the effective conductivity KE becomes highly dependent on grain size above this range and more sensitive to porosity if the radiative conductivity is that of a random porous medium (GB model). This directly scales with R between 10-4 and 10-1 W/m/K. Below the transition size, the effective conductivity is independent of the porosity according to Watson’s model. The radiative conduction may then be far from negligible even at temperatures as low as 80 K in such icy regoliths.
3. Results and discussion
These models of the effective conductivity provide very different behaviors and orders of magnitude depending on porosity, grain size and ice form. In this section we examine how the effective thermal inertia 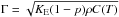 , which translates both the ability to conduct and to store heat in the regolith, varies accordingly as a function of these properties and temperature. The dichotomy in thermal inertia of Mimas terrains is also analyzed in light of these models. Finally, we explore the conditions to obtain a decrease of thermal inertia with solar distance. In this section, only the models that provide the highest and lowest guesses for thermal inertia are conserved, i.e., the tight contacts option (G+JKR model) and the loose contacts option (W model); both are combined with the BB model for radiative conductivity.
, which translates both the ability to conduct and to store heat in the regolith, varies accordingly as a function of these properties and temperature. The dichotomy in thermal inertia of Mimas terrains is also analyzed in light of these models. Finally, we explore the conditions to obtain a decrease of thermal inertia with solar distance. In this section, only the models that provide the highest and lowest guesses for thermal inertia are conserved, i.e., the tight contacts option (G+JKR model) and the loose contacts option (W model); both are combined with the BB model for radiative conductivity.
 |
Fig. 4 Thermal inertia |
3.1. Thermal inertia vs. regolith properties and temperature
The thermal inertia of a regolith with grains in tight contacts ranges from a few tens to few hundred J/m2/ K/s1/2 at T = 80 K, when the ice is in its crystalline form and grain size or porosity is in the considered ranges (Fig. 4). These values scale down to 5 to a few tens of J/m2/ K/s1/2 for amorphous ice. For loose contacts between grains, the thermal inertia ranges between a few and 100 J/m2/ K/s1/2. The volumetric heat capacity CV = (1−p)ρC(T) (in J/K/m3) and the conductivity by contacts in the solid phase both increase with decreasing porosity whereas the radiative conductivity decreases. Thermal inertia therefore significantly increases with decreasing porosity, when the conduction by contact dominates below the transition size. On the contrary, when heat transfer is dominated by radiation, the thermal inertia is less dependent on porosity given the antagonism between conduction and heat capacity (Fig. 4). This is true for both ice forms. The overall behavior of thermal inertia with size remains consistent with that of the effective thermal conductivity as expected with similar reversal sizes.
The temperature has been fixed so far to 80 K, which is typical of Saturn icy satellites. Given the significant contribution of radiative conductivity in a regolith of large grains, a variation of thermal inertia with temperature is expected, even at these low temperatures, besides the temperature dependency of KS(T) and C(T). Of most interest is also the opposite dependence of KS(T) for crystalline and amorphous forms, which decreases or increases with temperature respectively. The temperature dependence of thermal inertia is shown in Fig. 5 for tight or loose contacts for two grain sizes, which are about the transition sizes delimiting the contact-dominated region (left, R = 0.1 mm) from the radiation-dominated regime (right, R = 1 cm).
 |
Fig. 5 Thermal inertia versus temperature T for grain size R. Left panels: R = 100 μm. Right panels: R = 1 cm, tight contacts (top panels) or loose contacts (bottom panels). The thermal inertia is given for crystalline (full line) or amorphous (dotted line) ice forms for porosities p = 0.26 (black), p = 0.5 (red) and p = 0.84 (orange). The bulk thermal inertias of crystalline (dashed line) and amorphous (dot-dashed line) forms are also plotted. The contribution of radiative conductivity to thermal inertia is also plotted (−...− line). |
For crystalline ice form, the thermal inertia of small grains is dominated by conduction through contacts and is almost constant with temperature, regardless of the quality of contacts. This inertia ranges between 10 and few hundred J/m2/ K/s1/2 in case of tight contacts and only in the range 6–25 J/m2/ K/s1/2 if the contacts are loose. For large grains of crystalline ice, thermal inertia starts increasing with temperatures above 70–80 K, for porosities larger than 0.5. At lower temperatures, heat transfer through contacts still dominates. In the case of loose contacts, thermal inertia is then dominated by radiative conduction and increases with temperature.
The thermal behavior of the regolith of amorphous grains is different as expected. The effective thermal inertia increases with temperature regardless of the grain size and quality of contacts. This is all the more sensitive when contact conductivity dominates for small grains as it is all the more sensitive to the specific heat capacity C(T). Depending on the quality of contacts, the thermal inertia ranges from below one to a few tens J/m2/ K/s1/2 in the best case, and to only a few J/m2/ K/s1/2 for loose contacts. This inertia is dominated by radiative conductivity for large grains and follows a T2 dependency fixed by (KRC(T)1/2) at temperatures above 50 K.
Thus the thermal inertia may be very temperature dependent, either due to thermophysical properties or to the contribution of radiative heat transfer through the pores. The thermal inertia may vary by more than an order of magnitude or more between 20 and 120 K. The ice form has a strong impact on its magnitude and its temperature dependence. During diurnal cycles, temperatures at the surface of icy saturnian satellites vary between 50 and more than 100 K (Howett et al. 2010). Inverting their diurnal temperature cycle with a model which assumes a thermal inertia independent of temperature might then introduce a bias in its estimation if the crystalline grains are cm sized, which might be more important for amorphous ice.
3.2. Implications for Mimas thermal dichotomy
Howett et al. (2011) have discovered a large dichotomy in thermal inertia on the surface of Mimas, the leading face of this synchronous icy satellite region R2, 0°N–140°W), which is of significantly higher thermal inertia, Γ2 = 66 ± 23J/m2/ K/s1/2, compared to the trailing one (region R1, 0°N–195°W), with Γ1 ≤ 16J/m2/ K/s1/2. The thermal anomaly is correlated with a IR-to-UV color ratio anomaly observed by the ISS cameras (Schenk et al. 2011). Such anomalies have also been observed, to a lesser extent, on other Saturn satellites, Tethys and Dione (Howett et al. 2012, 2014). The shape of the anomaly appears to be correlated with the oval shape of a zone bombarded by high energy electrons (Paranicas et al. 2012, 2014; Schenck et al. 2011). The NIR albedo of the trailing face is known to be larger than the one of the leading face (Buratti et al. 1998; Emery et al. 2005). The absorption bands of water ice on the leading face are deeper, which is understood as the presence of larger grains (Emery et al. 2005; Filacchione et al. 2007, 2012). Buratti et al. (2011) propose grain sizes in the range 20–100 μm for the leading face and 10–50 μm for the trailing face, whereas Filacchione et al. (2012) do not specifically analyze this dichotomy and propose an average size range for Mimas regolith of 30 μm–7.5 mm. Crystalline ice is clearly detected on both faces owing to the absorption band at 1.65 μm and the shift of the 2.0-μm band toward 2.05 μm (Cruikshank et al. 2005; Filacchione et al. 2010). However this does not exclude the existence of amorphous ice, which can be better asserted from the 3.1 μm band (Hansen & McCord 2004). It is not clear from the recent literature if amorphous ice is definitely ruled out by VIMS data as the Fresnel peak typical of crystalline water ice at 3.1 μm is obvious only in the spectra of Saturn outer satellites (Filacchione et al. 2010). Most recently, Scipioni et al. (2015), studying the intensity of this peak on Mimas, concluded there is a much higher crystallinity on the leading face compared to the trailing face, where this peak is not observed or attenuated by more than 80%. They found no evidence of the oval feature seen in ISS images. As sunlight is absorbed in the very first mm of the surface in the 2-to-3 μm wavelength range, i.e. about the first layer of water ice grains, VIMS measurements may not be sensitive to the effects of bombardment by electrons that penetrate at cm depths, which is comparable to the diurnal thermal skin depth probed by CIRS in the infrared. There are also two spectral features, which are a diagnosis of crystalline ice in the thermal infrared at 44 and 62 μm (Moore & Hudson 1992). Observations by CIRS of some Saturnian satellites, in particular the nearly pure water ice-covered Enceladus and Tethys, conclude that the very flat spectra in this range may be indicative of a highly porous regolith of tiny amorphous grains according to Carvano et al. (2007). They apparently did not test the presence of crystalline water ice. No similar study can be found for Mimas. The effect of a bombardment by electrons of high energy on a regolith is uncertain. If this bombardment certainly excites and ionizes matter by energy deposition and may induce radiolysis, amorphization, sputtering, or desorption, it is not known how it can modify the thermal properties (Baragiola 2003; Paranicas et al. 2014) and eventually sinter grains to increase the thermal conductivity or decrease the porosity.
The constraints provided by Howett et al. (2011) on the thermal inertias of region R1 (trailing, low inertia) and region R2 (leading, high inertia) have been applied to the different models described above to tentatively translate them into constraints on porosity, grain size R or ice form. These constraints are reported in Fig. 4 and implications on p and R are reported in Fig. 6 as a function of the ice form. Only results obtained with the JKR and W models, coupled with the BB model of radiative conductivity, are plotted, i.e. tight versus loose contacts cases. Conclusions drawn with the JKR model are essentially similar for the GB model but for porosities about 10% lower. If the water ice were crystalline over the thermal skin depth, the thermal inertia Γ2 of the leading face would be easily explained by a regolith of grains larger than a cm, which is dominated by radiative conductivity regardless of the quality of contacts. This range of sizes is not compatible with NIR spectral observations. If the contacts are loose, Γ2 may also be that of a regolith of grains that are smaller than 30 μm, which fits both Buratti et al. (2011) and Filacchione et al. (2012) derivations. The low thermal inertia of the trailing face can hardly be reproduced with tight contacts. Such a low thermal inertia is better reproduced assuming loose contacts of about 100 μm- to 6 mm-sized crystalline grains. In this case porosity cannot be constrained. This range of size may be compatible with Filacchione et al. (2012) results but are excluded by Buratti et al. (2011). If there is mostly amorphous ice within the thermal skin depth sounded by the thermal wave on the trailing face of Mimas, i.e. 0.5 cm (Howett et al. 2011), its low thermal inertia may be that of a regolith of grains smaller than a few mm. This is compatible with size constraints previously mentioned. Its porosity depends on the quality of contacts. A regolith of grains larger than a cm or of grains smaller than 100 μm and porosity below 0.4, i.e. compacted and dominated by conduction through contacts, can account for the large thermal inertia for the leading face, which is a configuration that is also compatible with NIR constraints on size.
In conclusion, constraints on the thermal inertia as measured by CIRS on two regions of the leading and trailing faces are easy to reconcile with VIMS estimations of the size of grains if amorphous water ice is present at depths of a few cm. This constrains the regolith grains on the leading face to be tiny (R ≤ 100 μm) and compacted (p ≤ 0.4). Were the amorphous ice present at cm depth, it would have yielded a compaction of the regolith of the leading side by a factor of 2 compared to the trailing face. As suggested by the Scipioni et al. study on the very first layer of grains, the leading face might be more crystalline than the trailing face, which would have stood amorphous at cm depth. Radiation is expected to yield amorphization of crystalline ice. An upper layer of crystalline ice would imply that this amorphization does compete with a thermal processing on the surface. If the ice is crystalline at cm depth, the compatibility of CIRS measurements with NIR spectroscopy requires tight contacts between grains on the leading face, and loose contacts would require to have smaller grains there, i.e., smaller than 30 μm. One should then understand how a crystalline ice form can be conserved at depth despite bombardment. If amorphous ice were present at cm depth on the trailing face and crystalline on the leading face, one might expect higher dielectric constant from microwave echo as amorphous ice is slightly denser. Nonetheless the signal might be dominated by the effect of porosity which has a stronger effect on the signal (Kofman et al. 2015).
 |
Fig. 6 Constraints set on porosity p and grains size R by the observed thermal inertias of region R1 of the trailing face of Mimas (dark gray, Γ1 ≤ 16J/m2/ K/s1/2) and region R2 of the leading face (light gray, Γ2 = 66 ± 23J/m2/ K/s1/2) of Mimas (Howett et al. 2011). Left panels: crystalline water ice. Right panels: amorphous water ice. Both tight (top panels) and loose (bottom panels) contacts cases are considered too (see Fig. 5 for details). Temperature is assumed to be 80 K here. |
 |
Fig. 7 Thermal inertia versus grain size R (top panels) or heliocentric distance D (bottom panels), considering the crystalline ice (left panels) or amorphous ice (right panels) forms. Porosity is fixed at p = 0.5, bolometric Bond albedo A = 0.5 and emissivity ϵ = 1. Both tight (full line) or loose (dashed line) contacts are considered in each case. Data from Table 2 are plotted. Mimas data are plotted as a black symbol for both R1 (trailing) and R2 regions. The best fit of Γ(D) with the data is plotted also (dot line, see text). |
3.3. Thermal inertia vs. heliocentric distance
Measurements of the thermal inertia of icy atmosphereless bodies such as Jupiter and Saturn satellites exist but are missing for those of Uranus and Neptune. The Herschel and Spitzer telescopes have provided new insights on the thermal properties of the TNOs and other Centaurs (Fornasier et al. 2013; Lellouch et al. 2013). These estimates should be compared with care as they are not provided by data sets of equivalent wealth, or derived from similar transient phenomena with similar thermal models. Values for both the Jovian and Kronian icy satellites are illustrative of this discrepancy (Table 2, Fig. 7 bottom). Thermal inertias of Europa, Ganymede, and Callisto have been estimated either from eclipse cooling observed from Earth (Morrison & Cruikshank 1973) or from their diurnal cycle captured by the Voyager-IRIS thermal infrared spectrometer or the Galileo-PPR Photopolarimeter (Spencer 1987; Spencer et al. 1999). The thermal inertias measured from eclipse events are five times as low as the ones derived from diurnal cycles, a difference which appears to be significant. It has been interpreted as a change in thermal inertia with depth as both thermal events are expected to probe different skin depths. For the Saturnian satellites, thermal inertias have been derived from diurnal cycles (Howett et al. 2010). The large error bars account for an actual dispersion due to dichotomies observed at much higher spatial resolution by the CIRS instruments (Howett et al. 2011, 2012, 2014; see Sect. 3.2). They are comparable with eclipse measurements of the Galilean satellites or may also be considered as systematically lower than Galilean inertias measured during diurnal cycles. The thermal inertia of Centaurs and TNOs remains indeed difficult to determine as no eclipse nor diurnal cycles have yet been observed. The inertia is, hence, evaluated through the classical conversion of the beaming factor, a complex function of thermal inertia, roughness and spin state. Assumptions on spin orientation/rate and surface roughness allow us to derive some values that are then highly model dependent. Lellouch et al. (2013) provided average values for the population of Centaurs (≤25 AU) and TNOs located between 43 and 51 AU. These values are actually very low. Yet Centaurs, which orbit close to Saturn distance, have thermal inertias very consistent with that of some of its satellites. Quaoar, which is further away, does not either exhibit a very different thermal inertia. The average thermal inertia of classical TNOs or Plutinos about 47 AU appears very low about 2 ± 0.5J/m2/ K/s1/2 (Lellouch et al. 2013). Water ice has been detected in its crystalline form on the surface of all the individual objects listed in Table 2 (De Bergh et al. 2013). On Haumea in particular, a mixture of amorphous and crystalline ice better fits the data (Pinilla-alonso et al. 2009).
Thermal inertia measurements of icy bodies in the solar system (in J/m2/ K/s1/2).
It appears as a general trend (Fig. 7, bottom) that the thermal inertia of these icy surfaces effectively scales down by about two orders of magnitude between 5 and 50 AU, with a dispersion of about one order of magnitude at a given distance D. One finds here as a rough estimate Γ(D) = γDβ where 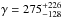 and the slope β = −1.21 ± 0.23, which is a smoother slope compared to Lellouch et al. (2013) work, which gives a slope of −1.7 fitted on all the Centaurs and TNOs population they observed. Lellouch et al. of course questioned this dependence of thermal inertia to heliocentric distance. They separately examined the expected dependence Γ(D) due to ice form only in D− 1/2 for amorphous ice and D0 for crystalline ice, or due to dominant radiative conductivity, i.e., D-1, therefore, not steep enough to explain the observed dependence. They also consider the scaling effect of porosity on thermal inertia, considering the fractal porous model elaborated by Shoshany et al. (2002) for cometary ice, which may be able to explain the very low thermal inertias.
and the slope β = −1.21 ± 0.23, which is a smoother slope compared to Lellouch et al. (2013) work, which gives a slope of −1.7 fitted on all the Centaurs and TNOs population they observed. Lellouch et al. of course questioned this dependence of thermal inertia to heliocentric distance. They separately examined the expected dependence Γ(D) due to ice form only in D− 1/2 for amorphous ice and D0 for crystalline ice, or due to dominant radiative conductivity, i.e., D-1, therefore, not steep enough to explain the observed dependence. They also consider the scaling effect of porosity on thermal inertia, considering the fractal porous model elaborated by Shoshany et al. (2002) for cometary ice, which may be able to explain the very low thermal inertias.
We studied the order of magnitude and temperature dependence of thermal inertia obtained by coupling thermophysical properties of both ice forms with heat transfer processes (radiation or conduction by contacts) in the previous section. It has been shown that heat transfer by radiation or temperature-dependent bulk thermophysical properties of water ice may yield large variations of thermal inertia for a given regolith structure. The equilibrium temperature TEQ of atmosphereless icy bodies is expected to vary with the heliocentric distance D along D− 1/2 according to TEQ = ((1−A)S/ 4σϵD2)0.25. The solar constant S = 1370 W/m2, σ is the Stefan constant and A is the bolometric Bond albedo. We may then effectively expect a systematic decrease of thermal inertia versus heliocentric distance, in particular, for an amorphous ice form (Fig. 5).
The dependence of thermal inertia versus grain size and heliocentric distance is shown in Fig. 7. The case of tight and loose contacts and crystalline versus amorphous ice forms are also considered. Porosity is assumed to be p = 0.5, and the Bond albedo A = 0.5 and ϵ = 1. As expected, the thermal inertia of a regolith of crystalline grains does not vary a lot with solar distance for sub-cm-sized grains with tight contacts (Fig. 7, bottom left). The thermal inertia, in this case, is expected to be large and almost independent of temperature and, hence, of the heliocentric distance D, as KE ~ KC ∝ KS ∝ T-1 and C(T) ∝ T. At low temperature, beyond D = 20 AU, the steeper decrease of C(T) with T slightly impacts the thermal inertia. Low thermal inertias of a few 10 J/m2/ K/s1/2 can be obtained with tight contacts and small grains for porosities smaller than 0.85. Lower thermal inertias are only accessible with normal porosities and loose contacts. In this case, radiative heat transfer can prevail down to sub-mm sizes as close as Jupiter distance (Fig. 7, top left). Thermal inertias, in this case, range then between 10 and a few tens J/m2/ K/s1/2 below 14 AU, regardless of the size. Thermal inertia of a few can be obtained only with sub-mm to sub-cm grains in size beyond Uranus orbit when radiative conductivity is prevailing. For a radiative-dominated regolith, for crystalline grains larger than 1 mm or so, the thermal inertia is expected to depend on T2 ∝ D-1 as the radiative contribution of conductivity scales as T3 and the heat capacity of water ice as T. This is actually observed on Fig. 7 (bottom) in case of loose contacts and grains larger than 1 mm. If grains are smaller, the thermal inertia is almost independent of temperature and D, but beyond 20 AU, C(T) starts to significantly decrease according to Eq. (1).
When ice is in amorphous form, its bulk conductivity scales down to an order of magnitude and increases with temperature. When heat transfer through contacts dominates in a bed of sub-mm-sized grains, thermal inertia is no larger than 30 J/m2/ K/s1/2 above the Jupiter orbit and decreases with heliocentric distance ∝ D-1 for the same reasons as explained above. It may as low as 4 J/m2/ K/s1/2 at 50 AU. In case of loose contacts, thermal inertia is below 10 J/m2/ K/s1/2 above D = 14 AU for sub-mm grains and always lower than this at 50 AU, whatever the grain size. For grains smaller than a few tens of μm, the thermal inertia Γ ∝ D− 1/2 as KE ∝ KS ∝ T and Γ ∝ (T2)1/2 ∝ T ∝ D− 1/2. This agrees with similar discussion provided by Lellouch et al. (2013) but adding here the dependency on the grain size and domains of predominance of solid versus radiative conductions. Radiative conduction dominates for R ≥ 100 μm and Γ ∝ D-1. But due to the rapid decrease of the specific heat capacity with temperature beyond 50 AU, the slope is a bit steeper, β ~ −1.3.
 |
Fig. 8 Thermal inertia versus heliocentric distance D, considering either tight (full line) or loose contacts (dashed line), amorphous ice form, grain size R = 1 mm and emissivity ϵ = 1. Left panel: as a function of Bond albedo A for p = 0.5. Right panel: as a function of porosity p for A = 0.5. See Fig. 7 for further details. |
The range of inertias of both Jovian and Kronian satellites is compatible with regoliths of sub-cm-sized grains of moderate porosity, either made of crystalline ice if the contacts are loose or of amorphous ice regardless of the quality of contacts. Inertias lower than 60 J/m2/ K/s1/2 can hardly be explained by tight contacts between grains unless the porosity is larger than 0.8. The low thermal inertias of Centaurs can hardly be explained by crystalline grains unless their regoliths are made off 100 μm to mm sized grains with loose contacts. This is even more difficult for most TNOs but if their thermal inertia is about 10 J/m2/ K/s1/2. It is straightforward to reproduce the dependence of thermal inertia with heliocentric distance and values as low as a few J/m2/ K/s1/2 for moderate porosities and grain sizes ranging from 10 μm to 1 cm with grains of amorphous ice. The quality of contacts simply constrains the possible range of sizes. Also inertias below 1 J/m2/ K/s1/2 beyond 50 AU can be reproduced mainly because of the very low specific heat capacity of water ice at low temperatures. According to Mastrapa et al. (2013), there is evidence for the presence of both crystalline and amorphous forms of water ice from Jupiter to the Kuiper belt. The balance between the thermal crystallization of amorphous ice on the surface and the amorphization at depth by particle bombardment may fix the relative proportion in the near surface. Amorphous ice is most probably at the equivalent temperatures of the trans-Neptunian orbits and crystallization may happen on the largest, maybe geologically active bodies.
The Bond albedo A directly impacts the equilibrium temperature at the surface and therefore its thermal inertia. The thermal inertia of a regolith of mm-sized grains and porosity p = 0.5 decreases by a factor 3 at Jupiter orbit or a factor of 5 at 50 AU as A varies between 0.1 and 0.9 (Fig. 8), regardless of the type of contacts. This is about half the dispersion observed at a given D. The dwarf planet Haumea, which exhibits the lowest thermal inertia of our sample, is also a very bright object with a geometric albedo in visible of about 80% (Fornasier et al. 2013). Hence, the low thermal inertia of that planet may be effectively due to a lower temperature and higher albedo compared to objects orbiting in the neighborhood, such as Orcus, whose albedo is about 23% (Fornasier et al. 2013) and whose thermal inertia about three times as large. The porosity of the regolith directly affects the heat transfer processes and the thermal inertia at a given temperature as shown in Fig. 5. Thermal inertia is very sensitive to porosity in the case of tight contacts, whereas it is almost insensitive to porosity in case of loose contacts, as expected. Consequently, the thermal inertia of a regolith of mm-sized amorphous grains with A = 0.5 can vary by similar amounts at 5 and 50 AU when porosity varies from 0.26 to 0.84 for tight contacts. Dispersions in Bond albedo A (or equivalently emissivity), porosity p, or grain size R among icy bodies at some heliocentric distance may perfectly explained the dispersion observed in thermal inertia, without considering further vertical variations of these properties within the regolith over thermal skin depths, i.e., a few cm typically.
4. Conclusions
The objective here was to understand why the thermal inertias of surfaces of icy atmosphereless bodies observed in the solar system are so low, how the thermal dichotomy between Mimas leading and trailing faces can be understood in terms of changes in regolith properties and, finally, how/if the very low thermal inertia of Centaurs and TNOs or the apparent decrease of the thermal inertia of icy atmosphereless with heliocentric distance can be explained and with what implications on their structure. Different models, derived either from theoretical or experimental considerations and commonly used in the literature dealing with heat transfer in packed beds, have been implemented and/or coupled to estimate the thermal inertia of an icy regolith as a function of the size of grains, its porosity, the ice form and the temperature.
On the one hand, it is difficult to obtain thermal inertias as low as a few tens J/m2/ K/s1/2 beyond Jupiter orbit with crystalline ice grains and plausible sizes or porosity, if the conductivity by contacts is as efficient as Hertz or derived theories propose. Only loose contacts, as observed in some laboratory experiments, can yield such values, for a regolith of sub-mm-sized grains. On the other hand, this is straightforward if amorphous ice is considered as the primary material at cm depths because of its conductive properties are derived from samples obtained by compression of crystalline ice and not by vapor deposition. This is valid for any kind of sub-cm-sized grains and normal regolith porosities. The quality of contacts just controls the range of porosity and sizes.
We examined the thermal dichotomy between leading and trailing faces of Mimas and the low thermal inertia of the trailing face. The high thermal inertia of the leading face can be explained by a regolith of crystalline grains of any porosity and grain sizes with tight contacts, eventually sintered by the bombardment of high energy electrons. A regolith of large cm-sized grains dominated by radiative conductivity is also possible but contradictory to other NIR spectroscopy measurements. For loose contacts, it can also be reproduced by grains as small as 30 μm and porosity ≤0.7; hence, heat transfer happens through contacts. The regolith on the trailing face has to be made of grains in the 200-μm to 2-mm range in size on the trailing face with loose contacts. If the ice is amorphous at cm depth, the low thermal inertia of the trailing face can be reproduced with grains no larger than a few mm, and the porosity is ruled by the quality of contacts. If it is amorphous, the regolith on the leading face has then to be dominated by radiative heat transfer in between large cm-sized grains or by grains that are smaller than 100 μm and compacted (p ≤ 0.4). Here again spectroscopic observations favor the latter scenario of compaction for this ice form.
The effective thermal inertia of a regolith of crystalline grains is about constant with temperature, but for grains larger than a cm, whereas that of a regolith of amorphous ice increases with it, in all cases of sizes and porosity, because of both the temperature dependence of thermophysical properties and the radiative conduction. This yields a significant decrease of thermal inertia with heliocentric distance. The very low thermal inertia of TNOs and the general trend of decreasing thermal inertia of icy atmosphereless surfaces with distance is easily explained by moderately porous regoliths of sub-cm-sized grains made of amorphous ice. In such regoliths, heat transfer by radiative conduction indeed dominates over solid conduction through contacts, for sizes greater than 100 μm.
As a consequence, the temperature dependency of the thermophysical properties and radiative conduction should be systematically included in thermal models used for the inversion of thermal inertia from observed thermal cycles of these icy moons as well as small bodies such as 67P for which thermal data as well as radar sounding are available. This kind of study may also deserve some development into other icy compounds and eventually mixtures. Also measurements of thermal inertia versus depth as derived from different transient phenomena such as eclipse or diurnal cycles should be studied to test the hypothesis of amorphous ice underneath layers. Radar sounding may also provide hints about this if the data are available.
Acknowledgments
This work was supported by the Centre National d’Études Spatiales (CNES) and CEA (Commissariat à l’Énergie Atomique et aux Énergies Alternatives). A.L. is supported by ANR Exodunes (ANR-12-BS05-001-03/EXODUNES) and Labex Univearths (ANR-10-LABX-0023,ANR-11-IDEX-0005-02). We thank A. Le Gall and S. Rodriguez for fruitful input and support. We thank the referee for fruitful comments on this work and close inspection of the proposed model. This work also benefitted from the mild and inspiring climate of Madrid city.
References
- Andersson, O., & Suga, H. 1994, Solid State Commun., 91, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Argento, C., & Bouvard, D. 1996, Int. J. Heat Mass Transfer, 39, 1343 [CrossRef] [Google Scholar]
- Aumatell, G., & Wurm, G. 2014, MNRAS, 437, 690 [NASA ADS] [CrossRef] [Google Scholar]
- Baragiola, R. A. 2003, Planet. Space Sci., 51, 953 [NASA ADS] [CrossRef] [Google Scholar]
- Breitbach, G., & Barthels, H. 1980, Nucl. Technol., 49, 392 [Google Scholar]
- Buratti, B. J., Mosher, J. A., Nicholson, P. D., et al. 1998, Icarus, 136, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Buratti, B. J., Brown, R. H., Clark, R. N., et al. 2011, 42nd Lunar and Planetary Science Conf., LPI Contribution, 1608, 1634 [Google Scholar]
- Capria, M. T., Tosi, F., De Sanctis, M. C., et al. 2014, Geophys. Res. Lett., 41, 1438 [NASA ADS] [CrossRef] [Google Scholar]
- Carlslaw, H. S., & Jaeger, J. C. 1959, Conduction of Heat in Solids, 2nd edn. (Oxford: Clarendon Press) [Google Scholar]
- Carvano, J. M., Migliorini, A., Barucci, A., et al. 2007, Icarus, 187, 574 [NASA ADS] [CrossRef] [Google Scholar]
- Chan, C. K., & Tien, C. L. 1973, ASME J. Heat Transfer, 95, 302 [Google Scholar]
- Cruikshank, D. P., Owen, T. C., Dalle Ore, C., et al. 2005, Icarus, 175, 268 [NASA ADS] [CrossRef] [Google Scholar]
- De Bergh, C., Schaller, E. L., Brown, M. E., et al. 2013, in The Science of Solar System Ices, eds. M. S. Gudipati & J. Castillo-Rogez (Springer), 107 [Google Scholar]
- Derjaguin, V. M., et al. 1975, Colloid Interface Sci., 53, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Delbo, M., dell’Oro, A., Harris, A. W., et al. 2007, Icarus, 190, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Dullien, F. A. 1991, Porous Media, Fluid Transport and Pore Structure (New York: Academic Press) [Google Scholar]
- Emery, J.-P., Burr, D. M., Cruikshank, D. P., et al. 2005, A&A, 435, 353 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferrari, C., & Reffet, E. 2013, Icarus, 223, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Fornasier, S., Lellouch, E., Müller, T., et al. 2013, A&A, 555, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Filacchione, G., Capaccioni, F., McCord, T. B., et al. 2007, Icarus, 186, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Filacchione, G., Capaccioni, F., Clark, R. N., et al. 2010, Icarus, 206, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Filacchione, G., Capaccioni, F., Ciarniello, M., et al. 2012, Icarus, 220, 1064 [NASA ADS] [CrossRef] [Google Scholar]
- Groussin, O., Sunshine, J. M., Feaga, L. M., et al. 2013, Icarus, 222, 580 [CrossRef] [Google Scholar]
- Gundlach, B., & Blum, J., 2012, Icarus, 219, 618 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gundlach, B., & Blum, J., 2013, Icarus, 223, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Gundlach, B., & Blum, J. 2015, ApJ, 798, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Gundlach, B., Kilias, S., Beitz, E., et al. 2011, Icarus, 214, 717 [NASA ADS] [CrossRef] [Google Scholar]
- Gusarov, A. V., Laoui, T, Froyen, L., & Titov, V. I. 2003, Int. J. Heat Mass Transfer, 46, 1103 [CrossRef] [Google Scholar]
- Hansen, O. L. 1973, Icarus, 18, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, G. B., & McCord, T. B. 2004, JGR, 109, E01012 [Google Scholar]
- Howett, C. J. A., Spencer, J. R., Pearl, J., et al. 2010, Icarus, 206, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Howett, C. J. A., Spencer, J. R., Schenk, P., et al. 2011, Icarus, 216, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Howett, C. J. A., Spencer, J. R., Hurford, T., et al. 2012, Icarus, 221, 1084 [NASA ADS] [CrossRef] [Google Scholar]
- Howett, C. J. A., Spencer, J. R., Hurford, T., et al. 2014, Icarus, 241, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Jagota, A., & Hui, C. Y. 1990, J. App. Mechanics, 57, 789 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, K. L. 1985, Contact Mechanics (Cambridge: Cambridge University Press) [Google Scholar]
- Johnson, K., Kendall, K., & Roberts, A. D. 1971, Proc. Roy. Soc. London A, 324, 301 [Google Scholar]
- Kaplar, C. W. 1963, Proc. of the Permafrost Int. Conf., 293 [Google Scholar]
- Kiuchi, M., & Nakamura, A. M. 2014, Icarus, 239, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Klinger, J. 1980, Science, 209, 271 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kofman, W., Herique, A., Barbin, Y., et al. 2015, Science, 349, aab0639 [Google Scholar]
- Kouchi, T., Greenberg, J. M., Yamamoto, T., et al. 1992, ApJ, 388, L73 [Google Scholar]
- Lellouch, E., Santos-Sanz, P., Lacerda, P., et al. 2013, A&A, 557, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindgren S. 1970, in Proc. IAHR symposium, ice and its action on hydraulic structures, 6.7.1 [Google Scholar]
- Mastrapa, R. M. E., Grundy, W. M., & Gudipati, M. S. 2013, in The Science of Solar System Ices, eds. M. S. Gudipati & J. Castillo-Rogez (Springer), 371 [Google Scholar]
- Moore, M. H., & Hudson, R. L. 1992, ApJ, 401, 253 [NASA ADS] [Google Scholar]
- Morrison, D., & Cruikshank, D. P. 1973, Icarus, 18, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Newmann, S. F., Buratti, B. J., Brown, R. H., et al. 2008, Icarus, 193, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Paranicas, C., Roussos, E., Krupp, N., et al. 2012, Planet. Space Sci., 61, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Paranicas, C., Roussos, E., Decker, R. B., et al. 2014, Icarus, 234, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Pinilla-Alonso, N., Brunetto, R., Licandro, J., et al. 2009, A&A, 496, 547 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piqueux, S., & Christensen, P. R. 2009, J. Geophy. Res., 114, E09005 [Google Scholar]
- Presley, M. A., & Christensen, P. R. 1997, JGR, 102, E3, 6551 [Google Scholar]
- Reffet, E., Verdier, M., & Ferrari, C. 2015, Icarus, 254, 276 [NASA ADS] [CrossRef] [Google Scholar]
- Rubiolo, P., & Gatt, J.-M. 2002, Int. J. Therm. Sci., 41, 401 [CrossRef] [Google Scholar]
- Schenk, P., Hamilton, D. P., Johnson, R. E., et al. 2011, Icarus, 211, 740 [NASA ADS] [CrossRef] [Google Scholar]
- Scipioni, F., Schenk, P., & Tosi, F. 2015, 46th Lunar and Planetary Science Conference, LPI Contribution, 1832, 1919 [NASA ADS] [Google Scholar]
- Sirono, S., & Yamamoto, T. 1997, Planet. Space Sci., 45, 827 [NASA ADS] [CrossRef] [Google Scholar]
- Shoshany, Y., Prialnik, D., & Podolak, M. 2002, Icarus, 157, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Shulman, L. M. 2004, A&A, 416, 187 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Slavin, A. J., et al. 2002, Int. J. Heat Mass Transfer, 45, 4151 [CrossRef] [Google Scholar]
- Spencer, J. R. 1987, Ph.D. Thesis, University of Arizona, USA [Google Scholar]
- Spencer, J. R., Lebofsky, L. A., & Sykes, M. V. 1989, Icarus, 78, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Spencer, J. R., Tamppari, L. K., Martin, T. Z., et al. 1999, Science, 284, 1514 [NASA ADS] [CrossRef] [Google Scholar]
- Ulrichs, J., & Campbell, M. J. 1969, Icarus, 11, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Van Antwerpen, W., du Toit, C. G., & Rousseau, P. G. 2010, Nuclear Engineering and Design, 240, 1803 [Google Scholar]
- Watson, K. 1964, Ph.D. dissertation, Calif. Inst. of Technol., Pasadena, USA [Google Scholar]
- Winter, D. F., & Saari, J. M. 1969, ApJ, 156, 1135 [NASA ADS] [CrossRef] [Google Scholar]
- Zehner, P., & Schlunder, E. U. 1970, Chemie Ing. Techn., 42, 933 [Google Scholar]
All Tables
Model expressions for Hertz factor h, porosity influence φ(p) on solid phase conductivity KC and exchange factor FE for radiative conductivity KR.
Thermal inertia measurements of icy bodies in the solar system (in J/m2/ K/s1/2).
All Figures
 |
Fig. 1 Left panel: radiative conductivity KR as a function of porosity p and grain size R, at mean temperature T = 80 K, emissivity ϵ = 1, solid thermal conductivity KS,C(T) = 567 /T for the crystalline ice form. Curves correspond to Breitbach and Barthels (BB, full line) and Gundbach and Blum (GB, dotted line) models. Right panel: temperature dependence of the radiative conductivity for p = 0.5 and R = 1 cm. Model curves are also plotted for emissivity ϵ = 0.5 in red (BB: dashed line; GB: dot-dashed line). |
| In the text | |
 |
Fig. 2 Contact conductivity KC of a packed bed of grains of size R (from yellow to dark red) as a function of its porosity p at temperature T = 80 K and emissivity ϵ = 1. Left panel: crystalline ice form. Right panel: amorphous ice form. Curves correspond to Watson theory (W, full line; loose contacts), Gusarov model for porosity coupled with JKR contact theory (G+JKR, dashed line; tight contacts) and Gundbach and Blum (GB, dotted line; tight contacts) models. |
| In the text | |
 |
Fig. 3 Effective thermal conductivity KE as a function of grain size R at T = 80 K, emissivity ϵ = 1 for both crystalline (full line) and amorphous (dotted line) ice forms. Top left panel: high (G+JKR); Top right panel: intermediate (GB); Bottom panels: low (W) contact conductivities are shown, coupled with either Breitbach and Barthels (+BB) or Gundlach and Blum (+GB) models for radiative conductivity (−...− line). Colors correspond to increasing porosity: from p = 0.26 (black), p = 0.5 (red) to p = 0.84 (orange). |
| In the text | |
 |
Fig. 4 Thermal inertia |
| In the text | |
 |
Fig. 5 Thermal inertia versus temperature T for grain size R. Left panels: R = 100 μm. Right panels: R = 1 cm, tight contacts (top panels) or loose contacts (bottom panels). The thermal inertia is given for crystalline (full line) or amorphous (dotted line) ice forms for porosities p = 0.26 (black), p = 0.5 (red) and p = 0.84 (orange). The bulk thermal inertias of crystalline (dashed line) and amorphous (dot-dashed line) forms are also plotted. The contribution of radiative conductivity to thermal inertia is also plotted (−...− line). |
| In the text | |
 |
Fig. 6 Constraints set on porosity p and grains size R by the observed thermal inertias of region R1 of the trailing face of Mimas (dark gray, Γ1 ≤ 16J/m2/ K/s1/2) and region R2 of the leading face (light gray, Γ2 = 66 ± 23J/m2/ K/s1/2) of Mimas (Howett et al. 2011). Left panels: crystalline water ice. Right panels: amorphous water ice. Both tight (top panels) and loose (bottom panels) contacts cases are considered too (see Fig. 5 for details). Temperature is assumed to be 80 K here. |
| In the text | |
 |
Fig. 7 Thermal inertia versus grain size R (top panels) or heliocentric distance D (bottom panels), considering the crystalline ice (left panels) or amorphous ice (right panels) forms. Porosity is fixed at p = 0.5, bolometric Bond albedo A = 0.5 and emissivity ϵ = 1. Both tight (full line) or loose (dashed line) contacts are considered in each case. Data from Table 2 are plotted. Mimas data are plotted as a black symbol for both R1 (trailing) and R2 regions. The best fit of Γ(D) with the data is plotted also (dot line, see text). |
| In the text | |
 |
Fig. 8 Thermal inertia versus heliocentric distance D, considering either tight (full line) or loose contacts (dashed line), amorphous ice form, grain size R = 1 mm and emissivity ϵ = 1. Left panel: as a function of Bond albedo A for p = 0.5. Right panel: as a function of porosity p for A = 0.5. See Fig. 7 for further details. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.