| Issue |
A&A
Volume 588, April 2016
|
|
|---|---|---|
| Article Number | A42 | |
| Number of page(s) | 10 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201527566 | |
| Published online | 15 March 2016 | |
Spin-up of massive classical bulges during secular evolution
1 Inter-University Centre for Astronomy
and Astrophysics, Post Bag
4, Ganeshkhind,
411007 Pune, India
,
e-mail:
kanak@iucaa.in
2
Max-Planck-Institut für Extraterrestrische Physik,
Giessenbachstrasse,
85748
Garching,
Germany
e-mail:
gerhard@mpe.mpg.de
3
Instituto de Astrofisica de Canarias, 38205, La Laguna, Tenerife, Spain
e-mail:
imv@iac.es
Received: 15 October 2015
Accepted: 21 December 2015
Context. Classical bulges in spiral galaxies are known to rotate, but the origin of this observed rotational motion is not well understood. It has been shown recently that a low-mass classical bulge (ClB) in a barred galaxy can acquire rotation by absorbing a significant fraction of the angular momentum emitted by the bar.
Aims. Our aim here is to investigate whether bars can also spin up more massive ClBs during the secular evolution of the bar, and to study the kinematics and dynamics of these ClBs.
Methods. We use a set of self-consistent N-body simulations to study the interaction of ClBs with a bar that forms self-consistently in the disk. We use orbital spectral analysis to investigate the angular momentum gain by the classical bulge stars.
Results. We show that the ClBs gain on average 2−6% of the disk’s initial angular momentum within the bar region. Most of this angular momentum gain occurs via low-order resonances, particularly 5:2 resonant orbits. A density wake forms in the ClB which corotates and aligns with the bar at the end of the evolution. The spin-up process creates a characteristic linear rotation profile and mild tangential anisotropy in the ClB. The induced rotation is small in the centre, but is significant beyond ~2 bulge half mass radii, where it leads to mass-weighted V/σ ~ 0.2, and reaches a local Vmax/σin ~ 0.5 at around the scale of the bar. The resulting V/σ is tightly correlated with the ratio of the bulge size to the bar size. In all models, a box/peanut bulge forms suggesting that composite bulges may be common.
Conclusions. Bar-bulge resonant interaction in barred galaxies can provide some spin-up of massive ClBs, but the process appears to be less efficient than for low-mass ClBs. Further angular momentum transfer due to nuclear bars or gas inflow would be required to explain the observed rotation if it is not primordial.
Key words: galaxies: bulges / galaxies: structure / galaxies: kinematics and dynamics / galaxies: spiral / galaxies: evolution
© ESO, 2016
1. Introduction
Classical bulges (hereafter ClBs) are the central building blocks in many early-type spiral galaxies. Classical bulges might have formed as a result of major mergers during the early phase of cosmic evolution (Kauffmann et al. 1993; Baugh et al. 1996; Hopkins et al. 2009; Naab et al. 2014), or through a number of other mechanisms such as the monolithic collapse of primordial gas clouds (Eggen et al. 1962), the coalescence of giant clumps in gas-rich primordial galaxies (Noguchi 1999; Immeli et al. 2004; Elmegreen et al. 2008), violent disk instability at high-redshift (Ceverino et al. 2015), multiple minor mergers (Bournaud et al. 2007; Hopkins et al. 2010), and accretion of small companions or satellites (Aguerri et al. 2001). Although most of these studies do not provide quantitative predictions for the bulge kinematics, it is generally believed that ClBs formed through these processes have low rotation compared to the random motion. For example, Naab et al. (2014) showed that spheroids produced by minor and major mergers (which include ClBs) in full cosmological hydrodynamical simulations have a wide range of rotational properties; the massive ones have V/σ less than 0.5. Elmegreen et al. (2008) reported dispersion dominated clump-origin ClBs with upper limit on V/σ ~ 0.4−0.5, where V is the rotation velocity and σ is the central velocity dispersion. A similar study by Inoue & Saitoh (2012) suggests that clump-origin bulges have exponential surface density profiles and rotate rapidly with V/σ ~ 0.9, resembling pseudobulges (Kormendy & Kennicutt 2004). However, using cosmological hydrodynamical simulations with continuous gas accretion, Ceverino et al. (2015) showed that massive classical bulges with non-zero angular momenta are produced at high redshift, but provided no estimate on the bulge V/σ. Overall, there is no clear quantitative picture of the rotational motion induced during the formation of classical bulges in numerical simulations.
Various observational measurements have confirmed that ClBs in spiral galaxies possess rotation about their minor axis and in most cases in the same sense as the disk rotates (Kormendy & Illingworth 1982; Cappellari et al. 2007; Fabricius et al. 2012). Disk galaxies both barred (e.g. NGC 1023, NGC 3992) and unbarred (e.g. NGC 4772, NGC 2841) host ClBs with a wide range of masses and sizes (Kormendy & Illingworth 1982; Kormendy 1982; Laurikainen et al. 2007; Cappellari et al. 2007). More recently, Fabricius et al. (2012) have obtained detailed kinematic observations of a large sample of bulges including ClBs (whose classification is based primarily on the bulge Sersic index). From these studies it is known that ClBs rotate typically with V/σ close to an oblate isotropic rotator model (Binney 1978), i.e. faster than low-luminosity elliptical galaxies but more slowly than pseudobulges. The origin of the rotational motion observed in ClBs remains unclear.
Recent cosmological hydrodynamical simulations, which include feedback and smooth accretion of cold gas through cosmic filaments, show that exponential disks could have assembled around merger-built ClBs and grown through the galaxy’s assembly history (Governato et al. 2007; Agertz et al. 2011; Brook et al. 2012). Once such a disk becomes massive and dynamically cold, its self-gravity may induce a bar instability leading to rapid formation of a bar, which would then interact with the preexisting ClB (Hernquist & Weinberg 1992; Athanassoula & Misiriotis 2002; Saha et al. 2012). In particular, Saha et al. (2012) showed that an initially non-rotating low-mass ClB could absorb a significant fraction of the angular momentum emitted by the bar and end up rotating within ~2 Gyr. However, it is not clear yet how more massive ClBs would react to the bar.
The goal of this paper is to investigate whether angular momentum transfer from the bar is an important process for the origin of angular momentum in ClBs embedded in spiral galaxies. To this end, we use collisionless N-body simulations to study the secular evolution in a set of model galaxies with initially non-rotating ClBs with different masses and sizes. Our simulation results show that massive ClBs could indeed be spun up in their outer parts, typically in less than half of the Hubble time. In these models, a box/peanut bulge always forms alongside the secular evolution, suggesting that composite bulges may be common.
The paper is organized as follows. In Sect. 2, we describe the initial galaxy models and the set-up for the N-body simulations. Section 3 describes the growth of a bar and its size evolution in these models. The transfer of angular momentum and the orbital analysis to account for the resonant trapping are described in Sect. 4. The kinematic properties of the these bulges are described in Sect. 5. Finally, a discussion of the results and the conclusions from this work are presented in Sect. 6.
2. Initial galaxy models with massive bulges
We present here a set of seven galaxy models constructed using the self-consistent method of Kuijken & Dubinski (1995). Each galaxy model consists of a live disk, a dark matter halo, and a bulge. The initial disk is modelled with an exponentially declining surface density in the radial direction with a scale-length Rd, mass Md, and with a sech2 distribution of stars with vertical scale-height hz. The initial radial velocity dispersion of the disk stars follows an exponential distribution with a radial scale-length Rσ = 0.5Rd such that the disk has a constant scale-height throughout. The live dark matter halo is modelled with a lowered Evans model and the classical bulge with a King model. The dark matter halo has a core in the inner regions of the galaxy model and produces a nearly flat rotation curve in the outer parts of the disk. For details on constructing these models, the readers are referred to Saha et al. (2010, 2012).
 |
Fig. 1 Initial total circular velocity curves a); the total circular velocity curves at 4 Gyr b); Toomre Q profiles c); and Mass-size relation for the initial ClBs d). |
Initial bulge, disk, and halo model parameters, ordered by the ratio of ClB to disk mass.
We scale each model such that the initial disk scale-length Rd = 4 kpc and the circular velocity at ~8.5 kpc is ~200 kms-1. The initial circular velocity curves for all the models are shown in Fig. 1a. Each model has a characteristic profile for the Toomre Q(R) = σr(R)κ(R)/3.36GΣ(R), where σr, κ, and Σ denote the radial velocity dispersion, epicyclic frequency, and the surface density of stars (see Fig. 1c). The stellar disks in our sample range from dynamically cold to fairly hot. Table 1 summarizes the initial parameters of the disk, bulge, and dark halo.
The bulges in our galaxy models are initially non-rotating and dispersion dominated. The Sersic indices for these King model bulges are generally close to 1 or less. Recent findings show that barred galaxies can have classical bulge like components with Sersic indices close to 1 or less (Laurikainen et al. 2007; Erwin et al. 2015). The density profiles in the inner region are flatter than R1/4 profiles, which are known to represent the surface brightness profiles of traditional ClBs (de Vaucouleurs 1953; Fisher & Drory 2010). Unlike R1/4 profiles, the density profile of a King model bulge has a well-defined outer boundary – defined by the truncation radius Rb given in Table 1 – and other well-studied properties, which motivated us to use them as a simple model for the bulges. Setting up of the stellar kinematics for the bulge stars is relatively straightforward since it is modelled by an analytic DF (King model, fb(E)) that only depends on the energy integral (E). Assigning a velocity to a bulge star is done in the following way: we find the local maximum of the DF corresponding to a star’s position, and then employ an acceptance-rejection technique to find a velocity. The three components of a star’s velocity (vx,vy,vz) are randomly selected from a velocity sphere with radius equal to the local escape velocity. The velocity ellipsoid is isotropic by construction. The DF accepts three free parameters, of which σb determines the velocity dispersion of the bulge stars; the higher the σb, the larger the value of the velocity dispersion. Modelled in this way, our initial ClBs are kinematically hot spheroidal stellar systems that are similar to typical observed ClBs.
To further compare our initial ClBs with observed ClBs, we performed a 2D bulge-disk decomposition of our initial galaxy models. We first made FITS files for all the galaxy models and analysed them with GALFIT (Peng et al. 2002). In Fig. 1d we show the effective radii and masses for our initial ClBs, and compare them with the relation 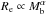 with α = 0.3 for observed ClBs found by Gadotti (2009). Most of our initial ClBs follow this relation closely, while models RHG109 and RCG076 are 1σ away from the mean relation.
with α = 0.3 for observed ClBs found by Gadotti (2009). Most of our initial ClBs follow this relation closely, while models RHG109 and RCG076 are 1σ away from the mean relation.
We evolved each galaxy model in isolation to examine the evolution of the bulge shape, morphology, and kinematics. The simulations were performed using the Gadget code (Springel et al. 2001), which uses a variant of the leapfrog method for the time integration. The forces between the particles were calculated using the Barnes & Hut (BH) tree with some modification with a tolerance parameter θtol = 0.7 (Springel et al. 2001). We computed the virial equilibrium condition of a galaxy model at different times using the Gadget output; although some of the models were initially out of equilibrium (by about a few percent), we found that they settled down close to virial equilibrium (by about a percent or less) within a rotational time scale. A total of 2.2 × 106 particles were used to simulate each model galaxy, of which 1.0 × 105 in the ClB, 1.05 × 106 in the disk, and 1.05 × 106 in the dark matter halo. The softening lengths for the disk, bulge, and halo were all unequal and were chosen so that the maximum force from particles of all species (bulge, disk, halo) was nearly the same (McMillan & Dehnen 2007).
3. Growth of a bar and its size evolution
Although about 70% of disk galaxies in the local universe are barred (Eskridge et al. 2000; Barazza et al. 2008), the formation of a bar is still not fully understood. The growth rate of a bar in a disk galaxy depends on various parameters of the disk and its gravitational interaction with the surrounding dark matter halo and preexisting ClB (if present). Numerous studies of N-body simulations show that a bar forms and grows rapidly in a cold rotating stellar disk with Toomre Q close to 1 (Hohl 1971; Sellwood & Wilkinson 1993; Athanassoula 2002; Dubinski et al. 2009, and references therein). Swing amplification (Toomre 1981) and cooperation of orbital streams (Earn & Lynden-Bell 1996) are thought to play a key role in the bar growth. The linear growth of a bar is directly affected by the Toomre Q of the stellar disk as can be seen from Fig. 3. A bar grows rapidly in a cool disk, whereas it grows rather slowly in a hotter disk (Saha et al. 2010). The slow growth of a bar occurs through non-linear processes; in particular, the resonant gravitational interaction with the surrounding dark matter halo is known to play a major role. This has been investigated by several authors in the past (Debattista & Sellwood 1998; Athanassoula 2002; Holley-Bockelmann et al. 2005; Weinberg & Katz 2007; Ceverino & Klypin 2007; Saha & Naab 2013).
 |
Fig. 2 Face-on surface density maps for all model galaxies after 4 Gyr of evolution. |
 |
Fig. 3 Time evolution of the bar strength in our galaxy models with pre-existing classical bulges. |
 |
Fig. 4 Upper panels: distribution of bulge stars with frequency (Ω−ΩB) /κ at different times throughout the secular evolution in model RHG097. Lower panels: net change in the angular momentum of the selected stars with respect to the previous time. The vertical dotted lines indicate the most important resonances (from left to right): −1:1, 4:1, 3:1, 5:2, and 2:1. As time progresses, more stars are trapped by the ILR of the bar in the stellar disk. However, most of the angular momentum transfer occurs through the 5:2 resonance. |
The role of a pre-existing ClB alone on the formation and evolution of a bar has not been fully investigated. Bar formation could, in principle, be hampered by a central mass concentration (Hasan et al. 1993; Sellwood & Moore 1999; Athanassoula et al. 2005) because the bulge could cut the feedback loop required for swing amplification by placing an inner Lindblad resonance (ILR) near the centre of a galaxy. In previous studies (e.g. Saha et al. 2012), a low-mass initially non-rotating ClB facilitated the bar growth by absorbing angular momentum through the ILR. Later, Saha & Gerhard (2013) investigated the effect of varying the degree of initial rotation in the preexisting ClB, but a detailed investigation of the effect of massive bulges on bar formation is yet to be done.
All the galaxy models in our simulation sample have a preexisting ClB of different mass and size (see Table 1), and they all form a bar in their stellar disks. Figure 2 shows surface density maps for all stars in each galaxy model at the end of 4 Gyr. The models are arranged such that the initial value of the bulge-to-disk mass ratio increases gradually from the top left corner (RCG076) of Fig. 2 to the bottom right corner (RHG097). We note that Toomre Q alone is not the factor that decides the final outcome of these models. Dark matter distribution and the bulge might also play an important role. Most of these models do not form long-lived two-armed spirals.
In Fig. 3 we show the time evolution of the bar amplitude (A2/A0) in all our models. A2 and A0 are the m = 2 and m = 0 Fourier component of the surface density, respectively. The fastest bar growth is seen in model RCG100 (Q = 1.4). From Figs. 1a and 3, we see that generally the steeper the slope of the initial rotation curve, the faster the growth rate of a bar (see model RCG100 versus RCG099 and RHG076). However, the correspondence between growth rate and slope of the rotation curve is not one-to-one. For instance, the linear growth rate of the bar in RCG076 is higher than RCG110, although the latter has a steeply rising rotation curve. Faster bar growth is also supported by higher values of 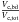 (see Table 1). We note that the bar in model RHG109 (Q = 2.8) is the weakest of all.
(see Table 1). We note that the bar in model RHG109 (Q = 2.8) is the weakest of all.
Once formed, the size of a bar increases as it exchanges angular momentum with the surrounding dark matter halo and the pre-existing bulge (Saha et al. 2012). In our simulations, we calculate the bar sizes at different epochs using the method explained in Saha & Gerhard (2013). As these bars grow and become self-gravitating, they undergo the well-known buckling instability that leads to the formation of a boxy/peanut bulge (Combes & Sanders 1981; Pfenniger & Norman 1990; Raha et al. 1991; Martinez-Valpuesta & Shlosman 2004). The galaxy models with prominent boxy/peanut bulges end up with a peak in the rotation curve in the boxy bulge region (see Fig. 1b). The rotation velocities shown in Fig. 1b are calculated at the end of 4 Gyr; by that time nearly all the bars are fully grown and have gone through the buckling instability. The final bulges in our simulations are thus composite bulges, which are a superposition of a ClB and a boxy/peanut bulge formed from the disk stars.
4. Angular momentum transfer and orbital analysis
A bar grows by trapping more and more orbits in its main orbital families (e.g. x1 orbit family). During the process, the stars lose angular momentum to the dark matter halo and the ClB in the model. Since the distribution function, f(E), of the initial ClB is described by a King model where it is a function of energy alone, the gain of angular momentum by the bulge at a given resonance is always positive (Saha et al. 2012). The dark matter haloes in our model galaxies also gain angular momentum, but here we are concerned with investigating the structural and kinematic changes in the ClB that are brought about by the angular momentum gain. To understand the impact of a bar on the pre-existing ClB, we compute the angular momentum transfer between the bar and the bulge in our simulation using orbital spectral analysis (Binney & Spergel 1982; Martinez-Valpuesta & Shlosman 2004; Martinez-Valpuesta et al. 2006). We focus in particular on two models, RHG097 and RCG076, which have the most massive and the least massive ClBs in our sample with Mb/Md = 0.43 and 0.11, respectively (see Table 1).
Figure 4 shows the results of the orbital spectral analysis for the bulge stars in model RHG097 at different times during the evolution. As in the case of a low-mass ClB (see Saha et al. 2012), more and more bulge stars get trapped by the 2:1 resonance of the rotating potential. However, unlike the low-mass case, not much angular momentum is gained through the ILR of the bar by this ClB. In fact, at ~2 Gyr (second panel in Fig. 4), the bulge stars are seen to be losing angular momentum through the ILR and this continues subsequently with gradually diminishing magnitude (except at ~4 Gyr, fourth panel from left). In essence, we find that the massive ClB in RHG097, on average, loses angular momentum through the 2:1 resonance. However, and interestingly, we find that a lot of angular momentum is gained via 5:2 resonant orbit families (corresponding to the peak around (Ω−Ωb) /κ = 0.4 in Fig. 4), and this occurs consistently throughout the evolution. In N-body bars, these 5:2 orbits are known to be stable periodic orbits like the 3:1 and 4:1 families inside the corotation of the bar (Voglis et al. 2007).
Figure 5 shows the results from the spectral analysis of model RCG076. We found a similar trend to model RHG097: a fraction of ClB stars in both models is gradually trapped at the 2:1 resonance of the bar. This persists in all ClBs in our simulations (see Table 1). However, the details and the dominant mode of angular momentum transfer vary. At t = 1.96 Gyr (second panel from left in Fig. 5), the initial bulge of RCG076 loses angular momentum through the 2:1 resonance, but at subsequent times it gains angular momentum consistently through 2:1 orbits. This ClB also gains angular momentum through other resonances; during the early phase of bar growth it gains angular momentum through the 3:1 resonant orbits, but gradually the peak shifts from 3:1 to 5:2 resonance (see the rightmost panel in Fig. 5). It is interesting to note that these resonances are broader than the usual 2:1 resonance, a feature that is common in the bulges of both RHG097 and RCG076 as well as in the bulge discussed in Saha et al. (2012). In other words, associated with these resonances (i.e. 3:1, 5:2), there are many off-resonant particles that contribute to the net angular momentum transfer. While the two ClBs in models RHG097 and RCG076 gain angular momentum through 5:2 resonance, we do not see any angular momentum transfer through the −1:1 orbital families outside corotation, which contributed in the case of the low-mass ClB studied by Saha et al. (2012) using 10 million particles. It is not clear to us whether this is due to the lower particle resolution in the current models (2.2 million particles). Since a low-resolution noisy simulation could artificially enhance the star-star encounters and knock stars off their resonant orbits, Holley-Bockelmann et al. (2005) and Dubinski et al. (2009) suggested – based on their explicit study on the model resolution and resonant behaviour – that models with a few million particles generally show convergent behaviour.
Other than resonant orbit families, there is also a continuous (chaotic orbits) component of angular momentum transfer of comparable importance in both models RHG097 and RCG076 (around Ω−Ωp/κ ≃ −0.3 in Figs. 4 and 5). We have changed the numerical resolution to calculate the potential on a finer grid and repeated the above analysis to rule out numerical artefacts. Saha et al. (2012) also found significant contributions to the net angular momentum gain of the ClB via non-resonant chaotic orbits. For the two bulges in RHG097 and RCG076, the sign of the angular momentum transfer changes during the evolution. They both gain angular momentum initially via the non-resonant orbits, but in the later phases these bulges mostly lose angular momentum via the stochastic orbits. Over the entire period of evolution, the non-resonant stochastic orbits cause a net loss of angular momentum from these bulges. However, we have verified that the total angular momentum gain through resonant and non-resonant orbits was positive at all times. In the following, we look at the density wakes created in these bulges by the bar.
4.1. Density wakes and bulge harmonics
In this section, we examine the density wakes in the ClBs, primarily the l = 2,m = 2 spherical harmonic modes, as the bulge stars interact with the bar. Figure 6 shows the density perturbation corresponding to the l = 2,m = 2 spherical harmonic mode projected onto the equatorial plane of the bulge at different times during the evolution of RHG097. This density wake arises naturally as the bulge stars interact gravitationally with the rotating bar potential. If dark matter particles interact with the stellar bar, a so-called halo-bar is created in the dark matter halo (Debattista & Sellwood 2000; Holley-Bockelmann et al. 2005; Sellwood & Debattista 2006; Athanassoula 2007; Weinberg & Katz 2007; Saha & Naab 2013). In the present case, we see that the perturbed density in the ClB corresponding to this l = 2,m = 2 mode becomes stronger as time progresses, in proportion to the number of trapped bulge stars at the 2:1 resonance (see upper panels of Figs. 4 and 5). The disk bar rotates anticlockwise and its instantaneous position angle is denoted by the dashed line (see Fig. 6).
 |
Fig. 6 Density wake mode (l = 2,m = 2) in the ClB of RHG097. Dashed lines in all panels indicate the location of the bar in the stellar disk while solid lines denote the phase angle corresponding to the bar mode in the classical bulge (ClB). Towards the later phases of the evolution, the ClBb becomes progressively stronger. The red arrow denotes the rotation of the disk bar. We note that at 1 Gyr, a clear bar has not developed yet. The unit of time is in Gyr. |
Initially, the density wake appears in the outer parts of the ClB of RHG097 in the form of a spiral-like feature (at about 1.5 Gyr when the disk bar forms), becomes stronger, and eventually takes the shape of a bar-like mode, although not as clear as in model RCG076 (shown below). The phase of the l = 2,m = 2 mode in the bulge of RHG097 reveals that the disk-bar and the bulge-bar are nearly aligned with each other during the entire evolution. Although there are instances when the two bars are clearly misaligned by a very small angle (mostly in the outer parts; see Fig. 6). This misalignment can cause dynamical friction (Chandrasekhar 1943; Tremaine & Weinberg 1984) thereby leading to the transfer of angular momentum either from the disk-bar to the bulge or vice versa. Figure 4 shows that there is little angular momentum exchange via the 2:1 resonance probably because of the small angle misalignment between the two bars of RHG097.
A similar analysis to the one above is shown in Fig. 7 for the low-mass bulge model in RCG076. The development of a bulge-bar through the l = 2,m = 2 mode follows a similar evolution as in model RHG097, albeit with some differences. As time progresses, the bulge in RCG076 grows a more pronounced bulge-bar. Initially, the density wake lags behind the disk-bar. At t = 1.48 Gyr, a part of the bulge-bar appears to be leading the disk-bar. However, during the later phases of evolution, this bulge-bar lags behind the disk-bar and gains angular momentum through the l = 2,m = 2 mode, in compliance with the angular momentum gain via 2:1 resonant orbits (Fig. 5). So in this case, we have a consistent picture of angular momentum transfer via the 2:1 resonance and the misalignment of bulge-bar and disk-bar.
Inspection of Figs. 6 and 7 shows that the peak of the l = 2,m = 2 density wake develops at different spatial locations in the two bulges; for the massive ClB (RHG097) it is pronounced in the outer parts, while for the low-mass case (RCG076) it is confined to an intermediate radial range. Thus, only the stars in the outer parts of the ClB in model RHG097 take part in the rotational motion (see the line-of-sight velocity maps in Fig. 8). It is likely that both figure rotation and streaming motion within the bulge-bar contribute to the net rotational motion.
5. Bulge kinematics
The orbital configuration of the ClBs in our model galaxies changes as a result of the angular momentum gain via the bar-bulge interaction, and this must manifest itself in the kinematic properties of the ClBs. In this section we focus on the stellar kinematics, in particular on the rotational motion of the classical bulge component induced by the angular momentum gain. By separating the ClB particles from the boxy/peanut bulge that forms from the disk through the bar buckling instability, we investigate the dependence of the acquired rotational motion in the ClBs on various parameters.
5.1. Rotation and dispersion profiles
In Fig. 8 we show the evolution of the massive ClB model RHG097 through surface density, line-of-sight velocity, and dispersion maps in edge-on projection. As the bulge gains angular momentum, it starts picking up rotation. Signs of systematic rotation are obvious at t = 2 Gyr, and at t = 4 Gyr, the ClB rotates faster, with (V/σ) ~ 0.5 in the outer parts. It is interesting to note that the inner parts (R< 2Rb,1/2) of this ClB do not show much rotational motion, which is mostly confined to the outer parts of the ClB. At the end of 4 Gyr, the initially non-rotating ClB has also become slightly rounder and hotter at the centre.
 |
Fig. 8 Surface density (upper panel), line-of-sight velocity and velocity dispersion maps (2nd to 4th panels) of the ClB in RHG097 at different times during the evolution. These images are taken at 90° projection (edge-on view) and the major axis of the bar is aligned with the X-axis. Clear signatures of rotation are seen at 4 Gyr. The colour bar at the top represents density, middle the velocity, and bottom the velocity dispersion. |
In Fig. 9, we show radial profiles of rotational velocity, V(R); velocity dispersion, σ(R); and local V(R) /σin, where σin denotes the average velocity dispersion in the central region (within 0.5Rb,1/2), for four ClBs after 4 Gyr of evolution. We illustrate models RHG097, RCG100, and RCG101 in order of decreasing bulge-to-disk mass ratio, and the relatively compact bulge model RHG109. The slope of the rotational velocity is approximately the same for all four bulges shown in the figure. This is also true for the remaining ClBs in our sample. The mean velocity dispersion profiles are also nearly identical for all these bulges except RHG109, which has lower velocity dispersion throughout. The V/σin profiles for the four bulges are shown at the bottom panel of Fig. 9. In all cases, rotational motion becomes significant in the outer parts of the bulge, for R ≥ 0.5Rd ≃ 2Rb,1/2.
 |
Fig. 9 Rotation, velocity dispersion, and local V/σ radial profiles for the four ClBs in models RHG097, RCG100, RCG101 and RHG109. The blue and black arrows show the half-mass radii for the two bulges of RHG109 and RHG097, respectively. |
In some of the models in which the bar grows rapidly, reaching its peak amplitude (A2,max) within a billion years (e.g. RCG100 and RCG101), the bulge stars acquire significant rotation already within 2 Gyr. Thereafter, over the next 3−4 Gyr, the rotational profiles in these bulges change insignificantly. On the other hand, in models that grow their bar rather slowly and reach peak amplitude over 1−3 Gyr, the rotation velocity in the ClBs continues to change until the bar growth approximately saturates at around 4 Gyr.
Comparing the rotational profiles of our simulated ClBs with those in observed barred galaxies is not straightforward because the kinematic data in external galaxies include both the ClB stars and the stars in the disk and a possible boxy bulge. Recently, Fabricius et al. (2012) analysed a large sample of galaxies containing ClBs residing in both barred and non-barred galaxies. The rotation profiles of the ClB host galaxies in their sample have a wide range from shallow rising profiles to steeply rising profiles often associated with steeply falling velocity dispersion. Visual comparison of the V/σ profiles of their bulges with our simulated ClBs suggest that some of the shallow-rising profiles could be similar to our spun-up ClBs. The amplitude of the rotational profiles (V/σ(R)) for the ClB host galaxies reached within their bulge radius is ~0.5−1.0 (see Fig. 13 in Fabricius et al. 2012). However, we note that their bulge radius is not simply related to the effective radius Re; for their entire sample, it is typically ~2Re. The V/σ(R) reached by the rotation profiles of our spun-up ClBs are ~0.2 at 2Rb,1/2. Beyond this radius, V/σ(R) for our ClBs keeps increasing, reaching V/σ(R) ~ 0.5 at ~4Rb,1/2.
However, the final bulge in our models is always a composite bulge composed of the pre-existing ClB and the boxy bulge formed from the disk. Fig. 10 shows the line-of-sight velocity, dispersion, and surface density profiles of the composite bulge (ClB and boxy bulge combined) of model RHG097. The inner parts of this galaxy model show a moderately rising rotation profile and declining dispersion. The size of the boxy bulge is about 0.6Rbar ≃ 0.6Rd, not much greater than ~2Rb,1/2 of the ClB, which is ≃ 0.5Rd. At this radius, the local V/σ ~ 1.0. The slope of V/σ(R) profile for this composite bulge resembles many of the observed pseudobulges (Fabricius et al. 2012). A more detailed comparison with observations is outside the scope of this paper.
Finally, we discuss the three-dimensional nature of the induced rotational motion in our ClBs. None of the massive bulges in our sample rotates cylindrically after 4−5 Gyr, contrary to the case of the low-mass ClB investigated by Saha et al. (2012). Evidently, the orbital changes that occurred in the high-mass bulges as a result of their interaction with the bar are weaker than in the low-mass case.
 |
Fig. 10 Surface density (top), mean line-of-sight velocity, and dispersion profiles (middle panel) for the composite bulge of model RHG097. The local V/σ profile is shown in the bottom panel. |
 |
Fig. 11 Fractional kinetic energy associated with the rotational motion for the four bulges in RHG097, RCG100, RCG101 and RHG109 in radial bins. The blue and black arrows show the half-mass radii for two bulges RHG109 and RHG097 respectively. |
5.2. Induced rotational kinetic energy and anisotropy
In Fig. 9 we note that 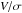 rises in the outer parts of the ClBs, whereas the central parts of the bulge remain with small rotation (
rises in the outer parts of the ClBs, whereas the central parts of the bulge remain with small rotation (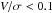 ). This can also be readily seen from the velocity maps of the ClB of RHG097 (see Fig. 8). Both these facts have prompted us to investigate the actual rotational energy that is being imparted by the bar to these bulges. The random kinetic energy of a group of stars moving in the equatorial plane of the bulge, using cylindrical coordinates, is given by
). This can also be readily seen from the velocity maps of the ClB of RHG097 (see Fig. 8). Both these facts have prompted us to investigate the actual rotational energy that is being imparted by the bar to these bulges. The random kinetic energy of a group of stars moving in the equatorial plane of the bulge, using cylindrical coordinates, is given by 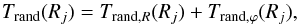 (1)where
(1)where ![\begin{equation} T_{{\rm rand},R}(R_j)= \frac{1}{2} \sum_{i=1}^{N_j} {{m_i [v_R(i)- {\bar{v}}_{R}]^2}}, \end{equation}](/articles/aa/full_html/2016/04/aa27566-15/aa27566-15-eq114.png) (2)and
(2)and ![\begin{equation} T_{{\rm rand},\varphi}(R_j)= \frac{1}{2} \sum_{i=1}^{N_j} {{m_i [v_{\varphi}(i) - {\bar{v}}_{\varphi}]^2}} , \end{equation}](/articles/aa/full_html/2016/04/aa27566-15/aa27566-15-eq115.png) (3)where \begin{lxirformule}$N_j$\end{lxirformule} is the number of bulge stars in the jth radial bin, Rj denotes its radius, mi is the mass of each bulge star, and
(3)where \begin{lxirformule}$N_j$\end{lxirformule} is the number of bulge stars in the jth radial bin, Rj denotes its radius, mi is the mass of each bulge star, and 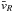 and
and 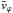 are the mean radial and azimuthal velocity of the stars.
are the mean radial and azimuthal velocity of the stars.
Similarly the rotational kinetic energy is given by 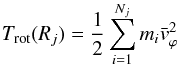 (4)so that the total kinetic energy of a group of stars moving in the equatorial plane is
(4)so that the total kinetic energy of a group of stars moving in the equatorial plane is 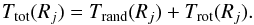 (5)Figure 11 shows the radial distribution of the fractional rotational kinetic energy in the final ClB bulges (used Eqs. (1)−(5)). The figure clearly shows that the inner regions (R< 2Rb,1/2) of these ClBs do not acquire much rotation from the bar; the final rotational kinetic energy amounts to about 5% of the total planar kinetic energy after the evolution. It is the outer regions that acquire most of the angular momentum transferred, where for R> 2Rb,1/2 typically 30−40% of the planar kinetic energy is in rotation for most of the ClBs. A possible explanation for this is given in Sect. 4.1. In terms of mass, this rotating region broadly contains about 40% or less of the total bulge mass.
(5)Figure 11 shows the radial distribution of the fractional rotational kinetic energy in the final ClB bulges (used Eqs. (1)−(5)). The figure clearly shows that the inner regions (R< 2Rb,1/2) of these ClBs do not acquire much rotation from the bar; the final rotational kinetic energy amounts to about 5% of the total planar kinetic energy after the evolution. It is the outer regions that acquire most of the angular momentum transferred, where for R> 2Rb,1/2 typically 30−40% of the planar kinetic energy is in rotation for most of the ClBs. A possible explanation for this is given in Sect. 4.1. In terms of mass, this rotating region broadly contains about 40% or less of the total bulge mass.
In Fig. 12, we show the radial variation of the radial, azimuthal and vertical velocity dispersion (σR,σϕ and σz) for four ClBs at the end of 4 Gyr. Initially, all the bulges were isotropic by construction. Of the four ClBs, RHG109 was spun-up significantly less than the other three after 4 Gyr of evolution. In all four ClBs, the final azimuthal velocity dispersion is slightly higher than the radial and vertical dispersions, with the largest effect in the outskirts where rotation velocity is also highest. Thus Fig. 12 shows that these spun-up bulges tend to become tangentially anisotropic.
 |
Fig. 12 Radial variation of the radial, tangential, and vertical velocity dispersions in the four bulges in RHG097, RCG100, RCG101 and RHG109 after 4 Gyr evolution. The blue and black arrows show the half-mass radii for two bulges RHG109 and RHG097, respectively. |
5.3. V/σ for the spun-up bulges
Here we plot our spun-up ClBs on the (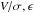 ) plot (Kormendy & Illingworth 1982) to further illustrate their rotational properties. We note that while this is easily done in simulations because of the unique ID attached to each particle, comparing with observed ClBs is non-trivial because it is difficult to separate classical bulge stars from stars in the boxy bulge in observations. First, we calculate
) plot (Kormendy & Illingworth 1982) to further illustrate their rotational properties. We note that while this is easily done in simulations because of the unique ID attached to each particle, comparing with observed ClBs is non-trivial because it is difficult to separate classical bulge stars from stars in the boxy bulge in observations. First, we calculate 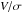 values in the traditional sense. We record the peak velocity, Vm, which is taken to be a simple average of the outer velocities in the radial range ~0.9−1.2Rd (excluding outliers such as the point with ~100 km s-1 in model RCG100; see Fig. 9). This value is divided by the inner velocity dispersion,
values in the traditional sense. We record the peak velocity, Vm, which is taken to be a simple average of the outer velocities in the radial range ~0.9−1.2Rd (excluding outliers such as the point with ~100 km s-1 in model RCG100; see Fig. 9). This value is divided by the inner velocity dispersion, 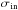 , computed by taking an average within the half-mass radius of the ClB after 4 Gyr. The resulting V/σ values are listed as
, computed by taking an average within the half-mass radius of the ClB after 4 Gyr. The resulting V/σ values are listed as 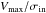 in Table 2.
in Table 2.
In addition, we also calculate 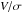 from the edge-on kinematic maps of our evolved ClBs, following Binney (2005), and denote these by
from the edge-on kinematic maps of our evolved ClBs, following Binney (2005), and denote these by 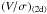 . Thus, we compute the surface density-weighted velocity and velocity dispersion both in the inner (R< 2Rb,1/2) and outer parts (R> 2Rb,1/2). Consistent with the results of the last section, the
. Thus, we compute the surface density-weighted velocity and velocity dispersion both in the inner (R< 2Rb,1/2) and outer parts (R> 2Rb,1/2). Consistent with the results of the last section, the 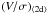 in the inner parts are small (< 0.1). In the rest of the paper we show the
in the inner parts are small (< 0.1). In the rest of the paper we show the 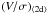 values for the outer parts only.
values for the outer parts only.
 |
Fig. 13
|
Bar size and bulge kinematics at the end of 4 Gyr.
We calculate the ellipticities (ϵ) of the ClBs by the method of diagonalizing the moment-of-inertia tensor. The intrinsic ellipticity of the bulge is then ϵ = 1−c/a, where c/a is the ratio of the minor to major axis. In edge-on projection (where the inclination angle is 90° with respect to the line of sight), the apparent ellipticity would be equal to the intrinsic ellipticity derived using the moment-of-inertia method. We compared these axis ratios with those obtained using IRAF ellipse fitting, and the agreement between the two methods is fairly good.
Figure 13 shows the well-known 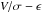 plot for all the ClBs in our model galaxies after 4 Gyr. Ellipticities and
plot for all the ClBs in our model galaxies after 4 Gyr. Ellipticities and 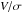 values at this time are also tabulated in Table 2. Four of the initially non-rotating ClBs from our simulated sample have final
values at this time are also tabulated in Table 2. Four of the initially non-rotating ClBs from our simulated sample have final 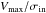 values which formally put them on the oblate isotropic rotator line (Binney 1978), while the remaining three bulges did not spin up as much. For all our ClBs, the outer
values which formally put them on the oblate isotropic rotator line (Binney 1978), while the remaining three bulges did not spin up as much. For all our ClBs, the outer 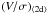 values are lower than the
values are lower than the 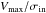 because the induced rotation profiles in these ClBs have a shallow rise and reach their maxima in the outermost parts, which contain little mass. The final
because the induced rotation profiles in these ClBs have a shallow rise and reach their maxima in the outermost parts, which contain little mass. The final 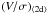 may be slightly on the low side in our models, however, because the initial ClBs were modelled as King profiles in which the density of stars drops to zero rapidly in the outer parts marked by the truncation radii and contain fewer stars. In contrast, the observed ClBs which follow Sersic profiles r1 /n (e.g. Caon et al. 1993) with n ~ 4 have less steeply falling density and contain a larger number of stars at the outer parts. Our analysis reveals that it is the outer part of the massive bulges that gain most of the angular momentum transferred by the bar. Having these outer parts well populated by stars on stable orbits would ensure effective transfer of angular momentum transfer via resonances. We, therefore, expect angular momentum transfer and the bulge spin-up to be greater for less steep bulge profiles as might be the case in observed ClBs.
may be slightly on the low side in our models, however, because the initial ClBs were modelled as King profiles in which the density of stars drops to zero rapidly in the outer parts marked by the truncation radii and contain fewer stars. In contrast, the observed ClBs which follow Sersic profiles r1 /n (e.g. Caon et al. 1993) with n ~ 4 have less steeply falling density and contain a larger number of stars at the outer parts. Our analysis reveals that it is the outer part of the massive bulges that gain most of the angular momentum transferred by the bar. Having these outer parts well populated by stars on stable orbits would ensure effective transfer of angular momentum transfer via resonances. We, therefore, expect angular momentum transfer and the bulge spin-up to be greater for less steep bulge profiles as might be the case in observed ClBs.
The two star symbols show the equivalent 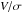 values for the low-mass ClB model of RCG004 from Saha et al. (2012). They are considerably higher than for the massive bulge models reported here. The ClB in this model had significantly lower mass (0.067Md) but similar Rb,1/2/Rd ≃ 0.21. Clarifying the origin of this difference will require a more extensive parameter study of the evolution of low-mass bulges in bar unstable disks.
values for the low-mass ClB model of RCG004 from Saha et al. (2012). They are considerably higher than for the massive bulge models reported here. The ClB in this model had significantly lower mass (0.067Md) but similar Rb,1/2/Rd ≃ 0.21. Clarifying the origin of this difference will require a more extensive parameter study of the evolution of low-mass bulges in bar unstable disks.
 |
Fig. 14 Dependence of V/σ on the ratio of bulge size to bar size of the embedded ClBs at the end of 4 Gyr. Initially, all the bulges were non-rotating. The star signs indicate the ClB of RCG004, as in Fig. 13. |
In addition to our simulated ClBs, in Fig. 13 we have overplotted six ClBs in barred galaxies (NGC 1023, NGC 2859, NGC 2880, NGC 3521, NGC 3992, and NGC 4260) and seven ClBs in non-barred galaxies (NGC 4698, NGC 4772, NGC 3898, NGC 3245, NGC 3031, NGC 2775, and NGC 2841) taken from Fabricius et al. (2012). In most cases, the ClBs in barred galaxies rotate faster than their counterparts in non-barred galaxies. Whether in these galaxies the bar might be responsible, in part, for spinning up these ClBs will require a separate investigation.
Figure 14 shows the dependence of normalized 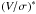 on the ratio of bulge size to bar size (Rb/Rbar). For the normalization we used the relation
on the ratio of bulge size to bar size (Rb/Rbar). For the normalization we used the relation 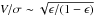 . For all bulges (except RCG076) the final
. For all bulges (except RCG076) the final 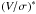 at 4 Gyr, as well as
at 4 Gyr, as well as 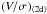 following Binney (2005), correlate closely with increasing ratio Rb/Rbar. This suggests that the dynamics of the ClB spin-up depends on the relative size of the bar. It is possible that there is an optimal size for the rotating bar to provide the most angular momentum transfer to the ClB through resonant angular momentum transfer and dynamical friction on the bulge stars (see Sect. 4.1); however, this needs additional models with large ClBs. Certainly, from the models studied here, the spin-up of ClBs is not efficient when the ClB is too compact.
following Binney (2005), correlate closely with increasing ratio Rb/Rbar. This suggests that the dynamics of the ClB spin-up depends on the relative size of the bar. It is possible that there is an optimal size for the rotating bar to provide the most angular momentum transfer to the ClB through resonant angular momentum transfer and dynamical friction on the bulge stars (see Sect. 4.1); however, this needs additional models with large ClBs. Certainly, from the models studied here, the spin-up of ClBs is not efficient when the ClB is too compact.
6. Conclusions and discussion
We have used self-consistent N-body simulations of disk galaxies to study the interaction of massive ClBs with the bar that forms in the disk. We find that significant angular momentum is transferred by resonant gravitational interaction from the bar to the ClB in all cases on a time scale of a few Gyr. We have analysed the angular momentum transfer using orbital frequency analysis and examining the barred density wake in the bulge. Because most of the angular momentum is transferred to the outer parts of the ClB in our models, it is likely that the induced rotation in Sersic bulges would be higher than in those studied here. Our main conclusions from this work are as follows:
-
1.
Massive classical bulges gain as much specific angular momentum through spin-up by the bar as do lower-mass bulges.
-
2.
Most of the angular momentum transfer occurs through low-order resonances. In particular, we found that a lot of angular momentum can be transferred via 5:2 resonant orbits, which are common in the models studied here.
-
3.
The bar generates a density wake in the bulge due to trapped 2:1 orbits. For lower mass bulges in our sample, such a wake is found to be misaligned with the bar and causes angular momentum transfer, while for higher mass bulges the misalignment is not substantial. At later phases of evolution, the bulge density wake aligns with the bar and evolves into the bulge-bar.
-
4.
The spin-up process creates a characteristic linear rotation profile such that significant rotation is induced beyond ~2Rb,1/2. Typical mass-weighted V/σ beyond ~2Rb,1/2 are ~0.2, and the local Vmax/σin reached at the largest radii are ~0.5.
-
5.
Contrary to the case of the low-mass ClBs studied in Saha et al. (2012), Saha & Gerhard (2013), the rotation induced in the ClB is not cylindrical.
-
6.
The spin-up process also creates mild tangential anisotropy in the outer regions of the ClBs studied here.
-
7.
In all models a box/peanut bulge also forms through the bar-buckling instability. The final systems therefore have a composite bulge with the ClB superposed on the slightly larger box/peanut bulge. This suggests that composite bulges may be common in galaxies.
The main result of this paper is that comparatively massive bulges are also affected by the angular momentum transfer mechanism from the bar, which was previously investigated only for low-mass ClBs, both non-rotating (Saha et al. 2012) and rotating (Saha & Gerhard 2013). In our sequence of models, the spin-up is most efficient when the size of the bar is somewhat larger than the ClB, but not too large. This suggests that larger effects might be expected in the presence of gas, which would favour higher pattern speeds and mass inflow. If nuclear bars formed as a result of central mass build-up, they could lead to additional angular momentum transfer. These effects merit future investigation.
Acknowledgments
The authors thank the referee, Frédéric Bournaud, for thoughtful comments which helped improve the clarity of the paper.
References
- Agertz, O., Teyssier, R., & Moore, B. 2011, MNRAS, 410, 1391 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aguerri, J. A. L., Balcells, M., & Peletier, R. F. 2001, A&A, 367, 428 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Athanassoula, E. 2002, ApJ, 569, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Athanassoula, E. 2007, MNRAS, 377, 1569 [NASA ADS] [CrossRef] [Google Scholar]
- Athanassoula, E., & Misiriotis, A. 2002, MNRAS, 330, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Athanassoula, E., Lambert, J. C., & Dehnen, W. 2005, MNRAS, 363, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Barazza, F. D., Jogee, S., & Marinova, I. 2008, ApJ, 675, 1194 [NASA ADS] [CrossRef] [Google Scholar]
- Baugh, C. M., Cole, S., & Frenk, C. S. 1996, MNRAS, 283, 1361 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J. 1978, MNRAS, 183, 501 [NASA ADS] [Google Scholar]
- Binney, J. 2005, MNRAS, 363, 937 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J., & Spergel, D. 1982, ApJ, 252, 308 [NASA ADS] [CrossRef] [Google Scholar]
- Bournaud, F., Jog, C. J., & Combes, F. 2007, A&A, 476, 1179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brook, C. B., Stinson, G., Gibson, B. K., et al. 2012, MNRAS, 419, 771 [NASA ADS] [CrossRef] [Google Scholar]
- Caon, N., Capaccioli, M., & D’Onofrio, M. 1993, MNRAS, 265, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., Emsellem, E., Bacon, R., et al. 2007, MNRAS, 379, 418 [NASA ADS] [CrossRef] [Google Scholar]
- Ceverino, D., & Klypin, A. 2007, MNRAS, 379, 1155 [NASA ADS] [CrossRef] [Google Scholar]
- Ceverino, D., Dekel, A., Tweed, D., & Primack, J. 2015, MNRAS, 447, 3291 [NASA ADS] [CrossRef] [Google Scholar]
- Chandrasekhar, S. 1943, ApJ, 97, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Combes, F., & Sanders, R. H. 1981, A&A, 96, 164 [NASA ADS] [Google Scholar]
- de Vaucouleurs, G. 1953, MNRAS, 113, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Debattista, V. P., & Sellwood, J. A. 1998, ApJ, 493, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Debattista, V. P., & Sellwood, J. A. 2000, ApJ, 543, 704 [NASA ADS] [CrossRef] [Google Scholar]
- Dubinski, J., Berentzen, I., & Shlosman, I. 2009, ApJ, 697, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Earn, D. J. D., & Lynden-Bell, D. 1996, MNRAS, 278, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Eggen, O. J., Lynden-Bell, D., & Sandage, A. R. 1962, ApJ, 136, 748 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G., Bournaud, F., & Elmegreen, D. M. 2008, ApJ, 688, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Erwin, P., Saglia, R. P., Fabricius, M., et al. 2015, MNRAS, 446, 4039 [NASA ADS] [CrossRef] [Google Scholar]
- Eskridge, P. B., Frogel, J. A., Pogge, R. W., et al. 2000, AJ, 119, 536 [NASA ADS] [CrossRef] [Google Scholar]
- Fabricius, M. H., Saglia, R. P., Fisher, D. B., et al. 2012, ApJ, 754, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Fisher, D. B., & Drory, N. 2010, ApJ, 716, 942 [NASA ADS] [CrossRef] [Google Scholar]
- Gadotti, D. A. 2009, MNRAS, 393, 1531 [NASA ADS] [CrossRef] [Google Scholar]
- Governato, F., Willman, B., Mayer, L., et al. 2007, MNRAS, 374, 1479 [NASA ADS] [CrossRef] [Google Scholar]
- Hasan, H., Pfenniger, D., & Norman, C. 1993, ApJ, 409, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Hernquist, L., & Weinberg, M. D. 1992, ApJ, 400, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Hohl, F. 1971, ApJ, 168, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Holley-Bockelmann, K., Weinberg, M., & Katz, N. 2005, MNRAS, 363, 991 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Cox, T. J., Younger, J. D., & Hernquist, L. 2009, ApJ, 691, 1168 [Google Scholar]
- Hopkins, P. F., Bundy, K., Croton, D., et al. 2010, ApJ, 715, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Immeli, A., Samland, M., Gerhard, O., & Westera, P. 2004, A&A, 413, 547 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Inoue, S., & Saitoh, T. R. 2012, MNRAS, 422, 1902 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., White, S. D. M., & Guiderdoni, B. 1993, MNRAS, 264, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J. 1982, ApJ, 257, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J., & Illingworth, G. 1982, ApJ, 256, 460 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J., & Kennicutt, Jr., R. C. 2004, ARA&A, 42, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Kuijken, K., & Dubinski, J. 1995, MNRAS, 277, 1341 [CrossRef] [Google Scholar]
- Laurikainen, E., Salo, H., Buta, R., & Knapen, J. H. 2007, MNRAS, 381, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Martinez-Valpuesta, I., & Shlosman, I. 2004, ApJ, 613, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Martinez-Valpuesta, I., Shlosman, I., & Heller, C. 2006, ApJ, 637, 214 [NASA ADS] [CrossRef] [Google Scholar]
- McMillan, P. J., & Dehnen, W. 2007, MNRAS, 378, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Naab, T., Oser, L., Emsellem, E., et al. 2014, MNRAS, 444, 3357 [NASA ADS] [CrossRef] [Google Scholar]
- Noguchi, M. 1999, ApJ, 514, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2002, AJ, 124, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Pfenniger, D., & Norman, C. 1990, ApJ, 363, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Raha, N., Sellwood, J. A., James, R. A., & Kahn, F. D. 1991, Nature, 352, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Saha, K., & Gerhard, O. 2013, MNRAS, 430, 2039 [NASA ADS] [CrossRef] [Google Scholar]
- Saha, K., & Naab, T. 2013, MNRAS, 434, 1287 [NASA ADS] [CrossRef] [Google Scholar]
- Saha, K., Tseng, Y., & Taam, R. E. 2010, ApJ, 721, 1878 [NASA ADS] [CrossRef] [Google Scholar]
- Saha, K., Martinez-Valpuesta, I., & Gerhard, O. 2012, MNRAS, 421, 333 [NASA ADS] [Google Scholar]
- Sellwood, J. A., & Debattista, V. P. 2006, ApJ, 639, 868 [NASA ADS] [CrossRef] [Google Scholar]
- Sellwood, J. A., & Moore, E. M. 1999, ApJ, 510, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Sellwood, J. A., & Wilkinson, A. 1993, Rep. Prog. Phys., 56, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., Yoshida, N., & White, S. D. M. 2001, New Astron., 6, 79 [Google Scholar]
- Toomre, A. 1981, in Structure and Evolution of Normal Galaxies, eds. S. M. Fall, & D. Lynden-Bell, 111 [Google Scholar]
- Tremaine, S., & Weinberg, M. D. 1984, MNRAS, 209, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Voglis, N., Harsoula, M., & Contopoulos, G. 2007, MNRAS, 381, 757 [NASA ADS] [CrossRef] [Google Scholar]
- Weinberg, M. D., & Katz, N. 2007, MNRAS, 375, 425 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Initial bulge, disk, and halo model parameters, ordered by the ratio of ClB to disk mass.
All Figures
 |
Fig. 1 Initial total circular velocity curves a); the total circular velocity curves at 4 Gyr b); Toomre Q profiles c); and Mass-size relation for the initial ClBs d). |
| In the text | |
 |
Fig. 2 Face-on surface density maps for all model galaxies after 4 Gyr of evolution. |
| In the text | |
 |
Fig. 3 Time evolution of the bar strength in our galaxy models with pre-existing classical bulges. |
| In the text | |
 |
Fig. 4 Upper panels: distribution of bulge stars with frequency (Ω−ΩB) /κ at different times throughout the secular evolution in model RHG097. Lower panels: net change in the angular momentum of the selected stars with respect to the previous time. The vertical dotted lines indicate the most important resonances (from left to right): −1:1, 4:1, 3:1, 5:2, and 2:1. As time progresses, more stars are trapped by the ILR of the bar in the stellar disk. However, most of the angular momentum transfer occurs through the 5:2 resonance. |
| In the text | |
 |
Fig. 5 Same as in Fig. 4, but for model RCG076. |
| In the text | |
 |
Fig. 6 Density wake mode (l = 2,m = 2) in the ClB of RHG097. Dashed lines in all panels indicate the location of the bar in the stellar disk while solid lines denote the phase angle corresponding to the bar mode in the classical bulge (ClB). Towards the later phases of the evolution, the ClBb becomes progressively stronger. The red arrow denotes the rotation of the disk bar. We note that at 1 Gyr, a clear bar has not developed yet. The unit of time is in Gyr. |
| In the text | |
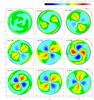 |
Fig. 7 Same as in Fig. 6, but for RCG076. |
| In the text | |
 |
Fig. 8 Surface density (upper panel), line-of-sight velocity and velocity dispersion maps (2nd to 4th panels) of the ClB in RHG097 at different times during the evolution. These images are taken at 90° projection (edge-on view) and the major axis of the bar is aligned with the X-axis. Clear signatures of rotation are seen at 4 Gyr. The colour bar at the top represents density, middle the velocity, and bottom the velocity dispersion. |
| In the text | |
 |
Fig. 9 Rotation, velocity dispersion, and local V/σ radial profiles for the four ClBs in models RHG097, RCG100, RCG101 and RHG109. The blue and black arrows show the half-mass radii for the two bulges of RHG109 and RHG097, respectively. |
| In the text | |
 |
Fig. 10 Surface density (top), mean line-of-sight velocity, and dispersion profiles (middle panel) for the composite bulge of model RHG097. The local V/σ profile is shown in the bottom panel. |
| In the text | |
 |
Fig. 11 Fractional kinetic energy associated with the rotational motion for the four bulges in RHG097, RCG100, RCG101 and RHG109 in radial bins. The blue and black arrows show the half-mass radii for two bulges RHG109 and RHG097 respectively. |
| In the text | |
 |
Fig. 12 Radial variation of the radial, tangential, and vertical velocity dispersions in the four bulges in RHG097, RCG100, RCG101 and RHG109 after 4 Gyr evolution. The blue and black arrows show the half-mass radii for two bulges RHG109 and RHG097, respectively. |
| In the text | |
 |
Fig. 13
|
| In the text | |
 |
Fig. 14 Dependence of V/σ on the ratio of bulge size to bar size of the embedded ClBs at the end of 4 Gyr. Initially, all the bulges were non-rotating. The star signs indicate the ClB of RCG004, as in Fig. 13. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


