| Issue |
A&A
Volume 588, April 2016
|
|
|---|---|---|
| Article Number | A59 | |
| Number of page(s) | 8 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201527307 | |
| Published online | 17 March 2016 | |
Photometry of dust grains of comet 67P and connection with nucleus regions
1 INAF-Astronomical Observatory of Padova, Vicolo dell’Osservatorio 5, 35131 Padova, Italy
e-mail: gabriele.cremonese@oapd.inaf.it
2 Center of Studies and Activities for Space (CISAS) “G. Colombo”, University of Padova, via Venezia 15, 35131 Padova, Italy
3 Dipartimento di Fisica e Astronomia, University of Padova, Vic. Osservatorio 3, 35122 Padova, Italy
4 Max-Planck-Institut für Sonnensystemforschung, Justus-von-Liebig-Weg 3, 37077 Göttingen, Germany
5 LESIA, Observatoire de Paris, PSL Research University, CNRS, Sorbonne Universités, Univ. Paris Diderot, Sorbonne Paris Cité, UPMC Univ. Paris 06, 5 place J. Janssen, 92195 Meudon Pricipal Cedex, France
6 Aix-Marseille Université, CNRS LAM (Laboratoire d’Astrophysique de Marseille), UMR 7326, 13388 Marseille, France
7 Centro de Astrobiologia, CSIC-INTA, 28850 Torrejon de Ardoz, Madrid, Spain
8 International Space Science Institute, Hallerstrasse 6, 3012 Bern, Switzerland
9 Scientific Support Office, European Space Research and Technology Centre/ESA, Keplerlaan 1, Postbus 299, 2201 AZ Noordwijk ZH, The Netherlands
10 Department of Physics and Astronomy, Uppsala University, Box 516, 75120 Uppsala, Sweden
11 PAS Space Research Center, Bartycka 18A, 00716 Warszawa, Poland
12 Institut für Geophysik und extraterrestrische Physik, TU Braunschweig, 38106 Braunschweig, Germany
13 University of Maryland, Department of Astronomy, College Park, MD 20742-2421, USA
14 LATMOS, CNRS/UVSQ/IPSL, 11 boulevard d’Alembert, 78280 Guyancourt, France
15 CNR-IFN UOS Padova LUXOR, via Trasea 7, 35131 Padova, Italy
16 University of Trento, via Sommarive 9, 38123 Trento, Italy
17 Department of Industrial Engineering, University of Padova, via Venezia 1, 35131 Padova, Italy
18 INAF Osservatorio Astronomico di Trieste, via Tiepolo 11, 34014 Trieste, Italy
19 Instituto de Astrofísica de Andalucía-CSIC, 18008 Granada, Spain
20 Deutsches Zentrum für Luft- und Raumfahrt (DLR), Institut für Planetenforschung, Rutherfordstrasse 2, 12489 Berlin, Germany
21 National Central University, Graduate Institute of Astronomy, 300 Chung-Da Rd, 32054 Chung-Li, Taiwan
22 Operations Department, European Space Astronomy Centre/ESA, PO Box 78, 28691 Villanueva de la Canada, Madrid, Spain
23 Department of Information Engineering, University of Padova, via Gradenigo 6/B, 35131 Padova, Italy
24 Physikalisches Institut der Universität Bern, Sidlerstr. 5, 3012 Bern, Switzerland
Received: 4 September 2015
Accepted: 19 January 2016
Aims. Multiple pairs of high-resolution images of the dust coma of comet 67P/Churyumov-Gerasimenko have been collected by OSIRIS onboard Rosetta allowing extraction and analysis of dust grain tracks.
Methods. We developed a quasi automatic method to recognize and to extract dust tracks in the Osiris images providing size, FWHM and photometric data. The dust tracks characterized by a low signal-to-noise ratio were checked manually. We performed the photometric analysis of 70 dust grain tracks observed on two different Narrow Angle Camera images in the two filters F24 and F28, centered at λ = 480.7 nm and at λ = 743.7 nm, respectively, deriving the color and the reddening of each one. We then extracted several images of the nucleus observed with the same filters and with the same phase angle to be compared with the dust grain reddening.
Results. Most of the dust grain reddening is very similar to the nucleus values, confirming they come from the surface or subsurface layer. The histogram of the dust grain reddening has a secondary peak at negative values and shows some grains with values higher than the nucleus, suggesting a different composition from the surface grains. One hypothesis comes from the negative values point at the presence of hydrated minerals in the comet.
Key words: comets: general / comets: individual: 67P/Churyumov-Gerasimenko
© ESO, 2016
1. Introduction
Comets are known to be the most pristine objects in our solar system. Their study therefore provides unique knowledge of the materials and the processes that formed and shaped the early solar nebula, leading then to form planets and moons.
Comets have two main constituents: refractory dust and volatile solid ices. Although historically these objects were considered as dirty snowballs with ices as main matrix component, there is evidence that in many cases the dust is comparable in mass to the ice, if not even dominant (Küppers et al. 2005).
The ESA Rosetta mission has been orbiting the Jupiter-family comet 67P/Churyumov-Gerasimenko (67P) since the beginning of August 2014. The instruments onboard the spacecraft are providing an unprecedented view of a cometary nucleus and its inner coma environment. Among these instruments, the OSIRIS two-camera telescope (Keller et al. 2007) is giving a vivid picture of the dust surrounding the nucleus. A previous study of the dust/ice ratio in comet 67P, using remote and in situ Rosetta instruments data, proved that the dust is dominant with the aforementioned ratio ~4 (Fulle et al. 2015a). Thus the knowledge of the composition of the dust particles released from the nucleus tell us what the components of the abundant refractory materials are that form the comet and what the relationship is with the surface materials. This provides hints about the dust release process in the comet and the mechanisms that are regulating the onset of the activity. Recently, Schulz et al. (2015) analyzed several dust grains collected with the COSIMA instrument and found that at heliocentric distances greater than 3 AU, such grains are most likely coming from a dusty crust that quenches the material outflow activity at the comet surface. After reaching a heliocentric distance lower than 3 AU, the nucleus would then shed its mantle, and unprocessed material starts to supply the developing coma, radically changing its dust component.
Name of the NAC-OSIRIS images utilized for the dust grains analysis.
During its continuous monitoring of the nucleus and inner coma, OSIRIS took several images of dust grains. We focus our analysis on images acquired on 10 September 2014, when 67P was at heliocentric distance rh = 3.395 AU and Rosetta was about 29 km from the comet. The images were acquired with the Narrow Angle Camera (NAC) in the blue (F24, centered at 480.7 nm) and in the red (F28, centered at 743.7 nm) filters. In Table 1 we report the names of the images utilized. The images were acquired every 20 s with an exposure time of about six seconds. All the images were obtained at a phase angle of 93°.
We analyzed six pairs of images and found 70 grain tracks. No track is visible on more than one pair, where we measured the photometry of each track and derived their reddening color, both giving clues to their composition. We decided to only work on this set of images, even if OSIRIS obtained several other sets of images of the dust grains in subsequent months, but with different phase angles, distances from the comet, and heliocentric distances. This would have meant adding more uncertainties into the statistics and the comparison because of the different physical and thermal conditions during the observations. Moreover, the grain photometry was compared with nucleus colors obtained with the same observational geometry as the grain data in order to constrain the possible source on the surface. The results of our analysis are shown in this paper.
2. Data analysis
The main aim of this work is to perform a photometric analysis of the dust tracks visible on pairs of images obtained with different filters, thereby i) getting the reddening of each dust grain and ii) comparing it with the reddening of some nuclear region. To apply the same procedure for extracting the track size, we realized a semi-automatic method of recognizing the tracks on both images and making the photometric calculations in a similar way to aperture stellar photometry.
A Laplace filtering is used to detect the regions in which the presence of a grain generates a peak in the second spatial derivative of the image. The signal-to-noise ratio (S/N) of the faintest tracks is around three, which makes difficult to detect them automatically with respect to the sky background; moreover, some tracks have a few pixels along their length with lower S/N producing interruptions along the track, when using a fixed threshold in the S/N. To avoid this problem, a Boolean mask is applied to the images assuming a threshold chosen with a trial-and-error procedure because of the different background between the images. The masks pass through a process of morphologic operator dilatation and erosion (see Fig. 1) to fill the interruptions due to the noise and grain rotation (Fulle et al. 2015b).
 |
Fig. 1 a) An example of the result of the Laplace filtering of the difference of two following NAC images. b) Boolean mask of the grain track identified by the definition of an adequate threshold. c) Result of the dilatation process. Finally, d) shows the result (after erosion filtering). In red is the isocurve of the border of the grain and in green the ellipsoid fit (expanded for visibility) used to distinguish the grain from other features by eccentricity. |
 |
Fig. 2 Definition of the trapezoid that approximates a grain signal both in FWHM a) and length b) definition. Blue indicates the image signal with a cross signature for selected points, an empty circle for outliers, and in green the first and second approximations of the stretch. |
At the end of this process, the obtained Boolean mask is considered as float function with codomain between 0 and 1. The boundary of the track is defined as the isocurve of the function with value 0.5 to define the correct grain track. This procedure allows the grain tracks to be defined automatically in any single image. During this process even some noise peaks and stars might be considered as grains. Fitting the obtained curves with ellipses (see Fig. 1d) allows separating the grain track from the noise, or star, thereby imposing a lower limit on the eccentricity of the ellipses. Each track is divided locally in columns or rows, depending on whenever the inclination of the track on the frame is larger or lower than 45°, and generating local sections of the track. Owing to pixel discretization, all the columns represent a function with a maximum next to the center of the track. The set of peaks in the sections can be used to define the effective inclination of the same track. This information is needed to rotate the image domain in order to have track length on the x-axis. This allows a horizontal slide of the rotated image, which can be used for defining the length (see Fig. 2).
The signal is now used to fit the grain track by an isosceles trapezoid along the direction of the moving grain through the following steps:
- 1.
Definition of a centroid;
- 2.
Definition of the best fit with a trapezoid centered on the centroid (first estimate affected by the definition of the centroid);
- 3.
Second estimate of the centroid by minimizing the fit error by moving the trapezoid defined over the signal;
- 4.
Definition of the trapezoid on the newly extracted centroid.
This process allows the length l of the grain track and its centroid xc to be defined. In this way the constrained data can be used to define the average cross track full width at half maximum (FWHM). The length of the tracks rotated on the correct direction allows (as shown in Fig. 2) oversampling the data and leads to a better approximation of the trapezoid even for small FWHM.
The background to be removed is calculated as the average signal around the track outside a rectangle of the same width and length of the track, centered on the track centroid and having the same orientation (Fig. 3).
 |
Fig. 3 Red line represents the final definition of the track depending on length, FWHM and centroid. The green line defines the maximum extension of the track to be used for the flux calculation. Lines are plotted on the difference between two images acquired from different positions and filters. |
It allows a second and more precise cycle of estimate of the track parameters defining centroids, lengths, and width of the tracks. In Fig. 4 we show the position of all the detected dust grains, measured on the 12 frames, projected on the image plane.
Summary of OSIRIS images used for the analysis of the color of several nucleus regions.
The data set we analyzed did not allow for deriving the orbital elements because the observed arcs were extremely short. An interesting attempt to determine the osculating orbital elements was explained in a previous paper of the OSIRIS team (Davidsson et al. 2015), but it used more WAC images of the same grain, thereby providing much better constraints with respect to the images used in this work. The possible velocitiy and size ranges may be assumed to be similar to what the OSIRIS and GIADA suggested in the related work (Rotundi et al. 2015) at the same heliocentric distances range. In the case of outflowing and ejected grains, we may have a size range of 2–15 mm and a velocity range of 2–24 m s-1, while for bound grains we may have 0.2–2 m at the outermost limit of the grain cloud and 4–40 cm for grains at 130 km from the spacecraft and a mean proper grain velocity lower than 0.36 m s-1.
 |
Fig. 4 All the 70 dust grains measured with the circle diameter related to the track length. The red circles have positive reddening, while it is negative for the blue ones. |
3. Color of the dust grains
ITo characterize the photometric properties of the dust grains, we calculated the pixel-by-pixel reddening in the two filters. The reddening, expressed in %/100 nm, is therefore computed as (Jewitt & Meech 1986; A’Hearn et al. 1984): 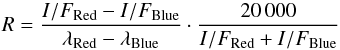 (1)where I/FRed and I/FBlue are intended as the Akimov corrected reflectance in the two filters.
(1)where I/FRed and I/FBlue are intended as the Akimov corrected reflectance in the two filters.
The results of our measurements are shown in Fig. 5 as a histogram of the overall dust reddening values, and the main parameters measured for each grain are reported in Table A.1. To estimate the errors associated to the whole process, standard bidirectional rect were generated, and a white noise was added with the same standard deviation of the background measured on the NAC images.
The calculated errors on the track length and width measurements were propagated to the flux, obtaining an average photometric uncertainty of 7%, which is very good considering that the S/N is lower than 10 for most of the grain tracks. Then we propagated the photometric errors to the reddening calculation and found increasing values that approach the reddening zero. This is clear from a mathematical point of view with the difference of the colors at the numerator and their sum at the denominator, because it corresponds to the two fluxes being very similar. The reddening error for each grain is reported in Table A.1. We have decided to plot all the reddening values, even in the case of high error since they are concentrated close to the zero value and do not influence the two peaks.
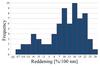 |
Fig. 5 Histogram of the measured grain reddening. |
Some reddening values are quite far from the peak of the histogram pointing at grains that may have a different composition. After an accurate check of all the photometric parameters obtained for each grain, we are confindent that the values at the extremes of the distribution might be real.
4. Colors of nucleus regions
To compare the colors of the grains with the observed color of the nucleus surface, we considered a series of images of the nucleus acquired in the same two filters used to observe the grains. We selected the images obtained at phase angles comparable with the phase at which the grains observation were performed, and found a suitable mapping set at phase 93° summarized in Table 2. This dataset was acquired from a spacecraft-comet distance of about 28 km, resulting in a linear spatial scale at the images of 0.52 m/pixel.
All OSIRIS images are calibrated in radiance (expressed in W m-2 nm-1 sr-1) using the OSIRIS standard calibration pipeline described in Tubiana et al. (2015) and Magrin et al. (2015), and then converted to reflectance (also known as radiance factor) using 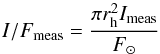 (2)where Imeas is the measured radiance, F⊙/π is the solar irradiance at 1 AU measured at the central wavelength for each filter, and rh is the heliocentric distance of the comet in AU.
(2)where Imeas is the measured radiance, F⊙/π is the solar irradiance at 1 AU measured at the central wavelength for each filter, and rh is the heliocentric distance of the comet in AU.
Given the high value of the observing phase angle and the very rough surface of the comet, we considered it important to take the effects of illumination and observing conditions into account before deriving the nucleus color. We therefore applied a photometric correction based on Akimov parameterless function following the method used by La Forgia et al. (2015) in the analysis of Philae landing site. Their results indeed indicate that this method represents the best approximation to a more complex Hapke model with the advantage that the parameter is free.
 |
Fig. 7 Orientation of 67P nucleus at the observing time and portion of the nucleus observed for each slope map panel in Fig. 6. |
 |
Fig. 8 Normalized histograms of the reflectance distribution for each slope map panel in Fig. 6 (black curve) and comparison with the grains one (red curve). The histograms have a bin equal to 3 in reddening. |
The Akimov corrected reflectance is therefore computed, for each pixel of the images, using 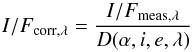 (3)where α, i, and e are the phase, incident, and emission angles, respectively. Here, D(α,i,e,λ) is the disk function, which describes how the reflectance varies over the surface at a constant phase angleIt is given by
(3)where α, i, and e are the phase, incident, and emission angles, respectively. Here, D(α,i,e,λ) is the disk function, which describes how the reflectance varies over the surface at a constant phase angleIt is given by 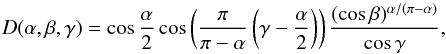 (4)with β and γ being the photometric latitude and longitude, respectively, which in turn depend on the incidence, emergence, and phase angles as follows:
(4)with β and γ being the photometric latitude and longitude, respectively, which in turn depend on the incidence, emergence, and phase angles as follows:  The computation of i, e, and α, for each pixel, required a high-resolution shape model of the surface, in order to correctly take the local topography into account. For this application we used the SPG model of Preusker et al. (2015), together with the most up-to-date NAIF-SPICE kernels and its IDL code toolkit (Acton 1996), to produce high-resolution synthetic images and maps of incidence, emergence, and phase angles. The used SPG shape model of 67P consists of about 16 million facets with 2 m horizontal sampling and a typical vertical accuracy at the decimeter scale.
The computation of i, e, and α, for each pixel, required a high-resolution shape model of the surface, in order to correctly take the local topography into account. For this application we used the SPG model of Preusker et al. (2015), together with the most up-to-date NAIF-SPICE kernels and its IDL code toolkit (Acton 1996), to produce high-resolution synthetic images and maps of incidence, emergence, and phase angles. The used SPG shape model of 67P consists of about 16 million facets with 2 m horizontal sampling and a typical vertical accuracy at the decimeter scale.
Small errors in the pointing of the spacecraft and/or small differences between the geodetic datum of the shape model reference frame compared to that of the used recent SPICE kernels cause a few pixel offset between the original images and the synthetic ones. The perfect alignment has been searched with a cross-correlation semi-automatic method looking for χ2 minima. We excluded all the non-illuminated (i> 90°) and the non-observable (e> 90°) regions from the analysis, but they are unfortunately quite extended on the frames because of the high observing phase.
The images in different filters are not acquired simultaneously but sequentially, and owing to the rotation of the comet and the spacecraft movements, they need to be co-registered for a correct color analysis. Therefore a control-point procedure has been developed to coregister the blue and red images together and obtain a reliable color cube for each set. A variable number of control points from 10 to 50 has been provided for each set, depending on the visible region and on the features observable in the frames.
The slope maps for all frames are shown in Fig. 6. Given the small field of view of each frame and the high observing phase casting large shadows, it is quite hard to recognize the nucleus regions that were imaged. Therefore we used the SPG shape model and the SPICE kernels to produce a synthetic projection of the nucleus with the observing conditions of each frame, and we highlighted the observed frame in each panel with a red square (Fig. 7).
Various morphological regions are imaged, and they show a variable color distribution over the nucleus. The average reddening of all the regions is 17.22%/100 nm, which is consistent with the high global nucleus spectral slope measured at lower phase angles and the high phase reddening reported by Fornasier et al. (2015).
To compare the nucleus region colors with the colors of the grains, we plotted the histograms of the reddening distribution for each panel in Fig. 6 and overplotted the histogram of the reddening distribution of the grains in red (Fig. 8).
The nucleus histograms are much narrower in all cases and are very similar for the various regions over the surface. The histogram in the top righthand panel, which refers to Set 4 turns out to be slightly bluer than the other, with a peak value at 16%/100 nm, which agrees with the colors observed in the neck-Hapi region (Fornasier et al. 2015; Capaccioni et al. 2015).
5. Conclusion
The comparison between the colors measured on the dust grains and some nuclear regions reported in Fig. 8 shows that the grain histogram is slightly shifted toward the blue part of the spectrum with a peak value between 12 and 16%/100 nm and a much wider spread with respect to the nucleus. It means that most of the grains come from the surface or at a different depth from the surface.
The grains having a color that is not included in the peak superimposed on the nucleus may have different compositions and origins. The dust grains histogram has a secondary peak around –8 because the 16 grains have a negative reddening, pointing at a completely different slope to the nucleus. Even if we have only two points in the reflectance curve of the grains, we may suggest some hypotheses that assume that an absorption band is falling within the bandwidth of one of the two filters used.
The negative values might be due to the grains characterized by an absorption within the spectral range of 712–776 nm (F28 filter; see also Fig. 1 of Oklay et al. 2015 for such minerals seen through OSIRIS NAC filters), for instance the 700 nm feature associated with hydrated minerals as observed in some asteroids, Fe2+−− > Fe3 + (Vilas & Gaffey 1989), or they may have a higher abundance of ice giving a bluer color.
We have also found 13 grains that have a reddening greater than 17, therefore higher than the surface. In this case the grains may have an absoprtion in the spectral range of 443–518 nm (F24 filter), and even in this case it could be a feature at 430 nm associated with hydrated minerals, Fe3+ (Vilas et al. 1993), as observed in some asteroids. We may also have another interesting analog observed on the Earth, because in some measurements performed in the Antarctic region on glacier ice and snow (Warren et al. 2006), it has been found that the water ice may have an absorption in the range 390–470 nm. However, the absorption by water ice is so weak in this spectral region that its observability is dominated by the small amount of absorptive impurities present in the ice, and the position of the λmin depends on this amount. If the process of freezing is slow enough, it can cause the rejection of the impurities, yielding the very pure water ice pieces characterized by this absoprtion.
These hypotheses could be confirmed by the recent activity observed in the Imhotep region (Groussin et al. 2015) that shows new small features having a higher albedo that is most likely due
to exposed water ice or maybe to hydrated minerals that were buried below a dust deposit. In similar events we may have the release of tiny water ice particles.
Acknowledgments
OSIRIS was built by a consortium of the Max-Planck-Institut für Sonnensystemforschung in Göttingen, Germany; CISAS-University of Padova, Italy; the Laboratoire d’Astrophysique de Marseille, France; the Instituto de Astrofísica de Andalucia, CSIC, Granada, Spain; the Research and Scientific Support Department of the European Space Agency, Noordwijk, The Netherlands; the Instituto Nacional de Técnica Aeroespacial, Madrid, Spain; the Universidad Politechnica de Madrid, Spain; the Department of Physics and Astronomy of Uppsala University, Sweden; and the Institut für Datentechnik und Kommunikationsnetze der Technischen Universität Braunschweig, Germany. The support of the national funding agencies of Germany (DLR), Italy (ASI), France (CNES), Spain (MEC), Sweden (SNSB), and the ESA Technical Directorate is gratefully acknowledged. We thank the ESA teams at ESAC, ESOC, and ESTEC for their work in support of the Rosetta mission.
References
- Acton, C. H. 1996, Planet. Space Sci., 44, 65 [NASA ADS] [CrossRef] [Google Scholar]
- A’Hearn, M. F., Schleicher, D. G., & Millis, E. A. 1984, AJ, 89, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Capaccioni, F., Coradini, A., Filacchione, G., et al. 2015, Science, 347 http://www.sciencemag.org/content/347/6220/aaa0628.full.pdf [Google Scholar]
- Davidsson, B. J. R., Gutiérrez, P. J., Sierks, H., et al. 2015, A&A, 583, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fornasier, S., Hasselmann, P. H., Barucci, M. A., et al. 2015, A&A, 583, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fulle, M., Della Corte, V., Rotundi, A., et al. 2015a, ApJ, 802, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Fulle, M., Ivanovski, S. L., Bertini, I., et al. 2015b, A&A, 583, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Groussin, O., Sierks, H., Barbieri, C., et al. 2015, A&A, 583, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jewitt, D., & Meech, K. J. 1986, ApJ, 310, 937 [NASA ADS] [CrossRef] [Google Scholar]
- Keller, H. U., Barbieri, C., Lamy, P., et al. 2007, Space Sci. Rev., 128, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Küppers, M., Bertini, I., Fornasier, S., et al. 2005, Nature, 437, 987 [NASA ADS] [CrossRef] [Google Scholar]
- La Forgia, F., Giacomini, L., Lazzarin, M., et al. 2015, A&A, 583, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magrin, S., La Forgia, F., Da Deppo, V., et al. 2015, A&A, 574, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oklay, N., Vincent, J.-B., Sierks, H., et al. 2015, A&A, 583, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Preusker, F., Scholten, F., Matz, K.-D., et al. 2015, A&A, 583, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rotundi, A., Sierks, H., Della Corte, V., et al. 2015, Science, 347 http://www.sciencemag.org/content/347/6220/aaa3905.full.pdf [Google Scholar]
- Schulz, R., Hilchenbach, M., Langevin, Y., et al. 2015, Nature, 518, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Tubiana, C., Güttler, C., Kovacs, G., et al. 2015, A&A, 583, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vilas, F., & Gaffey, M. J. 1989, Science, 246, 790 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Vilas, F., Hatch, E. C., Larson, S. M., Sawyer, S. R., & Gaffey, M. J. 1993, Icarus, 102, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Warren, S. G., Brandt, R. E., & Grenfell, T. C. 2006, App. Opt., 45, 5320 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A
Main parameters measured for each grain: length and FWHM of the tracks in the two filters F24 and F28 and the calculated reddening.
All Tables
Summary of OSIRIS images used for the analysis of the color of several nucleus regions.
Main parameters measured for each grain: length and FWHM of the tracks in the two filters F24 and F28 and the calculated reddening.
All Figures
 |
Fig. 1 a) An example of the result of the Laplace filtering of the difference of two following NAC images. b) Boolean mask of the grain track identified by the definition of an adequate threshold. c) Result of the dilatation process. Finally, d) shows the result (after erosion filtering). In red is the isocurve of the border of the grain and in green the ellipsoid fit (expanded for visibility) used to distinguish the grain from other features by eccentricity. |
| In the text | |
 |
Fig. 2 Definition of the trapezoid that approximates a grain signal both in FWHM a) and length b) definition. Blue indicates the image signal with a cross signature for selected points, an empty circle for outliers, and in green the first and second approximations of the stretch. |
| In the text | |
 |
Fig. 3 Red line represents the final definition of the track depending on length, FWHM and centroid. The green line defines the maximum extension of the track to be used for the flux calculation. Lines are plotted on the difference between two images acquired from different positions and filters. |
| In the text | |
 |
Fig. 4 All the 70 dust grains measured with the circle diameter related to the track length. The red circles have positive reddening, while it is negative for the blue ones. |
| In the text | |
 |
Fig. 5 Histogram of the measured grain reddening. |
| In the text | |
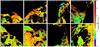 |
Fig. 6 Slope maps of all image set, as reported in Table 2. |
| In the text | |
 |
Fig. 7 Orientation of 67P nucleus at the observing time and portion of the nucleus observed for each slope map panel in Fig. 6. |
| In the text | |
 |
Fig. 8 Normalized histograms of the reflectance distribution for each slope map panel in Fig. 6 (black curve) and comparison with the grains one (red curve). The histograms have a bin equal to 3 in reddening. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


