| Issue |
A&A
Volume 587, March 2016
|
|
|---|---|---|
| Article Number | A141 | |
| Number of page(s) | 7 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201527862 | |
| Published online | 03 March 2016 | |
Magnetised accretion discs in Kerr spacetimes
II. Hot spots
1 Instituto Argentino de Radioastronomía (CCT La Plata, CONICET), C.C.5, (1894) Villa Elisa, Buenos Aires, Argentina
e-mail: fgarcia@iar-conicet.gov.ar
2 Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de La Plata, Paseo del Bosque, B1900 FWA La Plata, Argentina
3 Grupo de Gravitación, Astrofísica y Cosmología, Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de La Plata, Paseo del Bosque, B1900 FWA La Plata, Argentina
e-mail: iranea@fcaglp.unlp.edu.ar
4 Perimeter Institute for Theoretical Physics, Waterloo, Ontario, N2L 2Y5, Canada
e-mail: tjohannsen@pitp.ca
5 Department of Physics and Astronomy, University of Waterloo, Waterloo, Ontario, N2L 3G1, Canada
Received: 30 November 2015
Accepted: 26 January 2016
Context. Quasi-periodic variability has been observed in a number of X-ray binaries that harbor black hole candidates. In general relativity, black holes are uniquely described by the Kerr metric and, according to the cosmic censorship conjecture, curvature singularities always have to be clothed by an event horizon.
Aims. In this paper, we study the observed light curves that arise from orbiting hotspots in thin accretion discs around Kerr black holes and naked singularities, and the effect introduced by the presence of an external magnetic field.
Methods. We employ a ray-tracing algorithm to calculate the light curves and power spectra of these hot spots as seen by a distant observer for uniform and dipolar magnetic field configurations, assuming a weak coupling between the magnetic field and the disc matter.
Results. We show that the presence of an external dipolar magnetic field leads to potentially observable modifications of these light curves for both Kerr black holes and naked singularities, while an external uniform magnetic field has practically no effect. In particular, we demonstrate that the emission from a hotspot, which is orbiting near the innermost stable circular orbit of a naked singularity in a dipolar magnetic field, can be significantly harder than the emission of the same hotspot in the absence of this type of magnetic field.
Conclusions. The comparison of our model with observational data may allow us to study the geometry of magnetic fields around compact objects and to test the cosmic censorship conjecture in conjunction with other observables, such as thermal continuum spectra and iron line profiles.
Key words: black hole physics / accretion, accretion disks / magnetic fields / gravitation / X-rays: binaries / relativistic processes
© ESO, 2016
1. Introduction
Understanding the fate of an initial mass distribution after its gravitational collapse is still one of the most active fields of research within the general relativistic community. Although general relativity predicts the appearance of spacetime singularities, the formation of an event horizon that covers them is not necessarily required.
Back in 1969, Penrose (1969) proposed the cosmic censorship conjecture (CCC; see Penrose 1998, for a review on the subject). The weak form of the CCC states, in simple language, that in the final state of the gravitational collapse of “normal” matter, each spacetime singularity must be hidden behind an event horizon. Whether this conjecture is valid or not is amongst the most important open problems in classical theory of general relativity. Although great efforts – following different lines of thought – have been made over the last 40 years, there is still no definitive answer to the question whether the (weak and strong) CCC are valid or not (see Joshi 2008, and references therein).
To date, there is still no conclusive observational evidence of the actual nature of compact objects and no direct evidence of an event horizon has been found yet (but see, e.g., Broderick et al. 2009). For this reason, finding observable features that could help to distinguish between black holes (BH) and naked singularities (NS) should be considered relevant since they could shed some light on the validity of the CCC.
The study of potentially observable differences between accretion discs around BHs and NSs is important as it may give us an observational tool to determine the nature of the central object. Circular equatorial orbits of particles that comprise the disc are a key ingredient in the study of more realistic disc models. Stuchlík (1980) studied circular equatorial orbits in the spacetime of a rotating NS in detail. A recent comparative study of properties of accretion discs around BHs and NSs can be found in Kovács & Harko (2010) and references therein.
The physics of accretion discs is governed by a combination of different complex processes: gravitomagnetohydrodynamics, turbulent viscous fluids, and radiation fields, among others. The theoretical interpretation of observations of compact X-ray sources is extremely relevant to the understanding of compact-object stellar astrophysics (see, e.g., Lewin & van der Klis 2010). Such studies reveal that magnetic fields are usually associated with accretion discs around compact objects. Understanding this connection could serve as a tool for providing information related to the nature of the central compact object and to discard controversial theoretical models such as NSs.
The presence of magnetic fields affects the trajectories of particles orbiting around a rotating compact object and changes the location of the innermost stable circular orbit (ISCO; Prasanna & Vishveshwara 1978; Wiita et al. 1983; Iyer et al. 1985; Ranea-Sandoval & Vucetich 2014). These modifications may give rise to observable quantities that could be used to distinguish between different theoretical models for compact objects.
Recently, Ranea-Sandoval & García (2015) proposed a model of magnetised accretion discs that were formed in generalised Kerr spacetimes. The model is based on the analysis of the circular equatorial trajectories followed by charged particles in a Kerr spacetime under the presence of an external magnetic field, previously developed by Ranea-Sandoval & Vucetich (2014). In their paper, the authors study the simplest exact solutions to the Maxwell equations in a Kerr background, as obtained by Petterson (1975), introducing two particular magnetic field configurations: uniform and dipolar.
Even though there are studies that predict the linear instability of completely collapsed objects without event horizons, such as NSs (see, e.g., Dotti et al. 2008, 2012, for studies related to the Kerr solution and Cardoso et al. 2008, and Pani et al. 2010, for superspinars), through this work, we study potentially observable differences in the light curves that are produced by a hotspot orbiting at the innermost regions of an accretion disc that is formed around both BHs and NSs, with the idea of developing a tool to probe the nature of the spacetime in the strong gravitational regime close to fully-collapsed objects.
We extend the model presented in Ranea-Sandoval & García (2015) that is based on an adapted version of the free source code YNOGK (Yang & Wang 2013), as well as on the ray-tracing code developed by Psaltis & Johannsen (2012). This version allows us to consider Kerr NSs and to include magnetic field effects on the trajectories that are followed by particles with an effective electric charge. Using our machinery, we model the observed light curves of hotspots that are formed in magnetised accretion discs in a Kerr background and analyse their power spectra. The developed tool provides the possibility to perform an analysis that is independent of the thermal continuum spectra and broad iron-Kα emission line methods, which have proved very useful for measuring the spin parameters of a number of compact objects that assume a Kerr background. See McClintock et al. (2014) and Reynolds (2014) for respective reviews.
Another observational characteristic of the X-ray emission from BH candidates is its high-frequency variability, detected in their power spectra, known as quasi-periodic oscillations (QPOs; van der Klis et al. 1985; Middleditch & Priedhorsky 1986). This particular feature is often observed at commensurate integer ratios in accreting systems with a central compact object in the case of high-frequency QPOs (Miller et al. 2001; Remillard et al. 2002). These observations are a promising probe of the innermost part of the accretion disc and of the nature of the compact object itself (see, e.g., Lamb & Miller 2003; Psaltis 2004). Furthermore, they can be used as a tool to infer the spin parameter of the compact object (e.g., Peres et al. 1997; Stella & Vietri 1998, 1999; Silbergleit et al. 2001; Kluźniak & Abramowicz 2001; Abramowicz et al. 2003).
The comparison between observational data from X-ray binary systems and our theoretical model might be a useful tool to get insight into the physical properties related to the dark massive compact objects present in such binary systems and also to test Penrose’s conjecture in astrophysical environments. Moreover, as we take into account the effect of magnetic fields on observable quantities, this work represents a new tool to estimate the strength and geometry of magnetic fields in the neighborhood of an accretion disc.
The work is organised as follows: in Sect. 2, we present the basics of magnetised accretion discs and hot spots, as well as a description of the theoretical framework used. In Sect. 3, we describe our numerical code. Section 4 is devoted to the presentation of our results for light curves and power spectra for corotating hotspots in accretion discs that are formed in a generic Kerr background spacetime with an external (uniform or dipolar) magnetic field. Finally, we discuss our results and present conclusions in Sect. 5.
2. The model
Shakura & Sunyaev (1973) and Page & Thorne (1974) set the grounds for studying geometrically thin, optically thick accretion discs in astrophysical environments.
Magnetic fields play a decisive role in regard to gas dynamics in jet physics and accretion processes in compact objects. Page-Thorne accretion discs are formed by matter particles orbiting around the central object, which follow time-like circular equatorial geodesics. To model magnetised accretion discs, we incorporate the corrections to circular trajectories followed by charged particles in a Kerr spacetime with an external global magnetic field (Ranea-Sandoval & Vucetich 2014).
Like other accretion discs models, the one proposed by Ranea-Sandoval & García (2015) is not completely self consistent. Matter in the disc and the magnetic field do not alter the spacetime geometry. Moreover, the magnetic field structure is not tied to the plasma motion. For these reasons, in this paper we only consider magnetic fields of small strengths that weakly interact with the plasma.
2.1. The Kerr spacetime
A completely collapsed object with mass M and angular momentum J ≡ aM is described by the vacuum solution to the Einstein field equations obtained by Kerr (1963): 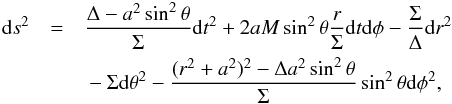 (1)where Δ ≡ r2−2Mr + a2, Σ ≡ r2 + a2cos2θ. Here, we use Boyer-Lindquist coordinates and (+ ,−,−, −) metric signature. In this section, we also use geometric units and set c = G = 1, where c and G are the speed of light and the gravitational constant, respectively.
(1)where Δ ≡ r2−2Mr + a2, Σ ≡ r2 + a2cos2θ. Here, we use Boyer-Lindquist coordinates and (+ ,−,−, −) metric signature. In this section, we also use geometric units and set c = G = 1, where c and G are the speed of light and the gravitational constant, respectively.
In the sub-extreme case, (0 ≤ | a | <M), the Kerr spacetime harbours a BH with two horizons located at the roots of the function Δ1. In the extreme case, (| a | = M), the two horizons merge since the root of Δ becomes a double root. In both cases, the outer horizon causally disconnects the interior domain from the external universe, hiding the curvature singularity. In the super-extreme case, (| a | >M), the ring singularity is causally connected to future null infinity as no horizons are present, because the roots of the function Δ become complex. In this case, the spacetime harbours what is usually called a Kerr NS. We note, however, that causality is violated everywhere around a Kerr NS, because any event in that spacetime can be connected to any other event by both a future- and a past-directed timelike curve (Carter 1968, 1973).
2.2. Magnetised accretion discs
Following Ranea-Sandoval & García (2015) we incorporate two different magnetic field configurations: the simplest uniform (U) case and a dipolar (D) one, which could be generated through the Poynting-Robertson cosmic battery mechanism (Contopoulos & Kazanas 1998; Contopoulos & Papadopoulos 2012).
The four-vector potential in the uniform case can be expressed as (Petterson 1975) 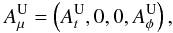 (2)where
(2)where ![\begin{eqnarray} &&A_t^{\rm U} = -aB\left(1-\frac{Mr}{\Sigma}\left(2- \sin ^2 \theta\right)\right), \nonumber \\ &&A_\phi^{\rm U} = \frac{B \sin ^2 \theta}{2\Sigma} \left[\left(r^2+a^2\right)^2 - \Delta a^2 \sin ^2 \theta -4Ma^2r\right] , \end{eqnarray}](/articles/aa/full_html/2016/03/aa27862-15/aa27862-15-eq17.png) (3)and where B is the magnetic field strength. For this magnetic field configuration, the coupling constant between the effective charge and the magnetic field strength is defined as
(3)and where B is the magnetic field strength. For this magnetic field configuration, the coupling constant between the effective charge and the magnetic field strength is defined as 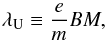 (4)where e and m are the charge and rest mass of the particles, respectively.
(4)where e and m are the charge and rest mass of the particles, respectively.
For the dipolar case (Petterson 1975), the non-zero components of the four-vector potential 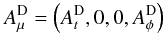 (5)can be written as
(5)can be written as 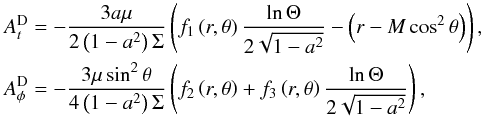 (6)where μ is the magnetic dipole moment (assumed to be aligned with the spin axis), fi(r,θ),i = 1,2,3, are functions defined as
(6)where μ is the magnetic dipole moment (assumed to be aligned with the spin axis), fi(r,θ),i = 1,2,3, are functions defined as ![\begin{eqnarray} &&f_1\left(r,\theta\right) \equiv r\left(r-M\right)+\left(a^2-Mr\right)\cos ^2 \theta , \nonumber \\ &&f_2\left(r,\theta\right) \equiv \left(r-M\right)a^2\cos ^2 \theta + r\left(r^2+Mr+2a^2\right) , \nonumber \\ &&f_3\left(r,\theta\right) \equiv - \left[r\left(r^3+ a^2r-2Ma^2\right)+\Delta a^2 \cos ^2 \theta \right], \end{eqnarray}](/articles/aa/full_html/2016/03/aa27862-15/aa27862-15-eq26.png) (7)and the function Θ is given by
(7)and the function Θ is given by 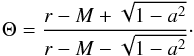 (8)For this magnetic field configuration, the coupling constant between the effective charge and the magnetic field strength is
(8)For this magnetic field configuration, the coupling constant between the effective charge and the magnetic field strength is 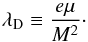 (9)
(9)
2.3. Emission from a hotspot
The simplest model of a hotspot was developed by Stella & Vietri (1998, 1999) and assumes that isotropic, monochromatic emission originates from a small region that corotates with the accretion disc following a circular trajectory. In this so-called blob model, the emissivity is assumed to be a Gaussian distribution of the distance from the centre of the hot spot: 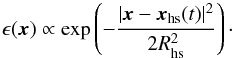 (10)Here, the spatial 3-vector, x, is given in pseudo-Cartesian coordinates for the Kerr spacetime. The size, Rhs, of the hotspot has to be small compared to the radial coordinate of its centre. If this were not the case, as the model assumes that all points belonging to the hotspot have the same 4-velocity of the “guiding” trajectory of the centre, tidal effects would eventually destroy the hotspot.
(10)Here, the spatial 3-vector, x, is given in pseudo-Cartesian coordinates for the Kerr spacetime. The size, Rhs, of the hotspot has to be small compared to the radial coordinate of its centre. If this were not the case, as the model assumes that all points belonging to the hotspot have the same 4-velocity of the “guiding” trajectory of the centre, tidal effects would eventually destroy the hotspot.
To properly compute the observed light curve, it is essential to take into account the time delay effects in Kerr spacetime. After obtaining the hotspot trajectory that has been parametrised via the coordinate time t, a ray-tracing map between the disc and the observer must be used to obtain the observed flux as a function of time. For each photon bundle intersection point, one can calculate a position-dependent time delay, Δt. This means that, to calculate the associated observer time, tobs, it is first necessary to determine the position of the hot spot at emission time, tem = tobs−Δt, which is different for each point of the accretion disc.
Repeating this procedure along the whole rotation period results in a time-dependent spectrum or spectrogram. After integration over frequencies the light curve is obtained. In this paper, we will set the arbitrary phase to the value φ = 0.5 at the time when the emission peaks for each light curve.
The flux from a hotspot experiences variations as a result of two fundamental processes since the hotspot is orbiting around the compact object. Frequency shifts of the emitted photons, (usually called redshifts, defined as g ≡ νobs/νem, where νobs and νem are the observed and emitted frequency of a given photon, respectively), as well as flux amplifications and deamplifications occur owing to Doppler boosting, gravitational lensing, and relativistic beaming.
3. The numerical code
 |
Fig. 1 Snapshots of the motion of a hotspot formed near the ISCO of a black hole with a spin a = 0.5rg (left panels) and a naked singularity with a spin a = 2rg (right panels), both observed at an inclination of i = 75° at four different phases φ. The colour bar indicates the observed flux in arbitrary units. The impact parameters α and β are expressed in gravitational radii. |
In this section we present how our numerical code operates to obtain the light curve of a corotating hot spot in a magnetised accretion disc that generalises the classical model, the Page & Thorne (1974) model.
To obtain the light curves as seen by a distant observer at an arbitrary position, we incorporate a ray-tracing technique to calculate the geodesics of photons between a plane placed at the position of the observer and the surface of the disc. For this purpose, we adapted both the public semi-analytic code YNOGK (Yang & Wang 2013) and the fully-numerical code from Psaltis & Johannsen (2012) to incorporate the orbits that correspond to circular trajectories followed by charged particles coupled to a magnetised Kerr spacetime through different values of the λU,D parameters, generalising the equations to allow for the appearance of NSs for | a | >M. With this machinery we proceed as follows:
-
We calculate the properties of circular trajectories followed bymatter in the disc at radii rhs.
-
We evaluate the orbital velocity at the hotspot radius to define the phases.
-
For each discrete phase, we obtain the image of the hotspot and we evaluate the relativistic effects experienced by photons that are emitted from the disc as they travel to the observer by means of the ray-tracing code.
For the calculations presented in this paper, phase and energy spaces are discretised to 100 steps, and snapshot images are constructed using a 500 × 500 pixel resolution. We also fixed rhs = 1.1rISCO and Rhs = 0.1rhs as we are only interested in the imprints of the motion of a compact hotspot at the innermost region of the accretion disc. Although this definition places a small part of the hotspot inside the ISCO, this does not affect our results, since our numerical code only considers photons that originate from the disc, with r>rISCO.
In Fig. 1 we show selected snapshots of the observed flux of a hotspot that is located at the innermost part of a non-magnetised accretion disc and formed around a BH with spin parameter a = 0.5rg (left panels) and an NS with spin parameter a = 2rg (right panels), as seen by a distant observer at an inclination angle of 75°. The different colours indicate the observed flux in arbitrary units, and α and β are coordinates in the observer’s plane, expressed in gravitational radii rg ≡ GM/c2.
A clear difference between the two opposite cases can be observed at phase φ = 1 where, in the case of the NS, two different images of the same hotspot can be observed (due to light-bending effects and the absence of an event horizon). This secondary image arises because the corresponding photons make one full revolution around the NS. A similar feature was observed in the paper of Li & Bambi (2014). In the BH case, the emission of the hotspot is negligible for ~ 70% of the time, becoming important only in the 0.35−0.65 phase range. Thus we selected snapshots at φ = 0.4, 0.5, 0.6, and 1.0. On the contrary, in the NS case, the hot spot is brighter for roughly half of the period and thus we chose equidistant phases φ = 0.25, 0.5, 0.75, and 1.0 to illustrate the snapshots.
The strong elongation of the observed image of the hotspot at φ ~ 0.5 (for the BH) and φ ~ 0.25 (for the NS) is a direct consequence of relativistic time dilation. As we mentioned, the phase is arbitrarily chosen so that the observed emission peaks at φ = 0.5. In both the BH and NS cases, this phase corresponds approximately to the moment when the hotspot velocity points in the direction to the observer, as a consequence of Doppler boosting.
4. Results
Having presented the central aspects of our model and numerical code, we now focus on our results and their implications. We divide these into two subsections: one for the light curves and one for the power spectra.
 |
Fig. 2 Light curves of corotating hotspots at the innermost part of accretion discs around a BH with rotational parameter a = 0.95rg (black lines) and a NS with a = 1.10rg (gray lines) viewed at inclinations of i = 30° (top panels) and i = 75° (bottom panels), respectively. Solid lines are used for non-magnetised accretion discs and dashed and dotted lines correspond to uniform and dipolar magnetised cases, respectively. The left panels show the total light curves which are fainter in the case of NSs. The center and right panels show the same light curves, separated into soft and hard energy bands with redshifts g ≤ 0.9 and g> 0.9, respectively. A dipolar magnetic field configuration leads to noticeable changes in the shapes and amplitudes of these light curves, while a uniform magnetic field configuration has practically no effect on the light curves. |
4.1. Light curves of hotspots in magnetised accretion discs
Implementing the numerical algorithm described in the previous section, we have been able to generate a family of theoretical light curves that have been emitted by corotating hotspots formed in magnetised accretion discs around both BHs and NSs.
In Fig. 2 we show the light curves of hotspots formed in the innermost part of magnetised accretion discs. In the left panels, we show the total flux as a function of the phase angle. The top and bottom panels correspond to inclinations of i = 30° and i = 75°, respectively. Clear differences can be seen between those formed around a = 0.95rg BHs (black lines) and a = 1.10rg NSs (grey lines) which are fainter in the latter case. Moreover, narrower (broader) light curves are found for high (low) inclinations. The presence of a uniform magnetic field barely affects the light curves, while the presence of a dipolar one strongly changes their shapes, as it is larger in the innermost parts of the disc.
When the observed photons are separated into soft (g ≤ 0.9) and hard (g> 0.9) energy bands (central and right panels, respectively), where g is the photon redshift, the light curves can have a very different shape. At high inclinations, in the case of either a BH or an NS, as well as at low inclinations, in the case of a NS in the presence of a dipolar magnetic field, the light curve has two peaks in the soft energy band, one before and one after the phase that corresponds to the peak of the total light curve. These peaks are an interesting characteristic for determining the parameter λD.
In the hard energy band, the contribution of the hard flux to the total observed flux is negligible for low inclinations, except in the case of a dipolar magnetic field around NSs (see top right panel of Fig. 2). The explanation for this phenomenon lies on the fact that the ISCO is closer to the curvature singularity than in the non-magnetised case (Ranea-Sandoval & García 2015), which causes the effect of the Doppler boosting to be sufficiently strong enough to overcome the effect of the gravitational redshift.
The origin of the wiggle and second bump present in the top panels of Fig. 2 for the a = 1.10rg NS with λD = 0.1 can be traced to the appearance of the secondary image (see right bottom panels of Fig. 1). This particular (and potentially observable) feature could be used as a tool to distinguish the nature of the central compact object.
4.2. Power spectra and quasi-periodic oscillations
 |
Fig. 3 Fundamental modes and lowest-order harmonics of the light curves presented in Fig. 2. The number of potentially observable modes and their relative amplitudes are strongly dependent on the type of the compact object, the inclination angle i, and the presence of a dipolar magnetic field. At small inclinations, the modes in the hard energy band are only visible, in the NS case, in a magnetised accretion disc with λD = 0.1, which makes this a particularly interesting tool for determining the parameter λD. |
Innermost stable circular orbits and orbital frequencies associated with the hot spots.
Computing the fast-Fourier transforms (FFTs) of the simulated light curves allows us to obtain the corresponding signals in the frequency domain. These frequencies can, in principle, be compared with the high-frequency X-ray variability seen in the observational data from X-ray binary systems. Here, we focus on the fundamental mode and higher-order harmonics of each light curve. In Table 1, we show the locations of the ISCO and the corresponding fundamental modes of the orbiting hotspot for BHs with spins a = 0.5rg and 0.95rg, as well as for NSs with spins a = 1.10rg and 2.0rg, assuming typical masses of 5 M⊙ and 10 M⊙ for each case.
In Fig. 3, we present FFTs of the light curves shown in Fig. 2. The mode patterns are strongly dependent on the inclination angle, i, both in the number of potentially observable modes and in their relative amplitudes. Differences for large inclinations (bottom panels) between the FFTs of the light curves in the soft and hard energy bands are evident. For small inclinations, FFTs in the hard energy band are only visible in the NS case in a magnetised accretion disc with λD = 0.1, which makes this an interesting tool for a determination of the parameter λD. For large inclinations, the situation changes and modes are visible in both the soft and hard energy bands. The variations between magnetised and non-magnetised FFTs are too small to be detectable.
5. Discussion
One of the main problems in general relativity and high-energy astrophysics is related to the question whether the CCC is valid or not. Astrophysical studies of compact objects are highly important as they can provide a unique tool for testing the validity of the weak CCC. In this sense, the development of theoretical tools that can be used to determine the nature of the compact object in an X-ray binary system has been an area of great activity during recent decades.
The nature and strength of the magnetic field in the region very close to the compact object that is present in these type of binaries is of great interest and could help us to better understand the complex scenario for the formation of accretion discs. Since most of the estimates for the magnetic fields found around compact objects are currently obtained by means of the properties of the non-thermal radiation that is produced far away from the disc, as well as using Faraday rotation measurements (see, e.g., Marrone et al. 2007; Eatough et al. 2013), the study of the effects caused by an external magnetic field on the emission of hotspots of accretion discs becomes relevant for these purposes.
Motivated by these two reasons, we continued the work presented in Ranea-Sandoval & García (2015) and developed a new tool that can be used to estimate the presence of a magnetic field in the neighbourhood regions of an accretion disc formed around a Kerr compact object. In the framework of the magnetised Page-Thorne accretion disc model, which was developed by Ranea-Sandoval & García (2015), we studied non-magnetised accretion discs, recovering well-known results from Page & Thorne (1974). We also extended these results by analysing the effects of an external uniform or dipolar magnetic field on the ho spot light curves and power spectra. For the first time we present light curves of hotspots formed in accretion discs around NSs.
We showed that the presence of an external dipolar magnetic field leads to potentially observable modifications of the light curves and power spectra for both Kerr BHs and NSs, while an external uniform magnetic field has practically no effect. In particular, we demonstrated that the emission from a hotspot orbiting near the ISCO of a NS in a dipolar magnetic field can be significantly harder than the emission of the same hotspot in the absence of this kind of magnetic field, at least for the spin values we considered.
Very precise detections of fundamental modes and higher-order harmonics of QPOs in X-ray binaries will become possible with future X-ray missions such as the Large Observatory For X-ray Timing (LOFT; Feroci et al. 2014). Observations of QPOs could also provide a test of the Kerr nature of BH candidates and, thereby, of general relativity (Johannsen & Psaltis 2011; Bambi 2012). A direct image of a handful of supermassive BHs and, hence, of an event horizon may be obtained by the Event Horizon Telescope (Doeleman et al. 2009a,b; Fish et al. 2009).
Acknowledgments
We thank the referee, Ulf Torkelsson, for valuable comments that helped us to improve our paper. We are grateful to Dr. M. M. Miller Bertolami for lending us the computer with which most of the numerical calculations were performed for this paper. I.F.R.S. acknowledges support from Universidad Nacional de La Plata. I.F.R.S. and F.G. are fellows of CONICET. T.J. was supported, in part, by Perimeter Institute for Theoretical Physics. Research at Perimeter Institute is supported by the Government of Canada through Industry Canada and by the Province of Ontario through the Ministry of Research and Innovation.
References
- Abramowicz, M. A., Karas, V., Kluźniak, W., Lee, W. H., & Rebusco, P. 2003, PASJ, 55, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Bambi, C. 2012, J. Cosmol. Astropart. Phys., 9, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Broderick, A. E., Loeb, A., & Narayan, R. 2009, ApJ, 701, 1357 [NASA ADS] [CrossRef] [Google Scholar]
- Cardoso, V., Pani, P., Cadoni, M., & Cavaglià, M. 2008, Class. Quant. Grav., 25, 195010 [NASA ADS] [CrossRef] [Google Scholar]
- Carter, B. 1968, Phys. Rev., 174, 1559 [NASA ADS] [CrossRef] [Google Scholar]
- Carter, B. 1973, in Black Holes, eds. C. DeWitt, & B. S. DeWitt (New York: Gordon and Breach) [Google Scholar]
- Contopoulos, I., & Kazanas, D. 1998, ApJ, 508, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Contopoulos, I., & Papadopoulos, D. B. 2012, MNRAS, 425, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Doeleman, S. S., Agol, E., Backer, D., et al. 2009a, Astro2010: The Astronomy and Astrophysics Decadal Survey, Science White Papers, No. 68 [Google Scholar]
- Doeleman, S. S., Fish, V. L., Broderick, A. E., Loeb, A., & Rogers, A. E. E. 2009b, ApJ, 695, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Dotti, G., Gleiser, R. J., Ranea-Sandoval, I. F., & Vucetich, H. 2008, Class. Quant. Grav., 25, 245012 [NASA ADS] [CrossRef] [Google Scholar]
- Dotti, G., Gleiser, R. J., & Ranea-Sandoval, I. F. 2012, Class. Quant. Grav., 29, 095017 [NASA ADS] [CrossRef] [Google Scholar]
- Eatough, R. P., Falcke, H., Karuppusamy, R., et al. 2013, Nature, 501, 391 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Feroci, M., den Herder, J. W., Bozzo, E., et al. 2014, SPIE, 9144, 2 [Google Scholar]
- Fish, V. L., Broderick, A. E., Doeleman, S. S., & Loeb, A. 2009, ApJ, 692, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Iyer, B. R., Vishveshwara, C. V., Wiita, P. J., & Goldstein, J. J. 1985, Pramana, 25, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Johannsen, T., & Psaltis, D. 2011, ApJ, 726, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Joshi, P. S. 2008, Gravitational Collapse and Spacetime Singularities (Cambridge University Press) [Google Scholar]
- Kerr, R. P. 1963, Phys. Rev. Lett., 11, 237 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Kluźniak, W., & Abramowicz, M. A. 2001, ArXiv e-prints [arXiv:astro-ph/0105057] [Google Scholar]
- Kovács, Z., & Harko, T. 2010, Phys. Rev. D, 82, 124047 [NASA ADS] [CrossRef] [Google Scholar]
- Lamb, F. K., & Miller, M. C. 2003, ArXiv e-prints [arXiv:astro-ph/0308179] [Google Scholar]
- Lewin, W., & van der Klis, M. 2010, Compact Stellar X-ray Sources (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Li, Z., & Bambi, C. 2014, Phys. Rev. D, 90, 024071 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Marrone, D. P., Moran, J. M., Zhao, J.-H., & Rao, R. 2007, ApJ, 654, L57 [NASA ADS] [CrossRef] [Google Scholar]
- McClintock, J. E., Narayan, R, & Steiner, J. F. 2014, Space Sci. Rev., 183, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Middleditch, J., & Priedhorsky, W. C. 1986, ApJ, 306, 230 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, J. M., Wijnands, R., Homan, J., et al. 2001, ApJ, 563, 928 [NASA ADS] [CrossRef] [Google Scholar]
- Page, D. N., & Thorne, K. S. 1974, ApJ, 191, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Pani, P., Barausse, E., Berti, E., & Cardoso, V. 2010, Phys. Rev. D, 82, 044009 [NASA ADS] [CrossRef] [Google Scholar]
- Penrose, R. 1969, Nuovo Cimento Rivista, 1, 252 [Google Scholar]
- Penrose, R. 1998, in Black Holes and Relativistic Stars, ed. R. M. Wald (Chicago, IL: University of Chicago Press), 103 [Google Scholar]
- Peres, C. A., Silbergleit, A. S., Wagoner, R. V., & Lehr, D. E. 1997, ApJ, 476, 589 [NASA ADS] [CrossRef] [Google Scholar]
- Petterson, J. A. 1975, Phys. Rev. D, 12, 2218 [NASA ADS] [CrossRef] [Google Scholar]
- Psaltis, D. 2004, AIP Conf. Proc., 714, 29 [Google Scholar]
- Psaltis, D., & Johannsen, T. 2012, ApJ, 745, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Prasanna, A. R., & Vishveshwara, C. V. 1978, Pramana, 11, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Ranea-Sandoval, I. F., & García, F. 2015, A&A, 574, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ranea-Sandoval, I. F., & Vucetich, H. 2014, in Relativity and Gravitation, eds. J. Bičák, & T. Ledvinka, Springer Proceedings in Physics, 157, 453 [Google Scholar]
- Remillard, R. A., Muno, M. P., McClintock, J. E., & Orosz, J. A. 2002, ApJ, 580, 1030 [NASA ADS] [CrossRef] [Google Scholar]
- Reynolds, C. S. 2014, Space Sci. Rev., 183, 277 [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Silbergleit, A. S., Wagoner, R. V., & Ortega-Rodríguez, M. 2001, ApJ, 548, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Stella, L., & Vietri, M. 1998, ApJ, 492, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Stella, L., & Vietri, M. 1999, Phys. Rev. Lett., 82, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Stuchlík, Z. 1980, Bull. Astr. Inst. Czechosl., 31, 129 [Google Scholar]
- van der Klis, M., Jansen, F., van Paradijs, J., Lewin, W. H. G., et al. 1985, Nature, 316, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Wiita, P. J., Vishveshwara, C. V., Siah, M. J., & Iyer, B. R. 1983, J. Phys. A: Math. Gen., 16, 2077 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, X., & Wang, J. 2013, ApJS, 201, 6 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Innermost stable circular orbits and orbital frequencies associated with the hot spots.
All Figures
 |
Fig. 1 Snapshots of the motion of a hotspot formed near the ISCO of a black hole with a spin a = 0.5rg (left panels) and a naked singularity with a spin a = 2rg (right panels), both observed at an inclination of i = 75° at four different phases φ. The colour bar indicates the observed flux in arbitrary units. The impact parameters α and β are expressed in gravitational radii. |
| In the text | |
 |
Fig. 2 Light curves of corotating hotspots at the innermost part of accretion discs around a BH with rotational parameter a = 0.95rg (black lines) and a NS with a = 1.10rg (gray lines) viewed at inclinations of i = 30° (top panels) and i = 75° (bottom panels), respectively. Solid lines are used for non-magnetised accretion discs and dashed and dotted lines correspond to uniform and dipolar magnetised cases, respectively. The left panels show the total light curves which are fainter in the case of NSs. The center and right panels show the same light curves, separated into soft and hard energy bands with redshifts g ≤ 0.9 and g> 0.9, respectively. A dipolar magnetic field configuration leads to noticeable changes in the shapes and amplitudes of these light curves, while a uniform magnetic field configuration has practically no effect on the light curves. |
| In the text | |
 |
Fig. 3 Fundamental modes and lowest-order harmonics of the light curves presented in Fig. 2. The number of potentially observable modes and their relative amplitudes are strongly dependent on the type of the compact object, the inclination angle i, and the presence of a dipolar magnetic field. At small inclinations, the modes in the hard energy band are only visible, in the NS case, in a magnetised accretion disc with λD = 0.1, which makes this a particularly interesting tool for determining the parameter λD. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


