| Issue |
A&A
Volume 587, March 2016
|
|
|---|---|---|
| Article Number | A88 | |
| Number of page(s) | 8 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201527626 | |
| Published online | 23 February 2016 | |
Dust production in debris discs: constraints on the smallest grains
LESIA-Observatoire de Paris, UPMC Univ. Paris 06, Univ.
Paris-Diderot,
92195
Meudon
France
e-mail:
philippe.thebault@obspm.fr
Received: 23 October 2015
Accepted: 4 January 2016
Context. The surface energy constraint puts a limit on the smallest fragment ssurf that can be produced after a collision. Based on analytical considerations, this mechanism has been recently identified as being having the potential to prevent the production of small dust grains in debris discs and to cut off their size distribution at sizes larger than the blow-out size.
Aims. We numerically investigate the importance of this effect to find out under which conditions it can leave a signature in the small-size end of a disc’s particle size distribution (PSD). An important part of this work is to map out, in a disc at steady-state, what is the most likely collisional origin for μm-sized dust grains, in terms of the sizes of their collisional progenitors.
Methods. For the first time, we implement the surface energy constraint into a collisional evolution code. We consider a typical debris disc extending from 50 to 100 au and two different stellar types: sun-like and A star. We also consider two levels of stirring in the disc: dynamically “hot” (⟨e⟩ = 0.075) and “cold” (⟨e⟩ = 0.01). In all cases, we derive ssurf maps as a function of target and projectile sizes, st and sp, and compare them to equivalent maps for the dust-production rate. We then compute disc-integrated profiles of the PSD and estimate the imprint of the surface energy constraint.
Results. We find that the (sp,st) regions of high ssurf values do not coincide with those of high dust production rates. As a consequence, the surface energy constraint generally has a weak effect on the system’s PSD. The maximum ssurf-induced depletion of μm-sized grains is ~30% and is obtained for a sun-like star and a dynamically “hot” case. For the e = 0.01 cases, the surface energy effect is negligible compared to the massive small grain depletion that is induced by another mechanism: the “natural” imbalance between dust production and destruction rates in low-stirring discs.
Key words: planetary systems / circumstellar matter
© ESO, 2016
1. Introduction
Circumstellar debris discs have been detected around main-sequence stars because of the excess luminosity produced by μm- to mm-sized dust. Because of its relatively short lifetime, this dust cannot be primordial and is thought to be steadily replenished by a chain of erosive collisions starting from a reservoir of large, planetesimal-like, parent bodies (e.g. Wyatt 2008; Krivov 2010). In an idealized case, the size distribution of bodies within such a collisional cascade should settle toward a power law of the form dN ∝ sqds, where the index q is close to −3.5 (Dohnanyi 1969). Such a power law has the interesting characteristics that, while most of the disc’s mass is contained in the biggest objects of the cascade, most of the geometrical cross section should be contained in the smallest grains of size smin. This means that, at all wavelengths λ ≲ 2πsmin, the disc’s luminosity should be dominated by these smallest grains.
Determining smin is consequently of crucial importance. Luckily, for most stars, stellar radiation pressure imposes a “natural” minimum cut-off size that is, in principle, easy to estimate. Indeed, because this pressure is both ∝1 /s and, like stellar gravity, ∝1 /r2 (r being the radial distance to the star), there is a minimum size sblow below which radiation pressure overcomes gravity and grains are quickly blown out from the system. Because small grains are probably produced from parent bodies on Keplerian orbits, the criteria for estimating sblow is given by β(sblow) = FRad.Press./Fgrav. = 0.5 (for parent bodies on circular orbits). For typical astro-silicates (Draine 2003), values for β range from ~0.5 μm for solar-type stars to 2−10 μm for late-type A stars (Krivov 2007)1. As a consequence, in scattered light, disc luminosities should always be dominated by grains close to sblow, and, for A stars, sblow grains should also dominate the thermal flux up to mid-IR wavelengths.
However, observations have sometimes challenged this basic view. Some discs have, for example, been found to contain important quantities of sub-micron grains below sblow (Ardila et al. 2004; Fitzgerald et al. 2007; Johnson et al. 2012). While there does not seem to be one single straightforward scenario for the presence of such tiny particles, some possible explanations have been suggested. One of them is that, at very small sizes, the β(s) curve starts to decrease with decreasing s before reaching a constant value that can be <0.5 for K, G or F stars, thus placing sub-micron grains on bound orbits (Johnson et al. 2012). Another possibility is that we are witnessing a powerful collisional chain-reaction, called an “avalanche”, of high-β particles that are passing through a dense ring of larger grains (Grigorieva et al. 2007).
1.1. Discs with “too large” minimum dust sizes
Here we will focus on the opposite problem, i.e., the systems for which the observationally derived smin has been found to be larger than sblow. The existence of such systems was first unambiguously determined by Pawellek et al. (2014), who considered a sample of 34 resolved discs2 and found that, while discs around A-star have smin ~ sblow, the smin/sblow ratio increased towards low-mass stars and could reach ~10 for solar-type stars. These results were later confirmed by Pawellek & Krivov (2015), who showed that the ssmin/sblow trend is robust and does not depend on material compositions or grain porosity.
These results seem to be in contradiction with the aforementioned behaviour expected in discs where a size distribution in dN ∝ sqds holds down to the blow-out size sblow, for which luminosities should be dominated by grains close to the blow-out size. Interestingly, numerical investigations of the collisional evolutions of debris discs have shown that, at least in the small-size domain, size distributions can in fact significantly depart from an idealized dN ∝ sqds power-law. The simulations of Thebault et al. (2003), Krivov et al. (2006), Thebault & Augereau (2007) have indeed shown that size-distributions can exhibit pronounced “wavy” patterns in the ≲100sblow domain, triggered by the absence of potential destructive projectiles below sblow. However, this waviness cannot deprive the system from grains close to sblow, and, generally, it even has just the opposite effect, inducing a density peak of grains in the 1.5−2sblow region (Thebault & Augereau 2007).
A possible cause of small-grain depletion could be the well-known Poynting-Robertson drag, which causes small particles to slowly spiral starwards. However, this effect is likely to be only noticeable for tenuous discs for which the collisional timescale of small grains becomes larger than tPR (Wyatt 2005). The first plausible mechanism for small-grain depletion that could also work for bright discs was proposed by Thebault & Wu (2008), who showed that, in discs with a low dynamical excitation (low orbital eccentricities e and inclinations i), there is an imbalance between the production and destruction rates of small grains. Indeed, while their production rate is controlled by the erosion of larger particles and is thus low because of these particles’ low ⟨e⟩, their destruction rate, which is controlled by impacts involving the small grains themselves, is much higher because these grains are placed on high-e orbits by radiation pressure regardless of the dynamical excitation in the rest of the system. As a result, depending on the value for ⟨e⟩, there could be a strong depletion of grains up to sub-mm sizes. The main issue with this scenario is that it requires values of ⟨e⟩ that could possibly be unrealistically low (see Sect. 4).
1.2. Maximum surface energy and minimum fragment size
Another, potentially more generic scenario has recently been proposed by Krijt & Kama (2014). It is based on an energy-conservation criteria, related to the physics of collisions themselves, which, remarkably enough, had never before been invoked in the context of debris discs. The argument is that a destructive collision cannot produce a size distribution of fragments that reaches an infinitely small value, as this would require an infinite amount of energy. This is because creating new fragments means increasing the amount of exposed surface, and this requires energy. There is thus a minimum size ssurf in the fragment distribution, which is given by the requirement that the total surface energy of all fragments cannot exceed the kinetic energy of the impact. For the specific case of a fully destructive impact between two equal-sized bodies and for a q = −3.5 size distribution, Krijt & Kama (2014) derived a relation linking ssurf to slfr, the size of the largest fragment, and the impactor’s size s0: 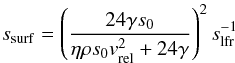 (1)where vrel is the impact velocity, γ is the surface energy per unit surface, and η is the fraction of the kinetic energy that is used to create a new surface. Interestingly, this formula gives the counter-intuitive result that, for a given vrel and a fixed slfr/s0 ratio (i.e., for self-similar impacts), the size of the smallest fragment increases with decreasing s0 sizes. For low-velocity impacts, low values of η and for material with high γ (like ice), ssurf can be significantly higher than sblow for s0 ≲ 1 m (see Fig. 1 of Krijt & Kama 2014).
(1)where vrel is the impact velocity, γ is the surface energy per unit surface, and η is the fraction of the kinetic energy that is used to create a new surface. Interestingly, this formula gives the counter-intuitive result that, for a given vrel and a fixed slfr/s0 ratio (i.e., for self-similar impacts), the size of the smallest fragment increases with decreasing s0 sizes. For low-velocity impacts, low values of η and for material with high γ (like ice), ssurf can be significantly higher than sblow for s0 ≲ 1 m (see Fig. 1 of Krijt & Kama 2014).
However, while deriving estimates of ssurf is analytically possible for one given collision, giving global estimates for a whole debris disc is a much more problematic task, since the values of ssurf will vary greatly depending on the absolute and relative sizes of the impacting objects. In their pioneering study, Krijt & Kama (2014) attempt to derive a disc-integrated ssurf by only considering impacts between equal-sized s0 objects and by restricting themselves to “barely catastrophic” impacts where each impactor is split into two identical fragments. This simplifying choice relied on two main assumptions: 1) for a given target size, and if slfr is fixed, it is with a projectile of the same size that the smallest “smallest fragments” should be obtained, hence the choice of equal-sized impacts as the most constraining ones, and 2) in a collisional cascade, small grains should preferentially originate from collisions that involve particles that are barely larger than themselves; so that even if collisions amongst large objets have very small ssurf values (because 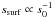 if slfr/s0 is fixed) the amount of small dust they produce cannot compensate for the amount of small dust “not produced” (because of their larger ssurf) by collisions amongst small grains, hence the focus on the smallest “barely catastrophic” impacts . Under these simplifying hypotheses, the disc-integrated
if slfr/s0 is fixed) the amount of small dust they produce cannot compensate for the amount of small dust “not produced” (because of their larger ssurf) by collisions amongst small grains, hence the focus on the smallest “barely catastrophic” impacts . Under these simplifying hypotheses, the disc-integrated  is then the ssurf obtained for the smallest s0 object that can be split in two by an impact at vrel
is then the ssurf obtained for the smallest s0 object that can be split in two by an impact at vrel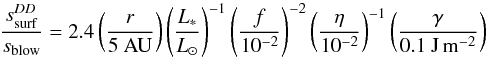 (2)where f = (1.25e2 + i2)0.5.
(2)where f = (1.25e2 + i2)0.5.
1.3. Need for a numerical approach
As rightfully stated by Krijt & Kama (2014) themselves, Eq. (2) should only be taken as an order of magnitude estimate, as it only takes into account a very limited range of collision types. But even this role as an order-of-magnitude indication should be taken with caution, because the simplifying assumptions that justify the predominant role of equal-sized barely-catastrophic impacts might not hold in a realistic disc. The first problem is that this predominant role has been inferred by assuming that slfr is fixed, which is far from being the case in realistic conditions, where slfr strongly depends on the two impactors’ mass ratio and on vrel (e.g. Leinhardt & Stewart 2012). Another problem is that it was derived assuming that a q = −3.5 power law holds for the whole size distribution, which several debris disc studies have shown to be erroneous, especially in the small grain-size domain. Last but not least, it neglects the contribution of cratering impacts, which might have a dominant role in the global dust production and destruction balance (Thebault & Augereau 2007; Kobayashi & Tanaka 2010)3.
Pawellek & Krivov (2015) improved on Eq. (2) by taking into account the fact that velocities of impacts involving small grains might have higher values because radiation pressure places small grains on highly eccentric or even parabolic orbits. This significantly reduces the values of 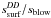 with respect to Eq. (2). Interestingly, this did not, however, improve the fit to the observationally-derived
with respect to Eq. (2). Interestingly, this did not, however, improve the fit to the observationally-derived 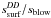 , for which the original Krijt & Kama (2014) formula seems to provide a better match (see Fig. 14 of Pawellek & Krivov 2015). However, even the improved formula used by Pawellek & Krivov (2015) is still a disc-averaged analytical estimate that relies on the same simplifying assumptions mentioned earlier.
, for which the original Krijt & Kama (2014) formula seems to provide a better match (see Fig. 14 of Pawellek & Krivov 2015). However, even the improved formula used by Pawellek & Krivov (2015) is still a disc-averaged analytical estimate that relies on the same simplifying assumptions mentioned earlier.
We propose here to take these studies a step further by incorporating, for the first time, the surface-energy constraint within a numerical collisional evolution code, estimating ssurf(i,j) for all pairs of impacting bodies of sizes si and sj and taking these values into account in the collision-outcome prescription of our code. We describe our numerical model and the set-ups for the different cases that we explore in Sect. 2. Results are presented in Sect. 3, where we first compare the ssurf(i,j) maps to equivalent (si, sj) maps for the level of dust production in the disc. We then display the steady state particle size distributions obtained for all considered cases, and investigate the signature of the surface-energy constraint by comparing these particle size distributions (PSDs) to those obtained for control runs without the ssurf criteria. In Sect. 4, we then discuss the importance of the surface-energy constraint, in particular with respect to the concurrent “low-stirring” dust-depletion mechanism identified by Thebault & Wu (2008).
2. Model
We use the statistical collisional model developed by Thebault et al. (2003) and later upgraded by Thebault & Augereau (2007). This has a “particle-in-a-box” structure, where particles are sorted into logarithmic size bins separated by a factor 2 in mass. It also has a 1D spatial resolution, being divided into radially concentric annuli. Collision rates between all size bins are computed using an estimate of the average orbital eccentricity and inclinations in each size bin. Crucially, the code takes into account the increased eccentricities, and thus impact velocities of small grains whose orbits are affected by stellar radiation pressure, as well as the fact that these grains are able to cross several concentric annuli (see Appendix of Thebault & Augereau 2007). Collision outcomes are then divided into two categories, cratering and fragmentation, depending on the ratio between the specific impact kinetic energy and the specific shattering energy Q ∗, which depends on object sizes and composition. In both regimes, the size of the largest fragment and the size distributions of the other debris are derived through the detailed energy-scaling prescriptions that are presented in Thebault et al. (2003) and Thebault & Augereau (2007).
The main upgrade for the present runs is that we implement a prescription for ssurf. We derive ssurf(i,j) for all possible colliding pairs of sizes si and sj and implement this parameter into our collision-outcome prescription: if, for a given collision between the bins “i” and “j”, ssurf(i,j) >smin−num (where smin−num is the smallest size bin considered in the code), we cut the post-impact fragment distribution at ssurf(i,j) instead of smin−num.
We estimate the values of ssurf(i,j) for both fragmenting and cratering impacts, using the equations presented in the Appendix of Krijt & Kama (2014): ![\begin{eqnarray} \label{sfrag} &&s_{\rm surf}= \left[ \frac{6\gamma \left( s_{i}^{3}+s_{j}^{3}\right)^{2}} {\eta\rho v_{\rm rel}^{2} (s_i s_j)^3} \right]^{2} s_{\rm lfr}^{-1} \,\,\,\,\,\,\,\rm{for \,\,fragmentation} \\ \label{scrat} &&s_{\rm surf}= \left( \frac{6\gamma \kappa} {\eta\rho v_{\rm rel}^{2} } \right)^{2} s_{\rm lfr}^{-1} \,\,\,\,\,\,\,\rm{for \,\,cratering} \end{eqnarray}](/articles/aa/full_html/2016/03/aa27626-15/aa27626-15-eq57.png) where we assume that i is the target and j the projectile (si ≥ sj). For the cratering case, κ is the ratio mcrat/mj, where mcrat is the total mass excavated from the target i. The crucial point here is that, instead of having to assume values for the largest fragment’s size slfr and the ratio κ, we can retrieve both quantities in a self-consistent way from our collision-outcome prescription.
where we assume that i is the target and j the projectile (si ≥ sj). For the cratering case, κ is the ratio mcrat/mj, where mcrat is the total mass excavated from the target i. The crucial point here is that, instead of having to assume values for the largest fragment’s size slfr and the ratio κ, we can retrieve both quantities in a self-consistent way from our collision-outcome prescription.
2.1. Set-up
Set-up for the numerical simulations.
We do not consider the full range of possible L∗/L⊙ explored by Pawellek & Krivov (2015), but restrict ourselves to the two illustrative cases of a sun-like L∗ = L⊙ star and a β-Pic-like A5V star with L∗ = 9 L⊙. We consider a reference debris disc extending from rmin = 50 au to rmax = 100 au. The disc’s total initial mass is Mdisc = 0.5 M⊕, distributed between smax−num = 50 m and smin−num = sblow, which corresponds to ~0.01 M⊕ of <1 mm dust4. The value of sblow is equal to 0.5 μm for the sun-like case (with 80 size bins from smax to sblow) and 4 μm for the A star one (71 size bins). As for the dynamical state of the disc, we consider one dynamically “hot” case with ⟨e⟩ = 0.075 and one dynamically “cold” case with ⟨e⟩ = 0.01. For each L∗ and ⟨e⟩ case, we run both a simulation taking into account the ssurf prescription and a reference case with no ssurf. We let the runs evolve for 107 yr, which is enough to reach a collisional steady-state in the dust size domain (<1 cm).
As for the free parameters of the ssurf prescriptions (Eqs. (3) and (4)), we adopt a conservative approach and chose, amongst the η and γ values considered by Krijt & Kama (2014), the ones that are in principle the most favourable to yielding large ssurf values. We thus take η = 0.01 (i.e., 1% of the kinetic energy is used for creating new surface) and γ = 0.74 J m-2, which is the value for water ice5.
All main parameters for the set-up are summarized in Table 1.
Main results for all four collisional runs.
3. Results
3.1. Dust progenitors and ssurf maps
 |
Fig. 1 Disc-integrated mean values of the ssurf/sblow ratio for all possible target-projectile pairs of sizes si and sj. Upper left panel: A-star primary and ⟨e⟩ = 0.075. Upper right: A-star primary and ⟨e⟩ = 0.01. Bottom left: solar-type primary and ⟨e⟩ = 0.075. Bottom right: solar-type primary and ⟨e⟩ = 0.01. The dashed white line delineates the si = sj diagonal of equal-sized impactors. |
 |
Fig. 2 Disc-integrated and normalized production rates of s ≤ 10 μm dust as a function of target and projectile sizes. These maps are estimated, at collisional steady-state, for the “control runs” where the ssurf criteria is turned off. This allows for an easy comparison with Fig. 1 by directly showing which high ssurf(i,j) regions will have a significant damping effect on the small-dust production rate. Upper left panel: A-star primary and ⟨e⟩ = 0.075. Upper right: A-star primary and ⟨e⟩ = 0.01. Bottom left: solar-type primary and ⟨e⟩ = 0.075. Bottom right: solar-type primary and ⟨e⟩ = 0.01. |
For each of the considered set-ups, Fig. 1 presents the ssurf(i,j) value for every pair of impacting target and projectile of sizes si and sj. We also show, as a useful comparison tool, the equivalent (si, sj) maps of the amount of μm-sized dust produced as a function of target and projectile sizes (Fig. 2).
3.1.1. A-star
For the dynamically “hot” (⟨e⟩ = 0.075) A-star case, Eq. (2) predicts a low 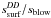 of only ~0.4, and our ssurf(i,j) map is in good agreement with this prediction, since almost all (i,j) impacts result in ssurf/sblow< 1 (Fig. 1a) . There is, admittedly, a very narrow range of impacts for which ssurf/sblow ≥ 1, but even there the ratio does not exceed 2. Moreover, this limited family of ssurf>sblow collisions corresponds to a region that has only a very limited contribution to the total dust production. The dust production is instead dominated by impacts that involve s ~ sblow = 5 μm projectiles and larger 5sblow ≲ s ≲ 20sblow targets (see Fig. 2a). This is because s ~ sblow grains are placed on high-e orbits by radiation pressure and impact all other grains at very high velocities. They are thus very efficient at fragmenting targets and producing dusty debris over a wide range of target sizes.
of only ~0.4, and our ssurf(i,j) map is in good agreement with this prediction, since almost all (i,j) impacts result in ssurf/sblow< 1 (Fig. 1a) . There is, admittedly, a very narrow range of impacts for which ssurf/sblow ≥ 1, but even there the ratio does not exceed 2. Moreover, this limited family of ssurf>sblow collisions corresponds to a region that has only a very limited contribution to the total dust production. The dust production is instead dominated by impacts that involve s ~ sblow = 5 μm projectiles and larger 5sblow ≲ s ≲ 20sblow targets (see Fig. 2a). This is because s ~ sblow grains are placed on high-e orbits by radiation pressure and impact all other grains at very high velocities. They are thus very efficient at fragmenting targets and producing dusty debris over a wide range of target sizes.
The situation is slightly different for the dynamically “cold” A-star case, for which the fraction of ssurf>sblow impacts is more extended and the maximum value for ssurf(i,j) reaches ~5 (Fig. 1b). This value is, however, well below the analytical prediction 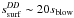 of Eq. (2). We note that these high-ssurf(i,j) impacts are located close the si = sj diagonal, which could appear to contradict Fig. B.1 of Krijt & Kama (2014), which shows instead a minimum of the ssurf curve for equal-sized impactors. But this is because this analytically-derived curve is only valid for fragmenting impacts, whereas here, with ⟨e⟩ = 0.01, the high-collisional-energy requirement for fragmentation can only be met when projectiles have sizes comparable to the target. All other cases result in cratering, for which ssurf are, in general, much smaller. As was the case for the ⟨e⟩ = 0.075 run, the (i,j) region of high ssurf values does not match the region of highest dust production, which corresponds, here again, to fragmenting impacts by s ~ sblow projectiles on 5sblow ≲ s ≲ 20sblow targets (Fig. 2b). Nevertheless, the contribution of the high- ssurf region is not fully negligible, so that we expect the maximum surface energy criteria to have at least some effect on the system’s evolution.
of Eq. (2). We note that these high-ssurf(i,j) impacts are located close the si = sj diagonal, which could appear to contradict Fig. B.1 of Krijt & Kama (2014), which shows instead a minimum of the ssurf curve for equal-sized impactors. But this is because this analytically-derived curve is only valid for fragmenting impacts, whereas here, with ⟨e⟩ = 0.01, the high-collisional-energy requirement for fragmentation can only be met when projectiles have sizes comparable to the target. All other cases result in cratering, for which ssurf are, in general, much smaller. As was the case for the ⟨e⟩ = 0.075 run, the (i,j) region of high ssurf values does not match the region of highest dust production, which corresponds, here again, to fragmenting impacts by s ~ sblow projectiles on 5sblow ≲ s ≲ 20sblow targets (Fig. 2b). Nevertheless, the contribution of the high- ssurf region is not fully negligible, so that we expect the maximum surface energy criteria to have at least some effect on the system’s evolution.
3.1.2. Solar-type star
For a Sun-like star, orbital velocities are lower and collisions less energetic than for an A-star for equivalent orbital parameters. The ssurf/sblow values are thus logically higher, as is clearly seen in Figs. 1c and d. The ssurf/sblow> 1 domain is much more extended than for an A star, with peak values reaching ~25 for the ⟨e⟩ = 0.075 case and even ≥100 for the dynamically cold case. As was already the case for the A-star runs, these peak ssurf values are located, in the (si, sj) map, on a line corresponding to the transition from cratering to fragmenting impacts6. For the ⟨e⟩ = 0.075 run, this transition always occurs for sj ≤ 0.5si, with a sj/si ratio that is decreasing towards larger sizes following an approximate law in s2/s1 ~ 0.4−0.1log (s2/ 10 μm)7. For ⟨e⟩ = 0.01, the peak ssurf line still corresponds to the fragmentation/cratering transition, but is now much closer to the si = sj diagonal, which reflects the fact that, for these lower impact velocities, it takes a larger projectile to fragment a given target.
We also note that, for both the ⟨e⟩ = 0.075 and ⟨e⟩ = 0.01 cases, there are no high ssurf/sblow values for impactors ≲10 μm. This is because such small grains have more energetic impacts (able to produce smaller fragments) because of their radiation-pressure-affected orbits. Incidentally, this s ≲ 10 μm region is the one where the μm-dust production is the highest (Figs. 2c and d). This means that a large fraction of the dust-generating impacts are, in fact, able to produce fragments down to the blow-out size. The regions of high ssurf/sblow> 5 only contribute to approximately 20% of the ≤10 μm dust production for both the ⟨e⟩ = 0.075 and ⟨e⟩ = 0.01 cases.
3.2. Size distribution
 |
Fig. 3 A-star case. Geometrical cross-section as a function of particle size, at t = 107 yr, integrated over the whole 50−100 au disc, for both the dynamically “hot” (⟨e⟩ = 0.075) and “cold” (⟨e⟩ = 0.01) cases. For each case, a reference run with the ssurf constraint switched-off is also presented. The two vertical dotted lines represent the analytical values given by Eq. (2). |
Figures 3 and 4 present the PSD, in terms of the differential distribution of geometric cross section dΣ / ds, at collisional steady-state8, for all four of the explored set-ups, as well as for the control runs where the ssurf constraint is ignored. Visualizing the dΣ / ds distribution allows us to immediately identify which particle sizes dominate the system’s optical depth, and thus its luminosity.
3.2.1. Generic features
Before assessing the additional effect of the ssurf constraint, let us first emphasise some characteristics of the obtained size distributions that are well known generic features of steady-state collisional discs, and that also affect the small-size domain of the PSDs.
A first “classic” result is that, for all cases, the size distribution displays a clear wavy structure in the ≲100 μm domain. This waviness is more pronounced than in Pawellek & Krivov (2015) because we consider a wider disc, so that small grains, placed on high-e orbits par radiation pressure, will be able to impact target particles at a higher impact angle and thus higher vrel. This will reinforce their shattering power and thus the amplitude of the size distribution wave (see Thebault & Augereau 2007, for a detailed discussion on “wave-enhancing” factors).
Another crucial result is the strong depletion of small particles for all ⟨e⟩ = 0.01 cases. This is the signature of the mechanism identified by Thebault & Wu (2008), i.e., the strong imbalance between the small-dust production and destruction rates for dynamically cold systems (see Sect. 1.1). As underlined by Pawellek & Krivov (2015), this effect is more pronounced for solar-type stars, for which we find a clear drop of the dΣ / ds curve at s ≲ 50sblow, than for A stars, where the PSD is roughly flat in the same s ≲ 50sblow domain. Nevertheless, for both cases the depletion of small grains is very strong, exceeding one order of magnitude as compared to a dynamically “hot” system.
3.2.2. Effect of the ssurf constraint
As expected from the ssurf(i,j) and dust-production maps (see Sect. 3.1), the effect of the ssurf constraint is very weak for the A-star runs. For the ⟨e⟩ = 0.075 case, the PSD is almost indistinguishable from the control run with ssurf switched off (Fig. 3). Some differences between the with- and without-ssurf runs are visible for the ⟨e⟩ = 0.01 case, but they remain relatively limited. Interestingly, they are not so much visible as a dearth of grains in the s ≤ 10−20 μm domain where the few ssurf ≥ sblow values lie (see Fig. 1b), but rather as an excess of larger particles in the ~30−50 μm range. This is a direct consequence of the specific dynamics, and thus destructive efficiency, of grains close to sblow. In the “ssurf-free” case, it is indeed this high destructive efficiency that is responsible for the strong depletion of 30−50 μm particles in the PSD (the first dip in the “wave”)9. So removing a small number of small destructive impactors will necessarily increase the number of 30−50 μm grains. And given that we start from a strongly depleted population of 30−50 μm particles in the ssurf-free case, their relative increase in the ssurf runs will be higher than the relative decrease of s ≤ 10−20 μm grains. And this is exactly what we observe (see Table 2): a ~5% depletion of s ~ sblow grains that causes a ~20% excess of s ~ 30 μm particles, which is the size of the biggest objects that can be destroyed by projectiles close to sblow. However, for this ⟨e⟩ = 0.01 case, the ssurf-induced depletions and excesses remain marginal when compared to the much more significant global depletion of s ≲ 50sblow grains caused by the low dynamical excitation of the system (see Discussion).
The imprint of the ssurf limit is, logically, much more visible around a Sun-like star (Fig. 4). Interestingly, this is especially true of the dynamically hot disc, for which the depletion of s ≤ 2sblow grains is close to 30%, and the related excess of 4sblow ≤ s ≤ 20sblow particles exceeds 40% (Table 2). For the ⟨e⟩ = 0.01 run, these excesses and depletions are only ~12% and ~14%, respectively. This is a rather counter-intuitive result, as Eq. (2) predicts a 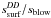 ratio that is 50 times higher for ⟨e⟩ = 0.01 than for ⟨e⟩ = 0.075, and even the more accurate Figs. 1c and d show peak ssurf(i,j) values that are still 6−7 times higher for the dynamically cold case. However, as discussed in Sect. 3.1.2, the crucial point is that these (si, sj) regions of high ssurf values do not match those of high dust production. Most of the dust is indeed created by collisions on s ≤ 10 μm (≲20sblow) targets (Fig. 2), for which ssurf rarely exceeds sblow (Fig. 1). Another reason for which the ssurf constraint only leaves a weak signature on the ⟨e⟩ = 0.01 system is that, in the s ≤ 100 μm range, the PSD is already massively depleted because of the dust production imbalance inherent to dynamically “cold” discs. This effect is even stronger than for the A-star case, with a depletion that reaches almost two orders of magnitude for s ~ sblow grains (Fig. 4).
ratio that is 50 times higher for ⟨e⟩ = 0.01 than for ⟨e⟩ = 0.075, and even the more accurate Figs. 1c and d show peak ssurf(i,j) values that are still 6−7 times higher for the dynamically cold case. However, as discussed in Sect. 3.1.2, the crucial point is that these (si, sj) regions of high ssurf values do not match those of high dust production. Most of the dust is indeed created by collisions on s ≤ 10 μm (≲20sblow) targets (Fig. 2), for which ssurf rarely exceeds sblow (Fig. 1). Another reason for which the ssurf constraint only leaves a weak signature on the ⟨e⟩ = 0.01 system is that, in the s ≤ 100 μm range, the PSD is already massively depleted because of the dust production imbalance inherent to dynamically “cold” discs. This effect is even stronger than for the A-star case, with a depletion that reaches almost two orders of magnitude for s ~ sblow grains (Fig. 4).
4. Discussion and conclusion
Figures 3 and 4 seems to indicate that the two dynamically “hot” cases bear some similarities with the prediction of Eq. (2) regarding the imprint of the ssurf constraint on the PSD. In the A-star case, this similarity is, of course, simply that the surface energy constraint has no effect on the PSD, but in the ⟨e⟩ = 0.01 case, we do indeed find a depletion of grains in the s ≤ 2sblow domain, which is roughly consistent with the 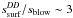 value given by Eq. (2). However, this quantitative agreement is probably largely a coincidence, firstly because the depletion of s ≤ ssurf grains does not come from the “smallest-barely-catastrophic-equal-size-impactors” collisions considered in deriving Eq. (2) (see Figs. 1c and 2c), and secondly because this depletion stops at s ~ 2sblow largely because of the “natural” waviness of the PSD, combined with the excess of ≥3sblow particles. We also note that this depletion is limited to ~30% and does not create a sharp cut-off in the size distribution. This limited amplitude, combined to the aforementioned excess of particles in the ~3sblow to ~20−30sblow range, renders the PSD plateau-like at sizes smaller than ~10sblow. It is thus difficult to define a proper smin for the size distribution, but, at least from a qualitative point of view, we confirm that, for this case, the maximum energy criteria does have a visible effect on the lower-end of the PSD.
value given by Eq. (2). However, this quantitative agreement is probably largely a coincidence, firstly because the depletion of s ≤ ssurf grains does not come from the “smallest-barely-catastrophic-equal-size-impactors” collisions considered in deriving Eq. (2) (see Figs. 1c and 2c), and secondly because this depletion stops at s ~ 2sblow largely because of the “natural” waviness of the PSD, combined with the excess of ≥3sblow particles. We also note that this depletion is limited to ~30% and does not create a sharp cut-off in the size distribution. This limited amplitude, combined to the aforementioned excess of particles in the ~3sblow to ~20−30sblow range, renders the PSD plateau-like at sizes smaller than ~10sblow. It is thus difficult to define a proper smin for the size distribution, but, at least from a qualitative point of view, we confirm that, for this case, the maximum energy criteria does have a visible effect on the lower-end of the PSD.
The situation is radically different for the dynamically cold cases, for which the simulated size distributions are much less affected by the ssurf constraint than would be expected from simple analytical estimates, which predict 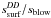 values in excess of 20, or even 150 (see Table 2). Even though we do find some (si, sj) target-projectile configurations that result in large ssurf comparable to these values (Fig. 1), the decisive point is that these collisions only have a marginal contribution to the disc’s total small-dust production. As a result, the differences with the reference ssurf-free cases’ PSDs remain very limited: for neither the A-star nor the Sun-like cases do we obtain a depletion that exceeds ~10% in the small grain domain close to sblow. Crucially, the ssurf constraint is never strong enough to change the size of grains that dominate the system’s geometrical cross-section, and thus its luminosity.
values in excess of 20, or even 150 (see Table 2). Even though we do find some (si, sj) target-projectile configurations that result in large ssurf comparable to these values (Fig. 1), the decisive point is that these collisions only have a marginal contribution to the disc’s total small-dust production. As a result, the differences with the reference ssurf-free cases’ PSDs remain very limited: for neither the A-star nor the Sun-like cases do we obtain a depletion that exceeds ~10% in the small grain domain close to sblow. Crucially, the ssurf constraint is never strong enough to change the size of grains that dominate the system’s geometrical cross-section, and thus its luminosity.
More importantly, we confirm that the most efficient way of depleting a collisional debris disc from its small grains is, by far, to reduce its dynamical excitation. The production/destruction imbalance mechanism identified by Thebault & Wu (2008) for low-stirring discs has an effect that exceeds, by more than one order of magnitude, that of the ssurf limit. This is true both for the amplitude of the small-grain depletion and for the size-range that is affected. For low ⟨e⟩ values, the size scold below which the PSD is depleted is, to a first order, given by the relation 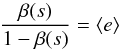 (5)which translates into
(5)which translates into 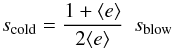 (6)leading to scold ~ 50sblow for our ⟨e⟩ = 0.01 case, a value that roughly agrees with the one obtained in the simulations (Figs. 3 and 4). It should be noted that this dominance of the low-stirring imbalance effect over the surface energy constraint is probably even stronger than that witnessed in Figs. 3 and 4, since we have taken, for our ssurf prescription, the parameters that were the most likely to lead to high ssurf values (see Sect. 2.1). On a related note, choosing disc configurations that enhance the amplitude of the surface-energy constraint, by, for instance, decreasing ⟨e⟩ or increasing [rmin,rmax], would not change this dominance either, because these configurations would also enhance the dust-production-imbalance effect by further decreasing the level of stirring in the disc.
(6)leading to scold ~ 50sblow for our ⟨e⟩ = 0.01 case, a value that roughly agrees with the one obtained in the simulations (Figs. 3 and 4). It should be noted that this dominance of the low-stirring imbalance effect over the surface energy constraint is probably even stronger than that witnessed in Figs. 3 and 4, since we have taken, for our ssurf prescription, the parameters that were the most likely to lead to high ssurf values (see Sect. 2.1). On a related note, choosing disc configurations that enhance the amplitude of the surface-energy constraint, by, for instance, decreasing ⟨e⟩ or increasing [rmin,rmax], would not change this dominance either, because these configurations would also enhance the dust-production-imbalance effect by further decreasing the level of stirring in the disc.
We emphasise that we did not attempt to fit observed smin/sblow trends with an exhaustive parameter exploration (⟨e⟩, Mdisc, [ rmin,rmax ], etc.) in the spirit of the Pawellek & Krivov (2015) study. Our goal was here to quantify, in a self-consistent way, the relative effects of the two potential dust-depletion mechanisms that are the surface energy constraint and the low-stirring dust-production imbalance. For the sake of clarity, and to clearly identify the mechanisms at play, we restricted our study to a reference wide disc and to the two illustrative reference cases of a sun-like and an A-type star. Test runs with a narrower, ring-like disc, have, however, been performed. They gave relatively similar results as to the relative imprint of the ssurf and low-stirring effects on the PSD, although with a less pronounced waviness in the PSD’s shape, which was to be expected, since small grains close to sblow will impact larger targets within a narrow ring at a lower velocity than they would have in an extended disc.
Despite this limited parameter exploration, we note however that our conclusions seem to agree with the numerical investigations of Pawellek & Krivov (2015), who were able to find a reasonable fit to the smin/sblow trend observed on their 34-stars sample with the low-stirring-induced mechanism alone. The main assumption for this fit to work is that, while the dynamical stirring of A stars should be of the order of e ~ 0.1, it should decrease towards lower mass stars and be as low as ~0.01 for solar-type objects. Such values might appear unrealistically low if we assume the classical view that debris discs are stirred by large lunar-to-Mars-sized large planetesimals (e.g., Thebault 2009). However, the level and the cause of stirring is still an open issue in present debris discs studies (see discussion in Pawellek & Krivov 2015). Moreover, we know of at least two discs, around the G0V-star HD 207129 (Löhne et al. 2012), and the K2V-star HIP 17429 (Schüppler et al. 2014), for which collisional modelling predicts ⟨e⟩ barely larger than 0.01.
5. Summary
Based on analytical considerations, the pioneering study of Krijt & Kama (2014) finds that the surface energy constraint, which limits the size of the smallest fragment produced after destructive collisions, could potentially affect the evolution of debris discs by limiting the smallest sizes of observable grains to a value ssurf larger than the blow-out size sblow.
Here we numerically quantify the importance of this mechanism by incorporating, for the first time, the surface energy constraint into a statistical code that follows the collisional evolution of a debris disc. Instead of relying on an analytical system-averaged value, we compute ssurf(i,j) for all impacting target-projectile pairs of sizes si and sj in the disc. We consider two stellar types, sun-like and AV5, and two levels of stirring for the disc, ⟨e⟩ = 0.075 and ⟨e⟩ = 0.01. Our main results and conclusions are as follows:
-
We confirm that, for all considered set-ups, there is a fraction of the (si, sj) space for which ssurf ≥ sblow, especially for low ⟨e⟩ and/or low-mass stars.
-
However, the (si, sj) regions of high ssurf do not coincide with the regions of high dust production. Indeed, most of the μm-sized dust is produced by impacts involving ~3−20sblow targets and small ≲2−3sblow projectiles, for which ssurf is, in general, smaller than the blow-out size. This is mainly due to the fact that impacts involving small grains are very energetic, because these particles are placed on high-e orbits by radiation pressure.
-
Because of this discrepancy between high-ssurf and dust-producing collisions, the global effect of the surface energy constraint is generally relatively limited. The only set-up for which it has a visible signature on the PSD is for a dynamically “hot” disc around a solar-type star. But even there, the depletion of small dust does not exceed 30%.
-
For the low ⟨e⟩ = 0.01 cases, which should in principle be the most favourable to strong surface-energy constraints, the depletion of small grains never exceeds 12% and is never able to change the sizes of particles that dominate the system’s geometrical cross-section.
-
At such low-stirring levels, the system’s PSD in the small size domain is, instead, totally dominated by another mechanism: the imbalance between small dust production and destruction rates identified by Thebault & Wu (2008) for low-e discs. This imbalance creates a depletion of small grains that is at least one order of magnitude more pronounced than that caused by the surface-energy constraint, and it affects grains over a much wider size range.
Even if its effect is not as decisive as could be analytically expected, we do, however, recommend implementing the surface-energy constraint in collisional-evolution codes, as it might leave visible signatures in the low-s end of PSDs for some star-disc configurations.
For subsolar stars, radiation pressure is too weak to overcome gravity, but stellar wind could play a similar role for active M stars like AU Mic (Augereau & Beust 2006; Schüppler et al. 2015).
There is an inherent degeneracy between grain size and disc radius that can only be broken for resolved systems (see discussion in Pawellek & Krivov 2015).
To their credit, Krijt & Kama (2014) briefly investigate the role of cratering impacts in their Appendix, but again assuming a fixed slfr/starget ratio (see Fig. B.1. of that paper).
This relatively sharp transition at the cratering/fragmentation boundary is due to the discontinuity in the ssurf prescriptions of Krijt & Kama (2014; Eqs. (3) and (4)) at this boundary (slfr = 2−1/3s1). More refined and self-consistent ssurf prescriptions should probably be derived in the future, but we chose to stick to the laws given by Krijt & Kama (2014) for this exploratory work.
This negative slope reflects the fact that, in the strength regime, the specific shattering energy Q ∗ decreases with increasing sizes (Benz & Asphaug 1999).
Or, more exactly, when steady-state is at least reached where it matters here, that is in the s< 1 cm domain. In the large-size domain, there is a difference of PSD slopes between the dynamically hot and cold discs that is due to the ⟨e⟩ = 0.01 systems not yet having had time to reach collisional steady-state for these larger objects yet. Collisional steady-state does indeed work its way up the PSD with time, at a rate that strongly increases with decreasing dynamical stirring (e.g., Löhne et al. 2008).
Acknowledgments
The author would like to thank M. Kama, S. Krijt and A. Krivov for fruitful discussions.
References
- Ardila, D. R., Golimowski, D. A., Krist, J. E. et al. 2004, ApJ, 617, 147 [Google Scholar]
- Augereau, J.-C., & Beust, H. 2006, A&A, 455, 987 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benz, W., & Asphaug, E. 1999, Icarus, 142, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Dohnanyi, J. S. 1969, J. Geophys. Res., 74, 2531 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2003, ARA&A, 41, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzgerald, M. P., Kalas, P. G., & Graham, J. R. 2007, ApJ, 670, 557 [NASA ADS] [CrossRef] [Google Scholar]
- Grigorieva, A., Artymowicz, P., & Thebault, P. 2007, A&A, 461, 537 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnson, B. C., Lisse, C. M., Chen, C. H., et al. 2012, ApJ, 761, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Kobayashi, H., & Tanaka, H. 2010, Icarus, 206, 723 [Google Scholar]
- Krijt, S., & Kama, M. 2014, A&A, 566, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krivov, A. V., Löhne, T., & Sremcević, M. 2006, A&A, 455, 509 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krivov, A. V. 2007, in 3dust in Planetary Systems, eds. H. Krueger., & A. Graps, 123 [Google Scholar]
- Krivov, A. V. 2010, RA&A, 10, 383 [Google Scholar]
- Leinhardt, Z. M., & Stewart, S. T. 2012, ApJ, 745, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Löhne, T., Krivov, A. V., & Rodmann, J. 2008, ApJ, 673, 1123 [NASA ADS] [CrossRef] [Google Scholar]
- Löhne, T., Augereau, J.-C., Ertel, S., et al. 2012, A&A, 537, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pawellek, N., & Krivov, A. 2015, MNRAS, 454, 320 [Google Scholar]
- Pawellek, N., Krivov, A., Marshall, J. P., et al. 2014, ApJ, 792, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Schüppler, Ch., Löhne, T., Krivov, A. V., et al. 2014, A&A, 567, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schüppler, Ch., Löhne, T., Krivov, A. V., et al. 2015, A&A, 581, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thebault, P. 2009, A&A, 505, 1269 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thebault, P., & Augereau, J. C. 2007, A&A, 472, 169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thebault, P., & Wu, Y. 2008, A&A, 481, 713 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thebault, P., Augereau, J. C., & Beust, H. 2003, A&A, 408, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wyatt, M. C. 2005, A&A, 433, 1007 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wyatt, M. C. 2008, ARA&A, 46, 339 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Disc-integrated mean values of the ssurf/sblow ratio for all possible target-projectile pairs of sizes si and sj. Upper left panel: A-star primary and ⟨e⟩ = 0.075. Upper right: A-star primary and ⟨e⟩ = 0.01. Bottom left: solar-type primary and ⟨e⟩ = 0.075. Bottom right: solar-type primary and ⟨e⟩ = 0.01. The dashed white line delineates the si = sj diagonal of equal-sized impactors. |
| In the text | |
 |
Fig. 2 Disc-integrated and normalized production rates of s ≤ 10 μm dust as a function of target and projectile sizes. These maps are estimated, at collisional steady-state, for the “control runs” where the ssurf criteria is turned off. This allows for an easy comparison with Fig. 1 by directly showing which high ssurf(i,j) regions will have a significant damping effect on the small-dust production rate. Upper left panel: A-star primary and ⟨e⟩ = 0.075. Upper right: A-star primary and ⟨e⟩ = 0.01. Bottom left: solar-type primary and ⟨e⟩ = 0.075. Bottom right: solar-type primary and ⟨e⟩ = 0.01. |
| In the text | |
 |
Fig. 3 A-star case. Geometrical cross-section as a function of particle size, at t = 107 yr, integrated over the whole 50−100 au disc, for both the dynamically “hot” (⟨e⟩ = 0.075) and “cold” (⟨e⟩ = 0.01) cases. For each case, a reference run with the ssurf constraint switched-off is also presented. The two vertical dotted lines represent the analytical values given by Eq. (2). |
| In the text | |
 |
Fig. 4 Same as for Fig. 3, but for a solar-type star. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


