| Issue |
A&A
Volume 587, March 2016
|
|
|---|---|---|
| Article Number | A154 | |
| Number of page(s) | 12 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201527532 | |
| Published online | 07 March 2016 | |
The atmosphere of comet 67P/Churyumov-Gerasimenko diagnosed by charge-exchanged solar wind alpha particles
1 Aalto University, School of Electrical EngineeringDepartment of Radio Science and Engineering, PO Box 13000, 00076 Aalto Finland
e-mail: cyril.simon.wedlund@gmail.com
2 Now at Department of Physics, University of Oslo, Box 1048 Blindern, 0316 Oslo, Norway
3 Swedish Institute of Space Physics, Box 812, 981 28 Kiruna, Sweden
4 Luleå University of Technology, Department of Computer Science, Electrical and Space Engineering, Rymdcampus 1, 981 28 Kiruna, Sweden
5 Belgian Institute for Space Aeronomy, Avenue Circulaire 3, 1180 Brussels, Belgium
6 Science Directorate, Chemistry and Dynamics Branch, NASA Langley Research Center, Hampton, Virginia, USA
7 SSAI, Hampton, Virginia, USA
Received: 9 October 2015
Accepted: 10 December 2015
Context. The ESA/Rosetta mission has been orbiting comet 67P/Churyumov-Gerasimenko since August 2014, measuring its dayside plasma environment. The ion spectrometer onboard Rosetta has detected two ion populations, one energetic with a solar wind origin (H+, He2+, He+), the other at lower energies with a cometary origin (water group ions such as H2O+). He+ ions arise mainly from charge-exchange between solar wind alpha particles and cometary neutrals such as H2O.
Aims. The He+ and He2+ ion fluxes measured by the Rosetta Plasma Consortium Ion Composition Analyser (RPC-ICA) give insight into the composition of the dayside neutral coma, into the importance of charge-exchange processes between the solar wind and cometary neutrals, and into the way these evolve when the comet draws closer to the Sun.
Methods. We combine observations by the ion spectrometer RPC-ICA onboard Rosetta with calculations from an analytical model based on a collisionless neutral Haser atmosphere and nearly undisturbed solar wind conditions.
Results. Equivalent neutral outgassing rates Q can be derived using the observed RPC-ICA He+/He2+ particle flux ratios as input into the analytical model in inverse mode. A revised dependence of Q on heliocentric distance Rh in AU is found to be Rh-7.06 between 1.8 and 3.3 AU, suggesting that the activity in 2015 differed from that of the 2008 perihelion passage. Conversely, using an outgassing rate determined from optical remote sensing measurements from Earth, the forward analytical model results are in relatively good agreement with the measured RPC-ICA flux ratios. Modelled ratios in a 2D spherically-symmetric plane are also presented, showing that charge exchange is most efficient with solar wind protons. Detailed cometocentric profiles of these ratios are also presented.
Conclusions. In conclusion, we show that, with the help of a simple analytical model of charge-exchange processes, a mass-capable ion spectrometer such as RPC-ICA can be used as a “remote-sensing” instrument for the neutral cometary atmosphere.
Key words: comets: general / comets: individual: 67P/Churyumov-Gerasimenko / instrumentation: detectors / solar wind / methods: analytical
© ESO, 2016
1. Introduction
In August 2014, the European Space Agency Rosetta spacecraft arrived in the vicinity of comet 67P/Churyumov-Gerasimenko (67P; e.g., Cochran et al. 2015) and started measuring its complex plasma environment, using notably the Rosetta Plasma Consortium (RPC), a suite of five science instruments measuring the plasma composition and dynamics, as well as the magnetic field (Carr et al. 2007). On this historic escort mission throughout the inner solar system, Rosetta has a unique vantage point on the evolution of the comet’s surface and space environment (Hansen et al. 2007). Comet 67P is a typical low-activity, short-period, Jupiter-family comet (orbital period of 6.5 years) with a perihelion at 1.3 AU close to Mars’ heliocentric distance (e.g., Schleicher 2006).
 |
Fig. 1 Sketch of low-charge solar wind charge-exchange processes in a cometary environment. Two processes are shown with solar wind protons and alpha particles, respectively, which transfer a single charge to water molecules. The depicted x,y,z Cartesian coordinate system is the one used in the analytical model. The comet picture is that of 67P (courtesy ESA/Rosetta). |
A comet is a near-airless body essentially made of water and carbon dioxide ice and dust. As it comes closer to the Sun, a thin atmosphere of sublimated neutral molecules – the coma – develops. In time, it becomes ionised through interactions with the EUV solar flux and the solar wind. The morphology of the coma gradually changes from a Moon-like solar wind interaction, where the nucleus is passively absorbing the solar wind, to one most resembling that of Mars or Venus, with solar wind mass loading playing an important role in the eventual formation of a bow shock (Breus et al. 1987).
Amongst all physico-chemical processes encountered in a cometary plasma (e.g., Coates & Jones 2009), charge exchange – or charge transfer – at comets (abbreviated CX in the following) plays a major role in the composition and dynamics of the plasma (Gombosi 1987; Dennerl 2010). Solar wind charge exchange is, for example, responsible for cometary X-ray emissions (Cravens 1997) that involve solar wind multiply charged heavy atoms (O7+, O6+). Through energy and momentum transfer, charge exchange may also be a powerful driver of the formation of cometopause and shock structures, as shown in the case of high-activity comets such as Halley (Gombosi 1987). The solar wind chiefly embeds protons and alpha particles, as well as energetic heavy ions, which can be detected by instruments onboard Rosetta. The RPC Ion Composition Analyser (RPC-ICA) is one such instrument (Nilsson et al. 2007, 2015a). Another instrument on Rosetta, the ion and electron sensor RPC-IES, was recently used by Burch et al. (2015) to detect H− ions, expected to arise from double electron capture in proton collisions with cometary neutrals.
Assuming no dissociation, the general form of charge transfer between solar wind-originating species X of charge n + (∀ positive integers n) and a cometary neutral molecule A is  (1)For a total transfer of one electron m = 1, n = 1 refers to H+ ions, while n = 2 refers to He2+ ions. Their respective X(n−m) + charge-exchange products are energetic neutral hydrogen atoms HENA and He+ ions (see Fig. 1). Cometary ions Am+, for example H2O+ ions, are also created.
(1)For a total transfer of one electron m = 1, n = 1 refers to H+ ions, while n = 2 refers to He2+ ions. Their respective X(n−m) + charge-exchange products are energetic neutral hydrogen atoms HENA and He+ ions (see Fig. 1). Cometary ions Am+, for example H2O+ ions, are also created.
On Rosetta, RPC-ICA measures the particle flux of high-energy solar wind ions and associated charge-exchanged products, such as H+, He2+, He+, or O6+, but also of low-energy cometary ions, such as water-family ions of mass-to-charge ratios m/Q> 18 amu/charge (Nilsson et al. 2015a,b). As shown by Nilsson et al. (2015a), a measure of the efficiency of charge-exchange processes can be attained by comparing the particle fluxes F of He+ ions with those of He2+; thus, this efficiency can be monitored throughout the escort phase of the Rosetta mission, as long as the solar wind penetrates the coma.
If the change in energy in the CX process is smaller than the initial energy of the impacting ion, then the energy per charge E/Q of the newly formed ion is increased. For example, if the impacting He2+ ion in the solar wind has an E/Q = 1 keV/charge, then the corresponding charge-exchanged He+ ion will have an E/Q ~ 2 keV/charge because the electric charge of the He+ ion is half that of the impacting He2+ ion. For the same reason, in the case of multiply charged ions, say O7+, the change in the charge in CX processes O7 + → O6 + → O5 +, etc., would, therefore, result in different E/Q values because of the decreasing electric charge of the charge-exchanged ion products (see, e.g., Kallio et al. 2008, Fig. 4, for details). This means that an energy-spectrogram instrument like RPC-ICA, which measures the energy per charge E/Q of an ion, can distinguish charge-exchanged ions from the original impacting ions. Also a particle instrument that would only measure the energy of the ion could not distinguish charge-exchanged ions from the impacting ions without an energy resolution high enough to measure the (small) energy exchange associated with the CX process. We define the efficiency as the ratio of the fluxes of charge-exchanged products to their parent solar wind ion:  (2)The parent solar wind ion flux FXn + measured by RPC-ICA is the local particle flux of initial solar wind ions already depleted at the spacecraft position, not that of the upstream solar wind ion flux, noted
(2)The parent solar wind ion flux FXn + measured by RPC-ICA is the local particle flux of initial solar wind ions already depleted at the spacecraft position, not that of the upstream solar wind ion flux, noted  . RPC-ICA flux datasets can be analysed to directly provide RF with a typical time resolution of a few minutes, a result unique to the Rosetta mission since no monitoring of charge-exchange processes at a comet has ever been achieved over such a wide variety of heliocentric distances. To analyse the large datasets produced, simple, fast models that take charge exchange into account are necessary.
. RPC-ICA flux datasets can be analysed to directly provide RF with a typical time resolution of a few minutes, a result unique to the Rosetta mission since no monitoring of charge-exchange processes at a comet has ever been achieved over such a wide variety of heliocentric distances. To analyse the large datasets produced, simple, fast models that take charge exchange into account are necessary.
After a description of He+-He2+ particle flux ratios, observations by RPC-ICA between 3.3 AU and 1.8 AU, an analytical model of charge-exchange processes is presented for He2+ and H+ solar wind ions that efficiently convert them into He+ ions (measured by RPC-ICA) and H energetic neutral atoms (ENAs), respectively. Finally, we show in this study that the ion spectrometer RPC-ICA may be used indirectly as a monitor of the comet’s neutral atmosphere and activity with respect to its heliocentric distance.
2. Observations
2.1. Instrument
RPC-ICA is a mass-resolving ion spectrometer built at the Swedish Institute for Space Physics (Kiruna, Sweden), consisting of an electrostatic arrival angle filter, an electrostatic energy analyser, and a magnetic momentum filter, designed to provide the 3D distribution of incoming positive ions. A detailed description can be found in (Nilsson et al. 2007) and only a short summary is presented here. RPC-ICA observations can be performed in 16 elevation steps and 16 azimuthal sectors. A full elevation scan takes 192 s (12 s per step) with a 5° stepping between 45° and 135° with respect to the vertical axis. Elevation binning is performed directly onboard the spacecraft with four different modes depending on the observation (1, 2, 4, or 8 bins), thus limiting the temporal resolution. Sixteen azimuth sectors of 22.5° each are recorded simultaneously by the detector sector anodes, but because of spacecraft shadowing and 90° elevation restrictions, RPC-ICA has a field of view of about 2.8π sr. Energy coverage ranges from 10 eV/charge to 40 keV/charge in 96 channels with a resolution of ΔE/E = 0.07.
The instrument has successfully detected heavy ions of cometary origin (slow/fast H2O+ and other water-family ions), as well as ions of solar wind origin (H+, He2+ and He+). For these detections, see Nilsson et al. (2015a). Nilsson et al. (2015b) recently discussed the evolution of the ion environment of the comet for pre-perihelion conditions between 3.3 AU and about 2.0 AU.
2.2. Data analysis and event selection
Events analysed in this paper were selected in the currently available RPC-ICA data from September 2014 until April 2015, as shown in Nilsson et al. (2015b). One event corresponds to at least several hours of continuous observation from RPC-ICA, and, when possible, up to six hours for any given day of observation, to average out the diurnal effects due to the rotation of the nucleus. The clearest solar wind ion signals were then visually inspected using the AMDA quicklook function (Jacquey et al. 2010). All events where solar wind H+ ions were contaminated by accelerated cometary ions were filtered away by choosing only the sector anodes which detect He2+ and He+ ions, usually within two to three anodes, i.e., a 44−66° angle. Cometary pickup ions are the focus of incoming studies by the ICA team (Béhar et al. 2016). The He2+ and He+ signals were identified using a simple energy discrimination depending on the event. In total, 45 events were selected from Sept. 2014 to April 2015, i.e., from 3.3 to 1.8 AU. A listing of these events is shown in Table 3.
Conversion from raw count rates measured by RPC-ICA to differential energy fluxes is achieved using an energy-dependent geometrical factor measured in the laboratory (Nilsson et al. 2007). Figure 2 presents a typical RPC-ICA observation on 24 January 2015 around 15:00 UT, showing the ion energy flux spectrum from three sector anodes (panel A). This date was chosen for its relatively good signal-to-noise ratio to illustrate the typical high-energy structures seen in RPC-ICA data. As pointed out earlier, what RPC-ICA measures is really the energy per charge E/Q in eV/charge, and depending on the species’ number of charges, a corresponding difference in energy will be seen in the spectra. In RPC-ICA measurements as in Fig. 2, four ion populations can usually be seen depending on E/Q: one at low energies between ~ 10−200 eV/charge (non-accelerated cometary water ions, not shown); a population around 600 eV/charge for the expected solar wind H+ signal, corresponding to a velocity of about 340 km s-1; a third population around 1200 eV/charge representing the signature of He2+ solar wind ions; finally, a fourth population at about 2400 eV/charge representing that of charge-exchanged He+ ions.
In panel B, the total He2+ and He+ ion fluxes versus time are extracted by identifying flux minima around the ion peaks. The fluxes are then integrated between these energy boundaries, i.e., 900−1600 eV/charge and 1800−3000 eV/charge for He2+ and He+ respectively (marked as dashed horizontal lines in panel A), yielding the total flux for each ion species. A running average over three elevation scans (3 × 192 s) is performed on each total flux to correct for elevation scan binning effects. For clarity, in panel B, ion fluxes are presented normalised to the first He+ flux value of the time interval. Variations of up to a factor 18 and to a factor 4 can be seen for He2+ and He+, respectively, which are most likely linked to variations in the solar wind and in cometary neutral atmosphere.
Ratios of He+ to He2+ fluxes can then be calculated, as shown in panel C. It is interesting to note that, though the time coverage is limited for this event, the flux ratios may seem to follow a somewhat periodical variation with time that is close to a sinusoid of period of about 6h, corresponding to about half a nucleus rotation (~ 12.4 h). This may be reminiscent of similar variations in neutral densities seen in the ROSINA-COPS data (Bieler et al. 2015), which were attributed to a variation in illumination angle (cosine of solar zenith angle) on the surface. Such variations are currently investigated further with longer data time spans.
Since we are interested in the overall impact of charge exchange on the cometary environment, a mean value of these particle flux ratios is calculated for each event separately (one value per event). Particle flux uncertainties are taken as the fluctuations ΔF of the flux signal around the mean, thus representing the natural variations in the signal across one event. The corresponding propagated statistical fluctuation ΔRF of the flux ratio may be estimated as (e.g., Howell 2014):  (3)which gives an indication of the variability of the flux ratio per one event. Panel D of Fig. 2 shows the corresponding cometocentric and heliocentric distances of Rosetta (of the order of 30 km and 2.5 AU, respectively) during the event.
(3)which gives an indication of the variability of the flux ratio per one event. Panel D of Fig. 2 shows the corresponding cometocentric and heliocentric distances of Rosetta (of the order of 30 km and 2.5 AU, respectively) during the event.
2.3. Observed He+/He2+ flux ratios
 |
Fig. 2 RPC-ICA observation on 24 January 2015 versus time. Panel A): differential energy flux spectrum in m2 s-1 eV-1 sr-1. Energy is given as E/Q in eV/charge. White dashed lines: energy limits used for the energy integration of the He2+ fluxes. Green dashed lines: energy limits for the integration of He+ fluxes. Panel B): integrated He2+ and He+ ion fluxes, normalised for clarity to the first value of the time series FHe+ at 11:03 UT. A running average window of 3 × 192 s is used on the two signals to correct for the instrument’s elevation binning. Panel C): final He+/He2+ flux ratio in %. Panel D): heliocentric distance in AU (left y-axis, solid line) and cometocentric distance in km (right y-axis, dashed line). |
Figure 3 (panel A) displays the He+/He2+ flux ratios derived from all 45 events with the above calculated statistical fluctuations. They all range between about 1% and 40%, depending on the position of the spacecraft (and the upstream column of atmosphere) and on the heliocentric distance (panels B and C).
Three trends can be seen. The first trend exhibits a near constant ratio from Sept. 2014 until the beginning of Dec. 2014. From Dec. 2014 to February 2015, ratios increase regularly while cometocentric distances remain approximately constant at about 25 km. These ratios thus reflect the effect of the decrease in the heliocentric distance from 3.3 to 2.5 AU: as neutral outgassing rates increase, the comet’s atmosphere becomes denser and more extended, and the charge exchange is more efficient at the same distance since the column of atmosphere traversed by the solar wind ions is larger. A third phase, from February to April 2015, witnesses a sudden drop in ratio values by a factor 2 followed by a slowly increasing behaviour, with cometocentric distances jumping from 25 km to 100 km. With respect to the first two phases, since the spacecraft is at larger distances from the comet, ratios are indeed expected to be lower. As the outgassing rate increases with diminishing heliocentric distances, this behaviour is mitigated. To interpret these ratios and decorrelate them with varying cometocentric distances, a quantitative model of charge-exchange efficiency is necessary. A new analytical model is presented in Sect. 3. Section 4.2 then presents a discussion of these ratios calculated by the analytical model and compared to RPC-ICA observations.
 |
Fig. 3 Panel A): RPC-ICA derived He+/He2+ ratios as gathered in 45 reference events between Sept. 2014 and Apr. 2015. Ratios calculated by the forward analytical model, with Q = QS13 from Snodgrass et al. (2013) and v0 = 700 m s-1 as input are displayed in red. Panel B): cometocentric distance in km. Panel C): heliocentric distance in AU. |
3. Analytical model of charge exchange at comets
A fast analytical solution of charge-exchange processes for H+ and He2+ solar wind ions at a comet is presented in this section, assuming no obstacle, a constant solar wind velocity, and no magnetic field effects, which results in beams of particles following straight trajectories and being continuously absorbed on their path. Inputs of such a model include neutral atmosphere and charge-exchange cross sections, the latter being described in Sect. 3.1.
3.1. Charge-exchange cross sections
The knowledge and book-keeping of cross sections is of paramount importance to the fine understanding of any physico-chemical reactions in a plasma, including charge-exchange reactions. Charge-exchange reactions at comets may be classified into two families, involving the two main constituents of the solar wind plasma, namely He2+ ions and H+ ions. Charge transfers will produce He+ ions and fast, so-called “energetic neutral atoms” (ENAs), in the form of HENA, respectively, as sketched in Fig. 1.
3.1.1. Charge exchange from solar wind alpha particles
He+ ions may be produced by different charge-exchange processes between the solar wind He2+ and the neutral environment of the comet (only the most important neutral species are hereby listed):  References for the cross sections for each process can be found in Barnett et al. (1990); Chanteur et al. (2009); Greenwood et al. (2004) for reactions (4), (5), and (8), respectively; and in Kusakabe et al. (2006) for reactions (7) and (6). Though no low-energy data is currently available for collisions with O, a good approximation, 4 × 10-20 m2, can be found in Chanteur et al. (2009) for energies of 1 keV. This order of magnitude is corroborated by a value of 9 × 10-21 m2 measured by McCullough et al. (1992) at 2 keV/amu. Following this, the estimate of Chanteur et al. (2009), recently used by Shematovich et al. (2013) for lack of measurements for Mars, would be an upper estimate. Cross sections at an energy of 0.83 keV/amu, corresponding to He2+ velocities of 400 km s-1, are collected in Table 1 with the associated estimated uncertainties.
References for the cross sections for each process can be found in Barnett et al. (1990); Chanteur et al. (2009); Greenwood et al. (2004) for reactions (4), (5), and (8), respectively; and in Kusakabe et al. (2006) for reactions (7) and (6). Though no low-energy data is currently available for collisions with O, a good approximation, 4 × 10-20 m2, can be found in Chanteur et al. (2009) for energies of 1 keV. This order of magnitude is corroborated by a value of 9 × 10-21 m2 measured by McCullough et al. (1992) at 2 keV/amu. Following this, the estimate of Chanteur et al. (2009), recently used by Shematovich et al. (2013) for lack of measurements for Mars, would be an upper estimate. Cross sections at an energy of 0.83 keV/amu, corresponding to He2+ velocities of 400 km s-1, are collected in Table 1 with the associated estimated uncertainties.
For low-energy collisions with H2O (E< 500 eV/amu), charge exchange followed by ionisation of H2O+ may dominate (Greenwood et al. 2004):  (9)leading to the formation of doubly charged water ions as shown in thermal electron spectroscopy experiments (Vavrukh et al. 2008). At higher collision energies, single electron charge exchange will dominate.
(9)leading to the formation of doubly charged water ions as shown in thermal electron spectroscopy experiments (Vavrukh et al. 2008). At higher collision energies, single electron charge exchange will dominate.
According to Chanteur et al. (2009), reactions (4) and (5) are typically dominant in a Mars-like magnetospheric environment. However, for a comet in the inner coma (i.e., with a cometocentric distance x< 500 km), the number density of H2O is about ten times denser than that of CO and more than 100 times that of any other neutral species (e.g., Tenishev et al. 2008), making the de facto reaction (8) the most efficient and likely process to occur for creating He+ ions. Farther away from the comet, i.e., at distances > 2 × 104 km, reactions (4) and (5) are expected to start dominating reaction (8), since water molecules will then be almost fully photodissociated (e.g., Festou 1981; Tenishev et al. 2008).
The dependence of He2++H2O cross sections with respect to He2+ velocity is presented in Fig. 4 (blue line) following Greenwood et al. (2004). The value at 400 km s-1 (see Table 1) is shown as a blue circle.
Main reactions creating He+ ions from charge exchange with solar wind alpha particles at an energy of 0.83 keV/amu.
3.1.2. Charge-exchange from solar wind protons
To create fast H ENAs from solar wind protons H+, collisions with the main ambient neutrals are considered: 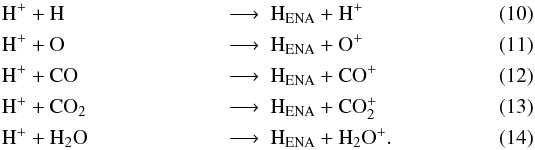 Cross sections are summarised in Table 2. For a proton impact on H2O, we use the experimental differential cross sections of Lindsay et al. (1997) measured at three different energies, i.e., at 500 eV, 1.5 kev, and 5 keV and interpolated at the solar wind velocity. The theoretical total charge-transfer cross section calculations of Mada et al. (2007) are in broad agreement with these measurements and provide the energy dependence at lower energy. The recommendation of Barnett et al. (1990) is also in good agreement with Lindsay’s experimental results though uncertainties in their review were undetermined and probably large under 600 eV energy.
Cross sections are summarised in Table 2. For a proton impact on H2O, we use the experimental differential cross sections of Lindsay et al. (1997) measured at three different energies, i.e., at 500 eV, 1.5 kev, and 5 keV and interpolated at the solar wind velocity. The theoretical total charge-transfer cross section calculations of Mada et al. (2007) are in broad agreement with these measurements and provide the energy dependence at lower energy. The recommendation of Barnett et al. (1990) is also in good agreement with Lindsay’s experimental results though uncertainties in their review were undetermined and probably large under 600 eV energy.
For comparison, cross sections for reaction (10), (11), (13), and (12) are given by Lindsay et al. (1996), Rudd et al. (1985b), and Kusakabe et al. (2000), respectively. The reported statistical uncertainties are of the order of 10% (Lindsay et al. 1997; Kusakabe et al. 2000), 20% (Rudd et al. 1985b). As for the production of He+ ions, since H2O number density is much higher than that of any other neutral component on the spatial scales considered in this article (see Tenishev et al. 2008) and owing to relatively large cross sections, process (14) is expected to dominate close to the comet. Cross sections for proton impact on water molecules are plotted in Fig. 4 with respect to the velocity of the impactor (i.e., solar wind protons). The value chosen at 400 km s-1 as in Table 2 is shown as a red circle.
 |
Fig. 4 Total charge-exchange cross section versus velocity of incident impactor: (a) α particles in reaction (8) He2+ + H2O and (b) protons in reaction (14) H+ + H2O. For He2+ impact on H2O, the data at 400 km s-1 (blue dot) of Greenwood et al. (2004) is used. For a proton impact at 400 km s-1, the interpolated experimental value of (Lindsay et al. 1997; red dot) lies between the “ORNL” recommendation of Barnett et al. (1990) and the theoretical curve of Mada et al. (2007). The experimental values of Berkner et al. (1970) and Cable (1970) are displayed for comparison with uncertainties. |
Main reactions creating H ENAs from charge-exchange processes with solar wind protons at an energy of 0.83 keV/amu.
3.2. Analytical model of charge-exchange
To assess charge-exchange processes in the environment of comet 67P, a simple line-of-sight analytical model for the creation of He+ ions and HENA atoms from solar wind impacting particles can be constructed. Several assumptions are made:
-
Solar wind ions and their charge-exchanged products (i.e.,He+) move along the Sun-comet axis along straight trajectories,
-
He+ ions are solely produced by CX with the cometary neutral atmosphere (here, H2O only),
-
Collisionless neutral atmosphere and spherical symmetry about the Sun-comet axis (using Haser-like profiles).
These assumptions are anticipated to be best when the studied comet has a low activity, typically for heliocentric distances of 2 AU and above.
Advantages of such an approach include simplicity and a fast algorithm, which can be automated to analyse large RPC-ICA datasets. The model can be used in forward and in inverse modes. In the forward analytical model, one starts from assuming a neutral outgassing rate (classically parametrised by the quantity Q in s-1) to calculate the corresponding X(n−m)+/Xn+ particle flux ratio, noted RF. In the inverse model, one uses the observed ratio at the position of Rosetta  to derive the equivalent Qobs value. Inputs and outputs of the model applied to He+ and He2+ species, in forward and inverse modes, are summarised in a synoptic form in Fig. 5. To broaden its application, the formalism described in the following sections is kept general.
to derive the equivalent Qobs value. Inputs and outputs of the model applied to He+ and He2+ species, in forward and inverse modes, are summarised in a synoptic form in Fig. 5. To broaden its application, the formalism described in the following sections is kept general.
 |
Fig. 5 Inputs and outputs of the analytical model in forward mode (left) and inverse mode (right) for He+ and He2+ ion species. The “forward” mode uses the recommended water outgassing rate QS13 of Snodgrass et al. (2013) to calculate theoretical flux ratios RF. The “inverse” mode uses RPC-ICA observations of He+/He2+ particle flux ratios |
3.2.1. Forward mode: from Q0 to RF
In the following, we choose a Cartesian system of coordinates centred on the comet nucleus, with the x-axis pointing towards the Sun (as in Fig. 1), as in the Comet-centred solar orbital coordinate system (CSO). Charge exchange will take place along straight trajectories on the path of the solar wind ions, i.e., at each point in the (+ x → −x) direction. The energy transfer (typically the difference between the ionisation potentials of species X and A, i.e., a few eV) is smaller than the energy of the collision (Sayers & Smith 1964): the velocity of the newly-born charge-exchanged ion is assumed to be the same as its parent solar wind ion.
For simplicity, the solar wind is considered to consist of mono-energetic particles with identical velocity vectors Usw = −Uswux. The flux of solar wind particles remaining after charge exchange with the cometary neutrals at position  from the comet is then obtained from the particle continuity equation in 1-D (e.g., Kallio et al. 1997):
from the comet is then obtained from the particle continuity equation in 1-D (e.g., Kallio et al. 1997):  (15)Here
(15)Here  represents the difference between the number of solar wind ions per unit surface and unit time entering a flux tube along the x-axis and the corresponding number of ions exiting this tube at position
represents the difference between the number of solar wind ions per unit surface and unit time entering a flux tube along the x-axis and the corresponding number of ions exiting this tube at position  after a charge-exchange collision occurs. The quantity
after a charge-exchange collision occurs. The quantity  is the inverse of the mean free path of neutral A: it depends on the charge-exchange cross section σCX (m-2), taken as constant in the model since solar wind ions are considered to have a beam-like structure of constant energy, and the number density of neutral species nA (m-3). When defining the column density of neutrals along the solar wind ion trajectory x as IA (m-2)
is the inverse of the mean free path of neutral A: it depends on the charge-exchange cross section σCX (m-2), taken as constant in the model since solar wind ions are considered to have a beam-like structure of constant energy, and the number density of neutral species nA (m-3). When defining the column density of neutrals along the solar wind ion trajectory x as IA (m-2)  (16)the remaining solar wind particle flux becomes
(16)the remaining solar wind particle flux becomes  (17)where
(17)where  is the initial upstream solar wind ion flux at position
is the initial upstream solar wind ion flux at position  .
.
Particle flux conservation states that in the stationary case, the particle flux of the solar wind ions and the charge-exchanged species is a constant:  (18)The particle flux of lost solar wind ions is equivalent to that of charge-exchanged species created at distance r:
(18)The particle flux of lost solar wind ions is equivalent to that of charge-exchanged species created at distance r:  (19)The ratio of X(n−m)+ to Xn+ ion fluxes is then
(19)The ratio of X(n−m)+ to Xn+ ion fluxes is then  (20)Another interesting particle flux ratio gives the so-called efficiency in converting solar wind ion fluxes into those of their charge-exchanged daughter species:
(20)Another interesting particle flux ratio gives the so-called efficiency in converting solar wind ion fluxes into those of their charge-exchanged daughter species:  (21)This quantity is of interest if one wants to investigate the percentage of lost ion fluxes in the CX process. In a complementary way, the remaining solar wind particle flux with respect to the initial solar wind ion particle flux is simply, following Eq. (17):
(21)This quantity is of interest if one wants to investigate the percentage of lost ion fluxes in the CX process. In a complementary way, the remaining solar wind particle flux with respect to the initial solar wind ion particle flux is simply, following Eq. (17):  (22)To calculate these ratios, it is first necessary to assume a neutral profile and determine the column density I. The classic spherically symmetric collisionless neutral density profile of Haser (1957) provides an expression of the number density of cometary species with Q0 molecules per second being released into the atmosphere at a homogeneous velocity v0 (m s-1):
(22)To calculate these ratios, it is first necessary to assume a neutral profile and determine the column density I. The classic spherically symmetric collisionless neutral density profile of Haser (1957) provides an expression of the number density of cometary species with Q0 molecules per second being released into the atmosphere at a homogeneous velocity v0 (m s-1):  (23)with
(23)with  and rc the radius of a supposed spherical comet, within which no outgassing takes place. The reaction rate
and rc the radius of a supposed spherical comet, within which no outgassing takes place. The reaction rate  is here the total photodestruction rate of species n, containing both photodissociation (index d) and photoionisation (index i):
is here the total photodestruction rate of species n, containing both photodissociation (index d) and photoionisation (index i):  Close to the comet (< 1000 km), the photodissociation exponential fall-off becomes negligible (e.g., Haser 1957; Gunell et al. 2015). Numerically evaluating the integral of Eq. (23) along the x axis enables the calculation of the theoretical ratio
Close to the comet (< 1000 km), the photodissociation exponential fall-off becomes negligible (e.g., Haser 1957; Gunell et al. 2015). Numerically evaluating the integral of Eq. (23) along the x axis enables the calculation of the theoretical ratio  defined by Eq. (20). Applied to He+ and He2+ species, this particle flux ratio is directly comparable to the RPC-ICA flux ratios under the model’s assumptions since the flux of the charge-exchanged species is compared to that of the local parent species flux, not the upstream solar wind ion flux. With the forward model, maps of flux ratios around the comet can be produced. A numerical application is presented in Sect. 4.
defined by Eq. (20). Applied to He+ and He2+ species, this particle flux ratio is directly comparable to the RPC-ICA flux ratios under the model’s assumptions since the flux of the charge-exchanged species is compared to that of the local parent species flux, not the upstream solar wind ion flux. With the forward model, maps of flux ratios around the comet can be produced. A numerical application is presented in Sect. 4.
RPC-ICA events and ratio results from observations and from models.
3.2.2. Inverse mode: from RF to Q
At position  of observation, an ion spectrometer detects ion fluxes so that one can derive the observed particle flux ratios at this position, noted
of observation, an ion spectrometer detects ion fluxes so that one can derive the observed particle flux ratios at this position, noted  . From these observed ratios, the inverse analytical model calculates equivalent outgassing rates
. From these observed ratios, the inverse analytical model calculates equivalent outgassing rates  . From Eq. (20) applied to the observed ratio
. From Eq. (20) applied to the observed ratio  at position
at position  of observation near the comet, one can express the neutral column density:
of observation near the comet, one can express the neutral column density:  (24)In cases when
(24)In cases when  , i.e., when the outgassing rate is low (large heliocentric distances ≳ 3 AU), the column density reduces to
, i.e., when the outgassing rate is low (large heliocentric distances ≳ 3 AU), the column density reduces to  . However, this approach breaks down at high cometary activity (small heliocentric distances) when the solar wind is expected to be significantly slowed down by the increased mass loading. Thus, measurement of a particle ion flux ratio at one point of a spacecraft orbit gives information on the column density at that point.
. However, this approach breaks down at high cometary activity (small heliocentric distances) when the solar wind is expected to be significantly slowed down by the increased mass loading. Thus, measurement of a particle ion flux ratio at one point of a spacecraft orbit gives information on the column density at that point.
Integrating the Haser model of Eq. (23) along the Sun-comet line of sight  , the equivalent outgassing rate Qobs can be linked to the column density Iobs:
, the equivalent outgassing rate Qobs can be linked to the column density Iobs:  (25)In turn, assuming an outgassing velocity v0, this Q value could be compared to ground-based optical observations of the comet’s light curve (e.g., Snodgrass et al. 2013) or, better, to other spacecraft in situ measurements of neutral densities, such as those of ROSINA-COPS onboard Rosetta (e.g., Bieler et al. 2015). A numerical application and results are shown in Sect. 4.
(25)In turn, assuming an outgassing velocity v0, this Q value could be compared to ground-based optical observations of the comet’s light curve (e.g., Snodgrass et al. 2013) or, better, to other spacecraft in situ measurements of neutral densities, such as those of ROSINA-COPS onboard Rosetta (e.g., Bieler et al. 2015). A numerical application and results are shown in Sect. 4.
4. Discussion
4.1. Charge-exchange efficiency
Theoretical ratios are calculated using the forward analytical model approach with assumptions for Q,v0, and rc. Considering a cometary atmosphere mostly made of H2O molecules, Q is usually in the range 1025−1028 s-1 for Jupiter-family comets, while v0 ~ 500−1000 m s-1 (e.g., Coates & Jones 2009).
The forward model inputs are summarised in Table 4. From various optical observations of the last pre-perihelion passage of comet 67P in 2008, Snodgrass et al. (2013) inferred an approximate Q value as a function of heliocentric distance Rh:  (26)This outgassing rate is used in the forward model to derive He+/He2+ ratios, noted
(26)This outgassing rate is used in the forward model to derive He+/He2+ ratios, noted  . For simplicity, a constant outgassing velocity of v0 = 700 m s-1 is first used, which corresponds to average velocities recorded by the microwave instrument MIRO onboard Rosetta (e.g., Gulkis et al. 2015; Gunell et al. 2015). The total photodestruction rate – dissociation and ionisation –
. For simplicity, a constant outgassing velocity of v0 = 700 m s-1 is first used, which corresponds to average velocities recorded by the microwave instrument MIRO onboard Rosetta (e.g., Gulkis et al. 2015; Gunell et al. 2015). The total photodestruction rate – dissociation and ionisation –  for the reaction H2O + hν is taken from the recommendations of Huebner et al. (1992) and Huebner & Mukherjee (2015) for low solar activity at 1 AU. The photorates are then scaled to the comet’s heliocentric distance by a factor
for the reaction H2O + hν is taken from the recommendations of Huebner et al. (1992) and Huebner & Mukherjee (2015) for low solar activity at 1 AU. The photorates are then scaled to the comet’s heliocentric distance by a factor  .
.
Table 3 lists the 45 events selected in this study, with dates/times, heliocentric and cometocentric distances, and their observed and theoretical ratios  and
and  . Since the cross section for charge exchange between He2+ and H2O is about twice as small as that between H+ and H2O, the efficiency of He2+ charge-exchange is expected to be lower, resulting in about twice as small ratios in the limit of low column densities. This trend is seen here with He2+ charge-exchange ratios
. Since the cross section for charge exchange between He2+ and H2O is about twice as small as that between H+ and H2O, the efficiency of He2+ charge-exchange is expected to be lower, resulting in about twice as small ratios in the limit of low column densities. This trend is seen here with He2+ charge-exchange ratios  reaching 5−10% and H+ charge-exchange ratios
reaching 5−10% and H+ charge-exchange ratios  reaching 10−20% on average at the radial distance of the Rosetta spacecraft.
reaching 10−20% on average at the radial distance of the Rosetta spacecraft.
Figure 3 (panel A) shows the comparison of the forward model using as input QS13, in red, with the RPC-ICA flux ratios (triangles). Overall agreement between the calculated ratios and the observed ones is achieved for most of the events with comparatively the same trends (as previously emphasised in Sect. 2.3). However, differences of up to a factor 5 are also encountered for several events, suggesting that a temporary increased activity might have then taken place, resulting in high outgassing rates column densities, hence higher ratios. Such a punctual increase can in turn be related to either changed solar activity conditions or local effects at the comet’s nucleus. Such high outgassing rates would further invalidate the first-approximation asssumption of straight solar wind trajectories in the analytical model, so that these derived flux ratios should be interpreted with extra caution.
The application of this approach to one event, recorded on 24 January 2015 (event #28), is now presented. At the position (−1.3,−8.2,26.5) km from the comet and 2.47 AU from the Sun, RPC-ICA detected a particle flux ratio He+/He2+ of  , where an energy-dependent geometric factor correction g = 4.92 × 10-5/ 3.18 × 10-5 = 1.54 was applied (e.g., Nilsson et al. 2015a, supplementary material). The corresponding column density was then about 3.26 × 1018 m-2 on this date and location, using the cross sections defined in Table 1 and Eq. (24).
, where an energy-dependent geometric factor correction g = 4.92 × 10-5/ 3.18 × 10-5 = 1.54 was applied (e.g., Nilsson et al. 2015a, supplementary material). The corresponding column density was then about 3.26 × 1018 m-2 on this date and location, using the cross sections defined in Table 1 and Eq. (24).
Because the Haser neutral profile provides the expression of the number density at each point around the comet, one can calculate the 3-D He+-He2+ and HENA-H+ flux ratios with respect to the initial solar wind ions, i.e.,  (Eq. (21)). As pointed out earlier, these ratios are a measure of the efficiency of the charge exchange in the close environment of the comet. For event 28, when the activity was still quite low, an outgassing rate of Q = 1.1 × 1026 s-1 for v0 = 700 m s-1 was chosen, using the pre-perihelion recommendation of Snodgrass et al. (2013) scaled to a heliocentric distance of 2.47 AU. The respective efficiency ratios in the symmetric plane along the Sun-comet axis x are shown in Figs. 6 and 7 for event #28. At this distance from the Sun, the effective conversion of solar wind particles to charge-exchanged species H+ and He+ may reach typical values of 10−40% and 20−60%, respectively, in the terminator plane of the comet at positions (x = 0,y,z). At zenith (x = 2,y = 0,z = 0) on the comet’s Sun-facing side, these flux ratios
(Eq. (21)). As pointed out earlier, these ratios are a measure of the efficiency of the charge exchange in the close environment of the comet. For event 28, when the activity was still quite low, an outgassing rate of Q = 1.1 × 1026 s-1 for v0 = 700 m s-1 was chosen, using the pre-perihelion recommendation of Snodgrass et al. (2013) scaled to a heliocentric distance of 2.47 AU. The respective efficiency ratios in the symmetric plane along the Sun-comet axis x are shown in Figs. 6 and 7 for event #28. At this distance from the Sun, the effective conversion of solar wind particles to charge-exchanged species H+ and He+ may reach typical values of 10−40% and 20−60%, respectively, in the terminator plane of the comet at positions (x = 0,y,z). At zenith (x = 2,y = 0,z = 0) on the comet’s Sun-facing side, these flux ratios  reach values of about 39.3% and 66.5% for He+-He2+ and HENA-H+, respectively.
reach values of about 39.3% and 66.5% for He+-He2+ and HENA-H+, respectively.
As the comet moves closer to the Sun, the outgassing rate is expected to become significantly higher. Because the water density around the comet increases, this in turn influences the charge-exchange rate. Figure 8 shows the predicted percentage of lost solar wind He ions due to charge-exchange with H2O with a varying distance to the Sun: the ratio is here
ions due to charge-exchange with H2O with a varying distance to the Sun: the ratio is here  of Eq. (22). We start at the 3.3 AU where Q = 1.4 × 1025 s-1 for outgassing velocity of 700 m s-1, then move on to 2.5 AU and finally to 1.8 AU. Since the velocity of the outgassing neutral is also expected to vary with heliocentric distance, the effect of a 400 m s-1 velocity on the 1.8 AU ratios is shown. As calculated from equation (23), the column density varies in
of Eq. (22). We start at the 3.3 AU where Q = 1.4 × 1025 s-1 for outgassing velocity of 700 m s-1, then move on to 2.5 AU and finally to 1.8 AU. Since the velocity of the outgassing neutral is also expected to vary with heliocentric distance, the effect of a 400 m s-1 velocity on the 1.8 AU ratios is shown. As calculated from equation (23), the column density varies in  , so that the effect of decreasing v0 at constant outgassing rate Q is equivalent to increasing Q at a constant velocity.
, so that the effect of decreasing v0 at constant outgassing rate Q is equivalent to increasing Q at a constant velocity.
 |
Fig. 6 Particle flux ratio |
 |
Fig. 7 Particle flux ratio |
 |
Fig. 8 Theoretical normalised remaining solar wind H+ (dashed lines) and He2+ (solid lines) particle flux ratios |
4.2. Outgassing rates
From the RPC-ICA derived He+-He2+ ratios, one can use the inverse analytical model to derive the equivalent outgassing rates Qobs, as shown in Fig. 9 with the corresponding propagated statistical fluctuations. Comparison with the recommended Q value of Snodgrass et al. (2013) (QS13, Eq. (26)) with heliocentric distance dependence  ) shows good agreement with RPC-ICA-derived Q values. Moreover, the
) shows good agreement with RPC-ICA-derived Q values. Moreover, the  curve most of the time remains within the event-by-event fluctuations, as already pointed out in Sect. 4.1.
curve most of the time remains within the event-by-event fluctuations, as already pointed out in Sect. 4.1.
 |
Fig. 9 Panel A): outgassing rates QH2O in s-1 derived from RPC-ICA (triangles with standard deviation) between Sept. 2014 and Apr. 2015 with a constant outgassing velocity of 700 m s-1. The red curve shows the Q value recommended by Snodgrass et al. (2013) by remote sensing from Earth for the last pre-perihelion passage of comet 67P. Panel B): corresponding heliocentric distance in AU. |
 |
Fig. 10 Outgassing rates Q derived from RPC-ICA as a function of heliocentric distance Rh, assuming a constant outgassing velocity of 700 m s-1. A least-squares fit is performed on the data (black solid line, Qfit) and compared to the previous measurements of Snodgrass et al. (2013; grey solid lines, QS13). This is a log 10−log 10 plot i.e., the x-axis is also logarithmically spaced. |
To compare more precisely with Snodgrass et al. (2013), a simple function of the form  is used to fit the retrieved Q values from RPC-ICA. This is equivalent to a linear fit on log Q of the following form:
is used to fit the retrieved Q values from RPC-ICA. This is equivalent to a linear fit on log Q of the following form:  (27)A least-squares fit on the retrieved log Q yields log α = 66.903 and β = 7.06 ± 0.81 (when taking the statistical fluctuations of Qobs into account). Consequently, the fitted revised Q value was
(27)A least-squares fit on the retrieved log Q yields log α = 66.903 and β = 7.06 ± 0.81 (when taking the statistical fluctuations of Qobs into account). Consequently, the fitted revised Q value was  (28)Figure 10 shows the retrieved outgassing rates from RPC-ICA with respect to the heliocentric distance and the final linear fit (solid black line). The figure is in log 10−log 10 scale to emphasise the linear dependence. For comparison, the results of Snodgrass et al. (2013) are also shown (grey solid line). At large heliocentric distances (> 2.8 AU), the fitted RPC-ICA results are in relatively good agreement with those of Snodgrass et al. (2013). When coming closer to the Sun, however, the departure between the two curves becomes more pronounced.
(28)Figure 10 shows the retrieved outgassing rates from RPC-ICA with respect to the heliocentric distance and the final linear fit (solid black line). The figure is in log 10−log 10 scale to emphasise the linear dependence. For comparison, the results of Snodgrass et al. (2013) are also shown (grey solid line). At large heliocentric distances (> 2.8 AU), the fitted RPC-ICA results are in relatively good agreement with those of Snodgrass et al. (2013). When coming closer to the Sun, however, the departure between the two curves becomes more pronounced.
It is necessary to assess how the model’s assumptions (Sect. 3) may impact the quality of the Q-value retrievals by examining the sources of uncertainty. Instrument-wise, one of the major uncertainties regards the calibration, and especially the determination of the geometrical factor, which depends on energy. A systematic variation in the geometric factor by any factor (around its average value of 1.5) will impact the parameter α but not the slope of the line. Model-wise, H2O was taken as the sole neutral constituent of the cometary atmosphere: this condition might not be met close to the comet, where CO and CO2 may play a large role and are expected to be of the order of 10% of the number density of H2O (Bieler et al. 2015). This could result in an underestimation of the charge-exchange ratios in the forward model approach of the order of 10%. Similarly, the constant outgassing velocity has an impact, albeit limited, on the retrieval process. To test this, Qobs values were calculated using a constant velocity of 400 and 1000 m s-1. The fitted exponents β in Eq. (27) remained nearly identical, i.e., 7.06 ± 0.01. This is expected since the effect of increasing the velocity uniformly increases the Q values but does not affect the line’s slope. However, the intercept α will be modified accordingly: if the velocity increases by a factor 2.5, α will also be multiplied by a factor close to 2.5 to a first approximation. Neutral velocity and density data from ROSINA-COPS (e.g., Bieler et al. 2015) could be used to mitigate the assumption of constant velocities.
Even though the solar wind deflection observed by RPC-ICA is in the range of 25−50° for the same time period Nilsson et al. (2015a,b), the assumption of straight undisturbed trajectories along the solar wind direction seems, to a first-order approximation, to be sufficient to account for the global charge-exchange efficiency at 67P within this range of heliocentric distances. Preliminary cometary hybrid model simulations performed by the team in similar conditions show that this tendency may be reasonable up until about 2 AU, where significant deflections of the solar wind start to take place (figure not shown).
Consequently, RPC-ICA observations of He+ and He2+ give a useful first approximation of charge-exchange processes around the comet for low cometary activities. The heliocentric distance dependence of Q in  , unlike the pre-perihelion one in
, unlike the pre-perihelion one in  found by Snodgrass et al. (2013), may imply that the comet’s neutral outgassing activity has significantly changed since its last perihelion passage in 2008. When the comet starts its outbound leg after reaching perihelion, RPC-ICA will be used to continue monitoring the charge-exchange efficiency around the comet and new comparisons with previous passages will be performed.
found by Snodgrass et al. (2013), may imply that the comet’s neutral outgassing activity has significantly changed since its last perihelion passage in 2008. When the comet starts its outbound leg after reaching perihelion, RPC-ICA will be used to continue monitoring the charge-exchange efficiency around the comet and new comparisons with previous passages will be performed.
5. Conclusions
We have shown how an in situ ion instrument may be used to remotely probe the neutral environment of a comet by use of charge-exchange processes. Using a simple analytical model, the ion instrument RPC-ICA onboard Rosetta is capable of monitoring the evolution of the coma’s activity for heliocentric distances > 2 AU. Differences with previous remote-sensing ground-based observations (Snodgrass et al. 2013) show that the activity of the comet has significantly changed from the last perihelion passage in 2008, a change that might be due to differences in solar wind and cometary outgassing conditions.
Complementary information on the cometary densities and outgassing velocities could be achieved with another in-situ instrument onboard Rosetta, the pressure sensor ROSINA-COPS (Bieler et al. 2015): comparison with RPC-ICA derived outgassing rates is under way.
The main results of this study can be summarised as follows:
-
1.
A new dependence of the ougtassing rate on heliocentricdistance Rh is found to be
 s-1, as derived from RPC-ICA measurements.
s-1, as derived from RPC-ICA measurements. -
2.
A simple analytical model of charge-exchange efficiency at a comet is presented that can be applied to He+/He2+ ion particle flux ratio observations. To a first approximation, the solar wind is assumed to be following straight trajectories along the Sun-comet path, an assumption that may be sustainable without too much discrepancy for Rh ≳ 2 AU. The analytical model is applicable to other species and could be used, for instance, for heavier ions such as O6+ and O7+.
-
3.
Charge exchange is predicted to play a significant role in the ion composition of the comet’s ion and neutral environment, populating it with He+ ions and hydrogen ENAs and reaching high efficiencies closer to the comet.
Closer to the Sun, magnetic boundaries due to the interaction between the solar wind and the ionised coma start to form for Rh< 2 AU. At these distances, the role of charge exchange in the formation of these boundaries can only be investigated with the use of 3D self-consistent hybrid kinetic models that take all ionisation processes at the comet into account, such as photoionisation, charge exchange, electron impact ionisation, and electron recombination. Such a model is currently under development at Aalto University and includes the dynamics and asymmetries due to j × B and Lorentz forces and will be the core of a future dedicated study.
Acknowledgments
Rosetta is a European Space Agency (ESA) mission with contributions from its member states and the National Aeronautics and Space Administration (NASA). This study was supported by the Academy of Finland and, in part, by the Research Council of Norway grant No. 240000. The work on RPC-ICA was funded by the Swedish National Space Board under contracts 108/12 and 112/13. Work at the Belgian Institute for Space Aeronomy was supported by the Belgian Science Policy Office through the Solar-Terrestrial Centre of Excellence and by PRODEX/ROSETTA/ROSINA PEA 4000107705. First selection of events in this study was performed with the AMDA science analysis system provided by the Centre de Données de la Physique des Plasmas (CDPP) supported by CNRS, CNES, Observatoire de Paris and Université Paul Sabatier, Toulouse. G.G. is supported by the NASA Astrobiology Institute Grant NNX15AE05G and by the NASA HIDEE program Grant NNH15CO73C. C.S.W. thanks T.E. Cravens (University of Kansas, USA), W.J. Miloch (University of Oslo, Norway) and, last but not least, M. Simon Wedlund for useful discussions.
References
- Barnett, C. F., Hunter, H. T., Fitzpatrick, M. I., et al. 1990, NASA STI/Recon Technical Report N, 91, 13238 [Google Scholar]
- Béhar, E., Nilsson, H., Stenberg Wieser, G., et al. 2016, Geophys. Res. Lett., 43, DOI: 10.1002/2015GL067436 [Google Scholar]
- Berkner, K., Pyle, R., & Stearns, J. 1970, Nucl. Fus., 10, 145 [Google Scholar]
- Bieler, A., Altwegg, K., Balsiger, H., et al. 2015, A&A, 583, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Breus, T. K., Krymskii, A. M., & Luhmann, J. G. 1987, Geophys. Res. Lett., 14, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Burch, J. L., Cravens, T. E., Llera, K., et al. 2015, Geophys. Res. Lett., 42, 5125 [NASA ADS] [CrossRef] [Google Scholar]
- Cable, P. 1970, Ph.D. Thesis, University of Maryland [Google Scholar]
- Carr, C., Cupido, E., Lee, C. G. Y., et al. 2007, Space Sci. Rev., 128, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Chanteur, G. M., Dubinin, E., Modolo, R., & Fraenz, M. 2009, Geophys. Res. Lett., 36, 23105 [NASA ADS] [CrossRef] [Google Scholar]
- Coates, A. J., & Jones, G. H. 2009, Plan. Space Sci., 57, 1175 [NASA ADS] [CrossRef] [Google Scholar]
- Cochran, A. L., Levasseur-Regourd, A.-C., Cordiner, M., et al. 2015, Space Sci. Rev., 197, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Cravens, T. E. 1997, Geophys. Res. Lett., 24, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Dennerl, K. 2010, Space Sci. Rev., 157, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Festou, M. C. 1981, A&A, 95, 69 [NASA ADS] [Google Scholar]
- Gombosi, T. I. 1987, Geophys. Res. Lett., 14, 1174 [NASA ADS] [CrossRef] [Google Scholar]
- Greenwood, J. B., Mawhorter, R. J., Cadez, I., et al. 2004, Phys. Script. T, 110, 358 [Google Scholar]
- Gulkis, S., Allen, M., von Allmen, P., et al. 2015, Science, 347 [Google Scholar]
- Gunell, H., Mann, I., Simon Wedlund, C., et al. 2015, Planet. Space Sci., 119, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, K. C., Bagdonat, T., Motschmann, U., et al. 2007, Space Sci. Rev., 128, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Haser, L. 1957, Bull. Soc. Roy. Scie. Liège, 43, 740 [Google Scholar]
- Howell, D. C. 2014, Median Absolute Deviation (John Wiley & Sons, Ltd) [Google Scholar]
- Huebner, W. F., & Mukherjee, J. 2015, Plan. Space Sci., 106, 11 [Google Scholar]
- Huebner, W. F., Keady, J. J., & Lyon, S. P. 1992, Astrophys. Space Sci., 195, 1 [Google Scholar]
- Jacquey, C., Génot, V., Budnik, E., et al. 2010, AMDA, Automated Multi-Dataset Analysis: A Web-Based Service Provided by the CDPP (H. Laakso, M. Taylor, and C. P. Escoubet), 239 [Google Scholar]
- Kallio, E., Luhmann, J. G., & Barabash, S. 1997, J. Geophys. Res., 102, 22183 [NASA ADS] [CrossRef] [Google Scholar]
- Kallio, E., Wurz, P., Killen, R., et al. 2008, Plan. Space Sci., 56, 1506 [NASA ADS] [CrossRef] [Google Scholar]
- Kusakabe, T., Asahina, K., Gu, J. P., et al. 2000, Phys. Rev. A, 62, 062714 [NASA ADS] [CrossRef] [Google Scholar]
- Kusakabe, T., Miyamoto, Y., Kimura, M., & Tawara, H. 2006, Phys. Rev. A, 73, 022706 [NASA ADS] [CrossRef] [Google Scholar]
- Lindsay, B. G., Sieglaff, D. R., Schafer, D. A., et al. 1996, Phys. Rev. A, 53, 212 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lindsay, B. G., Sieglaff, D. R., Smith, K. A., & Stebbings, R. F. 1997, Phys. Rev. A, 55, 3945 [NASA ADS] [CrossRef] [Google Scholar]
- Mada, S., Hida, K.-N., Kimura, M., et al. 2007, Phys. Rev. A, 75, 022706 [NASA ADS] [CrossRef] [Google Scholar]
- McCullough, R. W., McLaughlin, T. K., Koizumi, T., & Gilbody, H. B. 1992, J. Phys. B Atom. Mol. Phys., 25, L193 [NASA ADS] [CrossRef] [Google Scholar]
- Nilsson, H., Lundin, R., Lundin, K., et al. 2007, Space Sci. Rev., 128, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Nilsson, H., Stenberg Wieser, G., Behar, E., et al. 2015a, Science, 347, 571 [Google Scholar]
- Nilsson, H., Stenberg Wieser, G., Behar, E., et al. 2015b, A&A, 583, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Preusker, F., Scholten, F., Matz, K. D., et al. 2015, A&A, 583, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rudd, M. E., Goffe, T. V., & Itoh, A. 1985a, Phys. Rev. A, 32, 2128 [NASA ADS] [CrossRef] [Google Scholar]
- Rudd, M. E., Kim, Y.-K., Madison, D. H., & Gallagher, J. W. 1985b, Rev. Mod. Phys., 57, 965 [NASA ADS] [CrossRef] [Google Scholar]
- Sayers, J., & Smith, D. 1964, Discuss. Faraday Soc., 37, 167 [CrossRef] [Google Scholar]
- Schleicher, D. G. 2006, Icarus, 181, 442 [CrossRef] [Google Scholar]
- Shematovich, V. I., Bisikalo, D. V., Stenberg, G., et al. 2013, J. Geophys. Res., 118, 1231 [CrossRef] [Google Scholar]
- Snodgrass, C., Tubiana, C., Bramich, D. M., et al. 2013, A&A, 557, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tenishev, V., Combi, M., & Davidsson, B. 2008, ApJ, 685, 659 [NASA ADS] [CrossRef] [Google Scholar]
- Vavrukh, M. V., Seredyuk, V. O., Seredyuk, B. O., & McCullough, R. W. 2008, Prob. Atom. Sci. Techn., 6, 84 [Google Scholar]
All Tables
Main reactions creating He+ ions from charge exchange with solar wind alpha particles at an energy of 0.83 keV/amu.
Main reactions creating H ENAs from charge-exchange processes with solar wind protons at an energy of 0.83 keV/amu.
All Figures
 |
Fig. 1 Sketch of low-charge solar wind charge-exchange processes in a cometary environment. Two processes are shown with solar wind protons and alpha particles, respectively, which transfer a single charge to water molecules. The depicted x,y,z Cartesian coordinate system is the one used in the analytical model. The comet picture is that of 67P (courtesy ESA/Rosetta). |
| In the text | |
 |
Fig. 2 RPC-ICA observation on 24 January 2015 versus time. Panel A): differential energy flux spectrum in m2 s-1 eV-1 sr-1. Energy is given as E/Q in eV/charge. White dashed lines: energy limits used for the energy integration of the He2+ fluxes. Green dashed lines: energy limits for the integration of He+ fluxes. Panel B): integrated He2+ and He+ ion fluxes, normalised for clarity to the first value of the time series FHe+ at 11:03 UT. A running average window of 3 × 192 s is used on the two signals to correct for the instrument’s elevation binning. Panel C): final He+/He2+ flux ratio in %. Panel D): heliocentric distance in AU (left y-axis, solid line) and cometocentric distance in km (right y-axis, dashed line). |
| In the text | |
 |
Fig. 3 Panel A): RPC-ICA derived He+/He2+ ratios as gathered in 45 reference events between Sept. 2014 and Apr. 2015. Ratios calculated by the forward analytical model, with Q = QS13 from Snodgrass et al. (2013) and v0 = 700 m s-1 as input are displayed in red. Panel B): cometocentric distance in km. Panel C): heliocentric distance in AU. |
| In the text | |
 |
Fig. 4 Total charge-exchange cross section versus velocity of incident impactor: (a) α particles in reaction (8) He2+ + H2O and (b) protons in reaction (14) H+ + H2O. For He2+ impact on H2O, the data at 400 km s-1 (blue dot) of Greenwood et al. (2004) is used. For a proton impact at 400 km s-1, the interpolated experimental value of (Lindsay et al. 1997; red dot) lies between the “ORNL” recommendation of Barnett et al. (1990) and the theoretical curve of Mada et al. (2007). The experimental values of Berkner et al. (1970) and Cable (1970) are displayed for comparison with uncertainties. |
| In the text | |
 |
Fig. 5 Inputs and outputs of the analytical model in forward mode (left) and inverse mode (right) for He+ and He2+ ion species. The “forward” mode uses the recommended water outgassing rate QS13 of Snodgrass et al. (2013) to calculate theoretical flux ratios RF. The “inverse” mode uses RPC-ICA observations of He+/He2+ particle flux ratios |
| In the text | |
 |
Fig. 6 Particle flux ratio |
| In the text | |
 |
Fig. 7 Particle flux ratio |
| In the text | |
 |
Fig. 8 Theoretical normalised remaining solar wind H+ (dashed lines) and He2+ (solid lines) particle flux ratios |
| In the text | |
 |
Fig. 9 Panel A): outgassing rates QH2O in s-1 derived from RPC-ICA (triangles with standard deviation) between Sept. 2014 and Apr. 2015 with a constant outgassing velocity of 700 m s-1. The red curve shows the Q value recommended by Snodgrass et al. (2013) by remote sensing from Earth for the last pre-perihelion passage of comet 67P. Panel B): corresponding heliocentric distance in AU. |
| In the text | |
 |
Fig. 10 Outgassing rates Q derived from RPC-ICA as a function of heliocentric distance Rh, assuming a constant outgassing velocity of 700 m s-1. A least-squares fit is performed on the data (black solid line, Qfit) and compared to the previous measurements of Snodgrass et al. (2013; grey solid lines, QS13). This is a log 10−log 10 plot i.e., the x-axis is also logarithmically spaced. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.






