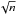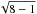| Issue |
A&A
Volume 587, March 2016
|
|
|---|---|---|
| Article Number | A158 | |
| Number of page(s) | 10 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201526852 | |
| Published online | 07 March 2016 | |
Richness-based masses of rich and famous galaxy clusters⋆,⋆⋆
INAF–Osservatorio Astronomico di Brera, via Brera 28, 20121 Milano, Italy
e-mail: stefano.andreon@brera.inaf.it
Accepted: 29 June 2015Received: 13 January 2016
We present a catalog of galaxy cluster masses derived by exploiting the tight correlation between mass and richness, i.e., a properly computed number of bright cluster galaxies. The richness definition adopted in this work is properly calibrated, shows a small scatter with mass, and has a known evolution, which means that we can estimate accurate (0.16 dex) masses more precisely than by adopting any other richness estimates or X-ray or SZ-based proxies based on survey data. We measured a few hundred galaxy clusters at 0.05 < z < 0.22 in the low-extinction part of the Sloan Digital Sky Survey footprint that are in the 2015 catalog of Planck-detected clusters, that have a known X-ray emission, that are in the Abell catalog, or that are among the most most cited in the literature. Diagnostic plots and direct images of clusters are individually inspected and we improved cluster centers and, when needed, we revised redshifts. Whenever possible, we also checked for indications of contamination from other clusters on the line of sight, and found ten such cases. All this information, with the derived cluster mass values, are included in the distributed value-added cluster catalog of the 275 clusters with a derived mass larger than 1014M⊙. Finally, in a technical appendix we illustrate with Planck clusters how to minimize the sensitivity of comparisons between masses listed in different catalogs to the specific overlapping of the considerd subsamples, a problem recognized but not solved in the literature.
Key words: catalogs / galaxies: clusters: general
Full Table 1 is available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/587/A158
A web front-end is available at the URL http://www.brera.mi.astro.it/~andreon/famous.html
© ESO, 2016
1. Introduction
Since Abell (1958) and Zwicky et al. (1961) we have known that the most massive clusters are also the richest. A precise quantification of the relation between mass and richness and, in particular, of the scatter between them has taken a long time to be established because direct estimates of mass not relying on hydrostatic or dynamical equilibrium, such as caustic (Diaferio & Geller 1997) or lensing (Broadhurst et al. 1995) masses, has only recently become available and robust (e.g., Serra et al. 2011; von der Linden 2014a).
This quantification is still in progress for most richness estimates. For example, “maxBCG” richnesses (Koester et al. 2007) a) include fore/background galaxies among cluster galaxies (Koester et al. 2007; Andreon & Hurn 2010); b) count galaxies within a noisy radius on average two times larger than r2001 (Becker et al. 2007; Johnston et al. 2007; Sheldon et al. 2009; Andreon & Hurn 2010); c) use an incorrect center 30% of the time (e.g., Johnston et al. 2007; Andreon & Moretti 2011); and d) for these reasons show redshift-dependent systematics (Becker et al. 2007; Rykoff et al. 2008; Rozo et al. 2009; Andreon & Hurn 2010; Andreon & Moretti 2011). Some other richnesses lack a mass calibration (e.g., those in Budzynski et al. 2014), have a preliminary one (e.g., those in Rykoff et al. 2014), have an unknown scatter with mass (e.g., those in Wiesner et al. 2015; Ford et al. 2015; and Oguri 2015), or a yet unquantified evolution (e.g., those in Koester et al. 2007). In these conditions, as for the “maxBCG” richnesses mentioned above or for richnesses in Rykoff et al. 2014 (see Andreon 2015 for the latter), systematics may appear. Not fully calibrated richnesses are not ready to be used to estimate cluster masses.
Other mass proxies share some of these shortcomings. For example, the integrated pressure YX used by Vikhlinin et al. (2009) to estimate cluster masses and, from these data cosmological parameters, has a yet uncharacterized evolution. In fact, Israel et al. (2014) found an higher normalization interpreted as possibly due to a Malmquist bias. The current calibration of the YSZ mass proxy returns cosmological parameters different from those derived mostly from the cosmic microwave background, which could suggest a calibration problem of up to 0.2 dex (Planck Collaboration XXIV 2015), or, using independent data, a mass bias (von der Linden 2014b) or a neglected evolution (Andreon 2014). The mass calibration of the South Pole significance parameter largely relies on simulations, given the scarcity of real data (Bocquet et al. 2015).
One proxy, n200, seems to be in better shape – it has a well-determined mean scaling, a known and small scatter, and a known and negligible evolution – as a result of calibration efforts using caustic masses from the Cluster Infall Regions (Rines et al. 2006), Hectospec Cluster Surveys (Rines et al. 2013), and weak lensing masses from Canadian Cluster Comparison Project (Hoekstra et al. 2012). A negligible scatter (0.02 dex) between a properly measured number of red galaxies and mass has been found around the relation 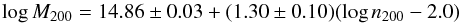 (1)with a tight upper limit on evolution with redshift up to z = 0.55 once the passive evolution of the red galaxies is accounted for (Andreon & Hurn 2010; Andreon & Congdon 2014; Andreon 2015). This 0.02 dex intrinsic scatter in mass is comparable to or better than the values derived for other proxies, such as the integrated pressure YSZ or pseudo pressure YX, X-ray luminosity LX, gas mass Mgas, and stellar mass (Andreon 2015). The n200 proxy performance, 0.16 dex, is comparable to or better than YSZ, maxBCG n200 (Andreon 2015), and LX (Andreon & Hurn 2010). We note that Eq. (1) refers to n200 values measured according to the prescriptions of Andreon & Hurn (2010) and not to other richness measurements even if they share the same symbol, such as “maxBCG” richnesses (Koester et al. 2007).
(1)with a tight upper limit on evolution with redshift up to z = 0.55 once the passive evolution of the red galaxies is accounted for (Andreon & Hurn 2010; Andreon & Congdon 2014; Andreon 2015). This 0.02 dex intrinsic scatter in mass is comparable to or better than the values derived for other proxies, such as the integrated pressure YSZ or pseudo pressure YX, X-ray luminosity LX, gas mass Mgas, and stellar mass (Andreon 2015). The n200 proxy performance, 0.16 dex, is comparable to or better than YSZ, maxBCG n200 (Andreon 2015), and LX (Andreon & Hurn 2010). We note that Eq. (1) refers to n200 values measured according to the prescriptions of Andreon & Hurn (2010) and not to other richness measurements even if they share the same symbol, such as “maxBCG” richnesses (Koester et al. 2007).
A small scatter between proxy and mass makes the proxy useful for predicting the mass of a cluster without a direct mass estimate. However, given that the proxy has to be measured within an aperture which is nothing else than a mass expressed in different units (for example, 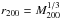 apart from obvious coefficients), an effective way to estimate the reference aperture (r200) is needed in order to use proxies to estimate masses. Andreon (2015) applies Kravtsov et al. (2006) idea of inferring both M200 and r200 at the same time exploiting the tight mass-proxy scaling. This was shown to minimally degrade the performance of richness as a way to estimate mass, leading to richness-based masses with 0.16 dex errors (Oguri 2014). The observationally inexpensive richness can therefore be used to estimate the mass of large samples of clusters for which either direct estimates are unavailable, are impossible to obtain, or just are not necessary. Unlike other mass proxies affected by dynamical or hydrostatic non-equilibrium, the cluster richness (the number of red galaxies) has the further advantage of also providing the mass of clusters out of equilibrium (interacting, merging, etc.).
apart from obvious coefficients), an effective way to estimate the reference aperture (r200) is needed in order to use proxies to estimate masses. Andreon (2015) applies Kravtsov et al. (2006) idea of inferring both M200 and r200 at the same time exploiting the tight mass-proxy scaling. This was shown to minimally degrade the performance of richness as a way to estimate mass, leading to richness-based masses with 0.16 dex errors (Oguri 2014). The observationally inexpensive richness can therefore be used to estimate the mass of large samples of clusters for which either direct estimates are unavailable, are impossible to obtain, or just are not necessary. Unlike other mass proxies affected by dynamical or hydrostatic non-equilibrium, the cluster richness (the number of red galaxies) has the further advantage of also providing the mass of clusters out of equilibrium (interacting, merging, etc.).
A large sample of clusters with homogeneously derived and calibrated masses has many possible uses: 1) understanding how cluster properties scale with mass; 2) performing other measurements of radial-dependent quantities at a fixed reference radius, such as the fraction of blue galaxies or the X-ray luminosity in a standardized aperture (as mentioned, r200 can be simply derived from the M200); 3) normalizing measurements whose definition requires knowledge of mass such as the star formation density; 4) combining clusters of different masses (and therefore sizes); 5) making available for study a larger sample of clusters with masses, allowing the characterization of trends that are hard to identify with smaller samples; 6) calibrating or checking the calibration of other mass proxies; etc.
In this paper, we measure the mass of 275 clusters at 0.05 <z< 0.22 in the Sloan Digital Sky Survey (SDSS) footprint at high Galactic latitude. This measurement requires that we first improve the approximate center and redshift of some of them. During the analysis, we also discover pairs of clusters on almost the same line of sight, which we list for later use (some other mass proxies and direct mass estimates are badly affected by this type of blends, such as weak lensing and SZ masses). The resulting sample differs from many catalogs of clusters with known richness because the reduced scatter of the adopted richness and the known calibration with mass allow us to derive accurate (0.16 dex) masses.
The Appendix compares richness-based masses to SZ-based masses for 107 clusters. To perform this comparison, we solve the common, yet unsolved, problem of minimizing the sensitivity of conclusions to the specific overlapping of the considered samples.
Throughout this paper, we assume ΩM = 0.3, ΩΛ = 0.7, and H0 = 70 km s-1 Mpc-1. Magnitudes are in the AB system, and all logarithms are in base 10. We use the 2003 version of the Bruzual & Charlot (2003) stellar population synthesis models with solar metallicity, a Salpeter initial mass function (IMF), and zf = 3.
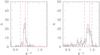 |
Fig. 1 Color histogram for the third nearest (left-hand panel) and third most distant (right-hand panel) clusters. The black (red) histogram is the color distribution in the cluster (control field) line of sight. The vertical red line indicates the expected color of an old passively evolving population, whereas the dashed lines mark the color range where red galaxies are counted. Error bars are |
2. Cluster sample and derivation of cluster richness and mass
Our starting sample considers clusters satisfying the following four conditions (logical “and” operator):
-
1.
Thet are listed a) in the Piffaretti et al.(2011) compilation of X-ray detected clusters and withlog LX ≳ 43.5 erg s-1 in the 0.1–2.4 keV band, where the X-ray threshold value is set to focus on massive clusters; b) in the Planck 2015 Catalog of Sunyaev-Zeldovich Sources (Planck Collaboration XXIV 2015); c) among clusters with at least 35 references in NED2 and | b | > 30 deg; and d) the Abell (1958) clusters with a redshift in NED and | b | > 30 deg.
-
2.
They are well inside the SDSS 12th data release (Alam et al. 2015) footprint, i.e., with centers more than 1 deg away from the SDSS boundary, and not severely masked by bright stars.
-
3.
They have a redshift in the range 0.05 <z< 0.22, the lower redshift boundary being set by the SDSS shredding problem, the high redshift boundary by the SDSS depth.
-
4.
They have low Galactic extinction, defined as Ar< 0.5 mag.
For each of these clusters, we derive n200 (richness) and, in turn, mass M200 strictly following Andreon (2015) to which we refer for details. Basically, we count red members within a specified luminosity range (only galaxies whose passive evolved magnitude is brighter than MV,z = 0 = −20 mag) and color range (within 0.1 redward and 0.2 blueward in g−r of the color–magnitude relation, our operational definition of “red”), as already done for other clusters (e.g., Andreon & Hurn 2010; Andreon 2012; Andreon et al. 2014). For each cluster, we extracted the galaxy catalogs from the SDSS 12th data release (Alam et al. 2015) and we used “cmodel” magnitudes for total galaxy magnitudes and “model” magnitude for colors. Colors are corrected for the color–magnitude slope (but this is a minor correction given the small magnitude range explored). Figure 1 shows, for the third nearest and most distant clusters, the color distribution and the adopted color ranges.
 |
Fig. 2 Spatial distribution of red galaxies of the third nearest (left-hand panel) and third most distant (right-hand panel) clusters. The inner (green) circle marks the derived r200 radius, the outer (red) circle indicates 3 Mpc at the cluster redshift. The cross indicates the cluster center as given in the literature. In the right panel there is another obvious galaxy overdensity, at (α,δ) ≈ (218.4,29.45). |
Some of the red galaxies in the cluster line of sight are actually in the cluster fore/background. The contribution from background galaxies is estimated, as usual, from a reference direction (e.g., Oemler 1974; Andreon et al. 2005). The reference direction is formed by three octants, free of contaminating structures (other clusters) and not badly affected by the SDSS imaging masks, of a corona centered on the studied cluster with inner radius 3 Mpc and outer radius 1 (if z> 0.07) or 2 (otherwise) degree(s), hence fully guaranteeing homogeneous data for cluster and control field. The color distribution of background galaxies, normalized to the cluster solid angle, is shown in Fig. 1 for the two example clusters.
Clusters position, redshift, mass, and cross-identifications.
The centers given in the literature are sometimes imprecise: Abell (1958) estimated them by eye, Planck has a poor point spread function and therefore large (1.5 arcmin) positional errors, and Piffaretti et al. and NED collect positions derived with a variety of methods from various sources sometimes having poor resolution or affected by unrelated point sources (as the Rosat All Sky Survey is). We estimate the cluster center iteratively as the median values of right ascension and declination of red galaxies within an aperture of 1.0 Mpc radius, starting the iteration on the literature center. We then iterate 11 times and take the last value as the final center. The initial and final center are indicated in Fig. 2 for the two example clusters. Andreon (2015) showed that results do not change when using another number of iterations because convergence is achieved earlier, whereas in Sect. 4 we show that the starting position does not matter when using duplicate clusters (objects with center offsets larger than 3 arcmin in different cluster catalogs, and therefore listed twice in our initial list of clusters to be analyzed). We note, however, that X-ray, SZ, and other types of optical centers may legitimately be different from our centers based on galaxy numbers.
As mentioned, the r200 radius is unknown for the studied clusters. We adopt, as proposed in Andreon (2015) for richness and in Kravtsov et al. (2006) for YX, an iterative approach to its determination, which exploits the almost scatter-less nature of the richness-mass relation: a radius r is taken (1.4 Mpc in our case), n (<r) estimated, then r is updated to the value appropriate for the derived richness (i.e., using Eq. (1), and noting that 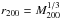 apart from obvious coefficients) and then the process is iterated 3 times. This procedure returns M200 with a total scatter of only 0.16 dex from true (Andreon 2015). The derived r200 is shown (inner circle) for the two example clusters in Fig. 2. In Andreon (2015) we show that adopting a different number of iterations does not change the results because convergence occurs earlier.
apart from obvious coefficients) and then the process is iterated 3 times. This procedure returns M200 with a total scatter of only 0.16 dex from true (Andreon 2015). The derived r200 is shown (inner circle) for the two example clusters in Fig. 2. In Andreon (2015) we show that adopting a different number of iterations does not change the results because convergence occurs earlier.
Since the mass-redshift relation is known to hold for log M200/M⊙> 14 (and we ignore if it holds at lower masses), only clusters more massive than this threshold are kept in the sample. To be more precise, the applied cut is log n200> 21.6. This leave us with a sample of 275 clusters. Figures 3 and 4 show the distribution of these 275 clusters in the sky and in the redshift-mass plane.
 |
Fig. 3 Sky distribution of the studied cluster sample. The SDSS footprint is clearly imprinted. |
 |
Fig. 4 Mass vs. redshift plot of the studied cluster sample. Mass has 0.16 dex errors, omitted to avoid crowding. |
The values of masses derived in this way are listed in Table 1 (entirely available at the CDS and also at http://www.brera.mi.astro.it/~andreon/famous.html with a front-end to the SDSS imaging service). These masses are the prime result of this work: while many literature papers report richnesses for cluster samples, these richnesses have a larger scatter with mass, often with an unknown or problematic mass calibration. The current work instead uses a precisely calibrated richness-mass scaling using a small scatter proxy. Radii can be derived using the M200 definition, whereas the originally measured richnesses are also listed. We remember that richness is within a cylinder of radius r200, whereas mass is deprojected (i.e., within a sphere) because the calibration, i.e., Eq. (1), returns the latter as a function of the former. Table 1 also lists other known identifications of the studied clusters when their reported coordinates are within 3.0 arcmin from the center determined in this work (5.0 armin for Abell 1958 and NED). The angular offset, in arcmin, is reported in parentheses. Table 2 shows the number of clusters in each subsample (Piffaretti et al. 2011; Planck Collaboration XXIV 2015, Abell 1958 and NED) and in their overlaps. Comments to a few individual clusters are listed in Appendix A.
Equation (1), used to estimate mass from richness, has a zero evolutionary term, in agreement with the small and statistically insignificant term determined in Andreon (2015), −0.1 ± 1.0, and with the tighter constraint derived in Andreon & Congdon (2014). A ten times larger term, 1.0, would induces a systematic error of ± 0.03 dex across the studied redshift range, negligible compared to our quoted error 0.16 dex. For this reason, we neglected the −0.1 ± 1.0 evolutionary term found in Andreon (2015).
Number of clusters in each subsample.
2.1. Can we apply the calibrating mass-richness relation to different cluster samples?
The mass calibration in Andreon (2015), i.e., Eq. (1), uses the observed number of galaxies to predict the mass of the cluster, and has been derived for a calibrating sample with a given selection function. One may therefore wonder if this may be used for the current, target, sample with a different selection function. The answer is yes, as we now illustrate. We consider the general case of a proxy x whose observed value has been calibrated against mass M (2)with some scatter σx, where we have absorbed in x the intercept and the possibly non-zero slope as well as the effect of the selection function and steep mass function of the calibrating sample. This relation does not change when another variable yobs showing some scatter σy with log M
(2)with some scatter σx, where we have absorbed in x the intercept and the possibly non-zero slope as well as the effect of the selection function and steep mass function of the calibrating sample. This relation does not change when another variable yobs showing some scatter σy with log M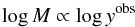 (3)is considered, available, and satisfies some constraints, which means that the cluster is included in the target sample. In fact, for each individual cluster, the relation in Eq. (2) is unaltered, neither the value of xobs nor M changes because another cluster property yobs is measured. The quantity xobs still provides an unbiased estimate of the cluster mass via Eq. (2). This make us free to use Eq. (2) (and Eq. (1), which has the coefficients explicitely given) for a sample selected by another observable3.
(3)is considered, available, and satisfies some constraints, which means that the cluster is included in the target sample. In fact, for each individual cluster, the relation in Eq. (2) is unaltered, neither the value of xobs nor M changes because another cluster property yobs is measured. The quantity xobs still provides an unbiased estimate of the cluster mass via Eq. (2). This make us free to use Eq. (2) (and Eq. (1), which has the coefficients explicitely given) for a sample selected by another observable3.
However, the data cloud satisfying the selection on yobs can obey a different relation as a result of sample selection effects. This can be easily understood when only log M> 15 clusters are kept in the sample, and where mass is estimated from a proxy y with negligible scatter with mass. At low xobs the M−xobs relation would no longer decrease with xobs, but instead would flatten at log M ~ 15 because clusters with log M< 15 are excluded by the selection (and log M ≫ 15 with low xobs become exceptionally rare). Equation (2) still provides an unbiased mass, but because of important selection effects the proxy vs. mass trend of the selected sample will appear to differ from a linear relation with slope one and zero offset, as detailed for the Planck subsample in Appendix B.
We also emphasize that while richness, and therefore richness-based masses, does not depend on the cluster status, other mass proxies assume a hydrostatic or dynamical equilibrium and are affected by an unknown hydrostatic bias. This too may lead to a possible systematic offset, or scatter, with our richness-based masses.
3. Value-added features of the cluster catalog
When deriving cluster masses we performed an extensive set of quality controls. Basically, every plot shown in this paper has been inspected for each and every cluster; SDSS images were inspected as well as individual spectra of the most important galaxies (typically the brightest cluster galaxy). During these controls we noted the following:
-
The cluster redshift listed in the literature (which comes from a variety of sources, including photometric redshift and perhaps sometimes from the redshift of one single galaxy) is inaccurate for 21 clusters by an amount that is easy to note for at least one of two reasons. First, the observed red sequence is not at the expected color. This is illustrated in Fig. 5 for Abell 1182: the observed red sequence is bluer than it should be for a z = 0.166 cluster. Indeed, the cluster is at z = 0.148, based on SDSS spectroscopy, a Δz ~ 0.02 offset from the literature (photometric in this case) redshift. If not corrected for, such a small offset might lead to an overestimation of the cluster mass of 0.09 dex, smaller than our quoted mass error. We note that on some rare occasions redshift offsets as small as Δz = 0.004 (as for Abell 1045, also known as MCXCJ1034.9+3041) have been detected from the color offset. Second, we queried the spectroscopic SDSS database and checked whether the redshift peak of the galaxies within r200 lies at the literature redshift. If not, we updated the literature redshift (an example is shown in Fig. 6, also in this case the redshift change lead to a negligible mass change). Of course, cluster parameters in Table 1 are estimated with the revised redshift, although this is a negligible correction4.

Fig. 5 Color histogram of Abell 1182. Symbols and error bars are as in Fig. 1, but in this figure we adopted the literature redshift z = 0.166 instead of the SDSS spectroscopic-based z = 0.148 we derived, showing how the color of the red sequence may pinpoint an approximate literature redshift.

Fig. 6 Redshift distribution of galaxies projected within the r200 radius of GCwM 170 (alias PSZ2G114.83+57.25, MCXCJ1325.8+5919, Abell 1744). The blue Gaussian is centered on the cluster redshift as given in the literature. The brighter cluster galaxy and five more galaxies are instead at Δz = −0.02 from the reported value.
-
Ten clusters listed in the literature are, on the r200 spatial scale, blends of widely separated (Δv > 1500 km s-1) clusters on the same, or nearby, line(s) of sight. These are recognized for having two red sequences at different colors and, when sufficient spectroscopic data are available, two or more redshift peaks (see Fig. 7 for an example). The ten blends are listed in Table C.1. This list constitutes a further result of this work because these clusters are likely blended in SZ too given the large Planck point spread function and the lack of redshift sensitivity, as well as in weak–lensing analysis (again because of the poor redshift sensitivity of shear). Indeed, one of this pair (Abell750/MS0906) is a known case of lensing blending (Geller et al. 2013). Seven out of ten have been detected via their intracluster medium in emission. Therefore, it does not seem that X-ray selected are immune to projection effects as one often reads in literature papers. It is true and obvious, however, that confusion effects are lower when a smaller aperture is adopted, as is compulsory in X-ray because of the shallowness of the signal at large radii and as is also feasible for richness. In fact, the clusters listed in Table C.1 could be not contaminated on smaller spatial scales, such as those probed by the X-ray emission and also by richness data when adopting a smaller aperture.

Fig. 7 Redshift distribution of galaxies projected within 1.4 Mpc of PSZ2G031.93+78.71. The two redshift peaks are separated by 2400 km s-1.
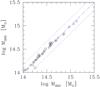
Fig. 8 Comparison of masses for 38 duplicate clusters (40 comparisons) with center coordinates that differ by more than 3 arcmin in different cluster catalogs. The solid line indicates equality, the corridor marks our mass error (±0.16 dex).
-
3.
On three occasions the SDSS photometry is corrupted, probably because of a background subtraction problem. This shows up as a rectangular region in the sky where galaxies are missing or have inappropriate colors for their spectroscopic redshift, notably a red sequence with the wrong color for the SDSS-measured spectroscopic redshift. We found the following clusters affected by the above, and therefore dropped from our list: Abell 1682 (alias MCXCJ1306.9+4633, alias PSZ2G114.99+70.36), Abell 2029 (also noted in Renzini & Andreon 2014), and MCXCJ0751.4+1730 (alias Abell 598).
4. Checks
A number of checks on the calibration and scatter of the richness-mass relation was done in our previous work using sample with well-measured (caustics, hydrostatic, or weak–lensing) masses. In addition to these,
-
38 cluster of our initial list of clusters to be an-alyzed (and with a derived mass larger thanlog M/M⊙> 14) were analyzed twice because they have center coordinates that differ by more than 3 arcmin (175 to 640 kpc, depending on redshift) in different cluster catalogs. These duplicate clusters (listed only once in our final catalog) are useful for estimating the noise introduced by our mass estimate procedure because they use different background areas and different starting centers. Figure 8 compares mass estimates for these duplicate clusters (there are 40 because two clusters appear in three catalogs). We found a scatter between the different mass estimates of the same cluster almost 10 times smaller than our quoted mass uncertainty. Therefore, the centering procedure and background estimates introduce a negligible error, independently confirming the tests in Andreon (2015).
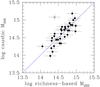
Fig. 9 Richness-based mass vs. caustic mass. The former only uses SDSS photometry, the latter abundant follow-up spectroscopy. The open point is Abell 1068, a cluster with a caustic mass of dubious quality.
-
35 clusters in Table 1 are also in the Hectospec Cluster Surveys (Rines et al. 2013) sample used by Andreon (2015) to calibrate the relation between mass and richness (Eq. (1)). The predicted mass, derived in this paper, vs. the caustic mass listed in Rines et al. (2013) is shown in Fig. 9. The scatter in mass at a given richness is 0.16 dex, i.e., what we reported in a similar analysis based on almost the same cluster sample. The outlier point is Abell 1068, having a caustic mass in disagreement with past mass measurements (see Andreon 2015, for details). This comparison differs from our past one by the use of a different starting center and, most of the times, a different background area. This comparison shows again that the centering procedure and background estimates introduce a negligible error into our masses. Comparison with caustic masses in the Cluster Infall Regions (Rines et al. 2006) shows a larger scatter because of the known lower precision of the centers used there (Andreon & Hurn 2010; Andreon 2015).
-
Out of the 71 clusters with YX-based mass listed in Planck Collaboration XXIX (2014), 11 are also in Table 1. The mass comparison is shown in Fig. 10. There is a good agreement, except for Abell 1795, a cluster with a complex X-ray morphology (a cavity, a cold front, and a cooling wake; see Walker et al. 2014; and Ehlert et al. 2015, and references therein). Although the agreement is promising, we emphasize once more that because the parent sample (the 71 clusters with YX) does not have a selection function, this comparison should be taken with caution, as discussed in detail for the larger sample of the Planck clusters in our Appendix B.
5. Summary and conclusions
In this paper we exploit the tight correlation between richness and mass, calibrated on more than one hundred clusters in Andreon (2015). By simply counting the number of red galaxies brighter than the appropriate limit, accounting for the fore/background, we estimated M200 and r200 of a sample of 275 clusters with log n200 > 21.6 corresponding to log M/M⊙ > 14 in the low-extinction part of the SDSS footprint and with 0.05 < z < 0.22. Position, redshift, and more importantly mass with a 0.16 dex precision is given in Table 1 for the 275 clusters. By adopting a low-scatter well-calibrated mass proxy, this catalog delivers masses whose precision exceeds those available by adopting any of the many proxies, including other richnesses, available in the literature. Our mass measurements are homogeneously derived using homogeneous data, making our catalog different from literature collections of heterogeneous measurements derived with a variety of methods using data of variable quality, such as the Piffaretti et al. (2011) or the Sereno (2015) catalogs.
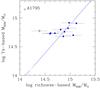 |
Fig. 10 Richness-based mass vs. YX-based mass. The former only uses SDSS photometry, the latter X-ray deep follow-up photometry and spectroscopy. The open point is Abell 1795, a well-known cluster with complex X-ray morphology. |
The derived masses are useful for a variety of purposes: to understand how a cluster property scales with mass, to perform measurements of radial-dependent quantities at a fixed, reference, radius (r200 can be simply derived from the listed M200 values), to normalize measurements whose definition requires knowledge of mass, to combine clusters of different masses, etc. The derived richness-based masses are unaffected by deviation of the cluster from dynamical or hydrostatic equilibrium because the proxy, i.e., the number of red galaxies, is unaffected by these deviations.
During the analysis, a much larger sample of clusters was individually scrutinized: about half of the analyzed clusters turned out to have log M/M⊙ < 14, several clusters were dropped because severely hidden by bright stars, a revision was needed for about a quarter of the sample (clusters with inaccurate redshifts or widely different centers in different catalogs), and we identify 10 “clusters” that are actually blends, on the r200 angular scale, of clusters at different redshifts on almost the same line of sight. These clusters are listed in Table C.1 for later use (other mass proxies are similarly badly affected).
Finally, in Appendix B we compare richness-based to SZ-based masses. To achieve this purpose, we solve the common, and yet unsolved, problem of minimizing the sensitivity of conclusions to the specific overlapping of the considered samples.
Abell 1182 has a mass below the limit for inclusion in the final catalog, and therefore is not listed in Table 1.
Acknowledgments
I thank the referee for the comments emphasizing the strengths of the catalog. Lucia Ballo is thanked for proposing the acronym adopted to name the clusters. This research has made use of the NASA/IPAC Extragalactic Database (NED).
References
- Abell, G. O. 1958, ApJS, 3, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Alam, S., Albareti, F. D., Allen de Prieto, C., et al. 2015, ApJS, 219, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Andreon, S. 2012, A&A, 548, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andreon, S. 2014, A&A, 570, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andreon, S. 2015, A&A, 582, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andreon, S., & Bergé, J. 2012, A&A, 547, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andreon, S., & Congdon, P. 2014, A&A, 568, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andreon, S., & Hurn, M. A. 2010, MNRAS, 404, 1922 [NASA ADS] [Google Scholar]
- Andreon, S., & Hurn, M. A. 2013, Statistical Analysis and Data Mining, 6, 15 [Google Scholar]
- Andreon, S., & Moretti, A. 2011, A&A, 536, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andreon, S., & Weaver, B. 2015, Bayesian methods for the physical sciences, Learning from examples in astronomy and physics (Springer) [Google Scholar]
- Andreon, S., Punzi, G., & Grado, A. 2005, MNRAS, 360, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Andreon, S., Newman, A. B., Trinchieri, G., et al. 2014, A&A, 565, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Becker, M. R., mc Kay, T. A., Koester, B., et al. 2007, ApJ, 669, 905 [NASA ADS] [CrossRef] [Google Scholar]
- Bocquet, S., Saro, A., Mohr, J. J., et al. 2015, ApJ, 799, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Broadhurst, T. J., Taylor, A. N., & Peacock, J. A. 1995, ApJ, 438, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Budzynski, J. M., Koposov, S. E., McCarthy, I. G., & Belokurov, V. 2014, MNRAS, 437, 1362 [NASA ADS] [CrossRef] [Google Scholar]
- Diaferio, A., & Geller, M. J. 1997, ApJ, 481, 633 [NASA ADS] [CrossRef] [Google Scholar]
- Ehlert, S., McDonald, M., David, L. P., Miller, E. D., & Bautz, M. W. 2015, ApJ, 799, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Ford, J., Van Waerbeke, L., Milkeraitis, M., et al. 2015, MNRAS, 447, 1304 [NASA ADS] [CrossRef] [Google Scholar]
- Geller, M. J., Diaferio, A., Rines, K. J., & Serra, A. L. 2013, ApJ, 764, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Hoekstra, H., Mahdavi, A., Babul, A., & Bildfell, C. 2012, MNRAS, 427, 1298 [NASA ADS] [CrossRef] [Google Scholar]
- Israel, H., Reiprich, T. H., Erben, T., et al. 2014, A&A, 564, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jenkins, A., Frenk, C. S., White, S. D. M., et al. 2001, MNRAS, 321, 372 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Johnston, D. E., Sheldon, E. S., Wechsler, R. H., et al. 2007, ArXiv e-prints [arXiv:0709.1159] [Google Scholar]
- Koester, B. P., McKay, T. A., Annis, J., et al. 2007, ApJ, 660, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Kravtsov, A. V., Vikhlinin, A., & Nagai, D. 2006, ApJ, 650, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Murray, S. G., Power, C., & Robotham, A. S. G. 2013, Astron. Comput., 3, 23 [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Oemler, A., Jr. 1974, ApJ, 194, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Oguri, M. 2014, MNRAS, 444, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Okabe, N., & Smith, G. P. 2015, MNRAS, submitted [arXiv:1507.04493] [Google Scholar]
- Piffaretti, R., Arnaud, M., Pratt, G. W., Pointecouteau, E., & Melin, J.-B. 2011, A&A, 534, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIX. 2014, A&A, 571, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIV. 2015, A&A, submitted [arXiv:1502.01597] [Google Scholar]
- Planck Collaboration XXVII. 2016, A&A, in press, DOI: 10.1051/0004-6361/201525823 [Google Scholar]
- Renzini, A., & Andreon, S. 2014, MNRAS, 444, 3581 [NASA ADS] [CrossRef] [Google Scholar]
- Rykoff, E. S., Rozo, E., Busha, M. T., et al. 2014, ApJ, 785, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Rines, K., & Diaferio, A. 2006, AJ, 132, 1275 [NASA ADS] [CrossRef] [Google Scholar]
- Rines, K., Geller, M. J., Diaferio, A., & Kurtz, M. J. 2013, ApJ, 767, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Rozo, E., Rykoff, E. S., Koester, B. P., et al. 2009, ApJ, 703, 601 [NASA ADS] [CrossRef] [Google Scholar]
- Rykoff, E. S., McKay, T. A., Becker, M. R., et al. 2008, ApJ, 675, 1106 [NASA ADS] [CrossRef] [Google Scholar]
- Sheldon, E. S., Johnston, D. E., Masjedi, M., et al. 2009, ApJ, 703, 2232 [NASA ADS] [CrossRef] [Google Scholar]
- Sereno, M. 2015, MNRAS, 450, 3665 [NASA ADS] [CrossRef] [Google Scholar]
- Sereno, M., Ettori, S., & Moscardini, L. 2015, MNRAS, 450, 3649 [NASA ADS] [CrossRef] [Google Scholar]
- Serra, A. L., Diaferio, A., Murante, G., & Borgani, S. 2011, MNRAS, 412, 800 [NASA ADS] [Google Scholar]
- von der Linden, A., Allen, M. T., Applegate, D. E., et al. 2014a, MNRAS, 439, 2 [NASA ADS] [CrossRef] [Google Scholar]
- von der Linden, A., Mantz, A., Allen, S. W., et al. 2014b, MNRAS, 443, 1973 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, S. A., Fabian, A. C., & Kosec, P. 2014, MNRAS, 445, 3444 [NASA ADS] [CrossRef] [Google Scholar]
- Wiesner, M. P., Lin, H., & Soares-Santos, M. 2015, MNRAS, 452, 701 [NASA ADS] [CrossRef] [Google Scholar]
- Zwicky, F., Herzog, E., Wild, P., Karpowicz, M., & Kowal, C. T. 1961, Catalogue of galaxies and of clusters of galaxies (Pasadena: California Institute of Technology) [Google Scholar]
Appendix A: Comments to individual clusters
-
GCwM 14 (Abell 67): possible multiple system
-
GCwM 23 (Abell 115, MCXCJ0055.9+2622, PSZ2G124.20-36.48): possible underestimated mass because of two bright stars
-
GCwM 62 (Abell 665, MCXCJ0830.9+6551, PSZ2G149.75+34.68): bimodal cluster
-
GCwM 92 (Abell 1033, MCXCJ1031.7+3502, PSZ2G189.31+59.24): bimodal cluster
-
GCwM 116 (Abell 1307, MCXCJ1132.8+1428, PSZ2G243.64+67.74): bimodal cluster
-
GCwM 181 (Abell 1800): bimodal cluster
-
GCwM 188 (Abell 1882) and GCwM 189 (MCXCJ1415.2-0030): these two clusters have the same redshift and have centers that are separated by about the estimated r200. If they are one single cluster, its mass is larger than both quoted values: if they are two separate clusters the quoted masses are overestimated.
-
GCwM 27, 99, 140, and 225 do not have any known identification in the input catalogs as a result of extreme recentering offsets.
Appendix B: Selection function, error, scatter, and mass function are important in mass-mass comparisons
 |
Fig. B.1 Richness-based M200 vs. Planck-based M500. Left-hand panel: points are color- and symbol-coded according to redshift. To avoid crowding, the error on abscissa is indicated in the bottom-right corner. Central and Left-hand panels: clusters are coadded in bins of 8. Bins are on the abscissa in the central panel, on the ordinate in the right-hand panel. Errors on the binned axis indicate the bin size, errors on the other axis is the error on the average (the scatter divided by |
It is just beginning to be recognized that the comparison between masses listed in different catalogs may be sensitive to the specific overlapping of the considered subsamples (e.g., Okabe & Smith 2015). Ignoring the selection function of the overlap may lead to claiming the existence of systematic differences between masses measured by different authors/methods/proxies when differences are instead the effect of the selection induced by only considering the overlap between the compared samples. Or, one may also miss an obvious systematic difference cancelled out by a selection effect. In this Appendix we go beyond the common and generic statements above by showing how to account for the selection using the subsample of Planck clusters. We emphasize that a naive comparison, not accounting for selection effects, would have claimed the masses derived here to show systematic differences with those derived by Planck whereas the found behavior is instead a manifestation of selection effects induced by Planck only seeing very massive clusters.
Our analysis makes some simplistic assumptions. In particular, we assume a) uncorrelated error and scatter between richness and YSZ; b) a step function to describe the Planck selection function; and c) that the Planck selection function does not depend on other other astronomical observables (such as Planck exposure time). This suffices to illustrate the dangers of a naive comparison: the observed trend may differ from a one-to-one relation without tilt or bias.
One handred and seven clusters in our sample have a match (<3′ offset) with a cluster in the second Planck catalog of SZ sources (Planck Collaboration XXIV 2015), 61 of which are in the cosmological sample. These clusters are listed in Table 1. These are a random sampling (in mass) of the Planck catalog because we analyzed all Planck clusters inside the SDSS (with 0.05 <z ≲ 0.22, depending on Galactic extinction) without retaining or discarding any of them because of their mass. In fact, our only mass-dependent selection is log M200/M⊙> 14, which is far more liberal than the original Planck catalog, log M500/M⊙ ≳ 14.4 (we also note the higher overdensity used for Planck masses). This can also be seen in Fig. B.1: there are no clusters at log M200/M⊙ ~ 14 because they are below the Planck sensitivity, while many of them are in our sample (see Fig. 4). The studied clusters are precisely in the redshift range where Planck Collaboration XXVII (2016) found a deficit of observed cluster counts for the cosmology (mostly) inferred from the cosmic microwave background (and therefore of utmost interest).
The comparison of the two mass estimates of individual clusters is shown in the left-hand panel of Fig. B.1. The two estimates of mass are correlated, although with some scatter, indicating that both are tracing the cluster mass. The trend identified by the points deviates by the naive expectation, a trend with slope one and intercept zero (depicted as a solid line in the figure) after accounting for differences in the density Δ adopted for the compared masses.
However, the trend (slope, shape, and scatter around the mean) are largely driven by the Planck selection effects (which dominates over our sample selection, as mentioned). This can be easily guessed by splitting the sample into two halves (below and above z = 0.17), and noting that points tend to “turn left” of the M200 = 1.3M500 (slanted) line when approacing the relevant Planck limiting mass. These are the expected (and observed in the case of simulated Euclid weak lensing masses, see Andreon & Bergé 2012) behavior of a sample affected by selection effects, as we now illustrate in detail.
A well-posed comparison of masses must account for the large population gradient (i.e., the cluster mass function), the unavoidable error, or scatter, of the mass proxies (which induces a Malmquist-like bias when joined to the population gradient, Andreon & Hurn 2010; Andreon & Hurn 2013; Andreon & Weaver 2015), and the Planck selection function. In passing, these make the locus of the expected YSZ-mass at a given richness-mass, E(log MPlanck | log Mrichness), different from the locus obtained the other way around, E(log Mrichness | log MPlanck). Furthermore, one of these locii is not even a straight line for input straight relations, as we now show.
The expected YSZ-based mass vs. richness-mass trends has been computed using a simulation, similar to Andreon & Bergé (2012) and Andreon & Congdon (2015): we extracted masses from a Jenkins et al. (2001) mass function at the mean redshift of the clusters entering in each mass bin using the halo mass calculator (Murray et al. 2013). About richness-based masses, their scatter is 0.16 dex and therefore are scattered by such an amount. Real observed data are calibrated on caustic masses to have slope one and zero intercept. Therefore, we also calibrate simulated observed data on true masses (we do not simulate a caustic estimate) in the same way. YSZ-based masses are derived from true M200 masses with M200 = 1.3M500, i.e., what one expects for a Navarro et al. (1997) profile of concentration of about 5 and scattered by 0.06 dex (the scatter of YSZ-based masses, Planck Collaboration XXIX 2014), and then removed from the simulated sample if less massive than the Planck limiting mass at the redshift of interest (e.g., log M500/M⊙ = 14.4 at z ~ 0.15, from Planck Collaboration XXIV 2015). With these simulated masses, we computed the mean YSZ-based mass in small bins of richness-based masses (green line in the central panel of Fig. B.1), E(log MPlanck | log Mrichness), and the other way around: the mean richness-based mass in small bins of YSZ-based mass, E(log Mrichness | log MPlanck) (green line in the right-hand panel of Fig. B.1). At low masses, because of the Planck selection function, E(log MPlanck | log Mrichness) must level off to a value largely set by the Planck selection function, as shown in the central panel by the green curve. The discontinuity at log M/M⊙ ~ 14.3 in the central panel is due to the change of mean redshift, and therefore of Planck limiting mass, of clusters of that richness-based mass. At high masses, E(log MPlanck | log Mrichness) converges to M200 = 1.3M500 (blue line). In the right-hand panel of Fig. B.1, the flattening above is absent because our catalog of richness-based masses is limited to a mass lower than the Planck limit, and therefore the relation is a straight line in the right-hand panel. We predict a bending of this line at log M200/M⊙ ~ 14 in the future when a comparison sample of less massive clusters will be available, precisely as the Planck subsample does at log M500/M⊙ ~ 14.4 when compared to our richness-based masses. This line differs from M200 = 1.3M500 because this relation holds for true values, while we are using observed values5.
We now consider the true data, i.e., the dots in central and right-hand panels of Fig. B.1, that are mean values in bins of 8 clusters in the catalog of the 107 clusters in the overlap of our catalog and the Planck catalog, starting the binning from the most massive cluster. At low masses, they follow the expected behavior, i.e., the green curves computed using the simulated data above, including the point with the lowest mass in the central panel, the latter due to the change of mean redshift. At high masses, the right-hand and central panels show an indication of an underestimation of Planck masses (lower than expectations, i.e., below the green line), in agreement with the mass-dependent bias suggested by von der Linden et al. (2014), Andreon (2015), and Sereno et al. (2015).
A naive inspection of the three panels would have lead to the wrong conclusions. In fact, masses deviate from the naive expectation (M200 = 1.3M500, the blue line, plotted in two of the panels) at low masses in all panels; however, this expectation is inappropriate for these data. An orthogonal or bisector fit would have incorrectly returned an agreement at high masses using the individual data points (left-hand panel), a mass tilt at low masses if E(log MPlanck | log Mrichness) were used (central panel), and an agreement at high masses if E(log Mrichness | log MPlanck) were used. To summarize, fitting the trend of two estimates of mass, or determining a mass bias, it is not just a matter of fitting the data cloud with an off-the-shelf (linear) fitter, unless the selection function is ignorable and the scatter/errors of the masses are negligible.
The use of the cosmological sample (61 clusters) does not alter our conclusions above, i.e., there is agreement with Planck masses at low masses only and the data trend may well be different from naive expectations.
We emphasize that for Planck clusters the expected trend can be computed because both types of masses are homogeneously measured and because of the controlled nature of the subsample being studied, having a known selection function. Such predictions, necessary to discriminate real trends from selection effects, are not possible with samples with unknown selection functions or with non-homogeneously measured masses, such as the current sample of clusters with weak-lensing masses.
Appendix C: List of blended clusters
Clusters blended on the r200 spatial scale.
All Tables
All Figures
 |
Fig. 1 Color histogram for the third nearest (left-hand panel) and third most distant (right-hand panel) clusters. The black (red) histogram is the color distribution in the cluster (control field) line of sight. The vertical red line indicates the expected color of an old passively evolving population, whereas the dashed lines mark the color range where red galaxies are counted. Error bars are |
| In the text | |
 |
Fig. 2 Spatial distribution of red galaxies of the third nearest (left-hand panel) and third most distant (right-hand panel) clusters. The inner (green) circle marks the derived r200 radius, the outer (red) circle indicates 3 Mpc at the cluster redshift. The cross indicates the cluster center as given in the literature. In the right panel there is another obvious galaxy overdensity, at (α,δ) ≈ (218.4,29.45). |
| In the text | |
 |
Fig. 3 Sky distribution of the studied cluster sample. The SDSS footprint is clearly imprinted. |
| In the text | |
 |
Fig. 4 Mass vs. redshift plot of the studied cluster sample. Mass has 0.16 dex errors, omitted to avoid crowding. |
| In the text | |
 |
Fig. 5 Color histogram of Abell 1182. Symbols and error bars are as in Fig. 1, but in this figure we adopted the literature redshift z = 0.166 instead of the SDSS spectroscopic-based z = 0.148 we derived, showing how the color of the red sequence may pinpoint an approximate literature redshift. |
| In the text | |
 |
Fig. 6 Redshift distribution of galaxies projected within the r200 radius of GCwM 170 (alias PSZ2G114.83+57.25, MCXCJ1325.8+5919, Abell 1744). The blue Gaussian is centered on the cluster redshift as given in the literature. The brighter cluster galaxy and five more galaxies are instead at Δz = −0.02 from the reported value. |
| In the text | |
 |
Fig. 7 Redshift distribution of galaxies projected within 1.4 Mpc of PSZ2G031.93+78.71. The two redshift peaks are separated by 2400 km s-1. |
| In the text | |
 |
Fig. 8 Comparison of masses for 38 duplicate clusters (40 comparisons) with center coordinates that differ by more than 3 arcmin in different cluster catalogs. The solid line indicates equality, the corridor marks our mass error (±0.16 dex). |
| In the text | |
 |
Fig. 9 Richness-based mass vs. caustic mass. The former only uses SDSS photometry, the latter abundant follow-up spectroscopy. The open point is Abell 1068, a cluster with a caustic mass of dubious quality. |
| In the text | |
 |
Fig. 10 Richness-based mass vs. YX-based mass. The former only uses SDSS photometry, the latter X-ray deep follow-up photometry and spectroscopy. The open point is Abell 1795, a well-known cluster with complex X-ray morphology. |
| In the text | |
 |
Fig. B.1 Richness-based M200 vs. Planck-based M500. Left-hand panel: points are color- and symbol-coded according to redshift. To avoid crowding, the error on abscissa is indicated in the bottom-right corner. Central and Left-hand panels: clusters are coadded in bins of 8. Bins are on the abscissa in the central panel, on the ordinate in the right-hand panel. Errors on the binned axis indicate the bin size, errors on the other axis is the error on the average (the scatter divided by |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.