| Issue |
A&A
Volume 587, March 2016
|
|
|---|---|---|
| Article Number | A140 | |
| Number of page(s) | 7 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201526083 | |
| Published online | 03 March 2016 | |
Orbits of maser stars in the rotating Galactic bar
Sterrewacht Leiden, PO Box 9513, 2300 RA Leiden, The Netherlands
Received: 12 March 2015
Accepted: 12 November 2015
Maser stars have been found with radial velocities up to +350 km s-1 and down to −350 km s-1 and exclusively within a few degrees from the Galactic centre. They form two spatially separated streams: one stream is at positive longitudes and consists of stars going away from us and the other is at negative longitudes consisting of stars approaching us. I show that closed orbits in a simple mass model for the bar explain quantitatively the existence of the two streams and the velocities observed. The mass of the bar is estimated on dynamical grounds: 3 × 1010 Msun.
Key words: Galaxy: bulge / Galaxy: center / Galaxy: kinematics and dynamics
© ESO, 2016
1. Introduction; Minkowski’s problem
Fifty years ago Minkowski (1965) published a review paper on the Galactic distribution of planetary nebulae (= PNe). Their distribution in longitude, latitude and radial velocity proved that almost all are part of the rotating Galactic disk. One thus expects all objects to have radial velocities lower than the maximum velocity of rotation, that is, below 220 km s-1 (Sofue 2013). Minkowski found contrary evidence: close to the Galactic centre the radial velocities of the PNe rose to + 270 km s-1. This is Minkowski’s problem: an unkown force near the Galactic centre accelerates the PNe to high velocities. PNe are faint objects and their detection is seriously hampered by interstellar extinction. This is not so for their close relatives, the maser stars, the first of which was found in 1968. They are detected at radio wavelengths independently of interstellar extinction. In 1975 Baud et al. (1975) reported the detection of a maser star at 20 arcmin from the Galactic centre and with a radial velocity of −340 km s-1. Over 1000 maser stars have been detected since then and almost all lie in the directions of the inner part of our Galaxy. In Table 1 I have listed 52 maser stars with velocities greater than +220 km s-1 or less than −220 km s-1. Minkowski’s problem still exists and the reasons why many stars have a velocity so high is unknown. In this paper, I propose that the rotating Galactic bar offers the solution: the stars follow elongated orbits inside the bar and they reach a high velocity when they pass the Galactic centre.
In several studies Maartje Sevenster has advocated the presence of the maser stars in the Galactic bar (Sevenster et al. 1999 and Sevenster 1999). This paper is a continuation of her work.
2. Distribution of maser stars in Galactic longitude and latitude and in radial velocity
Figure 1 shows the Galactic longitude and latitude (l,b)-distribution of maser stars and Fig. 2 the corresponding longitude–radial velocity (l,vrad)-diagram. The black points have been taken from the OH-maser star surveys by Sevenster et al. (1997a), Sevenster et al. (1997b) and Sevenster et al. (2001) that cover the northern and the southern sky using the VLA (Very Large Array) and the ATCA (Australia Telescope Compact Array), respectively. These surveys have been made under uniform conditions with respect to coverage on the sky, velocity range and sensitivity and are the best suited for statistical considerations. I have added 52 maser stars with a radial velocity | vrad | ≥ 220 km s-1 from Table 1. I will call these the high-velocity stars. In Fig. 2, I have also added groups of stars with velocities greater than + 150 km s-1 or less than −150 km s-1 from a survey by Babusiaux et al. (2014). Figure 3 shows the distribution in l and b of the high-velocity stars; in red the stars going away from us, in blue those approaching us.
Maser stars with vrad ≥ + 220 km s-1 or vrad ≤ −220 km s-1.
 |
Fig. 1 Distribution in longitude and latitude of the OH-maser stars in the surveys of Sevenster et al. The observations were limited to | b | ≤ 3deg. In red are shown the maser stars with a radial velocity | vrad | ≥ 220 km s-1 taken from Sevenster et al. (1997a,b, 2001) and from other surveys; see Table 1. |
Several comments in Figs. 1–3 are important. First, all high-velocity objects have been detected only in directions within 10 deg of the centre of our Galaxy. This is not a selection effect. For example, Eder et al. (1988) discovered 169 OH-maser stars more than 10deg from our Galactic centre and found no high-velocity objects in their velocity window with a width of 900 km s-1. In her survey Sevenster searched the area −45 deg < l < + 45 deg, −3 deg < b < + 3 deg at velocities between −300 kms and +400 km s-1 with the VLA and with the ATCA; she used a homogeneous detection limit and found high-velocity stars only near the Galactic centre. te Lintel Hekkert et al. (1991) searched for OH-maser stars in IRAS point sources over the northern and southern sky and detected 738 maser stars; only five had a high velocity and they all appear in Table 1. The same holds for the SiO-maser surveys by Messineo and by Deguchi, Fujii, Izumiura, and other Japanese observers.
Second, there is maximum (+ 350 km s-1) and a minimum radial velocity (−350 km s-1). These limits have not been caused by observational selection. Stars with velocities up to + 400 km s-1 or down to −400 km s-1 would have been found, if they existed.
Third, the average longitude of the red points in Fig. 3 equals +2.63 and the standard deviation is 2.93; for the blue points these values are −2.27 and 2.27: the red points are systematically at positive longitudes and the blue points at negative longitudes. There are two streams of high-velocity stars, one going away, the other coming. The trafic keeps left, British rule.
Fourth, the distribution in latitude ⟨ b ⟩ = −0.104 and the rms value =±1.33. This distribution is wider than that of the ensemble of all black points in Fig. 1. The mechanism that binds the stars to the Galactic plane is weaker at the Galactic centre.
There is no indication that the two streams seen in Fig. 3 are temporary: they must be the result of an equilibrium. Therefore the two streams are part of a closed loop of high-velocity stars. Finding the orbits of these stars is the goal of this paper.
 |
Fig. 2 Distribution in longitude and in radial velocity of the OH-maser stars from the surveys by Sevenster (black). High-velocity maser stars from various surveys (see Table 1) (red). Red squares indicate the number of stars in velocity intervals from a near-infrared survey by Babusiaux et al. (2014). The two horizontal red lines indicate the velocity limits of the high-velocity stars. |
 |
Fig. 3 Distribution in longitude and latitude of the high-velocity maser stars. The redshifted stars are largely at positive longitudes, the blueshifted stars at negative longitudes. Two horizontal lines at b = ± 4deg outline the search area. |
Maser stars both in OH and in SiO.
3. The nature of maser stars and of planetary nebulae
The first maser stars were detected by Wilson & Barrett (1968) who recorded an emission line at 1612 MHz from a few infrared stars in a survey by Neugebauer et al. (1965). Later it appeared that H2O- and SiO-maser stars also exist. A review of the early history of the detection of maser stars is given by Habing (1996). I will use the OH- and SiO-maser stars because they appear to belong to the same Galactic population. I will not use H2O-masers; surveys for these stars have been limited and samples are polluted with star formation masers, a problem that does not happen for OH- or for SiO-maser stars.
The maser star is a single star of intermediate mass during the last episode of its AGB-stage (see Habing & Olofsson 2003). In a short span of time the star throws off most of its envelope; the short duration of this episode makes the maser a rare phenomenon although the star itself is quite common. The star is surrounded by a dense circumstellar envelope. Solid particles and molecules form in this envelope. The solid particles convert all the stellar radiation into infrared photons and the simultaneous presence of an intense infrared field and of molecules leads to the maser amplification. Messineo (2004) used infrared data from various surveys and determined the interstellar extinction and the bolometric magnitude of the SiO-maser stars near the Galactic centre: −6 ≤ Mbol ≤ −4 with a peak at −5. Comparing this range in luminosity with model calculations led her to the conclusion that maser stars intially have a mass of 1 to 5 Msun and an estimated age between 0.8 and 5 Gyr.
In spite of their very different appearance PNe are astrophysically the same as maser stars but slightly more evolved. PNe data confirm the distribution in velocity and longitude obtained from the maser stars. Because the PNe sample is very incomplete close to the Galactic centre I will not discuss them further.
4. The effect of the Galactic bar
4.1. Evidence for a bar
The existence of a Galactic bar was first suggested by de Vaucouleurs (1964) as an explanation for radial velocities in the 21 cm line in the inner Milky Way, velocities that could not be explained by Galactic rotation. In the 1990s the discussion was resumed when much more detailed but similar measurements had been made in CO. This led to the conclusion that a bar had to be present (Binney et al. 1991; Englmaier & Gerhard 1999). Independent information came from asymmetries in the distribution of stars in the inner Galaxy (Whitelock & Catchpole 1992; Sevenster 1999). Surface photometry of the inner Galaxy in the infrared showed structures very suggestive of the existence of a bar, first the data of a japanese balloon survey (Blitz & Spergel 1991) and later superior COBE and Spitzer data (Binney et al. 1991; Bissantz & Gerhard 2002; Benjamin et al. 2005; Churchwell et al. 2009). Star counts have been used as well (e.g. Robin et al. 2012). The possibility of using “red clump” stars as objects with a well-known absolute magnitude makes star counts an attractive tool for the analysis (e.g. Wegg & Gerhard 2013; see their Fig. 13). All these attempts strongly support the existence of a bar in our Galaxy. Quantitatively uncertainty remains about the mass of the bar and how it joins the Galactic disk.
Hammersley et al. (2000) proposed what become known as the long bar with a length of 4 kpc and with an angle of 45deg to the Sun-Galactic centre line. His configuration of two different, partially coincident bars is dynamically unstable and that has led Martinez-Valpuesta & Gerhard (2011) to the explanation that the long bar is an extension of the main bar at both ends and thus it consists of the parts that connect the main bar to the molecular ring. A remarkable finding is the existence of star forming molecular clouds at each end of the extension (Hammersley et al. 1994; Ramírez Alegría et al. 2014).
4.2. A simple model for the stellar orbits in the gravitational potential of a rotating bar
I will use kpc, 106 yr (Myr) and solar mass, Msun, as units of distance, time and mass. In these units the gravitational constant, G, has the value 4.514 × 10-12 kpc3 Myr-2 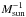 . A velocity of 1 kpc/Myr = 978 km s-1. The long axis of the bar is along the y-axis and it makes an angle β with the line Sun-Galactic centre. The Sun is located at (− rGCsinβ,rGCcosβ). The velocity of the Sun will be (vsuncosβ,vsunsinβ). I will use β = 25deg, rGC = 8.34 kpc and vsun = 255 km s-1 (Reid et al. 2014). The angular velocity of the bar, Ω will be taken equal to the velocity of the bar at its end points (220 km s-1) divided by the length of the bar (3 kpc).Thus Ω = 73 km s-1/kpc = 0.075 Mpc-1. The geometry used for the model calculations is shown in Fig. 4. Changes in the basic parameters by up to 20% do not affect the main conclusion.
. A velocity of 1 kpc/Myr = 978 km s-1. The long axis of the bar is along the y-axis and it makes an angle β with the line Sun-Galactic centre. The Sun is located at (− rGCsinβ,rGCcosβ). The velocity of the Sun will be (vsuncosβ,vsunsinβ). I will use β = 25deg, rGC = 8.34 kpc and vsun = 255 km s-1 (Reid et al. 2014). The angular velocity of the bar, Ω will be taken equal to the velocity of the bar at its end points (220 km s-1) divided by the length of the bar (3 kpc).Thus Ω = 73 km s-1/kpc = 0.075 Mpc-1. The geometry used for the model calculations is shown in Fig. 4. Changes in the basic parameters by up to 20% do not affect the main conclusion.
 |
Fig. 4 Geometry adopted in the model calculations. GC stands for Galactic centre. The bar is along the y-axis. The outline of the ellipsoid (the bar) is indicated by a black ellipse. In red inside the bar is the largest possible elliptical orbit (see text). The angle P-Sun-Star, α, is found by the relation asinα = ( | xs−xz | ) /d, where d is the distance between the Sun and the star. The angle P-Sun-GC is β. The longitude l = α−β. The Sun is located at (−8.0sinβ, 8.0cosβ kpc). The maximum and minimum velocity will be reached where the orbit cuts the x-axis. The units in x and in y are kpc. |
The velocity perpendicular to the Galactic plane will influence the radial velocity measurement of a star. The observations (Fig. 1), however, show that the amplitude of the oscillations in z is at most a few hundred parsecs and therefore the effect on the radial velocities is negligible (<200/8000). Consequently I put everywhere z = 0. The motion in this ellipsoid is a two-dimensional (x,y)-problem.
The bar will be approximated by a prolate spheroid of constant density ρ and with axes (ax,ay,az), where ax = az; the eccentricity equals 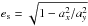 . The bar rotates at an angular frequency Ω.
. The bar rotates at an angular frequency Ω.
Inside the ellipsoid the gravitational potential is given by Binney & Tremaine (1987): 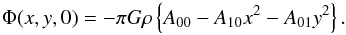 (1)Here A00,A10,A01 are functions of e; the expressions are given in Table 2.1 in Binney & Tremaine (1987).
(1)Here A00,A10,A01 are functions of e; the expressions are given in Table 2.1 in Binney & Tremaine (1987).
The orbits are described by the following two equations: ![\begin{eqnarray} &&\ddot{x}=-{{\partial\Phi}\over{\partial x}} + \Omega^2 x -2\Omega\dot{y} \\[2mm] &&\ddot{y}=-{{\partial\Phi}\over{\partial y}} + \Omega^2 y +2\Omega\dot{x}. \end{eqnarray}](/articles/aa/full_html/2016/03/aa26083-15/aa26083-15-eq69.png) The two equations are coupled through the Coriolis accelaration (−2Ωẏ, + 2Ωẋ). Therefore the free fall of the stars through the bar cannot be one-dimensional, i.e. linear. Next, observe that because
The two equations are coupled through the Coriolis accelaration (−2Ωẏ, + 2Ωẋ). Therefore the free fall of the stars through the bar cannot be one-dimensional, i.e. linear. Next, observe that because 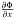 and
and 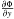 are linear in x and y, all terms in both equations are linear in x and y and their derivatives. This suggests that sinusoidal orbits may be a solution to the equations. Define Bx ≡ 2πGρAx and By ≡ 2πGρAy and substitute x = x0sinωt and y = y0cosωt in the equations of motions. It follows that
are linear in x and y, all terms in both equations are linear in x and y and their derivatives. This suggests that sinusoidal orbits may be a solution to the equations. Define Bx ≡ 2πGρAx and By ≡ 2πGρAy and substitute x = x0sinωt and y = y0cosωt in the equations of motions. It follows that ![\begin{eqnarray} && \omega^2 x_0 -B_x x_0 + \Omega^2 x_0 + 2\Omega \omega y_0 = 0 \\[2mm] &&\omega^2 y_0 -B_y y_0 + \Omega^2 y_0 + 2\Omega \omega x_0 = 0 . \end{eqnarray}](/articles/aa/full_html/2016/03/aa26083-15/aa26083-15-eq77.png) These equations have the trivial (and useless) solution x0 = y0 = 0. A non-zero solution exists if ω and f ≡ y0/x0 fulfil the equations
These equations have the trivial (and useless) solution x0 = y0 = 0. A non-zero solution exists if ω and f ≡ y0/x0 fulfil the equations ![\begin{eqnarray} &&\omega^2-B_x+\Omega^2+2\Omega\omega f =0 \\[2mm] &&\omega^2-B_y+\Omega^2+2\Omega\omega f^{-1} =0. \end{eqnarray}](/articles/aa/full_html/2016/03/aa26083-15/aa26083-15-eq81.png) The orbits are ellipses with axes (x0,y0), where x0 = y0/f; they all have the eccentricity
The orbits are ellipses with axes (x0,y0), where x0 = y0/f; they all have the eccentricity 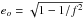 . For an ellipsoidal mass distribution with eccentricity es and density ρ, Eqs. (6) and (7) can be solved for f and ω. One can choose freely either x0 or y0, provided that x0<ax and y0<ay; thereafter the orbit is fixed. All ellipses corresponding to one value of (f,ω) form a family with the same eccentricity and orientation. The maximum velocity in the x- and y-directions is reached at x = 0 and y = 0, respectively, and is given by ωx0 and ωy0. Stars in an orbit with ω> 0 move in the clockwise direction, and in the other direction when ω< 0.
. For an ellipsoidal mass distribution with eccentricity es and density ρ, Eqs. (6) and (7) can be solved for f and ω. One can choose freely either x0 or y0, provided that x0<ax and y0<ay; thereafter the orbit is fixed. All ellipses corresponding to one value of (f,ω) form a family with the same eccentricity and orientation. The maximum velocity in the x- and y-directions is reached at x = 0 and y = 0, respectively, and is given by ωx0 and ωy0. Stars in an orbit with ω> 0 move in the clockwise direction, and in the other direction when ω< 0.
If f = 1 the ellipse becomes a circle. Then 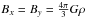 . Thus
. Thus 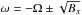 . In all practical cases Bx ≥ Ω2 and thus two values are found for ω, one larger than 0 and one smaller than 0, corresponding to either the clockwise or the anticlockwise direction.
. In all practical cases Bx ≥ Ω2 and thus two values are found for ω, one larger than 0 and one smaller than 0, corresponding to either the clockwise or the anticlockwise direction.
Graphs in f and ω show that there are four solutions (f,ω) that form two pairs, (f1,ω1), (− f1,−ω1) and (f2,ω2),(− f2,−ω2). Each pair represents the same orbit. One of the two values of f, say f1, is larger than 1 and corresponds to orbits elongated in the y-direction; the other, f2, has a value between 1 and 0 and corresponds to an orbit extended in the x-direction. The clockwise or anticlockwise direction is dictated by the value of f: if f> 1 the maximum velocity in the y-direction, ωy0, is f times the maximum in the x-direction and the coriolis-acceleration then decides in favour of the clockwise rotation. By the same argument the rotation will be anticlockwise if f< 1. One is reminded of the discussion on x1 and x2 orbits (Binney & Tremaine 1987, Figs. 3–14). Figure 5 shows orbits of different eccentricity inside the bar.
The calculations give us the values of ẋ and ẏ. To transform these into (vrad,vperp) (i) the rotational velocity of the bar (Δvx = Ωy) was added; (ii) the velocity of the Sun (vx = vsunsinβ,vy = vsuncosβ) was subtracted and (iii) the coordinates were rotated over an angle α (see Fig. 4). Figure 6 shows the traces in the lvrad-plane of the orbits from Table 3. From es = 0.4 to 0.95 the traces slowly increase in width but when the eccentricity reaches 0.99 there is a fundamental change in the loop: it widens strongly at positive longitude precisely as is observed (see Figs. 6 and 7).
4.3. Derivation of the orbits of the high-velocity stars
The elliptical orbits found in the preceding section directly explain the separation between the red and blue points in Fig. 3: the existence of the two streams. I thus look for orbits that pass the x-axis at x = ± x0 = ± 0.2 kpc with a velocity ẏ = 300 km s-1. I use es as free parameter and calculate the parameters ρ,f,ω for different values. The results are in Table 3 and in Fig. 5. In addition I show the trace of each orbit in the lvrad-diagram (see Fig. 6).
The remaining problem is to choose the right orbit from this table and these figures. Remarkably, three different arguments lead to the conclusion that the correct orbit is that with the highest eccentricity (es = 0.99). The first argument is from Fig. 2: it shows that the effect of the bar is already seen at longitude +12deg and since x0 = 0.2 and y0 = rGCsin12deg / sin143deg = 2.8 kpc it follows that f has to to be about 14.
The second argument comes from comparing Figs. 6 and 2: only the loop belonging to em = 0.99 is broad enough to include the stars of the highest velocity at each longitude.
Orbits inside the spheroid.
 |
Fig. 5 Orbits of different eccentricity but all passing the x-axis at x = ±0.2 with a velocity ẏ = 300 km s-1 using the parameters in Table 3; this table also gives the colour of each orbit. All orbits are in the clockwise direction. The units in x and in y are kpc. |
 |
Fig. 6 Traces in the lvrad-diagram of orbits of different eccentricity but all passing the x-axis at x = ± 0.2 with a velocity ẏ = 300 km s-1. The colouring is the same as in Fig. 5. |
 |
Fig. 7 (lvrad)-diagram with in green the largest possible orbit (x0 = 0, y0 = 3.0) in a model with dimensions (0.4,3,0.4). The symbols are the same as in Fig. 2. The density in the bar ρ = 15Msun pc-3, Ω = 0.074 Myr-1, β = 25deg. |
4.4. Bar and bulge
So far I have treated the bar as an object with a gravitational potential of its own. Clearly there are other main Galactic components to be considered. Therefore, I included a point source at the Galactic centre with mass Mps and a Galactic bulge with mass Mb. I used a Ferrer ellipsoid of rank n = 1 in which the density is constant on ellipsoids and where the density along the y-axis varies as 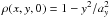 . The gravitational potential is therefore
. The gravitational potential is therefore 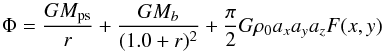 (8)where
(8)where 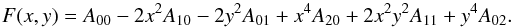 (9)The constants A00, etc. are integrals over (x,y) and are defined in Binney and Tremaine. I took Mps = 2 × 108Msun, Mb = 1 × 1010Msun and (ax,ay,az) = (0.4,3.0,0.4). There exists no analytic solution to the equations of motion and I therefore solved these numerically using a Runge-Kutta approximation. Figure 8 shows the lvrad-diagram of a calculation with the parameters as given above and with a central density in the Ferrer Bar of 16 Msun/ pc-3. The orbit is that of a star that starts at (x,y) = (0,3.0) with a velocity (vx,vy) = (0,0).
(9)The constants A00, etc. are integrals over (x,y) and are defined in Binney and Tremaine. I took Mps = 2 × 108Msun, Mb = 1 × 1010Msun and (ax,ay,az) = (0.4,3.0,0.4). There exists no analytic solution to the equations of motion and I therefore solved these numerically using a Runge-Kutta approximation. Figure 8 shows the lvrad-diagram of a calculation with the parameters as given above and with a central density in the Ferrer Bar of 16 Msun/ pc-3. The orbit is that of a star that starts at (x,y) = (0,3.0) with a velocity (vx,vy) = (0,0).
The main conclusion is that the presence of a bulge and a point source at the Galactic centre does not affect the main conclusion: the high velocities of the maser stars are nicely explained by a rotating bar.
 |
Fig. 8 Orbit of a star in the longitude-velocity diagram that starts at (x,y) = (0.0,3.0) with a velocity(vx,vy) = (0.0,0.0) in the gravitational field of a rotating bar plus the bulge plus a point source at the Galactic centre – see text (green). Maser stars from Sevenster’s survey and in red the high-velocity maser stars from Table 1 (black). |
5. Discussion and conclusion
The best model distribution has a high eccentricity, em = 0.99. The ellipsoid in which the closed loop is embedded has dimensions of (ax,ay,az = 0.4,3.0,0.4). This is in between two current but different bar models: the Galactic bar and the long bar (see e.g. Monari et al. 2014). The elongation (7:1) is high, but as argued above, the elongation is required by the observations because the maximum and the minimum radial velocity are close to l = 0deg. It is quite possible that the bar discussed here is a high-density ridge in a wider bar. Model calculations in a thicker model (1.0, 3.0, 1.0) show that the longitude of the maximum (minimum) radial velocity is unacceptably far away from l = 0deg. I also tested the model of a “demi-baguette” with dimensions (ax,ay,az) = (0.5,1.5,0.5). The resulting (l,vrad)-curve has the right range in vrad but the width of the loop is too small.
Where did these maser stars form? There is no evidence of star forming regions along the bar; also, numerical simulations imply that the bar was formed early in the history of our Galaxy. In the corners of the bulge the bulge stars appear indeed to be 10 Gyr old (e.g.Valenti et al. 2013). Maser stars are at most 5 Gyr old (Messineo 2004); where were they born? I suggest that this happened in the star forming region at each end of the bar (Hammersley et al. 1994; Ramírez Alegría et al. 2014). Martinez-Valpuesta & Gerhard (2011) and Gerhard & Wegg (2014) argued that there is a “bridge” between the molecular ring and the bar. In Fig. 8 the stellar velocities at the tips of the bar are zero in the frame of the bar and thus equal to those of the star forming regions there. This suggests that the stars that formed in the molecular ring at the end point of the bar may sometimes have wandered into the bar and in due time evolved into maser stars.
Maser stars develop into planetary nebulae and one expects the (lvrad)-diagram of the planetary nebulae to be the same as that of the maser stars. This is indeed the case, although the sample of PNe misses many objects at low Galactic latitude because of foreground extinction.
The mass of the bar in the best model is 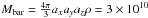 Msun. Dwek et al. (1995) analysed the infrared photometrical contours of the bulge of our Milky Way as measured by COBE/DIRBE and find for the bulge Lbar = 5 × 109Lsun, and thus M/L = 30 / 5.3 = 5.7. This value is uncertain because it is not clear that the bulge seen by COBE/DIRBE is the same as the bar I used here.
Msun. Dwek et al. (1995) analysed the infrared photometrical contours of the bulge of our Milky Way as measured by COBE/DIRBE and find for the bulge Lbar = 5 × 109Lsun, and thus M/L = 30 / 5.3 = 5.7. This value is uncertain because it is not clear that the bulge seen by COBE/DIRBE is the same as the bar I used here.
We will learn much more about the velocities of the maser stars discussed in this paper when their proper motions are derived. VLBI techniques allow a sufficiently accurate determination of maser positions with respect to quasars so that proper motions can be detected after a few years. This is the goal of the BAaDE project, a survey aiming to map the positions and velocities of up to 34 000 SiO maser stars in the Galactic bulge and inner Galaxy1.
Acknowledgments
I especially thank Anders Winnberg with whom I have collaborated very productively for almost 40 years on the properties of OH-maser stars, with the emphasis on their Galactic distribution. I thank Koen Kuijken and Huib Jan van Langevelde for reading successive drafts as this paper developed and I thank the latter for involving me in the BAaDE project. Piet van de Kruit and Amina Helmi asked critical and fruitful questions. I thank David Jansen and my son Martijn for software help with the figures.
References
- Babusiaux, C., Katz, D., Hill, V., et al. 2014, A&A, 563, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baud, B., Habing, H. J., Osullivan, J. D., Winnberg, A., & Matthews, H. E. 1975, Nature, 258, 406 [NASA ADS] [CrossRef] [Google Scholar]
- Benjamin, R. A., Churchwell, E., Babler, B. L., et al. 2005, ApJ, 630, L149 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J., & Tremaine, S. 1987, Galactic Dynamics (Princeton University Press) [Google Scholar]
- Binney, J., Gerhard, O. E., Stark, A. A., Bally, J., & Uchida, K. I. 1991, MNRAS, 252, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Bissantz, N., & Gerhard, O. 2002, MNRAS, 330, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Blitz, L., & Spergel, D. N. 1991, ApJ, 379, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Churchwell, E., Babler, B. L., Meade, M. R., et al. 2009, PASP, 121, 213 [NASA ADS] [CrossRef] [Google Scholar]
- de Vaucouleurs, G. 1964, in The Galaxy and the Magellanic Clouds, ed. F. J. Kerr, IAU Symp., 20, 195 [Google Scholar]
- Deguchi, S., Fujii, T., Izumiura, H., et al. 2000a, ApJS, 130, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Deguchi, S., Fujii, T., Izumiura, H., et al. 2000b, ApJS, 128, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Deguchi, S., Fujii, T., Miyoshi, M., & Nakashima, J.-I. 2002, PASJ, 54, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Deguchi, S., Fujii, T., Glass, I. S., et al. 2004, PASJ, 56, 765 [NASA ADS] [Google Scholar]
- Deguchi, S., Fujii, T., Ita, Y., et al. 2007, PASJ, 59, 559 [NASA ADS] [Google Scholar]
- Dwek, E., Arendt, R. G., Hauser, M. G., et al. 1995, ApJ, 445, 716 [CrossRef] [Google Scholar]
- Eder, J., Lewis, B. M., & Terzian, Y. 1988, ApJS, 66, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Englmaier, P., & Gerhard, O. 1999, MNRAS, 304, 512 [NASA ADS] [CrossRef] [Google Scholar]
- Fujii, T., Deguchi, S., Ita, Y., et al. 2006, PASJ, 58, 529 [NASA ADS] [Google Scholar]
- Gerhard, O., & Wegg, C. 2014, ArXiv e-prints [arXiv:1408.0219] [Google Scholar]
- Habing, H. J. 1996, A&ARv, 7, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Habing, H. J., & Olofsson, H., 2003, Asymptotic giant branch stars, Astron. Astrophys. Library (New-York, Berlin: Springer) [Google Scholar]
- Habing, H. J., Olnon, F. M., Winnberg, A., Matthews, H. E., & Baud, B. 1983, A&A, 128, 230 [NASA ADS] [Google Scholar]
- Hammersley, P. L., Garzon, F., Mahoney, T., & Calbet, X. 1994, MNRAS, 269, 753 [NASA ADS] [CrossRef] [Google Scholar]
- Hammersley, P. L., Garzón, F., Mahoney, T. J., López-Corredoira, M., & Torres, M. A. P. 2000, MNRAS, 317, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Imai, H., Deguchi, S., Fujii, T., et al. 2002, PASJ, 54, L19 [NASA ADS] [Google Scholar]
- Izumiura, H., Deguchi, S., Hashimoto, O., et al. 1995, ApJ, 453, 837 [NASA ADS] [CrossRef] [Google Scholar]
- Martinez-Valpuesta, I., & Gerhard, O. 2011, ApJ, 734, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Messineo, M. 2004, Ph.D. Thesis, Leiden University [Google Scholar]
- Messineo, M., Habing, H. J., Sjouwerman, L. O., Omont, A., & Menten, K. M. 2002, A&A, 393, 115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minkowski, R. 1965, in Galactic Structure, eds. A. Blaauw, & M. Schmidt, 321 [Google Scholar]
- Miyazaki, A., Deguchi, S., Tsuboi, M., Kasuga, T., & Takano, S. 2001, PASJ, 53, 501 [NASA ADS] [Google Scholar]
- Monari, G., Helmi, A., Antoja, T., & Steinmetz, M. 2014, A&A, 569, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neugebauer, G., Martz, D. E., & Leighton, R. B. 1965, ApJ, 142, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez Alegría, S., Borissova, J., Chené, A. N., et al. 2014, A&A, 564, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reid, M. J., Menten, K. M., Brunthaler, A., et al. 2014, ApJ, 783, 130 [Google Scholar]
- Robin, A. C., Marshall, D. J., Schultheis, M., & Reylé, C. 2012, A&A, 538, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sevenster, M. N. 1999, MNRAS, 310, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Sevenster, M. N., Chapman, J. M., Habing, H. J., Killeen, N. E. B., & Lindqvist, M. 1997a, A&AS, 122, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sevenster, M. N., Chapman, J. M., Habing, H. J., Killeen, N. E. B., & Lindqvist, M. 1997b, A&AS, 124, 509 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sevenster, M., Saha, P., Valls-Gabaud, D., & Fux, R. 1999, MNRAS, 307, 584 [NASA ADS] [CrossRef] [Google Scholar]
- Sevenster, M. N., van Langevelde, H. J., Moody, R. A., et al. 2001, A&A, 366, 481 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sjouwerman, L. O., van Langevelde, H. J., Winnberg, A., & Habing, H. J. 1998, A&AS, 128, 35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sofue, Y. 2013, PASJ, 65, 118 [NASA ADS] [Google Scholar]
- te Lintel Hekkert, P., Caswell, J. L., Habing, H. J., et al. 1991, A&AS, 90, 327 [NASA ADS] [Google Scholar]
- Valenti, E., Zoccali, M., Renzini, A., et al. 2013, A&A, 559, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Langevelde, H. J., Brown, A. G. A., Lindqvist, M., Habing, H. J., & de Zeeuw, P. T. 1992, A&A, 261, L17 [NASA ADS] [Google Scholar]
- Wegg, C., & Gerhard, O. 2013, MNRAS, 435, 1874 [Google Scholar]
- Whitelock, P. A., & Catchpole, R. 1992, in The Stellar Populations of Galaxies, ed. B. Barbuy & A. Renzini, IAU Symp., 149, 503 [Google Scholar]
- Wilson, W. J., & Barrett, A. H. 1968, Science, 161, 778 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Distribution in longitude and latitude of the OH-maser stars in the surveys of Sevenster et al. The observations were limited to | b | ≤ 3deg. In red are shown the maser stars with a radial velocity | vrad | ≥ 220 km s-1 taken from Sevenster et al. (1997a,b, 2001) and from other surveys; see Table 1. |
| In the text | |
 |
Fig. 2 Distribution in longitude and in radial velocity of the OH-maser stars from the surveys by Sevenster (black). High-velocity maser stars from various surveys (see Table 1) (red). Red squares indicate the number of stars in velocity intervals from a near-infrared survey by Babusiaux et al. (2014). The two horizontal red lines indicate the velocity limits of the high-velocity stars. |
| In the text | |
 |
Fig. 3 Distribution in longitude and latitude of the high-velocity maser stars. The redshifted stars are largely at positive longitudes, the blueshifted stars at negative longitudes. Two horizontal lines at b = ± 4deg outline the search area. |
| In the text | |
 |
Fig. 4 Geometry adopted in the model calculations. GC stands for Galactic centre. The bar is along the y-axis. The outline of the ellipsoid (the bar) is indicated by a black ellipse. In red inside the bar is the largest possible elliptical orbit (see text). The angle P-Sun-Star, α, is found by the relation asinα = ( | xs−xz | ) /d, where d is the distance between the Sun and the star. The angle P-Sun-GC is β. The longitude l = α−β. The Sun is located at (−8.0sinβ, 8.0cosβ kpc). The maximum and minimum velocity will be reached where the orbit cuts the x-axis. The units in x and in y are kpc. |
| In the text | |
 |
Fig. 5 Orbits of different eccentricity but all passing the x-axis at x = ±0.2 with a velocity ẏ = 300 km s-1 using the parameters in Table 3; this table also gives the colour of each orbit. All orbits are in the clockwise direction. The units in x and in y are kpc. |
| In the text | |
 |
Fig. 6 Traces in the lvrad-diagram of orbits of different eccentricity but all passing the x-axis at x = ± 0.2 with a velocity ẏ = 300 km s-1. The colouring is the same as in Fig. 5. |
| In the text | |
 |
Fig. 7 (lvrad)-diagram with in green the largest possible orbit (x0 = 0, y0 = 3.0) in a model with dimensions (0.4,3,0.4). The symbols are the same as in Fig. 2. The density in the bar ρ = 15Msun pc-3, Ω = 0.074 Myr-1, β = 25deg. |
| In the text | |
 |
Fig. 8 Orbit of a star in the longitude-velocity diagram that starts at (x,y) = (0.0,3.0) with a velocity(vx,vy) = (0.0,0.0) in the gravitational field of a rotating bar plus the bulge plus a point source at the Galactic centre – see text (green). Maser stars from Sevenster’s survey and in red the high-velocity maser stars from Table 1 (black). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


