| Issue |
A&A
Volume 587, March 2016
|
|
|---|---|---|
| Article Number | A90 | |
| Number of page(s) | 12 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201425396 | |
| Published online | 23 February 2016 | |
Hydraulic effects in a radiative atmosphere with ionization
1
Nordita, KTH Royal Institute of Technology and Stockholm
University, Roslagstullsbacken
23, 10691
Stockholm,
Sweden
e-mail:
palvi@iucaa.ernet.in
2
Inter University Centre for Astronomy and Astrophysics, Post Bag
4, Pune University Campus, Ganeshkhind, 411
007
Pune,
India
3
Department of Astrophysical Sciences and Princeton Plasma Physics
Laboratory, Princeton University, Princeton, NJ
08540,
USA
4
Department of Astronomy, AlbaNova University Center, Stockholm
University, 10691
Stockholm,
Sweden
5
JILA and Department of Astrophysical and Planetary Sciences,
University of Colorado, Boulder, CO
80303,
USA
6
Laboratory for Atmospheric and Space Physics, University of
Colorado, Boulder,
CO
80303,
USA
Received: 24 November 2014
Accepted: 14 September 2015
Context. In his 1978 paper, Eugene Parker postulated the need for hydraulic downward motion to explain magnetic flux concentrations at the solar surface. A similar process has also recently been seen in simplified (e.g., isothermal) models of flux concentrations from the negative effective magnetic pressure instability (NEMPI).
Aims. We study the effects of partial ionization near the radiative surface on the formation of these magnetic flux concentrations.
Methods. We first obtain one-dimensional (1D) equilibrium solutions using either a Kramers-like opacity or the H− opacity. The resulting atmospheres are then used as initial conditions in two-dimensional (2D) models where flows are driven by an imposed gradient force that resembles a localized negative pressure in the form of a blob. To isolate the effects of partial ionization and radiation, we ignore turbulence and convection.
Results. Because of partial ionization, an unstable stratification always forms near the surface. We show that the extrema in the specific entropy profiles correspond to the extrema in the degree of ionization. In the 2D models without partial ionization, strong flux concentrations form just above the height where the blob is placed. Interestingly, in models with partial ionization, such flux concentrations always form at the surface well above the blob. This is due to the corresponding negative gradient in specific entropy. Owing to the absence of turbulence, the downflows reach transonic speeds.
Conclusions. We demonstrate that, together with density stratification, the imposed source of negative pressure drives the formation of flux concentrations. We find that the inclusion of partial ionization affects the entropy profile dramatically, causing strong flux concentrations to form closer to the surface. We speculate that turbulence effects are needed to limit the strength of flux concentrations and homogenize the specific entropy to a stratification that is close to marginal.
Key words: radiative transfer / hydrodynamics / Sun: atmosphere / sunspots
© ESO, 2016
1. Introduction
In a series of a papers, Parker (1974, 1976, 1978) introduced the idea of hydraulic flux concentrations at the solar surface. Here the hydraulic device is formed by magnetic flux tubes of varying sizes and pumping is accomplished by turbulence. In these papers, he envisaged turbulent pumping (analogous to a water-jet vacuum pump) as the relevant driver, but other alternatives such as the negative effective magnetic pressure instability (NEMPI), first studied by Kleeorin et al. (1989, 1996), are possible and have also been discussed (Brandenburg et al. 2014).
These tubes can be concentrated further through what is known as convective collapse (Parker 1978; Spruit 1979). This process is similar to the onset of convection, which can either lead to downward or upward motion of the gas inside a vertical flux tube (see also Spruit & Zweibel 1979). In the former case, following the model of Spruit (1979), this can lead to a so-called collapsed state in which the field inside the tube increases from 1270 G to 1650 G. However, the collapsed state is not in thermal equilibrium, so the system will slowly return to an uncollapsed state. The detailed model of Spruit (1979) makes use of a realistic equation of state in which ionization plays an important role. While this is also the case in our models with partial ionization effects included, our models are always being pulled out of dynamical equilibrium by the applied negative effective magnetic pressure, which is not present in the model of Spruit (1979).
The flux concentrations of Parker are thought to be just around 100 km in diameter. Nevertheless, they might still be relevant for sunspots which can be more than a hundred times thicker. Indeed, in the cluster model of sunspots, an assembly of many such smaller tubes are thought to constitute a full sunspot. Even today, it is still unclear whether sunspots are monolithic or clustered (see review by Rempel & Schlichenmaier 2011). Nevertheless, the possibility of downward flows inside sunspots (as seen in Parker’s models of hydraulic magnetic flux concentrations) may be a more universal feature, which has also been identified as the driving mechanism for producing magnetic flux concentrations by NEMPI (Brandenburg et al. 2014) and has also recently been seen at the late stages of flux emergence (Rempel & Cheung 2014).
In most of the work that invokes NEMPI, an isothermal equation of state is used. This allows these effects to be studied in isolation from the downdrafts that occur in convection. However, it is important to assess the effects of thermodynamics and radiation, which might either support or hinder tube formation and amplification.
The goal of the present paper is to investigate how downward flows produce flux concentrations in a partially ionized atmosphere with full radiative transfer. We model the effects of an additional negative pressure by imposing an irrotational forcing function which corresponds to a localized gradient force of the form −∇φ on the righthand side of the momentum equation, where φ is a localized Gaussian profile function that emulates the effects of negative effective magnetic pressure in a controllable way. By imposing a vertical magnetic field, we force the resulting flow to be mainly along magnetic field lines. If φ is chosen to be negative, it corresponds to a negative extra pressure. Horizontal pressure balance then leads to a localized gas pressure and density increase and, consequently, to a downflow owing to the weight of this density enhancement. The return flow closes in the upper parts of this structure. The resulting flow convergence drives magnetic field lines together and thus forms the magnetic flux concentration envisaged by Parker (1974, 1976, 1978). These flux concentrations are also similar to those seen in studies of NEMPI with a vertical magnetic field (Brandenburg et al. 2013, 2014).
We construct hydrostatic equilibrium solutions using a method similar to that of Barekat & Brandenburg (2014), hereafter BB14. They fixed the temperature at the bottom boundary, which then also fixes the source function for the radiation field. Here we assume either a generalized Kramers opacity with exponents that result in a nearly adiabatic stratification in the deep fully ionized layers, or we use an H− opacity that is estimated from the number density of H− ions using the Saha equation with a corresponding ionization potential (Kippenhahn & Weigert 1990). For our investigation, we restrict ourselves to the ionization of hydrogen. This approach was also used by Heinemann et al. (2007) in simulations of the fine structure of sunspots.
A general problem in all approaches to time-dependent models of stellar atmospheres is the large gap between acoustic and thermal timescales. Their ratio is on the order of the ratio of the energy flux to 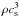 , where ρ is the density and cs is the sound speed. For the Sun, this ratio is less than 10-10 in the deeper parts of the convection zone (Brandenburg et al. 2005). This problem was identified long ago (Chan & Sofia 1986, 1989) and can be addressed using models that are initially in equilibrium (Nordlund et al. 2009). Another possibility is to consider modified models with a larger flux such that it becomes possible to simulate for a full Kelvin–Helmholtz timescale (Käpylä et al. 2013). This is also the approach taken here and it allows us to construct models whose initial state is very far away from the final one, as is the case with an initially isothermal model.
, where ρ is the density and cs is the sound speed. For the Sun, this ratio is less than 10-10 in the deeper parts of the convection zone (Brandenburg et al. 2005). This problem was identified long ago (Chan & Sofia 1986, 1989) and can be addressed using models that are initially in equilibrium (Nordlund et al. 2009). Another possibility is to consider modified models with a larger flux such that it becomes possible to simulate for a full Kelvin–Helmholtz timescale (Käpylä et al. 2013). This is also the approach taken here and it allows us to construct models whose initial state is very far away from the final one, as is the case with an initially isothermal model.
2. The model
2.1. Governing equations
We adopt the hydromagnetic equations for logarithmic density lnρ, velocity u, specific entropy s, and magnetic vector potential A, in the form 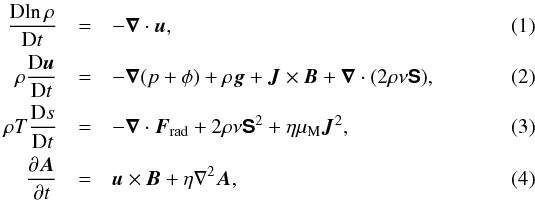 where D/Dt = ∂/∂t + u·∇ is the advective derivative, p is the gas pressure, g = (0,0,−g) is the gravitational acceleration, ν is the viscosity,
where D/Dt = ∂/∂t + u·∇ is the advective derivative, p is the gas pressure, g = (0,0,−g) is the gravitational acceleration, ν is the viscosity, 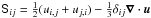 is the traceless rate-of-strain tensor and
is the traceless rate-of-strain tensor and 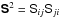 contributes to the (positive definite) viscous heating rate, B = B0 + ∇ × A is the magnetic field with
contributes to the (positive definite) viscous heating rate, B = B0 + ∇ × A is the magnetic field with 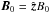 representing an imposed vertical magnetic field, J = ∇ × B/μM is the current density, μM is the magnetic vacuum permeability (not to be confused with the mean molecular weight μ, defined below), η is the magnetic diffusivity, and
representing an imposed vertical magnetic field, J = ∇ × B/μM is the current density, μM is the magnetic vacuum permeability (not to be confused with the mean molecular weight μ, defined below), η is the magnetic diffusivity, and 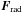 is the radiative flux. For the equation of state, we assume a perfect gas with p = (ℛ /μ)Tρ, where ℛ = kB/mu is the universal gas constant in terms of the Boltzmann constant kB and the atomic mass unit mu, T is the temperature, and the dimensionless mean molecular weight is given by
is the radiative flux. For the equation of state, we assume a perfect gas with p = (ℛ /μ)Tρ, where ℛ = kB/mu is the universal gas constant in terms of the Boltzmann constant kB and the atomic mass unit mu, T is the temperature, and the dimensionless mean molecular weight is given by 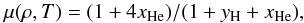 (5)where yH(ρ,T) is the ionization fraction of hydrogen and xHe is the fractional number of neutral helium, which is related to the mass fraction of neutral helium Y through 4xHe = Y/ (1 − Y). In the following, we use the abbreviation μ0 = 1 + 4xHe = (1 − Y)-1 = X-1, where X is the mass fraction of hydrogen (ignoring metals). In relating various thermodynamic quantities to each other, we introduce α = (∂lnρ/∂lnp)T, which is a known function of yH, as well as δ = (∂lnρ/∂lnT)p and the ratio γ = cp/cv of specific heats at constant volume and pressure, cv = (∂e/∂T)v and cp = (∂e/∂T)p, respectively, which are known functions of both yH and T; see Kippenhahn & Weigert (1990), Stix (2002), and Appendix A. When yH is either 0 or 1, we have α = δ = 1 and cv = (3/2) ℛ /μ with e = cvT. In general, however, we have e = (3/2) ℛT/μ + eH, where eH = yHℛTH/μ0 is the specific energy that is used (released) for ionization (recombination) and TH = χH/kB is the ionization temperature. Using χH = 13.6 eV for the ionization energy of hydrogen, we have TH ≈ 1.58 × 105 K.
(5)where yH(ρ,T) is the ionization fraction of hydrogen and xHe is the fractional number of neutral helium, which is related to the mass fraction of neutral helium Y through 4xHe = Y/ (1 − Y). In the following, we use the abbreviation μ0 = 1 + 4xHe = (1 − Y)-1 = X-1, where X is the mass fraction of hydrogen (ignoring metals). In relating various thermodynamic quantities to each other, we introduce α = (∂lnρ/∂lnp)T, which is a known function of yH, as well as δ = (∂lnρ/∂lnT)p and the ratio γ = cp/cv of specific heats at constant volume and pressure, cv = (∂e/∂T)v and cp = (∂e/∂T)p, respectively, which are known functions of both yH and T; see Kippenhahn & Weigert (1990), Stix (2002), and Appendix A. When yH is either 0 or 1, we have α = δ = 1 and cv = (3/2) ℛ /μ with e = cvT. In general, however, we have e = (3/2) ℛT/μ + eH, where eH = yHℛTH/μ0 is the specific energy that is used (released) for ionization (recombination) and TH = χH/kB is the ionization temperature. Using χH = 13.6 eV for the ionization energy of hydrogen, we have TH ≈ 1.58 × 105 K.
Instead of solving Eq. (3) for s, it is convenient to solve directly for T using the relation (Kippenhahn & Weigert 1990) 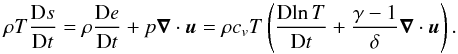 (6)The pressure gradient is computed as
(6)The pressure gradient is computed as 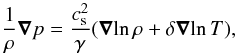 (7)where cs is the adiabatic sound speed with
(7)where cs is the adiabatic sound speed with 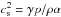 . This approach allows us to find the ionization fraction of hydrogen from the Saha equation as
. This approach allows us to find the ionization fraction of hydrogen from the Saha equation as 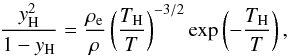 (8)where ρe = μ0mu(meχH/ 2πħ2)3/2 is the electron density.
(8)where ρe = μ0mu(meχH/ 2πħ2)3/2 is the electron density.
To compute 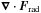 , we adopt the gray approximation, ignore scattering, and assume that the source function S is given by the frequency-integrated Planck function, so S = (σSB/π)T4, where σSB is the Stefan–Boltzmann constant. The negative divergence of the radiative flux is then given by
, we adopt the gray approximation, ignore scattering, and assume that the source function S is given by the frequency-integrated Planck function, so S = (σSB/π)T4, where σSB is the Stefan–Boltzmann constant. The negative divergence of the radiative flux is then given by 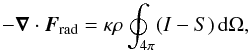 (9)where κ is the opacity per unit mass (assumed independent of frequency) and
(9)where κ is the opacity per unit mass (assumed independent of frequency) and 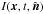 is the frequency-integrated specific intensity in the direction
is the frequency-integrated specific intensity in the direction 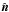 . We obtain I by solving the radiative transfer equation,
. We obtain I by solving the radiative transfer equation, 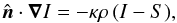 (10)along a set of rays in different directions
(10)along a set of rays in different directions 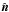 using the method of long characteristics. For the opacity, we assume either a Kramers-like opacity κ = κ0ρaTb with adjustable coefficients κ0, a, and b, or a rescaled H− opacity. In the former case, following BB14, it is convenient to express κ in the form
using the method of long characteristics. For the opacity, we assume either a Kramers-like opacity κ = κ0ρaTb with adjustable coefficients κ0, a, and b, or a rescaled H− opacity. In the former case, following BB14, it is convenient to express κ in the form 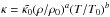 , where
, where 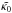 is a rescaled opacity and is related to κ0 by
is a rescaled opacity and is related to κ0 by 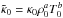 . With this choice, the units of
. With this choice, the units of 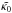 are independent of a and b, and always Mm-1 cm3 g-1 (=10-8 cm2 g-1). In the latter case we use for the H− opacity the expression (Kippenhahn & Weigert 1990)
are independent of a and b, and always Mm-1 cm3 g-1 (=10-8 cm2 g-1). In the latter case we use for the H− opacity the expression (Kippenhahn & Weigert 1990) 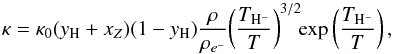 (11)where κ0 = σH−/ 4μ0mu is a coefficient, σH− = 4 × 10-17 cm2 is the cross section of H− (Mihalas 1978), xZ = 10-4 is the fraction of metals, TH− = χH−/kB and χH− = 0.754 eV are the ionization temperature and energy of H−, and ρe− = μ0mu(meχH−/ 2πħ2)3/2 is the relevant electron density.
(11)where κ0 = σH−/ 4μ0mu is a coefficient, σH− = 4 × 10-17 cm2 is the cross section of H− (Mihalas 1978), xZ = 10-4 is the fraction of metals, TH− = χH−/kB and χH− = 0.754 eV are the ionization temperature and energy of H−, and ρe− = μ0mu(meχH−/ 2πħ2)3/2 is the relevant electron density.
An important quantity in a radiative equilibrium model is the radiative conductivity K = 16σSBT3/ 3κρ. According to the results of BB14, K is nearly constant in the optically thick part. This implies that ρ ∝ Tn with n = (3 − b)/(1 + a) being effectively a polytropic index of the model provided n> −1.
For large values of T, the exponential terms in Eqs. (8) and (11) become unity, and only the terms 1 − yH ∝ ρ/T3/2 from Eq. (8) and an explicit ρ/T3/2 term in Eq. (11) remain. Therefore, κ ∝ ρ2T-3, i.e., a = 2 and b = −3, resulting in a stable stratification with polytropic index n = (3 + 3)/(1 + 2) = 2.
To identify the location of the radiating surface in the model, we compute the optical depth as 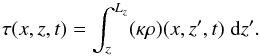 (12)The τ = 1 contour corresponds then to the surface from where most of the radiation escapes all the way to infinity. For the forcing function, we assume
(12)The τ = 1 contour corresponds then to the surface from where most of the radiation escapes all the way to infinity. For the forcing function, we assume ![\begin{equation} \phi=\phi_0 e^{-[x^2+(z-z_0)^2]/2R^2}, \end{equation}](/articles/aa/full_html/2016/03/aa25396-14/aa25396-14-eq101.png) (13)where φ0 is the amplitude with a negative value and R the radius of the blob-like structure.
(13)where φ0 is the amplitude with a negative value and R the radius of the blob-like structure.
2.2. Boundary conditions
We consider a two-dimensional (2D) Cartesian slab of size Lx × Lz with −Lx/ 2 <x<Lx/ 2, 0 ≤ z ≤ Lz. We assume the domain to be periodic in the x direction and bounded by stress-free conditions in the z direction, so the velocity obeys 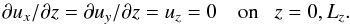 (14)For the magnetic field we adopt the vertical field condition,
(14)For the magnetic field we adopt the vertical field condition, 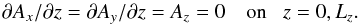 (15)We assume zero incoming intensity at the top, and compute the incoming intensity at the bottom from a quadratic Taylor expansion of the source function, which implies that the diffusion approximation is obeyed; see Appendix A of Heinemann et al. (2006) for details. To ensure steady conditions, we fix temperature at the bottom,
(15)We assume zero incoming intensity at the top, and compute the incoming intensity at the bottom from a quadratic Taylor expansion of the source function, which implies that the diffusion approximation is obeyed; see Appendix A of Heinemann et al. (2006) for details. To ensure steady conditions, we fix temperature at the bottom, 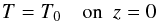 (16)while the temperature at the top is allowed to evolve freely. There is no boundary condition on the density, but since no mass is flowing in or out, the volume-averaged density is automatically constant (see Appendix C of BB14). Since most of the mass resides near the bottom, the density there will not change drastically and will be close to its initial value at the bottom.
(16)while the temperature at the top is allowed to evolve freely. There is no boundary condition on the density, but since no mass is flowing in or out, the volume-averaged density is automatically constant (see Appendix C of BB14). Since most of the mass resides near the bottom, the density there will not change drastically and will be close to its initial value at the bottom.
We use for all simulations the Pencil Code1, which solves the hydrodynamic differential equations with a high-order finite-difference scheme. The radiation and ionization modules were implemented by Heinemann et al. (2006). All our calculations are carried out either on a one-dimensional (1D) mesh with 576 or 1152 points in the z direction or on a 2D mesh with 1152 × 576 points in the x and z directions.
2.3. Parameters and initial conditions
To avoid very large or very small numbers, we measure length in Mm, speed in km s-1, density in g cm-3, and temperature in K. Time is then measured in kiloseconds ( ks). We adopt the solar surface value for the gravitational acceleration, which is then g = 274 km2 s-2 Mm-1 = 2.74 × 104 cm s-2. In most models we use (a,b) = (1,0) and 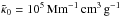 , which yields a top temperature of about 10 000 K (BB14). We also present results using the H− opacity. In both cases, the opacities are lowered by 5 to 6 orders of magnitude relative to their realistic values to allow thermal relaxation to occur within a few thousand sound travel times. As discussed in BB14, this also leads to a larger flux and therefore a larger effective temperature. For the H− opacity, we have applied a scaling factor of 10-6 in Eq. (11). In all the models we use ν = η = 10-3 Mm km s-1, corresponding to 1010 cm2 s-1. For the radius of the blob we take R = 1 Mm and for the magnetic field we take B0 = 1 kG.
, which yields a top temperature of about 10 000 K (BB14). We also present results using the H− opacity. In both cases, the opacities are lowered by 5 to 6 orders of magnitude relative to their realistic values to allow thermal relaxation to occur within a few thousand sound travel times. As discussed in BB14, this also leads to a larger flux and therefore a larger effective temperature. For the H− opacity, we have applied a scaling factor of 10-6 in Eq. (11). In all the models we use ν = η = 10-3 Mm km s-1, corresponding to 1010 cm2 s-1. For the radius of the blob we take R = 1 Mm and for the magnetic field we take B0 = 1 kG.
 |
Fig. 1 Comparison of ρ, T, s, yH, γ and cp along each row, top to bottom, from models with (solid, black) and without (dotted, blue) hydrogen ionization for Runs A, B and C along each column, left to right, and |
Summary of 1D runs leading to equilibrium solutions.
3. Results
 |
Fig. 2 Comparison of models with ρ0 = 0.002 g cm-3 (solid), 0.005 g cm-3 (dashed), and 0.01 g cm-3 (dotted lines). Here (a,b) is (1,0), corresponding to n = 1.5. |
First we run 1D simulations with φ0 = 0 and isothermal initial conditions using Kramers opacity and H− opacity. A summary of these runs is listed in Table 1. We use the resulting equilibrium solutions from the 1D runs as initial conditions for the 2D runs with φ0 ≠ 0.
3.1. Kramers opacity
As listed in Table 1, for Kramers opacity we use three pairs of (a,b), (1,−3.5), (1,0), and (1,1) in Runs A, B, and C, respectively. In the absence of ionization, the resulting equilibrium solutions have an optically thick part that is nearly polytropically stratified, i.e., ρ ∝ Tn, where n = (3−b)/(1 + a) = 3.25, 1.5 and 1, respectively are the polytropic indices (BB14) for Runs A, B and C; see Fig. 1. In the outer, optically thin part, the temperature in all cases is nearly constant and its value is compatible with (3/4)1/4 ≈ 0.93 times the effective temperature (Mihalas 1978). For γ = 5/3, a polytropic index of 3/2 corresponds to an adiabatic stratification. The pressure scale height, Hp = ℛT/μg, in the case of n = 1.5 is about 3 Mm in the upper parts of the model and increases to about 7 Mm at the bottom. In the 2D runs, for the Kramers opacity, we have only used (a,b) of (1,0), corresponding to n = 1.5.
In Table 1 we also list the height zτ = 1 of the photosphere, where τ = 1. For our models with Kramers opacity, the value of zτ = 1 is around 8 Mm, but comparing the models with T0 = 105 K and ρ0 = 0.002 g cm-3 using either Kramers or H− opacity (Runs C or E, respectively), we find that zτ = 1 doubles from about 7 Mm to 14 Mm, which is the reason we choose a shallower domain for our 2D experiments using H− opacity.
3.1.1. Vertical equilibrium profiles
In Fig. 1 we compare vertical profiles of various thermodynamic parameters in 1D models with (in solid black) and without (in dotted blue) partial ionization with φ0 = 0. Both models have in common that the temperature decreases approximately linearly with increasing z and then reaches a constant at a height where τ = 1 (in the one with ionization); this height is nearly the same in both cases. By requiring thermostatic equilibrium, Eq. (3) yields 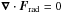 , and in the absence of ionization, it is seen that the solutions for the temperature profiles are linearly decreasing for τ ≫ 1 and nearly constant for τ ≪ 1 (BB14). The inclusion of ionization does not seem to affect the solutions for temperature profiles much. It can be seen that the polytropic density-temperature relation, ρ ~ Tn, nearly follows in the optically thick part (τ> 1) across all atmospheres with different polytropic indices. This is because in the optically thick part, the degree of ionization, yH remains nearly constant. In our models, the contribution of xZ is rather unimportant, because yH never drops to low values-even when xZ = 0; see the red dashed lines in Fig. 1. The remaining differences in the top layers are presumably still artifacts of using moderate resolution, as we have seen by comparison with lower resolution calculations which gave larger discrepancies in the top layers, but identical solutions in the deeper ones.
, and in the absence of ionization, it is seen that the solutions for the temperature profiles are linearly decreasing for τ ≫ 1 and nearly constant for τ ≪ 1 (BB14). The inclusion of ionization does not seem to affect the solutions for temperature profiles much. It can be seen that the polytropic density-temperature relation, ρ ~ Tn, nearly follows in the optically thick part (τ> 1) across all atmospheres with different polytropic indices. This is because in the optically thick part, the degree of ionization, yH remains nearly constant. In our models, the contribution of xZ is rather unimportant, because yH never drops to low values-even when xZ = 0; see the red dashed lines in Fig. 1. The remaining differences in the top layers are presumably still artifacts of using moderate resolution, as we have seen by comparison with lower resolution calculations which gave larger discrepancies in the top layers, but identical solutions in the deeper ones.
In the optically thin part, the models with ionization have lower densities compared to the models without ionization, thus increasing the density contrast. The specific entropy in the optically thick part is stratified according to the respective polytropic indices (stable when n = 3.25, marginal when n = 1.5, and unstable when n = 1; cf. BB14).
Interestingly with ionization, all the entropy profiles in Runs A, B, and C behave in a similar fashion near and above the height where τ = 1. Near τ = 1, there is a narrow layer where the vertical entropy gradient is negative, corresponding to Schwarzschild-unstable stratification and the possibility of convection. (We confirmed this and comment on it in the end of the discussion.) It can be seen from Fig. 1 that, on comparing the specific entropy profiles with the yH profiles, the extrema in the entropy profiles coincide with the ones in the corresponding yH profiles. This correspondence in the extrema between the two quantities, specific entropy and degree of ionization can be shown mathematically. We show in detail in Appendix B that, using the equation of state, the first law of thermodynamics, and the Saha ionization equation, for the case of τ ≫ 1, ![\begin{eqnarray} \dd s=\dd\yH{{\cal R}\over\mu_0}\left[{1\over A_v}{(n-3/2)\over(n+3/2)} - B_v\right], \label{dsdh1} \end{eqnarray}](/articles/aa/full_html/2016/03/aa25396-14/aa25396-14-eq172.png) (17)where Av and Bv are coefficients that are defined in Eq. (A.2) of Appendix A. In the case of τ ≪ 1, we have
(17)where Av and Bv are coefficients that are defined in Eq. (A.2) of Appendix A. In the case of τ ≪ 1, we have ![\begin{equation} \dd s=\dd\yH{{\cal R}\over\mu_0}\left[{1\over A_v}- B_v\right]. \label{dsdh2} \end{equation}](/articles/aa/full_html/2016/03/aa25396-14/aa25396-14-eq175.png) (18)From Eqs. (17) and (18), we find that the change in specific entropy is directly proportional to the change in degree of ionization and when dyH = 0, then ds = 0. Thus, the extrema in s directly correspond to extrema in yH.
(18)From Eqs. (17) and (18), we find that the change in specific entropy is directly proportional to the change in degree of ionization and when dyH = 0, then ds = 0. Thus, the extrema in s directly correspond to extrema in yH.
Interestingly, this kind of correspondence is observed even at τ ~ 1 from the Fig. 1 although it is only expected in the regimes of τ ≫ 1 and τ ≪ 1, see Eqs. (17) and (18). The hydrogen ionization fraction yH, reaches a minimum of about 0.2 (in Runs A and B) and about 0.4 (Run C) near the surface, but then increases again. This is because of a low density and the exponential decrease in the upper isothermal layer, leading to larger values of yH even when T is small. In the Sun, the surface temperatures are of course smaller still, and therefore yH ≈ 0 can then be reached. While the specific heats increase outward by a factor of about five to ten, their ratio, γ, decreases below the critical value of 5/3.
In Fig. 2 we compare models with three values of ρ0. We recall that ρ0 is the bottom value of the density of the initially isothermal model. Since temperature T0 is fixed at the bottom, the pressure scale height remains unchanged, but since the stratification evolves to a nearly adiabatic one, the density scale height becomes larger than the pressure scale height, so density drops more slowly and the bottom density becomes smaller by about two third; a corresponding expression for this is given by Eq. (C.5) in BB14. Models with larger values of ρ0 result in lower surface temperatures and lower degrees of ionization near the surface. However, for a given number of mesh points the height of the computational domain has to be reduced for larger values of ρ0, because the density drops then much faster to small values. This is just a numerical constraint that can be alleviated by using more mesh points.
 |
Fig. 3 Snapshots of Run F3 (fixed ionization, yH = 1) showing temperature (color coded), magnetic field lines, and velocity vectors at two times before and after the flux concentration develops. The solid yellow line at z ≈ 9 Mm indicates the τ = 1 surface while the dashed blue line indicates the height z0 where suction operates. |
3.1.2. Two-dimensional models
Next, we consider 2D models with φ0 ≠ 0. The 1D vertical equilibrium solutions form the initial condition here along z for all x. A summary of all 2D runs is given in Table 2. We consider first the case φ0 = −3 × 10-3 g cm-3 km2 s-2 using z0 = 3 Mm for the height of the blob. In Fig. 3 we show the result for Run F3 (fixed ionization, yH = 1) at t = 5 ks and 10 ks, while in Fig. 4 we show the result for Run K3a2 with partial ionization effects included at t = 1.6 ks and 2 ks.
 |
Fig. 4 Same as Fig. 3, but for variable partial ionization for Run K3a2 at two times just before and after the flux concentration develops. |
In both cases (Runs F3 and K3a2 in Figs. 3 and 4), we see the effects of downward suction. We also see how the magnetic field lines are being pushed together at a place above the blob where the return flow tries to replenish the gas in the evacuated upper parts (compare the flows at t = 5 ks and 10 ks). In the case of partial ionization (Run K3a2 in Fig. 4), the upper parts have a strongly negative specific entropy gradient, which leads to a strong concentration after a short time (t = 1.6 ks), and is most pronounced at a height considerably above the height of the blob. Thus, as compared to the case without partial ionization (Run F3), the inclusion of partial ionization (Run K3a2) causes the flux concentrations to form at the τ = 1 surface. This is a consequence of the highly unstable stratification just at the surface, so the resulting flow is primarily a consequence of triggering instability. By contrast, in Run F3 no such instability develops, so the flow characteristics reflects directly the nature of the driving. In Run K3a2 at the later time (t = 2 ks), however, when the magnetic structure has collapsed almost entirely, the converging inflow has stopped and there are now indications of an outflow.
 |
Fig. 5 Temperature versus optical depth and height at different times through x = 0 (solid lines and a dotted line for the last time) and x = Lx/ 2 (dashed lines) for Run K3a2 at times 1.6–1.9 ks. |
It is remarkable that at all times, the τ = 1 surface is approximately flat, so there is no Wilson depression in our models. To examine whether this is an artifact of the rather small values of opacity in our models, which results in comparatively larger radiative flux and radiative diffusivity, and therefore horizontal temperature equilibration, we ran a similar model, using however only vertical rays in the solution of Eq. (10). However, the results were virtually identical, suggesting that the absence of Wilson depression is not connected with the enhanced luminosity of our models that is used to reduce the Kelvin–Helmholtz timescale.
In Fig. 5 we show for Run K3a2 vertical temperature profiles though x = 0 (i.e., through the structure) and x = Lx/ 2 (away from it) as functions of τ and z. At x = 0, we clearly see that for τ ≫ 1, the temperature drops progressively below the value at x = Lx/ 2. At z = z0, the temperature is below 50 000 K at x = 0, while at x = Lx/ 2 we have 80 000 K. For τ< 1, the temperature is slightly enhanced at x = 0 compared to x = Lx/ 2. This is expected, because here the vertical gradient of specific entropy is positive, corresponding to stable stratification, so any downward motion would lead to enhanced entropy and temperature at that position.
 |
Fig. 6 Temperature and vertical magnetic field strength versus x at different times (1.4–2 ks) through z = 8 Mm for Run K3a2. |
In Fig. 6 we show the corresponding temperature and magnetic field profiles through a horizontal cut at z = 8 Mm, which is just beneath the surface. The temperature is reduced at the location of the structure, but there is also an overall increase in the broader surroundings of the structure, which we associate with the return flow from deeper down. The magnetic field enhancement reaches values of the order of about 50 kG (an amplification by a factor of 50) in a narrow spike. These structures are confined by the strong converging return flow. In Fig. 7, we compare such magnetic field profiles from Runs K3a1, K3a2 and K3a3 which have R = 0.5, 1.0, and 1.5, respectively, as listed in Table 2. It can be seen that at time t = 1.6 ks, the flux concentrations in Run K3a1 is still in the initial stages of formation, while for Runs K3a2 and K3a3, the field Bz at x = 0 has already increased to about 8 kG and 40 kG, respectively. This implies that for smaller values of R, the formation of flux concentrations is slower and vice-versa.
 |
Fig. 7 Comparison of vertical magnetic field strength from Runs K3a1, K3a2 and K3a3 at t = 1.6 ks. |
Summary of 2D models discussed in this paper.
The downward speed can become comparable with the local sound speed; see Figs. 8 and 9, where we compare two cases with different forcing amplitudes. Nevertheless, in both cases the speeds are similar. This implies that the vertical motion is essentially in free fall. To verify this, we note that the speed of a body freely falling over a distance Δz is 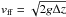 . Using Δz = 5 Mm, we find vff ≈ 50 km s-1, which is comparable with the speeds seen in Figs. 8 and 9. As expected from earlier polytropic convection models with ionization (Rast & Toomre 1993), the downflow advects less ionized material of lower γ and larger cp downward; see Figs. 10 and 11. Then again from time evolution plots of s and yH shown in Figs. 10 and 11, we find a correspondence between the profiles of specific entropy and yH, as expected according to Eqs. (17) and (18). Not surprisingly, the suction-induced downflow leads to values of s that, at larger depths inside the structure, agree with the photospheric values higher up. However, temporal changes in γ are not as dramatic as the changes with height. Inside the structure, the specific entropy has photospheric values also deeper down, and s is nearly constant (about 0.14 km2 s-2 K-1) in the range 3 Mm ≤ z ≤ 9 Mm at t = 1.9 ks.
. Using Δz = 5 Mm, we find vff ≈ 50 km s-1, which is comparable with the speeds seen in Figs. 8 and 9. As expected from earlier polytropic convection models with ionization (Rast & Toomre 1993), the downflow advects less ionized material of lower γ and larger cp downward; see Figs. 10 and 11. Then again from time evolution plots of s and yH shown in Figs. 10 and 11, we find a correspondence between the profiles of specific entropy and yH, as expected according to Eqs. (17) and (18). Not surprisingly, the suction-induced downflow leads to values of s that, at larger depths inside the structure, agree with the photospheric values higher up. However, temporal changes in γ are not as dramatic as the changes with height. Inside the structure, the specific entropy has photospheric values also deeper down, and s is nearly constant (about 0.14 km2 s-2 K-1) in the range 3 Mm ≤ z ≤ 9 Mm at t = 1.9 ks.
 |
Fig. 8 Vertical velocity at x = 0 versus height at different times (1.6–1.9 ks) for Run K3a2. |
 |
Fig. 9 Similar to Fig. 8, but for Run K3b with 10 times weaker suction. The red dash-dotted lines shows the profile of sound speed. |
 |
Fig. 10 Degree of ionization and ratio or specific heats versus height, from Run K3a2. |
 |
Fig. 11 Specific entropy and specific heat at constant pressure versus height, from Run K3a2. |
3.2. H− opacity
Finally, we compare with models using the H− opacity. Again, we use here the implementation of Heinemann et al. (2006, 2007), which was found to yield reasonable agreement with realistic opacities.
 |
Fig. 12 Profiles of T, s, ρ, yH, κ, and K for Run D, with H− opacity. The red symbol indicates the position of τ = 1. |
3.2.1. One-dimensional equilibrium models
In Fig. 12, we give 1D equilibrium solutions as functions of depth focusing on the top 5 Mm (Run D has a height of 9 Mm, where we have chosen T0 = 6 × 104 K). We find a stably stratified lower part with an unstable part just beneath the τ = 1 surface. The temperature decreases linearly from the bottom, where K is seen to be constant, indicating the regime where the diffusion approximation applies, similar to the other runs with Kramers opacity. However, close to the τ = 1 surface there is a short jump (decrease) in the temperature by a factor of ~2, unlike the runs with Kramers opacity, where the temperature profile simply turns from linearly decreasing to a constant value. The temperature profile eventually settles to a constant for z>zτ = 1. This jump in the temperature profile resembles the profile in Fig. 1 and Fig. 14 of Stein & Nordlund (1998), where again the jump is by a factor ~2 in temperature. It is attributed to the extreme temperature sensitivity of the H− opacity.
For comparison, we include Run E, for which we have chosen T0 = 105 K and a height of 20 Mm. The value of zτ = 1 is then nearly 14 Mm. Now, however, there is an extended deeper layer which is stably stratified.
 |
Fig. 14 Same as Fig. 5, but for Run H3 using the H− opacity with a scaling coefficient of 10-6. Note the increase in temperature at z ≈ 8 Mm. |
3.2.2. Two-dimensional models
In the 2D model with H− opacity, we chose φ0 = −3 × 10-3 g cm-3 km2 s-2 with z0 = 3 Mm for the height of the blob. In Fig. 13, we see that the flux concentrations form much above the blob location, close to the τ = 1 surface. This is again mainly due to the negative gradient in entropy just below τ = 1 surface as seen in Fig. 12. Furthermore, there is a very narrow dip in the τ = 1 surface in the lower panel of Fig. 13 at t = 1.1 ks, but is flanked by two peaks, which is due to the return flows.
Owing to the stable stratification of the lower part, the resulting speeds are much lower than those in Runs K3a2 and K3b. As a consequence, the cooling in the temperature profile due to the downflow of low entropy material, shown in Fig. 14, is decreased. Compared to the case of Kramers opacity in Fig. 5, most of the cooling here takes place to much lesser extent in depth. This is further limited because the stratification soon becomes unstable towards larger values of z.
Comparing with the deeper model, where T0 = 105 K (Run H10, whose equilibrium model was Run E), significant downflows can only be obtained when we place the blob higher up (z0 = 10 Mm) and increase the forcing (φ0 = −3 × 10-2 g cm-3 km2 s-2). This is because of the more extended stably stratified deeper layer. The maximum downflow speed is only 15 km s-1.
In reality, of course, strong convection would commence which would change the stratification in the deeper layers from stable to marginally stable, or even marginally unstable; see (Brandenburg 2015) for details. In this sense, the present case with H− opacity would in practice be close to the case with marginal background stratification studied in Sect. 3.1.2.
4. Conclusions
The inclusion of partial ionization along with radiative transfer forms an important step towards bridging the gap between idealized models of magnetic flux concentrations and more realistic ones. In this work, we have studied the effects of partial ionization firstly in 1D hydrostatic models of the atmosphere in thermal equilibrium and then in 2D hydraulic models of flux concentrations. In the radiative transfer module, we have used either Kramers opacity or H− opacity.
Comparison of the final 1D equilibrium atmospheres with and without partial ionization shows that, while the solutions do not differ much in the optically thick part, they are significantly different in the range 1 <τ< 100, especially with respect to the specific entropy and density profiles. An interesting feature is the narrow layer with a negative gradient in specific entropy close to the τ = 1 surface, which is persistent across different atmospheres with either Kramers opacity (for any polytropic index; shown for n = 3.25, 1.5 and 1) or the H− opacity. This minimum in the s profile is directly connected to the minimum in yH profile. In fact from Eqs. (17) and (18), it is clear that the extrema in s correspond to the extrema in yH. This unstable layer near τ = 1 is important since, in the 2D models, it causes the flux concentrations to form right at the surface.
In 1D models with H− opacity, the τ< 1 part is stably stratified as expected and here also a narrow unstable layer is seen close to surface. Due to the extreme sensitivity of the H− opacity to temperature, there is a distinctive jump (by a factor ~2) in the temperature profile after a prolonged decrease.
To study the effect of partial ionization on hydraulic flux concentrations, the model we used employed an artificially imposed source of negative pressure in the momentum equation. This work has demonstrated that such a forcing function can lead to a dramatic downflow that is channeled along vertical magnetic field lines. A corresponding return flow is produced that converges in the upper parts and draws vertical magnetic field lines together, which leads to significant magnetic field amplification. This strong amplification is connected with the high-speed descent of gas. It is much faster than what is expected based on the artificially applied pumping and it is, in fact, virtually independent of it. Weaker forcing only leads to a delay in what later always tends to develop into nearly free fall. We do not expect such rapid descent speeds to occur in the Sun, because there the gas is turbulent and will behave effectively in a much more viscous and also more irregular fashion, where downdrafts break up and change direction before they can reach significant speeds.
In the case of H− opacity, the flux concentrations are weaker because the deeper parts are stably stratified. Here again, the turbulence would have mixed the gas even before triggering downflows, so the background stratification would be more nearly adiabatic to begin with. This can be seen clearly from realistic solar simulations of Stein & Nordlund (1998); see their Fig. 13.
In models without partial ionization, flux concentrations form just above the height where the forcing function is placed, whereas in models including partial ionization, such flux concentrations form at the surface (where τ = 1). Here the specific entropy is unstably stratified and tends to drop by a significant amount. Under the influence of downward suction, this could still lead to significant descent speeds with a corresponding return flow as a result of mass conservation. The return flow, instead of closing near the height where the forcing function is placed, closes at the surface, from where the gas had earlier been pulled down.
It is surprising that the temperature reduction inside the downdrafts is rather modest and to some extent compensated for by the supply of hotter material from the converging return flow. Thus, the magnetic structure is in our case largely confined by dynamic rather than gas pressure. Therefore the changes in the thermodynamic properties across the flux tube are only moderate. As a consequence, the τ = 1 surface remains nearly flat.
In view of applications to sunspots, it would be important to consider the effects of turbulent convection and its suppression by the magnetic field. Such effects have been used in the models of Kitchatinov & Mazur (2000) that could explain the self-amplification of magnetic flux by a mechanism somewhat reminiscent of the negative effective magnetic pressure instability. In our model, convection would of course develop automatically if we only let the simulation run long enough, because the stratification is already Schwarzschild unstable. The degree to which the resulting convection contributes to the vertical energy transport should increase with increasing opacity, but with the rescaled opacities in our models it will be less than in the Sun.
Our findings also relate to the question of what drives turbulence in the bulk of the solar convection zone. Solving just the radiative equilibrium equations for the solar envelope would result in a stable stratification, because the standard Kramers opacity with a = 1 and b = −7/2, corresponding to a stable polytrope with n = 3.25. Yet, those layers are unstable mainly because of the continuous rain of low entropy material from the top (Spruit 1997; Brandenburg 2015). Clearly, a more detailed investigation of this within the framework of the present model would be needed, but this is well outside the scope of the present paper. Based on the results obtained in the present work, we can say that the effects of partial ionization and resulting stratification are of crucial importance for the production of strong magnetic flux amplifications just near the visible surface.
Acknowledgments
We are grateful to the referee for making a number of useful suggestions. PB thanks Nordita for support and warm hospitality while work on this paper was being carried out. She also acknowledges support from CSIR in India and use of high performance facility at IUCAA, India. This work was supported in part by the European Research Council under the AstroDyn Research Project No. 227952, and by the Swedish Research Council under the project grants 621-2011-5076 and 2012-5797. We acknowledge the allocation of computing resources provided by the Swedish National Allocations Committee at the Center for Parallel Computers at the Royal Institute of Technology in Stockholm and the National Supercomputer Centers in Linköping, the High Performance Computing Center North in Umeå, and the Nordic High Performance Computing Center in Reykjavik.
References
- Barekat, A., & Brandenburg, A. 2014, A&A, 571, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brandenburg, A. 2015 ApJ, submitted [arXiv:1504.03189] [Google Scholar]
- Brandenburg, A., Chan, K. L., Nordlund, Å., & Stein, R. F. 2005, Astron. Nachr., 326, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., Kleeorin, N., & Rogachevskii, I. 2013, ApJ, 776, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., Gressel, O., Jabbari, S., Kleeorin, N., & Rogachevskii, I. 2014, A&A, 562, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chan, K. L., & Sofia, S. 1986, ApJ, 307, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Chan, K. L., & Sofia, S. 1989, ApJ, 336, 1022 [NASA ADS] [CrossRef] [Google Scholar]
- Heinemann, T., Dobler, W., Nordlund, Å., & Brandenburg, A. 2006, A&A, 448, 731 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heinemann, T., Nordlund, Å., Scharmer, G. B., & Spruit, H. C. 2007, ApJ, 669, 1390 [NASA ADS] [CrossRef] [Google Scholar]
- Käpylä, P. J., Mantere, M. J., Cole, E., Warnecke, J., & Brandenburg, A. 2013, ApJ, 778, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Kippenhahn, R., & Weigert, A. 1990, Stellar structure and evolution (Berlin: Springer) [Google Scholar]
- Kitchatinov, L. L., & Mazur, M. V. 2000, Solar Phys., 191, 325 [Google Scholar]
- Kleeorin, N. I., Rogachevskii, I. V., & Ruzmaikin, A. A. 1989, Pis. Astron. Zh., 15, 639 [NASA ADS] [Google Scholar]
- Kleeorin, N., Mond, M., & Rogachevskii, I. 1996, A&A, 307, 293 [NASA ADS] [Google Scholar]
- Mihalas, D. 1978, Stellar Atmospheres (San Francisco: W. H. Freeman) [Google Scholar]
- Nordlund, Å, Stein, R. F., & Asplund, M. 2009, Liv. Rev. Sol. Phys., 6, 2 [Google Scholar]
- Parker, E. N. 1974, ApJ, 189, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1976, ApJ, 210, 816 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1978, ApJ, 221, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Rast, M. P., & Toomre, J. 1993, ApJ, 419, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Rempel, M., & Cheung, M. C. M. 2014, ApJ, 785, 90 [Google Scholar]
- Rempel, M., & Schlichenmaier, R. 2011, Liv. Rev. Sol. Phys., 8, 3 [Google Scholar]
- Spruit, H. 1997, Mem. Soc. Astron. It., 68, 397 [NASA ADS] [Google Scholar]
- Spruit, H. C. 1979, Solar Phys., 61, 363 [Google Scholar]
- Stein, R. F., & Nordlund, Å. 1998, ApJ, 499, 914 [Google Scholar]
- Spruit, H. C., & Zweibel, E. G. 1979, Solar Phys., 62, 15 [Google Scholar]
- Stix, M. 2002, The Sun: An introduction (Berlin: Springer-Verlag) [Google Scholar]
Appendix A: Thermodynamic functions
For completeness, we list here the relevant thermodynamic functions as implemented by Tobias Heinemann into the Pencil Code. We have 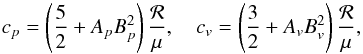 (A.1)as well as α = Ap/Av and δ = 1 + ApBp, where
(A.1)as well as α = Ap/Av and δ = 1 + ApBp, where ![\appendix \setcounter{section}{1} \begin{equation} \label{AB} \begin{array}{ll} A_p={\displaystyle{\yH(1-\yH)\over(2-\yH)\xHe+2}},\quad& B_p={\displaystyle{5\over2}+{\chi_{\rm H}\over\kB T}},\\ \\[2mm] A_v={\displaystyle{\yH(1-\yH)\over(2-\yH)(1+\yH+\xHe)}},\quad& B_v={\displaystyle{3\over2}+{\chi_{\rm H}\over\kB T}}\cdot \end{array} \end{equation}](/articles/aa/full_html/2016/03/aa25396-14/aa25396-14-eq245.png) (A.2)
(A.2)
Appendix B: Effect of partial ionization on entropy profile
On differentiating the equation of state, p = ℛTρ/μ, we have, 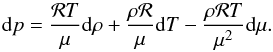 (B.1)Then we express dμ in terms of dyH using Eq. (5),
(B.1)Then we express dμ in terms of dyH using Eq. (5), ![\appendix \setcounter{section}{2} \begin{equation} {\dd p}=\frac{\rho {\cal R}T}{\mu_0}\left[\left({\dd\!\ln\rho} +{\dd\!\ln T}\right)(1+\yH+\xHe)+{\dd\yH}\right]. \label{diffpfinal} \end{equation}](/articles/aa/full_html/2016/03/aa25396-14/aa25396-14-eq250.png) (B.2)We substitute Eq. (B.2) into the equation for first law of thermodynamics, Tds = de + pdv, where v = ρ-1 is specific volume,
(B.2)We substitute Eq. (B.2) into the equation for first law of thermodynamics, Tds = de + pdv, where v = ρ-1 is specific volume, ![\appendix \setcounter{section}{2} \begin{eqnarray} {\dd s}=&&\frac{1}{T}\left[{\dd e} + {\dd(pv)} -\frac{1}{\rho}{\dd p}\right] \\[2mm] =&&\left(\frac{3{\cal R}}{2\mu_0}{\dd\!\ln T} -\frac{{\cal R}}{\mu_0}{\dd\!\ln\rho}\right) (1+\yH+\xHe) \nonumber \\[2mm] &&- \frac{{\cal R}}{\mu_0}{\dd\yH}\left[\frac{3}{2}+\frac{\chiH}{k_B T}\right], \label{dseq} \end{eqnarray}](/articles/aa/full_html/2016/03/aa25396-14/aa25396-14-eq253.png) where we have used e = (3/2) ℛT/μ + eH. Next, differentiate the Saha equation of ionization,
where we have used e = (3/2) ℛT/μ + eH. Next, differentiate the Saha equation of ionization, 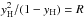 , where
, where 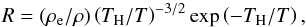 (B.5)
(B.5)
we have, 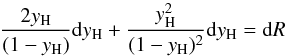 (B.6)and
(B.6)and ![\appendix \setcounter{section}{2} \begin{eqnarray} \label{dreq} \dd R &=& {\rhoe/\rho}\left({T_{\rm H}/ T}\right)^{-3/2} \exp\left(-{T_{\rm H}/ T}\right) \\ &&\times \left[-{\dd\!\ln\rho} -\frac{3}{2}{\dd\!\ln T}+ \frac{\chiH}{k_BT}{\dd\!\ln T}\right].\nonumber \end{eqnarray}](/articles/aa/full_html/2016/03/aa25396-14/aa25396-14-eq258.png) (B.7)After substituting Eq. (B.7) into Eq. (B.6), we obtain a relation between dyH, dlnT and dlnρ,
(B.7)After substituting Eq. (B.7) into Eq. (B.6), we obtain a relation between dyH, dlnT and dlnρ, ![\appendix \setcounter{section}{2} \begin{equation} {(2-\yH)\over \yH(1-\yH)}{\dd\yH} = \left[-{\dd\!\ln\rho} -\left(\frac{3}{2}- \frac{\chiH}{k_BT}\right){\dd\!\ln T}\right]. \label{dyeqfinal} \end{equation}](/articles/aa/full_html/2016/03/aa25396-14/aa25396-14-eq262.png) (B.8)Based on the behavior of temperature profile we can have two cases, the optically thick τ ≫ 1 and the optically thin τ ≪ 1. In the case of τ ≫ 1, ρ ∝ Tn and hence, dlnρ = n dlnT. We use this relation in Eq. (B.8), and have,
(B.8)Based on the behavior of temperature profile we can have two cases, the optically thick τ ≫ 1 and the optically thin τ ≪ 1. In the case of τ ≫ 1, ρ ∝ Tn and hence, dlnρ = n dlnT. We use this relation in Eq. (B.8), and have, 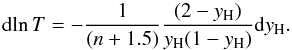 (B.9)In the optically thick part, T is large, thus TH(dT/T2) is small and can be neglected in Eq. (B.8). Again we use the relation dlnρ = n dlnT in Eq. (B.4) to eliminate dlnρ and finally substitute Eq. (B.9) into Eq. (B.4), to obtain,
(B.9)In the optically thick part, T is large, thus TH(dT/T2) is small and can be neglected in Eq. (B.8). Again we use the relation dlnρ = n dlnT in Eq. (B.4) to eliminate dlnρ and finally substitute Eq. (B.9) into Eq. (B.4), to obtain, ![\appendix \setcounter{section}{2} \begin{equation} \dd s=\dd\yH{{\cal R}\over\mu_0}\left[{(n-1.5)\over(n+1.5)}{(2-\yH)(1+\yH+\xHe)\over\yH(1-\yH)}- {3\over2} - {\chiH\over k_BT}\right]\cdot \label{dsdh11} \end{equation}](/articles/aa/full_html/2016/03/aa25396-14/aa25396-14-eq267.png) (B.10)In the case of τ ≪ 1, we use the fact that dlnT = 0 as T is nearly constant here and then obtain,
(B.10)In the case of τ ≪ 1, we use the fact that dlnT = 0 as T is nearly constant here and then obtain, ![\appendix \setcounter{section}{2} \begin{equation} \dd s=\dd\yH{{\cal R}\over\mu_0}\left[{(2-\yH)(1+\yH+\xHe)\over\yH(1-\yH)} - {3\over2} - {\chiH\over k_BT}\right]\cdot \label{dsdh22} \end{equation}](/articles/aa/full_html/2016/03/aa25396-14/aa25396-14-eq269.png) (B.11)Both Eqs. (B.10) and (B.11) can be written in the following form using expressions in Eq. (A.2),
(B.11)Both Eqs. (B.10) and (B.11) can be written in the following form using expressions in Eq. (A.2), ![\appendix \setcounter{section}{2} \begin{eqnarray} \label{dsdh111}&&\dd s=\dd\yH{{\cal R}\over\mu_0}\left[{1\over A_v}{(n-3/2)\over(n+3/2)} - B_v\right], \\ \label{dsdh222} &&\dd s=\dd\yH{{\cal R}\over\mu_0}\left[{1\over A_v}- B_v\right]. \end{eqnarray}](/articles/aa/full_html/2016/03/aa25396-14/aa25396-14-eq270.png) From Eqs. (B.12) and (B.13), its clear that the extrema in entropy profile correspond to the extrema in yH.
From Eqs. (B.12) and (B.13), its clear that the extrema in entropy profile correspond to the extrema in yH.
All Tables
All Figures
 |
Fig. 1 Comparison of ρ, T, s, yH, γ and cp along each row, top to bottom, from models with (solid, black) and without (dotted, blue) hydrogen ionization for Runs A, B and C along each column, left to right, and |
| In the text | |
 |
Fig. 2 Comparison of models with ρ0 = 0.002 g cm-3 (solid), 0.005 g cm-3 (dashed), and 0.01 g cm-3 (dotted lines). Here (a,b) is (1,0), corresponding to n = 1.5. |
| In the text | |
 |
Fig. 3 Snapshots of Run F3 (fixed ionization, yH = 1) showing temperature (color coded), magnetic field lines, and velocity vectors at two times before and after the flux concentration develops. The solid yellow line at z ≈ 9 Mm indicates the τ = 1 surface while the dashed blue line indicates the height z0 where suction operates. |
| In the text | |
 |
Fig. 4 Same as Fig. 3, but for variable partial ionization for Run K3a2 at two times just before and after the flux concentration develops. |
| In the text | |
 |
Fig. 5 Temperature versus optical depth and height at different times through x = 0 (solid lines and a dotted line for the last time) and x = Lx/ 2 (dashed lines) for Run K3a2 at times 1.6–1.9 ks. |
| In the text | |
 |
Fig. 6 Temperature and vertical magnetic field strength versus x at different times (1.4–2 ks) through z = 8 Mm for Run K3a2. |
| In the text | |
 |
Fig. 7 Comparison of vertical magnetic field strength from Runs K3a1, K3a2 and K3a3 at t = 1.6 ks. |
| In the text | |
 |
Fig. 8 Vertical velocity at x = 0 versus height at different times (1.6–1.9 ks) for Run K3a2. |
| In the text | |
 |
Fig. 9 Similar to Fig. 8, but for Run K3b with 10 times weaker suction. The red dash-dotted lines shows the profile of sound speed. |
| In the text | |
 |
Fig. 10 Degree of ionization and ratio or specific heats versus height, from Run K3a2. |
| In the text | |
 |
Fig. 11 Specific entropy and specific heat at constant pressure versus height, from Run K3a2. |
| In the text | |
 |
Fig. 12 Profiles of T, s, ρ, yH, κ, and K for Run D, with H− opacity. The red symbol indicates the position of τ = 1. |
| In the text | |
 |
Fig. 13 Same as Fig. 4, but for Run H3 using the H− opacity with a scaling coefficient of 10-6. |
| In the text | |
 |
Fig. 14 Same as Fig. 5, but for Run H3 using the H− opacity with a scaling coefficient of 10-6. Note the increase in temperature at z ≈ 8 Mm. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


