| Issue |
A&A
Volume 586, February 2016
|
|
|---|---|---|
| Article Number | A18 | |
| Number of page(s) | 2 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201527949 | |
| Published online | 20 January 2016 | |
Research Note
Bernoulli equation and the nonexistence of maximal jets
Centrum Astronomiczne im. M. Kopernika, Bartycka 18, 00-716 Warszawa, Poland
e-mail: aaz@camk.edu.pl
Received: 12 December 2015
Accepted: 28 December 2015
We discuss the idea of maximal jets introduced by Falcke & Biermann (1995, A&A, 293, 665). According to it, the maximum possible jet power in its internal energy equals the kinetic power in its rest mass. We show this result is incorrect because of an unfortunate algebraic mistake.
Key words: acceleration of particles / galaxies: jets / ISM: jets and outflows / magnetic fields / radiation mechanisms: non-thermal
© ESO, 2016
1. Introduction
Relativistic jets are common in active galactic nuclei. They accrete black-hole and neutron-star binaries, as well as γ-ray bursts, and occasionally appear in tidal disruption events. Calculating their properties is obviously of major importance.
We consider here a result of Falcke & Biermann (1995, hereafter FB95). It claims that there is an upper limit to a component of the jet power in its internal energy. This is an influential, highly cited paper. Here, we correct one of its results.
2. Maximal jets
We follow here the notation of FB95. The jet power, Qjet, and its mass flow rate, Ṁjet, can be connected to the mass flow rate through the accretion disc, Ṁdisc, thereby defining two dimensionless constants as in Eq. (1) of FB95: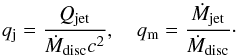 
(1)The Bernoulli equation is obtained by dividing the equations of energy and mass conservation. For a conservative jet with the mass dominated by protons, it is given by Eq. (27) of FB95, which can be expressed as 
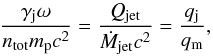(2)where ω and ntot are the density of the enthalpy (including rest mass) and of protons, respectively, and γj is the jet bulk Lorentz factor. The enthalpy density for a polytropic gas with the adiabatic index Γ is (as in Eq. (21) of FB95), 
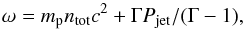(3)where Pjet is the jet pressure. Equation (2) implies that the maximum possible bulk Lorentz factor, corresponding to the complete conversion of the internal energy into the bulk motion, is γj,max = qj/qm. The sound speed in the jet frame, βs = (∂Pjet/∂ϵ)1 / 2, where ϵ is the internal energy density including the rest mass, can be written using the first law of thermodynamics (see, e.g., Königl 1980), 
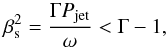(4)which is equivalent to Eq. (23) of FB95, and where the upper limit to the sound speed corresponds to the gas being extremely relativistic, ω ≫ mpntotc2. Equation (3) can be rewritten as 
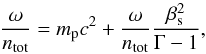(5)which has the solution of 
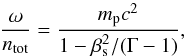(6)or equivalently using Eq. (2), 
(7)This equation yields the obvious result that the jet gas can be highly relativistic,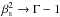 
, only for qm/qj ≪ 1 /γj, i.e., for jets with little relative matter content. On the other hand, βs = 0 corresponds to the jet with the maximum possible bulk Lorentz factor, equal to γj,max, after a conversion of all of the internal energy into bulk motion. We note that Eq. (6) is identical to Eq. (A8) of Fukue (2004) except for the g00 metric factor in the latter.
On the other hand, the version of our Eq. (7) in FB95, their Eq. (28),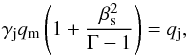 
(8)is incorrect because of an unfortunate error in the algebraic transformation. A similar (incorrect) form of the Bernoulli equation is also given in Eq. (1) of Falcke et al. (1993). It appears that the origin of this error is the fact that Eq. (8) is the non-relativistic limit of Eq. (7), and this would be true if the nonrelativistic form of the sound speed, 
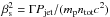, is applied.
As noted by FB95, the maximum value (corresponding to the maximum of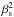 
) of the term in parentheses in Eq. (8) is 2. Given that, Eq. (2) implies that the maximum possible total enthalpy density is ω = 2ntotmpc2; i.e., the maximum internal enthalpy density equals ntotmpc2. Since the jet power equals the enthalpy flux, this implies in turn that the maximum possible component of the jet power in its internal enthalpy equals the jet kinetic power (i.e., in its rest mass). FB95 called this case the “maximal jet”. However, since Eq. (8) is incorrect, this theoretical concept is also incorrect. The correct form of Eq. (8) is given by Eq. (7), in which the term in brackets can be arbitrarily large, implying no limit on the internal power, hence no maximal jets. We also note that this maximum was supposed to correspond to 
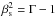, i.e., an extremely relativistic gas, which is not the case for ω = 2ntotmpc2. This incorrect concept has been adopted in a large number of papers (e.g., Falcke 1996; Markoff et al. 2001, 2003, 2005; Markoff & Nowak 2004; Maitra et al. 2009; Plotkin et al. 2015). In particular, the formula (8) for the maximal jet is one of the underlying assumptions of the complex jet model of Markoff et al. (2005), which is widely used to fit broad-band spectra of black-hole binaries and Sgr A*.
FB95 also considered equipartition between magnetic energy density, uB, and the particle internal energy density. If the latter equals the rest mass energy density, we have the magnetization parameter of σ ∼ 1 / 2, where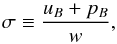 
(9)and pB is the magnetic pressure. We note that the magnetic enthalpy, uB + pB, should be included in the Bernoulli equation. This expresses how a jet can be accelerated at the expense of both the magnetic energy and the internal particle energy. Approximately, maximal jets with equipartition correspond to σ ∼ 1 / 2. This is similar to σ ≃ 1, up to which the magnetic-to-kinetic energy conversion via differential collimation of poloidal magnetic surfaces is efficient (Tchekhovskoy et al. 2009; Lyubarsky 2010; Komissarov 2011). However,
jets can have σ ≫ 1 initially, while blazar jets beyond radio cores have the opening angles Θj ∼ (0.1–0.2) /γj (Jorstad et al. 2005; Pushkarev et al. 2009; Clausen-Brown et al. 2013). Since σ ∼ (Θjγj)2 (Tchekhovskoy et al. 2009; Komissarov et al. 2009), some processes should be able to decrease σ to values ≪1.
3. Conclusion
We have clarified the issue of the existence of maximal jets, after correcting an algebraic error of FB95. We showed that the maximal internal enthalpy density in jets is not limited by the rest-mass energy density, and correspondingly, the internal jet power is not limited by the (rest-mass) kinetic jet power.
Acknowledgments
We thank Arieh Königl for valuable comments and for checking the results of this work and Heino Falcke for valuable discussions. This research has been supported in part by the Polish NCN grants 2012/04/M/ST9/00780 and 2013/10/M/ST9/00729.
References
- Clausen-Brown, E., Savolainen, T., Pushkarev, A. B., Kovalev, Y. Y., & Zensus, J. A. 2013, A&A, 558, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Falcke, H. 1996, ApJ, 464, L67 [NASA ADS] [CrossRef] [Google Scholar]
- Falcke, H., & Biermann, P. L. 1995, A&A, 293, 665 (FB95) [NASA ADS] [Google Scholar]
- Falcke, H.,Mannheim, K., & Biermann, P. L. 1993, A&A, 278, L1 [NASA ADS] [Google Scholar]
- Fukue, J. 2004, PASJ, 56, 959 [NASA ADS] [CrossRef] [Google Scholar]
- Jorstad, S. G.,Marscher, A. P.,Lister, M. L., et al. 2005, AJ, 130, 1418 [NASA ADS] [CrossRef] [Google Scholar]
- Komissarov, S. S. 2011, Mem. Soc. Astron. It., 82, 95 [NASA ADS] [Google Scholar]
- Komissarov, S. S.,Vlahakis, N.,Königl, A., & Barkov, M. V. 2009, MNRAS, 394, 1182 [NASA ADS] [CrossRef] [Google Scholar]
- Königl, A. 1980, Phys. Fluids, 23, 1083 [NASA ADS] [CrossRef] [Google Scholar]
- Lyubarsky, Y. E. 2010, MNRAS, 402, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Maitra, D., Markoff, S., Brocksopp, C., et al. 2009, MNRAS, 398, 1638 [NASA ADS] [CrossRef] [Google Scholar]
- Markoff, S., & Nowak, M. A. 2004, ApJ, 609, 972 [NASA ADS] [CrossRef] [Google Scholar]
- Markoff, S.,Falcke, H., & Fender, R. 2001, A&A, 372, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Markoff, S.,Nowak, M.,Corbel, S.,Fender, R., & Falcke, H. 2003, A&A, 397, 645 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Markoff, S., Nowak, M. A., & Wilms, J., 2005, ApJ, 635, 1203 [NASA ADS] [CrossRef] [Google Scholar]
- Plotkin, R. M.,Gallo, E.,Markoff, S., et al. 2015, MNRAS, 446, 4098 [NASA ADS] [CrossRef] [Google Scholar]
- Pushkarev, A. B.,Kovalev, Y. Y.,Lister, M. L., & Savolainen, T. 2009, A&A, 507, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tchekhovskoy, A.,McKinney, J. C., & Narayan, R. 2009, ApJ, 699, 1789 [NASA ADS] [CrossRef] [Google Scholar]
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.