| Issue |
A&A
Volume 586, February 2016
|
|
|---|---|---|
| Article Number | A26 | |
| Number of page(s) | 4 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201527444 | |
| Published online | 21 January 2016 | |
Quasars can be used to verify the parallax zero-point of the Tycho-Gaia Astrometric Solution
Lund Observatory, Department of Astronomy and Theoretical Physics, Lund University, Box 43, 22100 Lund, Sweden
e-mail: daniel.michalik@astro.lu.se; lennart@astro.lu.se
Received: 24 September 2015
Accepted: 25 October 2015
Context. The Gaia project will determine positions, proper motions, and parallaxes for more than one billion stars in our Galaxy. It is known that Gaia’s two telescopes are affected by a small but significant variation of the basic angle between them. Unless this variation is taken into account during data processing, e.g. using on-board metrology, it causes systematic errors in the astrometric parameters, in particular a shift in the parallax zero-point. Previously, we suggested an early reduction of Gaia data for the subset of Tycho-2 stars (Tycho-Gaia Astrometric Solution; TGAS).
Aims. We investigate whether quasars can be used to independently verify the parallax zero-point in early data reductions. This is not trivially possible as the observation interval is too short to disentangle parallax and proper motion for the quasar subset.
Methods. We repeat TGAS simulations but additionally include simulated Gaia observations of quasars from ground-based surveys. All observations are simulated with basic angle variations. To obtain a full astrometric solution for the quasars in TGAS we explore the use of prior information for their proper motions.
Results. It is possible to determine the parallax zero-point for the quasars with a few μas uncertainty, and it agrees to a similar precision with the zero-point for the Tycho-2 stars. The proposed strategy is robust even for quasars exhibiting significant spurious proper motion due to a variable source structure, or when the quasar subset is contaminated with stars misidentified as quasars.
Conclusions. Using prior information about quasar proper motions we could provide an independent verification of the parallax zero-point in early solutions based on less than one year of Gaia data.
Key words: astrometry / methods: data analysis / parallaxes / proper motions / quasars: general / space vehicles: instruments
© ESO, 2016
1. Introduction
The European space mission Gaia determines astrometry, photometry, and spectroscopy for more than one billion sources1 (Perryman et al. 2001; de Bruijne 2012). Important features of Gaia’s astrometric measurements are
-
the uniform scanning that ensures a relatively homogeneousall-sky performance;
-
the high accuracy of the final astrometric data, at a level of tens of μas for G = 15;
-
the relatively faint G ≃ 20 mag limit, which makes it possible to observe a large number of quasars, necessary for the determination of the reference frame and as an independent check of the parallax zero-point;
-
and the capability to measure absolute parallaxes by combining simultaneous measurements of different objects separated by a large angle on the sky.
For the last point, Gaia’s design includes two viewing directions separated by a large basic angle, which needs to be either perfectly stable or independently monitored. Gaia’s basic angle was designed to be very stable, while at the same time being measured on board with high accuracy through an interferometric device called the basic angle monitor (BAM; Mora et al. 2014).
Verification of the stability of the basic angle and of the quality of the on-board metrology can be done only partially through the analysis of the post-fit residuals of the astrometric solution; a full verification requires the use of external data. Quasars provide a clean and self-consistent approach, as they are so far away that their true parallaxes can safely be assumed to be zero. It is thus possible to determine the zero-point of the parallaxes measured by Gaia simply by taking the median of the resulting parallax distribution in a quasar subset and comparing it to the expected zero value. The width of this distribution gives an indication of the uncertainty of the obtained median value.
For a full five-parameter solution of the astrometric parameters (position, parallax, and proper motion), at least five distinct observations of each source are necessary, unless prior knowledge can be used to complement the observational data (Michalik et al. 2015b). A full five-parameter data reduction with less than one year of Gaia data is possible, for example, for the Tycho-2 (Tycho-Gaia Astrometric Solution, hereafter TGAS; Michalik et al. 2015a) and the Hipparcos stars (Hundred Thousand Proper Motions project, hereafter HTPM; Mignard 2009; Michalik et al. 2014). The Tycho-2 and Hipparcos catalogues contain extremely few extragalactic objects, which are not sufficient for an independent verification of the basic angle. Adding quasars to such early solutions requires prior information to overcome the ambiguity of parallax and proper motion. In this paper we explore which prior information can be used, and demonstrate the feasibility of adding quasars to the TGAS project for verification of the parallax zero-point in the light of basic angle variations.
2. Basic angle variations and metrology
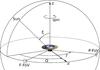 |
Fig. 1 Solar-aspect angle ξ and spin phase Ω define the orientation of the spacecraft relative to the Sun. x and z are axes fixed in the spacecraft reference system. The basic angle Γ separates the preceding and following fields of view (FoV), with x half-way between them. |
The two viewing directions of Gaia are separated by a basic angle Γ = 106.5deg. Basic angle variations are harmful to the resulting astrometry unless they are modelled as part of the data processing or corrected by means of data from the on-board metrology device, BAM. The BAM deploys a laser beam to create an interferometric pattern in each field of view (FoV). Variations in the basic angle cause a change in the relative phases of the fringes, which are measured by a dedicated BAM CCD adjacent to the main astrometric field of Gaia. It is desirable to verify that these measurements correctly characterize the variations for the entire focal plane. This can be done by comparing the BAM data with the variations determined from the astrometric observations themselves.
Gaia’s scanning requires a constant tilt ξ = 45deg of the spacecraft spin axis with respect to the Sun (de Bruijne 2012). The phase of the spacecraft relative to the Sun is therefore completely described by the angle Ω(t) giving the pointing of the satellite within its six-hour spin period (Fig. 1). Mora et al. (2014) reported an early analysis of BAM measurements finding stable periodic variations depending on Ω with an amplitude of about 1000 μas. This is much larger than expected from the design of the spacecraft; however, the effects on the astrometric results can be largely eliminated if the basic angle variations are determined with sufficient accuracy. The basic angle variations can be described by a Fourier expansion in terms of coskΩ and sinkΩ where k = 1,2,... is the order of the harmonics.
Dedicated simulations have shown that all but the cosΩ term can be solved with high accuracy using Gaia data alone, even with less than one year of observations. They are thus neglected throughout the rest of this article. However, the first cosine harmonic is virtually indistinguishable from a constant shift of the parallax zero-point (Lindegren et al. 1992, Sect. 6.1) and therefore impossible2 to determine from Gaia data alone. Lindegren (2004) relates the parallax zero-point Δϖ to the amplitude a1 of the cosΩ term and the spacecraft distance R (in au) from the Sun as 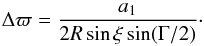 (1)In this paper we limit the further analysis to the first cosine term assuming a fixed amplitude a1 = 1000μas. For the observation interval used in the following simulations R evolves such that the expected average is Δϖ ≃ 871.9μas.
(1)In this paper we limit the further analysis to the first cosine term assuming a fixed amplitude a1 = 1000μas. For the observation interval used in the following simulations R evolves such that the expected average is Δϖ ≃ 871.9μas.
3. Quasar parallaxes in early solutions
We first repeat simulations of the TGAS scenario as described in Michalik et al. (2015a, Sect. 3), but perturb the observations by a periodic basic angle variation proportional to cosΩ with an amplitude of 1000 μas. Otherwise we follow the same assumptions as before, i.e. we simulate half a year of Gaia observations of the Hipparcos and Tycho-2 stars, and process them using the Hipparcos positions and proper motions and the Tycho-2 positions at 1991.25 as priors. As expected, the resulting parallax solution is strongly biased with a median parallax error (estimated minus true value) consistent with Eq. (1). This zero-point shift cannot be easily determined from the stellar observations themselves, and the recovery of absolute parallaxes in such a solution must instead rely on the correctness of BAM metrology, which can be verified by using external information.
Thus, it is desirable to include an additional subset of quasars. The true quasar parallaxes are known to be virtually zero. Therefore, the median of the quasar subset can be used to estimate the parallax zero-point of the astrometric solution. For our simulations the quasar subset is taken from the Gaia Initial Quasar Catalogue (GIQC; Andrei et al. 2014), which is a list of quasars produced in preparation for the Gaia mission. It is based mainly on the Large Quasar Astrometric Catalogue (LQAC; Souchay et al. 2012), which itself is based on the Sloan Digital Sky Survey (SDSS; Abazajian et al. 2009) and other ground-based surveys. It contains positions and approximate magnitudes for over one million objects. The source distribution is strongly inhomogeneous and shows the survey footprint. Within the magnitude limits of Gaia we use the ~190 000 entries flagged as “defining”, i.e. objects that are quasars with a high level of certainty based on their observational history and spectroscopic properties.
To account for the possibility that early Gaia solutions might not include observations for all of them, 150 000 (~80%) of the quasars listed in GIQC are randomly selected and the rest are discarded. From GIQC we use the position and magnitude to define the simulated “true” quasar sources. The true values of parallax and proper motion are initially set to zero.
To allow us to obtain a sensible five-parameter solution with a stretch of data as short as in a half-year TGAS solution, we need some prior information for the quasars. One could consider using the precisely known radio positions of VLBI quasars. Approximately 2500 ICRF sources with optical counterparts are expected to be bright enough to be detected by Gaia. However, this number of sources is too small to provide a statistically meaningful result. For the much larger number of GIQC quasars no reliable position information exists at a level that makes it usable as prior information. Even though we know that quasar parallaxes are supposed to be zero, we do not want to use this as prior information in the solution either, since we want to determine the parallax values freely from the Gaia data in order to verify the parallax zero-point. Instead, we suggest making use of the fact that quasars have negligible proper motions3 due to their cosmological distances. Incorporating this information as a prior in the early Gaia astrometric solutions will lift the parallax–proper motion degeneracy and is sufficient to obtain a good astrometric solution for the quasar subset.
We demonstrate the feasibility of the method through three different simulations. First we use a clean quasar sample with zero true proper motions and parallaxes. Then we relax these assumptions and introduce quasar structure variations, as well as contamination of the dataset with stellar sources. Table 1 shows the results of the three experiments (see below for further explanations).
3.1. Clean quasar sample
In the first experiment the simulated true parallaxes and proper motions in the quasar subset are strictly zero. To allow a full five-parameter astrometric solution we apply a prior of 0 ± 10μas yr-1 to each proper motion component. The prior uncertainty of 10 μas yr-1 is somewhat arbitrary, but provides enough weight to constrain the proper motions to negligible values without causing numerical difficulties. We incorporate the prior using Bayes’ rule as described in Michalik et al. (2015b).
We evaluate the resulting parallaxes separately for the stellar subset (Hipparcos and Tycho-2 stars) and the quasars. Table 1, experiment 1, presents the median value of the parallax errors (estimated minus true), the uncertainty of the median calculated using the bootstrap method, and the RSE 4 dispersion of the parallax errors for each of the subsets. The different columns give statistics for selections based on the individual formal standard uncertainties of the parallaxes. The median obtained for the quasar subset agrees with the corresponding stellar value to within a few μas, independent of the selection of sources.
Simulation results of three different experiments comparing the parallax median between the stellar subset and the quasars.
3.2. Spurious proper motion from variable source structure
Variation in the source structure of quasars can lead to shifts of their photocentres up to the milliarcsecond level (e.g. Popović et al. 2012; Porcas 2009; Taris et al. 2011). Linear trends of these shifts might lead to spurious proper motions measured for quasars and stable over years to decades. Titov et al. (2011) fitted long-term proper motions for 555 quasars from VLBI observations. The total proper motion 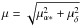 in μas yr-1 in their catalogue can be described by a log-normal distribution with mean 1.9 dex and standard deviation 0.61 dex. It is impossible to say whether these measurements give an optimistic or conservative characterization of spurious quasar proper motions on the much shorter time baselines of our simulations. Additionally, the morphology of the host galaxy might lead to a statistical increase in the centroiding error, and photometric variability of the nucleus together with the stable photocentre of the host galaxy might lead to an effect similar to “variability-induced movers” in binaries (Wielen 1996). Physically all of these effects are expected to be random and therefore should only increase the dispersion of the results but not the median values themselves.
in μas yr-1 in their catalogue can be described by a log-normal distribution with mean 1.9 dex and standard deviation 0.61 dex. It is impossible to say whether these measurements give an optimistic or conservative characterization of spurious quasar proper motions on the much shorter time baselines of our simulations. Additionally, the morphology of the host galaxy might lead to a statistical increase in the centroiding error, and photometric variability of the nucleus together with the stable photocentre of the host galaxy might lead to an effect similar to “variability-induced movers” in binaries (Wielen 1996). Physically all of these effects are expected to be random and therefore should only increase the dispersion of the results but not the median values themselves.
We use the statistical properties of the results by Titov et al. (2011) as the basis for simulations, but apply a factor of 10 to provide a conservative assumption on the total spurious motion. The individual components of the proper motion are computed as 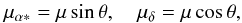 (2)where θ is a random position angle and log 10μ is taken from a normal distribution with mean value 2.9 dex and standard deviation 0.61 dex. The median value of the resulting μ is about 800 μas yr-1. While this spurious proper motion increases the RSE of the solution for the quasar subset, the agreement of median parallax between the quasars and the stellar subset remains at the previous level (see Table 1, experiment 2). This shows that significant spurious proper motions due to photocentre variability do not harm the proposed strategy.
(2)where θ is a random position angle and log 10μ is taken from a normal distribution with mean value 2.9 dex and standard deviation 0.61 dex. The median value of the resulting μ is about 800 μas yr-1. While this spurious proper motion increases the RSE of the solution for the quasar subset, the agreement of median parallax between the quasars and the stellar subset remains at the previous level (see Table 1, experiment 2). This shows that significant spurious proper motions due to photocentre variability do not harm the proposed strategy.
3.3. Contamination through misidentification
One potential problem with the use of quasars for the zero-point verification will be the identification of quasars in the Gaia observations. It is possible that a small fraction will be misclassified. Stars mistaken for quasars may have a noticeable parallax and proper motion which could contaminate the results obtained for the presumed quasar subset. To characterize the deterioration caused by misclassification, we replace 5% of the quasars by stellar sources. We assume that misclassification will be most prevalent for faint sources where no good spectra exist, and obtain true positions, parallaxes, and proper motions for contaminating stars from the Gaia Universe Model Snapshot (GUMS; Robin et al. 2012). We use the 7500 brightest stars fainter than magnitude 19. The results for experiment 3 in Table 1 present the combined evaluation of the quasar subset including the contaminating stars. Even with the contamination the median parallaxes of the quasar subset still agree to within a few μas with the values found for the other subsets.
4. Conclusions
We present a strategy to verify the parallax zero-point in a TGAS solution in the presence of basic angle variations. It uses quasars, which can only be included in the solution if prior information is applied. In the absence of accurate prior position information – available only for a small number of VLBI quasars – we propose to constrain their proper motions. Simulations show that this allows us to recover the parallax zero-point in a solution with half a year of Gaia data to within a few μas. This is true even if the quasars exhibit considerable variability in their photocentres, provided the resulting spurious proper motions are random from source to source. Furthermore, the scheme is robust to the quasar subset being contaminated by a significant fraction of stellar sources misclassified as quasars. In all cases the zero-point determined from the quasars agrees well with the theoretically expected parallax shift from the basic angle perturbations applied in the simulations.
Practical difficulties using quasars may arise from the colour calibration of the point spread function, which is based on stellar sources. Quasars, however, have very different spectra, which may require a separate calibration (U. Bastian, priv. comm.). Whether this can be overcome in practice remains to be seen.
Spurious proper motions caused by intrinsic variations in the quasars are discussed in Sect. 3.2. Additionally, the expected proper motion of the Galactocentric acceleration must be taken into account in the real data. This effect is a few μas yr-1 (Bastian 1995; Kovalevsky 2003) and does not affect the principle shown in this paper.
The “robust scatter estimate” (RSE) is defined as 0.390152 times the difference between the 90th and 10th percentiles of the distribution of the variable. For a Gaussian distribution it equals the standard deviation. Within the Gaia core processing community the RSE is used as a standardized, robust measure of dispersion(Lindegren et al. 2012) .
Acknowledgments
Uli Bastian, Anthony Brown, Jos de Bruijne, David Hobbs, Sergei Klioner, Timo Prusti, and an anonymous referee gave helpful comments on the draft manuscript, for which we are grateful. Thanks to Alexandre Andrei for providing the GIQC data and information about its content. This work was supported by the Gaia Data Processing and Analysis Consortium (DPAC) and uses the AGIS/AGISLab and GaiaTools software packages; special thanks to their maintainers and developers. We gratefully acknowledge financial support from the Swedish National Space Board, the Royal Physiographic Society in Lund, and from the European Space Agency (contract No. 4000108677/13/NL/CB). Quasar proper motion data were obtained through VizieR.
References
- Abazajian, K. N., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2009, ApJS, 182, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Andrei, H., Antón, S., Taris, F., et al. 2014, in Proc. Journées 2013 Systèmes de référence spatio-temporels, ed. N. Capitaine, 84 [Google Scholar]
- Bastian, U. 1995, in Future Possibilities for Astrometry in Space, eds. M. A. C. Perryman, & F. van Leeuwen, ESA SP, 379, 99 [Google Scholar]
- de Bruijne, J. H. J. 2012, Ap&SS, 341, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Kovalevsky, J. 2003, A&A, 404, 743 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L. 2004, Scientific requirements for basic angle stability monitoring, Gaia Data Processing and Analysis Consortium (DPAC) technical note GAIA-LL-057, http://www.cosmos.esa.int/web/gaia/public-dpac-documents [Google Scholar]
- Lindegren, L., Hog, E., van Leeuwen, F., et al. 1992, A&A, 258, 18 [NASA ADS] [Google Scholar]
- Lindegren, L., Lammers, U., Hobbs, D., et al. 2012, A&A, 538, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Michalik, D., Lindegren, L., Hobbs, D., & Lammers, U. 2014, A&A, 571, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Michalik, D., Lindegren, L., & Hobbs, D. 2015a, A&A, 574, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Michalik, D., Lindegren, L., Hobbs, D., & Butkevich, A. G. 2015b, A&A, 583, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mignard, F. 2009, The Hundred Thousand Proper Motions Project, Gaia Data Processing and Analysis Consortium (DPAC) technical note GAIA-C3-TN-OCA-FM-040, http://www.cosmos.esa.int/web/gaia/public-dpac-documents [Google Scholar]
- Mora, A., Biermann, M., Brown, A. G. A., et al. 2014, in SPIE Conf. Ser., 9143 [Google Scholar]
- Perryman, M. A. C., de Boer, K. S., Gilmore, G., et al. 2001, A&A, 369, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popović, L. Č., Jovanović, P., Stalevski, M., et al. 2012, A&A, 538, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Porcas, R. W. 2009, A&A, 505, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robin, A. C., Luri, X., Reylé, C., et al. 2012, A&A, 543, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Souchay, J., Andrei, A. H., Barache, C., et al. 2012, A&A, 537, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taris, F., Souchay, J., Andrei, A. H., et al. 2011, A&A, 526, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Titov, O., Lambert, S. B., & Gontier, A.-M. 2011, A&A, 529, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wielen, R. 1996, A&A, 314, 679 [NASA ADS] [Google Scholar]
All Tables
Simulation results of three different experiments comparing the parallax median between the stellar subset and the quasars.
All Figures
 |
Fig. 1 Solar-aspect angle ξ and spin phase Ω define the orientation of the spacecraft relative to the Sun. x and z are axes fixed in the spacecraft reference system. The basic angle Γ separates the preceding and following fields of view (FoV), with x half-way between them. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


