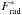| Issue |
A&A
Volume 586, February 2016
|
|
|---|---|---|
| Article Number | A88 | |
| Number of page(s) | 6 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201527438 | |
| Published online | 28 January 2016 | |
Scaling of the asymptotic entropy jump in the superadiabatic layers of stellar atmospheres
1 Niels Bohr Institute, University of Copenhagen Juliane Maries Vej 30 2100 Copenhagen Denmark
e-mail:
magic@nbi.dk
2 Centre for Star and Planet Formation, Natural History Museum of Denmark, Øster Voldgade 5–7, 1350 Copenhagen, Denmark
Received: 23 September 2015
Accepted: 3 December 2015
Context. Stellar structure calculations are able to predict precisely the properties of stars during their evolution. However, convection is still modelled by the mixing length theory; therefore, the upper boundary conditions near the optical surface do not agree with asteroseismic observations.
Aims. We want to improve how the outer boundary conditions are determined in stellar structure calculations.
Methods. We study realistic 3D stellar atmosphere models to find alternative properties.
Results. We find that the asymptotic entropy run of the superadiabatic convective surface layers exhibit a distinct universal stratification when normalized by the entropy minimum and jump.
Conclusions. The normalized entropy can be represented by a 5th order polynomial very accurately, and a 3rd order polynomial also yields accurate coefficients. This generic entropy stratification or the solar stratification, when scaled by the entropy jump and minimum, can be used to improve the modelling of superadiabatic surface layers in stellar structure calculations. Furthermore, this finding indicates that surface convection operates in the same way for all cool stars, but requires further scrutiny in order to improve our understanding of stellar atmospheres.
Key words: convection / hydrodynamics / radiative transfer / stars: atmospheres / stars: evolution / asteroseismology
© ESO, 2016
1. Introduction
In stellar evolution calculations, convection in the superadiabatic region (SAR) is commonly treated with the mixing length theory (MLT; see Böhm-Vitense 1958). However, as a result of the non-local and non-linear nature of surface convection, MLT cannot correctly model the complex SAR. The bulk of the convection zone is nearly adiabatic; i.e. compared to the adiabatic entropy value, sad, entropy fluctuations, δs, are small. At the optical surface (τRoss = 1) the optical mean free path for a photon becomes very large, leading to radiative losses and consequently to large-amplitude fluctuations, essentially driving convection (see Stein & Nordlund 1998; Nordlund et al. 2009). The radiative cooling at the surface leads to an entropy minimum, smin, and determines the upper boundary of the photospheric transition region. The resulting entropy-deficient plasma is buoyantly accelerated downwards and subsequent mixing of the downdraft with the stable background will rapidly diminish the entropy fluctuations within a few pressure scale heights. Ultimately, this creates an asymptotic entropy stratification in the SAR.
 |
Fig. 1 Entropy vs. density shown for different stellar parameters without and with normalization (a) and b), respectively). Each panel shows models with the same surface gravity, log g, and metallicity, [Fe/H], but different effective temperature, Teff (orange/brown lines). Furthermore, the location of the optical surface, τRoss = 1, and maximum in the entropy gradient, ds | max, are indicated (circle and triangle, respectively). In the left figure, the adiabatic entropy, sad, values are also shown (horizontal dotted lines). We note the differences in the axes between the top and bottom panels in a). |
Precise stellar evolutionary calculations are important for determining the age of stellar clusters, extragalactic population synthesis, and the characterization of exoplanet hosts. However, the SAR is a major source of uncertainty in stellar structure theory. This is reflected in asteroseismology, where so-called near-surface effects have to be corrected for, when stellar structure models are compared with observed p-mode oscillations frequencies (see Kjeldsen et al. 2008; Ball & Gizon 2014). Efforts are currently being made to implement results from 3D radiative hydrodynamic (RHD) simulations to improve stellar structure calculations, which is expected to enhance the accuracy of effective temperature, Teff, and radius predictions (Magic et al. 2015; Trampedach et al. 2014a,b; Salaris & Cassisi 2015). To improve MLT models, the entropy minimum and the entropy jump can be specified, which can be done by considering calibrations of T(τ) relations and a variable mixing length, αMLT, from 3D simulations. Nonetheless, even with this approach, MLT would still not properly account for the true structure of the SAR. Rosenthal et al. (1999) has already shown that, by appending depth dependent ⟨3D⟩ stratification of a solar model directly onto a 1D structure, p-mode oscillation frequency calculations can be improved considerably. Therefore, it would be desirable to do the same for the computation of stellar structures, even if implementing and interpolating ⟨3D⟩ stratifications onto 1D models is highly non-trivial.
In the present work, we report on our findings regarding a universal asymptotic stratification of the entropy jump in normalized ⟨3D⟩ entropy stratifications from the Stagger-grid, a grid of 3D RHD stellar atmosphere models (see Magic et al. 2013a). These generic depth dependent entropy stratifications are easily scaled, and can therefore potentially improve 1D stellar structure calculations. In addition, such scaling relations are also paramount for the theoretical understanding of surface convection.
2. Asymptotic entropy stratification
The average (specific) entropy1 plotted against the density shows a very steep drop towards the optical surface from the interior with decreasing density (Fig. 1a). Each entropy stratification is characterized by the entropy minimum, smin, and an asymptotic increase towards the adiabatic entropy of the deeper convection zone sad with increasing density. For higher effective temperature, Teff; lower surface gravity, log g; and lower metallicity, [Fe/H], the ⟨3D⟩ stratifications2 tend towards lower entropy and density. Concomitantly, the entropy jump decreases, but the asymptotic structure looks similar despite the different depth scales. In the metal-poor case ([Fe/H] = −2), it can be seen in Fig. 1a that, at high Teff, the entropy jump and minimum are similar to the solar metallicity case, while at lower Teff, both Δs and smin, are much smaller relative to the solar metallicity case. This is due to a lack of electrons at low [Fe/H] and Teff that are required for the dominant H−-opacity. At higher Teff, ionization of hydrogen results in more free electrons (see Magic et al. 2013a).
We consider the following normalizations: Shifting the entropy by its minimum and normalizing it by the entropy jump, Δs = sad−smin, i.e. 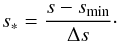 (1)Next, normalizing the density by its value at the peak of the entropy gradient, ds | max, and then taking the square root:
(1)Next, normalizing the density by its value at the peak of the entropy gradient, ds | max, and then taking the square root: 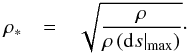 (2)The results of the normalization are shown in Fig. 1b. The entropy stratifications are now almost indistinguishable from one another and can basically be scaled from one to another. The simplicity of the outcome is remarkable, particularly when considering the complexity of the 3D RHD simulations from where the normalized entropy jump was derived. At the optical surface, i.e. where ⟨τRoss⟩ = 1, the opacity and density decreases significantly, which leads to radiative cooling in the thin photosphere3, and generates the entropy fluctuations. The fluctuations are partly advected by the horizontal deflection of velocity field, but primarily accelerated downwards by buoyancy. The downflows shear and mix (Kelvin-Helmholtz instability) with the layers below, which rapidly reduces the entropy fluctuations. This causes the asymptotic convergence of the entropy stratification. Furthermore, the process furthermore appears to be universal. The surface gravity sets the geometrical depth scale in the hydrostatic equilibrium, while the effective temperature, which is given by the radiative flux, sets the height of the entropy jump.
(2)The results of the normalization are shown in Fig. 1b. The entropy stratifications are now almost indistinguishable from one another and can basically be scaled from one to another. The simplicity of the outcome is remarkable, particularly when considering the complexity of the 3D RHD simulations from where the normalized entropy jump was derived. At the optical surface, i.e. where ⟨τRoss⟩ = 1, the opacity and density decreases significantly, which leads to radiative cooling in the thin photosphere3, and generates the entropy fluctuations. The fluctuations are partly advected by the horizontal deflection of velocity field, but primarily accelerated downwards by buoyancy. The downflows shear and mix (Kelvin-Helmholtz instability) with the layers below, which rapidly reduces the entropy fluctuations. This causes the asymptotic convergence of the entropy stratification. Furthermore, the process furthermore appears to be universal. The surface gravity sets the geometrical depth scale in the hydrostatic equilibrium, while the effective temperature, which is given by the radiative flux, sets the height of the entropy jump.
We have also marked the locations of the optical surface and the peak in entropy gradient in Fig. 1. One can see that the entropy minimum, which marks the upper boundary of the convection zone, lies well above the optical surface towards higher effective temperature. This is due to the vigorous velocities and overshooting, which renders the use of T(τ) relations, often fixed to τ = 2/3 in stellar structure computations, questionable. Also, the T(τ) relations are valid only for specific conditions. The metal-poor cool dwarf (right bottom panel in Fig. 1b), shows larger deviations from the universal entropy stratification most likely because this model exhibits a more adiabatic stratification, which should be considered as a limiting case for the universal entropy scaling.
3. Radiative cooling and convection
 |
Fig. 2 Normalized radiative flux |
Since the radiative cooling term, qrad, is responsible for creating the entropy jump, it is worthwhile to study the radiative flux for any related scaling properties. When comparing the radiative flux normalized to the total flux, 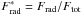 , with ρ∗, then different stellar parameters exhibit the same behaviour (Fig. 2). We find the peak of the entropy gradient coincides with the peak of the radiative cooling gradient.
, with ρ∗, then different stellar parameters exhibit the same behaviour (Fig. 2). We find the peak of the entropy gradient coincides with the peak of the radiative cooling gradient.
In order to make the relation between the entropy and the radiative flux clearer, we consider the entropy conservation equation 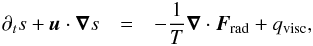 (3)which states that the radiative losses are a result of the entropy advection. The time derivative of the entropy becomes zero, while the viscous dissipations are negligible. Then, the spatial and temporal average, denoted by
(3)which states that the radiative losses are a result of the entropy advection. The time derivative of the entropy becomes zero, while the viscous dissipations are negligible. Then, the spatial and temporal average, denoted by  , gives
, gives 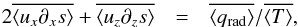 (4)which relates the radiative cooling in the photosphere to the total entropy advection. The horizontal entropy advection is symmetric, i.e.
(4)which relates the radiative cooling in the photosphere to the total entropy advection. The horizontal entropy advection is symmetric, i.e. 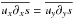 ; therefore, the twofold of x-direction gives the horizontal entropy advection. The RHS of Eq. (4) is the derivative of the vertical radiative flux, which determines the effective temperature, while the LHS of Eq. (4) contains the velocity, the entropy and geometrical depth scale. This illustrates the systematic variations of these values with stellar parameters within the Stagger-grid, which we reported in Magic et al. (2013a).
; therefore, the twofold of x-direction gives the horizontal entropy advection. The RHS of Eq. (4) is the derivative of the vertical radiative flux, which determines the effective temperature, while the LHS of Eq. (4) contains the velocity, the entropy and geometrical depth scale. This illustrates the systematic variations of these values with stellar parameters within the Stagger-grid, which we reported in Magic et al. (2013a).
 |
Fig. 3 Filling factor of the up- and downflows (solid and dashed lines) vs. normalized density ρ∗ for different stellar parameters. |
In Fig. 3, we show the filling factors of the up- and downflows. These are also very similar between the different 3D models. The upflows have a filling factor of 2/3 and the downflows 1/3, which was already reported by Stein & Nordlund (1998) for the solar case. This means that on average the downflows are compressed by a universal ratio of 2:1. This and the above findings are also connected to the scaling of the granulation pattern, which we found to scale with the pressure scale height in all Stagger-grid models (see Magic & Asplund 2014), and suggests that surface convection operates in the same way for all cool stars. Furthermore, we note that the asymptotic character of the entropy jump is also imprinted in the temperature and enthalpy, and becomes apparent when decomposing them into the non-adiabatic and adiabatic parts.
4. Fitting the normalized entropy jump
 |
Fig. 4 Fittings of the normalized ⟨3D⟩ entropy jump (dashed line) with the functions ζ3 and ζ5 (red and blue lines, respectively) for different models: Sun (Teff/ log g = 5777/4.44), turnoff star (6500/4.0), red giant (4000/2.0), and dwarf (4500/5.0) for solar metallicity ([Fe/H] = 0) and metal-poor ([Fe/H] = −2.0) models (upper and lower panels). We also depict the difference between the ⟨3D⟩ model and the fitted functions ζ3 and ζ5. |
 |
Fig. 5 The different coefficients for ζ3 from fits to different models. The different metallicities are indicated. |
We find that the normalized entropy jump can be reasonably fit with an asymptotic function, ζn, of the functional form 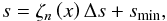 (5)with x = log ρ∗. A formulation for the ζn that matches s∗ well is a generic polynomial:
(5)with x = log ρ∗. A formulation for the ζn that matches s∗ well is a generic polynomial: 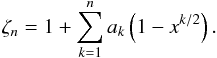 (6)Initially, we applied an asymptotic function; however, the resulting fits were insufficient, so that we found the polynomial to give a better fit. In Fig. 4 we show the results of the fitting for four different stellar models with two different metallicities in comparison with the ⟨3D⟩ entropy stratification. The differences, δ = s∗−ζn, are very small as shown. In fact, the root mean square and the maximum of the differences averaged over all models are 7.32 × 10-3 and 9.45 × 10-3 for the 3rd order function and 2.33 × 10-3 and 3.61 × 10-3 for the 5th order polynomial.
(6)Initially, we applied an asymptotic function; however, the resulting fits were insufficient, so that we found the polynomial to give a better fit. In Fig. 4 we show the results of the fitting for four different stellar models with two different metallicities in comparison with the ⟨3D⟩ entropy stratification. The differences, δ = s∗−ζn, are very small as shown. In fact, the root mean square and the maximum of the differences averaged over all models are 7.32 × 10-3 and 9.45 × 10-3 for the 3rd order function and 2.33 × 10-3 and 3.61 × 10-3 for the 5th order polynomial.
For the lower order, n = 3, we find that the coefficients vary around ak = −2, + 2,−0.75, as can clearly be seen in Fig. 5, i.e. the function 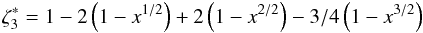 (7)fits the normalized entropy jump on average. We find the smallest residuals for n = 5, as shown in Fig. 4. However, we cannot find any correlations between the fitting coefficients and the stellar parameters. A better suited functional basis could be found; in particular, at the bottom the function ζn does not exactly exhibit an asymptotic behaviour by definition. Since an asymptotic functional basis resulted in worse fits, we preferred to use the presented generic polynomial.
(7)fits the normalized entropy jump on average. We find the smallest residuals for n = 5, as shown in Fig. 4. However, we cannot find any correlations between the fitting coefficients and the stellar parameters. A better suited functional basis could be found; in particular, at the bottom the function ζn does not exactly exhibit an asymptotic behaviour by definition. Since an asymptotic functional basis resulted in worse fits, we preferred to use the presented generic polynomial.
5. Depth dependent boundary for stellar structures
 |
Fig. 6 Reconstructed (red line) stratifications of the entropy, temperature and pressure (top, middle and bottom panels, respectively) from the generic function |
In stellar structure calculations, the entropy can be conveniently obtained by integrating 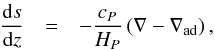 (8)where cP is the specific heat at constant pressure, HP the pressure scale height, and ∇sad = ∇−∇ad the superadiabatic gradient. Since the asymptotic entropy jump is universal, we can construct the thermal stratification in the superadiabatic layers using the generic entropy stratification scaled by the entropy jump and minimum. In Fig. 6, we show a constructed entropy stratification for the Sun using the generic function
(8)where cP is the specific heat at constant pressure, HP the pressure scale height, and ∇sad = ∇−∇ad the superadiabatic gradient. Since the asymptotic entropy jump is universal, we can construct the thermal stratification in the superadiabatic layers using the generic entropy stratification scaled by the entropy jump and minimum. In Fig. 6, we show a constructed entropy stratification for the Sun using the generic function 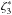 given in Eq. (7). Compared with the ⟨3D⟩ model, the differences between the two are remarkably small.
given in Eq. (7). Compared with the ⟨3D⟩ model, the differences between the two are remarkably small.
To construct such a stratification, we first consider the generic relation between s∗ and ρ∗ from Eq. (7). Then, for a given choice of stellar parameters Teff, log g, and [Fe/H], we determine Δs and smin, which are provided in Magic et al. (2013a) in the form of functional fits. We note that the entropy minimum sets the outer boundary, while the entropy jump determines the temperature gradient (∇ = ∇sad + ∇ad). With Eq. (5), we can now scale the entropy stratification. The density can be determined from Eq. (2) and the entropy peak, which is approximately located at the optical surface, i.e. ds | max ≈ τRoss = 2/3. Therefore, the adiabatic stratification with smin, where the entropy is constant, can be helpful for an initial estimate of the value of the density, at which ρ(ds | max). From the resulting ρ and s, we compute the thermal pressure, pth, from the equation of state. Then, the geometrical depth can be retrieved from the hydrostatic equilibrium, dpth/ dz = ρg. We note that the surface gravity is responsible for the scaling of the geometrical depth. The turbulent pressure (and velocity) has to be included in the hydrostatic equilibrium because it will elevate atmospheric structure (i.e. 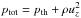 ). However, for simplicity we neglect the latter. The location of the optical surface can be retrieved from the optical depth, dτ/ dz = ρκ. Finally, with the constructed entropy and density stratification one can compute other thermodynamic quantities, such as temperature or internal energy, from the equation of state. We note that in the different constructed models shown in Fig. 6, we appended an isothermal atmosphere above the surface.
). However, for simplicity we neglect the latter. The location of the optical surface can be retrieved from the optical depth, dτ/ dz = ρκ. Finally, with the constructed entropy and density stratification one can compute other thermodynamic quantities, such as temperature or internal energy, from the equation of state. We note that in the different constructed models shown in Fig. 6, we appended an isothermal atmosphere above the surface.
This procedure can be used to construct depth dependent thermal stratifications to be used as outer boundary conditions for stellar structure computations. The physical complexity of the radiative transfer equation is then hidden in the dependence of Δs and smin on stellar parameters. This approach would reduce the deficiencies of MLT and the T(τ) relations since the mixing length is encoded in Δs and the outer boundary in smin. Such a simplified prescription of the superadiabatic layers could possibly improve the p-mode frequency disagreement (Christensen-Dalsgaard et al. 1988; Rosenthal et al. 1999). We note that our aim in the presented study is to illustrate the potential application of our findings for stellar structures. The method summarized above clearly needs further development for improved results.
6. Conclusions
The presented scaling relation for the entropy jump indicates that radiative losses in cool stars takes place in a fairly similar fashion. We found that the normalized entropy, as a function of the normalized density, can be fitted very well with a polynomial function. A robust and generic, yet simple description of the normalized entropy stratification can be achieved with a three-parameter function. This could be helpful for stellar structure computations by providing a simple description of the otherwise non-trivial superadiabatic region in cool stars. In particular, as corrections for the near-surface effects in asteroseismology this would constitute a large step forward in stellar structure modelling. We have shown that from the generic normalized entropy, we can construct stratifications by scaling the normalized entropy with the entropy jump and minimum, as outlined above. However, the method can benefit from some refinement in the future, for example by including the turbulent pressure in the hydrostatic equilibrium equation. Superadiabatic convection seems to take place in a similar manner, despite large differences in the physical conditions. The reason behind this has yet to be explored.
We computed the specific (thermodynamic) entropy by integrating the first law of thermodynamics ds = (dε−pth/ρ dlnρ) /T. Then we determined the spatial and temporal averages at constant geometrical height, which are the only averages that preserve the hydrostatic equilibrium (see Magic et al. 2013b, for more details).
Acknowledgments
This work was supported by a research grant (VKR023406) from VILLUM FONDEN.
References
- Ball, W. H., & Gizon, L. 2014, A&A, 568, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Böhm-Vitense, E. 1958, Z. Astrophys., 46, 108 [Google Scholar]
- Christensen-Dalsgaard, J., Dappen, W., & Lebreton, Y. 1988, Nature, 336, 634 [NASA ADS] [CrossRef] [Google Scholar]
- Kjeldsen, H., Bedding, T. R., & Christensen-Dalsgaard, J. 2008, ApJ, 683, L175 [NASA ADS] [CrossRef] [Google Scholar]
- Magic, Z., & Asplund, M. 2014, A&A, submitted [arXiv:1405.7628] [Google Scholar]
- Magic, Z., Collet, R., Asplund, M., et al. 2013a, A&A, 557, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magic, Z., Collet, R., Hayek, W., & Asplund, M. 2013b, A&A, 560, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magic, Z., Weiss, A., & Asplund, M. 2015, A&A, 573, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nordlund, Å., Stein, R. F., & Asplund, M. 2009, Liv. Rev. Sol. Phys., 6, 2 [Google Scholar]
- Rosenthal, C. S., Christensen-Dalsgaard, J., Nordlund, Å., Stein, R. F., & Trampedach, R. 1999, A&A, 351, 689 [NASA ADS] [Google Scholar]
- Salaris, M., & Cassisi, S. 2015, A&A, 577, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stein, R. F., & Nordlund, Å. 1998, ApJ, 499, 914 [Google Scholar]
- Trampedach, R., Stein, R. F., Christensen-Dalsgaard, J., Nordlund, Å., & Asplund, M. 2014a, MNRAS, 442, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Trampedach, R., Stein, R. F., Christensen-Dalsgaard, J., Nordlund, Å., & Asplund, M. 2014b, MNRAS, 445, 4366 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Entropy vs. density shown for different stellar parameters without and with normalization (a) and b), respectively). Each panel shows models with the same surface gravity, log g, and metallicity, [Fe/H], but different effective temperature, Teff (orange/brown lines). Furthermore, the location of the optical surface, τRoss = 1, and maximum in the entropy gradient, ds | max, are indicated (circle and triangle, respectively). In the left figure, the adiabatic entropy, sad, values are also shown (horizontal dotted lines). We note the differences in the axes between the top and bottom panels in a). |
| In the text | |
 |
Fig. 2 Normalized radiative flux |
| In the text | |
 |
Fig. 3 Filling factor of the up- and downflows (solid and dashed lines) vs. normalized density ρ∗ for different stellar parameters. |
| In the text | |
 |
Fig. 4 Fittings of the normalized ⟨3D⟩ entropy jump (dashed line) with the functions ζ3 and ζ5 (red and blue lines, respectively) for different models: Sun (Teff/ log g = 5777/4.44), turnoff star (6500/4.0), red giant (4000/2.0), and dwarf (4500/5.0) for solar metallicity ([Fe/H] = 0) and metal-poor ([Fe/H] = −2.0) models (upper and lower panels). We also depict the difference between the ⟨3D⟩ model and the fitted functions ζ3 and ζ5. |
| In the text | |
 |
Fig. 5 The different coefficients for ζ3 from fits to different models. The different metallicities are indicated. |
| In the text | |
 |
Fig. 6 Reconstructed (red line) stratifications of the entropy, temperature and pressure (top, middle and bottom panels, respectively) from the generic function |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.