| Issue |
A&A
Volume 586, February 2016
|
|
|---|---|---|
| Article Number | A1 | |
| Number of page(s) | 11 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201525709 | |
| Published online | 19 January 2016 | |
Heavy elements Ba, La, Ce, Nd, and Eu in 56 Galactic bulge red giants⋆
1 Universidade de São Paulo, IAG, Rua do Matão 1226, Cidade Universitária, 05508-900 São Paulo, Brazil
e-mail: mathieu.vanderswaelmen@iag.usp.br; b.barbuy@iag.usp.br
2 Laboratoire Lagrange (UMR 7293), Université de Sophia-Antipolis, CNRS, Observatoire de la Côte d’Azur, CS 34229, 06304 Nice Cedex 4, France
e-mail: vanessa.hill@oca.eu
3 Instituto de Astrofisica, Facultad de Fisica, Pontificia Universidad Catolica de Chile, Casilla 306, Santiago 22, Chile
e-mail: mzoccali@astro.puc.cl
4 Millennium Institute of Astrophysics, Casilla 306, Santiago 22, Chile
5 Departamento de Ciencias Fisicas, Universidad Andres Bello, Republica 220, Santiago, Chile
6 Vatican Observatory, V00120 Vatican City State, 00120 Vatican City State, Italy
7 Università di Padova, Dipartimento di Astronomia, Vicolo dell’Osservatorio 2, 35122 Padova, Italy
8 Observatoire de Paris-Meudon, 92195 Meudon Cedex, France
Received: 21 January 2015
Accepted: 21 September 2015
Aims. The aim of this work is the study of abundances of the heavy elements Ba, La, Ce, Nd, and Eu in 56 bulge giants (red giant branch and red clump) with metallicities ranging from -1.3 dex to 0.5 dex.
Methods. We obtained high-resolution spectra of our giant stars using the FLAMES-UVES spectrograph on the Very Large Telescope. We inspected four bulge fields along the minor axis.
Results. We measure the chemical evolution of heavy elements, as a function of metallicity, in the Galactic bulge.
Conclusions. The [Ba,La,Ce,Nd/Fe] vs. [Fe/H] ratios decrease with increasing metallicity, in which aspect they differ from disc stars. In our metal-poor bulge stars, La and Ba are enhanced relative to their thick disc counterpart, while in our metal-rich bulge stars La and Ba are underabundant relative to their disc counterpart. Therefore, this contrast between bulge and discs trends indicates that bulge and (solar neighbourhood) thick disc stars could behave differently. An increase in [La,Nd/Eu] with increasing metallicity, for metal-rich stars with [Fe/H] > 0 dex, may indicate that the s-process from AGB stars starts to operate at a metallicity around solar. Finally, [Eu/Fe] follows the [α/ Fe] behaviour, as expected, since these elements are produced by SNe type II.
Key words: stars: abundances / stars: atmospheres / Galaxy: bulge
© ESO, 2016
1. Introduction
Heavy elements (with Z> 30 K) are produced by neutron captures through s- and r-processes in a variety of sites. In strict terms, the s-process indicates a situation where no neutron captures take place on β-unstable nuclei, while the r-process indicates a situation where neutron captures occur before a radioactive β-decay. Different channels have been identified for s-element production (Käppeler et al. 1989, 2011; Busso et al. 1999; Frischknecht et al. 2012; Bisterzo et al. 2014): the weak component, contributing elements of A ≤ 90, takes place during He core and convective shell C burning of massive stars; and the main and strong components (A ~ 90−208) are produced in helium rich intershells of thermally pulsing asymptotic giant branch (AGB) stars (Bisterzo et al. 2011, 2014). According to, for example, Arlandini et al. (1999), Simmerer et al. (2004), the elements Ba, La, Ce, and Nd in the solar neighbourhood, are dominantly produced by the s-process. However, Truran (1981) suggested that, in very old stars, the abundances of these elements are the result of their r-process fraction produced at early times. This can apply to the Galactic bulge, which shows its bulk of stars as being very old (Zoccali et al. 2003; Clarkson et al. 2008). Of the 58 dwarf stars observed thanks to microlensing effects, Bensby et al. (2013) estimated that 22 % are younger than 5 Gyr and 38 % are younger than 7 Gyr (if He is standard), and these stars are among the more metal-rich stars. If a higher value of the He content is chosen, then age determination leads to a smaller fraction of stars younger than 6–8 Gyr. The old bulge stars could have their heavy element abundances produced by the r-process, as seems to be the case for metal-poor halo stars (e.g. Siqueira Mello et al. 2012).
The r-process is less well understood than the s-process, and there is still no consensus as to where the r-process takes place, as discussed in, for example, Wanajo & Ishimaru (2006), Kratz et al. (2007), Thielemann et al. (2011), Langanke & Thielemann (2013), Rosswog et al. (2014), among others. Recently, the hypothesis of r-element nucleosynthesis taking place in neutron star merger events is favoured by Rosswog et al. (2014) and Wanajo et al. (2014). These authors suggest that the strong r-process produces elements with A> 130, and the weak r-process yields elements with 50 <A< 130. Finally, massive spinstars can produce s-elements very early in the Galaxy, as proposed by Chiappini et al. (2011), Chiappini (2013).
The centre of our Galaxy hosts a dense stellar structure, and there is a strong debate concerning its formation process. The Galactic bulge shares chemical and kinematical properties compatible with a classic spheroid and a boxy bulge (Minniti 1996). Recently, Babusiaux et al. (2010, 2014), Hill et al. (2011), Bensby et al. (2013) and Rojas-Arriagada et al. (2014) have been able to identify two different stellar populations using chemical and kinematical properties of stellar samples. They found a stellar population that is old, metal-poor, alpha-element-rich, and has isotropic kinematics, and a younger population that is metal-rich with solar α-ratios and bar-like kinematics. Chemically and kinematically speaking, the metal-poor component has similarities with the thick disc, while the metal-rich component is more similar to an inner thin disc. Ness et al. (2013) carried out a large survey of bulge stars, and were able to separate up to five stellar populations in terms of kinematics and metallicity distributions. They also suspect that the different bulge components have an origin in the thin and thick discs of the Galaxy.
A number of scenarios have been described to explain how to form a spheroidal bulge. For instance, Eggen et al. (1962), Noguchi (1999), or Elmegreen et al. (2008) form a spheroidal bulge by gravitational collapse or hierarchical merging of subclumps formed in the disc. On the other hand, Jørgensen & Lindegren (2005) or Saha et al. (2010) are able to form a boxy bulge via heating processes after the formation of a dynamical bar due to disc instabilities. However, there is no consistent explanation of all the observational features of the bulge. This is expected, given that our Galaxy is an intermediate Sbc type spiral galaxy, and the bulges are considered to be true bulges in Sa and Sb type galaxies, and boxy bulges forming from the bar in Sc type galaxies (Saha et al. 2010).
Chemical abundances of α-elements have been used to obtain insights into the chemical history of the Galactic bulge (e.g. McWilliam & Rich 1994; Fulbright et al. 2007; Zoccali et al. 2006; Lecureur et al. 2007; Gonzalez et al. 2011; Hill et al. 2011). In the present work, we try to explore the possibility of using the abundances of heavy elements to characterise the bulge stellar population chemically, and to provide hints about nucleosynthesis processes and the kind of supernovae (SN) that enriched the Galactic bulge. We derive heavy element abundances for a sample of 56 bulge field stars observed at high spectral resolution with the FLAMES-UVES spectrograph at the Very Large Telescope, as described in Lecureur et al. (2007), Zoccali et al. (2006, 2008).
We compare our results with previous samples in the literature, for which heavy element abundances were derived in Galactic bulge stars. Johnson et al. (2012) derived abundances of the heavy elements La, Nd, and Eu in red giants in Plaut’s field, among which they found r-II stars (Johnson et al. 2013). Bensby et al. (2013) presented element abundances of 58 microlensed bulge dwarfs and subgiants of the Galactic bulge. Their study includes the abundances of the heavy element Ba.
In Sect. 2 we report our observations. In Sect. 3 we provide the atomic constants for the lines under study. In Sect. 4 we list the basic stellar parameters and describe the abundance derivation of heavy element. The results are derived in Sect. 5 and discussed in Sect. 6. Conclusions are drawn in Sect. 7.
2. Observations
The spectra we used for this study on heavy elements have already been used for light α-elements in Zoccali et al. (2006), Lecureur et al. (2007) and the iron-peak element Mn and Zn (Barbuy et al. 2013, 2015). These papers provide further details on the target selection, data reduction, and stellar parameters determination. We summarize these papers below.
Zoccali et al. (2006) obtained the spectra of 56 bulge giant stars with the multifibre spectrograph FLAMES/UVES (R ~ 45 000) at the UT2 Kuyen VLT/ESO telescope. The spectra, obtained with the UVES spectrograph, span a wavelength range from ~4800 to ~6800 Å, with a gap (inherent to the instrument design) between 5775 and 5825 Å. The targets are located in four different fields of the Galactic bulge: the Baade’s Window (l = 1.14°, b = -4.2°), a field at -6° (l = 0.2°, b = -6°), the Blanco field (l = 0°, b = -12°), and the field of NGC 6553 (l = 5.2°, b = -3°). Thirteen of our 56 stars are red clump (RC) stars and located in the Baade’s Window, the others are red giant branch (RGB) stars slightly brighter than the RC. Lecureur et al. (2007) performed the data reduction with the ESO FLAMES/UVES pipeline (debiasing, flat-fielding, spectrum extraction, wavelength calibration, order merging), and they performed the sky subtraction and the co-addition of multiple observations with IRAF tasks.
The stellar parameters (temperature Teff, surface gravity log g, overall metallicity [M/Fe], and microturbulence velocity vturb) were derived by Lecureur et al. (2007) for the RGB stars and by Hill et al. (2011) for the RC stars. The stellar parameters were derived by applying the standard spectroscopic criteria to their set of iron lines.
3. Abundances
3.1. Methods
We obtained element abundances through line-by-line spectrum synthesis calculations. We used the technique of line fitting described in Van der Swaelmen et al. (2013) to derive the elemental abundances, which is based on a weighted χ2 minimisation with weights inversely proportional to the computed blends from other species at each wavelength. We computed a grid of synthetic spectra using turbospectrum (code of line synthesis described in Alvarez & Plez 1998 and improved along the years by B. Plez) together with the grid of OSMARCS spherical model atmospheres1 (Gustafsson et al. 2008). We computed the synthetic spectra in spherical geometry, with LTE spherical radiative transfer. Our χ2 algorithm then found the best match between the synthetic and observed spectra. Figure 1 shows the fits to the observed spectrum of the RC star Bwc-4 for the lines of Ba, La, Nd, and Eu. Table 1 gives individual abundances for our bulge stars.
 |
Fig. 1 From top to bottom: fit of Ba ii line at 6496 Å, La ii line at 6390 Å, Nd ii line at 6740 Å, and Eu ii line at 6645 Å for BWc-4. Black crosses: observed spectrum; red solid line: best fit; blue solid lines: spectra computed for the best-fit value of [X/Fe] ± 0.3. |
Abundances line-by-line derived in the present work.
3.2. Line lists
We compiled the atomic line lists from the line database VALD2 (Kupka et al. 1999, 2000). We took into account the hyperfine structure (hfs) for Ba II (Rutten 1978: 6496.912 Å), La II (Lawler et al. 2001a: 6262.287 Å, 6320.430 Å, 6390.477 Å, and Eu II (Lawler et al. 2001b: 6645.064 Å). Table 2 lists the lines we used with their log gf.
Given the cool effective temperature (Teff ~ 4500 K) of our targets, molecules are expected to form in the atmosphere of our bulge stars and are responsible for molecular bands in the stellar spectra. Therefore, we included the molecular line lists of 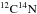 ,
, 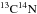 (Plez, priv. comm.) and TiO (Plez 1998) in the spectrum synthesis.
(Plez, priv. comm.) and TiO (Plez 1998) in the spectrum synthesis.
3.3. Initial chemical composition
We have to set CNO abundances before any abundance derivation since the CNO mix drives the equilibrium between atomic species, C, N and O, and molecular species, CN and CO, and therefore the CNO mixture controls the strength of CN features. Lecureur et al. (2007) measured individual [C/Fe] and [N/Fe] ratios for our bulge stars. Since they found no trend with metallicity and since their individual measurements suffer rather large uncertainties, we decided to use mean C and N abundances and we fixed the following values for any star of our sample: [C/Fe] =-0.05 dex and [N/Fe] =0.35 dex. Lecureur et al. (2007) also measured O and Mg abundances. However, O abundances are missing for some stars (e.g. BW-f8, BW-f4) because of telluric contamination (see revision of O abundances in Barbuy et al. 2015), and cannot be replaced by their Mg abundances since Mg does not trace O in the galactic bulge perfectly (e.g. McWilliam et al. 2008). Instead, we used the [O/Fe] of Lecureur et al. (2007) to build the following relation for [α/ Fe]: for [Fe/H] <-0.4 dex, [α/ Fe] =0.5 dex and for [Fe/H] ≥-0.4 dex, [α/ Fe] = −0.625 × [Fe/H] + 0.25.
Central wavelengths, excitation potential, and adopted oscillator strengths log gf values, taken from 1 Van der Swaelmen et al. (2013), otherwise VALD values.
3.4. μ Leonis as a benchmark star
We chose the metal-rich, thin-disc giant star μ Leonis as a reference star to calibrate our line list, and, in particular, to adjust the pseudo-log gf describing the CN lines. Our benchmark analysis is based on a spectrum of μ Leo taken at CFHT with ESPaDOnS (R ~ 80 000; see Lecureur et al. 2007). We made the same choice of stellar parameters as Lecureur et al. (2007): Teff =4540 K, log g = 2.3, [M/Fe] =0.3 dex and vturb =1.3 km s− 1. We also assumed the same abundance of C, N, and O as Lecureur et al. (2007): A(C = 8.85), A(N = 8.55) and A(O = 9.12), which translates in [C/Fe] =-0.01 dex, [N/Fe] =0.2 dex, [O/Fe] =-0.12 dex (solar composition from Grevesse & Sauval 1998). Table 3 lists the individual abundances we derived for μ Leo. Figure 2 shows example of fits.
 |
Fig. 2 From top to bottom: fit of Ba ii line at 6496 Å, La ii line at 6390 Å, and Eu ii line at 6645 Å for μ Leo (ESPaDOnS spectrum, see text for reference, degraded to UVES resolution). Black crosses: observed spectrum; red solid line: best fit; blue solid lines: spectra computed for the best-fit value of [X/Fe] ±0.3 dex. |
Individual abundances for μ Leonis derived from spectrum at different resolution and S/N.
3.5. Calibration of the line list
Our selected lines are sometimes affected by a blend with atomic or molecular (CN) lines since the blends are stronger at richer metallicities. However, molecules are often poorly known and it might be necessary to determine an astrophysical log gf. We sum up below a number of checks we made and the calibration we performed, when it was possible, based on high-resolution and high signal-to-noise ratio (S/N) μ Leo spectrum and the stellar parameters and CNO abundances given above.
Europium.
A strong CN band popped up in the synthetic spectrum of μ Leonis at 6644.5 Å when using the original CN line lists, but this molecular band is smaller in the observed spectrum. Since this CN band modifies the blue wing of the Eu line at 6645 Å, we adjusted the corresponding pseudo-log gf.
Barium.
The Ba line at 6496 Å is blended with CN lines. No adjustment was needed on the CN log gf. However, in our cool and metal-rich giants, the Ba line is strong (i.e. saturated and depends weakly on the abundance), and therefore, the abundance determination suffers large errors.
Lanthanum.
The La line at 6262 Å is blended with CN lines. We found that this line cannot be satisfactorily fitted in a high-resolution spectrum of the Sun, μ Leo, and Arcturus. In addition to the fact that the CN lines are poorly predicted, the shape of the La line due to the hyperfine structure never matches and is always broader than the observed line for our three reference stars. The hyperfine structure computed using the A and B coefficient of Lawler et al. (2001a), for the E =3250.35 cm− 1 and E =19 214.54 cm− 1 levels, is dominated by two components at ~6262.2 Å and ~6262.45 Å, which are too broadly separated compared to the observed profile.
Line lists predict the presence of a Co line and CN lines in the vicinity of the La line at 6320 Å. In the solar spectrum, the CN lines are completely negligible and we are left with the La and the Co lines. However, when [La/Fe] =0 dex and [Co/Fe] =0 dex, the synthetic profile is much deeper than the observed line (Fig. 3). One way to solve this problem is to consider this line as a pure La line and adjust the log gf accordingly, following Kovtyukh & Andrievsky (1999), who found log gf = −1.33 instead of −1.562 given by VALD. We tested different hypotheses: VALD log gf, considering a pure La line, considering a pure Co line or adjusted log gf so that the combination of La and Co fits the solar spectrum. However, none of the tested set of log gf allowed us to fit satisfactorily the line at 6320 Å in the spectrum of the Sun, μ Leo, and Arcturus simultaneously.
 |
Fig. 3 Synthesis of the line at 6320 Å in the solar spectrum: observed spectrum in black (Hinkle et al. 1995), La line alone in red, Co line alone in green, total blend in purple. |
As for the La line at 6390.48 Å, the hyperfine constants are provided by Lawler et al. (2001a). The line is contaminated by CN in its core, and some weaker CN components may appear before/after the blue/red wing of the La line (e.g. at 6389.6 Å, 6390 Å, 6391.2 Å). As we did for the Eu line, we adjusted the log gf of the CN contaminants close to the La line to fthe Sun and μ Leo simultaneously. We did not adjust the weaker CN lines that may appear before/after the blue/red wing of the La line since their depth is comparable to the noise level in our UVES spectra as seen in the second panel of Fig. 1. We recall that Fig. 2 shows the fits for the high S/N version of μ Leo’s spectrum, that is, a better S/N than our UVES spectra.
Given the above remarks, we decided to discard the La lines at 6262 Å and 6320 Å. Our final La abundance is therefore equal to the abundance derived from the La line at 6390 Å.
3.6. Robustness of the derived abundances
As a sanity check, we performed a second determination of abundances for the following lines: La ii line at 6390 Å and Ce ii line at 6043 Å. This second determination differs significantly from the main method described above by the assumptions, synthesis code, and abundance measurement.
We used the code PFANT06, described in Barbuy et al. (2003) and Coelho et al. (2005; see also Trevisan et al. 2011). The heavy element line list and oscillator strengths reported in Barbuy et al. (2014) were used. Here we take the individual Mg, C, N and O abundances derived in Lecureur et al. (2007) for the initial composition into account (unlike the averaged values used in Sect. 3.3). For the metal-poor stars with no oxygen derivation, B3-f2, B6-f5 and B6-f7, we assumed [O/Fe] =0.4 dex. Assuming a solar [O/Fe] would lead us to predict CN lines that are too strong, most obviously for the La line at 6390 Å blended with two CN A2Π−X2Σ lines ((ν′,ν′′) = (5,1) P1(J = 14) and (4,0) P2(J = 37)).
The observed spectra were smoothed with the Iraf task imfilter.gauss, using a σ = 2 px Gaussian function. The convolution of the synthetic spectra (to take the instrument convolution, macroturbulence profile, and rotation profile into account) and the normalisation of the observed and synthetic spectra were performed locally. The CN line lists were computed by Davis & Phillips (1963). We identified the best fit to the observed spectrum with a visual inspection (unlike the χ2 algorithm used in Sect. 3.1).
Figure 4 compares the abundances obtained with the χ2 best-fit procedure (Sect. 3.1) with those obtained with the visually accepted-fit procedure described above (Sect. 3.6). The mean and standard deviation of [E/Fe] second− [E/Fe] first are -0.03 dex and 0.16 dex for La at 6390 Å and 0.03 dex and 0.40 dex for Ce at 6043 Å, respectively. Given the differences (raw vs. smoothed observed spectrum, convolutions, normalisations, synthesis code, CN line lists, determination of the best fit), we observe an excellent agreement. The standard deviation given above is an estimator of the error on the individual abundance provided by those lines (see also Sect. 3.7).
 |
Fig. 4 Comparison of abundances derived by our two methods (first method described in Sect. 3.1, second method described in Sect. 3.6) for the La ii line at 6390 Å, Ce ii line at 6043 Å. |
3.7. Error budget
Random errors.
In order to estimate the typical (random) error bars on our individual abundances, we used our high-resolution, high S/N ESPaDOnS spectrum of μ Leo to run Monte Carlo simulations. We degraded the resolution towards the UVES resolution and we added Gaussian noise in the spectrum. We performed two S/N hypotheses (30 and 50) to match the low tail and high tail of our S/N distributions (see Table 2 in Lecureur et al. 2007). We created 101 realisations for each S/N hypothesis and derived the abundances. Results are given in Table 3. At a given S/N, when the resolution is decreased, the derived abundance tends to increase (up to ~0.1 dex in the case of Ce). At a given resolution, when the S/N decreases, the derived abundance tends to increase (<0.1 dex). Given the change of the abundance depending on the S/N and the standard deviations provided in the last two columns of Table 3, we consider that the conservative random errors on our derived abundances are 0.15 dex for Ba, La, and Eu and 0.20 dex for Ce and Nd in the metal rich part of our sample (to reflect their higher sensitivity to the resolution).
Systematic errors.
The uncertainties in stellar parameters given in Lecureur et al. (2007), were revised in Barbuy et al. (2013), which we adopt here, namely, ±150 K in temperature, ±0.2 in log g given that we used photometric gravities, ±0.1 dex in [Fe/H], and ±0.1 km s− 1 in microturbulence velocity. Table 4 reports the errors in the studied element abundances due to a change in one of the atmospheric parameters for star BWc-4. Since these parameters are covariant, the quadratic sum of individual errors represent an upper limit for the true uncertainties. The abundances are mainly sensitive to temperature and gravity.
Abundance uncertainties for star BWc-4, for uncertainties of ΔTeff =150 K, Δlog g = 0.2, Δvt =0.1 km s− 1 and Δ [M/H] =0.1 dex.
4. Results and discussion
As explained in Sect. 1, most of the heavy elements are made by both the s- and r-processes of neutron capture. However few elements, like Eu, are often considered as pure r-process elements since the r-process is thought to over-dominate the production. For instance, the r-process contribution to the solar Eu is 94 %, according to Arlandini et al. (1999), and 97 %, according to Sneden et al. (2008). On the other hand, for some elements, like Ba or La, the main contribution is thought to come from the s-process (though the r-process contribution is not negligible). For instance, ≈85 % of the solar Ba was produced by the s-process (Burris et al. 2000; Sneden et al. 2008).
In Sect. 4.1 we compare the present results with bulge data from Johnson et al. (2012) measured in Plaut’s field at l =0°, b =-8°, and l =-1°, b =-8.5°, microlensed dwarf stars by Bensby et al. (2013) and for stars in the metal-poor bulge globular cluster NGC 6522 (Barbuy et al. 2014). We also plot results for NGC 6266 (Yong et al. 2014a), which is projected towards the bulge, but is found at a rather large distance of 6.7 kpc from the Galactic centre, and therefore it is unclear if it is associated with the bulge component. In Sect. 4.2 we compare our results for the bulge with those for the Galactic thin disc and thick disc, reported by Bensby et al. (2005), Brewer & Carney (2006), Reddy et al. (2006) and Simmerer et al. (2004). Lastly, in Sect. 4.2 we compare our results to a sample of super-metal-rich stars, which were identified to be either old inner thin disc or bulge stars by Trevisan et al. (2011) and Trevisan & Barbuy (2014).
4.1. Chemical evolution of the Galactic bulge
Europium.
Figure 5 shows our bulge trend for [Eu/Fe]. For [Fe/H] ≥-0.5 dex, we clearly observe a decreasing [Eu/Fe] with increasing [Fe/H]. While our sample contains only a couple of stars with [Fe/H] ≤-0.5 dex, their abundance lie on a plateau of enhanced [Eu/Fe] in agreement with the constant Eu abundances derived in metal-poor bulge globular clusters (M22 as of Yong et al. 2014a or NGC 6522, Barbuy et al. 2014). At higher metallicities ([Fe/H] >-0.5 dex), our bulge [Eu/Fe] clearly decreases with increasing metallicity in agreement with the behaviour also observed by Johnson et al. (2012). Thus, we found for Eu the expected α-like behaviour for an r-element produced by massive stars (e.g. Fig. 14 in Sneden et al. 2008); the decreasing trend reflects the efficient production of iron by SN Ia after time delay between a few 100 Myr to ~1 Gyr (Ballero et al. 2007).
 |
Fig. 5 [Eu/Fe] vs. [Fe/H]. Symbols: black filled circles: present work; red filled downward triangles: Johnson et al. (2012); red crosses: Bensby et al. (2013); red empty squares: M62 (Yong et al. 2014b); red empty pentagons: NGC 6522 giants (Barbuy et al. 2014); green small dots: thick disc from Bensby et al. (2005), Brewer & Carney (2006), Reddy et al. (2006) and Simmerer et al. (2004); blue small dots: thin disc from Bensby et al. (2005) and Reddy et al. (2006). |
Barium, lanthanum, cerium and neodymium.
Figure 6 shows our bulge trends for Ba, La, Ce, and Nd, all belonging to the second peak of the s-process. We find that [Ba/Fe], [La/Fe], [Ce/Fe] and [Nd/Fe] decrease slightly with increasing metallicities. We obtain a very good agreement between our trends for [La/Fe] and [Nd/Fe] and those by Johnson et al. (2012). Our most metal-poor stars have a [Ba/Fe] and [La/Fe] compatible with results for the globular clusters NGC 6522 (Barbuy et al. 2014) and NGC 6266Yong et al. (2014a).
Ratios among neutron-capture elements can help to diagnose nucleosynthesis processes (e.g. Ishigaki et al. 2013). Figures 7 and 8 show [La,Ce,Nd/Ba] vs. [Fe/H] and [Ce,Nd/La] vs. [Fe/H] respectively. Those ratios are around the solar value for all metallicities, therefore, we can conclude that these elements are produced in the same stars or at least in the same proportions in any event.
 |
Fig. 7 [La,Ce,Nd/Ba] vs. [Fe/H]. Black dots: our bulge sample. |
In order to disentangle the contribution of the r- and s-process, it is useful to plot the abundances among the heavy elements, as for example ratios to a reference s-element, such as Ba or La, and a reference r-element, such as Eu. Figure 9 shows the trends for [Ba,La,Ce,Nd/Eu] vs. [Fe/H]. These trends show essentially that the dominantly s-elements Ba, La, Ce, and Nd are underabundant relative to the r-element Eu, and the ratio is below solar at the lower metallicities where [Eu/Fe] is overabundant (Fig. 5). The plots of [La/Eu] and [Nd/Eu] are better defined compared to those for Ba and Ce; see Sect. 3. We find a good agreement between our [La,Nd/Eu] trends and those of Johnson et al. (2012), as well as with the data of Yong et al. (2014a) for the metal-poor cluster M62. Our bulge metal-poor stars (-0.6 dex< [Fe/H] <0 dex) have mean [La,Nd/Eu] ratios comparable, within the uncertainties, to the value of the pure r-process ratio: for La, -0.17 dex (std. dev: 0.17 dex) vs. [Lar/ Eur] -0.4 dex (Arlandini et al. 1999); for Nd, -0.24 dex (std. dev: 0.16 dex) vs. [Ndr/ Eur] -0.35 dex (Arlandini et al. 1999; Sneden et al. 2008). On the other hand, the super-solar part of our sample exhibit higher ratios: for La, -0.06 dex (std. dev: 0.20 dex); for Nd, -0.12 dex (std. dev: 0.17 dex). This points to an increasing trend of [La,Nd/Eu] from -0.6 dex to 0.4 dex, that is, the rise of the s-process in the chemical enrichment history of the Galactic bulge. The Ba shows a similar behaviour, that is, the distribution is compatible with an increasing trend towards super-solar metallicities, but never reaches the pure r-process level. Also, the two most metal-poor stars (around -1.3 dex) exhibit very high [Ba,Nd/Eu]. Possibilities to explain such overabundances are discussed in Barbuy et al. (2014), Chiappini et al. (2011). It is also interesting to see that [La,Nd/Eu] ratios increase moderately with increasing metallicity for supersolar metallicities. There is a gap in metallicity at −0.2 < [Fe/H] <0 dex, and we cannot check where this increase in La, Nd starts. This finding, together with our previous finding of low (subsolar) [La,Nd,Ce/Fe] values in our sample, supports a scenario of a weak contribution of the s-process in the production of the second-peak elements.
 |
Fig. 9 [Ba,La,Ce,Nd/Eu] vs. [Fe/H]. Same symbols as in Fig. 5. Dotted and dashed blue lines: pure r-process values provided by Arlandini et al. (1999) and Sneden et al. (2008), respectively. |
4.2. Comparison between our sample vs. Galactic discs and bulge-like solar-neighbourhood stars
Figure 5 shows good agreement between our bulge [Eu/Fe] trend and the trends for the Galactic thick and thin discs derived by Bensby et al. (2005), Brewer & Carney (2006), Reddy et al. (2006), and Simmerer et al. (2004). It is not surprising, given the fact that Eu is processed by massive stars, and thus, is expelled in the interstellar medium at early stages of the galactic evolution.
Mean abundances and their associated standard deviation for our bulge Ba, La, Nd, Ce distributions.
If one compares the abundance diagrams of second peak s-elements obtained for the different galactic components (Fig. 6), we find that [Ba,La,Ce,Nd/Fe] ratios in bulge stars tend to lie above 0 dex for [Fe/H] < −0.2 − 0 dex and below 0 dex for [Fe/H] > 0 dex (Table 5), while the discs show a flatter distribution at all metallicities. Though the comparison between MW discs and bulge cannot be repeated over the full metallicity range of our bulge sample (paucity of data points above ~0.1 dex for the MW discs), our findings may suggest a decreasing trend for [Ba,La,Ce,Nd/Fe] in the bulge stars. We emphasize that μ Leo ([Fe/H] =0.3 dex) behaves like the metal-rich part of our sample: in particular, μ Leo has [La/Fe] =-0.36 dex and [Nd/Fe] =-0.7 dex, while our sample reaches [La/Fe] =-0.35 dex and [Nd/Fe] =-0.6 dex at similar metallicity. Systematic effects between dwarf and giant stars may explain the negative slope observed for our giant bulge stars. Assuming that the slope indeed has astrophysical origin, and since Ba, La, Ce, Nd are mainly produced by the s-process and Fe is mainly produced by SN Ia, the decrease of [Ba,La,Ce,Nd/Fe] with increasing metallicities could be due to a weak production of Ba, La, Ce, Nd by the s-process and/or a strong production of Fe by SN Ia. A very active production of iron by SN Ia is unlikely since it would affect other [X/Fe] vs. [Fe/H] diagrams (e.g. α-elements) and it would require a higher rate of binary system formation in the bulge than in the MW discs. On the other hand, it is more reasonable to assume a weaker contribution of the s-process, compared to the Galactic thin and thick discs, and therefore, assume that the second peak elements would be mainly produced by the r-process. The increase of [Ba,La,Ce,Nd/Eu] vs. [Fe/H] may indicate that the s-process from AGB stars starts to operate at a metallicity around solar (Fig. 9), that is, at a later epoch in the bulge history compared to the discs.
In order to better disentangle the Galactic populations, we plot [Ba/O] vs. [Fe/H] in Fig. 10. This figure shows that our [Ba/O] results overlap well the thick disc distribution from Bensby et al. (2005) and Reddy et al. (2006). Finally, all these stellar populations are clearly distinct from the thin disc in the metal poor regime, that is, where the thin and thick discs themselves are chemically distinct. On the other hand, the [Ba/O] distribution derived by Trevisan & Barbuy (2014) for bulge-like solar-neighbourhood stars is more similar to the thin disc distribution than our bulge distribution. This similarity reinforces the finding by Trevisan et al. (2011) and Trevisan & Barbuy (2014) that this sample should rather be associated with an old inner thin disc rather than a bulge-like population.
 |
Fig. 10 [Ba/O] vs. [O/H]. Same symbols as in Fig. 5 and black empty triangles: super metal-rich, bulge-like Trevisan & Barbuy (2014). |
5. Conclusions
The heavy elements appear to be a useful indicator of chemical enrichment in different environments. We find evidence for differences between their abundances in the thin and thick discs and bulge stars. We emphasize that the Fornax dSph or the Large Magellanic Cloud have their [Ba,La/Fe] ratios increasing with increasing metallicities (e.g. Tolstoy et al. 2009; McWilliam et al. 2013; Van der Swaelmen et al. 2013), making evident that the chemical enrichment of these galaxies is dominated by the s-process and the trends are clearly distinct from those of stellar populations in the Galaxy.
We have derived abundances of the neutron-capture elements Ba, La, Ce, Nd, and Eu in 56 bulge red giants. Their metallicities are in the range −1.3 < [Fe/H] <0.3 dex, which, if one follows the multiple populations proposed by Babusiaux et al. (2010), Hill et al. (2011), Ness et al. (2013), or Rojas-Arriagada et al. (2014), would mean that our sample includes stars in two stellar populations: old metal-poor with isotropic kinematics and metal-rich stars with bar-like kinematics. Even so, the behaviour of heavy-element-to-iron abundances vs. metallicity show some clear trends, among which we can cite as more important:
The dominantly r-element Eu shows a [Eu/Fe] vs. [Fe/H] ratio similar to that of alpha-elements (Fig. 5), that is, a flattening of the distribution towards low metallicities ([Fe/H]<~-0.5 dex), which is compatible with a plateau. The trend [Eu/Fe] vs. [Fe/H] also reveals a turnover at around [Fe/H] ~-0.6 dex due to Fe enrichment from type Ia SNe. It is interesting to compare the metallicity of the turnover with that for bulge microlensed stars by Bensby et al. (2013, their Fig. 25 located at around [Fe/H] ~-0.7 dex, and [Fe/H] ~-0.4 dex for thick disc stars, which can be seen in Fig. 9 of Bensby et al. (2004). This could indicate a small difference in the chemical enrichment of the bulge and thick disc (different SN II/SN Ia ratios along time). For [Fe/H] >-0.6 dex, there is a decreasing [Eu/Fe] vs. [Fe/H], reaching the solar value at the solar metallicity, and decreasing further for higher metallicities. On the other hand, in Fig. 9, the [La/Eu] and [Nd/Eu] seem to start increasing at around [Fe/H] ~-0.4 dex due to a triggering of s-element enrichment by AGB stars.
Figure 6 provide trends for [Ba/Fe], [La/Fe], [Ce/Fe] and [Nd/Fe] vs. [Fe/H], showing that they decrease steadily with increasing metallicities. One possible interpretation would be that the second peak elements are mainly produced by the r-process and that the decrease with metallicity is due to Fe enrichment by SN Ia. However, the increase of the [La/Eu] and [Nd/Eu] ratios with increasing metallicity for supersolar metallicities is due to s-element enrichment by AGB stars. Consequently, in that metallicity regime, the decrease in abundance (relative to iron) of the second peak neutron capture elements must be due to the s-process production not being quite strong enough to counterbalance the iron production by SN Ia.
For metal-poor stars in the range -0.6 dex< [Fe/H] <-0.3 dex, [La,Nd/Eu] ratios are located close to the pure r-process expected value (Arlandini et al. 1999; Sneden et al. 2008), indicating that for these older stars all these elements are produced by the r-process.
Finally, Fig. 10 showing [Ba/O] vs. [O/H] shows that our bulge stars and the thick disc data from Bensby et al. (2005) and Reddy et al. (2006) are compatible. The same figure shows that all these stellar populations are clearly distinct from the thin disc. Another interesting product of Fig. 10 is the comparison with metal-rich stars by Trevisan et al. (2011) and Trevisan & Barbuy (2014), indicating that their sample better resembles an old inner thin disc than a bulge-like population.
Models available at http://marcs.astro.uu.se/
Acknowledgments
We thank the anonymous referee for his/her remarks, which resulted in an improved discussion of the results. M.V.d.S. acknowledges a FAPESP post-doctoral fellowship No. 2013/50361-0. B.B. acknowledges partial financial support by CNPq and FAPESP. V.H. acknowledges support of the French Agence Nationale de la Recherche under contract ANR-2010-BLAN- 0508-01OTP. M.Z. and D.M. are supported by Fondecyt Regular 1110393 and 1130196, by the BASAL Center for Astrophysics and Associated Technologies CATA PFB-06, the FONDAP Center for Astrophysics 15010003, by the Chilean Ministry for the Economy, Development, and Tourism Programa Iniciativa Científica Milenio through grant IC120009, and awarded to the Millennium Institute of Astrophysics, MAS.
References
- Alvarez, R., & Plez, B. 1998, A&A, 330, 1109 [NASA ADS] [Google Scholar]
- Arlandini, C., Käppeler, F., Wisshak, K., et al. 1999, ApJ, 525, 886 [NASA ADS] [CrossRef] [Google Scholar]
- Babusiaux, C., Gómez, A., Hill, V., et al. 2010, A&A, 519, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Babusiaux, C., Katz, D., Hill, V., et al. 2014, A&A, 563, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ballero, S. K., Matteucci, F., Origlia, L., & Rich, R. M. 2007, A&A, 467, 123 [Google Scholar]
- Barbuy, B., Perrin, M.-N., Katz, D., et al. 2003, A&A, 404, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barbuy, B., Hill, V., Zoccali, M., et al. 2013, A&A, 559, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barbuy, B., Chiappini, C., Cantelli, E., et al. 2014, A&A, 570, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barbuy, B., Friaça, A. C. S., da Silveira, C. R., et al. 2015, A&A, 580, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Feltzing, S., & Lundström, I. 2004, A&A, 415, 155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Feltzing, S., Lundström, I., & Ilyin, I. 2005, A&A, 433, 185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Yee, J. C., Feltzing, S., et al. 2013, A&A, 549, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bisterzo, S., Gallino, R., Straniero, O., Cristallo, S., & Käppeler, F. 2011, MNRAS, 418, 284 [NASA ADS] [CrossRef] [Google Scholar]
- Bisterzo, S., Travaglio, C., Gallino, R., Wiescher, M., & Käppeler, F. 2014, ApJ, 787, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Brewer, M.-M., & Carney, B. W. 2006, AJ, 131, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Burris, D. L., Pilachowski, C. A., Armandroff, T. E., et al. 2000, ApJ, 544, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Busso, M., Gallino, R., & Wasserburg, G. J. 1999, ARA&A, 37, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Chiappini, C. 2013, Astron. Nachr., 334, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Chiappini, C., Frischknecht, U., Meynet, G., et al. 2011, Nature, 472, 454 [NASA ADS] [CrossRef] [Google Scholar]
- Clarkson, W., Sahu, K., Anderson, J., et al. 2008, ApJ, 684, 1110 [NASA ADS] [CrossRef] [Google Scholar]
- Coelho, P., Barbuy, B., Meléndez, J., Schiavon, R. P., & Castilho, B. V. 2005, A&A, 443, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davis, S. P., & Phillips, J. G. 1963, The red system (A2[pi]-X2[Sigma]) of the CN molecule (Berkley: University of California Press) [Google Scholar]
- Eggen, O. J., Lynden-Bell, D., & Sandage, A. R. 1962, ApJ, 136, 748 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G., Bournaud, F., & Elmegreen, D. M. 2008, ApJ, 688, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Frischknecht, U., Hirschi, R., & Thielemann, F.-K. 2012, A&A, 538, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fulbright, J. P., McWilliam, A., & Rich, R. M. 2007, ApJ, 661, 1152 [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez, O. A., Rejkuba, M., Zoccali, M., et al. 2011, A&A, 530, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hill, V., Lecureur, A., Gómez, A., et al. 2011, A&A, 534, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hinkle, K. H., Wallace, L., & Livingston, W. 1995, in Laboratory and Astronomical High Resolution Spectra, eds. A. J. Sauval, R. Blomme, & N. Grevesse, ASP Conf. Ser., 81, 66 [Google Scholar]
- Ishigaki, M. N., Aoki, W., & Chiba, M. 2013, ApJ, 771, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, C. I., Rich, R. M., Kobayashi, C., & Fulbright, J. P. 2012, ApJ, 749, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, C. I., McWilliam, A., & Rich, R. M. 2013, ApJ, 775, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, B. R., & Lindegren, L. 2005, A&A, 436, 127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Käppeler, F., Beer, H., & Wisshak, K. 1989, Rep. Prog. Phys., 52, 945 [Google Scholar]
- Käppeler, F., Gallino, R., Bisterzo, S., & Aoki, W. 2011, Rev. Mod. Phys., 83, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kovtyukh, V. V., & Andrievsky, S. M. 1999, A&A, 351, 597 [NASA ADS] [Google Scholar]
- Kratz, K.-L., Farouqi, K., Pfeiffer, B., et al. 2007, ApJ, 662, 39 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Kupka, F., Piskunov, N., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Kupka, F. G., Ryabchikova, T. A., Piskunov, N. E., Stempels, H. C., & Weiss, W. W. 2000, Balt. Astron., 9, 590 [NASA ADS] [Google Scholar]
- Langanke, K., & Thielemann, F.-K. 2013, Europhys. News, 44, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lawler, J. E., Bonvallet, G., & Sneden, C. 2001a, ApJ, 556, 452 [NASA ADS] [CrossRef] [Google Scholar]
- Lawler, J. E., Wickliffe, M. E., den Hartog, E. A., & Sneden, C. 2001b, ApJ, 563, 1075 [CrossRef] [Google Scholar]
- Lecureur, A., Hill, V., Zoccali, M., et al. 2007, A&A, 465, 799 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McWilliam, A., & Rich, R. M. 1994, ApJS, 91, 749 [NASA ADS] [CrossRef] [Google Scholar]
- McWilliam, A., Matteucci, F., Ballero, S., et al. 2008, AJ, 136, 367 [NASA ADS] [CrossRef] [Google Scholar]
- McWilliam, A., Wallerstein, G., & Mottini, M. 2013, ApJ, 778, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Minniti, D. 1996, ApJ, 459, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Ness, M., Freeman, K., Athanassoula, E., et al. 2013, MNRAS, 430, 836 [NASA ADS] [CrossRef] [Google Scholar]
- Noguchi, M. 1999, ApJ, 514, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Plez, B. 1998, A&A, 337, 495 [NASA ADS] [Google Scholar]
- Reddy, B. E., Lambert, D. L., & Allen de Prieto, C. 2006, MNRAS, 367, 1329 [NASA ADS] [CrossRef] [Google Scholar]
- Rojas-Arriagada, A., Recio-Blanco, A., Hill, V., et al. 2014, A&A, 569, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rosswog, S., Korobkin, O., Arcones, A., Thielemann, F.-K., & Piran, T. 2014, MNRAS, 439, 744 [NASA ADS] [CrossRef] [Google Scholar]
- Rutten, R. J. 1978, Sol. Phys., 56, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Saha, A., Olszewski, E. W., Brondel, B., et al. 2010, AJ, 140, 1719 [NASA ADS] [CrossRef] [Google Scholar]
- Simmerer, J., Sneden, C., Cowan, J. J., et al. 2004, ApJ, 617, 1091 [NASA ADS] [CrossRef] [Google Scholar]
- Siqueira Mello, C., Barbuy, B., Spite, M., & Spite, F. 2012, A&A, 548, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sneden, C., Cowan, J. J., & Gallino, R. 2008, ARA&A, 46, 241 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thielemann, F.-K., Hirschi, R., Liebendörfer, M., & Diehl, R. 2011, in Lect. Notes Phys., eds. R. Diehl, D. H. Hartmann, & N. Prantzos, (Berlin Springer Verlag), 812, 153 [Google Scholar]
- Tolstoy, E., Hill, V., & Tosi, M. 2009, ARA&A, 47, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Trevisan, M., & Barbuy, B. 2014, A&A, 570, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Trevisan, M., Barbuy, B., Eriksson, K., et al. 2011, A&A, 535, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Truran, J. W. 1981, A&A, 97, 391 [NASA ADS] [Google Scholar]
- Van der Swaelmen, M., Hill, V., Primas, F., & Cole, A. A. 2013, A&A, 560, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wanajo, S., & Ishimaru, Y. 2006, Nucl. Phys. A, 777, 676 [Google Scholar]
- Wanajo, S., Sekiguchi, Y., Nishimura, N., et al. 2014, ApJ, 789, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Yong, D., Alves Brito, A., Da Costa, G. S., et al. 2014a, MNRAS, 439, 2638 [NASA ADS] [CrossRef] [Google Scholar]
- Yong, D., Roederer, I. U., Grundahl, F., et al. 2014b, MNRAS, 441, 3396 [NASA ADS] [CrossRef] [Google Scholar]
- Zoccali, M., Renzini, A., Ortolani, S., et al. 2003, A&A, 399, 931 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zoccali, M., Lecureur, A., Barbuy, B., et al. 2006, A&A, 457, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zoccali, M., Hill, V., Lecureur, A., et al. 2008, A&A, 486, 177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Central wavelengths, excitation potential, and adopted oscillator strengths log gf values, taken from 1 Van der Swaelmen et al. (2013), otherwise VALD values.
Individual abundances for μ Leonis derived from spectrum at different resolution and S/N.
Abundance uncertainties for star BWc-4, for uncertainties of ΔTeff =150 K, Δlog g = 0.2, Δvt =0.1 km s− 1 and Δ [M/H] =0.1 dex.
Mean abundances and their associated standard deviation for our bulge Ba, La, Nd, Ce distributions.
All Figures
 |
Fig. 1 From top to bottom: fit of Ba ii line at 6496 Å, La ii line at 6390 Å, Nd ii line at 6740 Å, and Eu ii line at 6645 Å for BWc-4. Black crosses: observed spectrum; red solid line: best fit; blue solid lines: spectra computed for the best-fit value of [X/Fe] ± 0.3. |
| In the text | |
 |
Fig. 2 From top to bottom: fit of Ba ii line at 6496 Å, La ii line at 6390 Å, and Eu ii line at 6645 Å for μ Leo (ESPaDOnS spectrum, see text for reference, degraded to UVES resolution). Black crosses: observed spectrum; red solid line: best fit; blue solid lines: spectra computed for the best-fit value of [X/Fe] ±0.3 dex. |
| In the text | |
 |
Fig. 3 Synthesis of the line at 6320 Å in the solar spectrum: observed spectrum in black (Hinkle et al. 1995), La line alone in red, Co line alone in green, total blend in purple. |
| In the text | |
 |
Fig. 4 Comparison of abundances derived by our two methods (first method described in Sect. 3.1, second method described in Sect. 3.6) for the La ii line at 6390 Å, Ce ii line at 6043 Å. |
| In the text | |
 |
Fig. 5 [Eu/Fe] vs. [Fe/H]. Symbols: black filled circles: present work; red filled downward triangles: Johnson et al. (2012); red crosses: Bensby et al. (2013); red empty squares: M62 (Yong et al. 2014b); red empty pentagons: NGC 6522 giants (Barbuy et al. 2014); green small dots: thick disc from Bensby et al. (2005), Brewer & Carney (2006), Reddy et al. (2006) and Simmerer et al. (2004); blue small dots: thin disc from Bensby et al. (2005) and Reddy et al. (2006). |
| In the text | |
 |
Fig. 6 [Ba,La,Ce,Nd/Fe] vs. [Fe/H]. Same symbols as in Fig. 5. |
| In the text | |
 |
Fig. 7 [La,Ce,Nd/Ba] vs. [Fe/H]. Black dots: our bulge sample. |
| In the text | |
 |
Fig. 8 [Ce,Nd/La] vs. [Fe/H]. Same symbols as in Fig. 5. |
| In the text | |
 |
Fig. 9 [Ba,La,Ce,Nd/Eu] vs. [Fe/H]. Same symbols as in Fig. 5. Dotted and dashed blue lines: pure r-process values provided by Arlandini et al. (1999) and Sneden et al. (2008), respectively. |
| In the text | |
 |
Fig. 10 [Ba/O] vs. [O/H]. Same symbols as in Fig. 5 and black empty triangles: super metal-rich, bulge-like Trevisan & Barbuy (2014). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


