| Issue |
A&A
Volume 585, January 2016
|
|
|---|---|---|
| Article Number | A66 | |
| Number of page(s) | 11 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201527182 | |
| Published online | 18 December 2015 | |
A subsynchronously rotating pulsating subdwarf B star in a short-period binary with a white dwarf companion
1
Uniwersytet Pedagogiczny, Obserwatorium na Suhorze, ul. Podchorążych
2,
30-084
Kraków
Poland
e-mail:
sfbaran@cyf-kr.edu.pl
2
Nordic Optical Telescope, Rambla José Ana Fernández Pérez 7,
38711
Breña Baja,
Spain
3
Dr. Remeis–Sternwarte, Institute for Astronomy, University,
Erlangen-Nürnberg, Sternwartstr.
7, 96049
Bamberg,
Germany
4
Instituut voor Sterrenkunde, KU Leuven, Celestijnenlaan 200D,
3001
Leuven,
Belgium
5
Department of Physics, Astronomy, and Materials Science, Missouri
State University, Springfield, MO
65804,
USA
Received: 13 August 2015
Accepted: 2 October 2015
We present our analysis of KIC 7664467, an sdB pulsator that we have found to be residing in a 1.56-day binary system with a white-dwarf companion. This system was observed photometrically with the Kepler spacecraft and spectroscopically with ground-based telescopes. We analyzed the amplitude spectra detecting 61 periods, rotationally split multiplets, and an equally spaced sequence in period. These two features helped with the mode identification. We derived both the binary and rotation periods showing that this is another binary system with a subsynchronous sdB star. From our spectroscopy of the sdB star, we determined Teff = 27440 ± 120 K, log g = 5.38 ± 0.02 dex. The abundance pattern follows the general trend observed in sdB stars, where light metals are subsolar, while the Fe abundance is very close to the solar value. We found the N enrichment and low abundances of C and O that resemble the equilibrium abundances of the CNO cycle. We could also measure the Mg and Si abundances. Using the radial velocity amplitude K1 = 57(3) km s-1 and the Doppler boosting-dominated photometric signal at the orbital period, we constrained the companion to be a compact object, almost certainly a white dwarf.
Key words: asteroseismology / subdwarfs / stars: oscillations / stars: abundances
© ESO, 2015
1. Introduction
Subdwarf B stars (hereafter: sdB) are descendants of roughly 1 M⊙ main sequence stars. After the hydrogen is burned out in their cores, they rush toward the red giant branch to ignite helium. After helium ignition, sdB stars settle down on the hot end of the horizontal branch since unlike most red giant stars, sdB stars lose their hydrogen envelopes before the helium flash. A population study including several different envelope ejection mechanisms was presented by Han et al. (2002). Starting from a diverse population of binary systems and modeling the interactions during the red giant branch stage, they produce systems that include short-period binaries, such as sdB+white dwarf or sdB+main sequence stars, which are the products of common envelope ejection, long-period binaries, i.e., sdB+F/G/K, products of stable Roche lobe overflow, as well as single sdB stars being mergers of two objects.
Having no hydrogen fusion in their envelopes means that sdB stars do not climb up the asymptotic branch, but instead move directly to the white dwarf cooling track. The typical effective temperatures of sdB stars range from 20 000 K up to 40 000 K, while the surface gravity on a logarithmic scale is 5–6 dex. The surface metallicity abundance varies significantly from star to star.
The discovery of pulsations in sdB stars by Kilkenny et al. (1997) has opened up an excellent way to study their interiors by means of asteroseismology. Stellar pulsations force the entire star to shake according to the geometry of the modes driven in that star, hence modeling the interior includes information about the mass of the hydrogen envelope, chemical composition profiles, or the convective core.
At first, pulsating sdB (hereafter sdBV) stars were monitored only from the ground. Since observation runs were short and hampered by atmospheric transparency effects, it limited the lowest detectable amplitudes, which meant that rotational multiplets and period spacing among g-modes were not detected. Only with Kepler observations has significant progress been made. A few years coverage with high-precision photometric data helped us to lower the noise in amplitude spectra down to the parts per million (ppm) level, which uncovered tens or even hundreds of modes in one star. Such a large number of modes, particularly with low amplitudes, show rotational multiplets and asymptotic period spacings that allow us to make a mode identification, which is a necessary step toward modeling, and to derive stellar spin rates of sdB stars.
The analyses of many sdBV stars observed with the Kepler spacecraft have already been published. Apart from the single sdBV stars, those in binaries show additional features that can be used to determine binary system parameters or properties of the pulsating component itself, independently of asteroseismology. Since one of the proposed envelope-ejection mechanisms in the formation process of sdB stars is a common-envelope phase in binary evolution (Han et al. 2002), it is important to study the fraction of sdBV binaries in the original Kepler field of view. So far, four sdBVs have been found to have M dwarf companions and three sdBVs were found to have WD companions. In this paper we continue our work on pulsating sdBVs residing in non-eclipsing single-line spectroscopic binaries observed with the Kepler spacecraft, to disclose the fourth case of an sdBV with a white-dwarf companion, KIC 7664467. Three similar objects, KIC 11558725, KIC 7668647, and KIC10553698, were described by Telting et al. (2012, 2014a) and Østensen et al. (2014), respectively.
2. Spectroscopic data
We observed KIC 7664467 as part of our observing campaign to investigate the binary status of the 18 pulsating sdBV stars in the Kepler field (Telting et al. 2014b). From 2010 to 2012 we obtained 35 radial-velocity (RV) measurements of KIC 7664467.
The first two observations were made using the ISIS long-slit spectrograph on the William Herschel Telescope (WHT), equipped with the R600B grating and a 1.0 arcsec slit. Twenty-five spectra were collected with the ALFOSC spectrograph at the Nordic Optical Telescope (NOT) between May 2011 and September 2012, using an 0.5 arcsec slit with grism #16. In October 2012 we took five additional spectra. Since these were taken with a different instrument setup and an unknown RV-offset, they were not considered in the orbital analysis, even though the RV measurements fit the orbit relatively well. Finally, eight more spectra were taken on September 30 and October 1, 2012, with the Kitt Peak 4-m Mayall telescope (KPNO) with RC-Spec/F3KB, the kpc-22b grating and a 2 arcsec slit. All data we accepted for our analysis are listed in Table A.1 and presented in Fig. 1.
 |
Fig. 1 Color-coded plot of the radial-velocities of KIC 7664467. The dark blue circles represent WHT data, light blue ones show KPNO data, and red circles are NOT data. |
Exposure times were 900 s at the WHT and Mayall telescopes and 900 s or 1200 s at the NOT. The signal-to-noise ratio (S/N) of the spectra ranges between 48–52, 18–31, and 23–55, for these telescopes, respectively. The widths of the arc lines were 1.7 Å for the WHT and Mayall setups and 2.2 Å for the NOT.
All spectra were processed and RV extracted using standard IRAF tasks. For the ALFOSC data, an imaging-based flat-field frame, interpolated along the dispersion direction between UBV-band sky flats, was used to remove pixel-to-pixel variations. All spectra and their time stamps were shifted and transformed to the solar-system barycentric frame. Radial velocities were computed with FXCOR by cross-correlating the observed Hγ, Hδ, Hζ, and Hη lines with a synthetic template derived from a fit to a mean spectrum of the target. For the ALFOSC data, the final RVs were adjusted for the position of the target in the slit, judged from slit images taken just before and after the spectra.
Parameters of the orbital fit to the spectroscopic data.
 |
Fig. 2 Combined radial-velocity corrected WHT/NOT/KPNO spectrum of KIC 7664467 (black). The peak S/N of the combined spectrum is ~110. The continuum of the normalized spectrum was sampled in 100 Å sections. The model fit computed with TLUSTY/XTgrid and the fit residual (gray) were shifted vertically for clarity. Line identifications and equivalent widths in mÅ are given for only the strongest lines of the significant ions in the model. The atmospheric parameters of the model are given in Table 2. |
Assuming a circular orbit, we find a fit for which the root mean square (rms) matches the mean FXCOR RV error of 12.3 km s-1 quite well. Parameters of that fit are given in Table 1. If we fix the orbital period to the one found from the Kepler data (see next sections), we find the RV-amplitude of 57(3) km s-1.
As can be seen in Fig. 3, even with our large number of spectra, we were unsuccessful at properly sampling the minimum of the RV curve. This implies that the RV amplitude cannot be derived with the accuracy one may otherwise expect from these data. When computing the mass function, while assuming a typical value for the mass of the sdB star of 0.47 M⊙ (Fontaine et al. 2012), we find a lower limit of the companion’s mass of 0.24 M⊙, and a minimum distance between both components of 5 R⊙.
3. Model atmosphere analysis
KIC 7664467 was discovered by the Kepler compact pulsators survey (Østensen et al. 2010) and classified as a g-mode pulsator. Østensen et al. (2010) derived the effective temperature Teff = 26 800 ± 500 K, surface gravity log g = 5.37 ± 0.08 dex, and He abundance log (nHe /nH) = −2.8 ± 0.2 dex, using the metal-line blanketed local thermodynamic equilibrium (LTE) models of Heber et al. (2000).
To constrain the atmospheric parameters of KIC 7664467 further and estimate its metal abundance, we analyzed all the new low-resolution WHT/ISIS, NOT/ALFOSC, and KPNO/RC spectra with the TLUSTY/SYNSPEC non-LTE model atmosphere and spectral synthesis codes (Hubeny & Lanz 1995; Lanz & Hubeny 2003, 2007). TLUSTY calculates fully line-blanketed, plane-parallel model atmospheres with opacity sampling and departures from LTE for a set of elements. To simultaneously consider the atmosphere structure and the lines visible in the observations we included opacities of the first 30 elements in our synthetic spectra. We treated 13 elements in full non-LTE in both TLUSTY and SYNSPEC. Our models include the ions of H i, He i-ii, C i-v, N i-v, O i-v, Ne i-iv, Mg ii-iii, Si i-iv, P iv-v, S ii-vi, Ca i-iii, Fe ii-vi, and Ni iii-v, thereby providing 1322 energy levels in all. The remaining 17 elements were kept in LTE, and these elements were assumed not to contribute to the opacity in the atmospheric structure calculations. None of the 17 elements were found to be significant in the spectra. To simultaneously consider the atmosphere structure and the lines visible in the observations we included opacities of the first 30 elements in our synthetic spectra. The spectral analysis was performed with the steepest-descent iterative spectral analysis program XTgrid (Németh et al. 2012). By starting out from an approximate spectral model of an average sdB star, XTgrid makes successive updates of the atmospheric parameters to fit the observations and minimize the global χ2. The procedure does not require a model grid, new models are calculated in the direction of decreasing chi squares. To accelerate the fitting procedure, the complexity of our models increases with the goodness of fit. Usually 30 to 50 iterations and some 120 models are required to converge a fit. The final atmosphere model is sampled in 50 depth points and converged to a 0.1% relative change in the structural and atmospheric parameters. Statistical errors of the final parameters are evaluated by calculating new models in one dimension until the respective confidence limit is reached. The best fit is shown in Fig. 2, and the final parameters are listed in Table 2 together with error bars.
We convolved the spectra from the three instruments to 2.2 Å resolution and combined all observations to increase the S/N to ~110 and fit as many weak lines as possible. We found no signatures of the companion in the combined spectrum, so we proceeded with the analysis as if it were a single star. Rotational velocities of sdB stars are generally below 10 km s-1 (Geier & Heber 2012), therefore we assumed zero rotation in our analysis.
Metal absorption lines are weak in the optical spectra of hot stars, and one must be particularly careful when deriving metal abundances from low-resolution or low S/N data because some random noise features may coincide with metal lines. Global fitting procedures therefore need to keep track of the strongest lines that drive the fit and the error statistics of the observation to decide which elements are significant. We applied a post-fit check and found that beyond the obviously strong lines of H and He, significant are also the strongest lines of C, N, O, Mg, Si, and Fe. Owing to its strong line blanketing, Fe has a notable backwarming effect on the temperature structure and therefore on the Balmer line profiles even if Fe lines are weak.
The fitting procedure provided slightly asymmetric error bars as listed in Table 2. After making these symmetric we found that KIC 7664467 has an NLTE temperature of Teff = 27 440 ± 120 K, surface gravity of log g = 5.382 ± 0.019 dex, and He abundance of log (nHe /nH) = −2.57 ± 0.05 dex, which places it among most of the slow pulsating sdB stars. The metallicity of KIC 7664467 fits in the general abundance profile of sdB stars (Geier 2013): helium and light metals are depleted, while Fe is near or somewhat above the solar abundance. The nuclear history of sdB stars is not reflected by their surface parameters, because diffusion processes change their surface abundances (Michaud et al. 2011). Therefore abundance ratios show large star-to-star scatter. We found a N/O ratio of 4.28 in KIC 7664467, 0.27 in KIC 8302197 (Baran et al. 2015a), and 2.8 in KIC 7668647 (Telting et al. 2014a).
Parameters for the fits shown in Fig. 2, with respect to the solar abundances from Asplund et al. (2009) provided for comparison.
In spite of the relatively high S/N, we did not find any signatures of the companion in the spectrum. Deca et al. (2012) provide a useful correlation among visible and infrared color indices to find the spectral contribution of main-sequence companions to sdB stars. We collected optical photometry from the Naval Observatory Merged Astrometric Dataset (NOMAD; Zacharias et al. 2004) and infrared photometry from the 2MASS All-Sky Catalog (Skrutskie et al. 2006) that gave B − V = −0.56 and J − K = 0.59. Although KIC 7664467 is faint for a reliable 2MASS photometry, these values suggest that a main-sequence companion cannot be earlier than type M5. Such a companion would not be visible in our spectrum. Therefore, based on optical-infrared color indices and the spectral quality, we conclude that a possible companion can only be a late M-type main-sequence star or a white dwarf. In Sect. 5 we conclude that the lack of a reflection effect in the light curve of KIC 7664467 strongly favors a white dwarf or, even more, a compact companion.
For comparison with earlier works we also performed the classical fitting to the metal-line blanketed LTE grids of Heber et al. (2000) on the new high-S/N orbit-corrected mean spectra. We analyzed the spectrum from each observatory separately and made a weighted mean of the results. The LTE values for the physical parameters are Teff = 26 717 ± 70 K, log g = 5.340 ± 0.010 dex, and log(nHe/nH) = −2.660 ± 0.020 dex.
4. Photometric data
KIC 7664467 was observed by the Kepler spacecraft during the survey phase (Q2 in long cadence – LC and Q2.3 in short cadence – SC). These observations revealed stellar variability, which was interpreted with stellar oscillations. After this discovery, the star was monitored on a longer time scale during Q5-11 and Q13-Q17 and recorded in both SC and LC modes.
Since the analysis of the Q2.3 data was published by Reed et al. (2010), we focused on SC data obtained during Q5-17 in this work. The amplitude spectrum shows an intrinsic signal beyond the Nyquist frequency of LC data, therefore these data are not as useful and will not be considered in this analysis.
According to the Kepler database, a contamination factor for KIC 7664467 from neighboring stars reaches 0.228; however, this value was obtained based on incorrect Teff of the sdB star, which makes its application invalid. To avoid an unnecessary signal from any neighboring objects, we decided not to use fluxes from the optimal aperture, but we did use pixel tables to pull out Pixel Response Function fluxes1. These fluxes are based on PSF models linearly interpolated from the five reference models associated with the CCD channel, according to their positions. The PSF models account for intra-pixel variability and allow us to avoid a contamination from neighbors. Next, a detrending and 4σ clipping was applied to remove onboard systematics and outliers, respectively. Finally, we converted fluxes to parts per thousand (ppt) units. In total, we analyzed 1.38 million points described by a standard deviation of 5.75 ppt.
5. Orbital features
KIC 7664467 is a binary system with no eclipses or significant ellipsoidal variation. A lack of the former means an inclination below 88 deg, while an ellipsoidal deformation in this system may not be substantial enough to be detected. Recently, a beaming effect has been noticed in a number of the binaries observed with the Kepler spacecraft. This is a relativistic effect in which the luminosity of an object is magnified when heading toward us but dimmed when moving away from us. It was observed in three other sdB binaries, KIC 11558725, KIC 7668647, and KIC 10553698 (Telting et al. 2012, 2014a; Østensen et al. 2014), which are similar to our object, therefore we looked for a flux variation on a time scale of an orbital period, Porb = 1.56 days (details are given below), and correlated it with radial-velocity variations. We have phased time-series photometric and radial velocity data to the inferior conjunction at BJD = 2 455 832.951 defined from the radial velocities and folded the data into 50 phase bins (Fig. 3).
 |
Fig. 3 Photometric (black squares) and radial-velocity (blue dots) phased data overlapped with a sinusoidal fit representing the beaming effect obtained from radial-velocity data. The right vertical axis for RV data is reversed. |
The beaming effect can be used to evaluate the radial velocity of the detected companion and compared with the one derived from the spectroscopy. Similarly to Telting et al. (2012), we accepted a beaming factor to be 1.403(20). This value is derived following the procedure described in Bloemen et al. (2011), and worked fairly well for three other pulsating sdB stars analyzed by Telting et al. (2012, 2014a) and Østensen et al. (2014). Since the physical parameters of these stars, as well as KIC 7664467, are similar, we assumed that the above beaming factor will also work for our target star.
We used the Fourier technique to evaluate the amplitude and the orbital period of the binary variation; details on this technique will be provided in Sect. 6. We derived 255(7) ppm and 1.559049(27) days for the amplitude and period, respectively. Using equation 2 from Telting et al. (2012) and assuming D = 1, since no contamination from neighboring stars is involved, we derived the radial-velocity amplitude in the range of 54.9(1.1) km s-1, where the error reflects the photometric errors. This result agrees with the amplitude of the radial-velocity variation observed spectroscopically (Sect. 2), which implies that the companion to the sdB star does not contribute to the beaming, so must have a compact nature.
Recently, the previously known (Green et al. 2003) sdBV EQ Psc was found to have an M-dwarf (dM) companion from the orbital reflection effect seen by Kepler during K2 mission (Jeffery & Ramsay 2014). The system has an orbital period of 19.2 h, the longest period in any known sdB+dM system with a detected reflection effect. This orbital period is about half that of KIC 7664467, and while assuming reasonable masses for the components in these two binary systems, this implies that our system is roughly two times wider than EQ Psc. The Kepler light curve of EQ Psc has a rather high amplitude of 10.2 ppt at the orbital period and significant harmonic of 1.30 ppt in amplitude, while for KIC 7664467 we find no orbital signal down to 0.03 ppt after correcting for the beaming amplitude. The residual signal at the orbital frequency and any signal at its harmonics would indicate that the light curve contains other variations than just the relativistic Doppler boosting. We argue that for a system that is only twice as wide as EQ Psc, we should have detected the reflection effect in the Kepler data, in case the system included an M-dwarf companion. Since we do not see such an effect in the light curve, the companion to the sdBV in KIC 7664467 must be a white dwarf or an even more compact object. Although an NS or BH companion remains a theoretical possibility according to calculations, no such ultra-compact object has been found to orbit any of the >100 short-period sdB binaries studied to date (Podsiadlowski et al. 2002).
If we use a typical value for an sdB to be 0.5 solar masses, then the mass function gives M2 ≥ 0.24 M⊙. Then, if we adopt 0.6 for an average white dwarf, we derive the orbital inclination between 30 and 35 degrees.
6. Amplitude spectrum
We used the Fourier technique to identifythe periodic signals that exist in the photometric data. We calculated an amplitude spectrum and selected frequencies for a nonlinear least-squares fit. Each signal was presented in the form Aisin(ωit + φi). This iterative process followed the standard prewhitening procedure and continued until resolved peaks with amplitudes above a given threshold had been removed. This threshold follows Baran et al. (2015b) and was adopted at S/N = 5.5 (0.047 ppt). In addition, we searched for peaks below that threshold down to S/N = 4.3 (0.037 ppt), which is also used by others. We consider this extra set of peaks to be tentative.
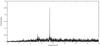 |
Fig. 4 Amplitude spectrum of KIC 8302197 limited to the very low frequencies. The dominant peak is a consequence of binarity. |
The analysis of Kepler Q2.3 data was published by Reed et al. (2010). They analyzed only one month of continuous data and detected six peaks above S/N = 4. The highest amplitude peak did not stand out above S/N = 10. A lower S/N, as compared to our analysis, is a consequence of short data coverage. All peaks were found in the frequency region characteristic of gravity modes. The residual spectrum did not show any leftovers at the frequencies of the pre-whitened peaks, which indicated that the peaks were stable over the month of monitoring.
In our analysis of Q5 – 17 data, the frequency resolution is 0.0131 μHz. It is defined as 1.5 /T, where T is the time baseline of the data. In our analysis we detected 58 periods, because of the high instability, additional three periods were inserted by hand. We found two significant signal at very low frequencies (Fig. 4). One of the signals at 7.423 μHz represents a flux variation that corresponds to the binarity. There are also residuals of another significant peak at 2.856 μHz, along with its low-amplitude harmonic at 5.712 μHz. The parent peak reaches 300 ppm in amplitude; however, it has been detrended out, therefore Fig. 4 shows only small residual peaks at their frequencies. In addition, our radial-velocity data folded over 0.247 days did not result in any coherent variation. This is clearly a hint that the peak in question does not represent any periodic variation in KIC 7664467. Keeping in mind that the extracted fluxes are not contaminated by neighbors, these peaks may originate in other stars not necessarily close to our object; it is known that the light reflection is present in Kepler photometer.
All other peaks detected in the amplitude spectrum of KIC 7664467 are associated with gravity modes and are listed in Table A.2. The amplitude spectrum is dominated by the frequency at ~247 μHz; however, its amplitude, 0.5 ppt, is one of the smallest among sdBV stars observed with the Kepler spacecraft. We confirm all frequencies reported by Reed et al. (2010) except their f2. This frequency could have been transient when observed in Q2.3. Our set of frequencies were also tested against the spurious signal listed in both Data Release Notes 12 2 and Baran (2013a) to avoid overinterpreting our solution. The residual amplitude spectrum still shows signal at the frequencies of the prewhitened peaks, which means that the oscillation modes are not stable, changing amplitudes and/or frequencies (phases).
The substantially larger number of frequencies detected in Q5 – 17 data, as compared to just six described by Reed et al. (2010), should significantly improve an application of asteroseismology since the stellar structure will be better constrained when more modes are brought into play, especially those that can be assigned a mode ID from multiplet splittings.
7. Multiplets
The Kepler spacecraft was able to provide almost continuous monitoring of many objects in the K1 field for up to 3.5 years. In the case of sdBV stars, it allowed us to detect multiplets in several of them (e.g., Baran et al. 2012; Telting et al. 2012; Baran 2012b; Baran & Winans 2012; Reed et al. 2014; Østensen et al. 2014; Telting et al. 2014a; Foster et al. 2015). Encouraged by these results, we searched for equidistant peak formations that could be associated with rotationally split modes. The range of the rotational splitting is fairly broad from 0.006 to 0.06 μHz, which is equivalent to roughly 90- to10-day rotation periods. The splitting in a particular star is usually unknown, and the presence of one fortuitous equally spaced peaks is not necessarily an indication of stellar rotation. However, a diversification of the Ledoux constant depending on modal degree may help for concluding which peaks create multiplets and which do not. For g modes, the Ledoux constant is tied to the modal degree by [ l(l + 1) ] -1, leading to the conclusion that the lowest l has the narrower splitting, while the high-degree modes have splitting of similar widths.
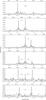 |
Fig. 5 Close-ups of the bulk of the g-mode region of the amplitude spectrum of KIC 8302197 with multiplet-like formations. The numbers in the plots indicate separations between peaks, and we rounded them up to two decimal places for clarity. |
 |
Fig. 6 Same as in Fig. 5 to show multiplet-like formations detected at the high end of frequencies of the g-mode region. |
In the amplitude spectrum of KIC 7664467, we have found several peaks that are indications of stellar rotation. We show them in Figs. 5 and 6. We started our multiplet-assignment seeking l = 1 or 2 since low-degree modes are the most likely to be detected in the amplitude spectra. The peaks at 246 and 363 μHz form two complete triplets with the narrowest splittings among all plotted multiplet candidates. In addition, we found doublets at 228, 242, and 372 μHz with a separation comparable to the former two. This indicates that all of the listed candidates are likely triplets. There are a few other cases with either one or two low-amplitude peaks and with spacings close to 0.17 μHz, as well as twice that value. A triplet missing the central peak has a similar spacing to high-degree modes and therefore needs to be cross-checked using other methods (Sect. 8). The narrowest splitting is 0.14, while the widest equals 0.17 μHz. We can only speculate that the splitting differs along a radial order. Taking an average value of splittings in the range of 0.14-0.19 μHz, we derive 35.1(6) days rotation period. It seems that KIC 7664467 is another example of subsynchronous rotation, rotating more slowly than revolving the system’s barycenter.
Having established the l = 1 triplets, we can search for higher modal degree modes. According to the Ledoux formula given earlier, the splitting in l = 2 quintuplets is 1.67 times wider than in l = 1 triplets, i.e., 0.23−0.28. Higher modal degree modes will have even wider splittings approaching the limit 0.28−0.34 in case of a very high degree.
Checking other multiplet candidates, we find only one spacing in the range of quintuplets. It is 0.22 μHz at 161.4 μHz. We do not detect three other potentially missing spacings. This makes the quintuplet assignment very doubtful. It leads to the conclusion that the quintuplets are very depleted in the amplitude spectrum of KIC 7664467.
Besides the multiplet candidates presented in Fig. 5, we also detected a few candidates at the higher frequencies. We are aware that some of the peaks are below 5.5σ, so we do not claim a convincing detection but indicate the possibility of additional signal at those frequencies. These are presented in Fig. 6. The spacings are wider than 0.3 μHz, which would indicate twice the l = 1 spacing. This explanation, however, is improbable since more than two peaks were typically found in each region. The only exception is a doublet at 909 μHz. If these candidates are not triplets, then they must be either combination frequencies or high-degree modes. We did not find enough peaks to explain such a long sequence of combination peaks, while multiplets of high-degree modes have already been detected in three other sdBV stars, KIC 10139546 by Baran & Østensen (2013), KIC 7668647 by Telting et al. (2014a) and KIC 3527751 by Foster et al. (2015). Therefore, we lean toward assigning these multiplets detected at higher frequencies with l ≥ 3−5.
8. Period spacing
An asymptotic period spacing has been detected in many g-mode-dominated sdBV stars. It is a very useful tool for mode identification. The gravity modes with the same modal degrees are equally spaced in periods and only differ in the radial order. Chemical discontinuities inside the stars may cause this sequence to be locally uneven. The period spacing has been established empirically to be on the order of 250 s and varies from star to star. Knowing the expected spacing makes finding particular modal degree sequences easier. In addition, fixed or suspected multiplets significantly help to start up the sequence, particularly when sequences are patchy.
 |
Fig. 7 Kolmogorov-Smirnov test to find the period spacings of the same modal degree sequences. A significant minimum of log Q indicates a frequent spacing of dipole modes at 263 s. |
Reed et al. (2010) report that the period spacing found in one-month survey data equals 260.02 s. We calculated the Kolmogorov-Smirnov test to confirm that value. The plot showing the result of our test clearly indicates that the most common spacing in period is 263 s (Fig. 7). Consistent with the lack of detected quintuplets (see Sect. 7), we find no Q-value minimum related to quadrupole modes. This test, however, does not indicate which peaks are spaced by 260 s , therefore we started our identification with a few modes, marked as triplets during the multiplet search, to check whether they are spaced by the expected 260 s on average. Then, we propagated the l = 1 sequence toward low and high frequencies to find more peaks that could complete the l = 1 sequence. In that way, we isolated 20 dipole modes with a separation between 200 and 300 s.
 |
Fig. 8 Close-up of the amplitude spectrum of KIC 7664467 displayed in period instead of frequency to show l = 1 sequence. |
In Fig. 8 we plotted a close-up of the amplitude spectrum with the bulk of the g modes. We marked l = 1 and 2 identifications with the numbers on top of the peaks. The asterisks denote which peaks are multiplets. The lowest and highest frequencies are not included in the plot. We included all our certain modal degree identifications in Table A.2. After having determined a number of modes through their multiplet splittings and establishing the main sequence of l = 1 modes through the regular spacings in the amplitude spectrum and through the KS test, we can construct an echelle diagram of all the detected modes. Figure 9 shows the modes listed in Table A.2 with period modulo ΔP on the x-axis plotted versus the period. In the left-hand panel we plotted modulo the ΔP derived with the KS test for l = 1 263 s, and in the right-hand panel we multiplied this ΔP with 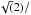
 to get the corresponding predicted asymptotic period spacing for l = 2 151 s. The curves from top to bottom show how the rotational splitting for Prot = 50+, d changes with increasing period. The double lines illustrates the uncertainty in period from the frequency resolution. In the figure, the l = 1 modes that show clear splittings are indicated with hollow blue bullets. Single pulsation peaks that follow the l = 1 sequence are illustrated with filled bullets, and the highest amplitude modes (A> 0.1 ppt) are plotted with larger symbols. Multiplets that match the l = 2 splitting are shown with outlined red boxes, and a few single modes that fall on the predicted l = 2 sequence, but not matching the l = 1 sequence have been indicated with filled boxes. Only one mode is too close to either sequence to be identified, and is indicated with a light-blue outlined box. The trapped modes discussed above are outlined with green diamonds. The modes that do not fit either sequence are shown with filled diamonds and are only found in the short-period region at the bottom of the diagrams. Comparing this echelle diagram with that of Østensen et al. (2014), we see that it shows many of the same features, even if the diagram is less complete due to fewer detected modes. The sequences rarely follow the asymptotic lines strictly, but instead meander around the mean line.
to get the corresponding predicted asymptotic period spacing for l = 2 151 s. The curves from top to bottom show how the rotational splitting for Prot = 50+, d changes with increasing period. The double lines illustrates the uncertainty in period from the frequency resolution. In the figure, the l = 1 modes that show clear splittings are indicated with hollow blue bullets. Single pulsation peaks that follow the l = 1 sequence are illustrated with filled bullets, and the highest amplitude modes (A> 0.1 ppt) are plotted with larger symbols. Multiplets that match the l = 2 splitting are shown with outlined red boxes, and a few single modes that fall on the predicted l = 2 sequence, but not matching the l = 1 sequence have been indicated with filled boxes. Only one mode is too close to either sequence to be identified, and is indicated with a light-blue outlined box. The trapped modes discussed above are outlined with green diamonds. The modes that do not fit either sequence are shown with filled diamonds and are only found in the short-period region at the bottom of the diagrams. Comparing this echelle diagram with that of Østensen et al. (2014), we see that it shows many of the same features, even if the diagram is less complete due to fewer detected modes. The sequences rarely follow the asymptotic lines strictly, but instead meander around the mean line.
 |
Fig. 9 Echelle diagrams for dipole (left panel) and quadrupole modes (right panel). |
9. Discussion and conclusions
We have identified and characterized the fourth sdBV+WD binary in the sample of hot subdwarf stars observed with Kepler. In Fig. 10 we show the location in the Kiel diagram of KIC 7664467 together with the other subdwarfs in the survey (Østensen et al. 2010, 2011). We updated the physical parameters for all the objects that were studied in detail and fit the spectroscopy on the same LTE grid as the one used in the survey papers. We also included the additional sdB stars observed in the NGC 6791 (Reed et al. 2012; Baran & Winans 2012, and references therein), as well as the BHBV (Østensen et al. 2012), which were not part of the original survey. The error bars of the points are 1-sigma formal fitting errors, but since all the stars are fit on the same grid, systematic effects should be small. For stars in binaries that have extensive spectroscopic series, such as KIC 7664467, the error bars are smaller than the point size. The stars labeled as NOV in the figure are those not observed to vary. Their error bars are not shown in order to avoid crowding the plot, but they are as big as the worst cases shown, since all are based on single spectra.
Among the g-mode pulsators, four are sdBV+WD, four are sdBV+dM, and eight are either apparently single or have low-mass planets as companions. We can also see from the figure that most of the studied pulsators are clustered at about 28 000 K. Three of the four in the group at 24 000 K are NGC 3791 objects, which could indicate that the properties of the EHB stars in this cluster are slightly different than the field stars that dominates among the original Kepler mission (K1) survey targets. While the observed pulsators seem to cluster, the different types of binaries and nonbinaries are spread out more. In the K1 survey, only two p-mode pulsators were found, and neither of those are in binaries. Hopefully, the current effort with K2 can help extend the statistics with respect to the p-mode instability strip.
Besides its binary nature with a pronounced Doppler boosting, KIC 7664467 is a g-mode pulsator. We analyzed all post-survey photometric data and detected only 61 periods. We looked for properties helpful in mode identification and found rotationally split multiplets and an equally spaced sequence of dipole modes. These analysis revealed modal degree assignment of all but one period. In a few cases, particularly at places where sequences of different degrees overlap and we did not detect multiplets, we limited the modal degree to the two lowest values. The azimuthal order is certain only in case of multiplets, while for other cases we arbitrarily assigned m values. The true values of radial orders cannot be derived from our analysis. A sequence of equally spaced periods can only give an arbitrary value. It should be kept in mind that incompleteness in sequences may lead to incorrect n assignment. Since rotationally split modes are an indication of the rotation period, we used them to evaluate its value, and we derived 35.1(6) days, which is comparable to the other sdBV stars observed with Kepler. We observed just one sdBV star from the ground with a convincing rotation period estimation equal to seven days (Baran et al. 2009). This period is a few times shorter and was the likely reason we were able to derive it from the ground data. A month-long period is long comparing to the usual few weeks of ground data coverage.
The rotation period of the sdB star in KIC 7664467 is longer than its binary period. This feature was detected in all Kepler sdBV for which the rotation periods were derived. We can divide this sample into two groups; three sdBs have rotation period of days and orbital period of hours (sdB+dM), while the three others have rotation periods of months and orbital periods of days (sdB+WD). Based on Claret & Cunha (1997), Zahn (1975) showed that for stars with radiative envelopes, the synchronization time scales with the orbital period to the power 17/3. Indeed, when comparing the seven subsynchronous Kepler sdBV binaries to those of comparable binaries, which are considered to rotate synchronously, the expected synchronization time scales are several hundred times longer. Therefore the seven binaries provide no good cases to constrain the formalism in Zahn (1975) for sdB stars, since these systems are not close enough to be fully synchronized. Their life on the horizontal branch will be too short to allow for synchronization. However, that they are so subsynchronous is remarkable and must mean that many of the sdB binaries are “born” as subsynchronous on the EHB and that the RGB progenitor has in fact lost a lot of rotational angular momentum while being converted into an sdB star. That the Kepler sdBV+dM systems, which have rotations derived seismically and which rotate about a factor of four faster than the Kepler sdBV+WD systems and than the apparently single Kepler sdBVs, all with seismic rotation measurements, may point out that the synchronization mechanism is, as expected, more effective in the former group because they have shorter orbital periods. Alternatively, the rotational discrepancy may point to the possibility that sdBV+dM systems are born on the horizontal branch with higher sdB rotation rates than newborn sdB+WD systems or newborn single sdBs have.
With low-resolution optical spectroscopy and NLTE model atmospheres, we derived Teff = 27 440 ± 120 K, log g = 5.382 ± 0.019 dex, and log (nHe /nH) = −2.57 ± 0.05 for the primary star. The derived metal abundances are consistent with other sdB stars. Light metals are depleted to one-tenth of the solar mixture, while the Fe abundance is close to the solar value that agrees with the predictions of atomic diffusion theory. The available blue spectra do not show any contribution from a cool companion. The amplitude of the Doppler-boosting signal in the Kepler light curve and the lack of a reflection-effect signal in the Kepler curve imply that the companion is a white dwarf.
 |
Fig. 10 Separations between reduced periods of dipole modes. |
Appendix A: Additional tables
Radial velocity data.
Frequency list obtained in a prewhitening process of KIC 7664467.
Acknowledgments
A.S.B. gratefully acknowledges financial support from the Polish National Science Center under project No. UMO-2011/03/D/ST9/01914. This paper is based on observations made with the Nordic Optical Telescope, operated on the island of La Palma jointly by Denmark, Finland, Iceland, Norway, and Sweden, in the Spanish Observatorio del Roque de los Muchachos (ORM) of the Instituto de Astrofisica de Canarias and the William Herschel Telescope also at ORM, operated by the Isaac Newton Group. Based on observations at Kitt Peak National Observatory, National Optical Astronomy Observatory, which is operated by the Association of Universities for Research in Astronomy (AURA) under cooperative agreement with the National Science Foundation. MDR and ASB were supported by National Science Foundation grant #1312869.
References
- Asplund, M., Grevesse, N., Sauval, A., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Baran, A. 2012, Acta Astron., 62, 179 [NASA ADS] [Google Scholar]
- Baran, A. 2013, Acta Astron., 63, 203 [NASA ADS] [Google Scholar]
- Baran, A., & Østensen, R. 2013, Acta Astron., 63, 79 [NASA ADS] [Google Scholar]
- Baran, A., & Winans, A. 2012, Acta Astron., 62, 343 [NASA ADS] [Google Scholar]
- Baran, A., Oreiro, R., Pigulski, A., et al. 2009, MNRAS, 392, 1092 [NASA ADS] [CrossRef] [Google Scholar]
- Baran, A., Reed, M., Stello, D., et al. 2012, MNRAS, 424, 2686 [NASA ADS] [CrossRef] [Google Scholar]
- Baran, A., Telting, J., Nemeth, P., Bachulski, S., & Krzesinski, J. 2015a, A&A, 573, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baran, A., Koen, C., & Pokrzywka, B. 2015b, MNRAS, 448, 16 [Google Scholar]
- Bloemen, S., Marsh, T., Østensen, R., et al. 2011, MNRAS, 410, 1787 [NASA ADS] [Google Scholar]
- Claret, A., & Cunha, N. 1997, A&A, 318, 187 [NASA ADS] [Google Scholar]
- Deca, J., Marsh, T., Østensen, R., et al. 2012, MNRAS, 421, 2798 [NASA ADS] [CrossRef] [Google Scholar]
- Fontaine, G., Brassard, P., Charpinet, S., et al. 2012, A&A, 539, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Foster, H., Reed, M., Telting, J., Østensen, R., & Baran, A. 2015, ApJ, 805, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Geier, S. 2013, A&A, 549, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Geier, S., & Heber, U. 2012, A&A, 543, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Green, E., Fontaine, G., Reed, M., et al. 2003, ApJ, 583, A31 [Google Scholar]
- Han, Z., Podsiadlowski, P., Maxted, P., Marsh, T., & Ivanova, N. 2002, MNRAS, 336 [Google Scholar]
- Heber, U., Reid, I., & Werner, K. 2000, A&A, 363, 198 [NASA ADS] [Google Scholar]
- Hubeny, I., & Lanz, T. 1995, ApJ, 439, 875 [Google Scholar]
- Kilkenny, D., Koen, C., O’Donoghue, D., & Stobie, R. 1997, MNRAS, 285, 640 [Google Scholar]
- Lanz, T., & Hubeny, I. 2003, ApJS, 146, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Lanz, T., & Hubeny, I. 2007, ApJS, 169, 83 [CrossRef] [Google Scholar]
- Michaud, G., Richer, J., & Richard, R. 2011, A&A, 529, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Németh, P., Kawka, A., & Vennes, S. 2012, MNRAS, 427, A2180 [NASA ADS] [CrossRef] [Google Scholar]
- Østensen, R., Silvotti, R., Charpinet, S., et al. 2010, MNRAS, 409, 1470 [NASA ADS] [CrossRef] [Google Scholar]
- Østensen, R., Silvotti, R., Charpinet, S., et al. 2011, MNRAS, 414, 2860 [NASA ADS] [CrossRef] [Google Scholar]
- Østensen, R., Degroote, P., Telting, J., et al. 2012, ApJ, 753, 17 [Google Scholar]
- Østensen, R., Telting, J., Reed, M., et al. 2014, A&A, 569, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Podsiadlowski, P., Rappaport, S., & Pfahl, E. 2002, ApJ, 1107 [NASA ADS] [CrossRef] [Google Scholar]
- Reed, M., Kawaler, S., Østensen, R., et al. 2010, MNRAS, 409, 1509 [NASA ADS] [CrossRef] [Google Scholar]
- Reed, M., Baran, A., Østensen, R., Telting, J., & O’Toole, S. 2012, MNRAS, 427, 1245 [NASA ADS] [CrossRef] [Google Scholar]
- Reed, M., Foster, H., Telting, J., et al. 2014, MNRAS, 440, 3809 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M., Cutri, R., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Telting, J., Østensen, R., Baran, A., et al. 2012, A&A, 544, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Telting, J., Baran, A., Németh, P., et al. 2014a, A&A, 570, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Telting, J., Østensen, R., Reed, M., et al. 2014b, in Hot Subdwarf Stars and Related Objects, eds. V. Van Grootel, B. Green, G. Fontaine, & S. Charpinet, ASP Conf. Ser., 481, 287 [Google Scholar]
- Zacharias, N., Monet, D., Levine, S., et al. 2004, BAAS, 36, 1418 [Google Scholar]
- Zahn, J.-P. 1975, A&A, 41, 329 [NASA ADS] [Google Scholar]
All Tables
Parameters for the fits shown in Fig. 2, with respect to the solar abundances from Asplund et al. (2009) provided for comparison.
All Figures
 |
Fig. 1 Color-coded plot of the radial-velocities of KIC 7664467. The dark blue circles represent WHT data, light blue ones show KPNO data, and red circles are NOT data. |
| In the text | |
 |
Fig. 2 Combined radial-velocity corrected WHT/NOT/KPNO spectrum of KIC 7664467 (black). The peak S/N of the combined spectrum is ~110. The continuum of the normalized spectrum was sampled in 100 Å sections. The model fit computed with TLUSTY/XTgrid and the fit residual (gray) were shifted vertically for clarity. Line identifications and equivalent widths in mÅ are given for only the strongest lines of the significant ions in the model. The atmospheric parameters of the model are given in Table 2. |
| In the text | |
 |
Fig. 3 Photometric (black squares) and radial-velocity (blue dots) phased data overlapped with a sinusoidal fit representing the beaming effect obtained from radial-velocity data. The right vertical axis for RV data is reversed. |
| In the text | |
 |
Fig. 4 Amplitude spectrum of KIC 8302197 limited to the very low frequencies. The dominant peak is a consequence of binarity. |
| In the text | |
 |
Fig. 5 Close-ups of the bulk of the g-mode region of the amplitude spectrum of KIC 8302197 with multiplet-like formations. The numbers in the plots indicate separations between peaks, and we rounded them up to two decimal places for clarity. |
| In the text | |
 |
Fig. 6 Same as in Fig. 5 to show multiplet-like formations detected at the high end of frequencies of the g-mode region. |
| In the text | |
 |
Fig. 7 Kolmogorov-Smirnov test to find the period spacings of the same modal degree sequences. A significant minimum of log Q indicates a frequent spacing of dipole modes at 263 s. |
| In the text | |
 |
Fig. 8 Close-up of the amplitude spectrum of KIC 7664467 displayed in period instead of frequency to show l = 1 sequence. |
| In the text | |
 |
Fig. 9 Echelle diagrams for dipole (left panel) and quadrupole modes (right panel). |
| In the text | |
 |
Fig. 10 Separations between reduced periods of dipole modes. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


