| Issue |
A&A
Volume 585, January 2016
|
|
|---|---|---|
| Article Number | A140 | |
| Number of page(s) | 14 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201527137 | |
| Published online | 12 January 2016 | |
Off-disk straylight measurements for the Swedish 1-m Solar Telescope
Institute for Solar Physics, Dept. of Astronomy, Stockholm University, Albanova University Center, 106 91 Stockholm, Sweden
e-mail: mats@astro.su.se
Received: 7 August 2015
Accepted: 27 October 2015
Context. Accurate photometry with ground-based solar telescopes requires characterization of straylight. Scattering in Earth’s atmosphere and in the telescope optics are potentially significant sources of straylight, for which the point spread function (PSF) has wings that reach very far. This kind of straylight produces an aureola, extending several solar radii off the solar disk.
Aims. We want to measure such straylight using the ordinary science instrumentation.
Methods. We scanned the intensity on and far off the solar disk by use of the science cameras in several different wavelength bands on a day with low-dust conditions. We characterized the far wing straylight by fitting a model to the recorded intensities involving a multicomponent straylight PSF and the limb darkening of the disk.
Results. The measured scattered light adds an approximately constant fraction of the local granulation intensity to science images at any position on the disk. The fraction varied over the day but never exceeded a few percent. The PSFs have weak tails that extend to several solar radii, but most of the scattered light originates within ~1′.
Conclusions. Far-wing scattered light contributes only a small amount of straylight in SST data. Other sources of straylight are primarily responsible for the reduced contrast in SST images.
Key words: instrumentation: miscellaneous / methods: observational / methods: data analysis / techniques: photometric
© ESO, 2016
1. Introduction
Careful measurements of the point spread function (PSF) in the Solar Optical Telescope (SOT) on the Hinode spacecraft (Wedemeyer-Böhm 2008) and comparison with synthetic data from magnetohydrodynamic (MHD) simulations (Wedemeyer-Böhm & Rouppe van der Voort 2009) have established that the granulation contrast in the synthetic data is correct. However, the contrasts measured in data from ground-based solar telescopes is far below that of the MHD data.
Like all of today’s major ground-based solar telescopes, the Swedish 1-m Solar Telescope (SST; Scharmer et al. 2003a), located in the Roque de Los Muchachos Observatory (ORM) on La Palma, has an adaptive optics (AO; Scharmer et al. 2003b) system that corrects for image degradation from wavefront aberrations caused by atmospheric turbulence. Science images are also routinely restored for residual aberrations by use of multi-frame blind deconvolution (MFBD; Löfdahl 2002) techniques like phase diversity (Löfdahl & Scharmer 1994) and multi-object MFBD (MOMFBD; van Noort et al. 2005). Both AO and MFBD techniques correct the wavefront aberrations only partially, a consequence of their being based on a finite number of AO mirror electrodes and on an expansion of the wavefront aberrations in a finite number of modes, leaving a tail of uncorrected high-order modes. If the correction is of sufficiently high order, the result is a diffraction-limited resolution but a Strehl ratio that is reduced due to a PSF “halo” of speckle noise from the uncorrected modes. This effect has already been simulated for stars, as well as for solar images, by Smithson & Peri (1989). Hardy (1998) discusses the effect, as do several authors represented in the collection edited by Roddier (1999). Scharmer et al. (2010) find that a significant part of the contrast reduction in SST data can be explained by the uncorrected modes. They also implemented a method for correcting the solar image contrast for this effect based on the known statistics of atmospheric turbulence and simultaneous measurements of Fried’s parameter r0 from a wide-field wavefront sensor.
Scharmer et al. (2011) demonstrate that the granulation contrast known from synthetic data can be used together with umbral intensities to constrain both the strength and the width of the straylight PSF. They conclude that the dominating straylight of the SST at the time of their observations was in the form of PSFs with narrow wings (~1′′ FWHM).
Continuing the search for contrast-reducing straylight in the SST, Löfdahl & Scharmer (2012) measured straylight originating in the post-focus optics of the SST. High-order modes from the deformable mirror (DM) contributed narrow-wing straylight (kernels with 90% enclosed energy within ~0.6′′) with a magnitude ranging from 34% of the total intensity at 390 nm to 18% at 854 nm, ghost images about ~1%, and an unidentified diffuse component that fitted well to a model with one or a few tenths of a percent of the intensity in 16′′ (blue) to 34′′ (red) wide wings.
The above results are based on data from different years and therefore cannot easily be combined into a current straylight budget for the SST, because several key optical components have recently been replaced, including the tip-tilt mirror and an upgrade of the AO from 37 to 85 electrodes. We refer the reader to Scharmer et al. (in prep.), who assess the current performance of the SST based on measurements of granulation contrast in a variety of wavelengths. We are led to a picture where the straylight from the post-focus optics has only small contributions from straylight with wings wider than ~1′′. However, the measurements do not include contributions from the telescope itself or scattering from aerosols suspended in the atmosphere. These sources can produce straylight with a much wider influence. Zwaan (1965) estimated that the contributed straylight is 4–10% of the intensity at disk center (DC) in measurements of the aureola with several different solar telescopes in the fifties and sixties. However, this was for sites and telescopes from an earlier era, and it seems likely that modern solar telescopes have better intrinsic straylight properties. Here, we aim to characterize the SST far wing straylight (FWS) by scanning the radial intensity distribution, both the limb-darkened intensity on the solar disk and the off-disk aureola, extending far outside the limb.
Radial intensity scanning has a long history with several different solar telescopes. Staveland (1970) scanned from 0.9 R⊙ to approximately 3 R⊙ with photometers in several wavelength bands on an off-axis mirror system of the Oslo Solar Observatory, finding scattering with ~100′′ wide wings in the visible. Pierce & Slaughter (1977) measured the solar limb darkening with a spectrometer “as the image drifted by diurnal motion across the entrance aperture”. They were also apparently the first to fit limb darkening data to fifth-order polynomials in μ (the cosine of the viewing angle), a type of fit that we also use. Martinez Pillet et al. (1990) and Martinez Pillet (1992) used a photometer to make similar drift scans with the Vacuum Newton Telescope at the Observatorio del Teide in Tenerife. They formulated and solved the radiative transfer problem for Earth’s atmosphere to model its scattering effects. The latter paper includes an overview of the 1992 state of art of measuring scattering and instrumental straylight for solar telescopes. We have not found any more recently published measurements of the scattered light PSF in high-resolution ground-based solar telescopes. In contrast, the major space-borne telescopes have recently had their scattered light characterized by Mathew et al. (2007; SoHO/MDI), Wedemeyer-Böhm (2008) and Mathew et al. (2009; Hinode/SOT/BFI), DeForest et al. (2009; TRACE), and Yeo et al. (2014; SDO/HMI).
In this paper we measure the radial intensity distribution from disk center out to several solar radii using the available science cameras and fit the measurements to a model involving both the straylight PSF and the solar limb darkening, as well as several other model parameters. These fits allow us to characterize the FWS PSF and its contribution to science data intensity on the entire disk. We describe the collection and radial binning of our data, and discuss the off-disk intensity in Sect. 2. In Sect. 3 we describe the model fitting. We discuss the results in Sect. 4.
2. Measurements and binning
2.1. Optics and instrumentation
The primary optical element of the SST is a singlet lens with a focal length of 20.3 m at 460 nm and a 98-cm aperture. A mirror at the primary focus reflects the light to a Schupmann corrector, which forms an achromatic focus through a field lens (FL) next to the primary focus.
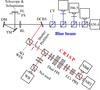 |
Fig. 1 Setup schematics. Light from the telescope enters through the target from upper left. TM = tip-tilt mirror; DM = deformable mirror; RL = reimaging lens; DCBS = dichroic beamsplitter; CT = correlation tracker; WFS = wavefront sensor; LCs = liquid crystal analyzer; FPI = Fabry–Pérot interferometer, PBS = polarizing beamsplitter, WB = wide band, NBT = narrow band transmitted, NBR = narrow band reflected. |
The setup following the Schupmann focus is illustrated in Fig. 1, in the caption of which acronyms for many optical elements are defined. The FL makes a pupil image in focus on the 85-electrode monomorph DM. The RL makes a converging F/46 beam parallel to the optical table. This beam is split by the 500 nm DCBS into a blue beam and a red beam. Both beams have several science cameras behind a variety of interference filters.
We did these observations in six different wavelength bands, from 396 nm in the violet to 854 nm in the near IR. We used two cameras with separate filters in the blue beam (λ< 500 nm) and four different CRISP (Scharmer et al. 2008) prefilters in the red beam.
The three CRISP Sarnoff CAM1M100 camera detectors are 1024 by 1024 pixels with an image scale of 0.̋059/pixel, making a FOV of 60′′, cadence ~37 Hz. The two blue MegaPlus II es4020 cameras have 2048 by 2048 pixel detectors with image scale 0.̋034/pixel, FOV 80′′, cadence ~10 Hz.
2.2. Data collection
Data were collected on 2014-04-27. This was a clear day with little dust, as quantified by a TNG aerosol count1 of 0.3 μg m-3. We cleaned the telescope lens from dust a few days before the observations. The observations are summarized in Table 1 and described in detail below.
Scan data collected on 2014-04-27.
The seeing was measured by the AO system while scanning on the disk but not off disk. The quality of the r0 measurements at the limb, while scanning rapidly, is unknown but based on the numbers logged over most of the disk we estimate that the seeing quality was very bad during most of the limb passages (r0 ≈ 4 cm) and never much better than that (r0< 9 cm). Due to limitations of the SH WFS, the seeing measurements of the SST AO lose their meaning for r0 ≲ 4 cm. But even assuming r0 = 1 cm, the FWHM of a long exposure PSF is only a few tens of arcsec at 854 nm, representing less than a percent of the solar radius.
We made “drift scans”, by pointing far off the limb on the hour angle (HA) angle axis, and then stopping the telescope tracking. Letting the Sun drift past the telescope, while collecting images, produces a scan along the HA axis. We henceforth refer to these scans as “HA scans”.
We also made scans in the perpendicular direction, along the declination angle (DA) axis. For this we used a script that sent instructions to the telescope pointing program, taking 20′′ DA steps while keeping HA zeroed, pausing to let the observer manually collect a set of 6 images. After making one such DA scan, we decided that operating the red and blue cameras at the same time while doing the steps was too tiresome and error prone. We then scanned one CRISP wavelength at a time (skipping 5576) and the blue cameras separately. Our intention was to analyze only the latter data but we later realized that the first scans were useful for checking the consistency of our measurements, so they appear below as “extra” data sets.
We did the usual dark and flat corrections on each image using code from the CRISPRED data pipeline (de la Cruz Rodríguez et al. 2015). From the flat fields we also established a mask to use in all later processing, where bad pixels and vignetted areas near the edges of the detectors are zeroed. For the Sarnoff cameras, the mask includes the vertical dividers between areas on the detectors that are read out separately.
2.3. Air mass
The amount of air between the telescope and the Sun varies with the angular distance from zenith. Therefore, so does the fraction of the light that is removed from the direct sunlight by the atmosphere. For the HA scans, the telescope is pointing in the same direction during the entire scan but for the DA scans we need to find out whether this affects our measurements significantly. The telescope software logs the pointing, so the zenith angle is readily available.
An estimate of the direct sunlight intensity at a certain height h above sea level is given by Honsberg & Bowden (2014), taking the varying properties of the atmosphere at different altitudes into account, 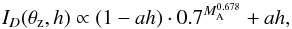 (1)where a = 0.14 km-1 and h ≈ 2.4 km for the SST. The relative air mass, MA, is the amount of air between the telescope and the Sun, normalized to unity at zenith. Kasten & Young (1989) give an approximation of MA, taking the curvature of the earth (and the atmosphere) into account,
(1)where a = 0.14 km-1 and h ≈ 2.4 km for the SST. The relative air mass, MA, is the amount of air between the telescope and the Sun, normalized to unity at zenith. Kasten & Young (1989) give an approximation of MA, taking the curvature of the earth (and the atmosphere) into account, 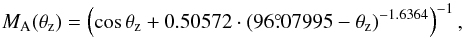 (2)where θz is the angular distance from zenith.
(2)where θz is the angular distance from zenith.
Equations (1) and (2) are both semi-empirical, involving measurements at specific sites. Therefore we have verified that they are valid for our site by comparison with intensity measurements from the SST SHABAR2. There is good agreement for θz< 70° (Sliepen 2015, priv. comm.).
With the DA zenith angles in Table 1 the variations in intensity are less than 0.22% during a single scan. This is negligible for our purposes so we made no correction for varying air mass.
2.4. Pointing and coordinate transformations
The Primary Image Guider (PIG; Sliepen & Sütterlin 2013) of the SST measures the pointing of the telescope on the solar disk by tracking the primary image at the bottom of the telescope vacuum tube. In addition to the solar disk, the instrument can see the field stop of the vacuum exit window. It can therefore keep track of what part of the disk is in the science FOV. The PIG logs disk coordinates with a modest accuracy of ~30′′ but the precision is much better, on the order of 1′′. After a calibration of the translation of the coordinate system, the expected accuracy should be as good as the precision, definitely better than image shifts from seeing. In order to properly model the data in 2D, we also need to find out the rotation angle between the logged coordinates and the coordinate system given by the pixel axes of the image data frames. Both calibrations can be done for each scan using images from the limbs.
The procedure is to find the images from each limb, that divide the FOV as evenly as possible (worked excellently for the HA scans, decently for the DA scans). We then fit a 2D model with free parameters including limb distance from FOV center, angle toward DC, logged limb image distance, blurring kernel width, and a multiplicative fudge factor (close to unity). For the limb darkening we used a fifth order polynomial in the cosine of the viewing angle, μ = cos(arcsin(r/R⊙)), apparently first done by Pierce & Slaughter (1977), 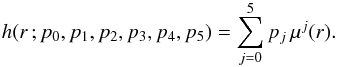 (3)We calculated
(3)We calculated 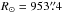 for 27 April 2014 using code from the get_sun subprogram in Solarsoft (Freeland & Handy 1998). For the pi parameters we used values interpolated in wavelength from the empirical data of Neckel & Labs (1994, their Table 1). Figure 2 shows the thus calculated limb darkening curves for our wavelengths.
for 27 April 2014 using code from the get_sun subprogram in Solarsoft (Freeland & Handy 1998). For the pi parameters we used values interpolated in wavelength from the empirical data of Neckel & Labs (1994, their Table 1). Figure 2 shows the thus calculated limb darkening curves for our wavelengths.
 |
Fig. 2 Limb darkening from Neckel & Labs (1994). |
For the initial estimates, we determined the position and orientation of the limb in each of the limb images with the following heuristics:
-
1.
Threshold a gradient image to get a mask that selects points thatare on or close to the limb,
-
2.
Find the coordinates of the thus selected limb point that is the one closest to the center of the FOV,
-
3.
Crop the image to as large an area as possible, which is centered on the selected limb point,
-
4.
Divide the cropped image into four equal parts, forming a quad cell where the maximum value indicates the image quadrant nearest to DC,
-
5.
Calculate the angle to DC within the quadrant as the arctangent of the two quad cell values surrounding the maximum cell.
This procedure gave good enough initial estimates for the model fit to converge nicely. For sample model fitting results, see Fig. 3. Evidently, the Neckel & Labs limb darkening curves were good enough for these fits. However, as we will see in the next section, they are not perfect fits to our data.
We performed these fits (as well as the fits in the following sections) in IDL with the MPFIT package (Moré 1978; Markwardt 2009).
 |
Fig. 3 Limb fit for the 630 nm HA scan. Within each subfigure, the top and bottom tiles represent the masked 1024 × 1024-pixel images of the two limbs, respectively. In b) and c), the rightmost tiles represent the differences between the model images and the observed images. |
2.5. Binning
For each image in a scan, we calculated the radial coordinate of each pixel-based on the coordinates logged by PIG and the transformation established from the limb images (see Sect. 2.4). This allowed us to radially bin the intensity data without being limited by the detector size, and then calculate the average intensity in each bin. We used a bin size of 10′′.
This resulted in approximately 3 × 107 contributing pixel values per bin in both red and blue cameras for the HA scans. For the less densely sampled DA scan data, we got 3 × 106 (red) and 1.3 × 107 (blue) pixel values per bin.
The binned intensity data are plotted in Fig. 4, normalized to DC intensity as given by the fits described in Sect. 3 below. In this figure, we have plotted the toward-DC halves (TDHs) of the scans with negative radial coordinates, while the from-DC halves (FDHs) are plotted with positive coordinates. The linear plots show the limb darkening for the different wavelengths, while the logarithmic plots show the faint off-disk straylight, demonstrating that there is signal all the way out to 3 R⊙.
Due to the smaller number of pixel values per bin, the CRISP DA scan data are noticeably noisier on the disk than the HA scan data (compare Figs. 4a to b and c to d). For both types of scan, the points within 0.1 R⊙ from DC are noisier because our scans did not go exactly through DC so for small r we get contributions from just a few pixels in the corners of image frames or none at all.
 |
Fig. 4 Binned and normalized intensity data (10′′ bins) of the HA and DA scans. Compare Fig. 2. Positive (negative) r correspond to scan direction away from (toward) DC. The 11:49 “extra” DA scans are omitted from these plots. |
The Neckel & Labs (1994) limb darkening curves fit several of our scans fairly well, as can be seen by comparing Fig. 4 with Fig. 2. However, the 396 nm data deviate from the regular progression with wavelength and the 854 nm data do not fall off with r quite as quickly as in the Neckel & Labs curve. We conjecture that the reason in both cases is that the filter passbands are completely within wide Ca ii lines. In the 396 nm case in the wing of the K line and near some deep blends and in the 854 nm case including the chromospheric line core. The Neckel & Labs measurements were done for continuum wavelengths.
2.6. The aureola intensity
The most interesting part of our scans are outside the limb, where the straylight forms an aureola. We plot them logarithmically in Fig. 5.
 |
Fig. 5 Aureola intensity of CRISP WB and blue scans. The dots represent the binned data, while the lines represent the fits described in Sect. 3, specifically the ones in Table 5. Normalization and δr from the fits. Note that the range on the vertical axis varies between the different plots. |
2.6.1. Deficiencies
We first address some deficiencies in the data. There is a leveling off at r> 2.5 R⊙ for the TDHs of the CRISP HA scans. This cannot be noise, since we do not see the same effect for r> 2.5 R⊙. It is also not seen in the blue data, so it must be originating in the red part of the beam, most likely vignetting or reflections within the CRISP optics. There is a glitch in the FDH of the 396 nm HA scan at r ≈ 2 R⊙, a premature ending of the FDH of the 538 nm HA scan at r ≈ 2.4, and all the TDHs of the DA scans starting at r ≈ 2.5 R⊙ rather than 3 R⊙.
2.6.2. Consistency
For the two blue wavelengths, 396 and 436 nm, there is a very good consistency in the off-disk intensity. Not only between the two halves of the scans, but also between scans collected at different times and between the orthogonal HA and DA scans.
For all the CRISP wavelengths, the FDHs of the HA scans show a near-limb (r< 1.4 R⊙) straylight component that is wider than that of the TDH. The far FDH components are also slightly (for 854 nm: significantly) higher than those of the TDHs. The far components of the DA scans are significantly lower than both halves of the HA scans, particularly so for the “extra” 854 nm scan.
For the two blue filters, the scans collected with different zenith distances are remarkably consistent, indicating an instrumental origin. For the three CRISP prefilters with both HA and DA scans, the DA scans are collected closer to zenith and also have less straylight, consistent with a significant atmospheric contribution that correlates with air mass. The average zenith distance of the 854 nm “extra scan” collected around 12 UT is approximately the same as for the DA scan collected after 14 UT (local noon in La Palma is a few minutes past 13 UT) and yet it shows even less intensity in the aureola. This is consistent with a decrease in the dust concentration with time and an insignificant atmospheric contribution to the blue scattered light. However, with a very sparse θz sampling and lacking a detailed record of the dust concentration, we do not believe our data support a detailed analysis with the aim of properly separating the atmospheric and instrumental contributions.
2.6.3. The CRISP FPI optics
In addition to the WB data discussed so far, with CRISP we simultaneously collected continuum NB data. As the WB data are dominated by the continuum wavelengths, this allows us to see whether any significant straylight comes from the FPI and LC optics of CRISP.
 |
Fig. 6 Consistency in HA scan aureola intensity, CRISP NB vs. WB. Normalization and δr from the 3-Gauss fit to the WB data. |
In Fig. 6 we compare the WB and NB continuum HA scan measurements. The WB data were normalized by the fits as above. The NB intensities were scaled to match the WB intensity near DC (but excluding the noisiest bins) to within a few percent, good enough for the following comparison. The difference between the aureola intensities recorded in the NB and the WB are minor compared to the noise in the NB data, as well as to the difference between the two halves of the WB scan, for the 538.0 nm, 557.6 nm, and 630.2 nm scans. A systematic difference at large r can be seen in the 854.2 nm scans but this is not necessarily due to an increase in straylight, as one could expect differences in the limb darkening between the NB continuum and the WB that is dominated by the chromospheric Ca II line.
3. The straylight PSF
3.1. Forward model
The 2D model involves a solar disk with limb darkening, convolution with a seeing PSF and 2–4 contributions from scattering with different widths, along with some other parameters. The model parameters are summarized in Table 2, along with their limits and initial values used in the fits. Below we describe the model in more detail.
Model parameters.
Far wing kernels.
The intensity at radial coordinate r is modeled as 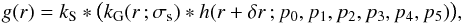 (4)where ∗ represents convolution, kS is a scattering kernel, and kG(r ;σs) is a Gaussian kernel representing seeing with the standard deviation σs as a free parameter. The intrinsic radial intensity distribution of the disk, h, includes a correction term, δr, in the radial coordinate. The limb darkening is modeled with the 5th-order polynomial, h, from Eq. (3). We tried using the coefficients measured by Neckel & Labs (1994, interpolation in their Table 1) but they caused significant errors near the limb and we suspected that they contributed to the problems we had with convergence (see Sect. 3.2 below). As mentioned above, the bad fits may be because of the non-photospheric contributions of the spectral lines within the passbands of some of the filters. We note also that Neckel & Labs discuss variations in their scans from scan to scan and from season to season, so their limb darkening parameters represent some sort of average. Hence, we made the limb darkening coefficients free model parameters.
(4)where ∗ represents convolution, kS is a scattering kernel, and kG(r ;σs) is a Gaussian kernel representing seeing with the standard deviation σs as a free parameter. The intrinsic radial intensity distribution of the disk, h, includes a correction term, δr, in the radial coordinate. The limb darkening is modeled with the 5th-order polynomial, h, from Eq. (3). We tried using the coefficients measured by Neckel & Labs (1994, interpolation in their Table 1) but they caused significant errors near the limb and we suspected that they contributed to the problems we had with convergence (see Sect. 3.2 below). As mentioned above, the bad fits may be because of the non-photospheric contributions of the spectral lines within the passbands of some of the filters. We note also that Neckel & Labs discuss variations in their scans from scan to scan and from season to season, so their limb darkening parameters represent some sort of average. Hence, we made the limb darkening coefficients free model parameters.
We model the scattering kernel as the sum of a Dirac delta function, δ, and a number of blurring kernels with the relative weights, ci, as free parameters, 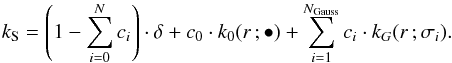 (5)The far wings kernel (FWK), k0(r ;•), is one of kM, kL, kG, or kV and • represents one or two parameters as needed, see Table 3. We found, however, that a single kernel would not produce good fits. We therefore added up to three less wide near-limb Gaussian kernels (NGKs), kG(r,σi).
(5)The far wings kernel (FWK), k0(r ;•), is one of kM, kL, kG, or kV and • represents one or two parameters as needed, see Table 3. We found, however, that a single kernel would not produce good fits. We therefore added up to three less wide near-limb Gaussian kernels (NGKs), kG(r,σi).
Convolution with FFT requires finite kernels. The wings of Lorentzian kernels do not drop to insignificant levels quickly, the same is true for Voigt and Moffat kernels for some parameter values. Therefore it is necessary to truncate the kernels at some radius, but we need to keep enough of the wings to completely characterize the straylight over the entire disk. If we want the light from the entire disk to potentially spread to every other point on the disk, we obviously need wings that extend to as far as 2 R⊙. To allow the entire disk to contribute to the measurements at 2 R⊙ outside the disk requires kernels that are truncated at r ≳ 4 R⊙. The kernels and the artificial images used for calculating the convolutions, including both the solar disk and enough surrounding empty space to protect against wrap-around contributions from the far wings, were represented as 2048 × 2048-pixel arrays.
3.2. Fitting the model to the scans
We fitted the binned scans separately for the two halves corresponding to positive and negative r.
Initially, we had problems making the model fit. The limb parameters δr and FWHMS tended to diverge before the limb darkening had converged. A major problem was that the limb darkening parameters would drive the solution in the wrong direction, long before the kernels had a chance to reproduce the off-disk straylight. Before we introduced the NGKs, the FWKs did not converge well and in particular left large residuals near the limb. But once introduced, the NGK fits would often degenerate by making ci go to zero or, for NGauss> 1, the widths becoming too small to recover after the limb darkening parameters had converged.
By trial and error, we arrived at the set of parameters described in the previous section and a procedure that led to convergence (in most cases, see below). For each data set, we called the mpfit program four times, with the results from one fit being used as an initial estimate for the following. The final columns in Table 2 show what parameters were fitted during each of the four fits, the others were fixed at their initial values or the values from the previous fit. In each fit, we minimized χ2 for different ranges in the radial coordinate, see Table 4. We used the numbers of contributing pixels to each bin as weights, this way the noisy bins near DC did not seem to cause any problems.
Ranges in r, consecutive fits.
We demonstrate the fitting using the 630.2 nm HA scan in the direction away from DC. The fits to other scans show similar behavior.
Figure 7 shows the fit errors over the entire radial range. The χ2 values are dominated by the noise on the disk. More relevant for our purposes (we are mostly interested in the off-disk part) are the errors off-disk. Unless stated otherwise, all χ2 values mentioned below are calculated for r>R⊙ + 30″.
 |
Fig. 7 Intensity and fit errors including the disk, NGauss = 1. HA scan at 630 nm, away from DC. The legends indicate the kernels used for the widest straylight component. |
 |
Fig. 8 Fit errors off-disk, different NGauss. HA scan at 630 nm, away from DC. The legends indicate the FWKs used in the fits. |
Zooming in on the off-disk errors, Fig. 8 demonstrates how the fit improves with increasing NGauss, the number of NGKs. NGauss = 1 and NGauss = 2 show undulating fit errors but with NGauss = 3 the errors are dominated by noise for three of the FWKs (while the Gaussian FWK has failed). This indicates that there is no point in using more NGKs.
 |
Fig. 9 Fitted FWS for 630 nm, NGauss = 3, HA scan away from DC. The total model intensity, g(r), is fitted to the measured data represented by the gray circles. |
The fit is robust in the sense that, except for the clearly failed Gaussian FWK, the different FWKs all agree on the total straylight fraction, as shown in Fig. 9.
In Fig. 10 we show the fitted straylight decomposed into contributions from the three NGKs and the Moffat FWK. The dominating component is the most narrow NGKs. Note also the excellent fit just outside the limb.
 |
Fig. 10 Fitted straylight components for 630 nm, NGauss = 3, Moffat, HA scan away from DC. The total model intensity, g(r), is fitted to the measured data represented by the gray circles. |
3.3. Results
The fits result in different combinations of the four kernels (the three NGKs and one of the four FWKs). Their FWHMs do not stray too far from their initial values, so the NGK widths are around 50′′, between 120′′ and 160′′, and around 400′′, respectively. The FWK widths stay within a factor of about 2 from R⊙. The ci parameters for the NGKs sum to a few percent, while c0 for the FWK is usually ≲1%.
The width of the blurring kernel, FWHMS ≲ 10″ for all wavelengths, which is well within what can be expected from seeing. It represents the combination of seeing, limb radiative transfer effects, and all major wavefront straylight with widths of the order 1′′.
We can compare the least wide NGK fits to the unidentified instrumental scattering from below the telescope field lens found by Löfdahl & Scharmer (2012). They measured on the order 0.3% (0.1%) straylight with a width of 20′′ (34′′) in 395.4 nm (630.2 nm). Unless the instrumental straylight has increased since 2010 when their data were collected, the now measured straylight must come from either the telescope itself or the atmosphere.
The sum of ci is the fraction of energy that is removed from the direct sunlight. However, the fraction of straylight in observed images is less because a significant fraction of the straylight is deposited outside the disk, particularly for the FWKs, which is why we can measure the straylight there. So the exact values of the fitted ci are not as interesting as the total straylight as a fraction of the direct intensity from the disk. At any point on or off the disk, the FWS corresponds to the summed contributions to g(r) from convolution of the limb darkening function, h(r), with the straylight kernel terms of kS.
 |
Fig. 11 Fitted FWS for all wavelengths, NGauss = 3, selected HA scan fits. The dotted lines in b) show the influence of an idealized sunspot at DC. |
Figure 11 shows the total FWS for one selected HA scan fit per wavelength. Figure 11a shows it normalized to the DC intensity, with drops toward the limb due to the limb darkening.
In Fig. 11b the FWS is normalized to the local intensity, which shows that the straylight is an approximately constant fraction of the local granulation intensity. The variations near to the limb are a consequence of the combination of limb darkening and the fact that the kernels have less disk to collect energy from there. The dotted lines in this plot show the influence on the straylight of an idealized sunspot at DC (a zero-intensity umbra with an arbitrary 13′′ radius). This changes the straylight by ~10% near the spot and not at all at distances ≳0.05 R⊙ (or 1′) from the spot.
Total far wing straylight, all scans.
Table 5 summarizes the results of fitting the model to all our data sets, including the 11:49 “extra” scans. Comparing with Fig. 5, we can note the following (with ± simply denoting the extremes of the estimates):
-
396.5 nm:
these highly consistent scanscorrespond to consistent estimates of straylight, 2.9 ± 0.5%. The exception is the HA FDH, for which the estimate is more than twice as high but χ2 is also higher because of the upward glitch at r = 2.4 R⊙.
-
436.4 nm:
these scans also look consistent, except for the two DA TDHs that both end with downward glitches at r ≈ 2.3 R⊙. Disregarding the lower estimates of the exceptions, we get 6.3 ± 2%.
-
538.0 nm:
these two scan halves look similar and the estimates are the same, 1.5%. The inconsistencies at r< 1.4 R⊙ do not appear to influence the estimate much. The leveling off at r> 3 R⊙ does not seem to have been a problem.
-
557.6 nm:
high consistency between the two halves of the HA scan result in the estimates 1.75 ± 0.05%. The DA scan is noisier and lower than the HA scan and the halves end at different r, resulting in the estimate 1.0 ± 0.3%.
-
630.2 nm:
these scans look similar to the 557.6 nm scans. The estimated stray light levels are lower than for 557.6 nm due to the LD not falling off as quickly near the limb. The HA scan estimate is consequently 1.4 ± 0.1%. Consistently, the DA TDH estimate is 0.7%. The DA FDH results can be disregarded, as the fits failed completely for all FWKs with the best χ2 several orders of magnitudes larger than for any other data.
-
854.2 nm:
the filter with the most inconsistent scans and scan halves, and also the noisiest DA scans. The HA estimate is consistent with the levels in the plot: 1.55 ± 0.25% with the FDH higher than the TDH. The DA scan results are less consistent with 0.9 ± 0.2% for DA and 1.3 ± 0.3% for DA “extra”.
3.4. The PSFs
Figure 12 shows the fitted PSFs. While the straylight at large r differs from scan to scan in each of the plots in Fig. 5, the far wings of the fitted scattering kernels are remarkably consistent. The variation is mostly in the r ≲ 0.5 R⊙ range.
In Fig. 13 we plot the PSFs times the radial coordinate, i.e., weighted by the annular surface area from which energy is redistributed by convolution. These plots show that the bulk of the FWS is scattered from within r ≲ 1′.
 |
Fig. 13 Scattering kernels radial contributions, rkS. Individually normalized to unit maximum. The vertical lines indicate r = 1′. Compare Fig. 12. |
4. Conclusion
We have measured the aureola intensity of the SST, out to 3 R⊙ and in several wavelengths. This allowed us to characterize the far wing straylight (FWS) PSFs, including the wings far enough to capture all stray light that can influence science image data on the entire disk. The measurements were done on a clear day without calima, with low amounts of dust in the atmosphere (TNG dust count: ~10-1μg m-3).
The FWS PSFs scatter light primarily from within r ≲ 1′ but have tails that extend to several solar radii.
Locally, the FWS of the SST is an approximately constant addition to science images of a few percent of the surrounding granulation intensity, much less than needed to explain the discrepancy between granulation contrast in observed and synthetic images. Particularly in CRISP data, the FWS is only ≲2%. Correcting rms contrast measurements for this would increase the contrast by the same fraction, such as from 10.0% of the average intensity to 10.2%. This is insignificant compared to the deficiencies in contrast of granulation data that are compensated for seeing effects by AO, MFBD restoration, and post-restoration deconvolution for uncompensated high-order wavefront modes reported by Scharmer et al. (2010). They measured 10% and 8.5% rms contrast in 538 nm and 630 nm, respectively, while MHD synthetic data at the same viewing angle has 17.4% and 13.3% rms contrast in the same wavelengths.
The measured FWS varies with wavelength and time, most likely due to a combination of varying zenith angle and variations in the dust concentration. Using scans from several days and zenith angles, Martinez Pillet et al. (1990) were able to separate the atmospheric scattering from the instrumental scattering of the Vacuum Newton Telescope and showed that the instrumental scattering was approximately constant (their Fig. 3). We do not have enough data for a similar separation. However, the very minor variations with zenith angle in the blue data are consistent with the measured FWS being dominated by non-varying scattering in the telescope. Allowing for an atmospheric contribution (certainly present for the redder CRISP wavelengths), the measured FWS represents an upper limit for the instrumental scattering of the SST.
Acquisitions of this kind of calibration data can be made in ≲10 min per CRISP prefilter (see Table 1), so FWS calibrations could be made routinely. As currently implemented, the calculations are quite time consuming but could be stream-lined and ported to C for speed and added as a voluntary step in the CRISPRED data reduction pipeline of de la Cruz Rodríguez et al. (2015). However, as SST data are mostly collected during low-dust conditions (calima often comes with hot weather and bad seeing) such calibrations would be routinely useful only when the more dominating sources of contrast-reducing straylight have been fully characterized.
The fact that the off-disk straylight is clearly above the noise level even in low dust conditions means the calibration should be even easier to measure in dustier conditions. Still, we did have problems making the models fit. If similar measurements are to be repeated, one may consider taking more data, i.e., scan slower than the Sun moves during a HA drift scan. This would be particularly useful near the limbs, where the intensity gradient is large. Collecting a limb image from at least one more position along the limb would make the coordinate transformations of Sect. 2.4 more well determined.
The concentration of airborne dust at ORM has been measured routinely since 2001 by the site-monitoring group of the Telescopio Nazionale Galileo (TNG), see (Lombardi et al. 2011, and references therein). With a cadence of two hours, they count dust particles in a range of sizes from 0.3 to 10.0 μm with different scattering properties. The summed contribution of the different particle sizes is plotted in their web site http://tngweb.tng.iac.es/weather/dust/. This number can serve as a proxy for the amount of dust above the site because the vertical distribution of (Saharan) dust over the Atlantic is such that elevated concentrations are measurable at 2 km elevation (Alpert et al. 2004). The range of such measurements for 2014 was roughly 10-2–102μg m-3. Calima conditions are characterized by a count of ≳101μg m-3.
The shadow band ranger (SHABAR) of the SST is one of a set of five, constructed by Sliepen et al. (2010). A SHABAR measures intensity variations (scintillation) in an array of photo diodes pointing toward the Sun. From those measurements it estimates the index of refraction structure parameter, 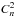 , along the line of sight. The average of the photo diode intensities is a measure of the direct sunlight.
, along the line of sight. The average of the photo diode intensities is a measure of the direct sunlight.
Acknowledgments
The Swedish 1-m Solar Telescope is operated on the island of La Palma by the Institute for Solar Physics of Stockholm University in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias. The author is grateful to Mikael Ingemyr and Pit Sütterlin for help with the observations, to Guus Sliepen for making it possible to do the DA scans, and to Göran Scharmer for discussions and helpful suggestions.
References
- Alpert, P., Kishcha, P., Shtivelman, A., Krichak, S. O., & Joseph, J. H. 2004, Atm. Res., 70, 109 [CrossRef] [Google Scholar]
- de la Cruz Rodríguez, J., Löfdahl, M., Sütterlin, P., Hillberg, T., & Rouppe van der Voort, L. 2015, A&A, 573, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- DeForest, C. E., Martens, P. C. H., & Wills-Davey, M. J. 2009, ApJ, 690, 1264 [NASA ADS] [CrossRef] [Google Scholar]
- Freeland, S. L., & Handy, B. N. 1998, Sol. Phys., 182, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Hardy, J. W. 1998, Adaptive Optics for Astronomical Telescopes (Oxford University Press), 448 [Google Scholar]
- Honsberg, C., & Bowden, S. 2014, PVCDROM (Photovoltaic Education Network), http://pveducation.org/pvcdrom [Google Scholar]
- Kasten, F., & Young, A. T. 1989, Appl. Opt., 28, 4735 [CrossRef] [Google Scholar]
- Löfdahl, M. G. 2002, in Image Reconstruction from Incomplete Data II, eds. P. J. Bones, M. A. Fiddy, & R. P. Millane, Proc. SPIE, 4792, 146 [Google Scholar]
- Löfdahl, M. G., & Scharmer, G. B. 1994, A&AS, 107, 243 [NASA ADS] [Google Scholar]
- Löfdahl, M. G., & Scharmer, G. B. 2012, A&A, 537, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lombardi, G., Zitelli, V., Ortolani, S., et al. 2011, MNRAS, 416, 1585 [NASA ADS] [CrossRef] [Google Scholar]
- Markwardt, C. B. 2009, in ASP Conf. Ser. 411, eds. D. A. Bohlender, D. Durand, & P. Dowler, 251 [Google Scholar]
- Martinez Pillet, V. 1992, Sol. Phys., 140, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Martinez Pillet, V., Ruiz Cobo, B., & Vazquez, M. 1990, Sol. Phys., 125, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Mathew, S. K., Martínez Pillet, V., Solanki, S. K., & Krivova, N. A. 2007, A&A, 465, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathew, S. K., Zakharov, V., & Solanki, S. K. 2009, A&A, 501, L19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moffat, A. F. J. 1969, A&A, 3, 455 [NASA ADS] [Google Scholar]
- Moré, J. 1978, in Numerical Analysis, ed. G. A. Watson (Springer-Verlag), Lect. Notes Math., 630, 105 [Google Scholar]
- Neckel, H., & Labs, D. 1994, Sol. Phys., 153, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Olivero, J. J., & Longbothum, R. L. 1977, J. Quant. Spectr. Rad. Transf., 17, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Pierce, A. K., & Slaughter, C. D. 1977, Sol. Phys., 51, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Roddier, F. 1999, Adaptive Optics in Astronomy (Cambridge University Press) [Google Scholar]
- Scharmer, G. B., Bjelksjö, K., Korhonen, T. K., Lindberg, B., & Pettersson, B. 2003a, in Innovative Telescopes and Instrumentation for Solar Astrophysics, eds. S. Keil, & S. Avakyan, Proc. SPIE, 4853, 341 [Google Scholar]
- Scharmer, G. B., Dettori, P., Löfdahl, M. G., & Shand, M. 2003b, in Innovative Telescopes and Instrumentation for Solar Astrophysics, eds. S. Keil, & S. Avakyan, Proc. SPIE, 4853, 370 [Google Scholar]
- Scharmer, G. B., Narayan, G., Hillberg, T., et al. 2008, ApJ, 689, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Scharmer, G. B., Löfdahl, M. G., van Werkhoven, T. I. M., & de la Cruz Rodríguez, J. 2010, A&A, 521, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scharmer, G. B., Henriques, V. M. J., Kiselman, D., & de la Cruz Rodríguez, J. 2011, Science, 333, 316 [NASA ADS] [CrossRef] [Google Scholar]
- Sliepen, G., & Sütterlin, P. 2013, in Synergies Between Ground and Space Based Solar Research, 1st SOLARNET – 3rd EAST/ATST meeting [Google Scholar]
- Sliepen, G., Jägers, A. P. L., Bettonvil, F. C. M., & Hammerschlag, R. H. 2010, in Ground-based and Airborne Telescopes III, eds. L. M. Stepp, R. Gilmozzi, & H. J. Hall, Proc. SPIE, 7733, 4 [Google Scholar]
- Smithson, R. C., & Peri, M. L. 1989, J. Opt. Soc. Am. A, 6, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Staveland, L. 1970, Sol. Phys., 12, 328 [NASA ADS] [CrossRef] [Google Scholar]
- van Noort, M., Rouppe van der Voort, L., & Löfdahl, M. G. 2005, Sol. Phys., 228, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Wedemeyer-Böhm, S. 2008, A&A, 487, 399 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wedemeyer-Böhm, S., & Rouppe van der Voort, L. 2009, A&A, 503, 225 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yeo, K. L., Feller, A., Solanki, S. K., et al. 2014, A&A, 561, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zwaan, C. 1965, Ph.D. Thesis, Rijksunitersiteit te Utrecht [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Setup schematics. Light from the telescope enters through the target from upper left. TM = tip-tilt mirror; DM = deformable mirror; RL = reimaging lens; DCBS = dichroic beamsplitter; CT = correlation tracker; WFS = wavefront sensor; LCs = liquid crystal analyzer; FPI = Fabry–Pérot interferometer, PBS = polarizing beamsplitter, WB = wide band, NBT = narrow band transmitted, NBR = narrow band reflected. |
| In the text | |
 |
Fig. 2 Limb darkening from Neckel & Labs (1994). |
| In the text | |
 |
Fig. 3 Limb fit for the 630 nm HA scan. Within each subfigure, the top and bottom tiles represent the masked 1024 × 1024-pixel images of the two limbs, respectively. In b) and c), the rightmost tiles represent the differences between the model images and the observed images. |
| In the text | |
 |
Fig. 4 Binned and normalized intensity data (10′′ bins) of the HA and DA scans. Compare Fig. 2. Positive (negative) r correspond to scan direction away from (toward) DC. The 11:49 “extra” DA scans are omitted from these plots. |
| In the text | |
 |
Fig. 5 Aureola intensity of CRISP WB and blue scans. The dots represent the binned data, while the lines represent the fits described in Sect. 3, specifically the ones in Table 5. Normalization and δr from the fits. Note that the range on the vertical axis varies between the different plots. |
| In the text | |
 |
Fig. 6 Consistency in HA scan aureola intensity, CRISP NB vs. WB. Normalization and δr from the 3-Gauss fit to the WB data. |
| In the text | |
 |
Fig. 7 Intensity and fit errors including the disk, NGauss = 1. HA scan at 630 nm, away from DC. The legends indicate the kernels used for the widest straylight component. |
| In the text | |
 |
Fig. 8 Fit errors off-disk, different NGauss. HA scan at 630 nm, away from DC. The legends indicate the FWKs used in the fits. |
| In the text | |
 |
Fig. 9 Fitted FWS for 630 nm, NGauss = 3, HA scan away from DC. The total model intensity, g(r), is fitted to the measured data represented by the gray circles. |
| In the text | |
 |
Fig. 10 Fitted straylight components for 630 nm, NGauss = 3, Moffat, HA scan away from DC. The total model intensity, g(r), is fitted to the measured data represented by the gray circles. |
| In the text | |
 |
Fig. 11 Fitted FWS for all wavelengths, NGauss = 3, selected HA scan fits. The dotted lines in b) show the influence of an idealized sunspot at DC. |
| In the text | |
 |
Fig. 13 Scattering kernels radial contributions, rkS. Individually normalized to unit maximum. The vertical lines indicate r = 1′. Compare Fig. 12. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



