| Issue |
A&A
Volume 585, January 2016
|
|
|---|---|---|
| Article Number | A9 | |
| Number of page(s) | 12 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201526866 | |
| Published online | 09 December 2015 | |
Size and albedo distributions of asteroids in cometary orbits using WISE data
1 Instituto de Astrofísica de Canarias (IAC), C/vía Láctea s/n, 38205 La Laguna, Tenerife, Spain
e-mail: jlicandr@iac.es
2 Departamento de Astrofísica, Universidad de La Laguna (ULL), 38205 La Laguna, Tenerife, Spain
3 Departamento de Astronomía, Facultad de Ciencias, Iguá 4225, 11400 Montevideo, Uruguay
4 Physics Department, University of Central Florida, PO Box 162385, Orlando, FL 32816.2385, USA
Received: 30 June 2015
Accepted: 15 September 2015
Context. Determining whether asteroids in cometary orbits (ACOs) are dormant or extinct comets is relevant for understanding the end-states of comets and the sizes of the comet population.
Aims. We intend to study the value distributions of effective diameter (D), beaming parameter (η), and visible geometric albedo (pV) of ACO populations, which can be derived from NASA’s Wide-field Infrared Explorer (WISE) observations, and we aim to compare these with the same, independently determined properties of the comets.
Methods. The near-Earth asteroid thermal model (NEATM) is used with WISE data and the absolute magnitude (H) of the ACOs to compute the D, pV and η.
Results. We obtained D and pV for 49 ACOs in Jupiter family cometary orbits (JF-ACOs) and 16 ACOs in Halley-type cometary orbits (Damocloids). We also obtained the infrared beaming parameter η for 45 of them. All but three JF-ACOs (95% of the sample) present a low albedo compatible with a cometary origin. The pV and η distributions of both ACO populations are very similar. For the entire sample of ACOs, the mean geometric albedo is p̅V = 0.05±0.02, (p̅V = 0.05±0.01 and p̅V = 0.05±0.02 for JF-ACOs and for Damocloids, respectively) compatible with a narrow albedo distribution similar to that of the Jupiter family comets (JFCs), with a p̅V ~ 0.04. The mean beaming parameter is η̅ = 1.0±0.2. We find no correlations between D, pV, or η. We also compare the cumulative size distribution (CSD) of ACOs, Centaurs, and JFCs. Although the Centaur sample contains larger objects, the linear parts in their log-log plot of the CSDs presents a similar cumulative exponent (β = 1.85 ± 0.30 and 1.76 ± 0.35, respectively). The CSD for Damocloids presents a much shallower exponent β = 0.89 ± 0.17.
Conclusions. The pV- and η-value distributions of ACOs are very similar to those of JF comet (JFCs) nuclei. The ACOs in Tancredi’s list are the best possible candidates to be dormant/inactive comets. The CSD for JF-ACOs is shallower and shifted towards larger diameters with respect to the CSD of active JFCs, which suggests that the mantling process has a size dependency whereby large comets tend to reach an inactive stage faster than small comets. Finally, the population of JF-ACOs is comparable in number with the population of JFCs, although there are more tens-km JF-ACOs than JFCs.
Key words: surveys / comets: general / minor planets, asteroids: general / infrared: planetary systems / catalogs
© ESO, 2015
1. Introduction
The classification criterion between asteroids and comets has evolved in recent decades, but the main phenomenological distinction remains unchanged: comets are active objects in the sense that they show gas and/or dust ejected from the surface at some point in their orbits, whereas asteroids do not. This statement is purely observational and makes no distinction among the different ways in which a body can lose mass.
There are some borderline cases between the asteroid and comet populations, usually called comet-asteroid transition objects, which include: (1) objects in typical cometary orbits that have never shown (or have not recently shown) any kind of activity, the asteroids in cometary orbits (ACOs); and (2) objects in typical asteroidal orbits that present some evidence of dust ejection, the active asteroids (AAs), a group that includes the so-called main belt comets (MBCs). Some AAs are designated comets because of the observed dust ejection, even though further analysis may later indicate that the dust is not produced by traditional cometary activity (i.e. sublimation or phase transition of volatiles), but from other physical phenomena, such as rotational spin-up, collisions, or thermal cracking.
To identify the transitional objects, several classification schemes have been used that are usually based on Tisserand’s parameter (TJ, Kresák 1979). TJ is a constant of motion in the restricted three-body problem and is related to an object’s encounter velocity with Jupiter. Most comets have orbits with TJ< 3, while the great majority of asteroids have orbits with TJ> 3. Only a few known comets, about 20 in the Jupiter family, have TJ> 3, with 2P/Encke being the most well known, but this is attributed to the long-term effects of non-gravitational forces (Fernández et al. 2002). Among asteroids with TJ< 3, aside from the ACOs mentioned above, are some members of the Cybele, Hilda, and Jupiter Trojan populations, and other objects close to the mean-motion resonances.
The problem with the usual TJ criterion is that it includes many objects with stable dynamical evolution incompatible with the chaotic dynamics of comets. Tancredi (2014) presented a much more restrictive criterion to identify ACOs, which ensures the selection of objects with a dynamical evolution similar to the population of periodic comets. Tancredi’s criterion is based on Tisserand’s parameter, the minimum orbital intersection distance (MOID) among the giant planets, and some information regarding the aphelion and perihelion distances, and it does not include objects in mean-motion resonances.
After applying a filter to the sample of >500 000 known asteroids to select only those with precise-enough orbits, Tancredi (2014) applied the proposed classification criterion to identify the ACOs. The resulting sample consists of ~331 ACOs, which are further classified in subclasses similar to the cometary classification: 203 objects belong to the Jupiter family group; 72 objects are classified as Centaurs; and 56 objects have Halley-type orbits (also known as Damocloids). These are the best known extinct/dormant comet candidates from a dynamical point of view.
To determine whether these objects truly are extinct/dormant comets or simply asteroids that have escaped from the main belt into cometary-like chaotic orbits, observations of other physical properties are needed. Recent studies of the surface properties of ACOs, including photometric and spectroscopic studies in the visible and near-infrared (Licandro et al. 2006, 2008; Alvarez-Candal & Licandro 2006; DeMeo & Binzel 2008; Alvarez-Candal 2013) and in the mid-infrared (Fernández et al. 2005; Licandro et al. 2009), feature a significant number of asteroids that do not satisfy Tancredi’s criterion. For example, Licandro et al. (2008) studied the visible and near-IR spectral properties of 39 ACOs, but only six appear in Tancredi’s list; in fact, based on their spectral properties, Licandro et al. (2008) warned that there are a significant number of objects in their sample that are likely “interlopers”. DeMeo & Binzel (2008) analysed the spectra of 55 ACOs (see their Table 3), and after removing six objects from the original list that were already identified as comets, only six out of the remaining 49 objects appear on Tancredi’s list. Fernández et al. (2005) computed the albedos of 26 ACOs using mid-IR observations. Two of them are presently classified as comets, and of the remaining 24 objects, 12 are on Tancredi’s list. In a recent paper, Kim et al. (2014) presented a compilation of the diameters and albedos of 123 ACOs obtained from different published databases, using their own selection criteria of ACOs; only 29 of these objects are on Tancredi’s list. Thus, the number of ACOs with spectral and thermal properties known is very small and the present knowledge of the physical properties of ACOs should be revised in view of Tancredi’s results.
The aim of this paper is to study the physical properties of ACOs, which can be derived by fitting a thermal model to NASA’s Wide-field Infrared Survey Explorer (WISE) observations. In particular, we present here the effective diameters (D), beaming parameters (η), visible geometric albedos (pV), and infrared-to-visible albedo ratios (RW1) using the method described in Alí-Lagoa et al. (2013). We compare our results to previous mid-infrared surveys of ACOs, such as that of Fernández et al. (2005), mentioned earlier, who used the near-Earth asteroid thermal model (NEATM; Harris 1998) to compute effective radii. Fernández et al. defined a comet-like albedo as being below 0.075, and they found that 64% ± 5% of their sample has comet-like albedos. They also found a very strong trend of albedo with TJ, with nearly all objects in their sample with TJ< 2.6 (and thus a higher probability of cometary origin) having comet-like albedos. Licandro et al. (2008) also found that the spectra of all objects with TJ< 2.7 in their sample are D- or P-type, which is typical of cometary nuclei.
We present results on ACOs that are part of two of the three populations in Tancredi (2014), those in Jupiter family comet orbits (JF-ACOs) and those in Halley-type orbits (the Damocloids), assuming they likely have an origin in two different comet reservoirs, the trans-neptunian belt and the Oort cloud, respectively. The WISE data for the population of Centaurs has already been analysed by Bauer et al. (2013); we combine our results with theirs to compare the cumulative size distributions (CSDs) of the three populations.
The paper is organized as follows. In Sect. 2, we briefly describe the WISE data set, the selection criteria and the thermal modelling used to derive D, η, and pV. We present our results in Sect. 3, which includes the pV and η distributions. The cumulative size distributions of the three ACO populations are presented in Sect. 4 and compared to that of Jupiter family comets. Finally, the discussion and conclusions are presented in Sect. 5.
2. Data and thermal modelling
The Wide-field Infrared Survey Explorer (WISE) is a space telescope launched by NASA in December 2009, which carried out an all-sky survey using four broadband filters with approximate isophotal wavelengths at 3.4, 4.6, 12, and 22 μm (named W1, W2, W3, and W4, respectively); see Wright et al. 2010 and references therein for a general description of the mission. The NEOWISE project managed the detection and archiving of all the observations of the more than 158 000 small solar system bodies acquired by WISE (see Mainzer et al. 2011a), and all of these observations have been reported to the IAU Minor Planet Center (MPC). The WISE All-Sky Single Exposure L1b Source Table, available via the IRSA/IPAC archive1, includes the corresponding magnitudes and uncertainties in the Vega system, as well as quality, contamination, and confusion flags that enable us to reject defective data (Cutri et al. 2012). Our rejection criteria, summarized next, are based on a combination of those used by Mainzer et al. (2011b, 2011c), Masiero et al. (2011), and Grav et al. (2012).
We downloaded all the data matching the MPC reported detections within a cone search radius of 1′′ centred on the MPC ephemeris of the ACO, and rejected those with artifact flags other than p, P, and 0 and quality flags other than A, B, and C. We also required the modified Julian date to be within four seconds of the time specified in the MPC. We ensured that the data are not contaminated by inertial sources by removing those points that return a positive match from the WISE Source Catalog within 6′′ if the flux of the inertial source is larger than 5% of that of the asteroid. We did not use data saturated to any extent, which translates to rejecting objects with magnitudes MW1 < 7.8, MW2 < 6.4, MW3 < 3.6, or MW4 < −0.6 (Cutri et al. 2012). All remaining observations in a given band are rejected if they are fewer than 40% of the data in the band with the maximum number of detections. Finally, we implemented the correction to the W3 and W4 isophotal wavelengths and zero magnitude fluxes to account for the red and blue calibrator discrepancy in W3 and W4 (Wright et al. 2010). The application of the above criteria results in a sample of 49 JF-ACOs and 16 Damocloids with WISE observations usable for our purposes.
Our method in fitting the WISE photometry and deriving effective diameters (D) and infrared beaming parameters (η) is described in Alí-Lagoa et al. (2013), but with an important caveat explained below. We used the NEATM of Harris (1998) and followed the implementation described in Mainzer et al. (2011b,c), Masiero et al. (2011), and Grav et al. (2012). As discussed in Appendix A of Alí-Lagoa et al. (2013), our results agree with the NEOWISE team’s within the typical error bars of the modelling.
The main difference here from the method in Alí-Lagoa et al. (2013) is that we do not use W2 data to avoid a potential bias in the beaming parameter determination related to the assumption that the infrared albedos at W1 and W2 are equal (pW1 = pW2). This was not problematic in the particular case of the B-types featured in Alí-Lagoa et al. because their average IR spectral slope, albeit ranging from slightly blue to moderately red (de León et al. 2012), is small, i.e. they are more neutral. When pW1 and pW2 are significantly different, however, said assumption causes the thermal part of the W2 flux to be miscalculated and introduces a small bias in the best-fitting values of D and η. Therefore, we only fit the beaming parameter if both W3 and W4 data are available and assume η = 1.0 otherwise2. We fit D in all cases and the corresponding visible albedos, pV, are derived by means of the relation ![\begin{equation} p_V = \left(1329\,\left[\mathrm{km}\right] \frac{10^{-H/5}}{D\,\left[\mathrm{km}\right]}\right)^2, \label{ec:pVHD} \end{equation}](/articles/aa/full_html/2016/01/aa26866-15/aa26866-15-eq33.png) (1)where H is the asteroid absolute magnitude taken from the IAU MPC website.
(1)where H is the asteroid absolute magnitude taken from the IAU MPC website.
Finally, the infrared albedo in filter W1 (pW1), is not fitted but computed from the following expression that follows the notation of Emery et al. (2007): 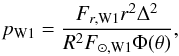 (2)where (r, Δ, θ) is the geometry of observation (the heliocentric distance r must be input in AU), F⊙ ,W1 the solar flux at 1 AU taken from the IR calibration of Rieke et al. (2008), Fr,W1 the reflected solar flux measured by the observer at wavelength W1, R the radius, and Φ(θ) a phase correction factor (recall that geometric albedo is defined at zero phase angle). We assume that the IAU H-G phase correction introduced by Bowell et al. (1989), namely,
(2)where (r, Δ, θ) is the geometry of observation (the heliocentric distance r must be input in AU), F⊙ ,W1 the solar flux at 1 AU taken from the IR calibration of Rieke et al. (2008), Fr,W1 the reflected solar flux measured by the observer at wavelength W1, R the radius, and Φ(θ) a phase correction factor (recall that geometric albedo is defined at zero phase angle). We assume that the IAU H-G phase correction introduced by Bowell et al. (1989), namely, 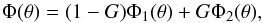 (3)holds for IR wavelengths. In Eq. (3), G is the so-called slope parameter, and Φ1 and Φ2 are empirical functions defined by Bowell et al. (1989). As G is not determined for the ACOs in our sample, we use the standard assumption G = 0.15. The reflected solar flux Fr,W1 is estimated by subtracting the model thermal flux at W1 from the observed flux. The former is usually negligible in comparison to the latter, though not always, in particular, for observations taken when r ≈ 1 AU.
(3)holds for IR wavelengths. In Eq. (3), G is the so-called slope parameter, and Φ1 and Φ2 are empirical functions defined by Bowell et al. (1989). As G is not determined for the ACOs in our sample, we use the standard assumption G = 0.15. The reflected solar flux Fr,W1 is estimated by subtracting the model thermal flux at W1 from the observed flux. The former is usually negligible in comparison to the latter, though not always, in particular, for observations taken when r ≈ 1 AU.
 |
Fig. 1 Determined geometric albedo pV of ACOs vs. Jupiter Tisserand’s parameter TJ. Big dots correspond to objets with determined η, while small dots correspond to ACOs with no η determination. The line at pV = 0.075 is the limit for a cometary-like albedo, according to Fernández et al. (2005). Only three JF-ACOs present a pV > 0.18 incompatible with a cometary origin. |
The assumption G = 0.15 may throw off the H, and derived albedo values. As shown by Pravec et al. (2012), H may be underestimated using this G-value, in particular for objects with H > 12. This implies that ACOs may actually have lower albedos. We discuss these implications in Sect. 5. In Tables 1 and 2 we list the JF-ACOs and Damocloids, respectively, that we included in this study, and also show the number of measurements from each of the WISE filters that we used in our analysis.
Observational circumstances of the ACOs in JFC orbits.
3. Results and analysis
The results of the thermal fits and albedo calculations are summarized in Tables 3 and 4. We obtained D and pV for 49 of the 203 JF-ACOs and 16 of the 56 Damocloids in Tancredi’s list (Tancredi 2014). This is the first published albedo determination for 34 of these 65 ACOs. For 32 of these JF-ACOs and 13 Damocloids, we also obtained η. We also were able to constrain the infrared-to-visible albedo ratio, RW1, i.e. pW1/pV, for four JF-ACOs and one Damocloid; unfortunately, there was not much reliable photometry in W1 and W2. This is to be expected for small, low-albedo objects such as ACOs, which have been observed by WISE at typically large heliocentric distances, as these bands are dominated by reflected light. This small number of RW1 values inhibit our ability to perform any statistical analysis similar to that in the case of B-type asteroids (see Ali-Lagoa et al. 2013).
Some of the objects in our survey have been studied previously by Fernández et al. (2005) and by Kim et al. (2014). In fact, Kim et al. analyzed some of the same WISE data. For the two objects studied by Fernández et al. and the 24 objects studied by Kim et al., which we include in our analysis, our results are in agreement with these earlier works.
3.1. Analysis of pV vs. TJ
Figure 1 presents the geometric albedo against the Tisserand parameter for all objects in our study. All but three objects present an albedo compatible with a primitive object. The JF-ACOs 2005 NA56, 2010 KG43, and 2010 DD2 have pV> 0.18, which is incompatible with a cometary origin and suggests that they may be scattered igneous asteroids. However, the data of these three asteroids are of lower quantity and quality; we were not able to determine η because they only have useful data in filter W3. On the other hand, only one Damocloid presents an albedo that is larger than a cometary-like albedo (pV ≤ 0.075, according to Fernández et al. 2005). The albedo of 2010 OR1, pV = 0.110 ± 0.022, is in any case a low albedo typical of primitive asteroids. Thus, 95% of the ACOs in this paper, 61 out of 65, are compatible with a cometary origin, and also not completely incompatible with the albedos of primitive class asteroids (Mainzer et al. 2011c). If we restrict ourselves to the subset of the 65 objects that have enough data to fit η, 45 objects, and consider an error bar up to 2σ, 100% of the sample has a cometary-like albedo.
Observational circumstances of the Damocloids included.
Results of thermal fits and albedo calculations for the ACOs in JFC orbits.
Results of thermal fits and albedo calculations for Damocloids.
3.2. Geometric albedo and beaming parameter distributions
The normalized histograms of Fig. 2 represent the beaming parameter (upper) and geometric albedo (lower) distributions of JF-ACOs and Damocloids with determined η (those with better WISE data) are presented.
 |
Fig. 2 Upper: beaming parameter distribution of JF-ACOs (red) and Damocloids (green) presented as normalized histograms; Lower: geometric albedo distribution of JF-ACOs (red) and Damocloids (green) with determined η. |
The albedo distributions of Damocloids and JF-ACOs are similar and narrow around the mean value, which indicates that both populations have similar surface properties. The mean geometric albedo (and 1σ standard deviation of the mean) for JF-ACOs is 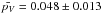 , whereas for Damocloids it is
, whereas for Damocloids it is 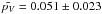 . If we assume that both distributions are compatible, the Kolmogorov-Smirnov test (K-S hereafter) cannot reject this null hypothesis with a high P-value of 0.67. Thus, for the entire sample of ACOs the mean geometric albedo is
. If we assume that both distributions are compatible, the Kolmogorov-Smirnov test (K-S hereafter) cannot reject this null hypothesis with a high P-value of 0.67. Thus, for the entire sample of ACOs the mean geometric albedo is 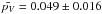 .
.
The η distributions of Damocloids and JF-ACOs look slightly different but are compatible within their error bars, with a mean beaming parameter 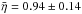 for the Damocloids and
for the Damocloids and 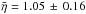 for the JF-ACOs. The K-S test gives us a borderline case3 with a P-value of 0.04. The reason for this is likely the presence of four JF-ACOs, which have somewhat elevated η ~ 1.21−1.6, but given the large error bars in η, we consider that both distributions are not incompatible at the P ≤ 0.01 level. Larger samples would be needed to be absolutely conclusive and it would also be interesting to have more data to confirm those objects with high η-values.
for the JF-ACOs. The K-S test gives us a borderline case3 with a P-value of 0.04. The reason for this is likely the presence of four JF-ACOs, which have somewhat elevated η ~ 1.21−1.6, but given the large error bars in η, we consider that both distributions are not incompatible at the P ≤ 0.01 level. Larger samples would be needed to be absolutely conclusive and it would also be interesting to have more data to confirm those objects with high η-values.
As we show later, the small differences in the 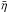 -values could be related to the fact that Damocloids were observed at slightly lower phase angles (mean phase angle
-values could be related to the fact that Damocloids were observed at slightly lower phase angles (mean phase angle 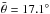 versus
versus 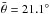 for the JF-ACOs). The only object with an η well above 1.0 is 2008 UD253, with η = 1.6 ± 0.7, but the uncertainty is large and so is < 1σ away from 1.0. If we had used a fixed η = 1.0 in the best-fitting size for the object would still result in a cometary-like albedo of pV = 0.047. For the entire sample of ACOs, the mean beaming parameter is
for the JF-ACOs). The only object with an η well above 1.0 is 2008 UD253, with η = 1.6 ± 0.7, but the uncertainty is large and so is < 1σ away from 1.0. If we had used a fixed η = 1.0 in the best-fitting size for the object would still result in a cometary-like albedo of pV = 0.047. For the entire sample of ACOs, the mean beaming parameter is 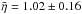 . This is compatible with the
. This is compatible with the 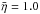 of the main belt asteroids measured with WISE (Masiero et al. 2011). On the other hand, Delbo et al. (2007) found a
of the main belt asteroids measured with WISE (Masiero et al. 2011). On the other hand, Delbo et al. (2007) found a 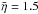 for near-Earth asteroids (NEAs), and Mainzer et al. (2011d) report a median η = 1.4 ± 0.5 for 313 NEAs. Our results are far from these values, although we emphasize that only two of our JF-ACOs are actually NEAs, 2009WF104 and 2009WO6, whose η-values, 1.15 and 1.16, are still closer to
for near-Earth asteroids (NEAs), and Mainzer et al. (2011d) report a median η = 1.4 ± 0.5 for 313 NEAs. Our results are far from these values, although we emphasize that only two of our JF-ACOs are actually NEAs, 2009WF104 and 2009WO6, whose η-values, 1.15 and 1.16, are still closer to 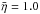 . Also, that a large fraction of NEAs in Delbo et al. and Mainzer et al. are S-types, which have different ensemble thermal properties than the primitive asteroids.
. Also, that a large fraction of NEAs in Delbo et al. and Mainzer et al. are S-types, which have different ensemble thermal properties than the primitive asteroids.
Even more relevant is to compare these distributions to those of comets. Fernández et al. (2013) presented mid-infrared measurements of the thermal emission from 89 nuclei of Jupiter family comets (JFCs) obtained with the Spitzer Space Telescope, and they were able to measure η for 57 of those nuclei. They derived the weighted mean and standard error on the mean of the η of the JFC population 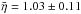 , which is very similar to the distribution we found for ACOs.
, which is very similar to the distribution we found for ACOs.
The comparison with the albedo distribution of JFCs is not straightforward; the albedo is computed using the diameter and the absolute magnitude, and the absolute magnitudes of comet nuclei are usually quite uncertain. It is a difficult task to measure them because a nucleus is usually embedded in a dust coma (see e.g. Licandro et al. 2000). By comparing the size distribution determined with Spitzer data and those determined using visible data, Fernández et al. (2013) conclude that “a geometric albedo of 0.04 is a reasonable assumption for visible-wavelength studies” in agreement with previous results by Lamy et al. (2004), which imply a narrow albedo distribution around a 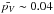 .
.
To test if this is compatible with the albedo distribution of ACOs found here, we constructed a synthetic set of albedo values as follows. We took Dμ = 10 km and Hμ = 14.10 so that the corresponding visible geometric albedo is pV ~ 0.04 (per Eq. (1)). Then, we generated 60 random values of size and absolute magnitude, each one drawn from Gaussian distributions with mean values Dμ and Hμ and standard deviations of 1.5 km (15% relative error in size) and 0.15 magn, respectively. The resulting pV distribution represents what we would obtain if we computed or measured the size and absolute magnitude for a single object with these levels of uncertainty, which we consider a plausible representation for a population of objects with the same visible geometric albedo. We used this pV distribution as the null hypothesis for a K-S test, and we obtained that it is not compatible with the albedo distribution of the ACOs. This means that, however small, there is a statistically significant shift between the assumed cometary nuclei pV = 0.04 and the ACOs visible geometric albedos. On the other hand, the null hypothesis was not rejected when we decreased H to 13.85, which corresponds to a slightly higher albedo value of 0.045, which in any case, is very close to the assumed mean cometary albedo. From this, we conclude that, accounting for our typical uncertainties, the pV distribution of the ACOs is similar to the pV distribution of comet nuclei: very narrow around a small typical geometric albedo pV = 0.045, an albedo value slightly larger, but still compatible with that assumed by Lamy et al. (2004) and Fernández et al. (2013) for comet nuclei.
3.3. Analysis of pV and η versus diameter
We also looked for possible correlations of pV and η with D. Figure 3 presents these scatter plots. First, we find there is no correlation between the albedo and the diameter, which is similar to the case of JFCs according to Fernández et al. (2013). Hence, it is reasonable to assume a common geometric albedo for all JFCs and JF-ACOs for statistical purposes, e.g. to compute their size distribution from their visible absolute magnitude, something that is frequently invoked when interpreting visible-wavelength photometry of JFCs.
Also, the three objects with high albedo values have very small diameters (D< 3.5 km), which may be the reason they have lower-SNR WISE data and thus poorly-constrained D and pV. On the other hand, these values of the diameter suggest that the Yarkovsky effect could have played an important role in their being scattered from the main belt.
 |
Fig. 3 Upper: beaming parameter vs. diameter distribution of JF-ACOs (filled circles) and Damocloids (open circles). A possible trend of η with D is shown. Lower: geometric albedo vs. diameter distribution of JF-ACOs and Damocloids. Large circles correspond to objects with η determined and small objects with not enough data to determine η. No correlation between pV and D is found. |
A possible trend of η with D is apparent in the upper panel of Fig. 3. In Sect. 3.4 we show that this is likely due to a phase angle effect.
3.4. Analysis of pV and η vs. the phase angle of the observations
We also searched for a correlation between geometric albedo and phase angle, and η with phase angle. Figure 4 shows pV vs. θ (lower plot) and η vs. θ (upper plot). No correlation is found between albedo and phase angle, but a correlation between beaming parameter and phase angle is evident. We find a best-fit linear relation of beaming parameter as a function of phase of η(θ) = (0.85 ± 0.03) + (0.008 ± 0.001) θ. This result is similar to that presented in Masiero et al. (2011): η(θ) = 0.79 + 0.011 θ.
 |
Fig. 4 Upper: beaming parameter vs. phase angle of JF-ACOs (filled circles) and Damocloids (open circles). A linear trend of η with θ is shown (see text); the red line is the correlation we found (η = 0.85 + 0.008 θ), the blue line is the linear regression (η = 0.79 + 0.011 θ) from Masiero et al. (2011). Lower: geometric albedo vs. θ distribution of JF-ACOs and Damocloids. Large circles correspond to objects with η determined and small objects with not enough data to determine η. No correlation between pV and θ is found. |
As discussed above, there is a difference between the JF-ACO and Damocloid η distributions, and a possible correlation between size and η (see Fig. 3). Once we correct the η-values as a function of θ, using the linear fit found above, the η distributions become even more similar (see Fig. 5). The K-S test distance is reduced and the P-value is 0.065, i.e. the distributions are not incompatible. Furthermore, after applying this correction to η, we found that the possible correlation of η with D also disappears (see Fig. 6).
 |
Fig. 5 Normalized histogram of η corrected to θ = 0 using the linear fit obtained in this paper. Both distributions are very similar. |
 |
Fig. 6 Beaming parameter corrected to θ = 0 using the linear fit obtained in this paper vs. diameter. The apparent trend of η with D in Fig. 3 is not anymore observed in this plot. |
Fernández et al. (2013) found that the beaming parameter of comet nuclei is uncorrelated with any observational or geometric parameter; in particular, they did not find a correlation with the phase angle, although their observations only covered a narrow range of phase angles (9 <θ< 17.5°). It is likely that this was too narrow a range to see the kind of correlation we report here for the ACOs, if it exists for the comet nuclei.
4. ACOs cumulative size distribution
 |
Fig. 7 Cumulative size distribution for JF-ACOs, Centaurs, and Damocloids (see text). |
Alvarez-Candal & Licandro (2006) studied the CSD of the population of JF-ACOs and derived a CSD power-law index of β = 2.55 ± 0.04. However, they used a sample of objects that was strongly contaminated by scattered asteroids because of their selection criteria.
We now present CSDs for the three groups of ACOs: Jupiter family, Damocloids, and Centaurs. The sample of objects in each group with reliable size estimates is rather small: 49 JF-ACOs, 16 Centaurs and 16 Damocloids. In the case of Centaurs, we used the results for the 16 objects presented in Bauer et al. (2013) that are in Tancredi’s list. These sample sizes are not sufficient by themselves however to find reliable CSDs. We follow the procedure presented by Tancredi et al. (2006) to enlarge the sample. We start with the sample of 203 JF-ACOs, 72 Centaurs, 56 Damocloids included in Tancredi’s list (2014). For each individual object, we assume a distribution of the albedo according to available information, to wit:
-
If a given object has a reliable measurement of the albedo with acertain error bar, we assume for this object an albedo distributionwith a Gaussian shape (within± 2σ), centred on the reported value and with σ equal to the reported error. The values for the JF-ACOs and Damocloids are taken from Tables 3 and 4, and those of the Centaurs from the albedos presented in Bauer et al. (2013).
-
If we do not have any information about the albedo of the object, we assume an albedo distribution with a normal shape (within ± 2σ ), centred at the mean and standard deviation of the values for each group.
Then, from the probability density function (PDF) of albedo for each individual object, following Eq. (7) of Tancredi et al. (2006), we compute the PDFs for the diameter for a given value of the absolute magnitude (H). In the case of ACOs, H is equivalent to the absolute nuclear magnitude (HN) used in the case of comets (see Tancredi et al. 2006). The values of H are taken from the Minor Planet Center. Adding the individual PDF pi(log D), we obtain the differential size distribution (in terms of log D) for the whole sample, from which we can easily compute the CSD.
The CSDs computed with this procedure for each ACO group are presented in Fig. 7. The size distributions are fitted to a power-law probability density p of the type 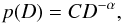 (4)where α is the constant exponential parameter known as the exponent and C a normalization constant. The power law represents asteroids down to some cut-off diameter (Dmin), giving the normalization constant
(4)where α is the constant exponential parameter known as the exponent and C a normalization constant. The power law represents asteroids down to some cut-off diameter (Dmin), giving the normalization constant 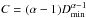 , provided α> 1. The cumulative distribution function (P) is then
, provided α> 1. The cumulative distribution function (P) is then 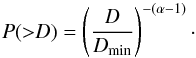 (5)The exponents of the distributions (α) and the cut-off diameters (Dmin) are estimated with a method, which combines a maximum-likelihood fitting method with goodness-of-fit tests based on the Kolmogorov-Smirnov statistic, as described by Clauset (2009) and Tancredi et al. (2015; see an example of the method below). The exponent of the CSDs (β = α−1), Dmin and the number of objects larger than Dmin (N( >Dmin)) are presented in Fig. 7.
(5)The exponents of the distributions (α) and the cut-off diameters (Dmin) are estimated with a method, which combines a maximum-likelihood fitting method with goodness-of-fit tests based on the Kolmogorov-Smirnov statistic, as described by Clauset (2009) and Tancredi et al. (2015; see an example of the method below). The exponent of the CSDs (β = α−1), Dmin and the number of objects larger than Dmin (N( >Dmin)) are presented in Fig. 7.
The linear part in the log-log plot of the CSDs for JF-ACOs and Centaurs are almost parallel with a similar cumulative exponent (β = 1.85 ± 0.30, = 1.76 ± 0.35, respectively). The CSD for Centaurs is shifted towards larger objects with respect to that for JF-ACOs. For example, for D> 30 km there are 25 times more Centaurs than JF-ACOs. The exponent for the Centaurs is similar to that obtained by Bauer et al. 2013 (β = 1.6 ± 0.30), although there are differences in the samples and computation method.
On the other hand, the CSD for Damocloids presents a much shallow exponent β = 0.89 ± 0.17. In the light of the hypothesis that all the ACOs are dormant comets, we have to bear in mind that the mantling process might alter the original size distribution. This process might be dependent on the size of the nucleus, chemical constituents, and number of perihelion passages. The time required for the mantling is expected to be much longer for the Damocloids than for the JF-ACOs because of their longer orbital periods. Nevertheless, if the mantling is only dependent on the number of passages, in a steady state scenario, the CSDs should not be affected. Therefore, the differences among the exponents may reflect a difference in the CSDs previous to the mantling process and/or mantling processes that depend on the size of the nucleus in different ways.
We conclude that the similarity in the exponent between JF-ACOs and Centaurs and the difference with the Damocloids reinforces the hypothesis that the populations of the former two populations have a common origin (in the transNeptunian belt), while the latter comes from a different origin (in the Oort Cloud).
Now we compare the CSD of JF-ACOs with the sample of active JFCs. The CSDs of the JFCs has been analysed by many authors: e.g. Lamy et al. (2004), Meech et al. (2004), Tancredi et al. (2006), Weiler et al. (2011), Snodgrass et al. (2011),and Fernández et al. (2013). There is no agreement among these authors and there has been a strong debate about the exponent of the CSDs. In our analysis we use the sample of diameters for the JFCs presented by Fernández et al. (2013). The sample includes 89 JFCs from their Table 7, plus nine objects already included in their analysis whose effective radii had been measured by spacecraft flybys or by earlier mid-IR photometry. The CSDs for JF-ACOs and JFCs are presented in Fig. 8. The computation of exponents of the distributions and the cut-off diameters was peformed with the method described above. As an example, in Fig. 9 we present the value of the Kolmogorov-Smirnov statistic as a function of the cut-off diameter (a) and the corresponding value of the maximum-likelihood exponent α (b) for the sample of JFCs. The KS-statistic is computed as the maximum distance between the size distribution of the data and the fitted model for each cut-off diameter. A similar plot could be presented for the JF-ACOs. The chosen value corresponds to the minimum KS-statistic at Dmin = 4.30 km, with a corresponding α = 3.30 (β = 2.30 ± 0.39). If a smaller cut-off diameter is selected, the value of α is drastically reduced. Fernández et al. (2013) reported an exponent β = 1.92 ± 0.23, computed as the median among different linear fits in several range of diameters. Although the two estimates overlap, we use our value to compare with the other samples for consistency.
 |
Fig. 8 Cumulative size distribution for JF-ACOs and JFCs. |
 |
Fig. 9 Value of the Kolmogorov-Smirnov test as a function of the cut-off diameter (lower plot) and the corresponding value of the maximum-likelihood exponent α (upper plot). |
From the comparison of the two CSDs (Fig. 8) we conclude that the CSD for JF-ACOs is shallower and shifted towards larger diameter with respect to the JFCs. In the context of the hypothesis that the JF-ACOs are dormant comets coming from the JFCs population, this result has several implications:
-
The largest JF-ACOs are much larger than the largest JFCs; e.g.there is only one JFC nucleus larger than 20 km, butthere are many JF-ACOs larger than this size.
-
The mantling process has a size dependency; large comets tend to acquire an inactive stage faster than small comets, which is consistent with previous results that suggest that larger comets develop insulating dust mantles faster (Licandro et al. 2000; Tancredi et al. 2006)
-
The number of JF-ACOs is higher than the JFCs for a given size, although we have to take into account that the sample of measured JFC nuclei is smaller than the known sample.
While for the sample of JF-ACOs, we are using the complete sample of discovered objects, we only use the sample of JFCs with measured absolute magnitudes, which is much smaller than the sample of discovered objects. In order to compare the numbers of the two population, we hence correct the CSDs of JFCs taking the incompleteness of the sample used to compute the CSD presented in Fig. 8 into account. Though we may expect that the incompleteness has some dependency on the nuclear magnitude and the diameter, in the absence of any further information we assume a constant incompleteness factor equal to the ratio of the total number of known JFCs over the sample with measured diameters (= 476/98).
In Fig. 10 we present the ratio between the differential (red line) and the cumulative (blue line) number of JF-ACOs over the number of JFCs (corrected for incompleteness) for a given diameter. These ratios are size-dependent: the ratios increase with increasing diameters. At D = 10 km, the differential ratio is 0.8 and the cumulative ratio is 1. Thus, we conclude that the population of JF-ACOs is comparable in number with the population of JFCs.
This result is in contradiction with previous estimates of a large population of dormant extinct comets, as has already been pointed out in Tancredi (2014). Shoemaker et al. (1994) estimated a ratio of extinct to active JFCs of ~7.5; and Levison & Duncan (1997) obtained a ratio of 3.5. Our results contradict these estimates based on the present-day number of JF-ACOs and JFCs.
Although the cumulative number of JF-ACOs and JFCs larger than a few km seem to be similar, we find that for very large objects (> 20 km), there is a prevalence of JF-ACOs over JFCs. There is a size over a few tens-km where only JF-ACOs have been observed. We can tentatively conclude that tens-km rapidly builds a insulating crust and/or they are physically unstable.
 |
Fig. 10 Ratio between the differential (red line) and the cumulative (blue line) number of JF-ACOs over the number of JFCs (corrected for incompleteness) for a given diameter (see text). |
5. Conclusions
In this paper we present the effective diameter (D), infrared beaming parameter η, and visible geometric albedos (pV) for 49 of the 203 JF-ACOs and 16 of the 56 Damocloids from the Tancredi 2014 list derived from applying the NEATM to their WISE data. The beaming parameter could be fitted for 32 of these JF-ACOs and 13 Damocloids.
All but three JF-ACOs present an albedo that is compatible with a cometary origin. The data quality of those three asteroids is relatively worse and that could explain the discrepancy. All Damocloids present an albedo typical of primitive asteroids and compatible with a cometary origin. Taking both populations, the albedo of 95% of the ACOs of our sample are compatible with a cometary origin. If we restrict our sample to those objects with enough data to fit η (45 objects), the result is 100%.
We did not find any correlation between: (1) the albedo and the Diameter; (2) the albedo and phase angle of the observation; (3) η and the albedo. On the other hand, we find a linear relation between η and phase angle θ (η = 0.85 + 0.008 θ) similar to that presented in Masiero et al. (2011) for the whole main belt data set (η = 0.79 + 0.011 θ). Applying this correction to the computed η values, we conclude that there is no correlation between η and D.
The pV and η distributions of Damocloids and JF-ACOs are similar, which is indicative that both populations have similar surface properties. Their albedo distributions are very narrow around their mean values: 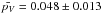 and
and 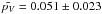 for JF-ACOs and for Damocloids, respectively. For the entire sample of ACOs, the mean geometric albedo is
for JF-ACOs and for Damocloids, respectively. For the entire sample of ACOs, the mean geometric albedo is 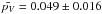 , compatible with a narrow albedo distribution around a
, compatible with a narrow albedo distribution around a 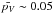 similar to the narrow albedo distribution around a
similar to the narrow albedo distribution around a 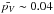 assumed by Fernández et al. (2013) for JFCs. As stated in Sect. 2, the determined albedo of ACOs may actually be smaller as we assumed G = 0.15 (see Pravec et al. 2012) because H may be underestimated for small objects (H> 12). In the extreme case that all the H values that we used were 0.5 mag too small (the maximum average difference found by Pravec et al.), all our pV would be 63% smaller, and our average
assumed by Fernández et al. (2013) for JFCs. As stated in Sect. 2, the determined albedo of ACOs may actually be smaller as we assumed G = 0.15 (see Pravec et al. 2012) because H may be underestimated for small objects (H> 12). In the extreme case that all the H values that we used were 0.5 mag too small (the maximum average difference found by Pravec et al.), all our pV would be 63% smaller, and our average 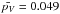 would drop down to 0.03. In any case, this bias would also affect the comet nuclei albedo determinations based on H, so this would not change the main conclusion that both populations have similar albedo distributions.
would drop down to 0.03. In any case, this bias would also affect the comet nuclei albedo determinations based on H, so this would not change the main conclusion that both populations have similar albedo distributions.
The η distribution of Damocloids looks slightly different than that of JF-ACOs, with a mean beaming parameter 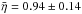 for the Damocloids and
for the Damocloids and 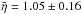 for the JF-ACOs. This difference is related to the higher phase angles at which the JF-ACOs were observed by WISE, however, and disappear when we apply the linear relation with θ to the computed η. For the entire sample of ACOs, the mean beaming parameter is
for the JF-ACOs. This difference is related to the higher phase angles at which the JF-ACOs were observed by WISE, however, and disappear when we apply the linear relation with θ to the computed η. For the entire sample of ACOs, the mean beaming parameter is 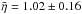 , which is compatible with the
, which is compatible with the 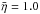 of the main belt asteroids (Masiero et al. 2011) and average beaming parameter of the JFC population
of the main belt asteroids (Masiero et al. 2011) and average beaming parameter of the JFC population 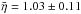 reported by Fernández et al. (2013).
reported by Fernández et al. (2013).
We conclude that the ACOs in Tancredi (2014) are likely dormant comets considering dynamical and surface properties criteria, and that Tancredi’s dynamical criteria to select dormant comet candidates are much better than those used before.
We also compare the CSD of JF-ACOs, Damocloids, Centaurs, and JFCs. The linear part in the log−log plot of the CSDs for JF-ACOs and Centaurs are almost parallel with a similar cumulative exponent (β = 1.85 ± 0.30 = 1.76 ± 0.35, respectively), with the CSD of Centaurs shifted towards larger objects than that of the JF-ACOs. The CSD for Damocloids presents a much shallow exponent β = 0.89 ± 0.17. The similarity in the exponent between JF-ACOs and Centaurs and its difference with the Damocloids’s reinforce the hypothesis that the populations of the first two has a common origin in the transNeptunian belt, while the Damocloids comes from the Oort Cloud.
Finally, the CSD for JF-ACOs is shallower and shifted towards larger diameters with respect to the CSD of active JFCs; there is only one JFC nuclei larger than 20 km, but there are many JF-ACOs larger than this size. The shallower slope for the JF-ACOs’ CSD means that, in relative numbers, there are fewer small members in the JF-ACO population than in JFC population. In the framework of the hypothesis that the JF-ACOs are dormant comets coming from the JFCs population, this result suggests that the mantling process has a size dependency. Two effects might be in action. First, JFCs might die by catastrophic disintegration, and this process should be more relevant for the smaller objects. Second, large comets tend to produce a thick crust, quenching the activity faster than small objects, due to the stronger gravitation field acting on the ejected particles, as suggested by Rickman et al. (1990), Licandro et al. (2000), and Tancredi et al. (2006).
We also show that the population of JF-ACOs is comparable in number with the population of JFCs, although there are more tens-km JF-ACOs than JFCs.
This is chosen based on the value distributions of all main belt asteroids reported in Masiero et al. (2011).
Acknowledgments
We acknowledge James Bauer for his useful comments, which improved this manuscript. V.A.-L. and J.L. acknowledge support from the project AYA2012-39115-C03-03 and ESP2013-47816-C4-2-P (MINECO, Spanish Ministry of Economy and Competitiveness). This publication uses data products from NEOWISE, a project of the Jet Propulsion Laboratory/California Institute of Technology, funded by the Planetary Science Division of the NASA. We made use of the NASA/ IPAC Infrared Science Archive, which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the NASA.
References
- Alí-Lagoa, V., de León, J., Licandro, J., et al. 2013, A&A, 554, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alvarez-Candal, A. 2013, A&A, 549, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alvarez-Candal, A., & Licandro, J. 2006, A&A, 458, 1007 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bauer, J. M., Grav, T., Blauvelt, E., et al. 2013, ApJ, 773, 22 [Google Scholar]
- Bowell, E., Hapke, B., Domingue, D., et al. 1989, in Asteroids II, eds. R. P. Binzel, T. Gehrels, & M. S. Matthews (Tucson: Univ. of Arizona Press), 524 [Google Scholar]
- Clauset, A., Shalizi, C. R.,& Newman, M. E. J. 2009, SIAM Rev. 51, 661 [Google Scholar]
- Cutri, et al., 2012, The WISE Explanatory Supplement, http://wise2.ipac.caltech.edu/docs/release/allsky/expsup/sec4_5.html [Google Scholar]
- de León, J., Pinilla-Alonso, N., Campins, H., Licandro, J., & Marzo, G. A. 2012, Icarus, 218, 196 [NASA ADS] [CrossRef] [Google Scholar]
- DeMeo, F., & Binzel, R. 2008, Icarus, 194, 436 [NASA ADS] [CrossRef] [Google Scholar]
- Kresák, L. 1979, Astron. Inst. Czechoslovakia Bull., 30, 291 [NASA ADS] [Google Scholar]
- Emery, J. P., Dalle Ore, C. M., Cruikshank, D. P., et al. 2007, A&A, 466, 395 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fernández, J., Gallardo, T., & Brunini, A. 2002, Icarus, 159, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Fernández, Y., Jewitt, D., & Sheppard, 2005, AJ, 130, 308 [NASA ADS] [CrossRef] [Google Scholar]
- Fernández, Y. R., Kelley, M. S., Lamy, P. L., et al. 2013, Icarus, 226, 1138 [NASA ADS] [CrossRef] [Google Scholar]
- Grav, T., Mainzer, A. K., Bauer, J., et al. 2012, ApJ, 744, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, A. W. 1998, Icarus, 131, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kim, Y., Masateru, I., & Fumihiko, U. 2014, ApJ, 789, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Lamy, P. L., Toth, I.,Fernandez, Y. R., & Weaver, H. A. 2004, in Comets II, eds. M. C. Festou, H. U. Keller, & H. A. Weaver (Tucson: University of Arizona Press), 223 [Google Scholar]
- Levison, H. F., & Duncan, M. J. 1997, Icarus, 127, 13 [Google Scholar]
- Licandro, J., Tancredi, G., Lindgren, M., Rickman, H., & Gil-Hutton, R. 2000, Icarus, 147, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Licandro, J., de León, J., Pinilla, N., & Serra-Ricart, M. 2006, Adv. Space Res., 38, 1991 [NASA ADS] [CrossRef] [Google Scholar]
- Licandro, J., Alvarez-Candal, A., de León, J., et al. 2008, A&A, 481, 861 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Licandro, J., Campins, H., Kelley, M., et al. 2009, A&A, 507, 1667 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mainzer, A., Bauer, J., Grav, T., et al. 2011a, ApJ, 731, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Mainzer, A., Grav, T., Masiero, J., et al. 2011b, ApJ, 736, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Mainzer, A., Grav, T., Masiero, J., et al., 2011c, ApJ, 741, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Mainzer, A., Grav, T., Bauer, J., et al. 2011d, ApJ, 743, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Masiero, J. R., Mainzer, A. K., Grav, T., et al. 2011, ApJ, 741, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Pravec, P., Harris, A. W., Kursinak, P., Galad, A., & Hornoch, K. 2012, Icarus, 221, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Rieke, G. H., Blaylock, M., Decin, L., et al. 2008, AJ, 135, 6 [Google Scholar]
- Rickman, H., Fernández, J. A., & Gustafson, B.A.S. 1990, A&A, 237, 524 [NASA ADS] [Google Scholar]
- Shoemaker, E., Weissman, P., Shoemaker, C., 1994. in Hazards Due to Comets and Asteroids, eds. T. Gehrels, M. S. Matthews, & A. M. Schumann (University of Arizona Press), 313 [Google Scholar]
- Tancredi, G. 2014, Icarus, 234, 66T [NASA ADS] [CrossRef] [Google Scholar]
- Tancredi, G., Fernández, J., Rickman, H., & Licandro, J. 2006, Icarus, 182, 851 [Google Scholar]
- Tancredi, G., Roland, S., & Bruzzone, S. 2015, Icarus, 247, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, E., Eisenhardt, P., Mainzer, A., et al. 2010, AJ, 140, 1868 [NASA ADS] [CrossRef] [Google Scholar]
- Weissman, P. R., Asphaug, E., & Lowry, S. C. 2005, in Comets II, eds. M. C. Festou, H. U. Keller, & H. A. Weaver (Tucson: University of Arizona Press), 337 [Google Scholar]
- Wolters, S., & Green, S. 2009, MNRAS, 400, 204 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Determined geometric albedo pV of ACOs vs. Jupiter Tisserand’s parameter TJ. Big dots correspond to objets with determined η, while small dots correspond to ACOs with no η determination. The line at pV = 0.075 is the limit for a cometary-like albedo, according to Fernández et al. (2005). Only three JF-ACOs present a pV > 0.18 incompatible with a cometary origin. |
| In the text | |
 |
Fig. 2 Upper: beaming parameter distribution of JF-ACOs (red) and Damocloids (green) presented as normalized histograms; Lower: geometric albedo distribution of JF-ACOs (red) and Damocloids (green) with determined η. |
| In the text | |
 |
Fig. 3 Upper: beaming parameter vs. diameter distribution of JF-ACOs (filled circles) and Damocloids (open circles). A possible trend of η with D is shown. Lower: geometric albedo vs. diameter distribution of JF-ACOs and Damocloids. Large circles correspond to objects with η determined and small objects with not enough data to determine η. No correlation between pV and D is found. |
| In the text | |
 |
Fig. 4 Upper: beaming parameter vs. phase angle of JF-ACOs (filled circles) and Damocloids (open circles). A linear trend of η with θ is shown (see text); the red line is the correlation we found (η = 0.85 + 0.008 θ), the blue line is the linear regression (η = 0.79 + 0.011 θ) from Masiero et al. (2011). Lower: geometric albedo vs. θ distribution of JF-ACOs and Damocloids. Large circles correspond to objects with η determined and small objects with not enough data to determine η. No correlation between pV and θ is found. |
| In the text | |
 |
Fig. 5 Normalized histogram of η corrected to θ = 0 using the linear fit obtained in this paper. Both distributions are very similar. |
| In the text | |
 |
Fig. 6 Beaming parameter corrected to θ = 0 using the linear fit obtained in this paper vs. diameter. The apparent trend of η with D in Fig. 3 is not anymore observed in this plot. |
| In the text | |
 |
Fig. 7 Cumulative size distribution for JF-ACOs, Centaurs, and Damocloids (see text). |
| In the text | |
 |
Fig. 8 Cumulative size distribution for JF-ACOs and JFCs. |
| In the text | |
 |
Fig. 9 Value of the Kolmogorov-Smirnov test as a function of the cut-off diameter (lower plot) and the corresponding value of the maximum-likelihood exponent α (upper plot). |
| In the text | |
 |
Fig. 10 Ratio between the differential (red line) and the cumulative (blue line) number of JF-ACOs over the number of JFCs (corrected for incompleteness) for a given diameter (see text). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


