| Issue |
A&A
Volume 585, January 2016
|
|
|---|---|---|
| Article Number | A21 | |
| Number of page(s) | 16 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201526796 | |
| Published online | 09 December 2015 | |
Magnetic and gaseous spiral arms in M83⋆
1 Institute of Continuous Media Mechanics, Korolyov str. 1, 614061 Perm, Russia
2 MPI für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
e-mail: rbeck@mpifr-bonn.mpg.de
3 Department of Physics, Moscow State University, 117588 Moscow, Russia
4 School of Mathematics and Statistics, Newcastle University, Newcastle upon Tyne NE1 7RU, UK
5 XMM-Newton Science Operations Centre, ESAC, ESA, PO Box 78, 28691 Villanueva de la Cañada, Madrid, Spain
6 Joint ALMA Observatory, Alonso de Cordova 3107, Santiago, Chile
Received: 19 June 2015
Accepted: 1 October 2015
Context. The magnetic field configurations in several nearby spiral galaxies contain magnetic arms that are sometimes located between the material arms. The nearby barred galaxy M83 provides an outstanding example of a spiral pattern seen in tracers of gas and magnetic field.
Aims. We analyse the spatial distribution of magnetic fields in M83 and their relation to the material spiral arms.
Methods. Isotropic and anisotropic wavelet transforms are used to decompose the images of M83 in various tracers to quantify structures in a range of scales from 0.2 to 10 kpc. We used radio polarization observations at λ6.2 cm and λ13 cm obtained with the VLA, Effelsberg and ATCA telescopes and APEX sub-mm observations at 870 μm, which are first published here, together with maps of the emission of warm dust, ionized gas, molecular gas, and atomic gas.
Results. The spatial power spectra are similar for the tracers of dust, gas, and total magnetic field, while the spectra of the ordered magnetic field are significantly different. As a consequence, the wavelet cross-correlation between all material tracers and total magnetic field is high, while the structures of the ordered magnetic field are poorly correlated with those of other tracers. The magnetic field configuration in M83 contains pronounced magnetic arms. Some of them are displaced from the corresponding material arms, while others overlap with the material arms. The pitch angles of the magnetic and material spiral structures are generally similar. The magnetic field vectors at λ6.2 cm are aligned with the outer material arms, while significant deviations occur in the inner arms and, in particular, in the bar region, possibly due to non-axisymmetric gas flows. Outside the bar region, the typical pitch angles of the material and magnetic spiral arms are very close to each other at about 10°. The typical pitch angle of the magnetic field vectors is about 20° larger than that of the material spiral arms.
Conclusions. One of the main magnetic arms in M83 is displaced from the gaseous arms similarly to the galaxy NGC 6946, while the other main arm overlaps a gaseous arm, similar to what is observed in M51. We propose that a regular spiral magnetic field generated by a mean-field dynamo is compressed in material arms and partly aligned with them. The interaction of galactic dynamo action with a transient spiral pattern is a promising mechanism for producing such complicated spiral patterns as in M83.
Key words: magnetic fields / magnetohydrodynamics (MHD) / galaxies: ISM / galaxies: individual: M83 / galaxies: spiral / galaxies: magnetic fields
Maps of M83 at various wavelengths are available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/585/A21
© ESO, 2015
1. Introduction
M83 (NGC 5236) is the nearest barred galaxy and is well studied at all wavelengths, including polarized and unpolarized radio continuum emission that traces the interstellar magnetic field. Early polarization observations of M83 were performed by Sukumar et al. (1987) at the wavelengths λ92 cm, λ20 cm, and λ6.3 cm at a resolution of 33″ × 55″, which corresponds to about 1.4 × 2.4 kpc at the assumed distance to the galaxy of 8.9 Mpc (Sandage & Tammann 1974)1, so that 1′ ≈ 2.6 kpc. Significant polarized emission has been detected, indicating that the galaxy hosts an ordered magnetic field approximately aligned with the spiral arms. Sukumar & Allen (1989a,b) observed the galaxy with the VLA at λ20 cm at a resolution of 30″ × 70″ and found that the regions where polarized emission is strongest are located outside the prominent optical spiral arms. However, the resolution of these observations was too low and Faraday depolarization at this wavelength was too strong to reach firm conclusions about the spatial distribution of the ordered magnetic field and its relation to the material spiral pattern. Neininger et al. (1991) observed M83 at λ2.8 cm and found ordered fields along the central bar and between the inner spiral arms. The Faraday rotation measures between these wavelengths indicated a bisymmetric field structure possibly driven by the bar (Neininger et al. 1993). More recent observations at λ12.8 cm with the ATCA data show the radio continuum emission from the bar and spiral arms in detail (Figs. 1 and 2).
Our aim is to determine the parameters of the spiral arms in M83, as seen in different tracers, and to study their morphological relations. We are particularly interested in the relative positions of gaseous and magnetic arms, especially those of the large-scale magnetic field. Beck & Hoernes (1996) discovered that the ordered magnetic field in the galaxy NGC 6946, traced by polarized radio continuum emission, concentrates in well-defined magnetic arms, which are interlaced with the gaseous arms. The comparative morphology of the spiral patterns visible in different tracers was discussed by Frick et al. (2000) who confirmed the conclusions of Beck & Hoernes (1996) and determined such parameters as the pitch angle, width, and arm-interarm contrast for the magnetic arms and those seen in optical red light. A remarkable feature of the spiral pattern in NGC 6946 is that the phase shift between the magnetic and stellar/gaseous arms is more or less constant with radius. In other words, the two spiral arm systems have similar pitch angles and do not intersect in the part of the galaxy explored.
The phenomenon of magnetic arms may be common among spiral galaxies. It was first observed in the spiral galaxy IC 342 by Krause et al. (1989; see also Krause 1993). However, the relation between magnetic and gaseous arms in IC 342 (Beck 2015) and other galaxies is not as simple and clear-cut as in NGC 6946. Another example is provided by M51 where the ordered magnetic field is maximum at the spiral arms traced by dust lanes in some regions and displaced from them at other locations (Fletcher et al. 2011). When applying a wavelet analysis with anisotropic wavelets, the pitch angle of the spiral arms in M51 was found to vary with the galacto-centric radius (Patrikeev et al. 2006). Systematic shifts between the spiral arm ridges in gas, dust, and magnetic field indicate a time sequence that is consistent with the gaseous spiral arms causing compression that results in a stronger magnetic field.
To assess the origin, role, and significance of magnetic arms and their relation to material arms, one needs a sample of galaxies with different spiral patterns. This paper adds one remarkable galaxy to this sample. We performed a systematic analysis of the spiral patterns in M83 using ancillary data and new observations and isotropic and anisotropic wavelet analysis similar to that of Frick et al. (2001) and Patrikeev et al. (2006). Our quantitative methods are free of restrictive ad hoc assumptions, such as logarithmic spirals with a fixed number of arms and constant pitch angles. To make our analysis more comprehensive, we used polarized radio continuum observations at λ6 cm (Fig. 1) and λ13 cm (Fig. 2), which are first published here.
The main message from the analysis performed here is that the configuration of magnetic and material arms in M83 is partly similar to M51. In both galaxies, the magnetic arms overlap the material pattern in large areas but not everywhere. Of course, the numbers of arms, their pitch angle, and other quantitative parameters are specific for each galaxy.
2. The data
2.1. ATCA radio continuum observations at λ13 cm
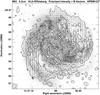 |
Fig. 1 Polarized radio continuum intensity (contours) and B vectors of M83 at λ6.17 cm, obtained by combining data from the VLA and Effelsberg telescopes, overlayed on an optical image from the Anglo-Australian Observatory by Dave Malin. The angular resolution is 22″. Faraday rotation of the B vectors has not been corrected, but is small because of the short wavelength and the low inclination of the galaxy. |
 |
Fig. 2 Polarized radio continuum intensity (contours) and B vectors of M83 at λ12.8 cm, observed with the ATCA telescope and overlayed onto an optical image from the Anglo-Australian Observatory by Dave Malin. The angular resolution is 22″. Comparison with Fig. 1 shows that the Faraday rotation of the B vectors is significant at this wavelength. |
We performed radio continuum observations of M83 with the Australia Telescope Compact Array (ATCA)2, consisting of six parabolic dishes, each of 22 m in diameter, forming an east-west radio interferometer.
We observed M83 with different baseline configurations (Table 1), each observation session lasting 12 h to achieve maximum uv coverage. The array was used in its five-telescope compact configuration ignoring the longest baselines (i.e., combinations with the Antenna 6) that are most prone to phase instabilities. The names of the configurations used in the table give approximately the largest baseline (750 m) used for this project. The full width at half maximum (FWHM) of the primary beam at λ13 cm is 22′, large enough to map the radio emission of M83 with an angular size of about 15′ at λ20 cm (Neininger et al. 1993). Also, the sampling of the shortest baselines is high enough to map the extended radio emission.
Each antenna receiver was used in the 128 MHz bandwidth continuum polarization mode. This bandwidth consists of 32 separately sampled channels. Linear polarization was measured using the orthogonal X and Y feeds on each antenna. Two frequencies (IFs) and the two polarization channels at each frequency were recorded simultaneously with 15 s time resolution.
For all observations the phase centre was set at 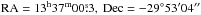 (J2000), which included an offset of 1′ south of the galaxy’s center, so as to place the observational phase center away from the bright nuclear emission of M83. This was done to check for systematic phase errors in the synthesis array that would be visible around the phase centre.
(J2000), which included an offset of 1′ south of the galaxy’s center, so as to place the observational phase center away from the bright nuclear emission of M83. This was done to check for systematic phase errors in the synthesis array that would be visible around the phase centre.
To calibrate the observations of M83, the phase calibrator QSO J1313−333 (unresolved at our baselines) was observed every half hour for about 5 min. The primary calibrator PKS 1934−638, observed for a short time during each synthesis run, was used as an absolute flux density calibrator to which all other measurements were scaled.
Data processing was done with the AIPS software package. The data of linearly polarized intensity were calibrated within the MIRIAD (Multichannel Image Reconstruction Image Analysis and Display) package. The calibrated visibility data of M83 were converted into maps of the Stokes parameters I, Q, and U. The self-calibration has improved the total-power image of Fig. 4 (Panel 8). The Q and U maps were combined into a map of polarized intensity P = (Q2 + U2)1/2 (Fig. 2 and Panel 10 of Fig. 4). The positive bias due to rms noise has been corrected for the inner parts of the galaxy where the noise is smallest and almost constant.
ATCA configurations used to obtain the λ13 cm radio continuum data of M83.
The polarized emission at λ13 cm is strongest in the outer regions of the galaxy. The typical degrees of polarization are 2% in the central region and 30% in the outer galaxy. In contrast to λ13 cm, the polarized emission at λ6.2 cm (Fig. 1) is strongest in the central region, confirming that Faraday depolarization is strongest in this region (Neininger et al. 1993). In both maps, the rms noise increases with increasing distance from the map’s centre.
Comparison of the position angles χ of the B vectors between Figs. 1 and 2 reveals a generally clockwise rotation at λ13 cm. We computed classical Faraday rotation measures, defined as 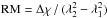 (Fig. 3). Classical RMs are not reliable in the inner part of the galaxy (<3′ radius) where Faraday depolarization is strong at λ13 cm. In the outer disk, RMs vary between about −60 rad m-2 and + 60 rad m-2. No systematic variation RM with azimuthal angle, a signature of a large-scale regular magnetic field in the disk, as in M51 (Fletcher et al. 2011) and in IC 342 (Beck 2015), and no traces of spiral arms are found, which is not surprising in view of the small magnetic field component of the disk field along the line of sight in a weakly inclined galaxy like M83. Furthermore, the strong depolarization at λ13 cm in the inner region leads to deviations of Faraday rotation angle Δχ from the λ2 law, so that classical RMs are not reliable and wide-band spectro-polarimetric data and application of RM Synthesis (Brentjens & de Bruyn 2005) are required to measure the large-scale fields.
(Fig. 3). Classical RMs are not reliable in the inner part of the galaxy (<3′ radius) where Faraday depolarization is strong at λ13 cm. In the outer disk, RMs vary between about −60 rad m-2 and + 60 rad m-2. No systematic variation RM with azimuthal angle, a signature of a large-scale regular magnetic field in the disk, as in M51 (Fletcher et al. 2011) and in IC 342 (Beck 2015), and no traces of spiral arms are found, which is not surprising in view of the small magnetic field component of the disk field along the line of sight in a weakly inclined galaxy like M83. Furthermore, the strong depolarization at λ13 cm in the inner region leads to deviations of Faraday rotation angle Δχ from the λ2 law, so that classical RMs are not reliable and wide-band spectro-polarimetric data and application of RM Synthesis (Brentjens & de Bruyn 2005) are required to measure the large-scale fields.
Still, the average rotation measure of ≃−11 ± 18 rad m-2 is useful as a measure of the rotation in the foreground of our Milky Way. The corresponding rotation angle is ≃−2° at λ6.2 cm and ≃−10° at λ13 cm. According to Oppermann et al. (2012), the foreground RMfg around the position of M83 is −34 ± 10 rad m-2. Since this value is an average over a much larger area, the difference could be due, for example, to Faraday rotation in the halo of M83 or to local variations in RMfg of the Milky Way.
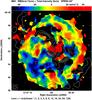 |
Fig. 3 Faraday rotation measures between λ6.17 cm and λ12.8 cm (colours) and total radio continuum intensity at λ6.17 cm (contours). The angular resolution is 30″. |
 |
Fig. 4 Maps of various tracers in M83: material tracers (H II, H I, CO, total neutral gas, warm dust, and cold dust) and tracers of the total magnetic field (mainly its small-scale part; I6 and I13) and its ordered component (P6, P13, and P6+P13), as indicated in the upper right corner of each frame. The coordinates are given in kpc, the intensity units are arbitrary units (H II), 1020 cm-2 (H I), K km s-1 (CO), 1020 cm-2 (gas), MJy/sterad (warm dust), Jy/beam (cold dust), μJy/beam (radio I6, I13, P6, P13, P6+P13). The axis scales are in kpc. |
2.2. APEX sub-mm observations of cold dust
The 870 μm data were obtained with the Large APEX Bolometer Camera (LABOCA; Siringo et al. 2009), a 295-pixel bolometer array for continuum observations, operated at the Atacama Pathfinder Experiment 12 m-diameter telescope (APEX)3 (Güsten et al. 2006) at Chanjantor, Chile. We observed M83 in June, August, and September 2008 in excellent weather conditions (the precipitable water vapour content ranged from 0.1 mm to 0.4 mm).
M83 was mapped in the spiral raster mode (in the five-of-the-dice pattern), providing a fully sampled map of the size 25′ × 25′ (compared to the LABOCA field of view of 11′ × 11′) in each scan. The total on-source integration time was about 11.5 h. The data were calibrated by observing Mars and Uranus together with the secondary calibrator J1246-258, and the flux scale was found to be accurate within 15%. The data were reduced using the BOA (BOlometer array Analysis) software (Siringo et al. 2009; Schuller et al. 2009). After flagging out bad and noisy pixels, the data were de-spiked, and correlated noise was removed for each scan. Then the 280 scans were combined (weighted by the squared rms noise) to produce the final map shown in the cold dust panel of Fig. 4.
2.3. Other data
In this paper the following data were used, referred to in Fig. 4 as indicated below:
-
H ii (Hα), ionized hydrogen: 3.9 m telescope of the Anglo-Australian Observatory (AAO) with the TAURUS II focal reducer, observed on 20 May 1990 (S. Ryder, priv. comm.);
-
H i, neutral hydrogen: VLA (Tilanus & Allen 1993);
-
CO, molecular hydrogen (traced by CO): SEST (Lundgren et al. 2004);
-
Gas, total neutral gas (H I + CO) (Lundgren et al. 2004);
-
Warm dust, infrared emission of warm dust at 12–18 μm: ISO (Vogler et al. 2005);
-
Cold dust, sub-mm emission of cold dust at 870 μm (Sect. 2.2);
-
I6, total radio continuum intensity at λ6 cm, combined from VLA and Effelsberg maps in total intensity (see Vogler et al. 2005, for details);
-
P6 and P13, linearly polarized radio continuum intensity at λ6 cm and λ13 cm (Figs. 1 and 2).
The infrared (warm dust) and H II maps provide a proxy to the star-formation rate in the starburst regions (mainly in the bar region) and elsewhere. Total radio continuum intensity has two components, a nonthermal (synchrotron) component, a tracer of the components of the total (turbulent + ordered) magnetic fields in the sky plane, and a thermal component, contributing about 12% in M83 at λ6 cm (Neininger et al. 1991), which is neglected in this paper.
Linearly polarized radio continuum intensity has a purely synchrotron origin. It is a tracer of ordered magnetic fields with a preferred orientation within the telescope beam if Faraday depolarization is small, which is generally the case in M83 at λ6 cm and also in the outer disks of M83 at λ13 cm.
The orientations of polarization “vectors” are ambiguous by multiples of 180°. As a consequence, the ordered magnetic fields as traced by linearly polarized emission can be either “regular” fields, preserving their direction on large scales, “anisotropic turbulent”, or “anisotropic tangled” fields with multiple field reversals within the telescope beam. To distinguish between these fundamentally different types of magnetic fields observationally, additional Faraday rotation data is needed. Faraday rotation is only sensitive to the component of the regular field along the line of sight. Owing to the irregular distribution of Faraday rotation measures in M83 (Fig. 3), we cannot distinguish between the components of ordered fields.
The maps of total emission at λ6 cm and λ13 cm (I6 and I13), representing the total magnetic field, are very similar, so that the λ13 cm map was not used for our analysis. The thermal contribution to the total radio emission of spiral galaxies at these wavelengths is generally less than 20% (Tabatabaei et al. 2007). The degree of polarization in M83 is largely below 20% at λ6 cm (Neininger et al. 1993) and even lower at λ13 cm (Fig. 2). The total radio emission at both wavelengths is thus dominated by unpolarized synchrotron emission from turbulent magnetic fields.
On the other hand, the maps of polarized emission at λ6 cm and λ13 cm (P6 and P13), representing the ordered magnetic field, are different. The signal-to-noise ratio is higher at λ13 cm because of the steep synchrotron spectrum, but Faraday depolarization is also stronger at this wavelength. As a result, the polarized emission at λ13 cm (Fig. 2) emerges mostly from the outer regions of the galaxy, while the lower sensitivity at λ6 cm (Fig. 1) restricts the detected polarized emission to the inner regions. The sum 1.91 P6 + P13 (P6+P13 in the following, see Fig. 4), where P6 is scaled by a factor of 1.91 to account for the average synchrotron spectral index of −0.9 (Neininger et al. 1993), is used to represent the polarized emission from the whole disk of M83. This procedure gives higher weights to the regions at intermediate distances from the centre that are seen in both polarization images, but this is not relevant to the purpose of this paper.
All the maps were smoothed to a common resolution of 12″, corresponding to 0.52 kpc at the assumed distance to M83, except for the CO map that has a resolution of 23″. As a consequence, the map of total neutral gas also has a resolution of 23″. All maps and their wavelet transforms presented here are in the sky plane: the galaxy is oriented nearly face-on, making a negligible correction for its inclination to the line of sight (24° – Tilanus & Allen 1993).
3. The method
In image analysis, wavelet-based methods are used to decompose a map into a hierarchy of structures on different scales. Wavelets are a tool for data analysis based on self-similar basis functions that are localized well in both the physical and wave-number domains. The localization of the basis functions in the physical space distinguishes the wavelet transform from the otherwise conceptually similar Fourier transform. One-dimensional and isotropic multi-dimensional wavelet transforms are based on the space-scale decomposition of the data. (In other words, the family of wavelets has two parameters, the location and the scale of the basis function.) Using the continuous isotropic wavelet transform, a 2D image is decomposed into a 3D cube of wavelet coefficients (obtained from the continuous wavelet transform by sampling it at a discrete set of scales) with the scale as the additional, third dimension. Cross-sections of the cube are slices that contain the image details on a fixed scale. As a result, the wavelet transform preserves the local properties of the image on all scales. If required, the original image can be synthesized from the cube by summing over all scales. (This procedure is called the inverse wavelet transformation.)
An anisotropic wavelet transform is the convolution of the image with a set of wavelets having different locations, sizes, and orientations. Such a family of basic functions is generated by the translations, dilations, and rotations of the basic wavelet. Applying the two-dimensional anisotropic wavelet transform to an image generates a four-dimensional data set that represents a space-scale-orientation decomposition. Fixing the space and scale parameters – based on some objective criteria – enables one to track the orientation of an elongated structure. An extended description of the continuum wavelet transform can be found in various books, for example, in Holschneider (1995). In extragalactic radio astronomy, galactic images have been analysed using isotropic wavelets by Frick et al. (2001), Tabatabaei et al. (2007, 2013a) and anisotropic wavelets by Patrikeev et al. (2006).
Both isotropic and anisotropic 2D wavelets can be constructed from a popular real-valued wavelet, the Mexican Hat (MH). In 1D, the MH is given by ψ(x) = (1−x2)exp(−x2/ 2). The MH can be generalized to 2D, leading to an isotropic basis function, 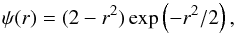 (1)where r = (x2 + y2)1/2. Another possibility is an anisotropic wavelet obtained by supplementing the 1D MH in one dimension with a Gaussian-shaped window along the other axis. The result is an anisotropic wavelet introduced by Patrikeev et al. (2006), called the Texan Hat (TH):
(1)where r = (x2 + y2)1/2. Another possibility is an anisotropic wavelet obtained by supplementing the 1D MH in one dimension with a Gaussian-shaped window along the other axis. The result is an anisotropic wavelet introduced by Patrikeev et al. (2006), called the Texan Hat (TH): 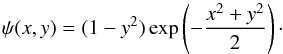 (2)This wavelet is sensitive to the structures elongated along the local x-axis. Rotation in the (x,y)-plane, x → (xcosϕ + ysinϕ), and y → (ycosϕ−xsinϕ) in Eq. (2), introduces the angle ϕ counted from the x-axis in the counterclockwise direction as the wavelet parameter. Finally, a set of basis functions of different sizes and orientations is obtained by applying both dilation and rotation to the basic wavelet. Since the TH is a symmetric with respect to rotation by 180°, ψϕ(x,y) = ψϕ + π(x,y), it is sensitive to the orientation of an elongated structure but not to its direction, which could be defined for structures in vector fields, such as magnetic field or velocity. The anisotropy of the TH makes it especially convenient in analyses of galactic spiral patterns. A detailed description of the technique and the illustration of how it works with test images and the spiral structure maps of the galaxy M51 were given by Patrikeev et al. (2006).
(2)This wavelet is sensitive to the structures elongated along the local x-axis. Rotation in the (x,y)-plane, x → (xcosϕ + ysinϕ), and y → (ycosϕ−xsinϕ) in Eq. (2), introduces the angle ϕ counted from the x-axis in the counterclockwise direction as the wavelet parameter. Finally, a set of basis functions of different sizes and orientations is obtained by applying both dilation and rotation to the basic wavelet. Since the TH is a symmetric with respect to rotation by 180°, ψϕ(x,y) = ψϕ + π(x,y), it is sensitive to the orientation of an elongated structure but not to its direction, which could be defined for structures in vector fields, such as magnetic field or velocity. The anisotropy of the TH makes it especially convenient in analyses of galactic spiral patterns. A detailed description of the technique and the illustration of how it works with test images and the spiral structure maps of the galaxy M51 were given by Patrikeev et al. (2006).
The continuous wavelet transform of a 2D map f(x), x = (x,y), is defined by 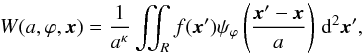 (3)where the integration is extended over the image area R, and the normalization factor a− κ allows one to fine-tune the interpretation of the wavelet transform: κ = 3/2 is for direct comparison of the wavelet spectra to the Fourier spectra, whereas κ = 2, used here, ensures that a power-law approximation to the wavelet spectrum has the same exponent as obtained from the second-order structure function (Frick et al. 2001). In the case of an isotropic wavelet, ϕ should be omitted in Eq. (3).
(3)where the integration is extended over the image area R, and the normalization factor a− κ allows one to fine-tune the interpretation of the wavelet transform: κ = 3/2 is for direct comparison of the wavelet spectra to the Fourier spectra, whereas κ = 2, used here, ensures that a power-law approximation to the wavelet spectrum has the same exponent as obtained from the second-order structure function (Frick et al. 2001). In the case of an isotropic wavelet, ϕ should be omitted in Eq. (3).
The maximum value of the wavelet transform W(a,ϕ,x) over all position angles ϕ for a given scale a, 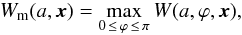 (4)can be used to quantify the anisotropic fraction of structures identifiable in the image. The orientation of the anisotropic structure is then given by the corresponding value of the position angle, ϕm, such that Wm = W(a,ϕm,x).
(4)can be used to quantify the anisotropic fraction of structures identifiable in the image. The orientation of the anisotropic structure is then given by the corresponding value of the position angle, ϕm, such that Wm = W(a,ϕm,x).
The distribution of the energy content of the signal, f2, on the scales and at the orientations can be characterized by the wavelet power spectrum, defined as the energy density of the wavelet transform on scale a and at orientation ϕ integrated over the image,  (5)The isotropic wavelet spectrum is obtained as
(5)The isotropic wavelet spectrum is obtained as 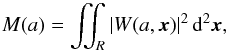 (6)where the wavelet coefficients W(a,x) are obtained using the isotropic wavelet (1).
(6)where the wavelet coefficients W(a,x) are obtained using the isotropic wavelet (1).
4. Results
We applied the MH and TH wavelet transforms to the maps of M83 presented in Sect. 2 with the aim of identifying structures (and their orientation, if appropriate) revealed in various tracers with particular emphasis on the spiral structure.
4.1. Isotropic wavelets: spectra and correlations
 |
Fig. 5 Wavelet power spectra of the M83 images, obtained with the isotropic 2D Mexican Hat from bottom to top: H II, H I, CO, total neutral gas, warm dust, cold dust, total synchrotron intensity at λ6 cm, polarized intensity at λ6 cm, polarized intensity at λ13 cm, and a weighted sum of the polarized intensities at λ6 cm and λ13 cm defined in Sect. 2.3. All the spectra have been multiplied by various factors chosen to avoid overcrowding of the curves: what matters is the relative distribution of the wavelet spectral power between scales in a given image rather than the relative power in different images. Error bars are evaluated from the variance of the sample mean. |
We start our analysis with the wavelet spectra M(a) calculated for each tracer using the isotropic MH, Eq. (1). Our aim here is to compare the dominant spatial scales of the different maps, i.e., the scales at which the wavelet power spectra have a maximum. The magnitudes of the maxima are not informative because they depend on the signal intensities measured in different units in some maps. To present the results in one plot, we multiplied each spectrum by a factor chosen to avoid excessive overlapping of the curves. The isotropic MH power spectra are shown in Fig. 5.
The spectra reveal that the distribution of the ISM seen in various tracers is characterized by certain dominant scales4. The maximum at the largest scales corresponds to the size of the galaxy as a whole, 2a ≈ 10′ in both polarized emission (either λ6 cm or λ13 cm) and H I. The images of I6, dust, total neutral gas, and H II are more compact, and the corresponding spectral maximum appears on smaller scales, 2a ≈ 5′–7′. The decrease in the spectra on the largest scales occurs due to the large void areas in the signal maps.
Maxima on smaller scales are produced by structures inside the galactic image, bar, and spiral arms. A maximum on the scale 2a ≈ 0.7′ is prominent in I6, dust, CO, and total neutral gas. The spectrum of H II also has a local maximum on this scale, but it is much broader and extends down to 2a ≈ 0.4′. The second maximum of the polarized intensity spectrum at λ6 cm (P6) is at 2a = 0.4′, probably reflecting sharp features in the bar. Remarkably, the spectrum of the other magnetic field tracer, the polarized emission at λ13 cm (P13), is quite different when it grows with a reaching a weak maximum at 2a ≈ 3′. The P13 map contains large structures that are absent in the other maps. This scale can be related to the outer, broad spiral arms. The H I spectrum is nearly flat on small scales with a weak, broad maximum at 0.2′ < 2a< 1′. The values of the peak scales should be considered with an uncertainty of about 20% because of the limited scale resolution of the wavelet.
The wavelet cross-correlation between two maps (1 and 2) is defined as (see Frick et al. 2001) ![\begin{equation} r_w(a) = \frac{\iint_R W_1(a,\vec x) W_2(a,\vec x) \,\dd^2 \vec x}{[M_1(a)M_2(a)]^{1/2}} , \label{cor_w} \end{equation}](/articles/aa/full_html/2016/01/aa26796-15/aa26796-15-eq103.png) (7)where the integration is carried over the map area. This quantity, designed to characterize scale-by-scale correlations in Maps 1 and 2, is sensitive to structures in the two maps that have similar scales and a similar position, but may not overlap as do, for example, spiral arm segments with a relative shift in position. The standard cross-correlation function fails to detect such subtle correlations, whereas examples presented by Frick et al. (2001) demonstrate the efficiency of the wavelet cross-correlation.
(7)where the integration is carried over the map area. This quantity, designed to characterize scale-by-scale correlations in Maps 1 and 2, is sensitive to structures in the two maps that have similar scales and a similar position, but may not overlap as do, for example, spiral arm segments with a relative shift in position. The standard cross-correlation function fails to detect such subtle correlations, whereas examples presented by Frick et al. (2001) demonstrate the efficiency of the wavelet cross-correlation.
The wavelet correlations have been calculated for all pairs of tracers in the whole scale range available. Figure 6 shows the cross-correlations of the total neutral gas and all other tracers in the upper panel, whereas the lower panel is for the scale-wise cross-correlation between the polarized emission P6+P13 and all other tracers.
 |
Fig. 6 Wavelet cross-correlations between the M83 maps as a function of scale (in arcmin). Correlations between the total neutral gas and other tracers (H II, H I, warm dust, I6, P6+P13) are shown in the upper panel and correlations of the polarized emission with other tracers in the lower panel. |
The tracers of matter (gas and dust) are more or less well correlated with each other. Not surprisingly, since they are not independent, this is true at all scales for the CO and the total neutral gas. Dust, H II and H I have maximum correlation with the total neutral gas near the scale 0.7−0.9′ (1.8–2.3 kpc). The correlation coefficient for dust and gas is about 0.7, while the correlation coefficient of H I and the total gas is below 0.4). In a striking contrast, the ordered magnetic field tracers are almost uncorrelated with the total neutral gas and dust on scales up to 2′ and even exhibit some anticorrelation (e.g. gas versus P13 on the scale of about 2′ and P6+P13 versus H II on the scale of about 1.5′).
The correlations between particular tracers can be summarized as follows. (We do not show all the plots.) The correlation between the total radio continuum (I6) and infrared (warm dust) intensities is high on all scales, similar to the situation in NGC 6946 (Frick et al. 2001; Tabatabaei et al. 2013b) and M33 (Tabatabaei et al. 2013a); this can be explained by the contributions of thermal radio emission and synchrotron emission from magnetic fields that are closely related to molecular gas (Niklas & Beck 1997). The correlation between the radio synchrotron and infrared intensities is known to be worse on small scales due to the propagation of cosmic-ray electrons (Tabatabaei et al. 2013a), so that the correlation coefficient is expected to be below 0.5 on scales that are smaller than the cosmic ray diffusion scale along the large-scale magnetic field of about 0.2′ or 0.5 kpc. The ratio of the ordered and turbulent field strengths q ≈ 0.5 follows from the average degree of synchrotron polarization of p ≈ 20% in the M83 disk at λ6 cm using the relation between p and q for a uniform cosmic-ray distribution (Eq. (2) in Beck 2007; under perfect equipartition between cosmic rays and magnetic field, q ≈ 0.43). With the former value of q, M83 fits the relation between the parallel diffusion scale and the degree of field ordering found by Tabatabaei et al. (2013a). A more detailed analysis would need a separation of synchrotron and thermal radio emission, which is beyond the scope of this paper.
The correlation between H II and infrared (warm dust) intensities is also high on all scales, except for a minimum around 2′, probably because of the bar that is bright in the infrared but weak in H II.
The I6, dust, and H II maps display high correlations on small scales (rw> 0.5 for 0.2′ < 2a< 1′), where correlations of the other tracers are weak. The maps of polarized intensity P6 and P13 display quite different properties. The P6 map shows little correlation with most tracers on all scales, except the largest ones, and an anticorrelation with H I on the scale 2a ≈ 2.5′. All correlations with P13 show an absence of correlation on small scales and have a deep minimum (anticorrelation) on the scale of about 3′ with H II, dust, CO, and I6 (but not with H I). We note that P13 and H I are the two maps with emission distributed over the largest areas, but just this pair of maps gives the minimum correlation over the whole range 0.2′ < 2a< 4′ (neither correlation nor anticorrelation). The highest anticorrelation (rw ≈ −0.4 is found between H II and P13 at 2a ≈ 3′. The H II and P6 have a weaker anticorrelation, r ≈ −0.2 at 2a ≈ 1.7′. The anticorrelation with H II around this scale indicates a general shift between the optical and magnetic spiral arms, similar to the shift in NGC 6946 (Frick et al. 2001).
On scales of ≤0.7′, corresponding to the maximum in the spectrum of P6, the emission emerges from the inner part of the galaxy. In P13, however, the emission from the central part of the galaxy is strongly suppressed by Faraday depolarization, and the larger scales attributed to the outer parts of the galaxy dominate in the wavelet spectrum. Thus the anticorrelation with P13 is probably the effect of depolarization.
4.2. Material versus magnetic patterns
A more detailed comparison of the spatial patterns in the interstellar matter and magnetic fields is facilitated by the use of the anisotropic wavelet introduced in Sect. 3. It is convenient to introduce a simple reference pattern of the dominant material structures shown in Fig. 7 that includes two spiral arms, labelled Arms I and II, emerging from the opposite ends of the bar shown by a thick straight line in the figure. Each arm is divided into three segments, a, b, and c, because some of them are not visible in all the tracers considered here.
 |
Fig. 7 Schematic representation of the spiral arms and bar (thick solid line) in M83. Each of the two arms (labelled I and II) is separated into three sections, labelled as a, b, and c and shown as solid, dotted, and solid lines, respectively. The background image represents the cold dust distribution. The axis scale is in kpc, assuming the distance to M83 of 8.9 Mpc. |
 |
Fig. 8 Anisotropic wavelet transforms of the total neutral gas on the scales 2a = 0.7′ (top) and 1.4′ (bottom). The wavelet orientation angles are shown by bars whose lengths are proportional to the magnitudes of the wavelet transform. The axis scale is in kpc. |
An anisotropic wavelet transform is useful on those scales where the spatial structures are clearly elongated, i.e., on the scales comparable to and exceeding their thickness, 0.5′ < 2a< 2′ in the case of M83. Figure 8 shows the anisotropic wavelet transform of the total neutral gas distribution obtained with the TH wavelet. A similar map for the polarized intensity P6 is shown in Fig. 9. We selected two representative scales to show in these figures, 2a ≈ 0.7′ and 1.4′ as suggested by the power spectra of Fig. 5. The maximum value Wm of the wavelet transform over all position angles ϕ on a given scale is shown as colour-coded, whereas the corresponding wavelet orientation angle ϕm is indicated with a bar.
Figures 8 and 9 demonstrate clearly that the distribution of polarized radio emission is more structured than that of the template pattern (Fig. 7). On the smaller scale, 0.7′, the bar is prominent in the total neutral gas, whereas the polarized structures are offset from the bar axis and are hardly aligned with it. Their overall pattern is similar to the barred galaxy NGC 1097, where it suggests the amplification of magnetic fields by compression and shearing gas flow in the dust lanes displaced from the bar axis (Beck et al. 2005).
On the larger scale, 1.4′, most features visible on the smaller scale remain, although some smaller structures of the upper panel have merged on this larger scale. The P6 map has a well-pronounced long arm extended from west to north in the outer part of the image (Part c of Arm I) apparently merging with Arm II in the east, but this appears to be an artefact of stronger, positively biased noise in polarized emission at large distances from the map centre that affects the wavelet transform.
The patterns isolated with the anisotropic TH wavelet in the material tracers are compared with those in the ordered magnetic field in Fig. 10 where the total neutral gas density is chosen as the reference variable. In all the panels, the solid line corresponds to 20% of the maximum intensity in the arm region5. Arm II is very visible in all three segments (IIa, IIb, and IIc) in the gas distribution. The CO distribution on this scale is very similar to that of the total neutral gas (unsurprisingly, because molecular gas dominates over H I in the inner part of the galaxy) and is not shown here. The only difference of the CO map is that the segments IIa, IIb, IIc are separated from each other by small gaps. The warm and cold dust have the same pattern as the gas, with the exception of the segment IIc. The H II image contains only the inner part of Arm II, while H I clearly displays the whole of Arm II. Concerning Arm I, only the first segment Ia is visible in gas, CO, and warm and cold dust. Its outer part Ic is prominent in the H I image but not in the other material tracers. To conclude, there are no discernible differences in the appearance, in various material tracers, of the bar as well as of Arms Ia, IIa, and IIb, whereas Arms Ib, Ic and IIc appear different in different material tracers.
The tracers of the total magnetic field, I6 and I13, are presumably dominated by small-scale, random magnetic fields. The structures in I6 and I13 are very similar to those in H II and the warm and cold dust, with the bar and Arms Ia and IIa being prominent. The spiral segments Ib and Ic are absent in I6 and I13.
The patterns in P13 and the combined P6+P13 are similar to each other on this scale with prominent outer spiral segments Ic and IIc, as well as Arm Ib. As we quantify below, the ridges in radio polarization are noticeably different from the gas ridges in the bar, often being shifted with respect to each other. Arm IIb is not visible in polarized radio emission, whereas Arm IIa is shifted with respect to IIa of the total neutral gas. The segment Ib occurs in P6+P13, thus delineating the whole Arm I. Arm IIc largely overlaps the corresponding gas arm in both P6 and P13. Remarkably, the polarized Arm IIa is displaced towards the outer galaxy with respect to the corresponding gas arms by 2–3 kpc, whereas Arm Ia is shifted inwards by a comparable magnitude. The mutual displacements of the gaseous and polarized arms are, on the one hand, systematic and coherent over several kiloparsecs along the arms, but on the other hand, they take different directions in different arms even in the same range of galacto-centric radii. Arm IIa (south-east of the galaxy, the “Gas” and “P6+P13” panels) shows the clearest picture of a polarized arm being parallel to the gaseous arm along about 8 kpc. On the other hand, in Arm IIc (the next outer arm in the south-east) a polarized arm overlaps the gaseous arm nearly perfectly at least along 12 kpc, and only its end deviates outwards from the gaseous arm. This implies that the mechanisms producing such a displacement are more complex than just advection of a large-scale magnetic field from the gaseous arms by the rotational velocity or the enhanced tangling of a large-scale magnetic field within the gas arms. Furthermore, Arms Ib and Ic appear mainly in the radio polarization data but not in the total radio intensity (dominated by small-scale magnetic fields) and are visible in only one material tracer, H I. The physical nature of the magnetic Arms IIc, Ib, and Ic is likely to be different from Arms I, IIa, and IIb (see Sect. 5). A more detailed comparison of the gaseous and magnetic spiral arms and their segments arms is presented in the next section.
 |
Fig. 10 Anisotropic (TH) wavelet transforms of various tracer distributions at 2a = 1′ are shown (dotted contour at 20% of the maximum intensity), together with the similar wavelet transform of the total neutral gas distribution (solid contour at 20% of the maximum intensity). The axis scale is in kpc. |
 |
Fig. 11 Elongated structures on the scale 2a = 1′ of the anisotropic wavelet transform in the tracer indicated in the upper right corner of each frame are shown with the solid contour drawn at 20% of the maximum intensity in that tracer in the arm region. Red dashes, representing the B vectors of the polarized radio emission at λ6 cm, with length proportional to the polarized intensity, are shown in the same regions. |
4.2.1. The orientations of the ordered magnetic field and the spiral arms
The wavelet representation allows us to investigate anisotropic structures on any given scale. Figure 11 helps for appreciating the complicated relation between the orientation of magnetic vectors and the orientation of structures in the distribution of the various tracers of spiral arms. The wavelet coefficients show the intensity of the signal that is smoothed over a domain of scale a. Thus, gaps in the original maps seen on smaller scales can be filled on larger scales.
The magnetic vectors (uncorrected for Faraday rotation) in the magnetic arms, shown in the lower left-hand panel of Fig. 11, are well (and yet imperfectly) aligned with the arms of polarized emission, while the magnetic vectors in the bar region are noticeably inclined to its axis, especially near the ends of the bar.
The near-alignment of magnetic field with the spiral structures requires quantifying. For this purpose, we compared the orientations of the magnetic field vectors (polarization angles) with the orientations of the anisotropic (elongated) structures on any given scale. Figure 12 shows the normalized angular power spectra M(a,ϕm) of the pitch angles ϕm of the structures on a fixed scale 2a = 1′ in the distributions of polarized intensity P6, labelled as “P6 pos.a”, and of the interstellar gas, i.e. the total neutral gas, “Gas pos.a”, and molecular gas, “CO pos.a”. Here, ϕm is measured from the tangent to the local circumference in the plane of the sky6. The spectra of Fig. 12 characterize the orientation of the ridges in the distributions of interstellar gas and polarized radio intensity on average over the corresponding region, the whole galaxy in the upper panel, and the spiral arm region in the lower panel.
Figure 12 also presents the angular spectrum M(ϕp) of the magnetic pitch angles ϕp derived from the polarized intensity at λ6 cm. This spectrum is defined as the integral of polarized intensities over all positions where the pitch angle of the magnetic field vectors at λ6 cm, χ, is equal to a given ϕp: 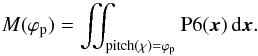 (8)The angle ϕp is also measured from the local circumference, thus representing the magnetic pitch angle (uncorrected for Faraday rotation, which is small at λ6 cm, and for the inclination of the galaxy to the line of sight, which is only modest).
(8)The angle ϕp is also measured from the local circumference, thus representing the magnetic pitch angle (uncorrected for Faraday rotation, which is small at λ6 cm, and for the inclination of the galaxy to the line of sight, which is only modest).
 |
Fig. 12 Angular wavelet power spectra of pitch angles ϕ on the scale 2a = 1′ normalized to unit maximum: the pitch angles ϕm of the structures of the polarized intensity P6 (black dotted), neutral gas (green), and CO (blue dashed). The spectrum of the pitch angles ϕp of the magnetic field vectors defined in Eq. (8) is shown with the red dot-dashed curve. The pitch angles are measured clockwise from the tangent to the local circumference on the sky plane. The upper panel shows the spectra for the whole galaxy, while the lower panel shows them for the region of spiral arms (i.e. with the bar region excluded). |
The most pronounced difference between the spectra shown in the two panels of Fig. 12 is in the position angles of the anisotropic CO structures dominated by the bar that provides a strong maximum at pitch angles ϕm of about 70°−80° (90° would correspond to a structure aligned along the radial direction). When the bar is excluded, this peak becomes twice lower than the other CO maximum centred at about 13°, with a half-width at half-maximum (HWHM) of 9° that arises from the spiral arms. The sharp peak in the spectrum for the total gas density is due to the gaseous spiral arms with a well-defined pitch angle ϕm of about 8° with a HWHM of 6°. We note that the pitch angles of the spiral arms in the total gas distribution show somewhat less scatter (narrower spectral maximum) than those in CO. The difference between the positions of the maxima in CO and the total gas is due to smaller pitch angles of spiral structures in the outer galaxy, which are traced by HI, while CO traces spiral features with larger pitch angles in the inner galaxy. A decrease in spiral pitch angles with increasing radius has been observed in many galaxies (e.g. Beck 2007, 2015; Van Eck et al. 2015).
The lower panel of Fig. 12 shows clearly that the distribution of the pitch angles of the structures ϕm prominent in polarized intensity (magnetic arms) is almost identical to the distribution of the CO structures: Most of the CO emission and polarized intensity are localized in regions with ϕ< 30°. The pitch angles of the polarization structures are only slightly larger (the peak pitch angles at ϕ ≈ 14°) than those of the total gas. It is notable that the pitch angles of the magnetic field vectors ϕp are concentrated at significantly different values, 20°–35° with a maximum at ϕ ≈ 26° and the HWHM of 15°. This difference cannot be explained by Faraday rotation in the foreground of the Milky Way, which is only about −2° at λ6 cm, as estimated from the B vectors at λ6 cm and λ13 cm (see Sect. 2.1).
To summarize, the peak pitch angles ϕm of the total gas and magnetic spiral arms are very close to each other at about 10°, whereas the magnetic field vectors have a different peak pitch angle ϕp of about 26° ± 15°, where the ranges represent the HWHM of the spectral maxima. The local differences between the pitch angles of the magnetic field vectors and the spiral arms can still be quite large (as is obvious from Fig. 14).
 |
Fig. 13 Position angles of the elongated structures of the total neutral gas (blue bars), obtained from the anisotropic wavelet transform on the scale 2a = 1′, and magnetic polarization angles (red bars); the isocontour of the total gas intensity at 20% of its maximum in the arms is shown as a dashed line. The upper panel shows the data points where the difference between two angles is between 3° and 33° with a positive value meaning a clockwise rotation with respect to the gas structure), as suggested by the relative shift of the corresponding peaks in the angular spectra (Fig. 12), while the lower panel shows the remaining data points. The axis scales are in kpc. |
 |
Fig. 14 As in Fig. 13, but with blue bars showing the position angles of the structures of the polarized intensity P6, the isocontour of P6 at 20% of its maximum intensity shown as dashed. The upper and lower panels show data points with the difference between the angles in the range −1° to 29° and out of this range, respectively. |
To confirm the identification of the regions that contribute to the maxima in the angular spectra of Fig. 12, we show in Fig. 13 the polarization vectors of the ordered magnetic field position angles of the gas structures in the regions that contribute to the maxima in their angular spectra. The upper panel shows the arm fragments where the orientation of the ordered magnetic field differs by 18° ± 15° from the local axis of a material arm, which is the case in most parts of Arms I and II.
The lower panel demonstrates that the two angles differ significantly and systematically in the bar, apart from localized regions elsewhere in the galaxy. Such deviations occur where the position angle of the gas arm turns sharply (arm sections Ib and IIb). This is a hint that different mechanisms can be responsible for the magnetic field alignment along the material arms in different parts of the galaxy.
 |
Fig. 15 Locations of the elongated structures, on the scale 2a = 1′, of the combined polarized radio emission (P6+P13; black isocontour at 20% maximum intensity) and in the distributions of H I (top panel) and warm dust (bottom panel), respectively, shown in colour and as dotted contours at 20% of its maximum intensity. The axis scale is given in kiloparsecs assuming the distance to M83 of 8.9 Mpc. The dashed ellipse shows the corotation radius. |
The analysis of the relative orientations of magnetic pitch angles and those of spiral arm segments is complicated by the fact that the magnetic and material arms often do not overlap, even if parallel to each other. In order to improve the comparison we take advantage of the fact, quantified above, that the pitch angles of the spiral arms in CO and P6 are very similar to each other, and present in Fig. 14 the polarization and position angles obtained from the magnetic tracer P6, which is the polarized intensity at λ6 cm. Now the area where the comparison is possible is substantially larger than in the previous figure, confirming that the ordered magnetic field is well aligned with the spiral arms along most sections of the Arms I and II (as discussed above, the two orientations differ systematically by an angle of about 10° which is difficult to discern visually), while there is little or no alignment in the bar region.
The reason for the misalignment in the bar region in Fig. 14 (bottom) is a structure in P6 that appears on large scales due to merging of smaller structures (Fig. 9 bottom). The existence of a smaller structure becomes clear from comparing P6 from Fig. 4 with P6 from Fig. 9. In the unfiltered map (Fig. 4), P6 is concentrated in two narrow features with a position angle of about 50°, running roughly parallel to the bar visible in I6, gas, and dust, with the polarization angles (Fig. 1) roughly aligned with them. At both ends of the bar, the position angles of the structures, as well as the polarization angles, jump by about 70°, to become oriented roughly in the north-south orientation. Most of these features are lost in Fig. 9 because the wavelet transform averages over small structures. In Fig. 9 bottom, the strongest wavelet structure near the centre is a combination of many narrow features in the original image and no longer resembles the bar. Not surprisingly, the structure position angles are between 80° and 130°, so completely different from those of the polarization angles.
H I and the combination of polarized emission at λ6 cm and λ13 cm cover the largest part of the galaxy and thus reveal the most extended spatial distributions. Only these two maps allow us to identify both arms along their whole lengths. Other tracers contain lacunae and often exhibit only short segments of arms, especially in the inner galaxy (e.g. in the H II map). The wavelet-filtered image of H I and an isocontour of combined polarized radio emission, P6+P13, are shown in Fig. 15 on the scale 2a = 1′. The spiral arms are very visible in both tracers. In H I, there are two bridges with large pitch angles (but not radial), which are seen in both tracers (Fig. 4). The figure supports the conclusion that all tracers show Arm II at the same positions, while the positions of Arm I display a systematic relative shift: the magnetic arm is shifted with respect to the H I arm, inwards in the inner galaxy (arm segment Ia) and outwards in the outer galaxy (Ib and Ic).
5. Discussion
A traditional approach to quantifying galactic spiral structures and estimating their pitch angles is based on the Fourier transform of the light (or any other suitable variable) distribution in azimuth (Puerari & Dottori 1992, and references therein). Such a spectral analysis involves a fit to an average pitch angle for a whole galaxy assuming the logarithmic-spiral shape of the arms. Given the complex structure of the spiral patterns with numerous branches and strong spatial variations of the pitch angle, etc., even in galaxies with grand-design patterns such as M51, the global approach to quantifying the spiral structure is rather restrictive. Puerari et al. (2014) attempted to improve the method in this respect by applying it to relatively narrow annuli rather than to a galaxy as a whole. However, a better way to resolve these problems would be to employ wavelet transforms, as we do here (see also Frick et al. 2000, 2001; Patrikeev et al. 2006). The wavelet-based approach is free of any model assumptions about the shape of the spiral arms, and their segments (such as a perfect m-armed pattern or a logarithmic spiral) allows for different widths of arms and inter-arm regions and works equally well for any structures, whether spiral, azimuthal, or radial.
5.1. Magnetic arms
M83 has well-defined magnetic arms where the ordered magnetic field is concentrated, which is visible as structures in polarized radio emission of about 1′ in width. Similar to the galaxy NGC 6946, the polarized arms appear to be more or less independent of the spiral patterns seen in other tracers, since they are displaced from the latter in large areas by about 20° along the azimuth on average in the mean shortest distance. This does not exclude a physical relation between them, which is suggested by their close spatial proximity and the fact that their axes are well aligned with each other. The mutual location of the gaseous and magnetic arms is diverse, with magnetic Arms Ib, Ic, and IIa extended along the inner edge of the corresponding gaseous arms, but magnetic Arm IIb and the inner part of Arm IIc superimposed on the corresponding gaseous arms (Figs. 8, 9, and 15).
This diversity suggests that a variety of physical mechanisms are responsible for the formation of the magnetic arms, possibly acting simultaneously. A remarkable feature of the large-scale galactic magnetic field that manifests itself as magnetic arms displaced from the gaseous arms is that its strength is greater where the gas density is lower. This may imply that the large-scale galactic magnetic fields are not frozen into the interstellar gas and thus need to be continuously replenished, presumably by the galactic mean-field dynamo action (Shukurov 2007). The only apparent alternative is that magnetic arms represent slow MHD density waves (Lou & Fan 1998, 2003; Lou & Bai 2006, and references therein). However, mean-field dynamo equations in a thin disk, either linear or nonlinear, do not admit wave-like solutions under realistic conditions even when generalized to include the second time derivative of the magnetic field (the telegraph equation; Chamandy et al. 2013, 2014). It cannot be excluded that more advanced nonlinear dynamo models, especially those with the direct coupling of the induction and Navier-Stokes equations, will reveal a new class of dynamo solutions reminiscent of the slow MHD waves.
There are several physical processes that can contribute to the formation of magnetic arms displaced from the gaseous arms:
-
1.
The mean-field dynamo action can be suppressed within the gaseous arms by either a presumably enhanced fluctuation dynamo driven by stronger star formation (Moss et al. 2013) or a stronger galactic outflow driven by stronger star formation (Sur et al. 2007; Chamandy et al. 2015; see also Shukurov 1998). A generic problem of such mechanisms is that they produce the desired displacement only within a few kiloparsecs of the corotation radius of the spiral pattern (Shukurov 1998; Chamandy et al. 2013, 2014), because the residence time of a volume element within a gaseous spiral arm is shorter than the dynamo time scale of order 5 × 108 yr at large distances from the corotation. A few mechanisms, briefly discussed below, have been suggested to produce magnetic arms displaced from the gaseous ones far away from the corotation radius.
-
2.
The model by Moss et al. (2013, 2015) assumes that a large-scale regular field is generated everywhere in the disk, while a small-scale dynamo injects turbulent fields only in the spiral arms. This gives polarization arms between the gaseous arms at all radii, but with pitch angles of the polarization structures and pitch angles of the polarization vectors that are significantly smaller than those of the gaseous arms, in contrast to the observations discussed in this paper.
-
3.
A finite mean-field dynamo relaxation time (a temporal non-locality of the mean electromotive force) does produce, under realistic parameter values, a displacement of up to 30° in azimuth at the corotation radius, with magnetic arms lagging behind the gaseous ones (Shukurov 1998; Chamandy et al. 2013). The ridges of magnetic arms thus produced have a systematically smaller pitch angle than do the gaseous spirals because of the action of differential rotation on the large-scale magnetic field. The pitch angle of the ordered magnetic field in M83 is, on average, larger than that of the material arms, contrary to this model (which, however, has not been specifically developed for M83).
-
4.
A different approach to the problem of displaced magnetic and gaseous spiral patterns emerges if the material pattern is not a solidly rotating structure, as suggested by the density wave theory, but rather a transient and evolving system of spiral arm segments produced by a bar, galactic encounters, local instabilities, etc., and wound up by the galactic differential rotation. As shown by Chamandy et al. (2013, 2014, 2015), the mechanisms mentioned above are relieved of their problems in this case, producing diverse interlaced or intersecting magnetic and gaseous spiral patterns depending on the relative contribution of each mechanism.
-
5.
Compression of the both the large-scale and turbulent magnetic fields in the gaseous arms enhances polarized synchrotron emission within them, also by amplifying the anisotropy of the random magnetic field (see Sect. 8 of Beck et al. 2005; Patrikeev et al. 2006; Fletcher et al. 2011). The resulting ridges of enhanced polarized emission are expected to be located at the inner edge of the material arms inside the corotation radius and at the outer edge outside the corotation. Offsets between the spiral arm ridges in various tracers, of a few 100 pc, are predicted by the density wave theory (Roberts 1969) and were detected in a wavelet analysis of M51 data (Patrikeev et al. 2006). Compression of a turbulent field aligns the magnetic arm along the shock front, while compression of an ordered field changes the pitch angle of the polarization angle to become more similar (but not identical) to the pitch angle of the material arm.
Most of these mechanisms (except those of Moss et al. 2013, 2015) are sensitive to the location of the corotation radius since advection of magnetic fields from the gaseous arms would unavoidably affect the relative positions of the magnetic and gaseous arms. It has been suggested that the corotation radius in M83 is about 2.3′–2.4′ (Kenney & Lord 1991; Rand et al. 1999; Hirota et al. 2014), about 6 kpc at a distance of 8.9 Mpc. As usual in barred galaxies, this radius is only slightly larger than the major axis of the bar. This does not allow us to clarify the role of the corotation radius in the formation of magnetic arms using M83 as an example.
The magnetic Arm IIb–IIc coincides with the corresponding material arm (Fig. 15). This may still be consistent with the mechanisms (3) or (4). The similarity of the magnetic pitch angles as compared to the pitch angles of the gas arms (Figs. 12 and 13) do not lend support to the mechanism (2). A regular field with a spiral pattern generated by a mean-field dynamo is possibly compressed and partly aligned in density waves interacting with the magnetic field. Another possibility may be associated with a coupling between magnetic fields and density waves.
Several narrow spiral arm segments are prominent in the dust emission in the inner galaxy (Fig. 4), which is indicative of compression. These features are visible in the anisotropic wavelet transform maps on the scale 0.7′ (Figs. 8 and 9, top panels). The features in total neutral gas and ordered magnetic field coincide with them in the west and north of the galaxy. Density wave models predict an offset of a few 100 pc between such features, corresponding to 0.1′, which cannot be resolved with the present observations. However, Patrikeev et al. (2006) find evidence of such offsets in the galaxy M51.
The magnetic Arm Ia–Ib is displaced from the corresponding material arm (Fig. 15). Its properties could be consistent with the mechanism (4) if the corotation radius of M83 is located at about 7 kpc at the assumed distance (Lundgren et al. 2004), and this is apparently the case. However, the displacement is too large to be consistent with density-wave compression. Alternatively, the whole of Arm I may be generated by the mean-field dynamo via the mechanisms (1)–(3). A rather good alignment of the polarization angles with the position angle is seen in the magnetic Arm I (Fig. 14, top panel). Such an alignment is facilitated by the mechanism (4).
An additional aspect of the magnetic field configuration in M83 is related to the presence of the bar. Although the bar of M83 is shorter (about 7 kpc) than that of NGC 1097 (of about 16 kpc), the ordered magnetic fields are inclined with respect to the bar in both galaxies (Fig. 13). The behaviour of polarization angles in the bar of M83 looks similar to the behaviour in NGC 1097 and NGC 1365, which are other barred galaxies (Beck et al. 2005), and indicates a non-axisymmetric gas flow in the bar region. Indeed, Fig. 1 shows that the magnetic field is inclined to the bar axis in the regions SE and NW of the bar (at x ≈ −2′,y ≈ 0′ and x ≈ + 3′,−2′<y< + 2′), seen also in the bottom left of Fig. 11, though less well owing to the wavelet smearing. Furthermore, the ordered magnetic field near the bar is concentrated in two narrow regions where the magnetic field vectors are aligned along the bar on the downstream (outer) sides of the bar (at x ≈ 0′,y ≈ + 2′ and y ≈ −1′). This is most visible in Fig. 1, but hardly in Fig. 11. This whole pattern is similar to what is observed in NGC 1097 and NGC 1365, though on a smaller scale. The inner region of IC 342 also shows magnetic fields strongly inclined to the bar (Beck 2015).
5.2. Magnetic field alignment with spiral arms
The application of anisotropic wavelet transform provides an excellent opportunity to estimate the pitch angles of various spiral structures without any model assumptions and to obtain their quantitative characteristics in a controlled manner. In particular, the estimates of the pitch angles from the angular spectra presented in Sect. 4.2.1 are perhaps the most reliable amongst the existing estimates of this kind. On average, the pitch angle of the magnetic field vectors at λ6.2 cm (presumably, mostly the regular field contaminated by an anisotropic random part) is larger than that of the material spiral arms by about 20°: the magnetic field lines form slightly more open spirals than the material arms. Van Eck et al. (2015) present a compilation of the measurements of magnetic and spiral-arm pitch angles in a sample of nearby galaxies (their Fig. 11 and the accompanying text) and conclude that they are closely correlated and yet gives a typical difference in their data of about 5°−10°, with the magnetic lines being more open than the spiral arms. M83 generally fits this relation.
6. Conclusions
Magnetic structures and their inter-relations with the material structures are more complicated in M83 than in NGC 6946 and M51, where they were previously investigated in some detail. The polarization angles in the vicinity of the bar of M83 are strongly inclined with respect to the orientation of the bar, possibly indicating non-axisymmetric gas flows, as also observed in other barred galaxies. The relative intensities of spiral structures at various scales, quantified by the wavelet power spectra, are similar for the dust, gas, and total magnetic field. The pattern of the total radio continuum emission, mainly associated with small-scale (turbulent) magnetic fields, looks more or less similar to the material pattern. On the other hand, ordered magnetic fields (traced by polarized radio emission) are distributed differently, showing weak correlation with other tracers.
We have identified two main material spiral arms that start at the ends of the bar. M83 also has well-defined magnetic arms where the ordered magnetic field is concentrated. The magnetic arms are partially displaced from the corresponding material arms (as in NGC 6946), while they partially coincide with the material arms in other regions similar to M51).
The magnetic Arm IIb–IIc (see Fig. 7 for the notation) coincides with the material arm, so behaves similarly to the outer south-western arms of M51 (Patrikeev et al. 2006). The polarization angles are mostly aligned with the orientations of the main material Arm II, but generally have pitch angles larger by about 20°. This could be a signature of a spiral field generated by the mean-field dynamo that is aligned by a still unknown mechanism, possibly interacting with density waves. Major deviations occur in two regions where the gas arms have a sharp bend (north-east and south-west of the bar), which the magnetic field does not follow. Figure 1 shows that the pattern of magnetic vectors at the bar ends in the north-east and south-west is smoother than the structure of gas and dust, which is not an effect of limited resolution.
The most prominent magnetic arm is displaced inwards with respect to the material Arm I in the south (Ia), located in the inter-arm space between the corresponding material arm and the bar (Fig. 15), resembling the magnetic arms in NGC 6946. The magnetic arm continues to the west and north, displaced outwards with respect to the material Arm Ic. The approximate alignment of the polarization angles with the magnetic arms (Fig. 14) was also found for the magnetic arms in NGC 6946.
The two types of magnetic arms may be different in their generation. A displacement can indicate generation by the mean-field dynamo, while coincidence could be due to shear or compression by density waves. A regular field generated by a mean-field dynamo can be compressed in material arms and thus be partly aligned with them. Interaction with nearby dwarf galaxies in the M83 galaxy group (Karachentsev et al. 2007) may also affect the gas kinematics and the magnetic field pattern; the dwarf galaxy NGC 5253 is possibly causing the warp in the H I disk (Rogstad et al. 1974). The coexistence of different generation mechanisms could be the result of the different timescales involved: While the dynamo operates on timescales of several rotation periods, density waves or disturbances by interaction act on shorter timescales. Dynamo models have indicated that gas streaming due to an encounter can enhance total and polarized emission without any increase in the regular magnetic field strength (Moss et al. 2014).
In summary, the modulation of the galactic dynamo by a transient spiral pattern is a promising mechanism for producing such complicated spiral patterns as in M83.
A better understanding of the structure and origin of the magnetic arms observed in M83 needs a high-resolution map of Faraday rotation to allow one to distinguish regular magnetic fields from the anisotropic magnetic fields produced by compression and shear in the bar and spiral arm regions. The radio polarization data presented in this paper are insufficient to provide reliable rotation measures because Faraday depolarization is strong in the inner galaxy at λ13 cm. Spectro-polarimetric observations and application of RM Synthesis (Brentjens & de Bruyn 2005) are desirable, e.g. with VLA data in the L-band (1–2 GHz) and S-band (2–4 GHz) giving a resolution in Faraday depth of ≃40 rad m-2. M83 is also proposed as a prime target for the Square Kilometre Array (SKA; Beck et al. 2015).
We neglect the small difference in the pitch angle measured in the plane of the galaxy because the inclination of M83 to the line of sight is only 24° (Tilanus & Allen 1993).
Acknowledgments
We thank Stuart Ryder for providing the Hα images of M83. We thank Sui Ann Mao and the anonymous referee for useful suggestions that helped to improve the paper. R.B. acknowledges support from the DFG Research Unit FOR1254. A.S. is grateful to STFC (grant ST/L005549/1) and the Leverhulme Trust (grant RPG-2014-427) for their support. P.F., R.S., and D.S. thank Prof. Michael Kramer for supporting several visits to the MPIfR.
References
- Beck, R. 2007, A&A, 470, 539 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, R. 2015, A&A, 578, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, R., & Hoernes, P. 1996, Nature, 379, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, R., Fletcher, A., Shukurov, A., et al. 2005, A&A, 444, 739 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, R., Bomans, D., Colafrancesco, S., et al. 2015, Advancing Astrophysics with the Square Kilometre Array (AASKA14), 94 [Google Scholar]
- Brentjens, M. A., & de Bruyn, A. G. 2005, A&A, 441, 1217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chamandy, L., Subramanian, K., & Shukurov, A. 2013, MNRAS, 428, 3569 [NASA ADS] [CrossRef] [Google Scholar]
- Chamandy, L., Subramanian, K., & Quillen, A. 2014, MNRAS, 437, 562 [NASA ADS] [CrossRef] [Google Scholar]
- Chamandy, L., Shukurov, A., & Subramanian, K. 2015, MNRAS, 446, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Fletcher, A., Beck, R., Shukurov, A., Berkhuijsen, E. M., & Horellou, C. 2011, MNRAS, 412, 2396 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Frick, P., Beck, R., Shukurov, A., et al. 2000, MNRAS, 318, 925 [NASA ADS] [CrossRef] [Google Scholar]
- Frick, P., Beck, R., Berkhuijsen, E. M., & Patrickeyev, I. 2001, MNRAS, 327, 1145 [NASA ADS] [CrossRef] [Google Scholar]
- Güsten, R., Nyman, L. Å., Schilke, P., et al. 2006, A&A, 454, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hirota, A., Kuno, N., Baba, J., et al. 2014, PASJ, 66, 46 [NASA ADS] [Google Scholar]
- Holschneider, M. 1995, Wavelets: Tool of Analysis (Oxford: Oxford University Press), 423 [Google Scholar]
- Karachentsev, I. D., Tully, R. B., Dolphin, A., et al. 2007, AJ, 133, 504 [NASA ADS] [CrossRef] [Google Scholar]
- Kenney, J. D. P., & Lord, S. D. 1991, ApJ, 381, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Krause, M. 1993, in The Cosmic Dynamo, eds. F. Krause, K. H. Rädler, & G. Rüdiger, IAU Symp., 157, 305 [Google Scholar]
- Krause, M., Hummel, E., & Beck, R. 1989, A&A, 217, 4 [NASA ADS] [Google Scholar]
- Lou, Y.-Q., & Bai, X.-N. 2006, MNRAS, 372, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Lou, Y.-Q., & Fan, Z. 1998, ApJ, 493, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Lou, Y.-Q., & Fan, Z. 2003, MNRAS, 341, 909 [NASA ADS] [CrossRef] [Google Scholar]
- Lundgren, A. A., Wiklind, T., Olofsson, H., & Rydbeck, G. 2004, A&A, 413, 505 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moss, D., Beck, R., Sokoloff, D., et al. 2013, A&A, 556, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moss, D., Sokoloff, D., Beck, R., & Krause, M. 2014, A&A, 566, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moss, D., Stepanov, R., Krause, M., Beck, R., & Sokoloff, D. 2015, A&A, 578, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neininger, N., Klein, U., Beck, R., & Wielebinski, R. 1991, Nature, 352, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Neininger, N., Beck, R., Sukumar, S., & Allen, R. J. 1993, A&A, 274, 687 [NASA ADS] [Google Scholar]
- Niklas, S., & Beck, R. 1997, A&A, 320, 54 [NASA ADS] [Google Scholar]
- Oppermann, N., Junklewitz, H., Robbers, G., et al. 2012, A&A, 542, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Patrikeev, I., Fletcher, A., Stepanov, R., et al. 2006, A&A, 458, 441 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puerari, I., & Dottori, H. A. 1992, A&AS, 93, 469 [NASA ADS] [Google Scholar]
- Puerari, I., Elmegreen, B. G., & Block, D. L. 2014, AJ, 148, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Rand, R. J., Lord, S. D., & Higdon, J. L. 1999, ApJ, 513, 720 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, W. W. 1969, ApJ, 158, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Rogstad, D. H., Lockhart, I. A., & Wright, M. C. H. 1974, ApJ, 193, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Sandage, A., & Tammann, G. A. 1974, ApJ, 194, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Schuller, F., Menten, K. M., Contreras, Y., et al. 2009, A&A, 504, 415 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shukurov, A. 1998, MNRAS, 299, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Shukurov, A. 2007, in Mathematical Aspects of Natural Dynamos, eds. E. Dormy, & A. M. Soward (Chapman & Hall/CRC), 313 [Google Scholar]
- Siringo, G., Kreysa, E., Kovács, A., et al. 2009, A&A, 497, 945 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sukumar, S., & Allen, R. J. 1989a, Nature, 340, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Sukumar, S., & Allen, R. J. 1989b, ApJ, 341, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Sukumar, S., Klein, U., & Gräve, R. 1987, A&A, 184, 71 [NASA ADS] [Google Scholar]
- Sur, S., Shukurov, A., & Subramanian, K. 2007, MNRAS, 377, 874 [NASA ADS] [CrossRef] [Google Scholar]
- Tabatabaei, F. S., Beck, R., Krause, M., et al. 2007, A&A, 466, 509 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tabatabaei, F. S., Berkhuijsen, E. M., Frick, P., Beck, R., & Schinnerer, E. 2013a, A&A, 557, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tabatabaei, F. S., Schinnerer, E., Murphy, E. J., et al. 2013b, A&A, 552, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tilanus, R. P. J., & Allen, R. J. 1993, A&A, 274, 707 [NASA ADS] [Google Scholar]
- Van Eck, C. L., Brown, J. C., Shukurov, A., & Fletcher, A. 2015, ApJ, 799, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Vogler, A., Madden, S. C., Beck, R., et al. 2005, A&A, 441, 491 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Polarized radio continuum intensity (contours) and B vectors of M83 at λ6.17 cm, obtained by combining data from the VLA and Effelsberg telescopes, overlayed on an optical image from the Anglo-Australian Observatory by Dave Malin. The angular resolution is 22″. Faraday rotation of the B vectors has not been corrected, but is small because of the short wavelength and the low inclination of the galaxy. |
| In the text | |
 |
Fig. 2 Polarized radio continuum intensity (contours) and B vectors of M83 at λ12.8 cm, observed with the ATCA telescope and overlayed onto an optical image from the Anglo-Australian Observatory by Dave Malin. The angular resolution is 22″. Comparison with Fig. 1 shows that the Faraday rotation of the B vectors is significant at this wavelength. |
| In the text | |
 |
Fig. 3 Faraday rotation measures between λ6.17 cm and λ12.8 cm (colours) and total radio continuum intensity at λ6.17 cm (contours). The angular resolution is 30″. |
| In the text | |
 |
Fig. 4 Maps of various tracers in M83: material tracers (H II, H I, CO, total neutral gas, warm dust, and cold dust) and tracers of the total magnetic field (mainly its small-scale part; I6 and I13) and its ordered component (P6, P13, and P6+P13), as indicated in the upper right corner of each frame. The coordinates are given in kpc, the intensity units are arbitrary units (H II), 1020 cm-2 (H I), K km s-1 (CO), 1020 cm-2 (gas), MJy/sterad (warm dust), Jy/beam (cold dust), μJy/beam (radio I6, I13, P6, P13, P6+P13). The axis scales are in kpc. |
| In the text | |
 |
Fig. 5 Wavelet power spectra of the M83 images, obtained with the isotropic 2D Mexican Hat from bottom to top: H II, H I, CO, total neutral gas, warm dust, cold dust, total synchrotron intensity at λ6 cm, polarized intensity at λ6 cm, polarized intensity at λ13 cm, and a weighted sum of the polarized intensities at λ6 cm and λ13 cm defined in Sect. 2.3. All the spectra have been multiplied by various factors chosen to avoid overcrowding of the curves: what matters is the relative distribution of the wavelet spectral power between scales in a given image rather than the relative power in different images. Error bars are evaluated from the variance of the sample mean. |
| In the text | |
 |
Fig. 6 Wavelet cross-correlations between the M83 maps as a function of scale (in arcmin). Correlations between the total neutral gas and other tracers (H II, H I, warm dust, I6, P6+P13) are shown in the upper panel and correlations of the polarized emission with other tracers in the lower panel. |
| In the text | |
 |
Fig. 7 Schematic representation of the spiral arms and bar (thick solid line) in M83. Each of the two arms (labelled I and II) is separated into three sections, labelled as a, b, and c and shown as solid, dotted, and solid lines, respectively. The background image represents the cold dust distribution. The axis scale is in kpc, assuming the distance to M83 of 8.9 Mpc. |
| In the text | |
 |
Fig. 8 Anisotropic wavelet transforms of the total neutral gas on the scales 2a = 0.7′ (top) and 1.4′ (bottom). The wavelet orientation angles are shown by bars whose lengths are proportional to the magnitudes of the wavelet transform. The axis scale is in kpc. |
| In the text | |
 |
Fig. 9 As in Fig. 8 but for P6, the polarized radio emission at λ6 cm. |
| In the text | |
 |
Fig. 10 Anisotropic (TH) wavelet transforms of various tracer distributions at 2a = 1′ are shown (dotted contour at 20% of the maximum intensity), together with the similar wavelet transform of the total neutral gas distribution (solid contour at 20% of the maximum intensity). The axis scale is in kpc. |
| In the text | |
 |
Fig. 11 Elongated structures on the scale 2a = 1′ of the anisotropic wavelet transform in the tracer indicated in the upper right corner of each frame are shown with the solid contour drawn at 20% of the maximum intensity in that tracer in the arm region. Red dashes, representing the B vectors of the polarized radio emission at λ6 cm, with length proportional to the polarized intensity, are shown in the same regions. |
| In the text | |
 |
Fig. 12 Angular wavelet power spectra of pitch angles ϕ on the scale 2a = 1′ normalized to unit maximum: the pitch angles ϕm of the structures of the polarized intensity P6 (black dotted), neutral gas (green), and CO (blue dashed). The spectrum of the pitch angles ϕp of the magnetic field vectors defined in Eq. (8) is shown with the red dot-dashed curve. The pitch angles are measured clockwise from the tangent to the local circumference on the sky plane. The upper panel shows the spectra for the whole galaxy, while the lower panel shows them for the region of spiral arms (i.e. with the bar region excluded). |
| In the text | |
 |
Fig. 13 Position angles of the elongated structures of the total neutral gas (blue bars), obtained from the anisotropic wavelet transform on the scale 2a = 1′, and magnetic polarization angles (red bars); the isocontour of the total gas intensity at 20% of its maximum in the arms is shown as a dashed line. The upper panel shows the data points where the difference between two angles is between 3° and 33° with a positive value meaning a clockwise rotation with respect to the gas structure), as suggested by the relative shift of the corresponding peaks in the angular spectra (Fig. 12), while the lower panel shows the remaining data points. The axis scales are in kpc. |
| In the text | |
 |
Fig. 14 As in Fig. 13, but with blue bars showing the position angles of the structures of the polarized intensity P6, the isocontour of P6 at 20% of its maximum intensity shown as dashed. The upper and lower panels show data points with the difference between the angles in the range −1° to 29° and out of this range, respectively. |
| In the text | |
 |
Fig. 15 Locations of the elongated structures, on the scale 2a = 1′, of the combined polarized radio emission (P6+P13; black isocontour at 20% maximum intensity) and in the distributions of H I (top panel) and warm dust (bottom panel), respectively, shown in colour and as dotted contours at 20% of its maximum intensity. The axis scale is given in kiloparsecs assuming the distance to M83 of 8.9 Mpc. The dashed ellipse shows the corotation radius. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


