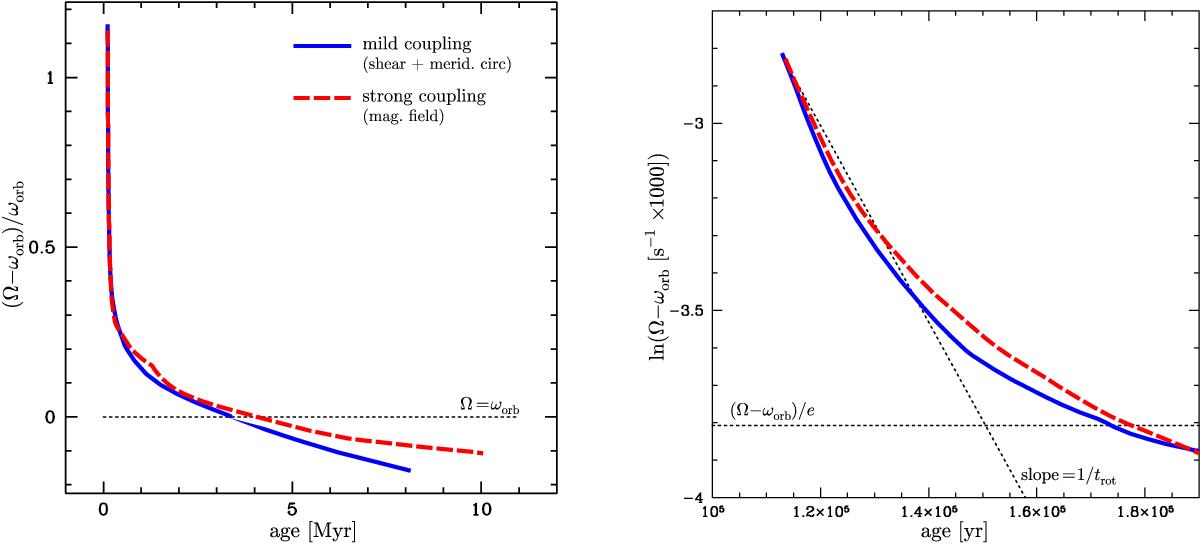
Left panel: evolution as a function of time of the surface angular velocity, Ω, minus the orbital angular velocity, ω_orb, normalised to the orbital angular velocity for a 15 M_⊙ model at Z = 0.014 beginning its evolution on the ZAMS with an initial rotation around 420 km s^-1 and an orbital period equal to 1.4 days. Its companion has 10 M_⊙. The solid (blue) line corresponds to models computed with a mild coupling mediated by shear and meridional currents. The dashed (red) line corresponds to models with a strong coupling mediated by an internal magnetic field (solid body rotation). The horizontal dotted line has an ordinate equal to 0, i.e. its intersection with the other curves indicates when an equality between Ω and ω_orb is obtained. Right panel: evolution as a function of time of Ω − ω_orb (natural logarithm) for the same models as in the left panel. The horizontal dotted line is at an ordinate equal to (Ω − ω_orb) /e. The other dotted line has a slope equal to 1 /t_rot as given by Eq. (6) in Paper I.