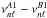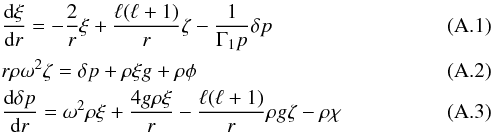| Issue |
A&A
Volume 584, December 2015
|
|
|---|---|---|
| Article Number | A71 | |
| Number of page(s) | 4 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201527447 | |
| Published online | 24 November 2015 | |
Research Note
Scaled models, scaled frequencies, and model fitting
Astronomy Unit, Queen Mary University of London,
Mile End Road,
London
E1 4NS,
UK
e-mail:
I.W.Roxburgh@qmul.ac.uk
Received: 24 September 2015
Accepted: 3 November 2015
I show that given a model star of mass M, radius R, and density profile ρ(x) [x = r/R], there exists a two parameter family of models with masses Mk, radii Rk, density profile ρk(x) = λρ(x) and frequencies νknℓ = λ1/2νnℓ, where λ,Rk/RA are scaling factors. These models have different internal structures, but all have the same value of separation ratios calculated at given radial orders n, and all exactly satisfy a frequency matching algorithm with an offset function determined as part of the fitting procedure. But they do not satisfy ratio matching at given frequencies nor phase shift matching. This illustrates that erroneous results may be obtained when model fitting with ratios at given n values or frequency matching. I give examples from scaled models and from non scaled evolutionary models.
Key words: stars: oscillations / asteroseismology / stars: interiors / methods: analytical / methods: numerical
© ESO, 2015
1. Scaled models
Consider a reference Model A with mass MA, radius RA, and density profile ρA(xA), where xA = r/RA is the fractional radius, and a scaled Model B of mass MB, radius RB density profile ρB(xB) = λρA(xA) where xB = r/RB and λ is a scaling factor. Both models satisfy the hydrostatic and mass equations 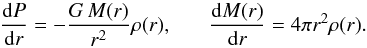 (1)The mass variable M(x) of the 2 models are given by
(1)The mass variable M(x) of the 2 models are given by 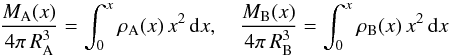 (2)and as ρB(x) = λρA(x) it follows that
(2)and as ρB(x) = λρA(x) it follows that 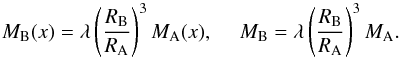 (3)The pressures PA(x),PB(x) satisfy
(3)The pressures PA(x),PB(x) satisfy 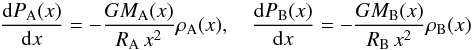 (4)so
(4)so 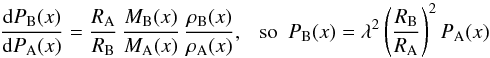 (5)and
(5)and 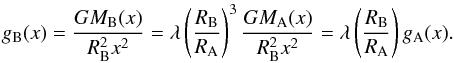 (6)
(6)
2. Scaled frequencies
For simplicity of presentation I first consider radial (ℓ = 0) oscillations where the equations governing the Lagrangian pressure perturbation δp, and radial displacement ξ, with angular frequency ω, can be written as (cf. Roxburgh 2008)  Defining y = ξ/R and x = r/R then for the scaled Model B
Defining y = ξ/R and x = r/R then for the scaled Model B 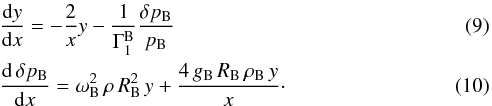 Taking
Taking 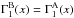 , (a good approximation in the fully ionised interior) then, since both y and δp/p are invariant under the scaling, Eq. (9) is invariant under the scaling from the reference model. Substituting the scaling relations
, (a good approximation in the fully ionised interior) then, since both y and δp/p are invariant under the scaling, Eq. (9) is invariant under the scaling from the reference model. Substituting the scaling relations 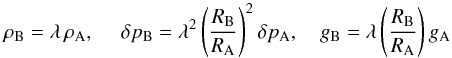 (11)into Eq. (10) then, with a little manipulation, one obtains
(11)into Eq. (10) then, with a little manipulation, one obtains 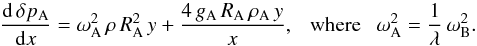 (12)To summarise, given λ,RB then the scaled models satisfy
(12)To summarise, given λ,RB then the scaled models satisfy 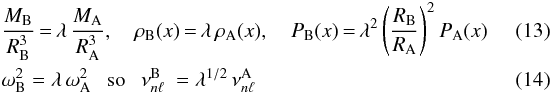 where I have anticipated the result (derived in the Appendix) that these relations hold for modes any angular degree ℓ.
where I have anticipated the result (derived in the Appendix) that these relations hold for modes any angular degree ℓ.
If λ = 1 then one recovers the well known result that the frequencies νnℓ are invariant under a scaling with M/R3 constant.
3. An example
To illustrate these results I take for the reference Model A a solar model based on Model S of Christensen-Dalsagaard et al. (1996), the scaled Model B has a radius RB = 0.95 RA and λ = (RA/RB)2 = 1.108..., so MB = 0.95 MA and the models have the same c2(x) = Γ1P/ρ (cf. Eqs. (13)); but they do not have the same c2(r) as a function of radius r. The run of density ρ(r) and c2(r) for the two models are shown in Fig. 1, clearly Model B does not have the same interior structure as Model A.
 |
Fig. 1 Internal structure of Model A and the scaled model, Model B. Top panel: variation of c2(r) for Models A and B; Bottom panel: density ρ(r) in the two models. |
4. Model fitting with separation ratios
Since the frequencies scale like λ1 / 2 the frequencies of Model B are not equal to the frequencies of Model A. Nevertheless the ratios of small to large separations, which is often used in surface layer independent model fitting, are identical when calculated at the same radial order n. This is illustrated in the top panel of Fig. 2 for the separations r02(n) defined as (cf. Roxburgh & Vorontsov 2003a,b) 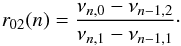 (15)The frequency set for Model A has 13 frequencies for ℓ = 0,1,2 in the range 2000−3700 μHz with error estimate of 0.15 μHz
(15)The frequency set for Model A has 13 frequencies for ℓ = 0,1,2 in the range 2000−3700 μHz with error estimate of 0.15 μHz
The separation ratios are one way of determining the inner phase shift differences δ2(ν) − δ0(ν) as a function of frequency, which is determined by the inner structure of the star {ρ(r),c2(r)} almost independent of the structure of the outer layers, and comparing ratios at the same n is not, in general, the same as comparing at the same frequency (cf. Roxburgh & Vorontsov 2013). To test whether a model and star have the same interior structure, and hence the same δ2(ν) − δ0(ν) one has to interpolate in the model values of r02(n) to determine the values of δ2(ν) − δ0(ν) at the same frequencies. The result of doing this for Model B is shown if the bottom panel of Fig. 2. They ratios do not agree – as one would expect since Model B does not have the same inner structure as Model A. With an error estimate of 0.15 μHz on the frequencies of Model A, the resulting χ2 (per degree of freedom) of the fit is 2.47. The probability of such a large value of χ2 being due to a chance realisation of errors is 0.003.
The reason for the exact fit of the r02(n) ratios is quite simply that all frequencies of Model B are the same multiple of those of Model A, 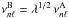 , and the ratios as defined in Eq. (17) are independent of λ
, and the ratios as defined in Eq. (17) are independent of λ
This illustrates the importance of comparing ratios interpolated to the same frequencies when searching for a model fit to an observed star (cf. Roxburgh & Vorontsov 2013).
 |
Fig. 2 Comparison of separation ratios r02 of Model A and the scaled Model B. Top panel: comparison at the same n where the fit is exact; bottom panel: comparison at the same frequencies, which is equivalent to comparing inner phase shift differences; were the two models to have the same interior structure agree these would be the same. |
5. Model fitting by comparing frequencies
Shortly after Kjeldsen et al. (2008) suggested that one could model the unknown effects of the stellar surface layers by scaling the solar offset to other stars, I suggested (erroneously!) that one could treat the offset as unknown and solve for it as part of a model fitting procedure (e.g. Roxburgh 2009). I subsequently realised that such a technique suffered from the same problems as comparing separation ratios at the same n values rather than at the same frequencies, as I now demonstrate.
In this algorithm one compares observed and model frequencies after having subtracted off an ℓ independent function of frequency ℱ(ν) from the frequency differences 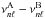 , defining the goodness of fit χ2 as
, defining the goodness of fit χ2 as 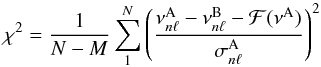 (16)where
(16)where 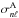 are the error estimates on
are the error estimates on 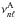 (taken to be the observed star), N is the number of frequencies and M the number of parameters in ℱ(ν) which are adjusted to minimise χ2 (M ≤ number of ℓ = 0 modes). The difference between this and the Kjeldsen et al. (2008) method is that in their method ℱ(ν) is assumed known in terms of the frequencies
(taken to be the observed star), N is the number of frequencies and M the number of parameters in ℱ(ν) which are adjusted to minimise χ2 (M ≤ number of ℓ = 0 modes). The difference between this and the Kjeldsen et al. (2008) method is that in their method ℱ(ν) is assumed known in terms of the frequencies 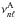 and
and 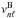 , whereas here it is to be determined as part of the fitting process.
, whereas here it is to be determined as part of the fitting process.
Since for the scaled models 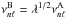 the χ2 for any value of λ is reduced to zero on taking ℱ(ν) = [ 1−λ1 / 2 ] ν, implying that all such models fit the interior structure of Model A, which is not the case.
the χ2 for any value of λ is reduced to zero on taking ℱ(ν) = [ 1−λ1 / 2 ] ν, implying that all such models fit the interior structure of Model A, which is not the case.
Models A1 and B1.
6. A non scaled example
It might be thought that the results in the previous two sections are special since I took a scaling that gives 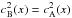 but this is not the case. Any scaled model with will give equality of the ratios at the same n values but not at the same frequencies if λ ≠ 1, independent of the radius of Model B, which could be the same as that of Model A.
but this is not the case. Any scaled model with will give equality of the ratios at the same n values but not at the same frequencies if λ ≠ 1, independent of the radius of Model B, which could be the same as that of Model A.
 |
Fig. 3 Comparison of separation ratios r02 of Model A1 and B1. Top panel: comparison at the same n where the fit is good with a χ2 = 0.43; bottom panel: fit at the same frequencies which is equivalent to comparing inner phase shift differences which would agree were the two models to have the same interior structure. The continuous curves are the inner phase shift differences δ2(ν) − δ0(ν) for the 2 models. |
 |
Fig. 4 Residuals of the fit of the frequency differences |
But perhaps a more convincing case is to compare two separate models which are not obtained by scaling and do not necessarily have the same variation of Γ1(x). Such an example is afforded by comparing 2 models, A1 and B1, constructed using my evolution code (Roxburgh 2008), with GS98 relative abundances (Grevesse & Sauval 1998), OPAL opacities (Iglesias & Rogers 1996) supplemented by Wichita opacities at low temperatures (Ferguson et al. 2005), the EOS5 equation of state (Rogers & Nayfonov 2002), NACRE reaction rates (Angulo et al. 1999), the mixing length model of convection and an Eddington atmosphere. The properties of the two models are given in Table 1 where XH is the initial hydrogen abundance, Z the heavy element abundance, α the mixing length parameter, Xc the central hydrogen abundance and age9 the age in units of 109 yr. The radius and luminosity of Model B1 differ from those of Model A by less than 5%. The frequency set of Model A1 (taken as the observed star) has 14 ℓ = 0,1,2 modes, and again I take an error estimate of 0.15 μHz on the frequencies.
The top panel of Fig. 3 shows the ratios compared at the same n values, the agreement is good with a χ2 of the fit = 0.43, naively suggesting a good fit between Models A1 and B1 whereas, when compared at the same frequency as in the bottom panel, the χ2 = 3.78 of the fit is very large. The continuous curves in this figure are the inner phase shift differences of the 2 models, which should agree if Model B1 is a good fit to Model A1, which it is not.
I then tested the fit of Model B1 to Model A1 using the frequency comparison algorithm defined in Eq. (18). Figure 4 shows the residuals of the best fit of the frequency differences νA − νB to a function ℱ(ν), which has a χ2 = 0.45, again naively suggesting a good fit of the 2 models whereas, as seen from the inner phase shift differences shown in Fig. 3, this is not the case.
I also determined the quality of fit using the phase matching algorithm described in Roxburgh & Vorontsov (2003b) and Roxburgh (2015a); this gave a χ2 = 2.35, still very large although smaller than that from comparing the r02(ν) of the 2 models. This is to be expected since the error estimates of frequency differences is ~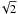 larger than that on individual frequencies.
larger than that on individual frequencies.
7. Conclusions
From a given model star (Model A) with a density profile ρA(x) where x = r/R is the fractional radius, one can generate a two parameter family of models, the parameters being the radius R, and a scaling factor λ, where the density ρ(x) of a member of the family is λρA(x). The frequencies of the models scale with λ1 / 2 and the mass with λ(R/RA)3 The family of scaled models all have the same separation ratios as a function of radial order n, and give an exact fit to to frequency fitting algorithm with an “offset” function of frequency determined by a best fit algorithm, even though they have a different interior density and pressure structure ρ(r),P(r), demonstrating that these algorithms can give erroneous results. Model fitting techniques that compare separation ratios at the same frequency or phase matching do not suffer from this problem.
I give a specific example of a model where the scale factor and radius are such that the sound speed profile c(x) is the same in both the reference model and the scaled model. I then give an example of the problem using non scaled models calculated with a stellar evolution code.
These results underline the importance when model fitting of comparing separation ratios at the same frequency, which reproduce the inner phase shift differences and therefore test how well the inner structure of a given model fits that of an observed star (cf. Roxburgh & Vorontsov 2013). It also shows that the frequency matching algorithm with a surface offset determined by the fitting process can give erroneous results. The phase match model fitting algorithm (Roxburgh & Vorontsov 2003b; Roxburgh 2015a) and a new algorithm using ϵ values (Roxburgh 2015b) where νnℓ = Δ (n + ℓ/ 2 + ϵnℓ), do not suffer from these problems.
Acknowledgments
I gratefully acknowledge support from the Leverhulme Foundation under grant EM-2012-035/4 and from the UK Science and Technology Facilities Council (STFC) under grant ST/M000621/1.
References
- Angulo, C., & the NACRE consortium 1999, Nucl. Phys. A, 656, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen-Dalsgaard, J., Dappen, W., Ajukou, S. V., et al. 1996, Science, 272, 1286 [CrossRef] [Google Scholar]
- Ferguson, J. W., Alexander, D. R., Allard, D. T., et al. 2005, ApJ, 623, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Kjeldsen, H., Bedding, T. R., & Christensen-Dalsgaard, J. 2008, ApJ, 683, L175 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, F. J., & Nayfonov, A. 2002, ApJ, 576, 1064 [Google Scholar]
- Roxburgh, I. W. 2008, Ap&SS, 316, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Roxburgh, I. W. 2009, Presentation at meetings: Synergies between solar and stellar modelling, Rome, June 22−26, New Insights into the Sun, the potential of a new generation of solar-stellar diagnostics, Ponte de Lima, Portugal, September 16−18 [Google Scholar]
- Roxburgh, I. W. 2015a, A&A, 574, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roxburgh, I. W. 2015b, A&A, in press, DOI: 10.1051/0004-6361/201526593 [Google Scholar]
- Roxburgh, I. W., & Vorontsov, S. V. 2003a, A&A, 411, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roxburgh, I. W., & Vorontsov, S. V. 2003b, Ap&SS, 284, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Roxburgh, I. W., & Vorontsov, S. V. 2013, A&A, 560, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Scaling for modes of all ℓ values
The full equations governing the oscillations can be written in terms of the Lagrangian pressure perturbation δp, radial perturbation ξ, tangential displacement ζ, gravitational potential perturbation φ and angular frequency ω as (cf. Roxburgh 2008)
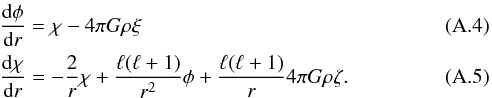 Dimensionally the gravitational potential φ and the derivative χ are
Dimensionally the gravitational potential φ and the derivative χ are 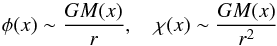 (A.6)and hence scale like
(A.6)and hence scale like 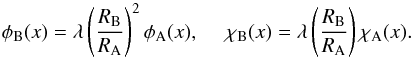 (A.7)Defining y = ξ/R,z = ζ/R, Eqs. (A.1)−(A.5) for Model B become
(A.7)Defining y = ξ/R,z = ζ/R, Eqs. (A.1)−(A.5) for Model B become ![\appendix \setcounter{section}{1} \begin{eqnarray} && {{\rm d}y\over {\rm d}x} = -{2\over x} y+ {\ell(\ell+1)\over x} z -{1\over\Gamma^{\rm B}_1} {\delta p_{\rm B}\over p_{\rm B}}\\ && R_{\rm B}^2 \, {x\, \rho_1 \,\omega_{\rm B}^2 \,z} = \delta p_{\rm B} + \rho_{\rm B}\, g_{\rm B}\, R_{\rm B} \, y + \rho_{\rm B} \, \phi_{\rm B} \\[5pt] && \hskip-1pt{1\over R_{\rm B}}\hskip-1pt{{\rm d}\,\delta p_1\over {\rm d}x}\hskip-2pt=\hskip-2pt\omega_{\rm B}^2\,\rho_{\rm B}\, R_{\rm B}\, y \!+\! \hskip-0pt{4\,g_{\rm B}\, \rho_{\rm B}\over x}y \!- \!{\ell(\ell\!+\!1)\over x} \rho_{\rm B}\,g_{\rm B}\,z \hskip-0pt -\hskip-0pt\rho_{\rm B}\,\chi_{\rm B}\quad\quad\quad \\[4pt] && {{\rm d}\phi_{\rm B}\over {\rm d}x} = R_{\rm B}\,\chi_{\rm B} - 4\,\pi \,G\,\rho_{\rm B}\, R_{\rm B}^2 \,y \\[4pt] && {{\rm d}\chi_{\rm B}\over {\rm d}x} = -{2\over x}\chi_{\rm B}+{\ell(\ell+1)\over R_{\rm B}\,x^2}\phi_{\rm B} + {\ell(\ell+1)\over x} 4\pi\, G\,R_{\rm B}\,\rho_{\rm B}\, z. \end{eqnarray}](/articles/aa/full_html/2015/12/aa27447-15/aa27447-15-eq115.png) Substituting the scaling relations as in Eqs. (11) and (A.7) into Eqs. (A.8)−(A.12) one obtains the same equations for the reference model variables with subscript A provided
Substituting the scaling relations as in Eqs. (11) and (A.7) into Eqs. (A.8)−(A.12) one obtains the same equations for the reference model variables with subscript A provided 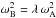 , exactly as in the analysis for radial ℓ = 0 modes.
, exactly as in the analysis for radial ℓ = 0 modes.
Hence for any RB and λ we have the scaling relations 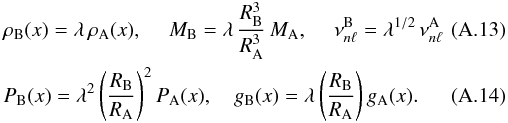
All Tables
All Figures
 |
Fig. 1 Internal structure of Model A and the scaled model, Model B. Top panel: variation of c2(r) for Models A and B; Bottom panel: density ρ(r) in the two models. |
| In the text | |
 |
Fig. 2 Comparison of separation ratios r02 of Model A and the scaled Model B. Top panel: comparison at the same n where the fit is exact; bottom panel: comparison at the same frequencies, which is equivalent to comparing inner phase shift differences; were the two models to have the same interior structure agree these would be the same. |
| In the text | |
 |
Fig. 3 Comparison of separation ratios r02 of Model A1 and B1. Top panel: comparison at the same n where the fit is good with a χ2 = 0.43; bottom panel: fit at the same frequencies which is equivalent to comparing inner phase shift differences which would agree were the two models to have the same interior structure. The continuous curves are the inner phase shift differences δ2(ν) − δ0(ν) for the 2 models. |
| In the text | |
 |
Fig. 4 Residuals of the fit of the frequency differences |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.